2. 浙江大学 软弱土与环境土工教育部重点实验室, 浙江 杭州 310058;
3. 浙江大学城市学院 工程学院, 浙江 杭州 310015;
4. 浙江大学宁波理工学院 土木建筑工程学院, 浙江 宁波 315100
2. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China;
3. School of Engineering, Zhejiang University City College, Hangzhou 310015, China;
4. School of Civil Engineering and Architecture, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China
阻尼是指体系振动过程中能量耗散的特性, 阻尼模型及参数选取对建筑结构、地基地震响应分析至关重要.由于具有形式简单、数学处理方便等优点, 瑞利阻尼在动力问题分析中得到广泛应用[1-2].
瑞利阻尼模型最早是由Caughey[3]提出的广义瑞利阻尼模型退化而来, 可以实现基于正交模态解耦的复杂动力方程,在早期研究中得到广泛应用.大量研究围绕瑞利阻尼系数的选取.Idriss等[4]采用基频确定瑞利阻尼系数, Yoshida等[5]定义一个结构敏感的频率范围来计算瑞利阻尼系数, 楼梦麟等[6]利用实际地震波的分析结果, 开展回归分析, 得到一个阻尼系数转换频率取值的经验公式, 邹德高等[7]提出同时考虑结构频率特性和地震动频谱特性来确定瑞利阻尼系数, 楼梦麟等[8]建议可以通过比较土层基频与地震波主频来确定瑞利阻尼系数.丁海平等[9-11]对现有的系数确定方法进行改进或优化.楼梦麟等[12-15]对不同参数选定方法得到的计算结果进行比较, 指出不合理的瑞利阻尼系数会导致较大的计算误差.
尽管瑞利阻尼能够较好地表征结构振动过程中的能量耗散, 并在地表分析中得到较多的应用, 但模型的物理意义尚不甚明确, 将瑞利阻尼应用于动响应分析可能会隐含各种问题.Nielsen等[16-17]指出以总位移表述运动方程时包含了与质量比例阻尼有关的外部阻尼力;Chen等[18]指出Abaqus/Explicit分析中, 忽略刚度比例阻尼会产生高频振荡;Hall[17]通过算例分析发现, 若瑞利阻尼取值无上限, 则会得到与实际不符的较大阻尼力, 特别是在非线性问题中, 如果采用初始刚度求解瑞利阻尼, 则会使计算结果偏不安全.
由于瑞利阻尼是目前地震响应分析中经常采用的阻尼模型之一, 本文试图从一个视角阐析瑞利阻尼模型的物理意义, 揭示模型参数对动力响应, 特别是应力响应的影响.
1 瑞利阻尼的物理意义在体系振动过程中, 能量耗散机制十分复杂, 产生阻尼的因素众多, 但总体上可以归结为两大类.一类是由材料本身的黏滞性引起的, 表现为应力不仅与应变有关, 还与应变的速率有关, 本文称这一类阻尼为材料阻尼.另一类为体系振动过程中支座摩擦、空气阻力等外部环境引起的能量耗散, 本文统称为环境阻尼.体系振动过程中的能量耗散源于材料阻尼和环境阻尼共同作用.
目前, 已有大量的材料阻尼本构模型被提出, 由弹簧和黏壶并联得到的Kelvin模型[19]是其中最简单的模型之一, 可以表述为
| $ \mathit{\boldsymbol{\sigma = D\varepsilon + \eta \dot \varepsilon }}. $ | (1) |
式中:σ和ε分别为应力和应变矢量,
将式(1) 代入虚功方程
| $ \int_\mathit{\Omega } {{{\left( {{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\varepsilon }}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}{\rm{d}}V} = \int_\mathit{\Omega } {{{\left( {{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{f}}{\rm{d}}V} + \int_{{\mathit{\Gamma }_{\rm{t}}}} {{{\left( {{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{u}}} \right)}^{\rm{T}}} \cdot \mathit{\boldsymbol{\bar t}}{\rm{d}}\mathit{\Gamma }} $ | (2) |
的左端, 利用位移插值u=N·d, 可得
| $ \int_\mathit{\Omega } {{{\left( {{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\varepsilon }}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}{\rm{d}}V} = {\left( {{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{d}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{K}} \cdot \mathit{\boldsymbol{d + }}{\mathit{\boldsymbol{C}}_{\rm{M}}} \cdot \mathit{\boldsymbol{\dot d}}} \right), $ | (3) |
| $ \mathit{\boldsymbol{K}} = \int_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{d}}V} , $ | (4) |
| $ {\mathit{\boldsymbol{C}}_{\rm{M}}} = \int_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\eta B}}{\rm{d}}V} . $ | (5) |
式中:f和t分别为给定的体积力和表面力矢量, d和
当黏性系数矩阵η和弹性系数矩阵间满足η=βD时,
| $ {\mathit{\boldsymbol{C}}_{\rm{M}}} = \beta \mathit{\boldsymbol{K}}. $ | (6) |
外部环境引起的阻尼作用通常与体系振动速度有关, 作用方式非常复杂.为了简化起见, 假定环境阻尼作用可以等效为与速度相关的体积力fE, 并表示为
| $ {\mathit{\boldsymbol{f}}_{\rm{E}}} = - \mu \left( \mathit{\boldsymbol{v}} \right) \cdot \mathit{\boldsymbol{v}}. $ | (7) |
将式(7) 代入式(2) 右端的第一项, 可以求得环境阻尼作用对应的等效节点力为
| $ {\mathit{\boldsymbol{F}}_{\rm{E}}} = - {\mathit{\boldsymbol{C}}_{\rm{E}}}\mathit{\boldsymbol{\dot d}}, $ | (8) |
| $ {\mathit{\boldsymbol{C}}_{\rm{E}}} = \int_V {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mu \left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{N}}{\rm{d}}V} . $ | (9) |
式中:CE为环境阻尼引起的阻尼矩阵.当μ(v)为常数, 且与质量密度ρ成正比, 即μ(v)=αρ时,
| $ {\mathit{\boldsymbol{C}}_{\rm{E}}} = \alpha \mathit{\boldsymbol{M}}, $ | (10) |
| $ \mathit{\boldsymbol{M = }}\int_\mathit{\Omega } {{\mathit{\boldsymbol{N}}^{\rm{T}}}\rho \mathit{\boldsymbol{N}}{\rm{d}}V} . $ | (11) |
式中:M为一致质量阵.
将式(6)、(10) 叠加, 总阻尼阵C可以表示为
| $ \mathit{\boldsymbol{C}} = \alpha \mathit{\boldsymbol{M}} + \beta \mathit{\boldsymbol{K}}. $ | (12) |
式中:C为瑞利阻尼阵, α和β为相应的瑞利阻尼系数.
综上分析可以看出, 瑞利阻尼的刚度相关部分反映了材料对动力响应的阻滞作用, 表现为应力不仅与应变有关, 而且与应变率相关;瑞利阻尼的质量相关部分反映了环境对结构体系振动的阻滞作用.瑞利阻尼模型是一种综合反映材料和环境对结构体系动力响应阻滞作用的最简单模型, 只需2个材料参数.
需要指出的是, 瑞利阻尼模型的提出仅基于离散的结构体系, 与材料的性质无关, 因此在有限元软件中计算应力时, 没有考虑应变率对应力的贡献, 导致计算应力与实际应力存在差异.
2 一维黏弹性振动问题为了进一步验证瑞利阻尼模型物理意义的合理性, 揭示模型参数对动力响应, 特别是应力响应的影响, 分别采用解析和数值方法对比分析均质等截面杆件一维黏弹性动力响应问题, 给出该问题的描述和解析解.如图 1所示, 杆件长L=10 m, 截面面积A=1 m2, 弹性模量E=25 MPa, 质量密度ρ=1 800 kg/m3, 采用瑞利阻尼.在初始时刻, 杆件处于静止状态, 初始速度和初始位移均为0.杆件左端(x=0 m)均匀分布幅值p=50 Pa的随时间t正弦变化的荷载f(t), 杆件右端(x=L)自由.

|
图 1 均质连续的等截面一维黏弹性杆 Fig. 1 One-dimensional viscoelastic rod of homogeneous and continuous with constant section |
黏弹性杆件振动的控制方程和相应的定解条件如下:
| $ E\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \beta E\frac{{{\partial ^3}u}}{{\partial {x^2}\partial t}} = \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}} + \alpha \rho \frac{{\partial u}}{{\partial t}};0 < x < L,t > 0. $ | (13) |
| $ u = 0,\frac{{\partial u}}{{\partial t}} = 0;0 < x < L,t = 0. $ | (14) |
| $ \frac{{\partial u}}{{\partial x}} + \beta \frac{{{\partial ^2}u}}{{\partial x\partial t}} = - \frac{{f\left( t \right)}}{{EA}};x = 0,t > 0. $ | (15) |
| $ \frac{{\partial u}}{{\partial x}} + \beta \frac{{{\partial ^2}u}}{{\partial x\partial t}} = 0;x = L,t > 0. $ | (16) |
式中:u为沿x方向的位移.
求解上述定解问题, 可得解析解.限于篇幅, 省略推导过程, 仅给出解的最终形式:
| $ u\left( {x,t} \right) = \bar u\left( {x,t} \right) + \sum\limits_{k = 0}^\infty {{T_k}\left( t \right)\cos \left( {{\gamma _k}x} \right)} . $ | (17) |
式中:
| $ {\gamma _k} = k{\rm{\pi }}/L,k = 0,1,2, \cdots , $ | (18) |
| $ {T_k}\left( t \right) = \frac{1}{{\rho \left( {{r_{k2}} - {r_{k1}}} \right)}}\left[ {{K_{k2}}\left( t \right) - {K_{k1}}\left( t \right)} \right]. $ | (19) |
其中,
| $ \begin{array}{l} {h_k}\left( \tau \right) = \frac{{2\rho }}{L}\int_0^L {\left[ {\frac{E}{\rho }\left( {\frac{{{\partial ^2}\bar u}}{{\partial {x^2}}} + \beta \frac{{{\partial ^3}\bar u}}{{\partial {x^2}\partial \tau }}} \right) - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left( {\frac{{{\partial ^2}\bar u}}{{\partial {\tau ^2}}} + \alpha \frac{{\partial \bar u}}{{\partial \tau }}} \right)} \right]\cos \left( {{\gamma _k}x} \right){\rm{d}}x.\\ {r_{k1,k2}} = \\ \;\;\; - \frac{1}{2}\left[ {\left( {\frac{E}{\rho }\beta \omega _k^2 + \alpha } \right) \pm \sqrt {{{\left( {\frac{E}{\rho }\beta \omega _k^2 + \alpha } \right)}^2} - 4\frac{E}{\rho }\omega _k^2} } \right].\\ \bar u\left( {x,t} \right) = \left\{ \begin{array}{l} \frac{{{{\left( {L - x} \right)}^2}}}{{2EAL}} \cdot f\left( t \right),\beta = 0;\\ \frac{{{{\left( {L - x} \right)}^2}}}{{2EAL}} \cdot \int_0^t {\frac{{f\left( \tau \right)}}{\beta }{{\rm{e}}^{\frac{\tau }{\beta }}}{\rm{d}}\tau \cdot {{\rm{e}}^{ - \frac{1}{\beta }}},\beta \ne 0} . \end{array} \right. \end{array} $ | (20) |
将位移解代入几何关系, 可得杆件应变解:
| $ \varepsilon \left( {x,t} \right) = \frac{{\partial \bar u\left( {x,t} \right)}}{{\partial x}} - \sum\limits_{k = 0}^\infty {{\gamma _k}{T_k}\left( t \right)\sin \left( {{\gamma _k}x} \right)} . $ | (21) |
利用应力和应变关系, 可得杆件应力解:
| $ \begin{array}{*{35}{l}} \sigma \left( x,t \right)=E\left[ \frac{\partial \bar{u}\left( x,t \right)}{\partial x}+\beta \frac{{{\partial }^{2}}\bar{u}\left( x,t \right)}{\partial x\partial t} \right]- \\ \ \ \ \ \sum\limits_{k=0}^{\infty }{E{{\gamma }_{k}}\sin \left( {{\gamma }_{k}}x \right)\left[ {{T}_{k}}\left( t \right)+\beta {{{\dot{T}}}_{k}}\left( t \right) \right]}. \\ \end{array} $ | (22) |
如果忽略应变率对应力的贡献, 可得如下形式的应力解:
| $ {\sigma ^ * }\left( {x,t} \right) = E\left[ {\frac{{\partial \bar u\left( {x,t} \right)}}{{\partial x}} - \sum\limits_{k = 0}^\infty {{\gamma _k}{T_k}\left( t \right)\sin \left( {{\gamma _k}x} \right)} } \right]. $ | (23) |
上述一维黏弹性杆件振动问题可以采用有限单元法进行数值求解.本文采用ABAQUS软件进行数值分析, 选用四节点四边形平面单元, 单元纵向尺寸为0.25 m.采用HHT算法[20]进行动力隐式时程积分, 时间步长为0.001 s.
为了对比分析α和β对动响应, 尤其是应力响应的影响, 采用Yoshida等[5]提出的基于体系敏感频率范围的方法确定基准阻尼系数α和β.
| $ \left. \begin{array}{l} \xi = \frac{{\bar \alpha }}{{2{\omega _a}}} + \frac{{\bar \beta {\omega _a}}}{2},\\ \xi = \frac{{\bar \alpha }}{{2{\omega _b}}} + \frac{{\bar \beta {\omega _b}}}{2}. \end{array} \right\} $ | (24) |
式中:ξ为敏感频率上、下限对应的阻尼比, 本文取土体常用值0.05[21].Clough等[22]建议ωa取多自由度体系的基频, ωb在对动力响应有显著贡献的高阶振型频率中选取.本文分别取ωa、ωb为第1、3阶非零固有频率.经分析可知, ωa=1.19 rad/s、ωb=18.51 rad/s.由式(24) 可得, α=0.1 s-1, β=0.005 s.为了方便起见, 定义无量纲瑞利阻尼系数λα=α/α, λβ=β/β.
3 计算结果及分析分别对比分析α和β对动力响应的影响, 重点分析刚度相关阻尼项对应力计算值的影响.为了简单起见, 取激振频率ω=10π rad/s(5 Hz).
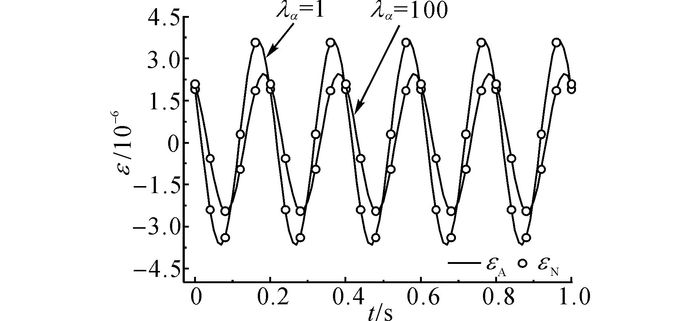
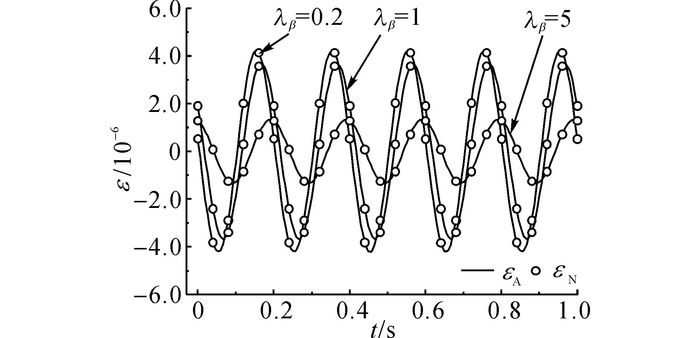
图 2、3分别给出λβ=1和λα=1时杆件中点(x=5 m)处的应变时程曲线.可见:1) 无论是α还是β变化, 应变数值解εN给出了与解析解εA几乎完全相同的结果, 说明有限元给出了可靠的应变解;2) 随着α或β的增加, 应变振动幅值减少, 响应滞后, 比较而言, 系数β的影响更明显.
|
图 2 λβ=1时杆件中点(x=5 m)应变时程曲线 Fig. 2 Strain time curve of rod midpoint (x=5 m) with λβ=1 |
|
图 3 λα=1时杆件中点(x=5 m)应变时程曲线 Fig. 3 Strain time curve of rod midpoint (x=5 m) with λα=1 |
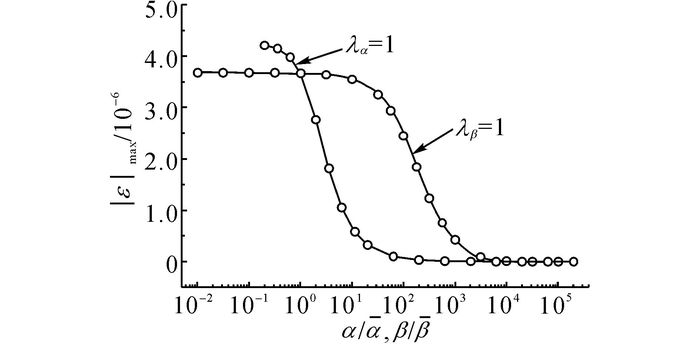
图 4给出当λβ=1和λα=1时, 杆件中点(x=5 m)处稳态应变幅值|ε|max随α和β的变化曲线.可见, 在基准瑞利阻尼系数附近, α的变化对动力响应的影响远小于β的变化, 说明材料阻尼是主要的结构能量耗散源.
|
图 4 不同λα或λβ时稳态应变幅值变化曲线(x=5 m) Fig. 4 Steady-state strain amplitude curve with different λα or λβ (x=5 m) |
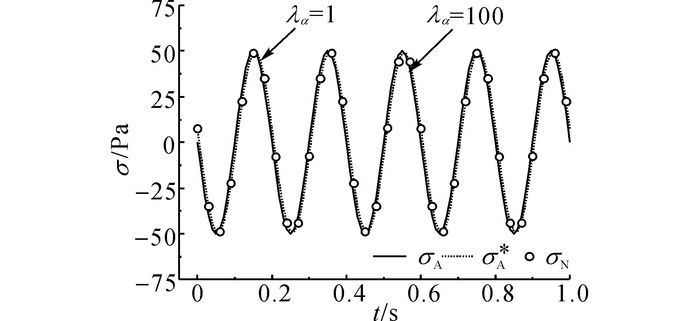
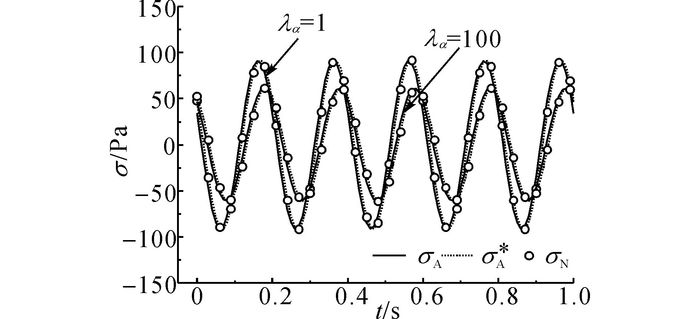
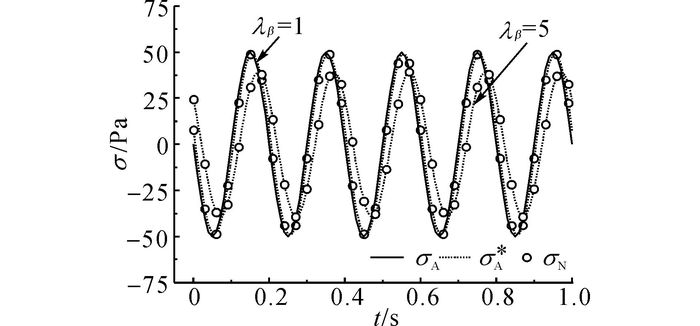
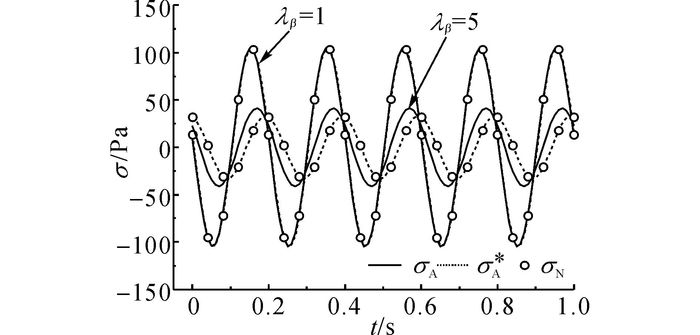
图 5、6给出当λβ=1时, 杆件左端(x=0 m)和中点(x=5 m)处应力时程曲线, 包括解析解σA、解析解σA*和数值解σN3种结果.图 5中, λα=1和λα=100时的曲线几乎完全重合.可以看出, 当λβ=1时, σA*和σN的结果一致, 但与σA的结果略有不同;α对σA和σA*差别的影响不大.图 7、8给出当λα=1时, 杆件x=0 m、x=5 m处的应力时程曲线.由图 7、8可以看出, σA*和σN的结果一致, σA和σA*间的差异随着β的增加而明显增大.尤其值得注意的是, x=0 m处的σA*不能满足边界条件, 而σA满足边界条件.说明现有有限元软件在分析瑞利阻尼的动响应问题时所求得的应力从理论角度上是不精确的.
|
图 5 λβ=1时杆件左端(x=0 m)应力时程曲线 Fig. 5 Stress time curve of rod left end (x=0 m) with λβ=1 |
|
图 6 λβ=1时杆件中点(x=5 m)应力时程曲线 Fig. 6 Stress time curve of rod midpoint (x=5 m) with λβ=1 |
|
图 7 λα=1时杆件左端(x=0 m)应力时程曲线 Fig. 7 Stress time curve of rod left end (x=0 m)with λα=1 |
|
图 8 λα=1时杆件中点(x=5 m)应力时程曲线 Fig. 8 Stress time curve of rod midpoint (x=5 m) with λα=1 |
为了进一步验证α和β对动力响应影响的上述规律, 取ω分别为5π rad/s和15π rad/s进行类似分析.
为了方便起见, 仅对比分析稳态响应振幅的变化而不分析相位差别.以杆件左端p为基准值, 对比分析3种稳态应力幅值|σA|max、|σA*|max和|σN|max, 定义如下形式的应力无量纲误差:
| $ \left. \begin{array}{l} {e_{\rm{A}}} = \frac{{{{\left| {{\sigma _{\rm{A}}}} \right|}_{\max }} - {{\left| {\sigma _{\rm{A}}^ * } \right|}_{\max }}}}{{\bar p}} \times 100\% ,\\ {e_{\rm{N}}} = \frac{{{{\left| {{\sigma _{\rm{A}}}} \right|}_{\max }} - {{\left| {{\sigma _{\rm{N}}}} \right|}_{\max }}}}{{\bar p}} \times 100\% . \end{array} \right\} $ | (25) |
表 1给出不同ω时杆件中点(x=5m)处的稳态应变幅值.表 2、3分别给出不同ω时杆件x=0 m和x=5 m处的稳态应力幅值和应力的无量纲误差.由表 1~3的计算结果可以看出:1) 当ω取不同值时, 随着α或β的变化, 杆件稳态响应的应变和应力幅值均表现出如上文所述的规律;2) 稳态应力幅值的无量纲误差与ω有关.
| 表 1 不同激振频率时杆件中点(x=5 m)应变幅值 Table 1 Strain amplitude of rod midpoint (x=5 m) with different exciting frequency |
| 表 2 不同激振频率时杆件左端(x=0 m)应力幅值及无量纲误差 Table 2 Stress amplitude and non-dimensional errors of rod left end (x=0 m) with different exciting frequency |
| 表 3 不同激振频率时杆件中点(x=5 m)应力幅值及无量纲误差 Table 3 Stress amplitude and non-dimensional errors of rod midpoint (x=5 m) with different exciting frequency |
从上文分析可以看出σN和σA*一致, 导致应力计算误差的原因在于有限元分析软件在计算应力时没有考虑阻尼刚度部分对应力的贡献.本节取λα=1, 利用σA和σA*对比分析β和ω对应力计算误差的影响.此处仅对比分析|σA*|max相对|σA|max的应力无量纲误差, 且不分析相位差别.
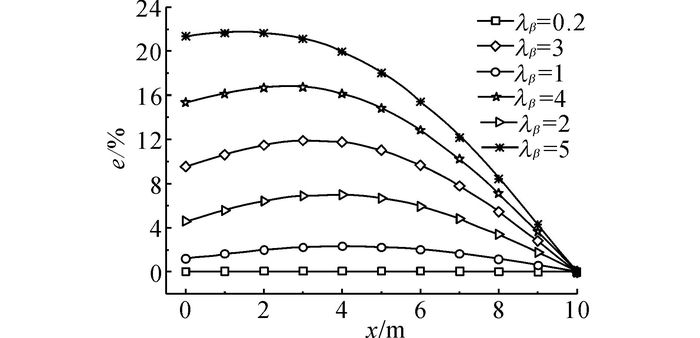
利用杆件非零基频, 定义无量纲激振频率λω=ω/ωa.图 9、10分别给出当λω=26和λβ=1时杆件沿纵向长度x的应力无量纲误差分布曲线.由图 9可见, e在杆件不同位置处起伏分布, 杆件右端因应力为0而误差很小.同时, e随着λβ的增加而不断加大, 当λβ=5时, 误差可以超过p的1/5.
|
图 9 λω=26时应力无量纲误差的分布曲线 Fig. 9 Distribution curve of non-dimensional stress errors with λω=26 |
|
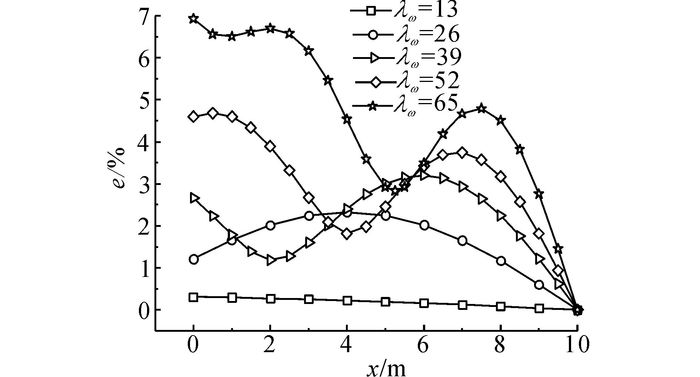
图 10 λβ=1时应力无量纲误差的分布曲线 Fig. 10 Distribution curve of non-dimensional stress errors with λβ=1 |
图 10表明, 随着ω的增加, e明显增大, 且在杆件内起伏分布更加明显, 这是由应力波在杆件内的波动传播特性决定的.当p不变时, 随着ω增加, 应变率增大, 导致e上升;同时, 随着ω的增加, 应力波波长减小, 导致应变率幅值和应力计算误差幅值在杆件内的起伏分布更加明显.
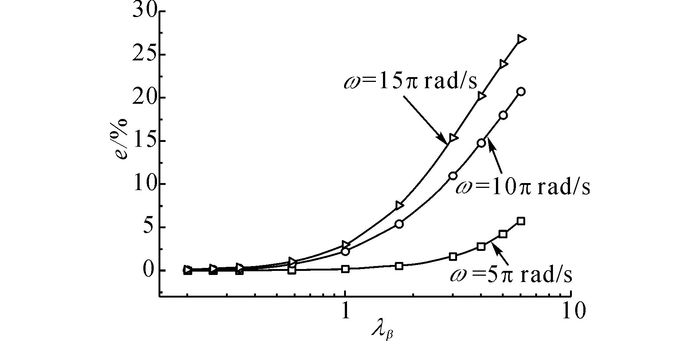
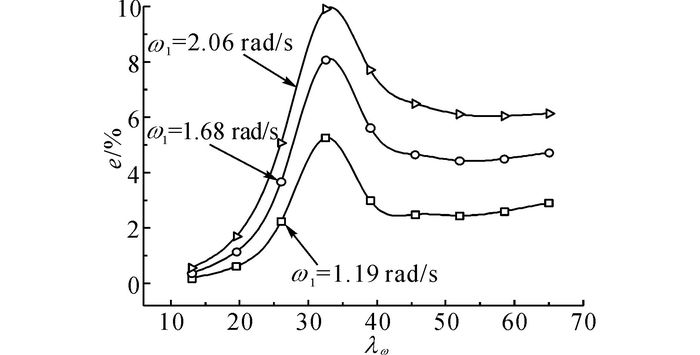
图 11、12分别给出杆件中点(x=5 m)处e随λβ和λω的变化曲线.图 11表明, 在不同ω下, e均随λβ的增加而增大.图 12表明, 杆件中点(x=5 m)处e随着λω的增加起伏变化, 且随着基频ω1的增加而增大, 原因是E增加引起与应变率相关应力项增大以及杆件内应力波的波动传播.
|
图 11 应力无量纲误差随λβ的变化曲线 Fig. 11 Changing curve of non-dimensional stress errors with different λβ |
|
图 12 应力无量纲误差随λω的变化曲线 Fig. 12 Changing curve of non-dimensional stress errors with different λω |
(1) 瑞利阻尼的刚度相关部分反映了材料对动力响应的阻滞作用, 表现为应力不仅与应变有关, 而且与应变率相关;瑞利阻尼的质量相关部分反映了环境对结构体系振动的阻滞作用.瑞利阻尼模型是一种综合反映材料和环境对结构体系动力响应阻滞作用的最简单模型.
(2) 随着α或β的增加, 应变振动幅值减少, 响应滞后, 比较而言, β的影响更明显.在基准瑞利阻尼系数附近, α的变化对动力响应的影响远小于β的变化, 材料阻尼是主要的结构能量耗散源.
(3) 现有的有限元分析考虑了材料阻尼作用和环境阻尼作用对动力平衡的影响, 可以给出可靠的位移、应变及其变化率的解;在应力计算中, 没有考虑材料阻尼的作用, 导致计算应力和实际应力存在差异, 并随着β和ω的增加而明显增大.计算应力不能满足力的边界条件, 因此从理论角度上是不正确的.
| [1] | LIANG Z, LEE G. Representation of damping matrix[J]. Journal of Engineering Mechanics, 1991, 117(5): 1005–1019. DOI:10.1061/(ASCE)0733-9399(1991)117:5(1005) |
| [2] |
黄宗明, 白绍良, 赖明. 结构地震反应时程分析中的阻尼问题评述[J].
地震工程与工程振动, 1996, 16(2): 95–105.
HUANG Zong-ming, BAI Shao-liang, LAI Ming. Review on the damping in the earthquake response time-history analysis of structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 1996, 16(2): 95–105. |
| [3] | CAUGHEY T, KELLY M. Classical normal modes in damped linear dynamic systems[J]. Journal of Applied Mechanics, 1965, 32(3): 583–588. DOI:10.1115/1.3627262 |
| [4] | IDRISS I, LYSMER J, HWANG R, et al. QUAD4: a computer program for evaluating the seismic response of soil structures by variable damping finite element procedures [R]. Berkeley: University of California, 1973. |
| [5] | YOSHIDA N, KOBAYASHI S, SUETOMI I, et al. Equivalent linear method considering frequency dependent characteristics of stiffness and damping[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(3): 205–222. DOI:10.1016/S0267-7261(02)00011-8 |
| [6] |
楼梦麟, 潘旦光. 滞后阻尼在土层时域分析中的应用[J].
同济大学学报, 2004, 32(3): 281–285.
LOU Meng-lin, PAN Dan-guang. Hysteretic damping application in time domain analysis of soil layer[J]. Journal of Tongji University, 2004, 32(3): 281–285. |
| [7] |
邹德高, 徐斌, 孔宪京. 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J].
岩土力学, 2011, 32(3): 797–803.
ZOU De-gao, XU Bin, KONG Xian-jing. Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response[J]. Rock and Soil Mechanics, 2011, 32(3): 797–803. |
| [8] |
楼梦麟, 邵新刚. 深覆盖土层Rayleigh阻尼矩阵建模问题的讨论[J].
岩土工程学报, 2013, 35(7): 1272–1279.
LOU Meng-lin, SHAO Xin-gang. Discussion on modeling issues of Rayleigh damping matrix in soil layers with deep deposit[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1272–1279. |
| [9] |
丁海平, 马俊玲. 基于场地特征周期的瑞利阻尼确定方法[J].
岩土力学, 2013(supple.2): 35–40.
DING Hai-ping, MA Jun-ling. A method for determining Rayleigh damping based on site characteristic period[J]. Rock and Soil Mechanics, 2013(supple.2): 35–40. |
| [10] |
潘旦光. 直接确定Rayleigh阻尼系数的一种优化方法[J].
工程力学, 2013, 30(9): 16–21.
PAN Dan-guang. An optimization method for thedetermination of Rayleigh damping coefficients[J]. Engineering Mechanics, 2013, 30(9): 16–21. |
| [11] |
董云, 楼梦麟. 基于结构基频确定Rayleigh阻尼系数的优化方法及其讨论[J].
湖南大学学报:自然科学版, 2014, 41(2): 8–13.
DONG Yun, LOU Meng-lin. An optimization solution for Rayleigh damping coefficients based on the fundamental frequency of structure[J]. Journal of HunanUniversity: Natural Sciences, 2014, 41(2): 8–13. |
| [12] |
楼梦麟, 殷琳. 关于高土坝地震反应分析中阻尼模型的讨论[J].
水力发电学报, 2009, 28(5): 103–107.
LOU Meng-lin, YIN Lin. Discussion on damping models for seismic response analysis of high earth dams[J]. Journal of Hydroelectric Engineering, 2009, 28(5): 103–107. |
| [13] |
马俊玲, 丁海平. 土层地震反应分析中不同阻尼取值的影响比较[J].
防灾减灾工程学报, 2013, 33(5): 517–523.
MA Jun-ling, DING Hai-ping. Comparative study on the influence of different damping values in soil seismic response analysis[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(5): 517–523. |
| [14] |
潘旦光, 高莉莉. Rayleigh阻尼系数解法比较及对结构地震反应影响[J].
工程力学, 2015, 6(32): 192–199.
PAN Dan-guang, GAO Li-li. Comparison of determination methods for Rayleigh damping coefficients and effects on seismic responses of structures[J]. Engineering Mechanics, 2015, 6(32): 192–199. |
| [15] |
朱秀云, 刘志凤, 潘蓉, 等. 瑞利阻尼系数确定方法对非岩性场地地震反应的影响分析[J].
工业建筑, 2015, 9(45): 31–36.
ZHU Xiu-yun, LIU Zhi-feng, PAN Rong, et al. Analysis of the influence of different methods for determing Rayleigh damping coefficient on non-rock site seismic response[J]. Industrial Construction, 2015, 9(45): 31–36. |
| [16] | NIELSEN A. On the use of Rayleigh damping for seismic analysis[J]. Proceedings of the ICE-Engineering and Computational Mechanics, 2009, 162(4): 215–220. |
| [17] | HALL J. Problems encountered from the use of Rayleigh damping[J]. Earthquake Engineering and Structural Dynamics, 2006, 35(5): 525–545. DOI:10.1002/(ISSN)1096-9845 |
| [18] | CHEN X, DUAN J, QI H, et al. Rayleigh damping in Abaqus/explicit dynamic analysis[J]. Applied Mechanics and Materials, 2014, 627(6): 288–294. |
| [19] | 龚晓南. 土塑性力学[M]. 杭州: 浙江大学出版社, 1999: 199-209. |
| [20] | 费康, 张建伟. ABAQUS在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2010: 250-255. |
| [21] |
申权. 土体阻尼测试新方法及其阻尼性能变化规律的研究[D]. 南昌: 南昌航空大学, 2013.
SHEN Quan. The new method to test soil damping and the change law of its damping performance [D]. Nanchang: Nanchang Hangkong University, 2013. |
| [22] | CLOUGH R, JOSEPH P. Dynamics of structures[M]. 3rd ed. New York: McGraw-Hill, 2003: 234-236. |



