2. 浙江大学 岩土工程研究所, 浙江 杭州 310058;
3. 湖南大学 土木工程学院, 湖南 长沙 410082
2. Institute of Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;
3. College of Civil Engineering, Hunan University, Changsha 410082, China
21世纪以来, 我国城市地铁建设高速发展, 地铁建设对周边环境的影响问题引起广泛关注[1-4].随着地铁线网的日益加密, 基坑开挖对邻近既有地铁隧道结构的影响问题越发突出.
基坑开挖卸载使得基坑周边一定范围内土体因应力状态改变而产生变形, 位于影响范围内的既有隧道结构将产生附加内力和变形, 严重时造成管片开裂漏水, 威胁地铁运营安全[5].国内外, 对已运营地铁隧道变形控制的要求十分严格.例如, 《上海市地铁沿线建筑施工保护地铁技术管理暂行规定》要求邻近施工影响下地铁隧道变形的曲率半径不小于15 000 m;相对弯曲不大于1/2 500;隧道结构的绝对水平位移和沉降量不超过20 mm.部分标准甚至要求隧道结构的绝对水平位移和沉降量不超过10 mm[6].研究基坑开挖对邻近既有地铁隧道的影响十分重要.
基坑开挖对邻近既有地铁隧道的影响与地层条件、基坑尺寸和支护形式、隧道与基坑相对位置等因素密切相关.基坑开挖过程中, 位于基坑外侧的地铁隧道以水平变形为主[7-10], 而下卧于基坑的地铁隧道则由于基坑开挖后地基土卸载回弹, 以上浮变形为主.针对基坑开挖过程下卧地铁隧道上浮变形的问题, 国内外多采用解析法[11-12]、离心模型试验[13]以及数值模拟[14-16]进行研究.除此之外, 实测分析是一种可靠的研究手段.刘庭金[17]基于隧道变形三维监测数据, 分析地铁车站上方基坑开挖过程地铁车站两侧盾构区间隧道的变形规律.魏刚[18]对国内14个基坑工程案例实测数据进行统计分析, 提出隧道最大隆起值的经验预测公式.可见, 关于基坑开挖对下卧隧道变形影响的研究已有不少.现有研究大多是针对规则多边形基坑, 地铁隧道位于基坑下方的长度一般不超过200 m;关于既有地铁隧道长距离共线下卧于地下通道明挖基坑的情况, 目前的研究报道不多.
本文以某地下通道项目一标工程580 m范围为背景, 基于通道基坑开挖过程隧道上浮实测数据, 介绍地下通道明挖施工过程中下卧地铁隧道的上浮变形过程和统计规律.采用二维有限元模型, 研究基坑开挖后下卧隧道上浮变形规律.
1 工程概况 1.1 明挖地下通道基坑明挖地下通道基坑桩号里程K1+040~K1+620, 全长580 m, 基坑宽度为38 m, 最大开挖深度约为12.5 m, 平面图和纵断面如图 1所示.里程K1+040~K1+520范围采用放坡结合
既有地铁隧道共线下卧于明挖地下通道, 衬砌内、外径分别为6.0 m和6.7 m, 环宽1.5 m, 厚度为0.35 m, 每环管片由6块管片通过弯螺栓连接, 管片混凝土强度等级为C50, 隧道拱顶埋深为16.5~23.5 m.其中, 左线隧道自里程K1+180开始进入围护桩内侧, 并逐渐平行于明挖基坑.按该地区在运营地铁隧道变形控制要求可知, 邻近工程施工造成的地铁隧道竖向和水平变形不得超过10 mm.为了确保基坑开挖过程中地铁隧道变形满足控制要求, 在纵向一定范围内坑底采用

|
图 1 场地平面及纵断面示意图 Fig. 1 Plan view and longitudinal section of site |
|
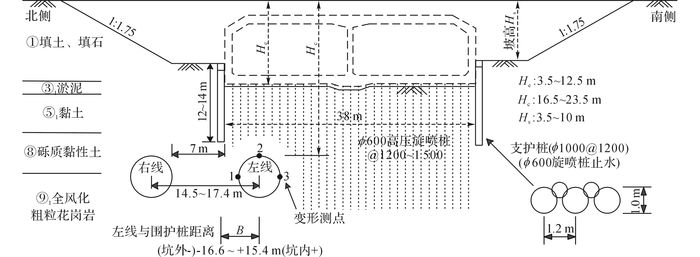
图 2 基坑典型断面示意图 Fig. 2 Typical cross section of excavation |
工程场地原始地貌为滨海滩涂地貌, 后经人工改造为平坦地貌, 地下水位位于地表下约3 m.表层广泛为人工填土层, 局部分布海积淤泥层和冲洪积黏土和粗砂层.地铁隧道主要位于该地区广泛分布的第四系中更新统残积层, 主要包括⑧ 砾质黏土层和⑨1全风化粗粒花岗岩层.① 人工填土层结构松散~稍密, 渗透性高;③1淤泥层呈流塑状且含有机质, 层厚0.3~3.8 m, 分布不均;⑤ 黏土层以可塑状为主, 层厚0.7~8.5 m不等;⑧ 砾质黏土层由下伏花岗岩风化残积而成, 可塑至硬塑状, 场地内普遍分布, 层厚多达10余米;隧道下卧⑨1全风化粗粒花岗岩层为Ⅲ级硬土, 层顶埋深多大于25 m.典型横断面如图 2所示, 地层的主要物理性质指标如表 1所示.表中, e0为孔隙比, ρ为密度, Ip为塑性指数, k为渗透系数, N为标贯击数.
| 表 1 土体基本性质指标 Table 1 Basic property index of soil |
该标段于2015年5月底动工, 为了控制地铁隧道变形, 同时保证施工进度, 纵向进行分段同步开挖.每段开挖长度约为100 m, 并按15 m/幅逐层挖深, 相邻开挖段约留50 m反压段.各开挖段开挖至设计标高后, 立即施工地下通道结构, 严控基坑暴露时间.截至2016年11月, 该标段基本完工.
2.1 地铁隧道上浮变形过程1) 闭合框架段.
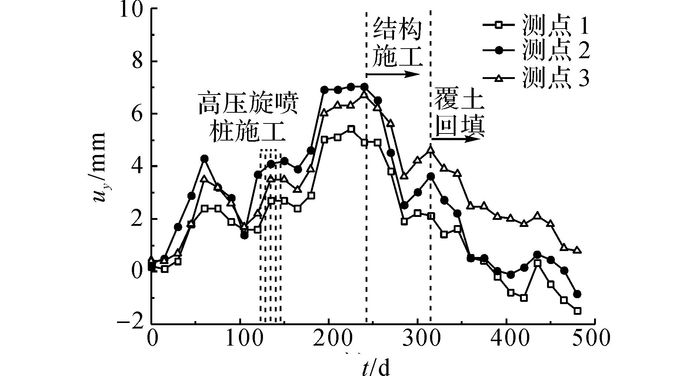
闭合框架段左线隧道的典型上浮发展曲线如图 3所示.图中,uy为隧道上浮变形.He=6.4 m, Hc=16.8 m, Hs=10 m, 围护桩长12 m, 隧道轴线与基坑北侧(邻近侧)围护桩水平距离B=+2.9 m.
|
图 3 K1+240断面左线隧道上浮实测结果 Fig. 3 Measured results of uplift of left line at K1+240 |
闭合框架段隧道上浮曲线主要包含2个上浮段和1个回落段.第一个上浮段的原因是隧道上方开挖2.9 m至冠梁平台, 开挖卸载使得隧道随着地基回弹而上浮;第二个上浮段是因围护桩内侧3.5 m厚土体开挖引起的.两个上浮段之间的稳定段主要的施工过程为边坡喷护和坑底高压旋喷桩加固.从高压旋喷桩施工时间与隧道上浮发展的对应情况来看, 高压旋喷虽然会破坏地基土的结构性造成土体扰动, 但不会导致下部隧道明显上浮, 且旋喷桩施工后上浮略有回落;回落段主要是由于通道结构施工并覆土回填(回填土层顶高于原地表约3 m), 隧道最终回到初始标高, 甚至略微出现沉降.
2) U型槽段.
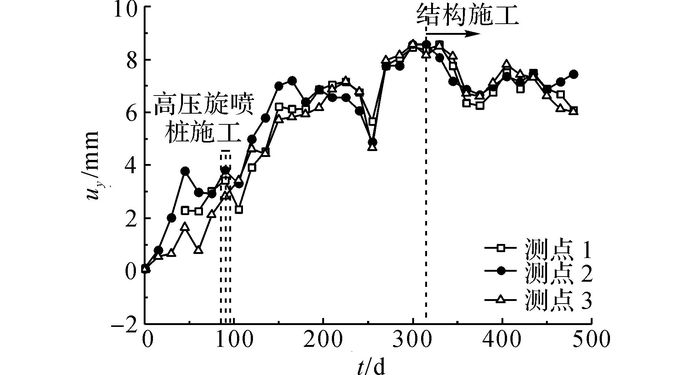
U型槽段左线隧道的典型上浮曲线如图 4所示.He=9.6 m, Hc=22.0 m, Hs=6.5 m, 围护桩桩长14 m, 隧道轴线与近侧围护桩水平距离B=+14.0 m.
|
图 4 K1+440断面左线隧道上浮实测结果 Fig. 4 Measured results of uplift of left line at K1+440 |
U型槽段隧道上浮段的规律与闭合框架段类似, 不同的是U型槽结构施工后, 隧道上浮虽然有所回落, 但回落量有限.主要原因是U型槽结构自重较小, 且无法进行覆土回填, 结构施工后地基土应力远小于先期水平, 地基土回弹变形无法完全恢复.
2.2 隧道整体变形统计规律1) 卸载率与上浮的关系.
隧道上浮变形与上方卸载程度有关, 可以用He与Hc的比值表征土体应力释放程度, 即卸载率a[18].统计纵向不同断面位置的卸载率和隧道上浮变形, 如图 5所示.结果表明, 实际工程条件下的地铁隧道上浮变形与卸载率存在较好的线性关系.

|
图 5 隧道上浮变形与卸载率的关系 Fig. 5 Relationship between tunnel uplift and unloadingratio |
尽管隧道纵向不同断面位置的地质条件略有差异, 但高压旋喷桩加固使得隧道周边土体的强度和刚度提高.在基坑开挖过程中, 加固后复合地基以弹性变形为主, 且回弹量取决于隧道上方应力释放程度, 故上浮变形与卸载率基本线性相关.
2) 水平位置与上浮的关系.
如图 6所示为隧道处于基底不同水平位置情况下的实测上浮统计结果.虽然不同数据点所对应断面位置的卸载率略有不同, 但综合考虑卸载率与上浮变形的近似线性关系和结果关于基坑中轴的对称性, 可以认为图 6中不同水平位置隧道上浮包线为抛物线, 即隧道越靠近基坑中轴线, 上浮变形相应越大.此外, 由于围护桩外侧土体未采取加固措施, 尽管卸载率相对较小, 但上浮变形依然较大.

|
图 6 不同水平位置下隧道实测上浮变形 Fig. 6 Influence of horizontal position on tunnel uplift |
基于隧道上浮变形实测统计规律, 为了研究一般条件下地下通道施工过程中共线下卧地铁隧道的上浮变形规律, 以该工程条件为背景, 但不考虑实际工程中为确保隧道变形满足控制标准所采取的地基加固措施, 采用Plaxis 2D平面应变有限元法, 开展数值模拟研究.
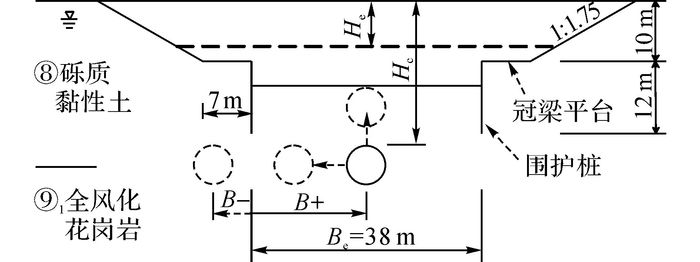
3.1 计算模型考虑纵向不同位置处地质条件、隧道拱顶埋深、隧道与围护桩的水平距离以及卸载率略有差异, 隧道上浮主要受隧道所处地层的回弹变形影响.为了研究隧道埋深和水平位置对上浮的影响, 模型条件如图 7所示.模型尺寸为150 m×50 m;地层简化成两层:砾质黏土层厚25 m, 下卧全风化花岗岩25 m.基坑宽度为38 m;围护桩长12 m;坡高取场地中较普遍的10 m, 坡度为1:1.75;围护桩顶设一道800 mm×800 mm钢筋混凝土支撑;地下水位为-3 m;隧道仅考虑一条线.
|
图 7 K1+560断面隧道上浮数值模拟结果与实测结果 Fig. 7 Numerical results and field measurements oftunnel uplift at K1+560 |
土体采用小应变硬化土(HSS)模型[19]、15节点三角形单元.
针对场地中分布较广的4层土, 采用薄壁取土器各钻取了3筒原状土, 并进行一系列室内试验.通过标准固结试验, 获得各层土参考压力100 kPa下的主固结切线模量Eoedref以及应力相关幂指数m;通过三轴固结排水(CD)试验, 获得100 kPa围压下对应50%峰值偏应力的参考割线模量E50ref及破坏比Rf;根据100 kPa围压下三轴固结排水(CD)加载-卸载-再加载试验中的卸载-再加载段斜率, 确定各层土的参考卸载模量Eurref;由三轴固结不排水(CU)试验, 获得各层土的强度指标c′和φ′.小应变剪切刚度G0ref根据现场波速测试结果由G0ref=ρVs2计算确定, 小应变刚度衰减至70%时对应的切应变γ 0.7的获取较复杂, 基于相关经验取法[20-22]确定.此外, 卸载泊松比采用Plaxis软件默认的0.2.各层土模型参数如表 2所示.
| 表 2 土层计算参数 Table 2 Soil parameters for calculation |
隧道衬砌采用板单元模拟成均质圆环, 但考虑纵向接缝对环向刚度的影响, 环向刚度有效率η取0.75[8].围护桩采用板单元模拟, 基于刚度等效原则确定刚度参数, 并考虑施工缺陷刚度折减20%[10].土与结构的相互作用通过Plaxis软件自带的界面单元加以考虑, 界面强度折减因子Rinter取软件默认的0.65.围护桩和隧道的结构参数如表 3所示.表中,d为等效厚度,γ为泊松比,EA为抗压刚度,EI为抗弯刚度.
| 表 3 围护桩和隧道衬砌计算参数 Table 3 Parameters for retaining pile and tunnel lining |
基于以上参数, 对U型槽段里程K1+560断面进行模拟.该位置基坑开挖过程未采取加固措施, 因此, 实测隧道上浮变形未受地基加固的影响, 避免了地基加固参数对计算结果的影响.土层自上而下分别为:人工填土9 m, 淤泥层1.7 m, 黏土层5.2 m, 砾质黏土层6.5 m, 下卧全风化花岗岩层, 潜水位于地表以下约2.7 m.He和Hs均为5.2 m, Hc约为20.0 m, 左线隧道轴线距基坑中轴线3.2m.不同开挖深度下左线隧道的上浮变形模拟结果和实测结果如图 7所示.数值模拟结果与实测结果较接近, 表 2的土层模型参数取值合理.
3.4 模型工况如图 8所示, 针对隧道埋深和水平位置两个因素, 进行两组共17种工况分析.分别如下:工况组1:B=+19.0 m;Hc取12、14、16、18、20、22、24 m共7种工况, 考虑隧道埋深的影响.工况组2: Hc=24 m;B取-5.0、-2.5、0、+2.5、+5.0、+7.5、+10.0、+12.5、+15.0、+17.5 m共10种工况, 考虑隧道水平位置的影响.各工况建模过程如下:1) 生成初始应力场;2) 生成既有隧道;3) 重置位移后, 按1 m/层开挖至冠梁平台;4) 激活围护桩;5) 按1 m/层进行围护桩内基坑开挖.卸载率由不同开挖步下开挖深度和隧道拱顶埋深的比值体现, 隧道水平位置通过隧道轴线与左侧围护桩距离B确定.

|
图 8 有限元模型示意图 Fig. 8 Schematic diagram of finite element model |
工况组1的模拟结果如图 9所示.如图 9(b)所示为将图 9(a)横坐标归一成卸载率后的结果.

|
图 9 隧道埋深对上浮变形的影响 Fig. 9 Influence of cover depth on tunnel uplift |
结果表明:低卸载率下, 隧道上浮变形与卸载率呈线性关系.随着卸载率的增大, 将向非线性关系转变, 且隧道埋深小相对埋深大的情况非线性关系更明显.当隧道埋深较大时, 相同卸载率下基坑开挖后隧道覆土厚度相对大, 坑底土体塑性变形区对隧道变形的影响相对较小.反之, 当隧道埋深较小时, 影响相对较大.地基加固的原理是使隧道上方土体的强度和刚度提高, 基坑开挖后隧道上方土体近似弹性回弹, 因此实测中有如图 5所示的线性关系.
通过计算结果可以发现, 在隧道拱顶埋深小于18 m或大于22 m的情况下, 埋深对曲线的影响不大.可能原因是当隧道拱顶埋深小于18 m时, 隧道结构均位于砾质黏土层中;当拱顶埋深大于22 m时, 隧道拱腰以下位于全风化花岗岩中, 基坑开挖过程中, 下卧隧道结构的上浮变形受卸载率和隧道下方地层条件的直接影响, 埋深的影响不大.
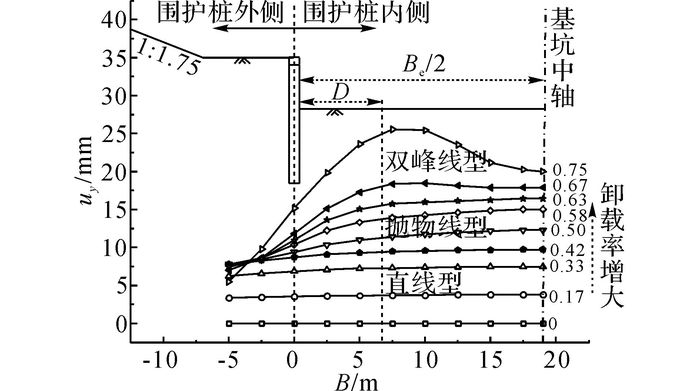
4.2 水平位置与上浮的关系工况组2的计算结果如图 10所示.图中, 每条曲线表示同一卸载率下不同水平位置处隧道上浮变形连成的包线.考虑计算结果关于基坑中轴的对称性, 当卸载率较小时, 隧道上浮包线为直线型;随着卸载率的增加, 上浮包线逐渐发展成抛物线型;最终演变成双峰线型.分析原因如下:a<0.42为放坡开挖阶段, 卸载后坑底较均匀回弹, 上浮包线呈直线型;随着卸载率的增加(a>0.42), 基坑进入围护开挖阶段, 围护桩内侧回弹量大于外侧, 且越靠近基坑中轴, 回弹量越大, 隧道上浮包线由直线型转变为抛物线型;当卸载率大于一定值(a>0.67) 时, 由于围护桩嵌入深度过小, 踢脚变形较大, 使得在距围护桩一定距离区间(Be/10~Be/3) 内, 隧道上浮变形大大增加, 隧道上浮包络线呈双峰线型.
|
图 10 隧道水平位置对上浮变形的影响 Fig. 10 Influence of horizontal position on tunnel uplift |
为了研究土与结构的相互作用、隧道下卧层卸载模量以及地基加固对隧道上浮变形的影响, 基于图 7的剖面对以上因素进行建模分析.隧道拱顶埋深取案例中较普遍的22 m, 基坑开挖深度14 m, 分析结果如下.
1) 土与结构相互作用的影响.
在该有限元模型中, 土与结构的相互作用关系不仅和土与结构间界面单元强度折减因子Rinter的取值有关, 而且受隧道刚度的影响.对以上2个因素进行敏感性分析, 结果如图 11所示.图中, η为隧道环向刚度有效率, η越大, 隧道刚度越大.Rinter越大, 表示隧道与周围土体的接触特性越好;当Rinter=1时, 隧道与周围土体变形始终耦合.
计算结果表明, 隧道刚度越大或者隧道结构与周围土体的接触特性越好, 基坑开挖后下卧隧道的上浮变形越小.尽管隧道结构与周围土体的接触特性对隧道上浮变形大小的影响更明显, 但影响程度均较有限.

|
图 11 隧道刚度和土与结构界面强度的影响 Fig. 11 Influence of tunnel stiffness and interface strength between tunnel and surrounding soil |
2) 隧道下卧土层卸载模量的影响.
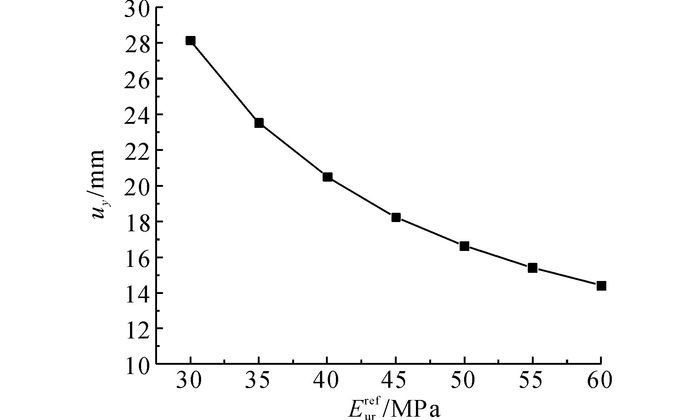
为了研究隧道下卧层土体卸载模量对隧道上浮变形的影响, 模型中, 通过改变隧道下卧层土体参考卸载模量的取值, 并使小应变刚度与参考卸载模量的比值恒定, 结果如图 12所示.可以发现, 随着隧道下卧层土体卸载模量的增大, 隧道上浮变形逐渐减小, 但减小幅度逐渐减小.
|
图 12 隧道下卧土层卸载模量的影响 Fig. 12 Influence of unloading modulus of soil underneath tunnel |
3) 基坑底地基加固的影响.
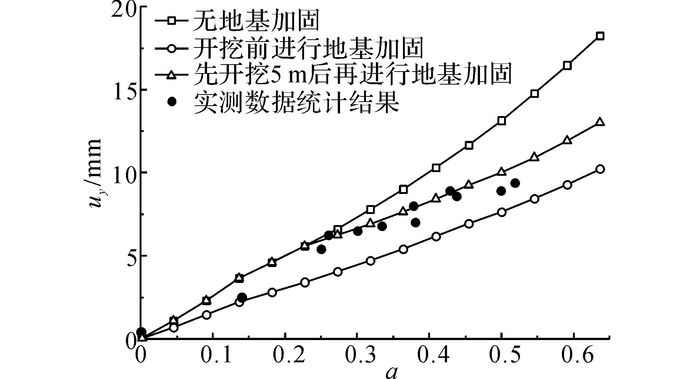
坑底地基的加固方案如图 2所示.隧道周围留3 m保护区, 加固深度至隧道拱底以下3 m.在模拟中, 将加固区土体刚度参数放大3倍[15], 以考虑地基加固的作用, 加固区强度指标c′=80 kPa, φ=33°.图 13给出无地基加固、开挖前进行地基加固以及先开挖5 m后(a>0.23后)再进行地基加固3种方案的模拟结果.结果表明, 在基坑开挖前, 先进行地基加固, 基坑开挖完成后, 隧道上浮变形约减小40%;若基坑先开挖5 m后再进行地基加固, 基坑开挖完成后, 隧道上浮变形减小比例仅20%左右.
|
图 13 地基加固的影响 Fig. 13 Influence of foundation reinforcement |
基坑开挖后, 下卧地铁隧道上浮变形过大将威胁地铁运营安全.在工程设计中, 通常以基坑开挖后隧道覆土厚度作为判定是否采取加固保护措施的依据.以该工程为例, 在初步方案中, 当基坑开挖后隧道覆土厚度满足大于1倍隧道直径的条件时, 不考虑地铁保护方案.根据上述研究可知, 基坑开挖后下卧地铁隧道上浮变形与卸载率以及隧道位置相关;此外, 是否采用加固保护方案, 应根据该地区要求的隧道变形控制标准确定.仅以隧道覆土厚度作为判定依据, 偏不安全.
为了使数值计算结果得到简便应用, 对图 9的曲线上、下边界进行拟合, 得到拟合曲线如下:
| ${{u}_{y\text{m}}}=\left\{ \begin{array}{*{35}{l}} 16.77{{a}^{3}}-5.52{{a}^{2}}+33.67a,12\text{m}\le {{H}_{\text{c}}}\le 18\text{m}; \\ 3.35{{a}^{3}}+5.85{{a}^{2}}+21.4a,22\text{m}\le {{H}_{\text{c}}}\le 24\text{m}\text{.} \\ \end{array} \right.$ | (1) |
式中:uym为基坑中轴下侧隧道上浮预估值.当隧道拱顶埋深为18~22 m时, 可以近似取上、下边界线性内插值.
在实际工程中, 围护桩嵌入深度一般不足以使踢脚产生过大变形, 故水平向隧道上浮包线往往呈抛物线型, 隧道越靠近基坑中轴, 上浮变形越大.数值模拟结果表明, 当隧道与围护桩距离大于1倍隧道直径时, 隧道上浮包线接近水平.将抛物线型上浮包线(0.42<a<0.67) 近似成分段线性, 基于图 10的规律且综合考虑卸载率和隧道下卧土层卸载模量的影响, 得到预估公式如下:
| $\begin{align} &{{u}_{y}}= \\ &\left\{ \begin{array}{*{35}{l}} \lambda \left[ 0.49\left( 1-B/D \right){{a}^{-0.67}}+B/D \right]{{u}_{y\text{m}}},&0\le B\le D; \\ \quad \quad \quad \quad \quad \quad \lambda {{u}_{y\text{m}}},&D<B\le {{B}_{\text{e}}}/2. \\ \end{array} \right. \\ \end{align}$ | (2) |
式中:B为隧道轴线与邻近侧围护桩的水平距离;D为隧道外径;Be为基坑宽度;λ为隧道下卧土层卸载模量的影响系数, 通过图 12所示的结果归一化拟合获得, 如下所示:
| $\lambda =6.14\exp \left( -E_{\text{ur}}^{\text{ref}}/15.32 \right)+0.68.$ | (3) |
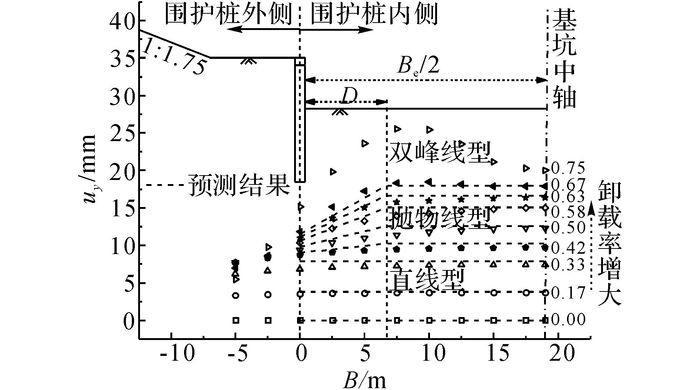
采用式(2) 预估得到的隧道上浮变形与数值模拟结果的对比如图 14所示.利用预估公式获得的结果与模拟结果较吻合.
|
图 14 预估结果与模拟结果对比 Fig. 14 Comparison between predicted and numericalresults |
类似案例中, 可以通过预估式(2) 初步估算地下通道基坑开挖后下卧地铁隧道的上浮变形, 并与隧道变形控制标准进行对比.若隧道上浮变形预估值超过控制标准, 则应考虑采取控制隧道变形的加固保护措施.
5 结论(1) 采用明挖法施工的地下通道, 地下通道结构自重不足以使因基坑开挖卸载导致的下卧隧道上浮变形完全回落.若要使下卧隧道恢复初始标高, 须进行超高回填.
(2) 地下通道基坑开挖后, 下卧隧道上浮变形与卸载率近似呈线性关系.当卸载率较低时, 隧道上浮变形与卸载率线性关系明显;随着卸载率的增大, 将向非线性关系转变, 且隧道埋深小相对埋深大的情况非线性关系更明显.
(3) 在坑底不同水平位置处, 隧道上浮变形连成的包线随着隧道上方卸载率的增加, 最初为直线型, 而后发展成抛物线型, 最终呈双峰线型.
| [1] |
黄润秋, 戚国庆. 地铁隧道盾构法施工对环境的影响研究[J].
岩石力学与工程学报, 2003, 22(supple.1): 2464–2468.
HUANG Run-qiu, QI Guo-qing. Study on the influence of subway by shield tunneling on environment[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(supple.1): 2464–2468. |
| [2] |
张书丰. 地铁盾构隧道施工期地表沉降监测研究[D]. 南京: 河海大学, 2004.
ZHANG Shu-feng. Study on measured ground settlement during shield tunneling of metro tunnel construction [D]. Nanjing: Hehai University, 2004. |
| [3] | CHEN R P, ZHUN J, LIU W, et al. Ground movement induced by parallel EPB tunnels in silty soils[J]. Tunneling and Underground Space Technology, 2011, 26(1): 163–171. DOI:10.1016/j.tust.2010.09.004 |
| [4] | CHEN R P, LI J, KONG L G, et al. Experimental study on face instability of shield tunnel in sand[J]. Tunneling and Underground Space Technology, 2013, 33(1): 12–21. |
| [5] | CHEN R P, MENG F Y, LI Z C, et al. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils[J]. Tunneling and Underground Space Technology, 2016, 58: 224–235. DOI:10.1016/j.tust.2016.06.002 |
| [6] |
胡海英, 张玉成, 杨光华, 等. 基坑开挖对既有地铁隧道影响的实测及数值分析[J].
岩土工程学报, 2014, 36(supple.2): 431–439.
HU Hai-ying, ZHANG Yu-cheng, YANG Guang-hua, et al. Measurement and numerical analysis of effect of excavation of foundation pits on metro tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(supple.2): 431–439. |
| [7] |
胡琦, 许四法, 陈仁朋, 等. 深基坑土体扰动及其对邻近地铁隧道的影响分析[J].
岩土工程学报, 2013, 35(supple.2): 537–541.
HU Qi, XU Si-fa, CHEN Ren-peng, et al. Influence of soil disturbance on metro tunnel in soft clay due to excavation of deep foundation pit[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(supple.2): 537–541. |
| [8] |
郑刚, 王琦, 邓旭, 等. 不同围护结构变形模式对坑外既有隧道变形影响的对比分析[J].
岩土工程学报, 2015, 37(7): 1181–1194.
ZHENG Gang, WANG Qi, DENG Xu, et al. Comparative analysis of influences of different deformation modes of retaining structures on deformation of existing tunnels outside excavations[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1181–1194. DOI:10.11779/CJGE201507003 |
| [9] |
郑刚, 杜一鸣, 刁钰, 等. 基坑开挖引起邻近既有隧道变形的影响区研究[J].
岩土工程学报, 2016, 38(4): 599–612.
ZHENG Gang, DU Yi-ming, DIAO Yu, et al. Influenced zones for deformation of existing tunnels adjacent to excavations[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 599–612. DOI:10.11779/CJGE201604003 |
| [10] |
陈仁朋, 孟凡衍, 李忠超, 等. 邻近深基坑地铁隧道过大位移及保护措施[J].
浙江大学学报:工学版, 2016, 50(5): 856–863.
CHEN Ren-peng, MENG Fan-yan, LI Zhong-chao, et al. Considerable displacement and protective measures for metro tunnels adjacent deep excavation[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(5): 856–863. |
| [11] |
吉茂杰, 刘国彬. 开挖卸荷引起地铁隧道位移预测方法[J].
同济大学学报, 2001, 29(5): 531–535.
JI Mao-jie, LIU Guo-bin. Predition method of displacement of subway tunnel due to excavation[J]. Journal of Tongji University, 2001, 29(5): 531–535. |
| [12] |
周泽林, 陈寿根, 陈亮, 等. 基坑施工对下卧地铁隧道上抬变形影响的简化理论分析[J].
岩土工程学报, 2015, 37(12): 2224–2234.
ZHOU Ze-lin, CHEN Shou-gen, CHEN Liang, et al. Analysis of uplift deflection of subway tunnel due to adjacent pit excavation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(12): 2224–2234. DOI:10.11779/CJGE201512012 |
| [13] | NG C W W, SHI J W, HONG Y. Three-dimensional centrifuge modeling of basement excavation effects on an existing tunnel in dry sand[J]. Canadian Geotechnical Journal, 2013, 50(8): 874–888. DOI:10.1139/cgj-2012-0423 |
| [14] | DOLEZALOVA M. Tunnel complex unloaded by a deep excavation[J]. Computers and Geotechnics, 2001, 28(6): 469–493. |
| [15] |
黄宏伟, 黄栩, HELMUTS F. 基坑开挖对下卧运营盾构隧道影响的数值模拟研究[J].
土木工程学报, 2012, 45(3): 182–189.
HUANG Hong-wei, HUANG Xu, HELMUT S F. Numerical analysis of the influence of deep excavation on underneath existing road tunnel[J]. China Civil Engineering Journal, 2012, 45(3): 182–189. |
| [16] |
黄兆纬, 黄信, 胡雪瀛, 等. 基坑开挖对既有地铁隧道变位影响及技术措施分析[J].
岩土工程学报, 2014, 36(supple.2): 381–385.
HUANG Zhao-wei, HUANG Xin, HU Xue-ying, et al. Influence of foundation pit excavation on displacement of existing metro tunnels and technical measures[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(supple.2): 381–385. |
| [17] |
刘庭金. 基坑施工对盾构隧道变形影响的实测研究[J].
岩石力学与工程学报, 2008, 27(supple.2): 3393–3400.
LIU Ting-jin. Study on shield tunnel deformation due to foundation pit construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(supple.2): 3393–3400. |
| [18] |
魏刚. 基坑开挖对下方既有盾构隧道影响的实测与分析[J].
岩土力学, 2013, 34(5): 1421–1428.
WEI Gang. Measurement and analysis of impact of foundation pit excavation on below existed shield tunnels[J]. Rock and Soil Mechanics, 2013, 34(5): 1421–1428. |
| [19] | BEN T. Small-strain stiffness of soils and its numerical consequences [D]. Germany: University of Stuttgart, 2007. |
| [20] |
汪中卫, 王海飙, 戚科骏, 等. 土体小应变试验研究综述与评价[J].
岩土力学, 2007, 28(7): 1518–1524.
WANG Zhong-wei, WANG Hai-biao, QI Ke-jun, et al. Summary and evaluation of experimental investigation on small strain of soil[J]. Rock and Soil Mechanics, 2007, 28(7): 1518–1524. |
| [21] |
王海波, 徐明, 宋二祥. 基于硬化土模型的小应变本构模型研究[J].
岩土力学, 2011, 32(1): 39–43.
WANG Hai-bo, XU Ming, SONG Er-xiang. A small strain constitutive model based on hardening soil model[J]. Rock and Soil Mechanics, 2011, 32(1): 39–43. |
| [22] |
王卫东, 王浩然, 徐中华. 上海地区基坑开挖数值分析中土体HS-Small模型参数的研究[J].
岩土力学, 2013, 34(6): 1766–1774.
WANG Wei-dong, WANG Hao-ran, XU Zhong-hua. Study of parameters of HS-Small model used in numerical analysis of excavations in Shanghai area[J]. Rock and Soil Mechanics, 2013, 34(6): 1766–1774. |


