2. 中山大学 数据科学与计算机学院, 广东 广州 510006
2. School of Data and Computer Science, Sun Yat-sen University, Guangzhou 510000, China
公共的物流服务平台能够广泛集成物流资源, 节约成本, 提升物流供应链的效率和竞争力.由于受到天气、实时路况、用户需求等各方面因素的支配, 公共物流服务平台的服务存在海量的可选组合.随着互联网技术的发展, 公共物流服务平台也在利用线上到线下(online to offline, O2O)模式提供服务, 物流平台的线上服务资源通常是由线下服务提供商提供, 线上服务要考虑线下的服务资源和服务提供商.在服务质量(quality of service, QoS)感知的情况下, 线上平台需要从线下服务提供商提供的海量服务资源中选出和规划合理的组合服务.这是一种典型的O2O服务场景中QoS感知的海量服务组合(service composition)[1]问题.处理海量服务组合时, 传统服务组合方法存在着效率不高和全局QoS性能低下等问题.而对于O2O服务, 以往研究侧重线上服务的属性, 当服务是数值计算类的自动化服务时很适合, 但当服务是由人或组织的线下活动参与提供时, 线上服务的质量会受到线下活动的极大影响.线上的服务组合往往隐含着线下服务提供商的协同工作, 并且人和组织的社会性使得服务的质量不仅受个体的影响, 还会受到个体之间的协作程度影响.这在以往的传统服务组合研究中很少涉及.
近年来, 服务组合研究得到服务计算领域众多研究者的关注.一些研究主要关注网络服务组合问题[2-4], 许多网络服务的研究主要关注用户侧的需求[5].在海量O2O服务的组合问题中, 研究焦点主要集中在QoS感知的网络服务组合方法, 少有学者关注提高线上海量服务组合算法执行效率和线下服务提供商之间的协作效率, 对服务组合质量的影响.
在服务计算的研究中, 有学者使用了社会关系方法.如可信的网络服务选取方法[6], 利用社会关系网络的社会性和专业性的分布式决策和传播的方法[7], 文献[8-9]在团队组建问题中加入社会关系等.社会关系理论在服务计算领域中产生了很多创新的研究和应用成果, 如团队组建和沟通成本的计算方法等, 但对于如何将社会关系理论应用在服务计算的过滤和优选过程,相关的研究成果较少.
目前已有学者在服务组合方法的研究中部分采用了社会关系理论, 如Deng等[2]使用社会网络理论, 提出了一种带有信任加强的服务推荐方法, 基于用户的信任关系和反馈进行推荐.Jiang等[10]使用了服务再利用的思想.以上研究通常都是以终端用户为导向, 从某种程度上使用了社会关系网络, 大部分的方法并没有从线下服务提供商的角度考虑优化其协作效率, 这可能会导致组合服务的QoS虽然很优秀, 但是在实际执行时却表现不理想的情况发生.
目前传统的组合服务方法通常没有相应的过滤机制, 但在服务量较大的情况下, 一些过滤方法被广泛采用.比如协作过滤, 如Yu等[11]提出基于用户的协作过滤方法(collaborative filtering, CF), 使用皮尔森相关系数(pearson correlation coefficient, PCC)来计算用户间的相似度, 还有用协同过滤的方法将服务组合问题转化为服务推荐问题[12]和引入Skyline服务并按照QoS聚合评分进行聚类[13].
由于问题相近, 可以考虑在海量服务环境中, 使用协作过滤的方法.但是, 服务过滤在加快算法执行速度的同时, 可能存在过滤粒度过大的问题, 将导致许多优质的服务被过滤掉, 引起局部收敛甚至找不到解.因此, 在海量服务环境中, 粒度过大的过滤算法的实际应用效果不理想.
海量O2O服务组合的优化问题最终目标是在海量服务中找出最优的服务组合, 以适应特定业务流程和用户的需求.该类问题通常需要QoS感知, 多采用启发式算法.目前以遗传算法为代表的元启发式算法在解决服务组合问题时, 大多将重心放在QoS指标的优化上面.在多QoS约束下, 随着种群数量的增加, 在较大搜索空间下算法的收敛速度较慢, 稳定性差.
针对海量服务组合, Brahmi等[14]利用服务间过往的合作关系来改进组合服务的优化率, 但是该方法单纯使用服务的合作关系作为启发信息, 缺乏稳定性.Shao等[15]考虑了物流服务中的服务组合情况, 为了应对服务量大的情况下服务组合过程效率低下的问题, 利用社会关系来引导A*算法的执行.该方法有着较好的优化率, 利用社会关系很好地加快了算法执行效率, 但依然存在需要对QoS进行聚合或只能应对单一QoS服务的问题.
综上所述, 社会关系理论已经在服务计算领域和服务组合方法中初步应用, 但如何基于社会关系理论进行海量O2O服务组合优化, 以此提高线上组合服务执行效率, 以及线下服务提供商之间的协作效率, 还面临着众多的挑战.
本文提出一种面向海量O2O服务组合的优化方法, 在传统服务组合方法的优化阶段前, 增加一个带有QoS感知的过滤阶段, 提高线上海量服务组合的算法执行效率;引入社会关系(social relation)理论[16], 在过滤和优化2个阶段增加社会关系元素, 利用QoS感知的服务组合优化算法, 提高线下服务提供商之间的协作效率, 同时保证线上服务质量.首先, 利用线下服务提供商之间的合作历史日志建立一个社会关系网络.其次, 提出一种社会关系扩展的Skyline服务过滤方法.最后, 在服务组合优化阶段, 基于社会关系提出2种新的社会进化算子来改进多目标遗传算法.
1 问题定义 1.1 网络服务定义1 网络服务(web service, WS). WS是由线下提供商提供的具有QoS指标的服务.将网络服务SW表示为一个4元组:
| $ {S_{\rm{W}}}{\rm{ = (id, qos, function, partner), }} $ |
其中, id为网络服务的唯一标识, 用来区分网络服务.qos是一个9元组:qos=(response_time, availability, through_out, success_rate, reliability, compliance, best_experience, citation_rate, latency), 分别表示该服务在这9项QoS指标的评价.function是服务的功能集合, 表示服务能够执行的任务类型.partner是一个服务的id集合, 表示服务的有效伙伴, 即与服务存在过有效合作的服务集合.
定义2 网络服务集合(web service set, WSS).网络服务集合SWS是一个由网络服务SW组成的, 大小为k的集合.SWS={SW1, SW2, SW3, …, SWk}, 表示该集合有k个服务.本文的目标是在该集合中选出最优的组合服务.
1.2 社会关系网络定义3 社会关系网络(social network, SN).是由多个服务连接构成的一个有权无向图, 表示为一个3元组NS=(V, E, W), 其中V是图中点的集合, 每个点v∈V代表一个网络服务SW.E是图中边的集合, 其中e∈E为图中的边.W是边上的权重, 表示服务间的沟通成本.
针对事件日志中的每一个事件Ei, 该事件的服务集合SWSi如果∀SWm, SWn∈SWSi, 则在社会关系网络NS中存在一条无向边e=〈vm、vn〉, 其中vm、vn分别对应SWm、SWn, 表示这2个服务之间存在过合作关系.
定义4 合作服务集合(cooperative collection of services, CCS).一个服务SW的合作服务集合CCS是由与该服务具有合作关系的其他服务组成的.在社会关系网络NS中, 表示为与SW对应的顶点u直接相连接的顶点集合, 即{∀v|v∈〈u, v〉}.
1.3 组合优化的适应度函数及社会进化算子定义5 组合服务(composition service, CS).组合服务SC表示为一个3元组SC=(SWS, BP, f), 其中SWS为该组合服务中所包含的服务集合;BP为该组合服务所针对的业务流程;f为一个映射关系f=SWS→BP, 表示组合服务中的服务与业务流程中的任务tP的对应关系, 即{∀SW∈SWS, tP∈BP, ∃f=SW→tP}.
定义6 适应度函数.用于评价服务组合的优化结果.对于一个个体(组合服务)SC=(SWS, BP, f), 定义其计算出来的QoS指标为一个列表:
| $ \begin{array}{l} {\rm{QoS}}({S_{\rm{C}}}) = \{ {\rm{Qo}}{{\rm{S}}_1}, {\rm{Qo}}{{\rm{S}}_2}, {\rm{Qo}}{{\rm{S}}_3}, \ldots, {\rm{Qo}}{{\rm{S}}_k}|{\rm{Qo}}{{\rm{S}}_i} \in \\ {A_{\rm{d}}}\parallel {\rm{Qo}}{{\rm{S}}_j} \in {M_{\rm{u}}}\}, \end{array} $ |
表示共有k个QoS指标.Ad和Mu分别表示加性指标和乘性指标, 任意QoS指标必定属于加性指标或者乘性指标.适应度函数Z定义如下:
| $ \begin{array}{l} Z({\rm{QoS}}({\rm{SC}})) = \\ \sum\limits_{\{ {\rm{Qo}}{{\rm{S}}_i} \in {\rm{Ad}}\parallel {\rm{Qo}}{{\rm{S}}_i} < {\rm{QoSCo}}{{\rm{n}}_i}\} } {(1 -\frac{{{\rm{Qo}}{{\rm{S}}_i} -{\rm{Qo}}{{\rm{S}}_{i, {\rm{min}}}}}}{{{\rm{Qo}}{{\rm{S}}_{i, {\rm{max}}}} -{\rm{Qo}}{{\rm{S}}_{i, {\rm{min}}}}}})} + \\ \sum\limits_{\{ {\rm{Qo}}{{\rm{S}}_j} \in Mu\parallel {\rm{Qo}}{{\rm{S}}_j} > {\rm{QoSCo}}{{\rm{n}}_j}\} } {\frac{{{\rm{Qo}}{{\rm{S}}_j} - {\rm{Qo}}{{\rm{S}}_{j, {\rm{min}}}}}}{{{\rm{Qo}}{{\rm{S}}_{j, {\rm{max}}}} - Qo{S_{j, {\rm{min}}}}}}} . \end{array} $ | (1) |
其中, QoSi, max和QoSi, min为组合服务集合中该项QoS指标的最大值和最小值, QoSConi为相应的QoS约束值.函数Z针对每一项QoS指标进行评分, 每一项QoS指标的评分都归一化到(0, 1], 指标满足约束并且优化程度越高则评分将越高, 不满足QoS约束的指标将被排除在外, 即得分为0.
为了在服务优化阶段进行社会关系的进化, 增加了社会变异算子和社会交叉算子, 如定义7和定义8所示.
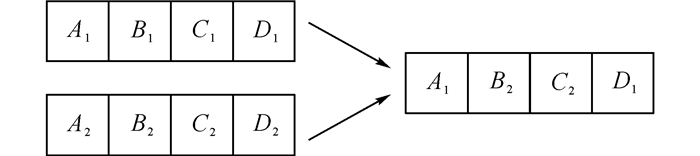
定义7 社会变异.区别于通常的变异过程, 通过计算个体与其邻居的沟通成本, 用较小的个体取代当前个体.社会变异后, 变异的基因为B(B1→Bi).那么变异后的服务Bi满足min (cost (A1, Bi)+cost (Bi, C1)), 即Bi在候选服务集合中与A1、C1的沟通成本最小, 如图 1所示.其中,cost (u, v)表示服务u和服务v的沟通成本[8]:
| $ {\rm{cost}}\left( {u, v} \right) = \frac{{{F_{{\rm{max}}}}}}{{\sum\limits_i^{i \in e\left( {u, v} \right)} {\left( {{\alpha _i}{\beta _i}g} \right)} }}. $ | (2) |

|
图 1 社会变异过程示意图 Fig. 1 Diagram of social mutation process |
定义8 社会交叉.社会交叉将由2个父代产生1个新的个体.假设父代分别为par1和par2, i表示其中一个父代, cost (i, prev)为其与前一个服务的沟通成本, 而cost (i, next)为其与后一个服务的沟通成本, 如图 2所示.父代i被选中为新个体的概率为
| $ {p_i} = 1 - \frac{{{\rm{cost}}(i, {\rm{prev}}) + {\rm{cost}}(i, {\rm{next}})}}{{\sum\nolimits_{_{j - 1}}^{^2} {\left( {{\rm{cost}}(i, {\rm{prev}}) + {\rm{cost}}(i, {\rm{next}})} \right)} }}. $ | (3) |
|
图 2 社会交叉过程示意图 Fig. 2 Diagram of social crossover process |
本文的服务组合问题除了需要满足用户的QoS约束之外, 还要通过降低服务组合的服务提供商之间的沟通成本, 提高其协作效率.
问题描述为:用户给出一组QoS约束QoSCon和业务流程BP, 通过服务组合的方法从服务集合SWS中找出能够满足用户需求的组合服务SC, 并且尽可能优化SC的各项QoS指标以及服务提供商之间的沟通成本, 即SC满足:1) 对于QoS为加性的指标, 要求QoS小于约束, 即QoSi < QoSConi;2) 对于QoS为乘性的指标, 要求QoS大于约束, 即QoSi > QoSConi;3) 线下服务提供商的总沟通成本最小, 即min(exp(SC)), 其中exp()表示服务组合SC的总沟通成本;4) 线上服务的总体QoS评价最大, 即max (Z(QoS(SC)).
2 海量O2O服务组合的优化 2.1 社会关系网络的建模方法本文从线下服务提供商过往合作的事件日志中, 建立社会关系网络模型并计算服务提供商之间的沟通成本.根据定义3, 线下服务提供商之间社会关系的紧密程度是通过社会关系网络中边上的权重来体现的, 综合考虑社会关系的影响因子——时间衰减因子α和评价因子β, 定义Fmax为所有服务之间最大的合作次数, 设u, v为2个服务, e(u, v)为事件日志中u, v参与的事件集合, g是该次事件e(u, v)中合作的评价, g∈(0, 10).
该式表明关系评价权重正比于最大合作次数, 反比于衰减因子和评价因子.本文采用等级评价法, “1级”表示评价分值最高, 以此类推.
算法1:社会关系网络生成算法
输入:候选服务集合SWS
输出:社会关系网络NS
步骤:
1. FOR每个服务SWi∈SWS DO
2. cost (SWi, SWj), SWj∈SWi.CCS //根据式(3) 计算与其合作服务集合CCS中各服务的沟通成本
3.建立以SWi为顶点的社会关系网络NSi
4. END FOR
5. FOR i=1 to N
6.将NSi并入社会关系矩阵NS
7.cost (SWi, SWj)←min (cost (SWi, SWj), cost (SWj, SWi))//得到2个服务的最小沟通成本
8. END FOR
2.2 社会关系扩展的Skyline服务过滤方法本文在传统的优化阶段前增加了QoS感知的过滤阶段, 其目的是从海量服务中选出1组候选集, 避免在优化阶段的大规模数据输入, 加快算法的收敛速度.由于过滤后的服务集是优化阶段的候选集, 过滤粒度不能太大, 在过滤掉较差的服务的同时, 保证优质的服务被保留下来.本文将过滤阶段分成2个阶段, 第1阶段为Skyline过滤阶段, 即仅保留Skyline服务;第2阶段为社会关系扩展阶段, 通过服务的合作服务集合来扩展候选集, 以保证大多数优秀的服务加入到最终的服务集合中.此方法称为基于社会关系扩展的Skyline过滤方法(social relation expanded Skyline filtering, SESF).SESF方法能够提高算法执行效率, 保留优秀的服务并且克服Skyline过滤粒度较大的问题, 保证后续优化阶段服务的多样性, 避免局部收敛.
3.2.1 Skyline服务过滤阶段为了快速的过滤掉较差的服务, 本文采用Skyline服务过滤方法.Skyline服务是通过Pareto支配关系根据服务的QoS指标对服务进行支配分级, 其中处于最高级别的服务被称为Skyline服务[14].Skyline服务能够保证选中的服务至少有1个优秀的QoS指标, 以此来粗略和有效地过滤大数量的服务, 但同时也造成一些优秀的非Skyline服务被过滤掉.因此通常的研究并不直接使用Skyline过滤, 而是在此基础上进行进一步处理.本文也是如此, 在下一阶段, 通过社会关系扩展的方法将本阶段过滤掉的优秀服务重新加入候选集.
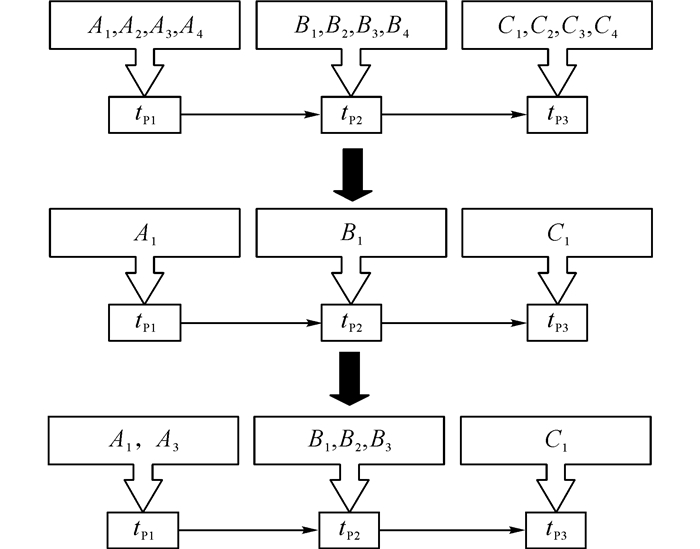
3.2.2 社会关系扩展阶段Skyline服务的合作服务集合也包含了大量优质的服务, 因此, 在第一阶段的Skyline服务被选出后, 从其合作服务集合中扩充服务到候选集.整个过程的示意图, 如图 3所示.其中, tP1、tP2、tP3为3个任务, Ai、Bi、Ci为对应的候选服务, 加粗字体表示为Skyline服务, 这3个服务的合作服务集合CCS分别为A1.CCS={A3, B2, C1}, B1.CCS={B3, A3}, C1.CCS={A1}, 那么在Skyline过滤之后, 只留下A1、B1、C1, 之后将它们的合作服务集合中的服务重新加入到候选服务集.
|
图 3 基于社会关系的候选服务集扩展过程 Fig. 3 Process of expansion of candidate services based on social relationship |
算法2:基于社会关系扩展的服务过滤算法
输入:候选服务集合SWS
输出:过滤后的服务集合
步骤:
1.FOR每个任务DO
2. 依次选出单个任务的Skyline服务
3. 选出所有的Skyline服务
4.END FOR
5. 首先在候选集中包含所有Skyline服务
6. FOR每个Skyline服务DO
7. 将Skyline服务的合作服务集合中的服务重新加入
8. END FOR
9. 将原本的服务集合替换为过滤后的服务集合
2.3 基于多目标遗传算法和社会进化算子的服务组合优化方法对多目标遗传算法的改进通常有2个方向, 一是对优化方法改进来保留更优秀的个体;二是通过改进进化算子来改进遗传算法(genetic algorithm, GA)的效率和实用性.本文将传统GA算法、多目标遗传算法NSGA-Ⅱ[17](non-dominated sorting genetic algorithm, NSGA)和NSGA-Ⅲ算法框架中的进化算子改进为社会变异和社会交叉2个算子, 而将具体的优化过程交给遗传算法本身的启发过程, 降低服务提供商之间的沟通成本.2种新的社会进化算子定义, 如定义7和定义8所述.社会变异使用有利于社会进化的基因代替原基因.
算法3:社会变异算法
输入:根据概率选出的要变异的基因组SC, 候选服务集SWS
输出:社会变异后的新基因组
步骤:
1.确定需要变异基因的位置
2. FOR基因组中的每个服务SWi∈SC DO
3. M←max (cost (SWi, prev)+cost (SWi, next))//用M标记变异基因的位置
4. END FOR
5.在候选服务集合中找出新基因
6. FOR候选服务集中的每个服务SWj∈SWS DO
7. new←min (cost (SWj, prev)+ cost (SWj, next)) //与相邻服务沟通成本最小的基因为新基因
8. END FOR
9. SWM←new //用新基因替换原基因
社会交叉通过计算父代个体以及每个服务与其相邻服务的沟通成本, 并沿最小沟通成本的方向进行交叉进化.
算法4:社会交叉算法
输入:第一个父个体par1;第二个父个体par2
输出:社会交叉后产生的新个体offSpring
步骤:
1. offSpring.set(0, par1.(0)) //首先设置子个体的第一个基因为par1的第一个基因
2.FOR i= 1 to基因长度N //逐个选择基因
3. 根据公式(2) 计算选择par1的第i个基因为子基因的概率pi
4. ran←random() //产生(0, 1) 的随机数
5. IF ran pi < THEN
6. offSpring.set(i, par1.(i) //设置par1的第i个基因为子基因
7. ELSE
8. offSpring.set(i, par2.(i)) //否则设置par2的第i个基因为子基因
9. END IF
10. END FOR
3 仿真结果与分析 3.1 实验数据的选择和仿真数据的生成 3.1.1 实验参数设置由于当前缺乏服务数量较大并且有事件日志和评价的数据集合, 为了验证本项目的算法在海量O2O服务环境中的执行效果, 本文采用QWS数据集[18]作为实验数据集, 通过取中后线性插值的方法, 对真实数据集进行扩展来构造仿真数据集.仿真数据集保留了真实数据的线性分布特征, 同时扩展了数据量.
QWS数据集是一类有确定QoS指标的网络服务数据集, 其中的大多数网络服务来源于网络上的公开资源如UDDI和搜索引擎等.本文采用的QWS公共数据集由365个服务源提供2 507条服务信息, 每个服务有9个QoS指标, 这些QoS指标全部经过商用工具验证, 验证时长为3 d, 周期为10 min.通过仿真的方法由2 507条服务扩展生成了10 000~800 000的数据集, 仿真的数据内容是服务的QoS指标.仿真数据描述如下.
1) 服务数据的生成方式:基于QWS数据集, 利用文献[19]中多个次优服务协作能够提供优质服务的思想, 将协同服务视作新服务来扩大数据集.具体算法是服务类别和服务名按平均分布扩展, QoS指标取中后线性插值;QoS指标数量:9个(响应时间, 可获取性, 吞吐量, 成功率, 可靠性, 一致性, 最佳体验, 引用率以及延迟);服务数量:10 000, 20 000, 50 000, 100 000, 200 000, 400 000, 800 000.
2) 事件日志的生成方式:利用已有的QoS指标和业务流程模型, 按交易次数随机选择若干服务提供商进行合作.若合作满足QoS约束将被记录进日志, 如不满足约束则会被放弃;交易次数:200, 600, 1 000, 2 000, 4 000, 8 000, 10 000, 40 000;交易评价分值:1~10(随机分配);评价次数:20~500(随机分配).
实验中使用的遗传算法参数设置如下.
GA算法:种群个数:153个, 判断收敛的代数:6代, 基因长度:10, 最大循环次数(代数):1 000代, 变异率:0.2, 社会变异率:0.5.
NSGA-Ⅱ算法:基本参数设置:同GA, 优先级比较策略:先比较Skyline级别, 再比较拥挤距离最后比较适应性.
NSGA-Ⅲ算法:基本参数设置:同GA, 根据数据规模设置种群规模;当种群个数为153时, 参照点设为3个;种群个数为415时, 参照点设为5个, 通过求解N元一次方程计算超平面截距.
3.1.2 模拟数据集的T检验结果将QWS数据集的原始数据与仿真生成的80万数据集2组数据集, 利用SPSS Statistics进行平均值等同性T检验, 结果如表 1所示.
| 表 1 QWS模拟数据集T检验结果 Table 1 T test result on QWS simulation data set |
根据表 1, 从QWS数据集的9个QoS指标进行的2组数据的T检验结果中的显著性(双尾)指标, 可以看出所有数据维度的显著性均大于0.5, 其中V2、V3、V4、V5等4项维度的显著性均大于0.8.根据T检验的结果, 可以认为仿真生成的数据集相对原始的数据集是符合原有分布特征, 并具备较强的相关性.采用QWS仿真数据集进行优化算法的研究符合显著性检测的要求.
3.2 实验结果以下实验结果, 如无特别说明, 均是在20万数据集上执行30次以后的平均值.
3.2.1 服务过滤方法的实验结果服务过滤阶段的有效性有2个方面的内容, 一是减少服务的数量, 服务组合优化阶段的服务数量应该被显著减少;二是尽量保留优秀的服务, 也就是说, 过滤前和过滤后, 服务组合的QoS值应该变化不大.为了说明本文算法在以上2个方面的有效性, 使用多目标遗传算法NSGA-Ⅱ来比较过滤前、后QoS指标的变化, 如图 4所示, 图中q为各类QoS指标, 无量纲;r为基于社会关系扩展的Skyline过滤(social-relation expanded Skyline filtration, SESF)前、后的QoS百分比.

|
图 4 基于社会关系扩展的过滤前、后的QoS指标对比 Fig. 4 Comparison of QoS before and after social-relation expanded Skyline filtration |
从图 4可以看出, 过滤算法造成的QoS损失在5%左右, 而社会关系过滤在2%左右.这表明, 过滤算法提升执行效率的同时, 造成了整体性能的损失, QoS的损失是由于过滤阶段造成的, 原因在于部分服务被过滤掉, 解空间从全解空间变为部分解空间.在增加了社会扩展方法后, 部分优质的服务重新加入解空间, 从而提升了3%左右的QoS.
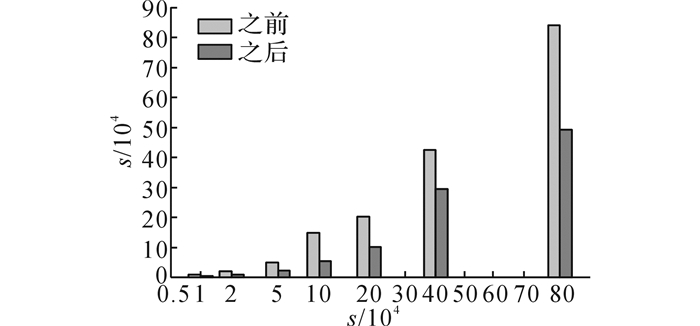
过滤前、后的数据量对比如图 5所示, 图中s为服务的数量.通过对7种数据集比较可以看出, 随着数据量的增加, 过滤方法始终能够过滤掉50%左右的服务, 原因在于社会关系扩展方法是线性的, 服务数量的增加也意味着合作伙伴数量的增加和社会关系网络的扩展.
|
图 5 基于社会关系扩展的过滤前、后的筛选数据量比较 Fig. 5 Comparison of filtration data amount before and after social-relation expanded Skyline filtration |
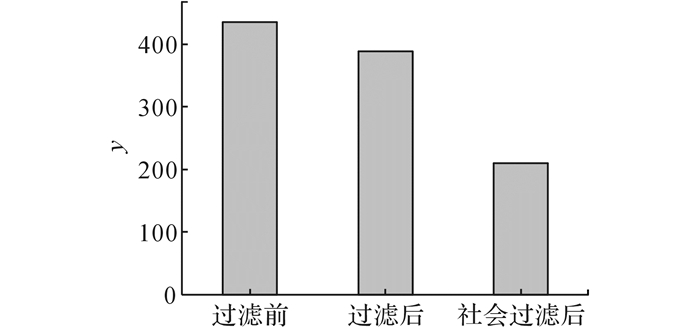
图 6和图 7是NSGA-Ⅱ算法的执行结果.图中y为收敛代数, 无量纲.图 6显示收敛代数从400代下降到200代左右, 原因是过滤算法过滤了解空间中大约50%的不利服务, 并且社会关系扩展保留了很多优秀的服务, 降低了收敛代数, 提升了算法的效率.图 7中的t为执行时间.图 7表明过滤算法也在一定程度上降低了执行时间, 通过过滤掉50%左右的服务数量, 将算法的执行时间降低了50%.与有过滤的过滤算法相比, 社会扩展的过滤算法由于社会关系扩展增加了额外的计算时间, 在时间性能上与普通过滤差别不明显.
|
图 6 NSGA-Ⅱ算法在SESF过滤前、后的收敛代数比较 Fig. 6 Comparison of NSGA-Ⅱ algorithm's convergence generations before and after SESF |

|
图 7 NSGA-Ⅱ算法在SESF过滤前、后的执行时间比较 Fig. 7 Comparison of NSGA-Ⅱ algorithm's execution time before and after SESF |
为了评估解的收敛性, 采用Deb等[17]提出的收敛性指标(convergence metric), 该指标定义如下.
令P*=(p1, p2, …p|p*|)为理想Pareto前沿面上均匀分布的Pareto最优解集合, A=(a1, a2, …, a|A|)是通过EMO算法得到的近似Pareto最优解集.对于集合A中的每个解, 可以通过下式得到该解距离P*的最小归一化欧式距离:
| $ {d_1} = \mathop {{\rm{min}}}\limits_{j = 1}^{|{P^*}|} \sqrt {\sum\limits_{m = 1}^k {{{\left( {\frac{{{f_m}({a_i}) - {f_m}({p_j})}}{{f_{_m}^{max} - f_{_m}^{min}}}} \right)}^2}} } . $ | (4) |
式中:fmmax和fmmin是参考集合P*中第m个目标函数的最大值和最小值.收敛性度量值被定义为集合A中所有点的归一化距离的平均值, 如下式所示:
| $ C\left( A \right) = \frac{1}{{|A|}}\sum\limits_{i = 1}^{|A|} {{d_i}} . $ | (5) |
采用文献[20]的盒图来分析文中6种算法独立运行30次的结果,可以得到解收敛性的统计特性.盒子的上、下2条线分别表示样本的上、下4分位数, 盒子中间的水平线为样本的中位数, 盒子的上、下虚线表示样本的其余部分.样本最大值为虚线顶端, 样本最小值为虚线底端, 盒子的切口为样本的置信区间.
本文采用传统GA算法、NSGA-Ⅱ、NSGA-Ⅲ算法、有社会扩展的GA、有社会扩展的NSGA-Ⅱ、和有社会扩展的NSGA-Ⅲ, 比较6种算法的收敛性, 根据30次独立运行得出的收敛性指标的统计盒图如图 8所示.

|
图 8 30次独立运行得出的6种算法收敛性指标的统计盒图 Fig. 8 Convergence metric box plots of six algorithms based on thirty independent runs |
从图 8可以看出, 对于GA、NSGAⅡ、NSGAⅢ、增加社会进化的3种算法在同一数据集上运行30次的结果中, NSGAⅡ相比其他算法表现得最好;对比其他算法, NSGAⅢ的解集更加分散;对比没有社会因子的算法, 增加社会进化因子后的算法收敛性均有10%左右的性能提升.
根据实验结果, 可以看出增加社会关系因子后, 由于算法倾向于社会进化的方向, 提高了算法的收敛性, 而其中表现最好的是NSGAⅡ算法, 表明在引进社会关系因子后, 以解稀疏度进行多目标优化的方式稍优于进行超空间均匀分布的方式.
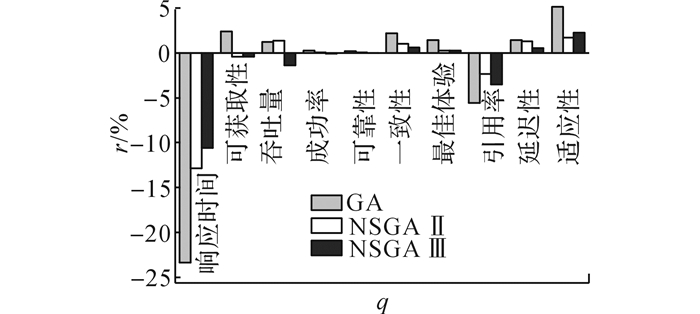
3.2.3 优化过程的QoS比较本文对提出的2种进化算子进行评估.社会进化算子的目的是在可接受的QoS损失下, 优化服务提供商之间的协作效率, 所以从QoS和沟通成本2方面来验证新的算子. QoS和适应度在社会关系算子增加前后的变化如图 9所示.如果仅从服务质量优化的角度来看, NSGA-Ⅱ和NSGA-Ⅲ表现出更好的性能.
|
图 9 增加社会进化算子后3种算法(GA、NSGAⅡ、NSGAⅢ)的QoS对比 Fig. 9 QoS comparison after social revolution operators added on three algorithms: GA, NSGAⅡ and NSGAⅢ |
相比不使用社会关系算子, 使用社会关系算子后, 一些QoS指标有轻微的降低, 平均在5%左右, 只有响应时间是13%的降幅.对于最重要的评价指标, 使用社会关系算子后, 适应度有2%~5%的提升.由于使用了服务过滤和新的进化算子, 基于社会关系的进化算法在提高协作效率的同时, 并没有恶化原算法的整体性能, 相反有一定程度的增强.
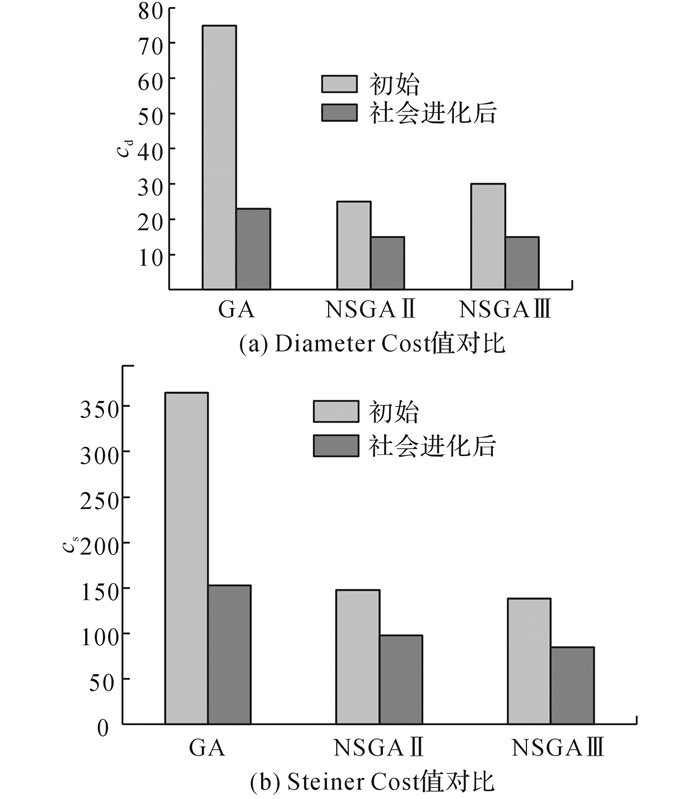
3.2.4 协作效率的比较协作效率能够通过服务提供商之间的沟通成本来衡量.根据文献[19], 使用Diameter Cost和Steiner Cost来比较沟通成本, 加入社会进化算子后3种算法的沟通成本对比, 如图 10所示, 图 10(a)中cd为Diameter Cost值, 图 10(b)中cs为Steiner Cost值.可以看出, 加入社会关系算子后沟通成本指标值降低了50%左右, 社会关系算子在降低沟通成本方面的作用明显.
|
图 10 加入社会进化算子前、后3种算法的沟通成本对比 Fig. 10 Comparison of communication costs among three algorithms before and after adding social revolution operators |
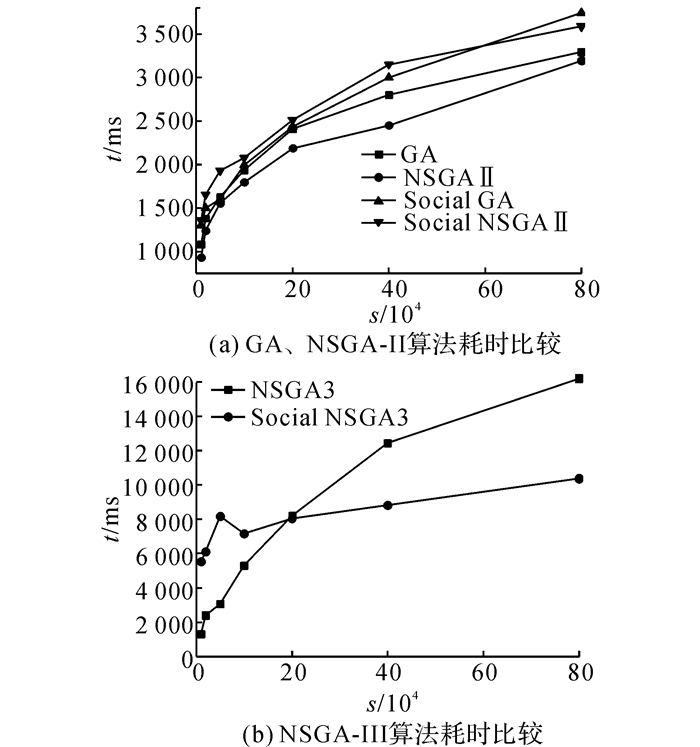
综合比较6种算法在独立运行30次以后的平均耗时情况, 可以分析6种算法对海量数据容量的响应情况, 以上实验均在Intel i7处理器2.9 GHz, 16 GB内存的PC上运行.实验运行结果如图 11所示, 图(a)是GA和NSGA-Ⅱ算法的耗时比较.
|
图 11 3种算法在加入社会进化算子前、后耗时比较 Fig. 11 Comparison of time cost before and after adding social revolution operators on three algorithms |
从图中可以看出, 加入社会进化算子后算法在运行时间上没有太大优势, 主要原因是在服务组合优化阶段, 新的社会进化算子增加了额外的计算时间, 特别是NSGA-Ⅲ较适合高维多目标优化, 部分操作计算耗时过多.但是随着数据量的增加, 耗时的增长率相对较慢, 在图 11(b)中表现更为明显.实验结果表明, 提出的算法更适于海量的网络环境.
4 结语本文讨论了面向海量O2O服务组合的优化问题.在给定QoS需求和业务流程的情况下, 提出了一种新的算法应用在QoS感知的海量O2O服务环境中, 综合考虑线上服务组合的算法执行效率和线下服务提供商之间的协作效率对服务质量的影响.利用线下服务提供商之间的合作历史, 建立其社会关系网络模型.将服务过滤阶段加入到传统的线上服务组合过程中, 在该阶段提出一种基于社会关系扩展的Skyline过滤方法, 通过快速减少服务数量来提高算法收敛速率, 同时在QoS感知情况下, 优质的服务被保留.在服务组合优化阶段, 提出社会交叉和社会变异这2种新的遗传算子, 在QoS感知情况下优化线下服务提供商之间的沟通成本, 以提高其协作效率.在3种遗传算法(传统的GA算法、NSGA-Ⅱ和NSGA-Ⅲ)上进行仿真实验, 实验结果表明, 该方法在海量O2O服务的环境中, 对整体服务组合质量影响较小的情况下, 提高了线上服务组合的算法执行效率, 以及线下服务提供商之间的协作效率.
未来的工作主要是进一步改进海量环境中现有算法的执行效率, 将算法移植到分布式环境中.由于数据集的选择对服务组合影响较大, 需要在不同以及更多的数据集上验证基于社会关系的方法正确性, 同时会考虑数据的可信度, 进行信任加强方法的研究.
| [1] | FANG Q, PENG X, LIU Q, et al. A global QoS optimizing web services selection algorithm based on MOACO for dynamic web service composition[C] // International Forum on Information Technology and Applications. Chengdu: IEEE, 2009:37-42. |
| [2] | DENG S, HUANG L, XU G. Social network-based service recommendation with trust enhancement[J]. Expert Systems with Applications, 2014, 41(18): 8075–8084. DOI:10.1016/j.eswa.2014.07.012 |
| [3] | SUI X, CHEN Z, MA J. Location sensitive friend recommendation in social network[C] // 2015 Asia-Pacific Web Conference. Guangzhou: Springer, 2015: 316-327. |
| [4] | LI M, XIANG Y, ZHANG B, et al. A trust evaluation scheme for complex links in a social network: a link strength perspective[J]. Applied Intelligence, 2016, 44(4): 969–987. DOI:10.1007/s10489-015-0734-2 |
| [5] | BLAKE M B, NOWLAN M F. A web service recommender system using enhanced syntactical matching[C]//2007 IEEE International Conference on Web Services. Salt Lake City: IEEE, 2007: 575-582. |
| [6] | WANG S, HUANG L, HSU C H, et al. Collaboration reputation for trustworthy Web service selection in social networks[J]. Journal of Computer and System Sciences, 2016, 82(1): 130–143. DOI:10.1016/j.jcss.2015.06.009 |
| [7] | LOUATI A, EL-HADDAD J, PINSON S. A distributed decision making and propagation approach for trust-based service discovery in social networks[C] // 2014 Joint International Conference on Group Decision and Negotiation. Toulouse: Springer, 2014: 262-269. |
| [8] | LAPPAS T, LIU K, TERZI E. Finding a team of experts in social networks[C] // Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris: ACM, 2009: 467-476. |
| [9] | JUANG M C, HUANG C C, HUANG J L. Efficient algorithms for team formation with a leader in social networks[J]. The Journal of Supercomputing, 2013, 66(2): 721–737. DOI:10.1007/s11227-013-0907-x |
| [10] | JIANG W, HU S, LEE D, et al. Continuous query for QoS-aware automatic service composition[C] // 2012 IEEE 19th International Conference on Web Services. Honolulu: IEEE, 2012: 50-57. |
| [11] | YU Y, CHEN J, LIN S, et al. A dynamic qos-aware logistics service composition algorithm based on social network[J]. IEEE Transactions on Emerging Topics in Computing, 2014, 2(4): 399–410. DOI:10.1109/TETC.2014.2316524 |
| [12] | ZHENG Z, MA H, LYU M R, et al. Wsrec: a collaborative filtering based web service recommender system[C] // 2009 IEEE International Conference on Web Services. Los Angeles: IEEE, 2009: 437-444. |
| [13] | ALRIFAI M, SKOUTAS D, RISSE T. Selecting skyline services for QoS-based web service composition[C] // Proceedings of the 19th International Conference on World Wide Web. Raleigh: ACM, 2010: 11-20. |
| [14] | BRAHMI Z, GAMMOUDI M M. QoS-aware automatic web service composition based on cooperative agents[C] // 2013 IEEE 22nd International Workshop on Enabling Technologies: Infrastructure for Collaborative Enterprises. Tunisia: IEEE, 2013: 27-32. |
| [15] | SHAO L, ZHANG J, WEI Y, et al. Personalized qos prediction forweb services via collaborative filtering[C] // 2007 IEEE International Conference on Web Services. Salt Lake City: IEEE, 2007: 439-446. |
| [16] | KUTER U, GOLBECK J. Semantic web service composition in social environments[M]. Berlin Heidelberg: Springer, 2009. |
| [17] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. DOI:10.1109/4235.996017 |
| [18] | AL-MASRI E, MAHMOUD Q H. The qws dataset[EB/OL]. [2013-03-12]. http://www.uoguelph.ca~qmahmoud/qws/indexhtml, 2008. |
| [19] | CHARD K, BUBENDORFER K, CATON S, et al. Social cloud computing: A vision for socially motivated resource sharing[J]. IEEE Transactions on Services Computing, 2012, 5(4): 551–563. DOI:10.1109/TSC.2011.39 |
| [20] |
公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J].
软件学报, 2009, 20(2): 271–289.
GONG Mao-guo, JIAO Li-cheng, YANG Dong-dong, et al. Evolutionary multi-objective optimization algorithms[J]. Journal of Software, 2009, 20(2): 271–289. |



