2. 安徽大学 计算机科学与技术学院, 安徽 合肥 230601;
3. 安徽大学 信息保障技术协同创新中心, 安徽 合肥 230601;
4. 安徽大学 计算机教学部, 安徽 合肥 230601
2. School of Computer Science and Technology, Anhui University, Hefei 230601, China;
3. Institute of Bio-inspired Intelligence and Knowledge Mining, Anhui University, Hefei 230601, China;
4. Computer Studies Department, Anhui University, Hefei 230601, China
流程相似性度量一直是工作流研究中的一个主要方向[1].业务流程作为企业的三要素之一, 在实际的业务流程管理中, 需要对2个业务流程进行比较, 以求得不同流程之间的相似性[2].在互联网大时代背景下, 如中国移动这类办公自动化的大集团公司, 其业务流程非常繁杂众多, 流程数量动辄数以万计, 且具有较大的冗余性[3].高效的流程相似性算法可以为基数庞大的流程比较、索引和搜索提供有效的保证[4].除此之外, 流程相似性计算同样被广泛地运用于组织合并、用户需求变更、模型仓库管理等多个领域[5].
主流的流程相似性算法一般基于以下3个方面展开:1) 任务标签、事件或其他建模元素; 2) 模型拓扑结构; 3) 过程模型的执行语义.殷明等[3]针对流程相似性研究, 总结提出了流程相似性算法应该满足的五大基本性质, 即:顺序结构漂移不变性、互斥结构漂移不变性、跨度负相关性、非替代无关递减性和循环序列长度负相关性.近年来, 流程相似性算法层出不穷, 经典的流程相似度算法有:TAR算法[6]、CF算法[7]、BP算法[8]、PTS算法[9], 还包括一些改进算法, 如:TAR++算法[10]和PTS++算法[5],但是仍然存在一些未能解决的问题, 具体表现为对一些常见模型的相似性度量与预期值不符、算法复杂度太高不适用于实际生产或不满足上述五大基本性质等.
本文基于标签Petri网对业务流程建模, 引入BP算法中行为轮廓[11]和变迁关系的概念, 定义5类变迁之间的基本关系, 对已有行为轮廓进行扩充.对传统的工作流网进行改进, 提出一种不同流程中映射变迁的关系相似性度量(transition relation similarity, TRS)方法, 从映射变迁结构相似性的角度, 给出计算流程相似度的新思路.
1 Petri网模型介绍 1.1 Petri网基本元素Petri网为简单的过程模型, 如图 1所示, 由下列几类基本元素构成:

|
图 1 简单的Petri网模型 Fig. 1 Simple Petri net model |
1) 库所(Place)圆形节点, 以○表示;
2) 变迁(Transition)方形节点, 以□表示;
3) 有向弧(Directed arc)库所和变迁之间的有向弧, 以有向线段“→”表示;
4) 令牌(Token)动态存在于库所中, 以“·”表示.
Petri网是一个三元组,N=(P, T, F),P={p1, p2, p3, …, pm}是库所的有限集合, T={t1, t2, t3, …, tn}是变迁的有限集合, 有P∪T≠∅且P∩T=∅.F代表流关系, 即有向弧的有限集合, F=(T×P)∪(P×T)={e1, e2, e3, …, ek}, “×”代表笛卡尔乘积.Petri网集合P∪T中的任意一个库所pi或变迁ti均为Petri网中的一个节点; Petri网集合F中的任意元素即为一条有向弧称为Petri网的边, 相同类型的2个节点之间不允许存在相连接的边.
1.2 Petri网基本概念前集与后集:对于一个Petri网结构N=(P, T, F), 设x∈(P∪T), 称∙x为x的前集或输入集, x∙为x的后集或输出集.特别地,当x∈T时, 称∙x为x的输入库所集合, 称x∙为x的输出库所集合[12].
顺序(Order)关系:对于一个Petri网结构N=(P, T, F), 设t1∈T, t2∈T, t2只能在t1发生后才有可能发生, t1和t2的发生存在直接的因果关系.顺序关系是不对称的, 且存在传递性, 如图 2所示.

|
图 2 Petri网的顺序(Order)关系示意图 Fig. 2 Diagram of relation Order in Petri net |
并发(And)关系:对于一个Petri网结构N=(P, T, F), 设t1∈T, t2∈T, t1和t2是相互独立的, 即(∙t1∪t1∙)∩(∙t2∪t2∙)=∅, t1和t2的发生不存在因果关系.并发关系是对称的, 且没有传递性.
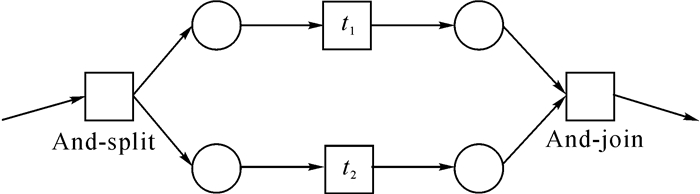
设And-split结构与And-join结构分别对应于一个变迁有多个输出库所和一个变迁有多个输入库所, 如图 3所示.And-split变迁表示通过该变迁使得多个任务可以同时被执行, 而And-join变迁只有当前任务都完成才能触发.
|
图 3 Petri网的并发(And)关系示意图 Fig. 3 Diagram of relation And in Petri net |
冲突(Xor)关系:对于一个Petri网结构N=(P, T, F), 设t1∈T, t2∈T, t1和t2的发生存在着冲突, 当其中某一个发生时另一个一定不会发生.冲突关系是对称的, 即“t1和t2冲突”与“t2和t1冲突”是等价的.
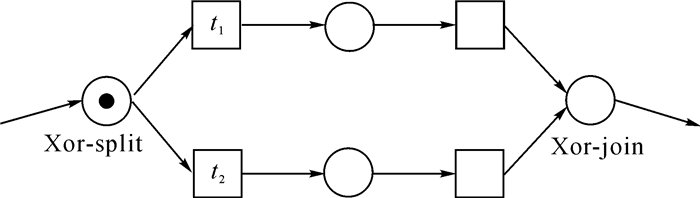
设Xor-split结构与Xor-join结构分别对应于一个库所有多条以其为始点的边和以其为终点的边, 如图 4所示, 库所中令牌用于对接下来发生的变迁进行选择.
|
图 4 Petri网的冲突(Xor)关系示意图 Fig. 4 Diagram of relation Xorin Petri net |
基于Petri网模型对系统流程进行建模, 用变迁表示资源的消耗、使用及系统状态产生的变化等.用库所表示系统中的资源, 如状态、条件、媒介等[13].库所可以容纳一定数量的令牌, 用来表示资源的数量, 若一个变迁的输入库所集合中存在足够数量的令牌使其使能, 则该变迁可以被触发(firing), 当变迁触发后会消耗一定数量的令牌, 并在其输出库所中生成新的令牌[14].
基于上述关系将系统流程构建成一个Petri网结构NPetri=(P, T, F), 若NPetri满足以下条件:
1)NPetri只存在一个起始库所s, 即∙s=∅;
2)NPetri只存在一个终止库所e, 即e∙=∅;
3) 若增加一个变迁t连接库所s和e, 即t∙={e}且∙t={s}.
Petri网NPetri=(P, T, F)∪{(e, s)}是强连通的, 如图 5所示.在此基础上引入标签的概念, 给变迁分配任务名称, 使得变迁跟实际流程中的任务对应起来, 构成工作流网, 其中M0为初始标识, 即初始的资源分布, M0:P→{0, 1, 2, …}.因此, 给定六元组工作流网为NW=(P, T, F, M0, s, e).

|
图 5 强连通Petri网示意图 Fig. 5 Diagram of strongly connected Petri net |
定义1 节点度数:对工作流网NW中的某一个节点v, 与之连接的边称为该节点的边.从该节点流出的边称为输出边, 简称出边, 记输出边的集合为Eo, |Eo|称为该节点的出度; 流向该节点的边称为输入边, 简称入边, 记输入边的集合为Ei, |Ei|称为该节点的入度, 显然, s的入度和e的出度均为0.出度与入度之和|Eo|+|Ei|, 称为节点的度数, 简称度, 记作Deg (v).
定义2 变迁可达关系:对工作流网NW中任意2个变迁t1∈T, tn∈T.若NW中存在一个由有限数量的边和节点组成的点边交替可执行序列Strace=(t1, …, ei, pj, ei+1, tk, …, tn), 使节点t1和tn分别位于序列的始点和终点, i, j, k∈N+, 则称t1和tn可达, 记作t1Rtn, R表示变迁可达关系, Strace称为t1和tn的可达路径.
在序列Strace中, 如果同一条边不出现2次, 则称此路径为简单可达路径, 同一节点不出现2次的简单可达路径称为基本可达路径.如果路径的始点t1和终点tn相重合, 即t1=tn, 则称此路径为可达回路, 没有相同边的可达回路称为简单可达回路, 通过各节点不超过一次的简单可达回路称为基本可达回路.Strace的长度|Strace|等于序列中所有边的数量和.
2 变迁相似性度量在普遍的业务流程管理中, 企业组织内的各个行为活动并不单独地属于某个特定的流程, 而是根据不同的工作需要, 某些行为活动会在不同的业务流程中多次出现, 配合其他的行为活动从而达到完成特定业务目标的作用[15].本文利用Petri网对业务流程进行建模研究, 变迁元素代表了实际业务流程中的行为活动, 库所代表了相关行为的条件或状态.在对不同的工作流网模型进行元素映射时, 主要通过对变迁与库所节点展开.
需要说明的是, 本文旨在提出一种流程模型相似度的度量方法, 只关注流程模型定义本身,因此, 对不同业务流程实例及其运行情况或令牌分布, 不予讨论.同时, 由于本文选取的角度是基于变迁映射的, 库所映射不在讨论范围之内.下面将从变迁映射展开对变迁关系相似度度量的具体研究.
2.1 变迁映射前文已经提及变迁元素对应的行为活动可以出现在不同的业务流程中, 在实际应用中, 一般可以通过行为活动的标识, 对不同流程中的相同行为进行识别和对应.本文在建模过程中将基于行为活动标识的互异性这一特性, 同样用行为的标识代替对变迁节点的标识.
通常情况下, 变迁的标识一般为一个字符串, 因此判断2个标识是否表示为同一个任务, 可以结合上下文的执行语义或行为相似度, 同时, 也可以通过判断2个字符串是否相等进行确定[15].本文的研究是在变迁映射的基础上展开的, 旨在研究2个不同业务模型的相似度.同时, 上文提到行为相似度与下文将提出的变迁关系相似度是2个完全不同的概念.前者用于对2个变迁进行映射, 后者指的是在良好的变迁映射的前提下, 求得不同工作流网模型中的同一个变迁节点在整体结构上的相似度.
2.2 变迁关系在工作流网的基础上, 任意2个变迁在整个工作流网的结构上存在着不同的关系, 为了便于表述, 在进行变迁关系相似性度量之前, 本文首先对变迁之间的关系进行如下定义.
定义3 强线性(Strong linear)关系:设流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e), 存在tm∈T, tn∈T且tm≠tn, tm和tn不在同一条可达回路上, 若∃p∈P使∃((tm, p)∈F∧(p, tn)∈F)或∃((tn, p)∈F∧(p, tm)∈F), 则称tm和tn存在强线性关系, 记为→或←, tm和tn的关系记为→(tm, tn)或←(tm, tn), 如图 6所示.显然, 由Petri网的规则可知, 强线性关系是反对称的且不满足传递性.将满足强线性关系的变迁对构成的集合称为强线性关系集合, 记作→A, 可知, →A⊆(T×T).

|
图 6 变迁tm和tn满足强线性关系→(tm, tn)示意图 Fig. 6 Diagram of strong linear relation →(tm, tn)between tm and tn |
定义4 弱线性(Weak linear)关系:设流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e), 存在不同变迁tm∈T, tn∈T且tm≠tn, tm和tn不在同一条可达回路上.若tm和tn不满足强线性关系, 但存在一个有限序列Strace, (|Strace| > 2), 使得tm至tn可达, 则称tm和tn存在弱线性关系, 关系符号记为~≻或≺~, tm和tn的关系记为~≻(tm, tn)或≺~(tm, tn)(箭头方向代表tm至tn路径Strace中起始点指向终点的方向), 如图 7所示.显然, 弱线性关系是反对称的且满足传递性, 将满足弱线性关系的变迁对构成的集合称为弱线性关系集合, 记作~≻A, 可知, ~≻A⊆(T×T).

|
图 7 变迁tm和tn满足弱线性关系~≻(tm, tn)示意图 Fig. 7 Diagram of weak linear relation ~≻(tm, tn)between tm and tn |
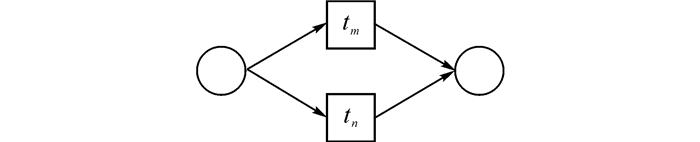
定义5 互斥(Mutex)关系:设流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e), 存在tm∈T, tn∈T且tm≠tn, tm和tn之间不存在任何可达路径, 同时tm和tn满足冲突关系, 则称tm和tn存在互斥关系, 关系符号记作+, tm和tn关系记为+(tm, tn), 如图 8所示.显然, 互斥关系是对称的且满足传递性, 即若存在+(tm, tn), 则一定存在+(tn, tm).特别地, 如果tm=tn, 则有+(tm, tm), 即变迁自身满足互斥关系.将满足互斥关系的变迁对构成的集合称为互斥关系集合, 记作+A, 可知, +A⊆(T×T).
|
图 8 变迁tm和tn满足互斥关系+(tm, tn)示意图 Fig. 8 Diagram of mutex relation +(tm, tn) between tm and tn |
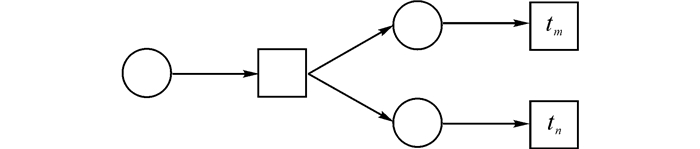
定义6 并行(Parallel)关系:设流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e), 存在tm∈T, tn∈T且tm≠tn, tm和tn不在同一条可达回路上, 同时, tm和tn满足并发关系.则称tm和tn之间存在并行关系, 关系符号记作‖, tm和tn关系记为‖(tm, tn), 如图 9所示.显然, 并行关系是对称的且满足传递性, 即若存在‖(tm, tn), 则一定存在‖(tn, tm).将满足互斥关系的变迁对构成的集合称为并行关系集合, 记作‖A, 可知, ‖A⊆(T×T).
|
图 9 变迁tm和tn满足并行关系‖(tm, tn)示意图 Fig. 9 Diagram of parallel relation ‖(tm, tn) betweentm and tn |
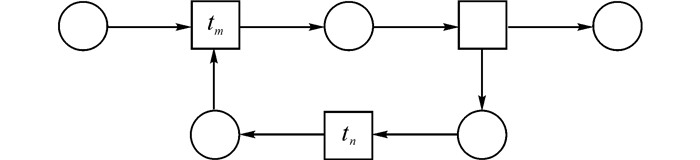
定义7 循环(Circulation)关系:设流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e), 存在tm∈T, tn∈T且tm≠tn, tm和tn之间在同一条可达回路上,则称tm和tn之间存在循环关系, 关系符号记作
|
图 10 变迁tm和tn满足循环关系↔(tm, tn)示意图 Fig. 10 Diagram of circulation relation ↔(tm, tn) between tm and tn |
基于上述5类变迁关系定义, 在前述六元组工作流网中, 加入一个关系类集合r, 构成本文所提出的七元组工作流网:N′W=(P, T, F, M0, r, s, e), 其中r={→, ~≻, +, ‖,
通过5类变迁之间的基本关系定义, 本文提出一种变迁关系相似性度量方法(TRS).上述部分介绍了行为轮廓提供一组行为的抽象, 其意义在于不用具体考虑行为的细节而仅仅关注行为在整体结构中的关系和可能的执行路径.
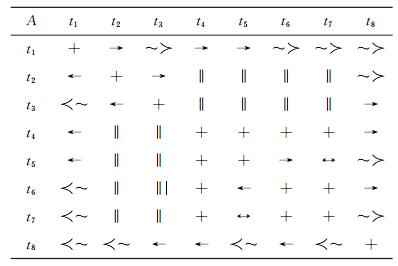
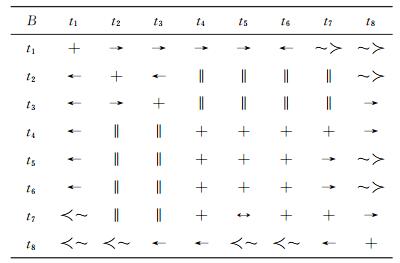
利用变迁之间的关系可以将行为轮廓通过变迁关系矩阵的形式表达出来, 称为变迁关系矩阵, 流程A和B的变迁关系矩阵如表 1和2所示.
| 表 1 流程A的变迁关系矩阵 Table 1 Transition relation matrix of process A |
| 表 2 流程B的变迁关系矩阵 Table 2 Transition relation matrix of process B |
由变迁关系的定义可知, 变迁关系矩阵是一个对称矩阵, 满足对称阵的基本性质.通过变迁关系矩阵可以很直观地得到各个变迁之间的关系, 同时在此基础上, 也便于研究映射变迁之间相似度问题.
为了更好地表述相关概念, 进行如下定义.
定义8 变迁关联集合:设流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e), 其行为轮廓为BA={→A, ~≻A, +A, ‖A,
| $ \begin{array}{l} \to A\left( {{t_m}} \right) = \{ < {t_m}, {t_n} >, < {t_n}, {t_m} > |{t_n} \in {T_A} \wedge ( \to ({t_m}, \\ {t_n}) \in \to A \vee \to \left( {{t_n}, {t_m}} \right) \in \to A)\} \sim \succ A\left( {{t_m}} \right) = \{ < {t_m}, \\ {t_n} >, < {t_n}, {t_m} > |{t_n} \in {T_A} \wedge \sim \succ \left( {{t_m}, {t_n}} \right) \in \to A \vee \sim \succ \\ \left( {{t_n}, {t_m}} \right) \in \sim \succ A\} + A\left( {{t_m}} \right) = \{ < {t_m}, {t_n} > |{t_n} \in {T_A} \wedge \\ \left( { + \left( {{t_m}, {t_n}} \right) \in + A \vee + \left( {{t_n}, {t_m}} \right) \in + A} \right)\} \parallel A\left( {{t_m}} \right) = \\ \{ < {t_m}, {t_n} > |{t_n} \in {T_A} \wedge (\parallel \left( {{t_m}, {t_n}} \right) \in \parallel A \vee \parallel \left( {{t_n}, {t_m}} \right) \in \\ \parallel A)\} \leftrightarrow A\left( {{t_m}} \right) = \{ < {t_m}, {t_n} > |{t_n} \in {T_A} \wedge ( \leftrightarrow ({t_m}, {t_n}) \in \\ \leftrightarrow A \vee \leftrightarrow ({t_n}, {t_m}) \in \leftrightarrow A)\} \end{array} $ |
令CA(tm)={→A(tm), ~≻A(tm), +A(tm), ‖A(tm), A(tm)}, 则称CA(tm)为变迁tm的关联集合.特别地, 变迁关联集合CA(tm)的模|CA(tm)|计算如下:
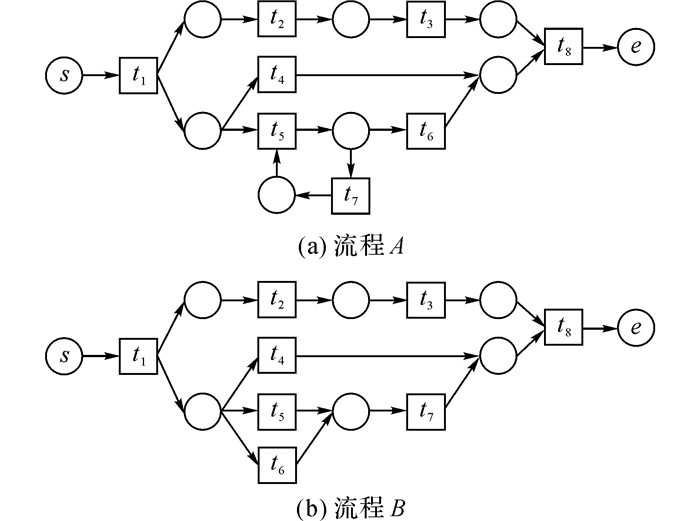
如图 11所示, 流程A的工作流网为NW(A)=(PA, TA, F, M0, s, e).其中, TA={t1, t2, t3, t4, t5, t6, t7}, 取t5∈TA, 由流程A关系矩阵易得:
| $ \begin{array}{*{20}{l}} { \to A\left( {{t_5}} \right) = \{ < {t_5},{t_6} > , < {t_1},{t_5} > \} ,\left| { \to A\left( {{t_5}} \right)} \right| = 2;}\\ { \sim \succ A\left( {{t_5}} \right) = \{ < {t_5},{t_8} > \} ,\left| { \sim \succ A\left( {{t_5}} \right)} \right| = 1;}\\ { + A\left( {{t_5}} \right) = \{ < {t_5},{t_4} > , < {t_5},{t_5} > \} ,\left| { + A\left( {{t_5}} \right)} \right| = 2;}\\ {\parallel A\left( {{t_5}} \right) = \{ < {t_5},{t_2} > , < {t_5},{t_3} > \} ,\parallel \left| {A\left( {{t_5}} \right)} \right| = 2;}\\ { \leftrightarrow A\left( {{t_5}} \right) = \{ < {t_5},{t_7} > \} ,\left| { \leftrightarrow A\left( {{t_5}} \right)} \right| = 1.} \end{array} $ |
|
图 11 流程A和流程B的工作流网示意图 Fig. 11 Workflow net diagram of process A and process B |
则
不失一般性, 可以得到以下推论:
对任意工作流网NW=(P, T, F, M0, r, s, e), 对∀t∈T, 有|C(t)|=|T|.
定义9 映射变迁关系相似度:设流程A、B的工作流网分别为NW(A)=(PA, TA, F, M0, s, e), NW(B)=(PB, TB, F, M0, r, s, e).
若∃tm:tm∈TA∧tm∈TB, 令:fInter(tm)A, B=CA(tm)∩CB(tm), 指tm在流程A、B中, 基于本文所提出的上述5类变迁关系, 求得的变迁关系交集, 其中,
| $ \begin{array}{*{20}{l}} {{C_A}\left( {{t_m}} \right) \cap {C_B}\left( {{t_m}} \right) = \left\{ { \to A\left( {{t_m}} \right) \cap \to B\left( {{t_m}} \right),} \right.}\\ { \sim \succ \left\{ {A\left( {{t_m}} \right) \cap \sim \succ B\left( {{t_m}} \right), + A\left( {{t_m}} \right) \cap + B\left( {{t_m}} \right),} \right.}\\ {\left. {\parallel A\left( {{t_m}} \right) \cap \parallel B\left( {{t_m}} \right), \leftrightarrow A\left( {{t_m}} \right) \cap \leftrightarrow B\left( {{t_m}} \right)} \right\}.} \end{array} $ |
令:fUnion(tm)A, B=CA(tm)∪CB(tm), 指tm在流程A、B中, 基于本文所提出的上述5类变迁关系, 求得的变迁关系并集, 同理,
| $ \begin{array}{*{20}{l}} {{C_A}\left( {{t_m}} \right) \cup {C_B}\left( {{t_m}} \right) = \left\{ { \to A\left( {{t_m}} \right) \cup \to B\left( {{t_m}} \right),} \right.}\\ { \sim \succ \left\{ {A\left( {{t_m}} \right) \cup \sim \succ B\left( {{t_m}} \right), + A\left( {{t_m}} \right) \cup + B\left( {{t_m}} \right),} \right.}\\ {\left. {\parallel A\left( {{t_m}} \right) \cup \parallel B\left( {{t_m}} \right), \leftrightarrow A\left( {{t_m}} \right) \cup \leftrightarrow B\left( {{t_m}} \right)} \right\}.} \end{array} $ |
由此定义映射变迁关系相似度计算方法如下:
| $ \begin{array}{*{20}{l}} {|{f_{{\rm{Inter}}}}{{\left( {{t_m}} \right)}_{A,B}}\left| = \right| \to A\left( {{t_m}} \right) \cap \to B\left( {{t_m}} \right)| + }\\ {| \sim \succ A\left( {{t_m}} \right) \cap \sim \succ B\left( {{t_m}} \right)\left| + \right| + A\left( {{t_m}} \right) \cap + }\\ {B\left( {{t_m}} \right)\left| { + \parallel } \right|A\left( {{t_m}} \right) \cap \parallel B\left( {{t_m}} \right)\left| + \right| \leftrightarrow A\left( {{t_m}} \right) \cap }\\ { \leftrightarrow B\left( {{t_m}} \right)\parallel = \sum {\left| {\Re A\left( {{t_m}} \right) \cap \Re B\left( {{t_m}} \right)} \right|} ,\left( {\Re \in r} \right);}\\ {|{f_{{\rm{Union}}}}{{\left( {{t_m}} \right)}_{A,B}}\left| = \right| \to A\left( {{t_m}} \right) \cup \to B\left( {{t_m}} \right)| + }\\ {| \sim \succ A\left( {{t_m}} \right) \cup \sim \succ B\left( {{t_m}} \right)\left| + \right| + A\left( {{t_m}} \right) \cup + B\left( {{t_m}} \right)| + }\\ {\parallel |A\left( {{t_m}} \right) \cup \parallel B\left( {{t_m}} \right)| + | \leftrightarrow A\left( {{t_m}} \right) \cup \leftrightarrow B\left( {{t_m}} \right)\parallel = }\\ {\sum {\left| {\Re A\left( {{t_m}} \right) \cup \Re B\left( {{t_m}} \right)} \right|} ,\left( {\Re \in r} \right).} \end{array} $ |
如图 11所示的流程A、B, 取t5∈TA, TB, 可得
| $ \begin{array}{l} {f_{{\rm{Sim}}}}{\left( {{t_5}} \right)_{A, B}} = \\ \left( {1 + 1 + 2 + 2 + 0} \right)/\left( {3 + 1 + 3 + 2 + 1} \right) = 0.6. \end{array} $ |
因此, 可以计算出流程A和B所有公共变迁节点的关系相似度.把每一个变迁及其关系相似度关联起来, 记作fSim(tm)-tm, 如上述变迁节点t5, 可改记为0.6-t5.
特别地, 在流程A和B中, 当∃tn:(tn∈TA∧tn∉TB)∨(tn∉TA∧tn∈TB), fSim(tn)=0.
3 实验与分析基于上文对映射变迁关系相似度的介绍及研究, 从映射变迁关系相似度和流程相似度计算2个方面进行具体的分析.需要说明的是, 工作流网模型是基于Petri网建立的, 属于静态模型, 下文提到的插入和删除操作只是用于对整体结构的模拟分析, 与Petri网的静态特性并没有矛盾.
3.1 变迁关系相似度实例对于2个不同的工作流网模型, 流程C和D, NW(C)=(PC, TC, F, M0, r, s, e), NW(D)=(PD, TD, F, M0, r, s, e).其变迁集合的关系可分为两大类(TC, TD均不为空集):1)TC∩TD=∅;2)TC∩TD≠∅.第一种情况下, C和D中不存在相同的变迁节点, 此时讨论变迁的关系相似度没有意义.下文只针对第二种情况, 即C和D中含有相同的变迁节点, 进行相关实验分析.
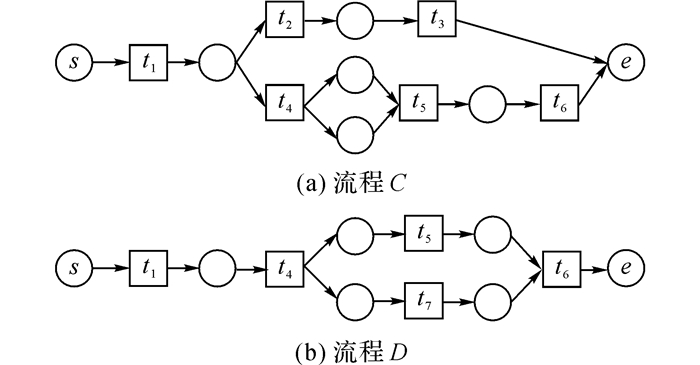
如图 12中(a)和(b)所示, TC={t1, t2, t3, t4, t5, t6}, TD={t1, t4, t5, t6, t7}.
|
图 12 流程C和D初始状态图 Fig. 12 Initial states of process C and process D |
令T′=TC∩TD={t1, t4, t5, t6}, 则对∨tm∈T′均可得fSim(tm)C, D, 计算结果如下:
| $ {f_{{\rm{Sim}}}}{\left( {{t_1}} \right)_{C, D}} = 0.57, {\rm{ }}{f_{{\rm{Sim}}}}{\left( {{t_4}} \right)_{C, D}} = 0.38, $ |
| $ {f_{{\rm{Sim}}}}{\left( {{t_5}} \right)_{C, D}} = 0.38, {\rm{ }}{f_{{\rm{Sim}}}}{\left( {{t_6}} \right)_{C, D}} = 0.22. $ |
由fSim(tm)C, D=|fInter(tm)C, D|/|fUnion(tm)C, D|, (m≤{|TA|, |TB|})可知, 在流程C和D中插入或删除变迁, 将会提高或降低映射变迁的关系相似度.鉴于实际工作流程会比较复杂, 为了便于叙述和讨论, 本实验选取的2个示例均不含重名变迁.
3.1.1 删除变迁对流程删除变迁, 需要存在变迁t, 且满足以下约束性条件:
1)TC∩TD≠∅, 且t∈(TC∪TD)-(TC∩TD);
2) Deg(t)=2;
3) 删除变迁t后, 对于∀tm∈TC∩TD, 有|(fInter(tm)C, D)′|=|fInter(tm)C, D|.
在包含变迁t的工作流网模型中删除变迁t, 并对其结构作出相应的调整, 会提高C和D中相同变迁节点的关系相似度.其中, 第二个条件是为了在执行删除操作后保持工作流模型的整体结构没有大的改变, 另外2个条件则是2个流程相似度提高的充分条件.
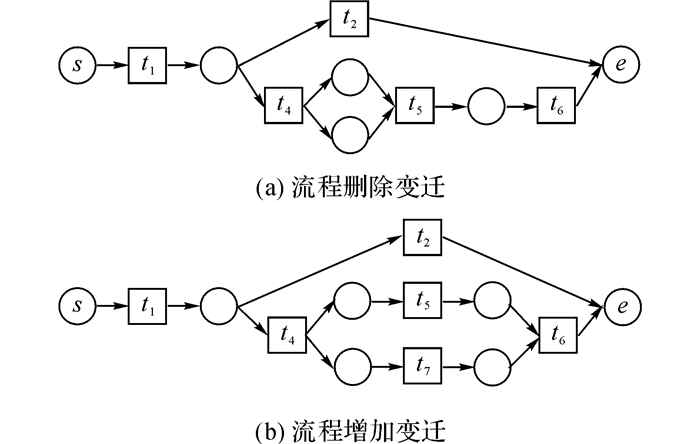
对于删除变迁操作, 如图 13(a)所示, 在流程C中删除变迁t3, 对其工作流网结构作出相应的调整.相应地, 可以得到fSim′(t1)C, D=0.67, fSim′(t4)C, D=0.43, fSim′(t5)C, D=0.43, fSim′(t6)C, D=0.25.比较fSim(tm)C, D和fSim′(tm)C, D可知,删除变迁操作使映射变迁的关系相似度有了较大的提高.
|
图 13 流程C删除变迁和流程D增加变迁状态转换 Fig. 13 State transition of process C by deleting transition and process D by adding transition |
类同于变迁, 在工作流网模型中, 对流程插入变迁, 需要存在变迁t, 且满足以下约束性条件:
1)TC∩TD≠∅, 且t∈[(TC∪TD)-(TC∩TD)];
2) Deg (t)=2;
3) 插入变迁t后, 对于∀tm∈TC∩TD, 有|(fInter(tm)C, D)″|>|fInter(tm)C, D|.
在不包含变迁t的工作流网模型中插入变迁t, 使得Deg(t)=2.同时, 在保持整体结构的前提下调整模型, 会提高流程C和D中相同变迁节点的相似度.
对于插入变迁操作, 如图 13(b)所示, 在流程D中插入变迁t2, 对其工作流网结构作出相应的调整,得到T″=T∪t2, 此时流程C和流程D的相同变迁节点的关系相似度如下:
| $ \begin{array}{l} {f_{{\rm{Sim}}}}^{\prime \prime }{\left( {{t_1}} \right)_{C, D}} = 0.71, {f_{{\rm{Sim}}}}^{\prime \prime }{\left( {{t_2}} \right)_{C, D}} = 0.71, \\ {\rm{ }}{f_{{\rm{Sim}}}}^{\prime \prime }{\left( {{t_4}} \right)_{C, D}} = 0.50, {f_{Sim}}^{\prime \prime }{\left( {{t_5}} \right)_{C, D}} = 0.50, {\rm{ }}\\ {f_{Sim}}^{\prime \prime }{\left( {{t_6}} \right)_{C, D}} = 0.33. \end{array} $ |
比较fSim(tm)C, D和fSim″(tm)C, D可知,插入变迁操作同样使映射变迁的关系相似度有了较大的提高.
3.2 仿真实验对变迁数量较多和结构比较复杂的工作流程模型, 选取如表 3所示的数据集进行仿真实验(2个模型为一组, 为了便于描述分别记作A′、B′).
| 表 3 仿真实验数据集 Table 3 Simulation experimental data sets |
对每一组模型执行有限次数满足上述条件的变迁删除操作, 删除变迁数量(number of deleting transitions, NDT)记为NDelete, 显然NDelete≤(|TA′∪TB′|-|TA′∩TB′|).相同变迁集合记作T′=TA′∩TB′, T′中元素的平均关系相似度(average relation similarity, ARS)记为
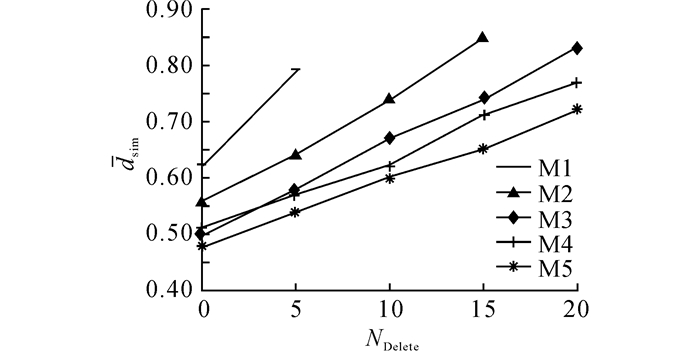
|
图 14 不同数据集下平均相似度随删除变迁数量的变化曲线 Fig. 14 Change curve of average similarity vary with numbers of deleting transition under different data sets |
类同于删除变迁, 对上述的数据集进行仿真实验, 对每一组模型执行满足上述条件的变迁插入操作有限次数, 插入变迁数量(number of inserting transitions, NIT)记为NInsert, 显然, NInsert≤(|TA′∪TB′|-|TA′∩TB′|).得到NInsert和
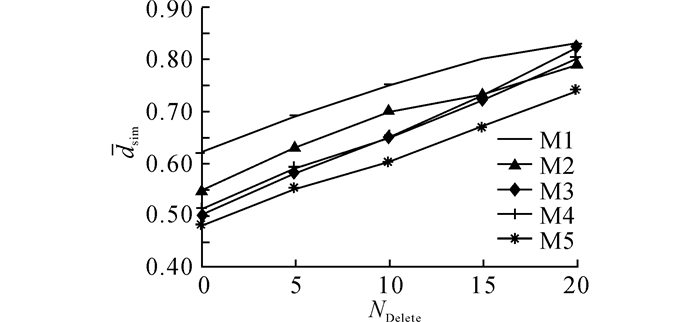
|
图 15 不同数据集下平均相似度随插入变迁数量的变化曲线 Fig. 15 Change curve of average similarity vary with numbers of adding transition under different data sets |
本文研究的是2个不同工作流网模型中相同变迁的关系相似性度量, 目的在于对流程整体相似性的度量.基于映射变迁的关系相似度, 可求得图 12中流程C和D初始的流程相似度, 计算公式为
| $ \begin{array}{l} {f_{Sim}}\left( {C, D} \right) = \\ \frac{{\sum (|{f_{{\rm{Inter}}}}{{\left( {{t_m}} \right)}_{C, D}}\left| / \right|{f_{{\rm{Union}}}}{{\left( {{t_m}} \right)}_{C, D}}|)}}{{\sum {f_{{\rm{Inter}}}}{{\left( {{t_m}} \right)}_{C, D}}\left| / \right|{f_{{\rm{Union}}}}{{\left( {{t_m}} \right)}_{C, D}})\left| { + (} \right|{T_C} \cup {T_D}\left| - \right|{T_C} \cap {T_D}|)}} \approx 0.34. \end{array} $ |
其中, tm∈TC∩TD,
通过如图 13所示的删除变迁和插入变迁操作, 同理可求得fSim′(C, D)≈0.47, fSim″(C, D)≈0.58.同初始的流程相似性比较可知, 约束性的增删变迁能较为显著地提高流程的相似性:
| $ \begin{array}{l} {f_{{\rm{Sim}}}}\prime C,D)/{f_{{\rm{Sim}}}}\left( {C,D} \right) = 138\% ,\\ {f_{{\rm{Sim}}}}^{\prime \prime }\left( {C,D} \right)/{f_{{\rm{Sim}}}}\left( {C,D} \right) = 171\% . \end{array} $ |
需要说明的是, 上述流程相似度计算方法是针对不含重名变迁的工作流网模型, 但在实际业务流程中, 工作流程含有重名任务的情况是常见的, 所以需要对流程模型进行消除重名变迁的处理.为了方便表述, 本文实验选取的都是不含重名变迁的模型.
为了进一步验证本文提出方法的有效性, 将约束性的增删变迁操作应用于其他的流程相似性算法, 如表 4所示.
| 表 4 不同流程相似性算法计算结果比较 Table 4 Comparison of calculation results by different process similarity algorithms |
针对不同的方法, 流程相似性的初始值会有所不同.本文的TRS方法是基于映射变迁关系, 立足于比较流程整体结构的相似度, 因此其流程相似性初始值较低于其他方法.在不同的流程相似性算法中, 约束性增删变迁操作均可提高流程相似性.然而, 通过比较约束性增删变迁操作对各算法流程相似性的提高程度可知, TRS方法具有更为显著的提高效果.
4 结语本文的主要贡献可以归纳为如下3点:
1) 基于标签Petri网对业务流程建模, 将传统的工作流网模型进行了变迁之间5类基本关系的定义, 构造了新的工作流网.对比已有的业务流程模型进行了结构描述功能方面的完善, 更加全面地刻画了流程行为之间的关系.
2) 在变迁映射的基础上, 提出了2个不同工作流网模型之间映射变迁关系相似性的概念, 反映了相同变迁节点在整体结构上的相似度, 并通过实验对映射变迁关系相似度进行了相关的分析.
3) 提出了一种基于映射变迁关系相似度的流程相似性度量方法提供了一种研究流程相似性的新方法.未来拟考虑从如下几个方面进行研究:
1) 在保证变迁关系相似度准确计算的前提下, 研究出一种对含有重名变迁的工作流网模型进行消除重名的处理算法.
2) 目前存在的流程相似性算法很多, 如CF、BP、PTS、TAR算法等, 在今后的研究中, 需要将本文提出的这种流程相似性度量方法与这些经典算法的效率和准确率进行多方面比较, 进一步降低算法的复杂度.
3) 本文提出的映射变迁的关系相似性度量方法还可以进一步被改进以提高效率和准确度,如何优化本文所提方法或如何找出一种更为高效的算法是未来的主要研究工作.
| [1] | LU Y, YU H, MING Z, et al. A similarity measurement based on structure of business process[C]// 20th IEEE International Conference on Computer Supported Cooperative Work in Design (CSCWD 2016). Nanchang: IEEE, 2016: 498-503. |
| [2] | MONTANI S, LEONARDI G, QUAGLINI S, et al. A knowledge-intensive approach to process similarity calculation[J]. Expert Systems with Applications, 2015, 42(9): 4207–4215. DOI:10.1016/j.eswa.2015.01.027 |
| [3] |
殷明, 闻立杰, 王建民, 等. 基于变迁紧邻关系重要性的流程相似性算法[J].
计算机集成制造系统, 2015, 21(2): 344–358.
YIN Ming, WEN Li-jie, WANG Jian-min, et al. Process similarity algorithm based on importance of transition adjacent relation[J]. Computer Integrated Manufacturing Systems, 2015, 21(2): 344–358. |
| [4] | SONG M, SUN Z, ZHANG Y, et al. Synthesis of 3D models by Petri net[J]. Journal of Zhejiang University SCIENCE C, 2013, 14(7): 521–529. DOI:10.1631/jzus.CIDE1305 |
| [5] |
董子禾, 闻立杰, 黄浩未, 等. 基于触发序列集合的过程模型行为相似性算法[J].
软件学报, 2015, 26(3): 449–459.
DONG Zi-he, WEN Li-jie, HUANG Hao-wei, et al. Behavioral similarity algorithm for process models based on firing sequence collection[J]. Journal of Software, 2015, 26(3): 449–459. |
| [6] | ZHA H, WANG J, WEN L, et al. A workflow net similarity measure based on transition adjacency relations[J]. Computers in Industry, 2010, 61(5): 463–471. DOI:10.1016/j.compind.2010.01.001 |
| [7] | DONGEN B F, MENDLING J, DER A W. Structural patterns for soundness of business process models[C]// 10th IEEE International Conference on Enterprise Distributed Object Computing. Hong Kong: IEEE, 2006: 116-128. |
| [8] | WEIDLICH M, ELLIGER F, WESKE M. Generalised computation of behavioural profiles based on petri-net unfoldings[C] // International Workshop on Web Services and Formal Methods. Berlin Heidelberg: Springer, 2010: 101-115. |
| [9] | WANG J, HE T, WEN L, et al. A behavioral similarity measure between labeled Petri nets based on principal transition sequences[C] // OTM Confederated International Conferences on the Move to Meaningful Internet Systems. Berlin: Springer, 2010: 394-401. |
| [10] | WANG S, YIN M, WANG Z, et al. TAR++: a new process model similarity algorithm based on the importance of TARs[C] // Asia-Pacific Conference on Business Process Management. Busan: Springer, 2015:98-112. |
| [11] | KUNZE M, WEIDLICH M, WESKE M. Behavioral similarity: a proper metric[C]. International Conference on Business Process Management. France: Springer, 2011: 166-181. |
| [12] |
丁力, 董利达, 朴云. 基于Petri网的并发编程死锁预防策略[J].
浙江大学学报:理学版, 2012, 39(1): 43–49.
DING Li, DONG Li-da, PIAO Yun. Deadlock prevention policy of concurrent programming based on Petri net[J]. Journal of Zhejiang University: Science Edition, 2012, 39(1): 43–49. |
| [13] | MA Z, LI Z, GIUA A. Design of optimal Petri net controllers for disjunctive generalized mutual exclusion constraints[J]. IEEE Transactions on Automatic Control, 2015, 60(7): 1774–1785. DOI:10.1109/TAC.2015.2389313 |
| [14] | QIAO Y, WU N Q, ZHOU M C. A Petri net-based novel scheduling approach and its cycle time analysis for dual-arm cluster tools with wafer revisiting[J]. IEEE Transactions on Semiconductor manufacturing, 2013, 26(1): 100–110. DOI:10.1109/TSM.2012.2222945 |
| [15] |
曹斌, 王佳星, 范菁, 等. 基于Petri网的流程间元素映射方法[J].
软件学报, 2015, 26(3): 474–490.
CAO Bin, WANG Jia-xing, FAN Jing, et al. Mapping elements between process models based on Petri net[J]. Journal of Software, 2015, 26(3): 474–490. |