随着信息技术的快速发展, 各种面向服务的应用大量涌现.服务组合的执行通常需要面临多个并发用户的动态环境, 这种环境常常会导致服务质量(quality of service, QoS)的降级甚至服务过载.因此, 考虑面向多用户的服务组合将更具现实意义.
由于面向多用户服务组合场景下的搜索空间更大(通常是面向单一需求的m倍, m为需求的数量), 很难找到多项式时间复杂度的算法[1-2].为了解决此问题, 可以将面向多用户的服务组合分解成2个问题[3]:一是如何对服务组合问题进行约束分解来降低服务组合的复杂度;二是在功能属性相同的服务类中, 如何根据多用户请求为每个用户选择合适的服务, 并且尽可能地避免服务过载.针对第一个问题, 可以采用基于服务类(功能属性相同的服务)的约束分解方法将面向多用户服务组合问题分解成基于局部约束的服务选择问题[3].针对第二个问题, 可以归类为人员分配或最优分配等匹配问题[4-5].本文重点是解决第二个问题, 将该问题称为面向多用户请求的服务选择问题.
在面向多用户请求的服务选择中, 如果一个服务同时被多个用户选择, 在短期内其实际性能表现可能远远低于用户的预期.造成该现象的原因主要包括2个方面.一方面没有合理分配服务资源, 例如:基于服务质量加权和的服务选择方法通常会选择加权和最大的服务, 如果在面向多用户请求的服务选择中仍然采用该方法, 那么就会导致很多个用户同时选择QoS较优的服务, 而很少人选取QoS较差的服务.另一方面, 服务QoS的不确定性(本文统称为稳定性)也是影响用户体验的重要因素, 如果用户选择了稳定性较差的服务, 那么该服务的QoS会随着网络环境[6]或者用户请求数量的变化而产生较大的波动, 从而导致服务QoS低于用户的期望值.因此, 面向多用户请求的服务选择存在巨大挑战.
针对以上问题, 本文提出一个较完整的解决方法:1) 提出一种基于离散系数的服务稳定性过滤方法, 该方法通过计算与更新服务QoS的离散系数动态地过滤掉稳定性较低的服务, 提高候选服务的稳定性;2) 提出一种双向服务选择方法, 确保每个QoS需求能够选择合适的服务, 同时每个服务也能匹配到合适的QoS需求.
1 相关工作在众多具有相同功能属性但非功能属性却不同的候选服务中选择满足用户需求的服务是服务计算领域研究的热点问题之一.目前关于服务选择这一主题, 已经有了较多的研究成果.
1.1 面向单用户请求的服务选择面向单用户的服务选择的方法大都是关注QoS优化, 从而提高用户的满意度.Ran[7]提出将用户的功能需求和QoS引入到服务发现中后, 基于QoS服务选择研究取得了长足的进展.Zeng等[8]提出将服务的多维QoS和用户偏好考虑到服务的组合中, 为服务组合提出了一个中间件平台, 并给出一种QoS的计算方法, 为用户选择QoS加权和最大的服务.刘书雷等[9]把服务动态选择全局最优化问题转化为一个带QoS约束的多目标服务组合优化问题, 利用多目标遗传算法的智能优化原理, 同时优化多个目标函数, 产生一组满足约束条件的Pareto优化服务聚合流程集.Victor等[10]为提高服务选择效率提出一种基于动态QoS网络(一种随着时间变化的动态贝叶斯网络)的服务选择方法.李玲等[11]全面考量QoS属性对服务最优选择的影响, 提出一种基于模糊层次分析法的多维QoS局部最优服务选择模型, 提高了聚合服务的成功率.QoS感知的服务组合优化问题已被证明是NP难问题[12].相对而言, 具有多项式时间复杂度的启发式算法由于其具有良好的计算性能和扩展性, 近年来得到广泛关注和研究[13-15].然而, 面对实际应用需求, 现有的启发式算法仍有较大提升空间, 针对这一问题, 白琳等[16]提出了基于服务功能规约的服务选择方法.该方法首先对用户需求进行合并形成大粒度服务需求, 然后针对大粒度服务需求进行服务组合.以上服务选择方法主要针对单个服务请求场景, 这些方法不能很好地解决面向多用户服务选择中存在的问题.
1.2 面向多用户请求的服务选择为了应对面向多用户服务选择中出现的问题, Dou等[17]针对多个用户同时请求同一种服务的情形, 提出了一种多属性决策方法.Liang等[4]提出了一种面向多用户的Web服务选择框架, 该框架首先预测缺失的QoS值, 然后用Kuhn-Munkres(KM)匹配算法完成服务选择.Kang等[5]根据服务需求与服务之间的匹配度, 利用欧氏距离及整数规划建立全局优化服务选择模型(global optimization service selection model, GOSSMR), 并结合实际情况提出通用可行的解决多请求的全局优化服务选择算法.Wang等[18]首先利用区间数帮助用户更好地表达QoS需求, 然后通过服务聚类减小候选服务规模, 最后通过服务调度达到负载均衡.Xu等[19]针对大规模用户需求的服务选择问题, 提出了一种面向服务的人工蜂群算法.以上服务选择方法没有考虑服务的稳定性, 如果某用户选择了一个稳定性较差的服务, 那么该服务很有可能无法满足用户的实际需求.
1.3 服务稳定性研究王尚广等[20]提出了一种基于云模型的不确定性QoS感知的Skyline服务选择方法.该方法首先通过云模型计算服务的稳定性, 然后采用Skyline计算提取Web服务中的Skyline服务, 剔除冗余服务, 最后采用混合整数规划在Skyline服务中进行服务选择.朱勇等[21]针对不同负载状态下服务QoS会发生变化的情况, 提出了一种基于负载等级的多维QoS模型, 该模型能够表示和评估不同负载等级下的服务QoS.Sun等[22]首先利用信息熵和方差过滤掉可靠性较低的服务, 然后设计了一个可靠性函数, 能快速选出最可靠的组合服务.Soumi等[23]提出了一种随机服务组合模型来解决服务QoS在实际部署中发生变化的问题.以上方法对服务稳定性进行了大量的研究并提出了一系列的解决方案, 能够有效地提高用户的体验.以上这些方法没有充分考虑服务的实时稳定性问题, 例如:以前不稳定的服务通过维护和性能改善变得稳定了, 而以前稳定的服务可能由于用户请求数量急剧增多而变得不稳定了.因此, 在进行服务选择时,需要考虑服务的动态稳定性问题, 并且尽量避免过多的计算开销.
2 相关概念介绍定义1 服务稳定性:将服务QoS随着外部条件(如:网络环境、用户请求数量等)变化产生的波动情况称为服务的稳定性.服务QoS波动越小, 服务稳定性越好;服务QoS波动越大, 服务的稳定性越差.
欧式距离能够衡量多维空间中两点之间的真实距离, 在众多领域中得到广泛应用.基于此, 本文在欧式距离中加上用户的权重(对每个QoS属性的偏好)来定义服务与需求之间的距离.
定义2 需求与服务之间的距离:在面向多用户请求的服务选择中, 现有m个需求(r1, r2, …, rm)以及n个服务(s1, s2, …sn).其中, 用户需求rj(1≤j≤m)用r维QoS向量表示, rj=(rj(q1), …, rj(qr)).服务si(1≤i≤n)用一个r维QoS向量表示, si=(si(q1), …, si(qr)).假设用户需求的信息可以提前获取, 则需求rj与服务si之间的距离由下式计算得:
| $ d\left( {{r_j}, {s_i}} \right) = \sqrt {\sum\limits_{k = 1}^r {\left( {{w_{jk}}{{\left( {{r_j}\left( {{v_k}} \right) - {s_i}\left( {{v_k}} \right)} \right)}^2}} \right).} } $ | (1) |
式中:k(1≤k≤r)表示QoS维度, rj(vk)为rj(qk)归一化之后的值, si(vk)为si(qk)归一化之后的值.wjk为需求rj中对第k维QoS的偏好程度, wjk可以由下式计算得出:
| $ {{w}_{jk}}=\text{ }{{{r}_{j}}\left( {{v}_{k}} \right)}/{\sum\limits_{k=1}^{r}{{{r}_{j}}\left( {{v}_{k}} \right)}}\; $ | (2) |
定义3 效用值:表示需求rj选择服务si时所获得的效用, 用uij表示, uij可由如下公式计算得出:
| $ {u_{ij}} = \sum\limits_{k = 1}^r {\left( {{s_i}\left( {{v_k}} \right){w_{jk}}} \right)} . $ | (3) |
定义4 需求-服务关系结点:每个需求-服务关系结点由3个元素构成, 可以用来表示需求与服务之间的关系, 简称关系结点.3个元素分别是:候选服务、效用值以及需求与服务之间距离.例如, 需求rj与服务si之间的关系可以表示为
| $ {\rm{rel}}\left( {{r_j}, {s_i}} \right) = \left( {{s_i}, d\left( {{r_j}, {s_i}} \right), {u_{ij}}} \right). $ |
定义5 偏好服务集合:能够表示同一个需求与所有服务之间关系的集合.例如:需求rj的偏好服务集合由n个需求-服务关系结点构成, 该集合可以表示为
| $ {\rm{srel}} = \left\{ {{\rm{rel}}\left( {{r_j}, {s_1}} \right), {\rm{rel}}\left( {{r_j}, {s_2}} \right)} \right., \ldots, \left. {{\rm{rel}}\left( {{r_j}, {s_n}} \right)} \right\}. $ |
定义6 支配关系:现有2个r维的QoS向量A和B.如果∀k∈[1, r], A(qk)≥B(qk)且∃k∈[1, y], A(qk) > B(qk), 则有A≺B, 称A支配B.即A每一个QoS属性都高于或等于B相应QoS属性且A至少有一个QoS属性高于B的对应QoS属性, 其中A(qk)和B(qk)分别表示A和B的第k维QoS.当支配关系表示服务与服务之间的关系时可以用来剔除那些被其他服务支配的冗余服务, 从而降低服务选择的搜索空间[19, 23].
定义7 服务负载[1]:服务si当前并发处理的用户请求数量称为服务负载, 用lsi表示.一个服务可以承受最大并发请求数量(即最大负载)表示为lsimax, 当并发请求数量超过最大负载时(即服务过载), 服务将拒绝部分服务请求.
3 基于离散系数的双向服务选择方法面向多用户请求的服务选择目标不仅需要为每个用户选择一个合适的服务, 还要较好地规避服务过载问题.为了解决以上问题, 提出一种基于离散系数的双向服务选择方法(dual service selection method based on coefficient of variation, DSS-CV), 该方法主要分为2个阶段:第1阶段提出基于离散系数的服务稳定性过滤方法, 目的是剔除掉稳定性较低的服务, 并减小候选服务的数量;第2阶段提出一种双向服务选择方法, 目的是合理分配用户需求.其中, 第1阶段是为了提高第2阶段服务选择的效率以及服务选择结果的满意率.
3.1 基于离散系数的服务稳定性过滤方法 3.1.1 服务稳定性分析在面向多用户的服务选择中, 除了网络环境等因素会影响服务的QoS, 同一个候选服务同时被多个用户选择也可能导致其服务QoS产生较大波动, 因此考虑服务的稳定性是必要的.首先, 通过一个例子来说明服务的稳定性.如表 1所示为2个服务s1和s2最近5次历史交易过程中响应时间的变化情况, 其中T为服务的响应时间.根据表 1中数据, 可以计算出s1的平均响应时间为17.0 s, s2的平均响应时间为16.8 s, s1的平均响应时间要小于s2的平均响应时间.
| 表 1 服务s1和s2的响应时间对比 Table 1 Comparison of response time for services s1 and s2 |
如果不考虑服务的稳定性选择平均响应时间较好的s2参加服务选择, 那么实际的响应时间很可能偏离预期响应时间, 这样会导致服务的响应时间无法满足用户的需求.此外, 还需要考虑服务的实时稳定性问题.例如, 某购票网站在非节假日时网页响应速度很快, 而节假日时网页响应速度很慢.因此服务的稳定性是动态变化的, 需要根据服务的运行情况不断地计算服务的稳定性.
3.1.2 离散系数计算在概率论与数理统计中, 离散系数(coefficient of variation)是一个统计量, 用来度量一个随机变量的稳定程度.典型的服务QoS属性有响应时间、可靠性、可用性、价格等, 其具体含义见文献[4], 与离散系数之间的关系可以分为相关和不相关.与离散系数大小相关的主要有响应时间、可靠性、可用性等;与离散系数大小不相关主要有价格等.本文主要考虑与离散系数相关的QoS值.离散系数越小,服务稳定性越高;反之,服务稳定性越低.本文将服务QoS的最近N次历史记录作为一组离散的随机变量, 每个候选服务的离散系数值计算如下:
| $ S_k^i = \sqrt {\frac{1}{{N - 1}}\sum\limits_{\alpha = 1}^N {{{\left( {{s_i}\left( {v_k^\alpha } \right) - \overline {E_k^i} } \right)}^2}} }, $ | (4) |
| $ \overline {E_k^i} = \frac{1}{N}\sum\limits_{\alpha = 1}^N {{s_i}\left( {v_k^\alpha } \right)} $ | (5) |
| $ C_k^i = \frac{{S_k^i}}{{\overline {E_k^i} }} \times 100\% . $ | (6) |
式中:Ski为服务si第k维QoS记录的标准差,
由于服务所处环境的动态变化以及服务本身性能的动态变化, 只有计算最近QoS历史记录的离散系数, 才能保证服务的实时稳定性.但是, 在进行服务选择时, 如果每个服务都需要计算最近QoS记录, 那么计算的代价将会很高.为了减小离散系数计算代价, 提出一种离散系数动态更新方法.
将QoS历史记录看作一组随机变量, 假设V为服务si的第k维QoS指标的实际执行记录归一化的结果,
通过计算出初始候选服务的离散系数的数值, 可以得到候选服务离散系数的集合C={C1, …, Ci, …, Cn}, 在离散系数的集合中Ci=C1i, …, Cki, …, Cri为第i个候选服务多维QoS的离散系数值.本文对集合C进行筛选, 选择出稳定性较高(即离散系数较小)的候选服务.
本文采用Skyline计算方法[20, 24]对候选服务进行筛选, 若一次求得的Skyline服务集合中服务数量太少, 则可在剩余服务中多次进行Skyline计算.如图 1所示为二维坐标2次Skyline计算示例, a表示服务的可用性.
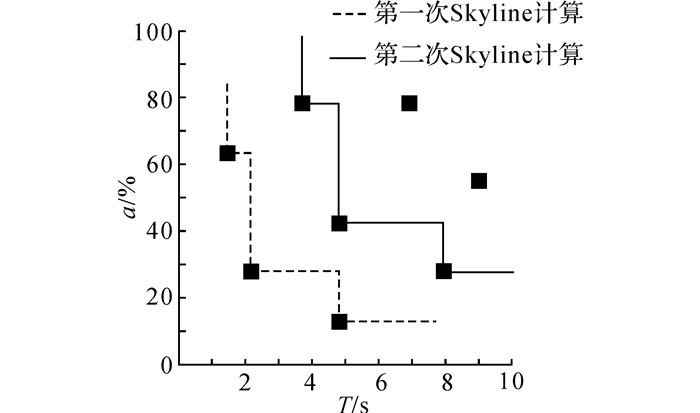
|
图 1 二维空间中的Skyline计算示例 Fig. 1 Example of skyline-based computing intwo-dimensional space |
通过离散系数计算可以将离散系数较大服务过滤掉, 这样不仅能够得到稳定性较高的候选服务, 同时还能大大减小候选服务的数量, 有利于提高服务选择的效率.
特别地, 对于QoS处于整体上升趋势的服务, 可将其分为2类进行讨论.第一类:上升趋势较小, 离散系数较低;第二类:上升趋势较大, 离散系数较高.对于前者, 该类服务稳定性较好, 与本文描述的高稳定服务一致, 这类服务在服务过滤时保留.对于后者, 该类服务稳定性较低.虽然该类服务能够满足一些用户的需求, 并且有时会比期望的QoS更好, 但是在其波动较大的情况下, 这类服务将被过滤.但事实上, 对于每个QoS属性而言, 都有一个允许的上界或下界, 即使服务的QoS波动再大, 上升趋势明显, 但是最终QoS值都会趋于稳定, 因此, 在其趋于稳定后, 本文通过动态更新离散系数, 最终将保留这类服务.
3.2 双向服务选择方法在约束分解已经完成的基础上, 针对同一个服务类(功能属性相同的服务), 当有n个服务处于可选择状态, 有m个用户正在请求该类服务, 需要为每个用户需求选择一个合适的服务, 同时较好地避免服务过载.延迟接受算法能够在双边匹配问题中使双方受益同时达到最大[25].在面向多用户请求的服务选择问题, 为了能够使需求匹配到较好的服务, 同时使服务能够匹配到合适的需求,本文将延迟接受算法的思想应用到面向多用户的服务选择中.但延迟接受算法无法直接运用到面向多用户请求的服务选择中.一方面, 伴随着互联网的不断普及、信息技术的不断发展、大数据以及云计算技术的飞速发展, 能满足用户功能需求的候选服务数量日益增多, 让用户给出对每个候选服务的偏好程度显然是不现实的.另一方面, 由于服务没有主观能动性, 服务无法判断接收到的需求QoS中哪些更适合自己.本文通过对由用户提议的延迟接受算法进行改进使其能够运用到面向多用户的服务选择中.首选通过服务过滤减小候选服务的数量, 然后根据式(3) 计算需求偏好集合, 效用值uij越大, 需求rj对服务sj越满意.当某一个服务接收到的请求数量大于当前负载lsij时, 服务会根据需求QoS与服务QoS之间的距离, 接受距离前lsij个较小的需求, 拒绝其他需求.
此外, 通过限制算法的最大迭代次数提高服务选择的效率, 在偏好服务集合中, 将这些服务按照效用值从低到高排序, 并按照效用值大小选择d个候选服务参与服务选择, 当需求第d次发出申请时, 默认需求-服务关系结点中d(rj, si)的值为0, 防止需求选择不到服务.
改进后的延迟接受算法称为双向服务选择算法, 算法的流程描述如下.
输入:m个用户需求QoS, n个服务QoS, 阈值d.//d表示每个需求从偏好服务集合中选取的服务数量
输出:服务选择方案.
1) 计算每个需求的偏好服务集合.
2) 对关系结点按照效用值从大到小进行排序.
3) 每个用户需求向产生效用值最高的候选服务发出申请.
4) 判断服务请求数量是否大于当前负载.若接收到的请求数量大于当前负载lsij, 则通过计算收到的需求与服务QoS之间的欧氏距离, 留下lsij个距离较近的请求, 拒绝掉其他请求.
5) 判断每个需求是否选择了服务.若某需求没有选择合适服务, 转步骤3.否则, 转步骤6.
6) 产生一个服务选择方案, 算法结束.
在以上算法中, 2) 计算时间复杂度最高.计算每个需求的偏好服务集合时间复杂度是O(mn), 针对一个需求, 基于效用值大小的排序时间复杂度是O(nlog n), 针对m个需求, 时间复杂度为O(mnlog n).因此2) 的时间复杂度为O(mnlog n).在4) 中,若有需求被某服务拒绝了,那么该需求会向其他候选服务发出请求,直到该需求匹配到候选服务. 6) 中服务选择方案用一个“0-1”矩阵X表示.矩阵X中xij的取值表示服务选择的策略, 当xij=1时, 表示第i个服务被第j个用户需求选择, 当xij=0时, 表示第i个服务没有被第j个用户需求选择.
4 仿真实验对比 4.1 实验配置本次实验的硬件环境的CPU为酷睿i7处理器, 主频为2.5 GH, 内存为8 GB, MatlabR2015a版本.实验中采用2个数据集,通过实验对比来验证本文提出方法的可行性和有效性.
1) 数据集1: WSDream Dataset[26]是现实世界采集的数据集, 包括接近200万条真实世界的QoS调用历史记录值, 每条QoS属性历史记录包含2个QoS属性:响应时间和吞吐量, 通过分布在世界各地的339名用户调用5 825个Web服务得到.该数据集还包括这339名用户及5 825个Web服务的详细信息.用户需求的数据是在一定范围用随机函数生成的.
2) 数据集2:用户需求数据集, 利用随机函数在一定范围内随机生成.
将每个服务QoS初始历史记录设置为20个.并且根据每个服务QoS历史记录计算出每个服务最初的离散系数.实验将进行30次服务选择, 实验结果为30次实验的平均值.Skyline的平均计算次数为n/20, n为候选服务的数量.将双向服务选择算法中阈值d的值设置为5.
4.2 用户满意率比较如果一个用户选择到的服务能够满足自己期望的需求, 那么称用户对该次服务选择结果是满意的;相反地, 如果一个用户选择到的服务无法满足自己期望的需求, 那么称用户对该服务选择结果是不满意的.假设在某时刻有m个并发的用户需求, 最终能够选择满意服务的用户数量m′与总用户需求数量m的比值称为该次服务选择的满意率:
| $ {r_{\rm{s}}} = \frac{{m'}}{m} \times 100\% . $ | (8) |
将DSS-CV方法的满意率与3种典型的面向多用户的服务选择方法GOSSMR[15]、FMA[16]和INSSM[17]进行比较,如图 2所示.用户需求的数量从50增至300, 服务的数量为200, 最终满意率为30次实验的平均值.
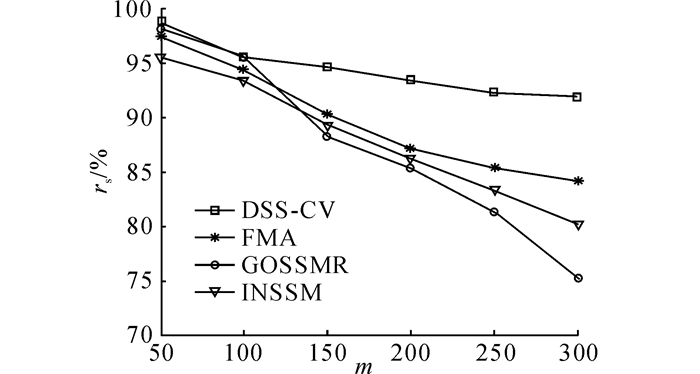
|
图 2 DSS-CV、GOSSMR、FMA和INSSM服务选择方法的满意率对比 Fig. 2 Comparison of satisfaction rate of four service selection methods: DSS-CV, GOSSMR, FMA and INSSM |
从图 2中可以看出, 随着用户需求数量的增多, 4种服务选择方法的满意率都在降低.相对于其他3种方法, 本文提出的DSS-CV方法执行结果的满意率始终处在较高的水平, 这是因为剔除掉了很多稳定性较低的服务, 并且所提出的双向服务选择方法有利于提高用户的满意率.其他3种方法执行结果的满意率随着用户需求的增多, 越来越低.这主要是因为服务QoS在服务选择过程中会随着网络环境、用户需求数量等因素的变化产生较大的波动.基于以上的实验与分析, 可以得出:在实际服务选择过程中, 考虑服务的稳定性并对稳定性较低的服务进行分析处理有利于提高服务选择结果的满意率.
4.3 计算时间对比将DSS-CV方法的计算时间与3种典型的面向多用户的服务选择方法GOSSMR、FMA和INSSM进行比较如图 3所示.服务数量n=100, 用户需求的数量m从50增加到300, TC表示计算时间.
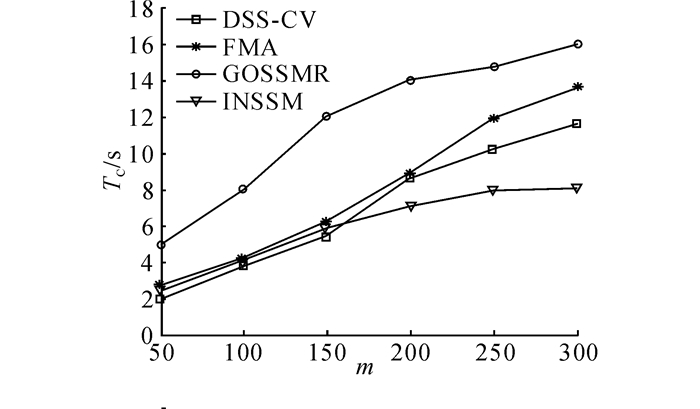
|
图 3 DSS-CV、GOSSMR、FMA和INSSM服务选择方法的计算时间比较 Fig. 3 Comparison of computation time of four service selection methods: DSS-CV, GOSSMR, FMA and INSSM |
从图 3可以看出, 随着服务数量的增多, 4种服务选择方法的执行时间都在增加.其中, GOSSMR方法一直都是耗时最多的, 该方法采用了“0-1”整数规划方法进行服务选择, 基于整数规划的服务选择方法是典型的NP问题, 因此算法时间执行时间很慢;INSSM方法虽然也采用了“0-1”整数规划方法, 但首先对候选服务进行聚类处理, 因此可以大大提高该方法的执行效率;本文提出的DSS-CV方法首先服务进行稳定性过滤, 剔除冗余服务, 能有效地提高了服务选择的效率.虽然随着候选服务数量的增多, INSSM执行时间比DSS-CV方法要低.从图 2可以看出, 相比于INSSM方法, DSS-CV方法可以有效地提高服务选择结果的满意率.
5 结语本文提出了一种基于离散系数的双向服务选择方法(DSS-CV), 利用服务过滤从候选服务中获得稳定性较高的候选服务, 提高了用户对服务结果的满意率和提高服务选择的效率.从服务和用户请求出发提出了一种双向服务选择方法, 保证每个用户需求可以选择一个合适的、稳定性较高的服务, 同时也可以较好地避免服务过载.
在实际应用中, 随着数据维数的增多, Skyline计算容易造成属性灾难问题.本文实验只采用了二维数据, 未来将继续探索新的服务过滤方法,并采用多维数据来提高实验的科学性.本文尚未考虑面向多用户的服务组合情况, 这是下一步的研究方向.
| [1] |
王忠杰, 徐飞, 徐晓飞. 支持大规模个性化功能需求的服务网络构建[J].
软件学报, 2014, 25(6): 1196–1211.
WANG Zhong-jie, XU Fei, XU Xiao-fei. Service network planning method for mass personalized functional requirements[J]. Journal of Software, 2014, 25(6): 1196–1211. |
| [2] | WANG S, WANG Z J. Mining bilateral patterns as priori knowledge for efficient service composition[C] // Proceedings of International Conference on Web Services. San Francisco: IEEE, 2016: 72-79. |
| [3] | JIN H, ZOU H, YANG F C, et al. A hybrid service selection approach for multi-user requests[C] // Proceedings of International Conference on High PERFORMANCE Computing and Communication and International Conference on Embedded Software and Systems. Liverpool: IEEE, 2012: 1142-1149. |
| [4] | LIANG Z J, ZOU H, GUO J, et al. Selecting Web service for multi-user based on multi-QoS prediction[C] // Proceedings of International Conference on Services Computing. California: IEEE, 2013: 551-558. |
| [5] | KANG G S, LIU J X, TANG M D, et al. Web service selection for resolving conflicting service requests[C] // Proceedings of International Conference on Web Services. Washington DC: IEEE, 2011: 387-394. |
| [6] | YANG M K, HU X H. SVM-based efficient QoS-aware runtime adaptation for service oriented systems[C] // Proceedings of International Conference on Web Services. San Francisco: IEEE, 2016: 396-403. |
| [7] | RAN S. A model for Web services discovery with QoS[J]. ACM SIGecom Exchanges, 2003, 4(1): 1–10. DOI:10.1145/844357 |
| [8] | ZENG L, BENATALLAH B, ANNE H H N, et al. QoS-aware middleware for Web services composition[J]. IEEE Transactions on Software Engineering, 2004, 30(5): 311–327. DOI:10.1109/TSE.2004.11 |
| [9] |
刘书雷, 刘云翔, 张帆, 等. 一种服务聚合中QoS全局最优服务动态选择算法[J].
软件学报, 2007, 18(3): 646–656.
LIU Shu-lei, LIU Yun-xiang, ZHANG Fan, et al. A dynamic Web services selection algorithm with QoS global optimal in Web services composition[J]. Journal of Software, 2007, 18(3): 646–656. |
| [10] | VICTOR W C, RAYMOND K W, CHEN F, et al. Service selection based on dynamic QoS networks[C] // Proceedings of International Conference on Services Computing. San Francisco: IEEE, 2016: 105-112. |
| [11] |
李玲, 刘敏, 成国庆. 一种基于FAHP的多维QoS局部最优服务选择模型[J].
计算机学报, 2015, 38(10): 1997–2010.
LI Ling, LIU Min, CHENG Guo-qing. A local optimal model of service selection of muti-QoS based on FAHP[J]. Journal of Software, 2015, 38(10): 1997–2010. DOI:10.11897/SP.J.1016.2015.01997 |
| [12] | CANFORA G, PENTA M D, ESPOSITO R, et al. A framework for QoS-aware binding and re-binding of composite web services[J]. Journal of Systems and Software, 2010, 81(10): 1754–1769. |
| [13] |
温涛, 盛国军, 郭权, 等. 基于改进粒子群算法的Web服务组合[J].
计算机学报, 2013, 36(5): 1031–1046.
WEN Tao, SHENG Guo-jun, GUO Quan, et al. Web service composition based on modified particle swarm optimization[J]. Chinese Journal of Computers, 2013, 36(5): 1031–1046. |
| [14] |
范小芹, 蒋昌俊, 方贤文, 等. 基于离散微粒群算法的动态Web服务选择[J].
计算机研究与发展, 2010, 47(1): 147–156.
FAN Xiao-qin, JIANG Chang-jun, FANG Xian-wen, et al. Dynamic Web service selection based on discrete partice swarm optimization[J]. Journal of Computer Research and Development, 2010, 47(1): 147–156. |
| [15] | HOSSAIN M S, MONIRUZZAMAN M, MUHAMMAD G, et al. Big data-driven service composition using parallel clustered particle swarm optimization in mobile environment[J]. IEEE Transactions on Services Computing, 2016, 9(1): 806–817. |
| [16] |
白琳, 叶丹, 魏峻, 等. 一种高效的基于服务功能规约的服务选择方法[J].
软件学报, 2015(8): 1886–1906.
BAI Lin, YE Dan, WEI Jun, et al. Efficient service selection approach based on functionality folding[J]. Journal of Software, 2015(8): 1886–1906. |
| [17] | DOU W C, LV C, ZHANG X Y, et al. A QoS-aware service evaluation method for co-selecting a shared service[C] // Proceedings of International Conference on Web Services, Washington DC: IEEE, 2011: 145-152. |
| [18] | WANG H Y, CHENG Y. Interval number based service selection for multi-users' requirements[C] // Proceedings of International Conference on Web Services. San Francisco: IEEE, 2016: 712-715. |
| [19] | XU X F, LIU Z Z. S-ABC: a service-oriented artificial bee colony algorithm for global optimal services selection in concurrent requests environment[C] // Proceedings of International Conference on Web Services. Anchorage: IEEE, 2014: 503-509. |
| [20] |
王尚广, 孙其博, 张光卫, 等. 基于云模型的不确定性QoS感知的Skyline服务选择[J].
软件学报, 2012, 23(6): 1397–1412.
WANG Shang-guang, SUN Qi-bo, ZHANG Guang-wei, et al. Uncertain QoS-aware skyline service selection based on cloud model[J]. Journal of Software, 2012, 23(6): 1397–1412. |
| [21] |
朱勇, 李伟, 罗军舟. 一种面向多用户的负载感知动态服务选择模型[J].
软件学报, 2014, 25(6): 1196–1211.
ZHU Yong, LI Wei, LUO Zhou-jun. Multi-user oriented load-aware dynamic service selection model[J]. Journal of Software, 2014, 25(6): 1196–1211. |
| [22] | SUN L, WANG S G, LI J L, et al. QoS uncertainty filtering for fast and reliable web service selection[C] // Proceedings of international conference on web services. Anchorage: IEEE, 2014: 550-557. |
| [23] | SOUMI C, ANSUMAN B. QSCAS: QoS aware web service composition algorithms with stochastic parameters[C] // Proceedings of International Conference on Web Services. San Francisco: IEEE, 2016: 388-395. |
| [24] | ALRIFAI M, SKOUTAS D, RISSE T. Selecting skyline services for QoS-based Web service composition[C] // Proceedings of the 19th International Conference on World Wide Web. North Carolina: IEEE, 2010. 11-20. |
| [25] | LI J. A note on roth's consensus property of many-to-one matching[J]. Mathematics of Operations Research, 2013, 38(2): 389–392. DOI:10.1287/moor.1120.0576 |
| [26] | ZHANG Y, ZHENG Z, LYU M R. WSPred: A time-aware personalized QoS prediction framework for web services[C] // Proceedings of International Symposium on Software Reliability Engineering. Tokyo: IEEE, 2011: 210-219. |


