关系网络由各个不同的社会个体成员构成, 这些社会个体成员拥有不同的兴趣、属性和行为等, 社会个体成员的相互联系形成了相对稳定的体系结构, 其中存在着不同的小群体, 各个群体之间的属性特征和行为特征都存在着很大的差别, 而群体内的各个成员之间的行为特征和属性特征的相似度却比较高.
关系网络分析是由Jacob提出的[1].在计算机科学中, 关系网络群体结构的研究不仅与计算机科学中的图形分割有关[2], 而且和社会学中的层次聚类[3]密切相关.目前, 国内外学者已经对聚类方法进行大量的研究, 其分类主要包括:划分方法、层次方法、密度方法、网格方法等.例如:K-均值算法[4]、K-中心点算法[5]属于划分方法;AGNES算法、DIANA算法[6]属于层次方法, 前者是凝聚层次的聚类算法, 后者是分裂层次的聚类算法;DBSCAN算法[7]和OPTICS算法属于密度方法;STING算法[8]和CLIQUE算法属于网格方法.
公安情报行业经常要对犯罪团伙的内部关系和团伙之间的关系进行准确、有效、及时的分析[9].公安行业面临的犯罪特点大多呈现出高度的关联性、团伙性、多变性和突发性[10], 虽然公安机关的现有工作模式都实现了信息化管理, 但部门之间协作程度不高[11], 各犯罪嫌疑人之间以及各案件之间的潜在关联关系难以挖掘并呈现给情报研判人员, 这些都会影响情报信息的研判效率和质量.因此, 在公安情报业务的具体场景下, 将群体(社区)发现领域的研究思想及人的历史行为数据结合起来, 利用人的行为共性建立行为共性网, 划分出人与人之间的群体关系, 确定多个群体之间及群体内部的联系紧密程度, 将社会关系网络挖掘应用于公安情报大数据分析是有效提高公安行业的案情分析能力的新思路.
1 相关工作 1.1 关键图谱关键图谱(KeyGraph)算法借助共生关键词提取文本主题关键词.该算法有2个显著特点:能提取文本中的高频关键词;能提取容易被忽略但能描述文本主旨的低频关键词.
该算法首先提取文本中的高频关键词作为实心顶点, 计算关键词共同出现的次数, 在共同出现次数大于给定参数的实心顶点之间绘制一条实边, 形成“共现关键词”图谱;其次找出图谱中的所有连通子图, 将找出的每个连通子图看成独立群体, 独立群体由高频关键词组成, 属公众知识;最后, 在图中添加能够将独立群体连接起来的新关键词, 该关键词必须满足与独立群体之间共同出现次数的要求, 这样的关键词被标记为虚心顶点.虚心顶点不频繁出现, 是隐藏在公众知识背后的知识, 因此被称为机会[12-13].
关键图谱的核心思想就是寻找对象之间共同出现的特征和属性, 这与“物以类聚, 人以群分”的自然规律相吻合, 在公安情报场景中, “共现”的思想将起到至关重要的作用.
1.2 图聚类算法聚类分析简称聚类, 是把数据对象划分成子集的过程.每个子集是一个簇, 簇中的对象彼此相似, 但与其他簇中的对象不相似.常用的聚类方法未考虑到关系网络或者图的聚类问题, 需要将图转化成非图结构的数据进行聚类.在图和网络数据上进行聚类分析, 主要存在两大挑战:如何度量图中2个对象之间的相似性;如何设计在图和网络数据上有效聚类的模型和方法.
针对如何更好地度量2个节点间的距离或者相似度这一关键问题, 本文不使用诸如欧式距离这样的传统距离度量, 而是尝试一种适合图的新的尺度来量化相似度.
SimRank是一种基于随机游走和图结构相似性的度量.SCAN (structural clustering algorithm for networks)[16]是一种定义于SimRank上的聚类算法.该算法规定了2个重要的概念.
1) 直接结构可达:对于核心对象p和q, 如果p在q的ε-邻域内, 称p是从q直接结构可达的.
2) 结构可达:如果存在一个对象链p1, p2, …, pn, 使得p1=q, pn=p, 并且对于pi∈D(1≤i≤n), pi+1是从pi关于ε和μ直接结构可达的, 称p是从q结构可达.
给定无向图G=(V, E), 对于顶点u∈V, u的邻域是Γ(u)={v|(u, v)∈E}∪{u}.使用结构情境相似性的思想, SCAN算法用规范化的公共邻域大小来度量2个顶点u和v(u, v∈V)之间的相似性, 即
| $ \sigma \left( {u, v} \right) = \frac{{\left| {\mathit{\Gamma }\left( u \right) \cap \mathit{\Gamma }\left( v \right)} \right|}}{{\sqrt {\mathit{\Gamma }\left( u \right)\mathit{\Gamma }\left( v \right)} }}. $ | (1) |
该计算值的大小表示2个顶点相似程度的高低.SCAN算法确定顶点属于哪个簇时用相似度阀值ε来衡量.对于顶点u∈V, u的ε-邻域定义为Nε(u)={v∈Γ(u)|σ(u, v)≥ε}.u的ε-邻域包含u的近邻, 与u的结构情境相似性至少为ε.在算法中, 核心顶点是簇内的顶点, 即u∈V是核心顶点, 如果|Nε(u)|≥μ, 其中μ是点数阀值.SCAN算法从核心点开始产生簇.如果顶点v在核心顶点u的ε-邻域, 则顶点v与顶点u属于同一个簇.
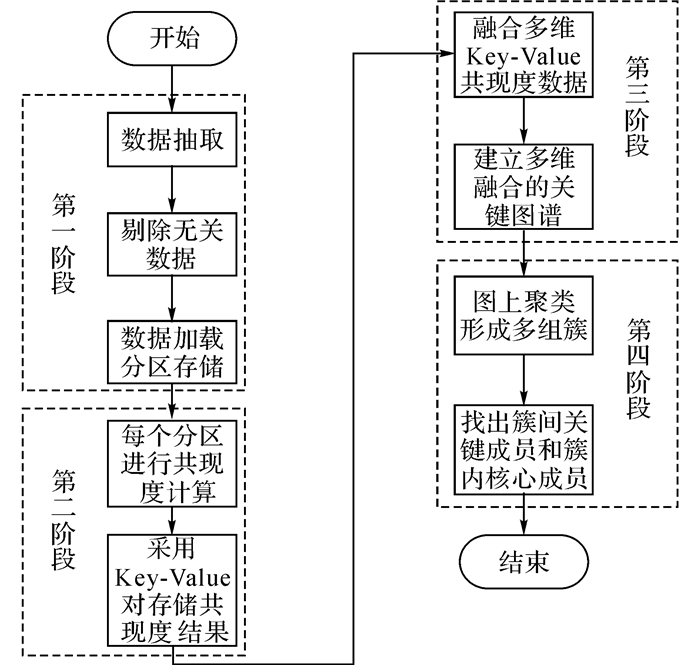
2 基于关键图谱的群体发现 2.1 系统架构本文提出基于关键图谱的群体发现(KeyGraph-based community detection, KCD)方法, 其流程如图 1所示.
|
图 1 基于关键图谱的群体发现算法(KCD)的流程图 Fig. 1 Flowchart for KeyGraph-based community detection (KCD) |
KCD方法主要分为4个阶段.第一阶段是对数据进行ETL(提取、转换、加载).为了解决海量结构化数据在传统关系型数据库和单机环境下不能满足计算性能和存储空间要求的问题, 需要利用数据分区的思想来重组数据存储结构, 方便第二阶段进行共现度的计算.第二阶段是对经过第一阶段预处理的数据, 利用局部性原理进行计算过程优化和计算结果的存储结构优化, 并形成Key-Value对的共现度数据, 完成从结构化数据到半结构化数据的转化.第三阶段是融合第二阶段的多维共现度数据, 计算对象之间的共现率, 通过设置参数“最小支持度”过滤噪音数据并建立关键图谱, 形成基于“共现关系”的关系网络图, 完成从半结构化数据到非结构化数据(图模型)的转化.第四阶段是在关键图谱上进行关系网络分析, 利用改进后的聚类算法SCAN求解出群体内部以及群体之间的成员联系, 并以图结构直观呈现.
2.2 数据组织与处理 2.2.1 共现定义数据分区的合理性对本文最终并行计算的性能将会产生很大影响.基于本文的研究内容和背景, 可以对公安局已有的网吧上网行为特征数据、旅馆住宿行为特征数据、铁路乘车行为特征数据进行充分的利用和挖掘.通过对公安民警多年的案件侦查和侦破经验的深入了解, 根据共现关系的思想, 提出如下定义.
定义1 同上网:在同一网吧中, 若有2个人的上网时间和下网时间间隔小于15 min, 则称这2个人同上网1次, 简称“同上网”.数学表述如下:若用P表示人员集合, W表示所有网吧集合, S表示所有上网记录集合, fplace表示求共同网吧函数, ftime表示求时间差函数(时间单位为s), fpeople表示求人员函数, 则
∀ a, b∈S, 若∃w∈W使得fplace(a, b)=w, 并且有ftime(a, b)≤15×60, 则
| $ {f_{{\rm{people}}}}\left( {a, b} \right) = \left( {{p_1}, {p_2}} \right), $ |
其中p1, p2∈P称p1和p2同上网一次, 采用三元组记法, 写为(p1, p2, 1).
定义1适用于集合S中任意2条记录, 统计上网三元组集, 可得出(p1, p2, n)表示p1和p2共同上网n次, n为自然数.
定义2 同住宿:同一旅馆中, 如有2个人的入住时间和退房时间间隔小于15 min, 则这2个人或同一住宿时间段内(例如:从某天中午12:00到第二天中午12:00) 入住房间号一样的2个人, 简称“同住宿”.数学表述如下:若用P表示所有人员集合, H表示所有旅馆集合, Z表示所有住宿记录集合, fhotel表示求共同旅馆函数, 则
∀ z1, z2∈Z, 若∃h∈H使得fhotel(z1, z2)=h,且ftime(z1, z2)≤15×60, 则
| $ {f_{{\rm{people}}}}\left( {{z_1}, {z_2}} \right) = \left( {{p_1}, {p_2}} \right), $ |
其中p1, p2∈P称p1和p2同住宿一次, 采用三元组记法, 写为(p1, p2, 1).
定义2适用于集合H中任意2条记录, 统计住宿三元组集, 可得出(p1, p2, m).表示p1和p2共同住宿m次, m为自然数.
定义3 同乘车:同一班次火车, 购票时间差在15 min之内的2个人, 简称“同乘车”.数学表述为:若用P表示所有人员集合, T表示所有火车班次集合, C表示所有火车购票记录集合, fwhich表示求共同火车班次函数, 则
∀ c1, c2∈C, 若∃t∈T使得fwhich(c1, c2)=t,且ftime(c1, c2)≤15×60, 则fpeople(c1, c2)=(p1, p2), 其中p1, p2∈P称p1和p2同乘车一次, 采用三元组记法, 写为(p1, p2, 1).
定义3适用于集合C中任意2条记录, 统计乘车三元组集, 可得出(p1, p2, s).表示p1和p2共同乘车s次, s为自然数.
2.2.2 多级分区公安情报的基础数据随着时间的推移呈现出的增长趋势超过线性的增长趋势, 而数据的存储粒度又必须采用低粒度级(即数据细节程度高)的存储.为了实现数据管理的便捷性和科学性, 采用基于空间分区的方式——按场所分区, 并在每个分区内部进行二级分区存储——按时间(跨度为天)分区, 能够减少共现权值计算的运行时间.这是因为共现定义规定, 2个人必须出现在同一场所才能算作是共现关系, 那么在对每个分区进行扫描、处理读取数据的时候, 要将该空间分区下的数据进行读取, 而不是读取所有空间的分区, 这样不仅从计算的数据量上呈数量级的减少计算时间, 还在读取的数据量上呈数量级的减少读取时间.按照空间分区的做法, 具体到同上网、同住宿、同乘车的场景中来说, 就是分别按照网吧分区、旅馆分区、车次分区.
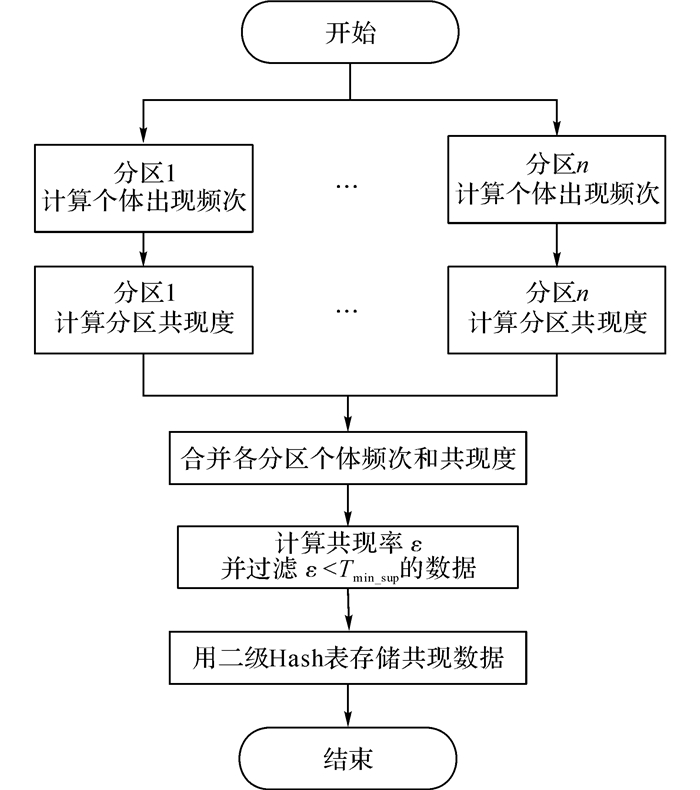
2.3 图谱数据计算与存储关键图谱的建立重点在于将关系数据转化成图数据, 计算节点之间的共现度, 整个过程的流程如图 2所示.
|
图 2 关键图谱数据计算流程图 Fig. 2 Calculation flowchart for Key-Graph data |
图谱计算一共分为3个阶段.第一阶段, 并行扫描各个一级分区的数据, 计算每个一级分区个体的出现频次, 然后将多个一级分区中相同个体的出现频次累加.第二阶段, 并行计算每个一级分区内个体与个体之间的共现次数, 多个一级分区中相同2个个体之间的共现次数累加.第三阶段, 计算每个个体的共现次数占该个体出现频次的比例, 对于比例小于阀值的数据, 认为是噪音数据并剔除.最终形成个体与个体之间的共现度, 并以二级Hash表的形式存储.
2.3.1 共现度计算在第一阶段, 每个分区中直接扫描一遍分区文件, 为每个分区申请一个Hash表, 在扫描的过程中逐条读取数据, 在每条数据中提取个体oi, 并在Hash表中查找个体oi对应的出现频次, 如果能够查找到则频次加1, 如果不能查找到则将Key-Value对 < oi, 1>添加到Hash表中.在第二阶段, 根据共现的定义, 在本文数据存储结构的前提下, 只有在每个二级分区内部的数据之间才会出现共现的2个人.在对实际数据的探索中发现每个分区的数据在10 MB以内, 因此, 在进行计算的时候可以根据物理机器内存将每个分区的数据一次性加载入内存.在内存中针对每一条数据ri取和该条数据在时间上相差近15 min(包括该时间之前和该时间之后)的数据集Ri, 产生该条数据ri的个体oi和数据集Ri 中的个体集Oi一一形成共现关系.若pj∈Ri, 则三元组(ri, pj, 1) 记录一对共现关系, 表示个体ri和个体pj共现一次.
2.3.2 共现关系去重在第二阶段的计算中, 由于每一对共现关系都会被计算2遍, 浪费了计算资源.为了减少重复计算, 优化计算效率.提出在分区内部针对每一条记录按时间升序排序, 这样每个分区数据在内存中都是按照时间的升序排序.对于每一条数据ri的个体oi, 计算其共现关系时只需要取ri以后的时间差小于15 min的数据, 即在时间上比ri大且不超过15 min的数据.这样每一对共现关系都会减少一次重复计算的计算量.
虽然在记录处理上按时间排序也会消耗资源, 但是本研究所用的数据在业务库中都是按照时间递推顺序产生, 在数据库中存储时,绝大部分记录是按照时间顺序依次写入并存储, 只有少量数据产生时, 并发读写的过程中会出现乱序存储的情况, 因此在将记录按照时间排序的过程中采用插入排序的方法十分高效, 时间复杂度基本为O(n), 小于进行一遍重复共现度计算时间复杂度Ο(kn), 其中k为以每条记录个体为核心时额外读取的平均记录数.
2.3.3 跨分区计算处理数据多级分区存储带来了计算性能的提升, 但同时也产生了麻烦.例如, 以上网数据来说, 某个体在24:00之前的5 min内在某网网, 而与其关系密切的另一个体因为上洗手间在24:00之后的5 min内才上机, 在对数据进行二级分区存储的时候, 会人为将这个2条同上网的数据记录分割不同的分区, 然而, 在进行共现度计算的时候又没有对这种情况进行处理, 从而可能导致重要的信息丢失.为了应对这种情况, 本文提出一种“补尾多读”的解决方法.
所谓“补尾多读”就是指在读每个分区的数据时, 当读到最后一条记录时, 需要将最后一条记录的时间取出来, 按照这个时间去寻找并读取下一天分区同地点和这个时间相差小于15 min的数据, 完成实际尾部最后一条数据的正确处理, 就保证了该分区的所有数据能够正确处理.
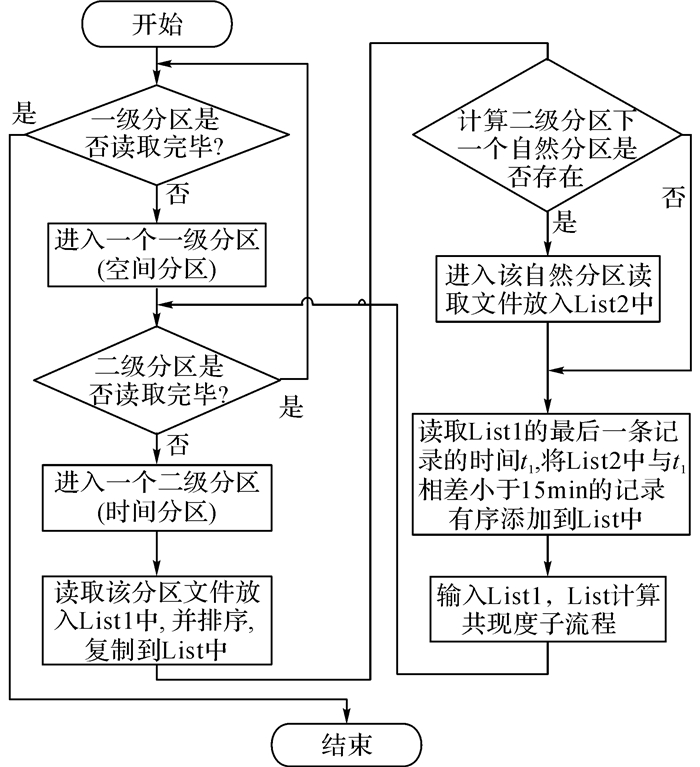
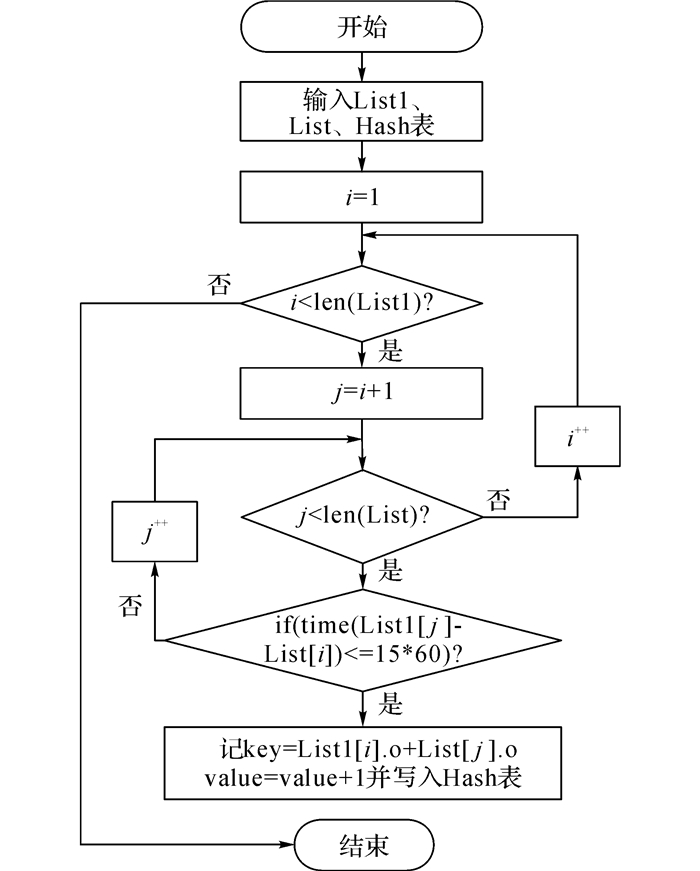
通过上述分区处理, 共现度的计算效率得到有效提升, 计算共现度的算法流程如图 3和4所示.
|
图 3 计算共现度的算法流程图 Fig. 3 Algorithm flowchart for co-occurrence calculation |
|
图 4 计算共现度的子流程图 Fig. 4 Sub-flowchart for co-occurrence calculation |
算法首先遍历一级分区, 在每个一级分区中, 进入二级分区, 将该二级分区的数据块读入到内存的List1中并排序, 复制List1到List中, 取出排序后最后一条记录的时间Tlast, 接着找到该二级分区的下一个自然分区, 将该分区中和Tlast时间差小于15 min的记录全部有序的加入到List中, 将List1和List输入到计算共现度子流程算法中进行共现度计算.多个一级分区之间计算共现度互不干扰, 可以采用并行处理.
计算共现度子流程算法外层遍历List1, 循环变量i=0, 内层遍历List, 其中内层遍历循环变量初始化j=i+1, 每次进入内层循环都比较外层循环当前记录的时间和内层循环当前记录的时间之差是否小于15 min.若是, 则外层循环当前记录的个体和内层循环当前记录的个体形成一次“共现关系”, 2个个体的共现度增加一次;若否, 则2个个体不形成共现关系, 直接进入下一次内层循环.
2.4 图谱数据聚类 2.4.1 分区数据合并分区数据合并采用一个全局Hash表来实现.首先, 对所有结果数据分区逐一扫描, 针对任意的2个对象Oi、Oj的Key, Ki, Kj, Hash函数使得Hash(Ki, Kj)映射到Hash表中的键Kij, 查询Hash表, 如果表中存在, 则用原来的value值Vij加上新的Vij形成新的值, 并保存;如果表中不存在, 则直接将新的Vij当成新的值保存.这样当所有结果数据分区扫描完成后, 所有的数据都合并到全局的Hash表中.
2.4.2 数据去噪针对已经合并的共现数据, 提出一种方法融合多个维度的数据, 使之成为一种综合权重评价该共现关系.定义一个共现率(co-occurrence rate)的概念, 对于2个个体A和B, 用FAB表示A和B在某种场合共同出现的次数, 即A和B在这种场合的共现度.CA和CB分别表示A和B在这种场合出现的总次数, 那么A和B之间的共现率RAB的计算公式为
| $ {R_{AB}} = \frac{{{F_{{\rm{AB}}}}}}{{\sqrt {{C_{\rm{A}}}{C_{\rm{B}}}} }}. $ | (2) |
共现率RAB同时考虑了A和B这2个个体在该场合的出现次数, 其RAB的取值范围为(0, 1.0), 共现率越接近1表示2个个体在该场合一同出现几率越大, 即2个人关系越密切.
引入最小支持度参数Tmin_sup, 对于一对共现关系来说, 如果共现率RAB < Tmin_sup, 则认为这对共现关系为噪音数据, 会对最终的聚类结果产生比较大的影响, 应该直接抛弃.
经过数据去噪后, 对剩下的数据遍历, 建立关键图谱.首先, 建立一张空的带权无向图:
| $ G = \left( {V, E, W} \right), V = \emptyset, E = \emptyset, W = \emptyset . $ |
即顶点、边、权重都为空, 其中V表示顶点集, E表示顶点之间的边集, W表示边上的权重集.然后逐一遍历Hash表中的每一项, 从Key求出2个节点的唯一标识, 并在图G中创建2个节点、2个节点之间的边以及边上的权重, 重复这一步骤直到整个Hash表遍历完成.
2.4.3 图谱数据聚类给定无向图G=(V, E), 对于顶点u∈V, u的邻域是Γ(u)={v|(u, v)∈E}∪{u}.使用情境相似性的思想, SCAN算法采用规范化的公共邻域大小来度量2个顶点u, v∈V.之间的相似性.该计算值越大, 2个顶点越相似.SCAN算法使用相似度阀值ε定义簇隶属关系.对于顶点u∈V, u的ε邻域定义为
| $ {N_\varepsilon }\left( u \right) = \left\{ {v \in \mathit{\Gamma }\left( u \right)|\sigma \left( {u, v} \right) \ge \varepsilon } \right\}. $ | (3) |
u的ε-邻域包含u的所有近邻, 与u的结构情境相似性至少为ε(ε≥0).在SCAN算法中, 核心顶点是簇内的顶点, 即如果|Nε(u)|≥μ, u∈V是核心顶点, 其中μ是点数阀值.如果u是v的ε邻域, 并且v是一个核心顶点, 则顶点u和顶点v必然属于同一个簇, 这是因为算法从核心顶点开始生成新的簇所导致的, 称u和v直接结构可达.
3 测试结果与分析 3.1 测试环境本文的所有测试都在安装操作系统为Ubuntu Desktop 14.04的一台物理服务器上进行, 服务器硬件配置如下:CPU为Intel® Xeon(R) CPU E5-2620 2.10 GHz*8, 内存为32 GB, 硬盘为1 TB, 千兆网卡.测试数据集来自某公安局真实上网数据, 包含上亿条上网记录.
3.2 评价指标在KCD方法的测试分析中, 主要是对聚类结果的优劣进行评价.由于在实际测试中并不能找出所有的标准聚类结果, 即不存在标准集, 该过程实际上是一个无监督的学习过程.对于聚类质量的评估, 本文采用模块化度量函数Q来进行评估, 该函数最早由Newman等[15]提出, Q函数的定义公式为
| $ Q = \sum\limits_{s = 1}^k {{{\left[{\frac{{{l_s}}}{L}-\left( {\frac{{{d_s}}}{{2L}}} \right)} \right]}^2}} . $ | (4) |
式中:L为图中边的数目, ls为第s个簇的顶点之间的边数, ds为第s个簇的顶点的度数和.模块化函数度量Q的值越大, 表明聚类效果越好.在实际数据中模块化度量函数Q的值一般为0.3~0.7, 高于0.7的情况十分少.
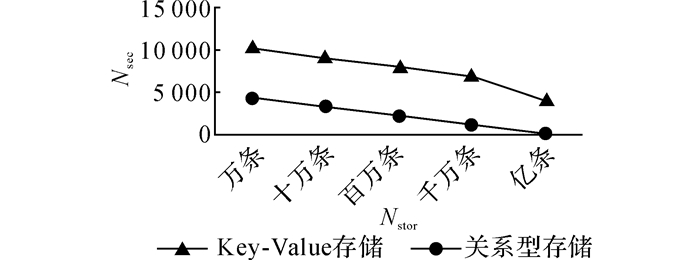
3.3 测试结果与分析 3.3.1 存储模型效率对比分析本文在共现关系的存储上选用Key-Value存储模型.Key-Value存储模型在本文的共现关系对的融合计算中表现出的性能很高.在多个分区合并共现度结果过程中, 需要将同一Key的Value进行累加, 这个过程分为2个步骤, 第一步查询库中是否存在Key;第二步如果库中存在Key则读取对应的Old_Value并和New_Value相加然后写入库中, 如果库中不存在Key, 则直接将New_Value写入库中.随着库中共现度Key-Value对增加, 采用关系型存储模型和Key-Value存储模型每秒能够处理的共现度条数如图 5所示.其中,Nsec为存储模型每秒处理的共现度条数,Nstor为库中共现度Key-Value对数.
|
图 5 不同存储方式下的共现度处理性能对比图 Fig. 5 Comparison of co-occurrence handling speed for different storage modes |
从图 5可以看出, 即使在关系型数据存储模型已经建立索引的情况下, 采用Key-Value存储模型仍全面优于关系型存储模型, 并且随着库中共现度数量的逐渐增加, 关系型存储的方案几乎无法使用, 而Key-Value存储模型虽然性能有所下降, 但依然保持相对较高的性能.
3.3.2 数据多级分区测试分析KCD方法中数据的多级分区存储为共现度的计算提供了极大的性能提升, 本小节通过不采用分区、采用一级分区、采用多级分区3个存储方案来讨论多级分区存储带来的优势.
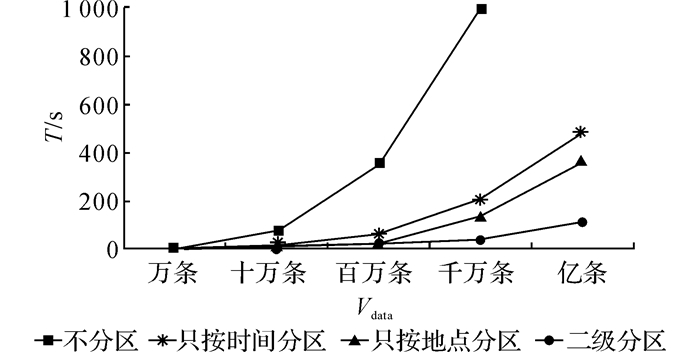
不采用分区指的是直接将源数据全部简单地放在一起, 在针对每条记录计算共现度时都需要遍历整个记录集, 逐一计算其他每条记录是否与该记录存在共现关系.这样将存在2个问题:1) 不是同一个场所产生的2条记录也会进行一次计算;2) 与该条记录时间相差太远的记录肯定不构成共现关系, 也会被计算.采用一级分区指的是对上述记录遍历一遍, 然后将每条记录存储到对应的分区, 这里有2种方案:1) 采用时间分区或者采用地点分区, 在计算共现度的时候只需要遍历分区内部的数据集;2) 采用按时间和地点的二级分区存储结构, 进一步缩小了计算共现度需要遍历的数据集.对于10 m的上网记录数据, 采用不同分区方法的处理性能如图 6所示.其中,T为处理时间,Vdata为数据集大小.
|
图 6 不同分区方法下的共现度处理性能对比图 Fig. 6 Comparison of co-occurrence handling speed for different partition methods |
从图 6可以看出, 采用两级分区的对源数据进行预处理的策略能够极大降低共现度计算时间的复杂度, 这主要是由于在计算每一条共现度时, 需要遍历的数据集成数量级级别的减少.
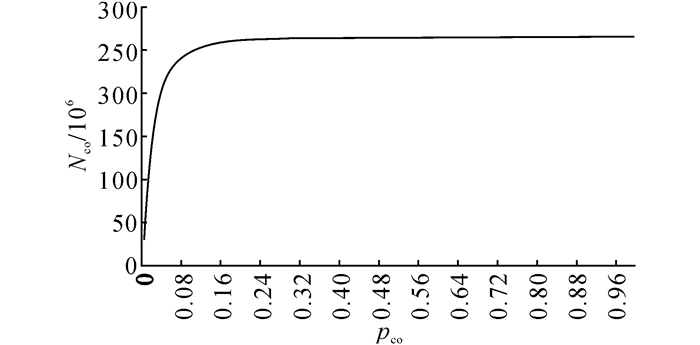
3.3.3 最小支持度对图谱大小的影响最小支持度Tmin_sup对噪音数据的过滤直接影响最终聚类中图的顶点数据和边数, 从而影响最终簇中成员和簇之间的联系, 因此, 针对实际数据设置一个适当的Tmin_sup对数据的过滤效果十分重要.图 7列出了上网数据共现对N数量的累积分布情况, 其中Nco为累计共现度数,pco为共现率.图中将节点之间的共现率R分为100个小区段, 每个区段之间的间隔精度为0.01.
|
图 7 累计共现对数量随共现率的折线图 Fig. 7 Accumulation of co-occurrence number varies with co-occurrence probability |
从图 7可以看出, 个体之间的共现率在0~0.1的共现对总数增长较快;共现率在0.10~0.24的共现对总数增长较为缓慢;共现率在0.24~1.00的共现对总数增长十分平缓, 趋于稳定.由于共现率是衡量2个个体在同一场合共现出现的指标, 共现率越低表明2个个体同时出现在该场景的概率就越低, 本研究应该取共现率较高且增长趋于稳定的共现对来建立关键图谱进行聚类, 即Tmin_sup≥0.10.
3.3.4 最佳ε、μ参数测试由3.3.3节分析知, 取Tmin_sup=0.27, 即将共现率≥0.27的点和边建立关键图谱, 然后进行聚类分析.如图 8所示为不同的ε、μ参数对聚类质量指数的影响曲线, 聚类质量指数用模块化度量函数Q来衡量, 其范围为0~0.1, 越接近1.0表明聚类的质量越高, 聚类产生的簇越接近真实簇.从图 8可以看出, 聚类质量指数的最大值>0.9, 这和该值的常规范围0.3~0.7不吻合, 通过进一步分析发现不管ε取何值, Q值都随着μ值的增加而下降, 这从侧面说明用来聚类的图G是不连通, 图G中包含若干个子图.

|
图 8 聚类质量的变化曲线图 Fig. 8 Changing curve of cluster quality |
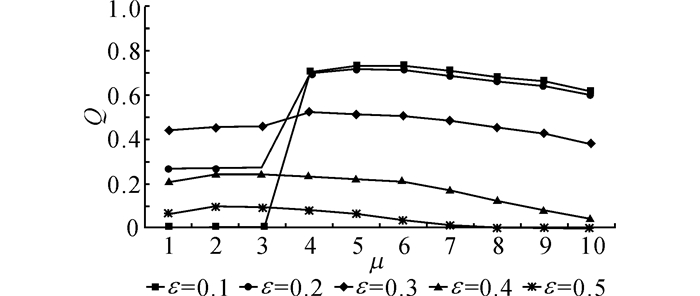
对于图G来说, 首先将其划分为若干个子图, 再对各个子图作聚类, 是本实验的重要步骤.通过对每个子图就行若干次试验, 最后随机从若干子图取100个样本的Q函数值作实验, 结果如图 9所示.从图 9可以看出, 当ε取值为0.1或0.2时, Q函数拥有较高的值在[0.5, 0.8], 而且当μ=5时分别可以得到ε=0.1或0.2时Q的最大值.在实际情况中, 考虑到噪音数据不可能完全去除, 因此, 取ε=0.2和μ=5作为最佳参数.
|
图 9 子图中聚类质量的变化曲线图 Fig. 9 Cluster quality varies in sub-graphs |
在对整个图G聚类时, 取ε=0.1和μ=1作为最佳参数, 此时SCAN算法退化为求连通子图算法;在针对子图进行聚类时, 取ε=0.2和μ=5作为最佳参数, 以此来达到使聚类质量指数最大化的目的, 从而使聚类效果最佳.针对不同的子图可能需要不同的参数, 因此应该ε=0.2和μ=5附近取多个不同的值来对比多个参数下的每个子图的聚类效果.
4 结语在分析公安机关现有业务数据的基础上, 利用关系网络分析方法, 加入对行为数据的量化处理, 提出了用人的行为数据挖掘行为特征相似的人群并将他们聚类的方法KCD, 完成公安情报中的共现关系网络挖掘, 有效弥补了公安情报场景中对行为数据利用的不足.
KCD方法通过对个人行为数据(上网、住宿、乘车等)的探索提出个体之间共现度的概念, 并给出了数据清洗过程和计算共现度的算法.针对个体行为数据, 提出基于地点和时间的二级分区数据存储结构对数据做预处理, 减少了共现度计算的时间复杂度, 提高了计算效率.针对共现度的存储模型, 提出利用两级Hash结构的Key-Value存储, 提高了关键图谱中的节点之间边的查询效率.针对计算多维度数据产生的不同维度的共现度以及计算共现度过程中产生的噪音数据, 通过计算各个维度所占的比例和引入最小支持度Tmin_sup对数据进行融合和过滤并建立多维度的关键图谱.将聚类中产生的中心点、离群点和公安情报领域的实际场景相结合, 指出重点研究中心点有极大机率找出关键个体.
目前在数据的利用上只考虑2个个体之间的粗略位置关系和时间关系.未来研究可以更深入地进行细节位置关系的探索, 例如:网吧数据中2个人是否邻座, 乘车数据中2个座位是否连号等, 以进一步提高群体发现的精确度.
| [1] | JACOB L. Moreno[EB/OL].[2016-10-01]. https://en.wikipedia.org/wiki/Jacob_L._Moreno. |
| [2] | WEST D B. Introduction to graph theory[M]. Upper Saddle River: Prentice hall, 2001: 1-36. |
| [3] | SCOTT J. Social network analysis[M]. Sage: socialogy, 2012: 109-127. |
| [4] | ALSABTI K, RANKA S, SINGH V. An efficientK-means clustering algorithm[C] // Proceeding of IPPS/SPDP Workshop on High Performance Data Mining, 1998. New York: ACM, 2011: 1-6. |
| [5] | KAUFMAN L, ROUSSEEUW P J. Finding groups in data: an introduction to cluster analysis[M]. New York: John Wiley and Sons, 2009. |
| [6] | KAUFMAN L, PETER J R. Finding Groups in Data: An Introduction to Cluster Analysis[M]. New York: John Wiley and Sons, 1990. |
| [7] | ESTER M, KRIEGEL H P, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C] // Proceeding of Second International Conference on Knowledge Discovery and Data Mining. Menlo Park: AAAI Press, 1996: 226-231. |
| [8] | WANG W, YANG J, MUNTZ R. STING: a statistical information grid approach to spatial data mining[C] // Proceeding of 23rd International Conference on Very Large Data Bases. San Francisco: Morgan Kaufmann, 1997: 186-195. |
| [9] |
张浩明. 数据挖掘在公安情报系统中的研究与应用[D]. 上海: 同济大学, 2008.
ZHANG Hao-ming. Research and application on data mining for systems of public security intelligence[D]. Shanghai: Tongji University, 2008. |
| [10] |
陆巧. 公安大情报应用体系建设研究[D]. 四川: 电子科技大学, 2013.
LU Qiao. Research on the construction of the application system of public security intelligence[D]. Sichuan: University of Electronic Science and Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10614-1013332466.htm |
| [11] |
杨正涛. 基于数据仓库的公安情报分析系统的设计与实现[D]. 四川: 电子科技大学, 2012.
YANG Zheng-tao. Design and implementation of public security information system based on data warehouse[D]. Sichuan: University of Electronic Science and Technology, 2012. |
| [12] | ZHANG Z, CHENG H, WANG X. From data mining to chance/sign discovery[J]. Computer Science, 2007, 10: 188–191. |
| [13] | ZHANG Z Y, CHENG H M, ZHANG S G. Research on approach of simple scenario map construction in chance discovery[J]. Computer Engineering, 2011, 37(8): 192–193. |
| [14] |
程泽凯, 张佳玉. 基于节点相似度的社团发现算法[J].
计算机工程与设计, 2014, 35(5): 1689–1693.
CHENG Ze-kai, ZHANG Jia-yu. Community discovery algorithm based on node similarity[J]. Computer Engineering and Design, 2014, 35(5): 1689–1693. |
| [15] | NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 |
| [16] | XU X, YURUK N, FENG Z, et al. Scan: a structural clustering algorithm for networks[C] // Proceedings of the 13rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose: ACM, 2007: 824-833. |


