2. 杭州萧山锦江绿色能源有限公司, 浙江 杭州 311203
2. Hangzhou Xiaoshan Green Energy Co. Ltd, Hangzhou 311203, China
垃圾焚烧能够较好实现垃圾处理技术的减容化、减量化、无害化和资源化.近十几年, 在国家相关产业政策的引导下, 国内垃圾焚烧行业取得了蓬勃的发展[1].从20世纪90年代开始, 国内多家科研结构对中国城市生活垃圾(municipal solid waste, MSW)燃烧机理进行了大量深入研究, 掌握了混合收集、水分高、成分复杂的城市生活垃圾的燃烧特性, 并根据我国对煤、煤矸石等劣质燃料循环流化床(circulating fluidized bed, CFB)燃烧技术的开发经验, 开发出了循环流化床垃圾焚烧锅炉.1998年,浙江大学开发的第一台流化床垃圾焚烧炉开始进行大规模焚烧处理, 对国内高水分、低热值且波动性大的生活垃圾表现出了极强的适应性[2].目前, CFB垃圾焚烧技术已经在国内的多个城市进行了推广应用, 截至2014年底, 国内已建成垃圾焚烧锅炉70余台, 日处理垃圾量6.4万吨[3], 为我国的垃圾焚烧处理行业作出了重要的贡献.
国内的城市生活垃圾多为混合收集, 导致入厂、入炉垃圾成分较为复杂, 表现出低热偏值、水分较高和波动性较大的特征[4].入炉垃圾的不均匀性迫使运行人员频繁地对锅炉的运行状态进行调整, 会给CFB垃圾焚烧锅炉的运行带来的不良的影响[5], 尤其是对床温的稳定控制, 当含水量很高、热值极低的垃圾进入炉膛, 会在短时间内造成床温急剧降低, 甚至熄火, 给锅炉的安全稳定运行带来隐患.另一方面, 为了促进垃圾焚烧企业运行管理水平的发展, 提升垃圾焚烧工艺的安全性、环保性和经济性, 国家住建部颁发的《生活垃圾焚烧厂评价标准(CJJ/T 137-2010)》设置了生活垃圾焚烧系统是否配套了自动燃烧控制(automatic combustion control, ACC)系统的评分选项, 而ACC系统实施的前提是保证控制系统具有可靠的垃圾热值反馈信号[6-7].同时, 垃圾焚烧企业在日常运行管理的过程中, 需要对垃圾的热值进行统计分析, 为企业管理人员掌握运行状况和制定运营策略提供依据.因此, 在焚烧过程中对垃圾的热值进行在线监视和软测量具有十分重要的意义.
目前, 还没有一种可靠的垃圾热值在线测量硬件设备应用于实际生产过程, 常见的垃圾热值测量方法主要包括实验法和软测量方法.实验方法主要是指采用弹式量热计的方法[8-9], 该方法的测量结果精确, 但该方法的样品预处理和后续试验过程耗时长、成本高[10], 难以满足实际生产过程对实时性和持续性的要求.另一种方法主要是指基于离线试验结果的经验计算模型, 主要分为基于工业分析的热值软测量模型[11]、基于元素分析的热值软测量模型[12-13]和基于垃圾物理组分的热值软测量模型[10, 14], 这3种类型模型都是通过对大量实验结果进行数据挖掘的得到的, 有一定程度的可靠性.然而, 这些方法自身就有实验法的限制, 而且, 垃圾是非均匀物质, 所取样品是否能够代表入炉垃圾的特性难以确定[6-7].因此, 这种方法目前主要用于离线的统计分析, 难以胜任实时且不间断的热值监测工作.
运行人员在司炉过程当中并不知道入炉垃圾的具体热值, 但是能通过相关焚烧参数综合判断出垃圾热值的变化趋势, 并估计出总体热值水平, 从而作出准确的操作.因此, 利用黑箱建模的方法将CFB垃圾焚烧锅炉运行状态参数作为模型的输入变量, 将垃圾热值的模糊水平作为模型的输出变量的软测量模型, 从而避开对垃圾成分进行离线测量的工作[7].随着电子技术、计算机技术和信息技术的发展, 集散控制系统(distributed control system, DCS)被广泛应用于CFB生活焚烧锅炉的运行过程, 包含温度、压力、流量等参数在内的过程数据都被完善得保存下来, 这些历史数据中包含丰富过程信息, 是人们认识和了解生产过程的重要途径之一, 具有很高的挖掘价值[15].但是, 在处理大型数据时需要高效的数据挖掘方法才能避免知识提取不完备和计算资源的过度消耗情况的发生.自适应模糊神经网络(adaptive neuro-fuzzy inference system, ANFIS)、多层感知器(multiple layer perceptron, MLP)神经网络、径向基函数(radial basis function, RBF)神经网络和支持向量机(support vector machine, SVM)等算法成为公众普遍认可的数据挖掘算法, 然而针对不同的对象, 这些算法的性能不尽相同, 相互之间的对比研究和联合使用受到了研究人员的关注[16-21].
模糊神经网络融合了神经网络并行计算、分布式信息存储、容错能力强、具备自适应学习功能等优点和模糊算法能够有效表达先验知识的能力, 具有成为构建不确定性和非线性模型的有力工具, 被广泛应用于预测系统、系统辨识、模式识别、故障诊断和一些非线性系统控制领域当中[22-25], 对于表征基于模糊经验判断的垃圾热值具有先天性的优势, 能够集中全厂最优秀的现场运行人员的经验和一些已被人们知晓的专家知识.减法聚类算法[26]能够在保证执行效率和挖掘质量的前提下从大型数据中提取出数据特征, 无需提前确定聚类数, 能够根据样本数据决定聚类中心, 十分适合用来确定ANFIS模型的初始结构参数.
本文从运行人员运行控制锅炉的角度出发, 在分析CFB生活垃圾焚烧锅炉运行机理和运行经验的基础上, 对垃圾热值的进行模糊划分以及选择入炉垃圾实时热值软测量模型的输入变量, 并重点论述基于减法聚类算法的自适应模糊神经网络(subtractive clustering based adaptive neuro-fuzzy inference system, SC-ANFIS)的入炉垃圾热值软测量方法.对比研究SC-ANIFS模型与MLP模型、RBF模型以及SVM模型在垃圾热值预测方面的性能和表现;比较SC-ANFIS模型预测的垃圾热值和弹筒量热计的测量的垃圾热值.
1 减法聚类算法和自适应模糊神经网络原理 1.1 减法聚类算法减法聚类算法[26]用于对建模数据样本的空间进行初始划分以及模糊规则的确定, K-均值聚类算法和模糊C-均值聚类算法均需要预设聚类中心的数目, 没有充分利用样本空间蕴含的对象特征信息.减法聚类算法基于山峰函数, 将每个数据点作为可能的聚类中心, 并根据各个数据点周围的数据点密度来计算改点作为聚类中心的可能性.
每个数据点作为聚类中心的可能性由下式定义:
| $ {P_i} = \sum\limits_{j = 1}^m {{\rm{exp}}} \left( {-\frac{{{{\left\| {{X_i}-{X_j}} \right\|}^2}}}{{{{({r_{\rm{\alpha }}}/2)}^2}}}} \right). $ | (1) |
式中:m为n维输入空间中全部的数据点数, Xi=[Xi1, Xi2, …, Xin]、Xj=[Xj1, Xj2, …, Xjn]是具体的数据点, rα为一个正常数, 定义了该点的邻域半径, ‖·‖符号表示欧式距离.被选为聚类中心的点具有最高的数据点密度, 同时该数据点周围的点被排除作为聚类中心的可能性.第一个聚类中心为Xc1, 数据点密度为Pc1.选出第一个聚类中心后, 继续采用类似的方法确定下一个聚类中心, 但需要消除已有聚类中心的影响, 修改密度指标的山峰函如下:
| $ {P_i} = {P_i}-{P_{{\rm{c1}}}}{\rm{exp}}\left( {{\rm{}}\frac{{-{{\left\| {{X_i}-{X_{{\rm{c1}}}}} \right\|}^2}}}{{{{({r_{\rm{\beta }}}/2)}^2}}}} \right). $ | (2) |
式中:rβ定义了一个密度指标显著减小的邻域, 为了避免出现十分接近的聚类中心, rβ>rα.循环重复上述过程直到所有剩余数据点作为聚类中心的可能性低于某一阈值, 即
| $ {P_{ck}}/{P_{{\rm{c1}}}} < \delta . $ |
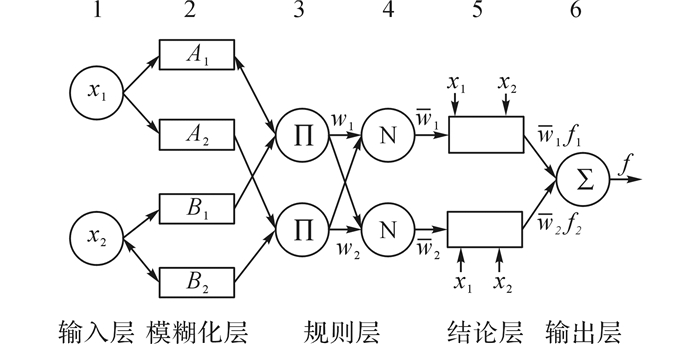
ANFIS是由Jang[27]提出的一种基于Takagi-Sugeno模型的一阶模糊神经网络.不失一般性, 假设一个双输入单输出的ANFIS系统(如图 1所示), 有2条IF-THEN模糊规则.
|
图 1 自适应模糊神经网络系统结构图 Fig. 1 Adaptive neuro-fuzzy inference system architecture |
规则1:
若x1 = A1, x2=B1, 则
| $ {f_1} = {r_1} + {p_1}{x_1} + {q_1}{x_2}. $ |
规则2:
若x1=A2, x2=B2, 则
| $ {f_2} = {r_2} + {p_2}{x_1} + {q_2}{x_2}. $ |
第1层为系统的输入层, 由2个节点组成, 作用是将输入向量x=[x1 x2]按原值传递到下一层.
第2层为模糊化层, 由4个节点组成, 作用是计算各输入分量属于各语言变量值模糊集合的隶属函数μij, 该层采用函数进行模糊化处理, 每个节点的输出:
| $ \mu _i^j = {\rm{exp}}\left( {-\frac{{{x_i}-{c_{ij}}}}{{{\sigma _{ij}}}}} \right), {\rm{ }}i = 1, 2, j = 1, 2. $ | (3) |
式中:cij和σij分别为隶属函数的中心和宽度.
第3层共有2个节点, 每个节点代表一条模糊规则, 作用是完成模糊逻辑的“与”操作, 采用Product推理计算出每条规则的适应度值, 即
| $ {w_1} = \mu _1^1\mu _2^1, {w_2} = \mu _1^2\mu _2^2. $ | (4) |
第4层为归一化层, 节点数与第3层一样, 所实现的是归一化计算, 即
| $ {{\bar w}_j} = \frac{{{w_j}}}{{{w_1} + {w_2}}}, j = 1, 2. $ | (5) |
第5层为结论层, 该层与第3层的节点数相同.其节点输出为
| $ {O_{4i}} = \overline {{w_i}} {f_i} = \overline {{w_i}} ({r_i} + {p_i}{x_1} + {q_i}{x_2}), i = 1, 2. $ | (6) |
第6层为输出层及去模糊化层, 只有一个节点, 使用面积中心法解模糊, 得到网络的最终输出为
| $ {O_5} = \frac{{{w_1}{f_1} + {w_2}{f_2}}}{{{w_1} + {w_2}}}. $ | (7) |
对于模糊神经网络模型的所有参数, 采用混合最小二乘法的梯度下降算法进行学习, 步骤如下:
1) 在固定型隶属函数的中心和宽度的前提下, 利用最小二乘法计算线性结论参数{r, p, q};
2) 固定结论参数, 采用误差反向传播算法对函数的中心和宽度进行学习可得
| $ S\left( {t + 1} \right) = S\left( t \right)-{\eta _s}\left( t \right)\frac{{\partial E}}{{\partial S}} + \alpha \Delta S\left( t \right), $ | (8) |
| $ \Delta S\left( t \right) = S\left( {t + 1} \right)-S\left( t \right), $ | (9) |
| $ E = \frac{1}{n}\sum\limits_{i = 1}^n {{{(f-{f_*})}^2}} . $ | (10) |
式中:S表示参数c和σ, ηs为学习率, α为动量项, f为预测输出, f*为实际输出.
利用训练样本数据, 重复上述步骤, 直到满足误差指标或者达到最大训练次数.
2 垃圾热值实时软测量模型设计本文的研究对象为处理量650 t/d的循环流化床生活垃圾焚烧锅炉, 其垃圾热值软测量模型的设计方法如图 2所示.从锅炉运行控制机理的角度出发, 在定性分析锅炉运行状态和垃圾热值之间潜在规律的基础上, 结合运行人员在长期实践中积累的经验, 选择垃圾热值软测量模型的输入变量, 然后对采集的数据样本进行数据预处理, 并进行归一化.利用减法聚类算法对处理后的样本空间进行划分, 以此来确定ANIFS模型的结构, 并进行学习、训练和验证, 最终将验证好的模型用于焚烧过程中垃圾热值的实时预测.这种建模方法所需设置的参数较少, 建模自动化程度高, 降低了建模的难度.同时, 基于机理和工艺的模型输入变量选择方法有利于提高垃圾热值软测量模型的外推性, 便于推广和使用.

|
图 2 循环流化床生活垃圾焚烧锅炉城市生活垃圾热值软测量模型设计方法 Fig. 2 Design methodology of heating value soft measurement of burning municipal solid waste (MSW) in circulating fluidized bed incinerators (CFBI) |
垃圾在循环流化床中的燃烧是一个十分复杂的物理化学变化过程, 垃圾在进入炉膛之后会经历几个过程:干燥加热、挥发分的析出和燃烧、焦炭燃烧.垃圾中质轻易碎的组分如纸张、塑料以及细颗粒等会在流化风的作用下进入炉膛上部, 经历干燥、挥发分的析出及燃烧以及残炭的燃烧等一系列过程;而密度较大、含水率高以及颗粒尺寸较大的组分, 如木头、厨余垃圾等终端速度大于流化速度的组分会落入密相区, 并在密相区中被床料加热、燃烧, 与煤的热量释放规律不同, 垃圾中高水分低热值的组分会在密相区中吸收大量的热, 而大量的挥发分在悬浮段燃烧[28-32].为了保证生活垃圾充分燃尽并降低污染物的排放, 《生活垃圾污染控制标准》(GB18485-2014) 对炉膛内焚烧温度和焚烧炉渣热灼减率制定了相应的要求, 因此, CFB生活垃圾焚烧锅炉在运行过程当中还需要添加适量的辅助燃煤.
结合上述生活垃圾在CFB锅炉中焚烧机理和现场运行人员的运行经验, 在判断生活垃圾热值高低的时候会综合考虑以下策略.
1) 入炉燃料是由煤和垃圾组成的, 对同一种煤, 热值比较稳定, 因此运行人员在判断入炉生活垃圾热值的高低时会将当前给煤量考虑进去.
2) 运行人员在司炉的时候, 有一个重要的任务就是将床温控制在850~950 ℃[33-34], 生活垃圾入炉后床温的变化情况是判断其热值最直接的参考依据, 在其他运行参数不变的情况下, 如果垃圾入炉后床温呈现出降低的趋势, 在维持同样水平的床温时, 投入的给煤量越多, 则垃圾的含水率越高, 热值越低, 反之则垃圾的热值越高.
3) CFB生活垃圾焚烧锅炉采用分级送风的方式, 密相区处于缺氧燃烧的状态, 而生活垃圾中的挥发分含量占有较高的比重, 通常是固定碳含量的5~7倍[4], 同时, 垃圾中的水分会降低挥发分的燃烧速率[35], 大量的挥发分在炉膛的中部和上部燃烧, 产生的热烟气会提高炉膛出口的温度[31, 36].如果生活垃圾进入炉膛后, 在未改变其他燃烧参数的状况下, 炉膛出口的温度呈现降低的趋势, 则表明入炉垃圾中挥发分的含量降低, 垃圾热值降低, 反之则说明垃圾的热值升高.
4) 在考虑床温、稀相区温度和炉膛出口温度的变化趋势时, 需要将这些温度的变化程度和温度水平同时考虑在内.
5) 锅炉在运行过程中会根据炉内流化状况、烟气含氧量和炉膛温度等参数调整一二次风量, 影响生活垃圾在炉内的燃烧过程, 因此要综合考虑风量变化带来的影响.
6) 入炉燃料的热值最终反映在锅炉的蒸发量上, 如果垃圾的热值稳定, 则锅炉的蒸发量与垃圾给料之间呈现正相关的关系;在给煤量和垃圾给料量一定的情况下, 如果蒸发量呈现下降的趋势, 意味着这段时间内垃圾的热值偏低;反之, 若锅炉的蒸汽品质长期维持在较高的水平, 说明垃圾的热值较高.
因此, 在构建CFB生活垃圾焚烧锅炉入炉垃圾热值的软测量模型过程中, 将垃圾给料量、给煤量、炉膛床温平均温度、床温平均温度变化速率、炉膛出口烟温、炉膛出口温度变化速率主蒸汽温度、主蒸汽流量、主蒸汽压力、一次风量、二次风量作为入炉垃圾热值软测量模型的输入变量.
在实际生产运行过程当中, 运行人员通过给煤机和垃圾给料机的变频反馈值来判断给煤量和垃圾给料量, 现场投用2台给煤机, 用这2台给煤机变频反馈值的和FC来表征给煤量;投用2台双螺旋垃圾给料机, 用2台给料机的变频反馈值的和FMSW来表征给料量;投用1台一次风机, 用一次风机变频反馈值FPA来表征一次风量;投用1台二次风机, 用二次风机变频反馈值FSA来表征一次风量;由于床温测点较多, 选用其平均值tM作为模型的输入;采用床温平均值5 s内的变化值ΔtM来表征床温的变化趋势:
| $ \Delta {t_{\rm{M}}}(k) = {t_{\rm{M}}}(k)-{t_{\rm{M}}}(k-5); $ |
炉膛出口温度有2个测点, 用其平均值tC作为模型输入;采用炉膛出口温度平均值5 s内的变化值ΔtC来表征炉膛出口温度的变化趋势,
| $ \Delta {t_{\rm{C}}}(k) = {t_{\rm{C}}}(k)-{t_{\rm{C}}}(k-5); $ |
主蒸汽温度只有1个测点, 用tS表示;主蒸汽压力只有1个测点, 用pS表示;主蒸汽流量只有一个测点, 用FS表示.因此, CFB生活垃圾焚烧锅炉的入炉垃圾热值软测量模型共有11个输入变量.
2.2 垃圾热值软测量模型输出变量的模糊等级划分CFB生活垃圾焚烧锅炉入炉垃圾热值软测量模型的输出用模糊语言的形式来表达, 将垃圾的热值Q划分为9个模糊等级, 其模糊子集为{负极大, 负大, 负中, 负小, 零, 正小, 正中, 正大, 正极大}, 用英文表示为{NEB, NB, NM, NS, ZE, PS, PM, PB, PEB}, 垃圾热值模糊等级划分是由经验丰富的现场运行人员根据长时间的运行经验而得出的判断.
如表 1所示为9组典型的CFB生活垃圾焚烧锅炉的运行工况及相应的入炉垃圾热值Q的模糊分类, 下面结合具体的运行参数说明入炉垃圾热值的分类方法.1) 通过垃圾给料机的变频反馈值FMSW和给煤机的变频反馈值FC判断入炉燃料中生活垃圾和煤占的比重, 通常垃圾热值越高, 给煤量越低, 对比NEB等级热值的垃圾和PEB等级热值的垃圾不难发现, 前者入炉燃料中煤的比重远远大于后者;2) 结合主汽流量FS、主蒸汽温度tS和主汽压力pS, 判断锅炉当前的运行负荷, 在同样给料和给煤的前提下, 负荷越高则表明燃料释放的热值越多, 入炉燃料热值越趋于高等级, 对比NS等级热值的垃圾和PS等级热值的垃圾, 可以发现后者FS、tS和pS均大于前者;3) 在实际运行过程中入炉燃料的热值从释放到被汽水工质吸收是一个大滞后的过程, 当入炉垃圾热值频繁波动时, 单纯依靠锅炉负荷难以判断垃圾热值的水平, 运行人员会参考床温平均温度tM、炉膛出口的平均温度tC判断入炉垃圾热值的水平, 在同样给料和给煤的前提下, 床温越低说明垃圾中的含水率越高, 炉膛出口温度越高说明垃圾中挥发分含量越高, 对比NS等级热值的垃圾和ZE等级热值的垃圾, 两者的入炉燃料构成和负荷都接近, 但是后者的TM和TC均大于前者;4)ΔtM和ΔtC通过炉膛中温度的变化, 间接反映了入炉燃料热值的波动情况, 以NB等级热值的垃圾为例, 该工况下的ΔtM和ΔtC均小于0, 说明此时入炉垃圾热值处于下降的趋势, 因此后续时间内的垃圾热值的等级不会超过NB, 除非ΔtM和ΔtC大于0;5) 一次风流量FPA和二次风流量FSA间接反映了入炉燃料中可燃物含量的比重, 可燃物含量越多, 则送风量越大, 对比NEB等级热值的垃圾和NB等级热值的垃圾, 可以发现, 后者总的送风量要高于前者.
| 表 1 CFB生活垃圾焚烧锅炉典型运行工况下垃圾热值模糊分类 Table 1 Fuzzy classification of HVs under characteristic operating conditions of CFB incinerator |
采用DELL OPTILEX 7010型台式机作为建模的硬件平台, CPU型号为i5-3570, 8 G内存.采用2013a版本的Matlab计算引擎作为建模的软件平台.
1) 样本的采集和数据预处理.从现场选取采集训练样本和测试样本, 尽量覆盖尽可能多的工况, 以保证训练样本的完备性.对样本集进行粗大误差处理和随机误差处理, 以摒除那些并不是反映对象真实情况的虚假信息, 将锅炉压火、给料机堵塞、结渣结焦等异常工况排除掉, 最终选择2 000组工况作为模型的训练样本.部分样本见表 1, 选取200组工况作为模型的预测性能的验证样本.为了避免预测模型的参数之间量纲和数量级的不同对模型性能造成的不良影响, 训练样本和测试样本的输入空间经过归一化处理后映射到[0,1].
2) 减法聚类获取ANFIS的初始结构.聚类半径是rα和rβ是影响减法聚类算法聚类效果的2个重要参数, 聚类半径太大则难以获取完备的初始模糊规则, 聚类半径太小会使后续会导致模糊神经网络结构的冗余[22], 经过粗调和细调之后将模糊半径设置为rα=0.38、rβ=1.5rα, 最终得到39个聚类中心, 即39条初始模糊规则, 部分聚类中心如表 2所示.
| 表 2 建模训练样本的减法聚类中心 Table 2 Subtractive clustering centers of training samples for modelling |
在构建对比模型时, 采用的训练样本和测试样本与ANFIS模型所采用的样本是一致的.
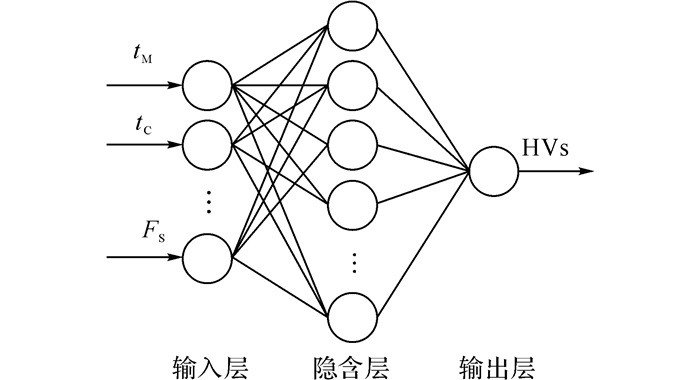
1) 创建BP神经网络模型.误差反向传播神经网络(back propagation neural network, BPNN)[16-17, 37]建模方法都是目前使用最为广泛的MLP神经网络模型, BP神经网络模型具有优良容错性、自学习的能力和非线性动力学特性, 本文采用3层结构的BP神经网络模型, 其结构如图 3所示.模型所采用的学习算法为动量反传和动态自适应学习率的梯度下降法, 隐含层节点的传递函数为Sigmod函数, 迭代次数为300次, 初始学习率为0.1, 训练目标为0.000 5.合理设置隐含层节点数是构建BP模型的关键之处, 节点数太少无法表达复杂的非线性关系, 节点数太多则会造成训练时间过长, 并且容易出现过拟合现象.目前, 隐含层节点数的设置还没有统一的标准, 本文利用粒子群优化算法[38](particle swarm optimization, PSO)对网络的节点数进行寻优, 最终确定隐含层的节点数是16.
|
图 3 基于BP神经网络模型的垃圾热值软测量模型 Fig. 3 Soft sensor of HVs based onback propagation neural network |
2) 创建RFB神经网络模型.RBF神经网络也是一种3层前馈网络, 拓扑结构和3层BP神经网络一样, 拥有输入层、隐含层和输出层, 但是隐含层是由径向基函数构成.RBF算法具有拓扑结构简单、收敛速度快、不易陷入局部最小点和鲁棒性好等优点而被广泛应用[16].同样, 构建RBF模型的关键也是确定隐含层神经元的个数, Matlab RBF神经网络工具箱利用扩展常数SPREAD确定隐含层神经元个数, 通常扩展系数越小, RBF模型的输出结果越光滑, 但是, 模型的泛化能力越低.本文采用PSO算法对SPREAD系数进行启发式搜索, 最终获得最优的扩展常数SPREAD为2.5.
3) 创建SVM模型.SVM是一种基于结构风险最小化思想的统计学习方法[20, 39], 先将样本数据通过映射到高维特征空间, 并采用极小化上界风险的方法进行非线性回归.建立精确的SVM模型需要确立惩罚因子C和径向基函数的核参数g, 本文利用PSO算法对SVM模型的C和g进行寻优[40], 得到最佳的参数C=100, g=1.18.
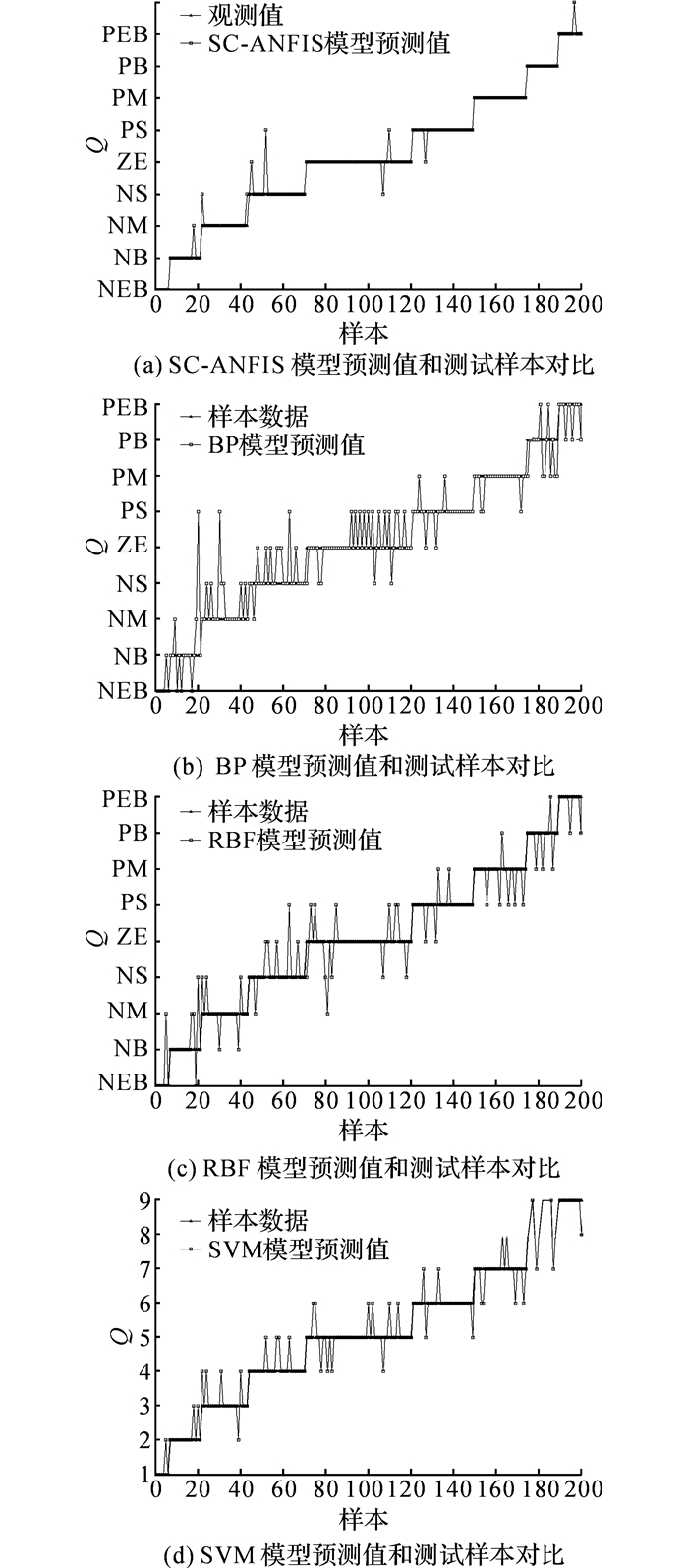
2.5 结果和讨论选取训练样本之外的验证样本200组, 将样本空间的输入变量, 分别输入上述各个模型, 预测垃圾的热值, 统计得到SC-ANFIS模型、BP神经网络模型、RBF神经网络模型和SVM模型的预测精度分别是95.5%、70%、79%和81.5%, 预测结果和样本数据之间的对比如图 4所示.
|
图 4 测试样本和不同模型预测值的对比 Fig. 4 Comparisons of heating values based on sample data and different predictive model |
从统计结果和对比图中可以得出以下结论:
1) BP模型的垃圾热值预测精度最低, 导致这一结果的原因有以下2个方面:最有可能的原因是BP神经网络模型的性能对初始权值和阈值有一定程度上的依赖, 通常对初始权值和阈值进行随机赋值, 如果初始权值和阈值设置的不理想, BP网络容易陷入局部最优值[41], 使得BP模型的预测精度和泛化能力下降;BP算法不善于表达基于规则的知识, 难以充分利用已有的经验知识, 而运行CFB垃圾焚烧锅炉的历史运行过程数据中包含了运行操作人员的经验和判断, 这部分知识没有得到充分的挖掘.
2) RBF模型和SVM模型的预测精度比较接近, 预测精度比BP模型要高5%以上, 说明在垃圾热值预测方面, 这2个模型在泛化能力和逃避局部极小值方面比未经优化的BP模型更优秀.但是相较于SVM模型, RBF模型某些点的预测误差超过了一个等级, 表明的SVM模型的稳定性更佳.
3) SC-ANFIS模型拥有最优秀的预测性能和可靠性, 能够将预测误差控制在5%以下, 并且预测误差均未超过1个等级, 说明该模型具有良好的学习能力和泛化能力, 能够充分表述运行操作人员的经验和决策, 能够自适应的从过程数据中反映出入炉垃圾热值的变化趋势.
3 与实际垃圾热值对比为了验证基于SC-ANFIS模型的实际应用效果, 将模型预测结果和实际的垃圾热值测量结果进行对比, 垃圾热值的测量过程是按照住房建设部颁发《生活垃圾采样和分析方法(CJ/T313-2009)》进行的, CFB垃圾焚烧锅炉的运行工况如表 1中所述, 每个工况下垃圾热值的实际预测结果和模型的软测量结果如表 3所示, 其中Qreal为实际热值.从表 3中可以看出, 在实际生产过程中, 基于SC-ANFIS的入炉垃圾热值软测量模型能够很好地反映出实际垃圾热值的变化趋势, 表明SC-ANFIS模型具有很强的学习能力和泛化能力, 能够适应复杂多变的现场运行工况, 将入炉垃圾热值的非线性变化特性表征出来.
| 表 3 城市生活垃圾实际热值与SC-ANFIS预测值对比 Table 3 Comparisons of MSW heating values based on experiment and subtractive clustering based adaptive neuro-fuzzy inference system (SC-ANFIS) predictivemodel |
(1) 基于减法聚类的模糊神经网络模型具有建模过程简便明了的特点, 需要设置的参数少, 无需太多经验就能够构建出高精度的模型, 为该建模方法的应用推广奠定了良好的基础.
(2) 通过基于减法聚类的模糊神经网络模型对流化床垃圾焚烧锅炉的相关运行参数进行挖掘, 能够构建入炉垃圾热值的实时软测量模型.从预测仿真结果来看, 该模型具有理想的预测精度和可靠性, 能够真实快速地反映出入炉垃圾热值的变化情况.
(3) 相较于目前应用广泛的BP神经网络模型、RBF神经网络模型和SVM模型, SC-ANFIS模型在循环流化床垃圾焚烧锅炉的入炉垃圾热值的软测量方面具有更高的预测精度和泛化能力, 在实际应用中更值得人们尝试.
(4) 基于减法聚类的模糊神经网络入炉垃圾热值软测量模型, 给研究人员和运行人员研究、了解流化床垃圾焚烧锅炉的入炉垃圾热值的特性提供了更多的途径.SC-ANFIS模型的计算速度很快, 具有良好的实时性, 能够胜任实时的垃圾热值监测任务, 能够在一定程度上为锅炉的运行和优化调整提供指导性的意见, 也能为锅炉的燃烧自动控制系统提供可靠的热值反馈信号.
| [1] |
马攀, 马增益, 陈继华, 等. 循环流化床垃圾焚烧炉混烧羊毛脂废料试验研究[J].
中国电机工程学报, 2012, 32(8): 6–11.
MA Pan, MA Zeng-yi, CHEN Ji-hua, et al. Experimental study on co-firing of lanolin waste and municipal solid waste in a circulating fluidized bed incinerator[J]. Proceedings of the CSEE, 2012, 32(8): 6–11. |
| [2] |
曹玉林, 严建华, 李晓东, 等. 垃圾与煤流化床混烧及其排放特性[J].
热力发电, 2005, 34(11): 57–63.
CAO Yu-lin, YAN Jian-hua, LI Xiao-dong, et al. Study on co-firing of coal and MSW and emission performance in a circulating fluidized bed incinerator[J]. Thermal Power Generation, 2005, 34(11): 57–63. DOI:10.3969/j.issn.1002-3364.2005.11.015 |
| [3] |
中国环境保护产业协会城市生活垃圾处理专业委员会. 城市生活垃圾处理行业2014年发展综述[J].
中国环保产业, 2015, 11: 17–24.
Specialized Committee of Urban Domestic Refuse of CAEPI. Development report on China treatment industry of urban domestic refuse in 2013[J]. China Environmental Protection Industry, 2015, 11: 17–24. DOI:10.3969/j.issn.1006-5377.2015.03.007 |
| [4] | ZHOU H, MENGA, LONG Y, et al. An overview of characteristics of municipal solid waste fuel in China: physical, chemical composition and heating value[J]. Renewable and Sustainable Energy Reviews, 2014, 36: 107–122. DOI:10.1016/j.rser.2014.04.024 |
| [5] | LIUKKONEN M, HILTUNEN T, HLIKK E, et al. Modeling of the fluidized bed combustion process and NOx emissions using self-organizing maps: an application to the diagnosis of process states[J]. Environmental Modelling and Software, 2011, 26(5): 605–614. DOI:10.1016/j.envsoft.2010.12.002 |
| [6] |
沈凯. 垃圾焚烧炉自适应控制策略及热值监测模型研究[D]. 武汉: 华中科技大学, 2005: 77-79.
SHEN Kai. Study on the adaptive control strategy of incinerators and the monitoring model of heating values[D]. Wuhan: Huazhong University of Science and Technology, 2005: 77-79. |
| [7] |
谢承利, 陆继东, 沈凯, 等. 基于焚烧运行参数的垃圾热值软测量模型[J].
燃烧科学与技术, 2007, 13(1): 81–85.
XIE Cheng-li, LU Ji-dong, SHEN Kai, et al. Indirect measurement model for waste heating value based on incineration operational parameters[J]. Journal of Combustion Science and Technology, 2007, 13(1): 81–85. |
| [8] | MCCAULEY B, REINHART D, SEIR H, et al. Municipal solid waste composition studies[J]. ASCE Practice Periodical of Hazardous and Radioactive Waste, 1997, 1(4): 158–163. DOI:10.1061/(ASCE)1090-025X(1997)1:4(158) |
| [9] | DAVID C, BRAINK K, JOHN M. Estimating the lower heating values of hazardous and solid wastes[J]. Air and Waste Manage Association, 1999, 49(4): 471–476. DOI:10.1080/10473289.1999.10463816 |
| [10] | LIN X, WANG F, CHI Y, et al. A simple method for predicting the lower heating value of municipal solid waste in China based on wet physical composition[J]. Waste Management, 2105, 36: 24–32. |
| [11] | Moh'd A, Hani A, Abu Q. Energy content of municipal solid waste in Jordan and its potential utilization[J]. Energy Conversation and Management, 2000, 41: 983–991. DOI:10.1016/S0196-8904(99)00155-7 |
| [12] | CHANG Y, LIN C, CHAN J, et al. Multiple regression models for the lower heating value of municipal solid waste in Taiwan[J]. Journal of Environmental Management, 2007, 85: 891–899. DOI:10.1016/j.jenvman.2006.10.025 |
| [13] | EBRU A, AHMET D. Energy content estimation of municipal solid waste by multiple regression analysis[C] // 5th International Advanced Technologies Symposium. Turkery:[s. n.] 2009. |
| [14] | DONG C, JIN B, LI D. Predicting the heating value of MSW with a feed forward neural network[J]. Waste Management, 2003, 23: 103–106. DOI:10.1016/S0956-053X(02)00162-9 |
| [15] | HEIKKINEN M, HILTUNEN T, LIUKKONEN M, et al. A modelling and optimization and optimization system for fluidized bed power plants[J]. Expert Systems with Applications, 2009, 36(7): 10247–10279. |
| [16] | YILMAZ I, KAYNAR O. Multiple regression, ANNRBF, MLP and ANFIS models for prediction of swell potential of clay soils[J]. Expert Systems with Applications, 2011, 38(5): 5958–5966. DOI:10.1016/j.eswa.2010.11.027 |
| [17] | MOGHADDAMNIA A, REMESAN R, HASSANPOUR M, et al. Comparison of LLR, MLP, Elman, NNARX and ANFIS Models-with a case study in solar radiation estimation[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2009, 71(8): 975–982. |
| [18] | ROOLHOLLAH N, GHOLAMALI H, KHOSRO A, et al. Uncertainty analysis of developed ANN and ANFIS models in prediction of carbon monoxide daily concentration[J]. Atmospheric Environment, 2010, 44(4): 476–482. DOI:10.1016/j.atmosenv.2009.11.005 |
| [19] | ZHANG Y, ZHOU Q, SUN C, et al. RBF neural network and ANFIS-based short-term load forecasting approach in real-time price environment[J]. IEEE Transactions on Power Systems, 2008, 23(3): 853–858. DOI:10.1109/TPWRS.2008.922249 |
| [20] | YANG S, Ross S. Comparison of support vector machine, neural network and CART algorithms for the land-cover classification using limited training data points[J]. ISPRS Journal of Photogrammetry andremote sensing, 2012, 70: 78–87. DOI:10.1016/j.isprsjprs.2012.04.001 |
| [21] | YILMAZ I. Comparison of landslide susceptibility mapping methodologies for Kouyulhisar, Turkey: conditional probability, logistic regression, artificial neural networks and support vector machine[J]. Environmental Earth Sciences, 2010, 614: 821–836. |
| [22] |
潘海鹏, 吕勇松. 时滞系统的模糊神经网络补偿控制[J].
浙江大学学报:工学版, 2010, 44(7): 1343–1347.
Pan Hai-peng, LV Yong-song. Fuzzy neural network control method with compensation for time-delay system[J]. Journal of Zhejiang University: Engineering Science, 2010, 44(7): 1343–1347. |
| [23] | CHEN M. A hybrid ANFIS model for business failure prediction utilizing particle swarm optimization and subtractive clustering[J]. Information Science, 2013, 220: 180–195. DOI:10.1016/j.ins.2011.09.013 |
| [24] |
李培强, 李欣然, 陈辉华, 等. 基于减法聚类的模糊神经网络负荷建模[J].
电工技术学报, 2006, 2(19): 2–6.
LI Pei-qiang, LI Xin-ran, CHEN Hui-hua, et al. Fuzzy neural network load modeling based on subtractive clustering[J]. Transactions of China Electrotechnical Society, 2006, 2(19): 2–6. |
| [25] | HOSSEIN A, TAGHANNSKI S, MASOUND K, et al. Implementing ANFIS for prediction of reservoir oil solution gas-oil ratio[J]. Journal of Natural Gas Science and Engineering, 2015, 15: 325–334. |
| [26] | CHIU S. Fuzzy model identification based on cluster estimation[J]. Journal of Intelligent and Fuzzy Systems, 1994, 2: 267–278. |
| [27] | JANG J. ANFIS: adaptive-network-based fuzzy inference system[J]. IEEE Transactions on Systems, Man and Cybernetics, 1993, 2(33): 665–685. |
| [28] |
闫涛. 循环流化床焚烧炉中生活垃圾燃烧特性研究[D]. 北京: 清华大学, 2004: 44-49.
YAN Tao. Research on combustion characteristics of municipal solid waste in circulating fluidized bed incinerator[D].Beijing: Tsinghua University, 2004: 44-49. |
| [29] |
刘青, 于海洋, 张守玉, 等. 循环流化床垃圾焚烧锅炉炉膛设计分析[J].
锅炉技术, 2007, 38(6): 20–25.
LIU Qing, YU Hai-yang, ZHANG Shou-yu, et al. Analysis for the design of circulating fluidized bed incinerator furnace[J]. Boiler Technology, 2007, 38(6): 20–25. |
| [30] | 徐旭常, 周力行. 燃烧技术手册[M]. 北京: 化学工业出版社, 2008: 578-581. |
| [31] |
江爱鹏. 城市生活垃圾典型组分的燃烧特性和排放特性研究[D]. 杭州: 浙江大学, 2002: 43-58.
JIANG Ai-peng. Research on combustion characteristics and emission performance of typical municipal solid waste components in circulating fluidized bed incinerator[D]. Hangzhou: Zhejiang University, 2002: 43-58. |
| [32] |
张衍国, 李海明, 李海清, 等. 垃圾焚烧炉内传热计算[J].
清华大学学报:自然科学版, 2001, 41(21): 95–98.
ZHANG Yan-guo, LI Hai-ming, LI Hai-qing, et al. Heat transfer in a municipal solid waste incinerator[J]. Journal of Tsinghua University: Natural ScienceEdition, 2001, 41(21): 95–98. |
| [33] |
张轩. 大型循环流化床床温动态模型与优化控制的研究[D]. 北京: 华北电力大学, 2013: 15-16.
ZHANG Xuan. Research on dynamic modeling and optimization control on the bed temperature of circulating fluidized bed Boiler[D]. Beijing: North China Electric Power University, 2013: 15-16. |
| [34] | CJJ/T 137-2010. 生活垃圾焚烧厂评价标准[S]. 北京: 中华人民共和国住房和城乡建设部, 2010. |
| [35] | SAITO M, AMGAI K, OGIWARA G, et al. Combustion characteristics of waste material containing high moisture[J]. Fuel, 2001, 8(9): 1201–1209. |
| [36] |
董长青, 金保升, 仲兆平, 等. 循环流化床掺烧生活垃圾实验研究[J].
东南大学学报:自然科学版, 2002, 3(21): 95–99.
DONG Chang-qing, JIN Bao-sheng, ZHONG Zhao-ping, et al. Experimental study on the co-firing of municipal refuse in a circulating fluidized bed[J]. Journal of Southeast University: Natural Science Edition, 2002, 3(21): 95–99. |
| [37] | LIUKKONEN M, HLIKK E, HILTUNNEN T, et al. Dynamic soft sensors for NOx emissions in a circulating fluidized bed boiler[J]. Applied Energy, 2012, 97: 483–490. DOI:10.1016/j.apenergy.2012.01.074 |
| [38] | BUYUKDA M. Co-combustion of peanut hull and coal blends: artificial neural networks modelling, particle swarm optimization and Monte Carlo simulation[J]. Bioresource Technology, 2016, 216: 280–286. DOI:10.1016/j.biortech.2016.05.091 |
| [39] |
李清毅, 周昊, 林阿平, 等. 基于网格搜索和支持向量机的灰熔点预测[J].
浙江大学学报:工学版, 2011, 45(2): 2181–2187.
LI Qing-yi, ZHOU Hao, LIN A-ping, et al. Prediction of ash fusion temperature based on grid search and support vector machine[J]. Journal of Zhejiang University: Engineering Science, 2011, 45(2): 2181–2187. |
| [40] |
赵志刚, 张纯杰, 苟向锋, 等. 基于粒子群优化支持向量机的太阳电池温度预测[J].
物理学报, 2015, 64(8): 1–7.
ZHAO Zhi-gang, ZHANG Chun-jie, GOU Xiang-feng, et al. Solar cell temperature prediction model of support vector machine optimized by particle swarm optimization algorithm[J]. Acta Physica Sinica, 2015, 64(8): 1–7. |
| [41] |
王德明, 王莉, 张广明. 基于遗传BP神经网络的短期风速预测模型[J].
浙江大学学报:工学版, 2012, 46(5): 837–841.
WANG De-ming, WANG Li, ZHANG Guang-ming. Short-term wind speed forecast model for wind farms based on genetic BP neural network[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(5): 837–841. |



