2. 天津大学 仁爱学院机械工程系, 天津 301636
2. Mechanical Engineering Department of Tianjin University Ren'Ai College, Tianjin 301636 China
排气歧管是发动机排气系统的重要组成部分, 直接与缸盖相连, 将高温废气传递给排气系统后续部件.随着发动机性能的不断提升以及排放法规的日趋严格, 发动机的排气温度也越来越高, 排气歧管受到的热负荷也随之加大.排气歧管在整个寿命周期内不仅受到高温燃气的侵蚀, 还要承受来自发动机的振动载荷.厚度小, 耐热性、热疲劳性更好的冲压不锈钢排气歧管逐步取代传统的铸铁排气歧管被越来越多地应用在汽油机上[1].
在耐热钢被越来越多地应用于排气歧管的同时, 振动疲劳破坏的危害逐渐被凸显出来.国内外学者针对排气歧管振动疲劳寿命的虚拟耐久疲劳预测进行了大量的研究工作.Sissa等[2]对一款增压柴油机的排气歧管分别进行了低周热疲劳以及高周振动疲劳寿命预测, 但并没有将热疲劳与振动疲劳结合起来.不能将热载荷与机械载荷共同作用视为两者的简单相加, 而是热载荷影响了结构刚度, 进而影响了机械载荷.Santacreu等[3]基于优化后的Taira模型、Larson-Miller模型对一款不锈钢排气歧管进行了热机耦合疲劳寿命预测.袁懋荣等[4]将热应力设为静载荷, 实现了热载荷与振动载荷的耦合, 对一款铸造排气歧管进行了疲劳寿命预测.有关热载荷对振动特性及振动疲劳寿命影响的研究还比较少[5-10].
在结构优化方面, 李建华[11]以轻量化为目标, 通过经验优化与形貌优化结合的方法对排气歧管进行了优化设计.范文杰等[12]提出了一种结构的多目标拓扑优化研究方法, 采用折衷规划法及平均频率法定义多目标拓扑优化的目标函数, 优化得到了同时满足静态刚度和低频振动要求的车架拓扑结构.Carpinelli等[13]提出了一种基于加权指数法的多目标优化方法, 通过加权指数法可以获得更多的Pereto前沿最优解, 求解速度快且准确率高.
为了深入研究温度及热应力分布对振动疲劳的作用机理及影响规律, 本文开展高温环境下的排气歧管振动特性及振动疲劳研究:将基于流固耦合分析得到的排气歧管温度分布映射到频率响应分析模型当中建立热机耦合模型;以温度及热应力分布为变量分别进行多个工况下的频率响应分析, 定性研究热载荷对排气歧管振动特性的影响;根据应力传递函数及激励处功率谱密度计算排气歧管振动疲劳, 分析热载荷对排气歧管振动疲劳寿命的影响.为了提高排气歧管振动疲劳寿命, 对发动机支架进行拓扑优化及基于加权指数法的多目标形貌设计, 在提高排气歧管整体刚度的基础上针对性地优化排气歧管的1、2、3、6阶固有频率, 提出发动机支架的优化设计方案.
1 基础理论 1.1 热机耦合对于多自由度线性结构, 考虑其承受随频率变化的载荷, 求解方程[14]为
| $ \boldsymbol{M}\left\{ {\ddot x} \right\} + \boldsymbol{C}\left\{ {\dot x} \right\} + \boldsymbol{K}\left\{ x \right\} = \left\{ {f\left( \omega \right)} \right\}{\rm{exp}}({\rm{i}}\omega t). $ | (1) |
式中:M为质量矩阵、C为阻尼矩阵、K为刚度矩阵, {x}、{ẋ}、{ẍ}分别表示位移向量矩阵、速度向量矩阵和加速度向量矩阵, ω为激励频率, i为虚数单位, t为时间.
频率响应的求解方法有直接法与模态法.模态法可利用结构振型减小计算规模, 为了提高计算效率, 选择模态法进行排气歧管频率响应分析.
在计算过程中, 引入假定解:
| $ \left\{ \boldsymbol{x} \right\} = \boldsymbol{\varphi} \left\{ {\varepsilon \left( \omega \right)} \right\}{\rm{exp}}({\rm{i}}\omega t). $ | (2) |
将变量从物理坐标u(ω)转换为模态坐标ε(ω), φ为初始相位.将式(2) 代入式(1), 并将阻尼分别加到每个模态上, 每个模态有形式方程如下式:
| $ -{\omega ^2}{m_j}\xi \left( \omega \right) + j\omega {b_j}\xi \left( \omega \right) + {k_j}\xi \left( \omega \right) = {p_j}\left( \omega \right). $ | (3) |
式中:mj、bj、kj、pj分别为第j阶模态质量、模态阻尼、模态刚度、模态力.
各阶模态响应为
| $ \xi \left( \omega \right) = \frac{{{p_j}\left( \omega \right)}}{{-{m_j}{\omega ^2} + j{b_j}\omega + {k_j}}}. $ | (4) |
在高温环境下, 热载荷会使得结构的刚度矩阵发生显著变化.首先, 材料弹性模量会随温度升高而降低, 使结构的初始刚度矩阵KL发生变化;此外, 热环境引起的热应力会改变结构的刚度分布, 产生附加热应力刚度矩阵Kσ, 这被称作是应力刚化现象;最后, 结构的非线性形变会产生附加形变刚度矩阵KNL, 因而考虑温度效应后, 结构的总刚度K为
| $ \boldsymbol{K} = {\boldsymbol{K}_{\rm{L}}} + {\boldsymbol{K}_\sigma } + {\boldsymbol{K}_{{\rm{NL}}}}. $ | (5) |
| $ {\mathit{\boldsymbol{K}}_{\rm{L}}} = \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{B}}_{\rm{L}}}\prime {\mathit{\boldsymbol{D}}_{\rm{T}}}{\mathit{\boldsymbol{B}}_{\rm{T}}}\rm{d}\mathit{\Omega }.} $ | (6) |
| $ {\mathit{\boldsymbol{K}}_{{\rm{NL}}}} = \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{B}}_{\rm{L}}}\prime {\mathit{\boldsymbol{D}}_{\rm{T}}}{\mathit{\boldsymbol{B}}_{{\rm{NL}}}}{\rm{d}}\mathit{\Omega }} + {\rm{ }}{\mathit{\boldsymbol{B}}_{{\rm{NL}}}}\prime {\mathit{\boldsymbol{D}}_{\rm{T}}}{\mathit{\boldsymbol{B}}_{\rm{L}}} + {\mathit{\boldsymbol{B}}_{{\rm{NL}}}}\prime {\mathit{\boldsymbol{D}}_{\rm{T}}}{\mathit{\boldsymbol{B}}_{{\rm{NL}}}}, $ | (7) |
| $ {\boldsymbol{\sigma} _{\rm{T}}} = {\boldsymbol{D}_{\rm{T}}}\left( {\varepsilon-{\varepsilon _0}} \right), $ | (8) |
| $ {\mathit{\boldsymbol{K}}_\sigma } = \int\limits_\mathit{\Omega } {H\prime {\sigma _{\rm{T}}}H{\rm{d}}\mathit{\Omega }} . $ | (9) |
式中:B、DT、H、σT分别为几何矩阵、弹性矩阵、形函数矩阵、热应力矩阵;带有下标L、NL与T的矩阵分别代表线性、非线性及热应力矩阵.
排气歧管长期工作在高温环境中, 为了计算结果的准确性, 在进行频率响应分析时需考虑热载荷对其振动特性的影响[15].排气歧管形变引起的形变附加刚度矩阵较小, 这里只考虑初始刚度矩阵的变化及附加热应力矩阵的影响.
1.2 振动疲劳排气歧管所受振动载荷大部分来自于工作中的发动机, 其振动属于随机振动, 需要较长的时域信号才能准确反映加载过程.在有限元分析当中对长时间的时域信号的处理是非常困难的, 因此随机振动疲劳不适合根据应力或应变的时域信号进行求解.在频域范围内, 把激励的时域信号转变为功率谱密度信号, 通过随机振动分析可得到响应功率谱密度函数:
| $ {S_\sigma }\left( \omega \right) = {H_\sigma }\left( \omega \right){S_{\rm{F}}}\left( \omega \right)H_\sigma ^{\rm{T}}\left( \omega \right). $ | (10) |
式中:Sσ(ω)为应力响应功率谱密度函数, SF(ω)为激励处的功率谱密度函数, Hσ(ω)为频率响应分析得到的响应应力传递函数.
Dirlik算法是通过对多种不同类型功率谱密度函数研究后得到的准经验模型, 是发展较为成熟的一种疲劳损伤算法, 现已集成在Fatigue等商业软件当中, 方便调取进行运算,其表达式为
| $ \begin{array}{l} p\left( S \right) = \frac{1}{\sigma }\left[{\frac{{{D_1}}}{Q}{\rm{exp}}\left( {-\frac{Z}{Q}} \right) + \frac{{{D_2}Z}}{{{R^2}}}{\rm{exp}}(-\frac{{{Z^2}}}{{2{R^2}}}) + } \right.\\ \;\;\;\;\;\left. {{D_3}Z{\rm{exp}}\left( {\frac{{-{Z^2}}}{2}} \right)} \right]. \end{array} $ | (11) |
式中:
| $ \begin{array}{l} {D_1} = \frac{{2({x_{\rm{m}}}-{\gamma ^2})}}{{1 + {\gamma ^2}}}, {D_2} = \frac{{1-\gamma-{D_1} + D_1^2}}{{1 - R}}, \\ {D_3} = 1 - {D_1} - {D_2}, {x_{\rm{m}}} = \frac{{{m_1}}}{{{m_0}}}\sqrt {\frac{{{m_2}}}{{{m_4}}}}, \\ Q = \frac{{1.25(\gamma - {D_3} - {D_2}R)}}{{{D_1}}}, Z = \frac{S}{\sigma }, \\ R = \frac{{\gamma - {x_m} - D_1^2}}{{1 - \gamma - {D_1} + D_1^2}}, \gamma = \frac{{{m_2}}}{{\sqrt {{m_0}{m_4}} }}. \end{array} $ | (12) |
其中,m1、m2、m3、m4为功率谱密度函数的4个惯性矩.
频域方法计算疲劳损伤可同时考虑动载荷及共振的影响, 因此计算结果与长时间历程的瞬态分析相比更加准确.Dirlik算法较为复杂, 但可应用各种不同工况的计算.其疲劳损伤公式为
| $ \begin{array}{l} D = \frac{{E\left[P \right]}}{C}{\sigma ^m}[{D_1}{Q^m}\mathit{\Gamma }\left( {1 + m} \right) + \\ \;\;\;\;\;\;\;\;\;\;{\left( {\sqrt 2 } \right)^m}\mathit{\Gamma }\left( {1 + \frac{m}{2}} \right)({D_2}{\left| R \right|^m} + {D_3})]. \end{array} $ | (13) |
式中:Γ为第二类欧拉积分又称Gamma函数.
1.3 多目标优化拓扑优化能在选定的设计空间内寻找最优材料分布, 从而在满足各种性能约束下得到最轻量化的设计.形貌优化是一种寻找形状最优化的方法, 即在板形结构中寻找最优的加强筋分布的概念设计方法[16].在薄壁冲压件的设计过程中, 通过形貌优化可以在不增加结构重量的同时提高结构刚度.
优化设计三要素为设计变量、目标函数、约束条件.在设计过程中通过改变设计变量从而提高产品性能;目标函数是关于设计变量的函数, 体现了对最优性能的要求;约束条件是对优化过程的限制, 即对设计变量和其他性能的要求[17].数学模型可表述为
1) 最小化目标函数:
| $ f\left( X \right) = f({x_1}, {x_2}, \ldots, {x_n}); $ | (14) |
2) 约束条件:
| $ \left. \begin{array}{l} {g_p}\left( X \right) \le 0, p = 1, 2, \ldots, m;\\ {h_k}\left( X \right) = 0, k = 1, 2, \ldots, {m_k};\\ x_{\rm{q}}^{\rm{L}} \le {x_1} \le x_{\rm{q}}^{\rm{U}}, q = 1, 2, \ldots, n. \end{array} \right\} $ | (15) |
式中:X=(x1, x2, …, xn)为设计变量、f(X)为目标函数、g(X)为不等式约束函数、h(X)为等式约束函数、n为变量分量的个数、U和L分别表示上、下限.
本文的多目标优化方法是通过加权指数法对子目标进行归一化, 将多个子目标转换为一个总目标.
| $ W = \sum\limits_{s- 1}^M {\left\{ {[{\rm{exp}}\;(p{\omega _s})-1]{\rm{exp}}(p{F_s})} \right\}} . $ | (16) |
式中:p为惩罚因子.ωs为第s个目标的权值, Fs为规范化的目标函数, M为子目标个数.
2 频率响应分析 2.1 模型建立及验证文中研究的排气歧管由441不锈钢冲压焊接而成, 不考虑冲压减薄率的情况下可认为各部件厚度均匀, 使用壳单元建模可以在大幅减少网格数量、提高计算速度的同时保证较好的计算精度.通过四边形网格(quads)划分网格, 网格大小为2 mm;将催化器载体及发动机简化为质点, 通过集中质量单元CONM2进行模拟;以发动机为激励源, 加载X、Y、Z三个方向的加速度激励信号[18];通过连续的ACM2焊点模型对焊接处进行模拟, 该模型由一层六面体单元与上、下两层壳单元组成, 各节点间通过RBE3单元实现连接;通过CBUSH弹簧阻尼单元模拟发动机悬置对系统的阻尼效果;排气歧管的模态及振动响应受到排气系统其他部件的影响, 同样通过弹簧阻尼单元对排气总管等部件对系统的阻尼效果进行模拟.
通过约束模态试验来验证有限元建模的准确性, 实验照片如图 1所示.建立与之对应的排气歧管有限元模型进行常温下约束模态分析, 其一阶模态振型图如图 2所示.将仿真模态频率与试验模态频率对比发现(见表 1), 其三阶模态频率误差均小于5%, 认为建模方法准确有效, 可应用于振动及疲劳寿命预测研究.表 1中, ft为试验模态频率, fs为仿真模态频率, δ为相对误差.

|
图 1 排气歧管模态试验现场图 Fig. 1 Scene photograph of exhaust manifold modal testing |
|
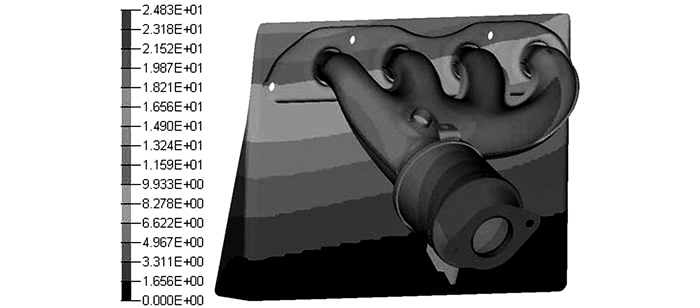
图 2 有限元仿真一阶模态振型图 Fig. 2 First modal shape of finite element analysis |
| 表 1 排气歧管仿真模态频率与实验模态频率对比 Table 1 Comparison between FEM analysis and experiment for modal frequencies of exhaust manifold |
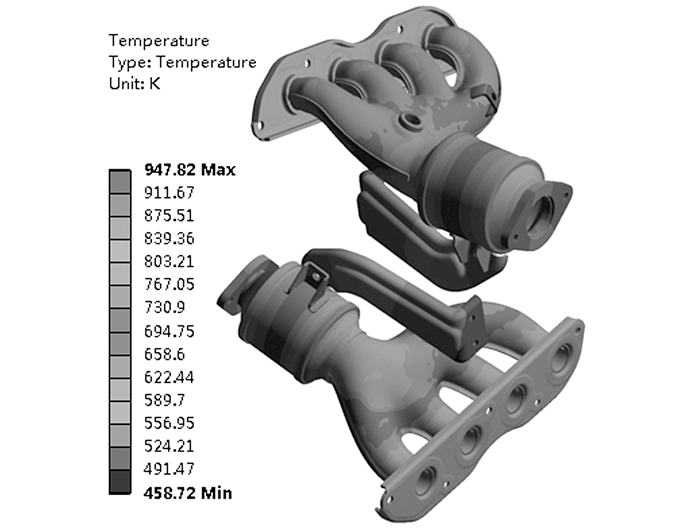
通过流固耦合温度场计算得到排气歧管的温度分布如图 3所示.进出口边界条件由一维仿真得到, 对排气歧管内外流场分别进行CFD模拟以获得内外壁面边界条件.根据壁面边界条件进行有限元温度场计算, 依照表面温度及对流换热系数分布修正CFD计算中的边界条件实现流固耦合温度场计算.
|
图 3 排气歧管有限元仿真温度场分布 Fig. 3 Exhaust manifold temperature field distribution of finite element analysis |
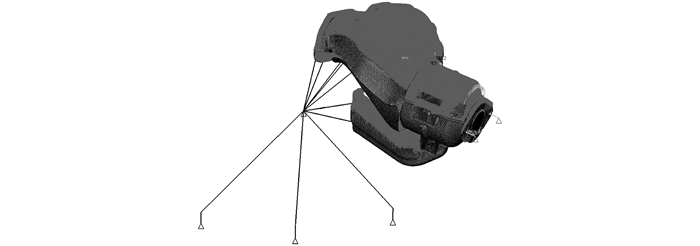
将计算得到的温度场映射到有限元模型上, 得到热机耦合的排气歧管有限元模型如图 4所示.在热机耦合分析中考虑材料属性随温度的变化, 441不锈钢弹性模量随温度变化如表 2所示.
|
图 4 热机耦合有限元模型 Fig. 4 Thermo-mechanical coupled FE model |
| 表 2 441不锈钢弹性模量表 Table 2 441 stainless steel elastic modulus table |
传递函数为线性定常系统在零初始条件下, 输出量的拉氏变换与输入量的拉氏变换之比.传递函数只与系统本身的参数有关, 与外界输入无关, 反映的只是系统本身的动态特性.
对系统施加单位加速度激励进行频率响应分析得到响应应力传递函数, 根据传递函数及激励点功率谱密度通过随机振动分析得到排气歧管有限元模型各点应力的PSD曲线从而进行疲劳寿命计算.若热载荷的存在对应力传递函数的计算结果产生较大的影响, 则会给后续的疲劳寿命计算带来较大的误差.为了研究热应力及温度分布对传递函数的影响, 分别进行以下4个工况的计算:A:考虑热应力及温度分布影响下的频率响应分析;B:考虑热应力分布影响下的频率响应分析;C:考虑温度分布影响下的频率响应分析;D:常温下的频率响应分析.
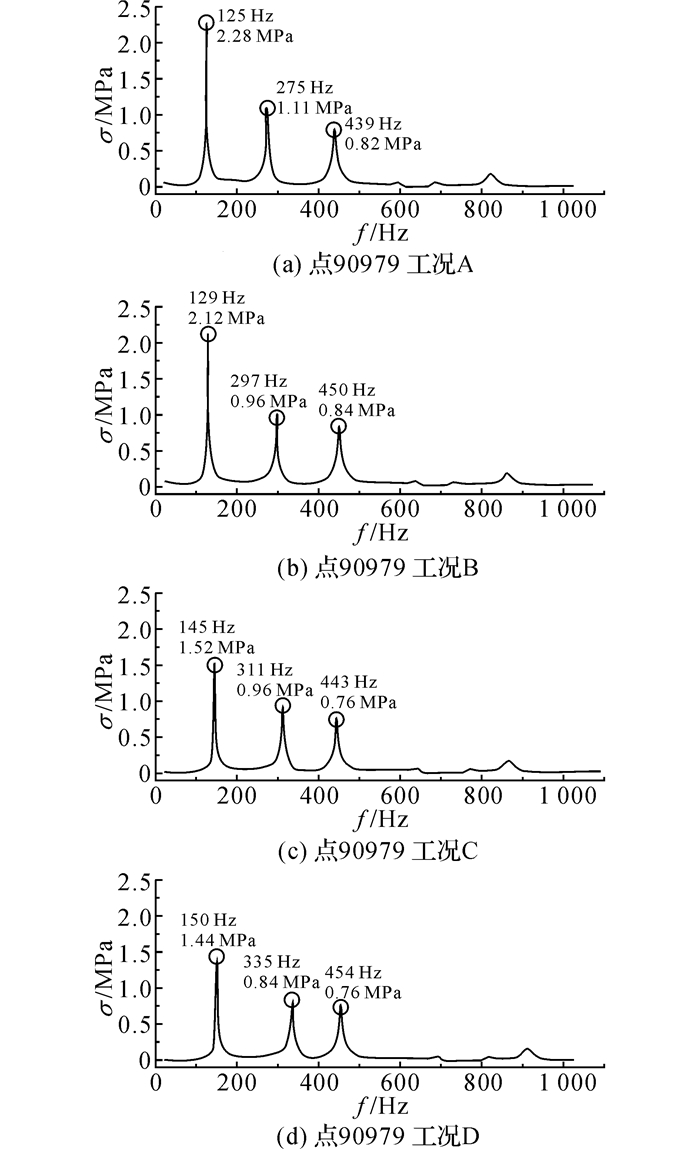
2.3 热载荷对振动特性的影响分析在排气歧管不同位置选点, 对以上4个工况进行对比分析, 发现不同位置、不同激励方向的应力传递函数有着较大区别, 同时热载荷对其造成的影响也并不完全一致.选取有代表性的2个点:点90979(发动机支架处)、点224344(排气支管处), 对不同工况下的应力传递函数进行对比分析,如图 5、6所示.
|
图 5 不同工况下点90979 Y向的应力传递函数 Fig. 5 Stress transfer function of Node 90979 in Ydirection under various operating conditions |

|
图 6 不同工况下点224344的X向应力传递函数 Fig. 6 Stress transfer function of Node 224344 in Xdirection under various operating conditions |
对比4个工况下传递函数峰值频率发现:工况A峰值频率最小, 工况D峰值频率最大, 热载荷的存在会明显降低其峰值频率的大小.对不同工况下排气歧管模态进行计算, 发现传递函数峰值频率与其固有频率相互对应, 且排气歧管不同位置对各阶固有频率的敏感程度不同.点90979对1、2、3阶固有频率对应的激励响应强烈, 而点224344对1、4、5阶固有频率对应的激励响应强烈.
根据振动分析的基本理论结合计算得到的应力传递函数分析发现, 当系统刚度提高时其响应应力幅值会随之增加.由表 2可以发现, 温度升高时材料的弹性模量下降, 从而刚度降低;应力刚化即结构在无应力状态和有应力状态下的刚度变化, 在有应力状态下, 结构某方向的刚度显著增大.
对比工况B与工况D发现, 考虑热应力分布计算得到的响应应力幅值较常温下要大.这是由于热应力的存在使得结构产生应力刚化效果, 由应力刚化引起的结构刚度的增大使得响应应力幅值增大.
对比工况C与工况D发现, 点90979与点224344的温度分布对其传递函数幅值影响规律并不一致.材料弹性模量随着温度的升高而降低, 排气歧管不同位置的温度不同, 其局部弹性模量变化规律也不相同, 加之排气歧管形状复杂, 因而温度分布对排气歧管不同位置传递函数的影响规律并不一致.排气管处温度较高, 局部刚度较低, 故排气管处的响应应力幅值较低.
对比工况A与工况D发现, 同时考虑热应力与温度分布计算得到的响应应力数值要明显大于常温工况, 较低的应力幅值在疲劳寿命分析时会得到过于乐观的寿命预测, 且传递函数峰值频率的改变也会对寿命预测结果产生影响.如果忽视热载荷的存在, 直接对高温环境中工作的排气歧管进行常温下的频率响应分析会造成较大误差, 因而对排气歧管进行热环境下的频率响应分析是很有必要的.
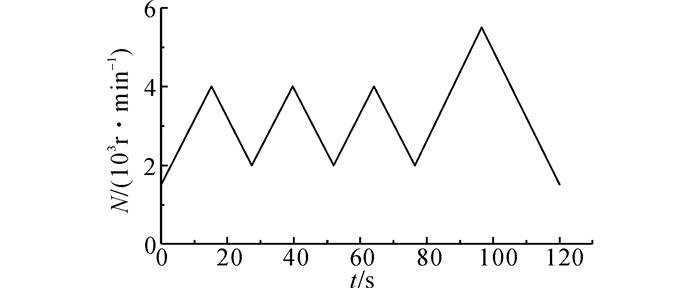
3 疲劳寿命分析排气歧管通过螺栓连接固定在发动机缸盖上, 其振动所受激励主要来自于发动机.汽车行驶过程中发动机转速会在较大范围内波动, 定转速下采集的激励信号无法反映排气歧管工作过程中所受到的激励.为了更好地对发动机整个寿命周期进行模拟, 在转鼓试验台上控制实验样车发动机转速变化如图 7所示, 并对发动机X、Y、Z三个方向(X为车头至车尾、Y为车内由左至右、Z为竖直方向由下至上)的加速度信号进行采集.
|
图 7 单个周期内发动机转速变化 Fig. 7 Variation of engine speed within one cycle |
信号周期为2 min, 发动机转速在1 500~5 500 r/min变化, 转速覆盖了发动机工作的主要转速区域, 发动机工作时主要工作转速范围在2 000~4 000 r/min, 故该转速区域所占整个信号比例较大.信号的采样频率为2 048 Hz, 信号测取采用LMS公司的Test.Lab测试系统、LMS SCM05数据采集仪, PCB三向加速度传感器安装于缸盖上以测取发动机振动产生的X、Y、Z三个方向的振动加速度信号,如图 8所示.

|
图 8 振动加速度信号采集试验现场图 Fig. 8 Scene photograph of vibration acceleration signal acquisition test |
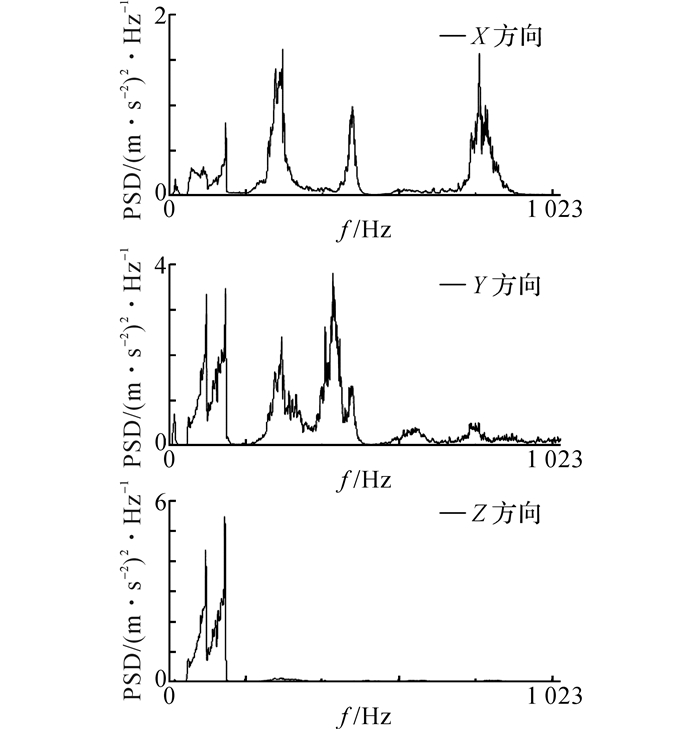
对转鼓实验中采集的时域信号进行傅里叶变换, 得到X、Y、Z方向的功率谱密度信号(power spectral density, PSD)如图 9所示.由于3个方向的振动是同时发生的, 信号间存在相关性, 为了响应应力功率谱密度计算的准确性, 需要对功率谱密度信号进行两两之间的相关性设置[19].最后得到的功率谱密度为一个3×3的矩阵:
| $ {\mathit{\boldsymbol{S}}_p}\left( \omega \right) = \left[{\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{xx}}\left( \omega \right)}&{{\mathit{\boldsymbol{S}}_{xy}}\left( \omega \right)}&{{\mathit{\boldsymbol{S}}_{xz}}\left( \omega \right)}\\ {{\mathit{\boldsymbol{S}}_{xy}}\left( \omega \right)}&{{\mathit{\boldsymbol{S}}_{yy}}\left( \omega \right)}&{{\mathit{\boldsymbol{S}}_{yz}}\left( \omega \right)}\\ {{\mathit{\boldsymbol{S}}_{xz}}\left( \omega \right)}&{{\mathit{\boldsymbol{S}}_{yz}}\left( \omega \right)}&{{\mathit{\boldsymbol{S}}_{zz}}\left( \omega \right)} \end{array}} \right]. $ | (17) |
|
图 9 激励处X/Y/Z三向加速度功率谱密度信号 Fig. 9 Power spectral density of acceleration of exciting source in X/Y/Z |
式中:Sxx(ω)、Syy(ω)、Szz(ω)为X、Y、Z三个方向的功率谱密度信号的自相关函数;Sxy(ω)、Sxz(ω)、Syz(ω)为两两方向功率谱密度信号间的互相关函数.
以Dirlik公式为评估模型, 使用Doodman直线方程修正平均应力对疲劳寿命的影响, 设置存活率为90%[20].根据激励信号功率谱密度及X、Y、Z方向的应力传递函数, 对不考虑热载荷与考虑热载荷这2种工况分别进行振动疲劳寿命计算, 寿命云图如图 10所示.

|
图 10 不同工况下排气歧管疲劳寿命计算结果对比 Fig. 10 Comparison of calculated results of exhaust manifold's fatigue life under various operatingconditions |
对比发现:在不考虑热载荷的工况中, 危险点出现在发动机支架弯折处, 其寿命为8.55×106 s,合237 5 h;在考虑热载荷的工况中, 排气前锥拐角处及发动机支架弯折处寿命较低, 最低寿命为6.02×106 s,合1 672.2 h, 与不考虑热载荷工况相比其最低寿命减少了42 %.以车辆运行平均时速80 km/h来估算, 这2种工况计算寿命分别为1.9×105 km与1.34×105 km, 与1.6×105 km的B10设计寿命相比, 不考虑热载荷会得到过于乐观的计算结果而忽视了产品设计上的缺陷.紧耦合式排气歧管的设计过程需要综合考虑安装位置、排气背压、管内流速、偏心度等因素, 对歧管形状的修改会涉及到众多参数的改变, 因此本文针对排气歧管寿命最低的发动机支架进行针对性优化.
4 多目标优化激励处的功率谱密度与排气歧管的传递函数共同决定了排气歧管不同位置的响应功率谱密度, 影响了排气歧管的疲劳寿命, 对支架进行针对性的优化设计需要综合考虑功率谱密度与传递函数的影响.

|
图 11 工况A下点90979的X、Y、Z向应力传递函数 Fig. 11 Stress transfer function of Node 90979 inX/Y/Z direction under operating condition A |
功率谱密度定义了激励信号的功率如何随频率分布, 可以理解为不同频率的激励出现的概率.功率谱密度函数值较高的频率代表了在此频率下的激励信号的出现频率较高, 如果排气歧管在该频率下的应力传递函数值较高则会造成较大的疲劳损伤.因此优化时应降低功率谱密度函数峰值频率附近的传递函数值.点90979位于发动机支架弯折处, 疲劳寿命较低为危险点, 其X、Y、Z方向的应力传递函数如图 12所示.
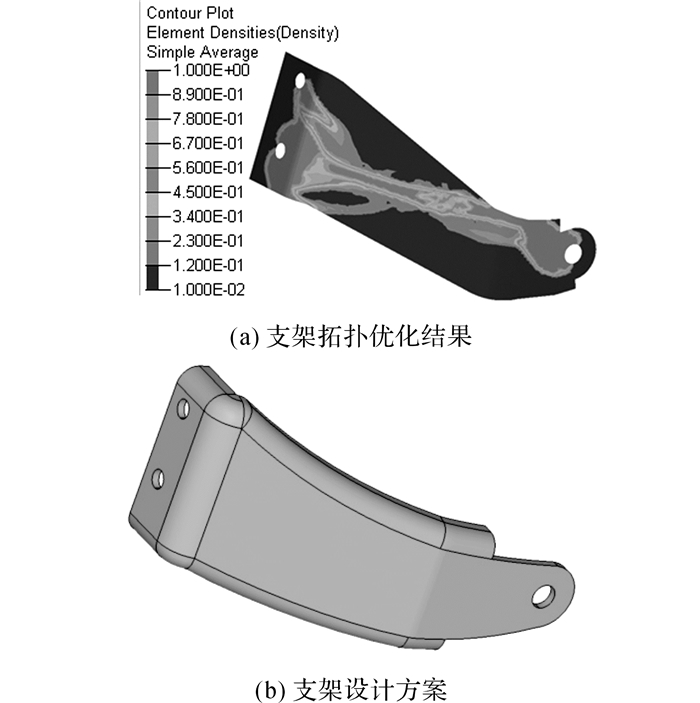
|
图 12 支架拓扑优化结果及对应设计方案 Fig. 12 Topology optimization results of bracket and corresponding design scheme |
X、Y、Z方向的功率谱密度函数均在50~180 Hz内存在峰值且函数值较高.受一阶模态频率影响, X、Y、Z方向的传递函数均在125 Hz出现峰值, 因此优化需要提高一阶模态频率使传递函数峰值频率尽可能远离50~180 Hz;Y向功率谱密度函数在220~500 Hz在范围内存在峰值且函数值较高, 同时Y向应力传递函数存在275、439 Hz两处峰值, 分别对应2、3阶模态频率, 需要对应优化提高2、3阶模态频率远离危险频率范围;虽然6阶模态对应的823 Hz处传递函数峰值较小, 但由于X向功率谱密度函数在对应频率范围内出现较大峰值, 为安全起见在优化过程中对6阶模态频率进行优化提高.根据以上分析得到优化的子目标:提高1、2、3、6阶固有频率.首先通过拓扑优化寻找最佳传力路径, 提高系统刚度.在拓扑优化的基础上通过多目标形貌优化寻找最优加强筋形状与位置, 达到优化目的.
4.1 拓扑优化以系统刚度最大化为目标进行拓扑优化, 将刚度最大化问题转化为柔度最小化问题, 柔度通过应变能进行定义[21].以去除加强筋的发动机支架为设计空间进行拓扑优化, 采用SIMP密度-刚度插值法进行计算.以整个系统柔度最小化为目标, 设计空间体积40 %上限为约束条件, 进行拓扑优化分析, 寻找最优材料分布.其目标函数及约束条件分别为
| $ \min :\lambda \left( X \right) = \lambda \left( {{x_1},{x_2}, \ldots ,{x_n}} \right),{V_{\rm{r}}}\left( X \right) \le 0.4. $ | (18) |
式中:λ为柔度, Vr为体积比.
分析结果显示,支架的最佳传力路径位于原始设计上方, 下方材料的存在并不能启到提高系统刚度的作用, 此处材料可以去除.在优化方案中, 在避免干涉的前提下尽可能使支架材料沿最佳传力路径分布, 同时在两侧进行翻边提高刚度.优化结果及优化后支架结构如图 13所示.
|
图 13 优化后的振动疲劳寿命 Fig. 13 Optimized vibration fatigue life |
不同子目标之间变化规律及数值大小各有不同, 为了准确反映各子目标变化对总目标的影响, 对目标函数进行规范化处理.
| $ {F_i} = \frac{{f_i^{{\rm{obj}}}-{f_i}}}{{f_i^{{\rm{obj}}}-f_i^{\min }}}. $ | (19) |
式中:fs为优化的第s个子目标, fsobj为第s个目标的目标值, fsmin为第s个目标的初始值.
多目标优化的子目标为提高1、2、3、6阶固有频率, 但模态频率的提高需要在一定范围内, 防止提高后的固有频率接近功率谱密度函数其他峰值频率.首先通过观察功率谱密度函数、传递函数峰值之间关系寻找各子目标理想值fside, 选择标准如下:保证fside在尽可能小的情况下避开X、Y、Z向功率谱密度函数的峰值频率.针对各子目标进行相同约束下单目标优化, 得到针对单个目标的优化最大值fsmax, 将fsmax目标的理想值fside进行比较, 如果fsmax高于理想值fside则fsobj取值为fside, 如果fsmax无法达到理想值则fsobj取值为fsmax:
| $ f_s^{{\rm{obj}}} = \left\{ \begin{array}{l} f_s^{{\rm{ide}}}, f_s^{{\rm{ide}}} \le f_s^{\max };\\ f_s^{\max }, f_s^{{\rm{ide}}} > f_s^{\max }. \end{array} \right. $ | (20) |
将式(13) 代入式(11) 中得到归一化函数:
| $ U = \sum\limits_{s- 1}^M {\left\{ {[{\rm{exp}}\;(p{\omega _s})-1]{\rm{exp}}(p\frac{{f_s^{{\rm{obj}}} -{f_s}}}{{f_s^{{\rm{obj}}} -f_s^{\min }}})} \right\}} . $ | (21) |
式中:ωs为第s个目标的权值且有
| $ \sum\limits_{s-1}^M {{\omega _s} = 1}, $ |
根据各阶模态频率对疲劳损伤的贡献度的不同, 设置权值:ω1=0.5, ω2=0.2, ω3=0.2, ω4=0.1.
形貌优化的设计区域为发动机支架中央处平面, 螺栓孔附近位置及两侧翻边为非设计区域.以最小化归一化函数为目标, 起筋角度为85°, 起筋高度为6 mm为约束条件, 进行形貌优化分析.其目标函数即约束条件分别为
| $ \begin{array}{l} {\rm{min}}:U\left( X \right) = U\left( {{x_1},{x_2}, \ldots ,{x_n}} \right),\\ \alpha \left( X \right) = 85^\circ ,h\left( X \right) = 6. \end{array} $ | (22) |
式中:α为起筋角度, h为起筋高度.
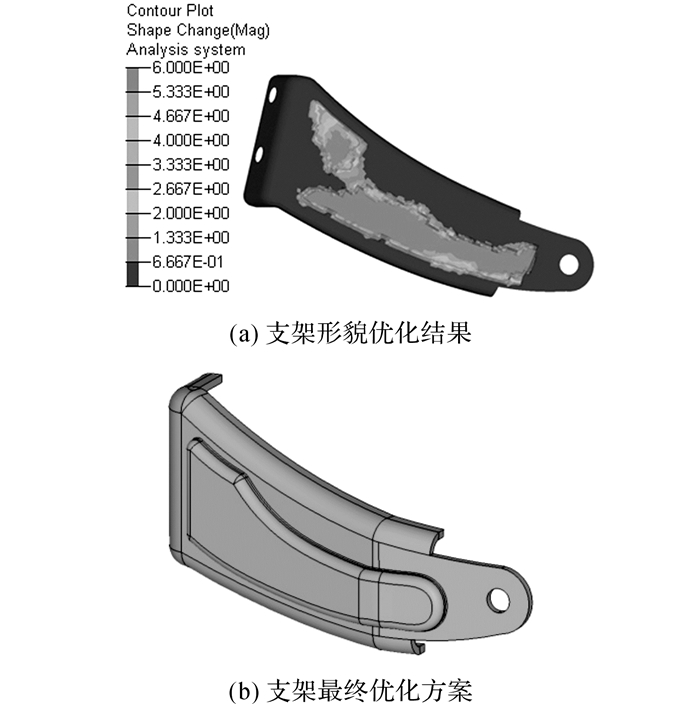
形貌的优化结果如图 14(a)所示.根据形貌优化结果对发动机支架进行重新设计, 最终得到的几何形状如图 14(b)所示.优化后的1、2、3、6阶固有频率分别由125、275、439、823 Hz提升到199、296、544、942 Hz.对优化后的排气歧管进行振动疲劳计算以验证优化效果, 得到寿命云图如图 13所示.

|
图 14 形貌优化结果及最终设计方案 Fig. 14 Topography optimization results and final design scheme |
优化后排气歧管最低点寿命为7.9×106 s,合2 194.4 h、安全行程约为1.76×105 km.较优化前最低寿命提高了31.2 %, 优化效果明显、满足设计要求.
5 结论(1) 应力刚化效果改变了排气歧管的刚度分布;温度升高引起的材料力学性能退化降低了排气歧管的刚度.结构刚度的改变使得传递函数峰值频率降低且应力幅值发生相应的改变.
(2) 排气歧管振动疲劳的危险点为发动机支架拐角处, 考虑热载荷的疲劳寿命较不考虑热载荷的疲劳寿命低42%, 未满足设计要求, 需要进行优化;热机耦合作用对振动疲劳寿命有较大影响, 对排气歧管进行热载荷下的振动疲劳寿命预测是很有必要的.
(3) 通过拓扑优化和基于加权指数法的多目标形貌优化对排气歧管发动机支架进行优化, 优化效果显著.振动疲劳寿命较优化前提高31.2%, 达到1.76×105 km的安全行程, 满足设计要求.与传统的经验优化相比, 这种优化方法可以更便捷准确的得到优化方案, 具有一定的实用价值.
| [1] |
杨云龙, 曹占义, 崔雷, 等. 汽车发动机排气歧管用耐热铸造合金的研究与发展[J].
汽车工艺与材料, 2009(5): 1–4.
YANG Yun-long, CAO Zhan-yi, CUI Lei, et al. The development and research of the casting heat resistant alloy used in car exhaust manifold[J]. Automobile Technology and Material, 2009(5): 1–4. |
| [2] | SISSA S, GIACOPINI M, ROSI R. Low-cycle thermal fatigue and high-cycle vibration fatigue life estimation of a diesel engine exhaust manifold[J]. Procedia Engineering, 2014, 74: 105–112. DOI:10.1016/j.proeng.2014.06.233 |
| [3] | SANTACREU P O, FAIVRE L, ACHER A. Life prediction approach for stainless steel exhaust manifold[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2012, 5: 904–910. DOI:10.4271/2012-01-0732 |
| [4] |
袁懋荣. 排气歧管热负荷与机械振动负荷的耦合分析[D]. 长春: 吉林大学, 2015.
YUAN Mao-rong. The couping analysis on thermal load and mechanical vibration load of exhaust manifold[D]. Changchun: Jilin University, 2015. |
| [5] | HA T K, JEONG H T, SUNG H J. High temperature bending fatigue behavior of stainless steels for automotive exhaust[J]. Journal of Materials Processing Technology, 2007, 187: 555–558. |
| [6] | WATANABE Y, SHIRATANI K, IWANAGA S, et al. Thermal fatigue life prediction for stainless steel exhaust manifold[R]. SAE Technical Paper, 1998. |
| [7] | MICHIUE M, NISHIO K, SUGIURA H, et al. Prediction of Vibration Fatigue Life for Motorcycle Exhaust Systems[R]. SAE Technical Paper, 2011. |
| [8] | DELPRETE C, SESANA R, VERCELLI A. Multiaxial damage assessment and life estimation: application to an automotive exhaust manifold[J]. Procedia Engineering, 2010, 2(1): 725–734. DOI:10.1016/j.proeng.2010.03.078 |
| [9] |
刘勇. 某发动机排气歧管的热疲劳分析与优化[D]. 重庆: 重庆理工大学, 2015.
LIU Yong. Thermal fatigue analysis and optimization of an engine exhaust manifold[D]. Chongqing: Chongqing University, 2015. |
| [10] |
马学军. 柴油机排气歧管的振动疲劳分析[D]. 太原: 中北大学, 2016.
MA Xu-jun. Vibration fatigue analysis of diesel engine exhaust manifold[D]. Taiyuan: North University of China, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10110-1016179877.htm |
| [11] |
李建华. 面向轻量化的发动机排气系统结构优化设计[D]. 武汉: 武汉理工大学, 2012.
LI Jian-hua.Optimized design of structure for exhaust systerm of engine based on lighting[D]. Wuhan: Wuhan University of Technology, 2012. |
| [12] |
范文杰, 范子杰, 苏瑞意. 汽车车架结构多目标拓扑优化方法研究[J].
中国机械工程, 2008, 19(12): 1505–1508.
FAN Wen-jie, FAN Zi-jie, SU Rui-yi. Research on multi-objective topology optimization on bua chassis frame[J]. China Mechine Press, 2008, 19(12): 1505–1508. DOI:10.3321/j.issn:1004-132X.2008.12.026 |
| [13] | CARPINELLI G, CARAMIA P, MOTTOLA F, et al. Exponential weighted method and a compromise programming method for multi-objective operation of plug-in vehicle aggregators in microgrids[J]. International Journal of Electrical Power and Energy Systems, 2014, 56: 374–384. DOI:10.1016/j.ijepes.2013.11.036 |
| [14] |
阚萍, 李源源, 吴道俊, 等. 基于频率响应分析的越野车车架疲劳寿命预估[J].
车辆与动力技术, 2011, 122(2): 9–13.
KAN Ping, LI Yuan-yuan, WU Dao-jun, et al. Fatigue life prediction of SUV frame based on frequency response analysis[J]. Vehicle and Power Technology, 2011, 122(2): 9–13. |
| [15] |
王佳莹. 考虑温度影响下结构振动疲劳寿命估算[D]. 南昌: 南昌航空大学, 2012.
WANG Jia-ying. Estimation of structural vibration fatigue life with temperature involved[D]. Nanchang: Nanchang Hangkong University, 2012. |
| [16] |
毕凤荣, 杜宪峰, 邵康, 等. 基于形貌优化的低振动柴油机机体设计[J].
内燃机学报, 2010(5): 459–463.
BI Feng-rong, DU Xian-feng, SHAO Kang, et al. Block design of diesel engine for low vibration based on topography optimization[J]. Transactions of CSICE, 2010(5): 459–463. |
| [17] |
孙晓辉, 丁晓红. 结构多目标拓扑优化设计[J].
机械设计与研究, 2012, 28(4): 1–4.
SUN Xiao-hui, DING Xiao-hong. Research on multi-objective topology optimization design methods for structure[J]. Machine Design and Research, 2012, 28(4): 1–4. |
| [18] | 庞剑, 谌刚, 何华. 汽车噪声与振动理论与应用[M]. 北京理大学出版社: 2008: 238-268. |
| [19] |
袁毅. 基于应力功率谱的结构振动疲劳寿命预测方法研究[D]. 长沙: 湖南大学, 2014.
YUAN Yi.Vibration fatigue life prediction method research based on stress power spectrum[D]. Changsha: Hunan University, 2014. |
| [20] | 王国军. MSC.FATIGUE疲劳分析实例指导教程[M]. 机械工业出版社: 2009: 168-196. |
| [21] |
刘林华, 辛勇, 汪伟. 基于折衷规划的车架结构多目标拓扑优化设计[J].
机械科学与技术, 2011, 30(3): 382–385.
LIU Lin-hua, XIN Yong, WANG Wei. Multi-objective topology optimization for an off-road vehicle frame based on compromise programming[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(3): 382–385. |


