在板料冲压成形中, 压边力的控制对于产品质量的好坏起着至关重要的作用:通过调节压边力可以改变毛坯与模具接触面间的摩擦力, 调节板料中的拉应力和切向应力, 从而达到控制金属流动, 避免产品起皱或者破裂的目的[1-2].一般认为, 压边力过小, 不能有效控制材料的流动, 导致板料容易起皱;压边力过大, 虽然可以避免起皱, 但是板料被拉破裂的趋势也会明显增加[1-2].因此, 在板料的冲压成形中, 需要对压边力进行合理的控制, 防止出现起皱和破裂, 保证产品质量.
对于压边力控制的研究, 主要包括两方面的内容:一是压边力的加载模式, 二是压边力的加载方法.压边力的加载模式主要分为2种, 即恒定压边力加载模式[3]和变压边力加载模式[4-6].前者实现方式相对比较简单, 对于外形结构简单的产品也能获得相对满意的产品质量, 因而得到了大量的应用;后者虽然在产品质量控制等方面优于前者, 但是实现起来相对比较复杂, 设备造价也比较高, 因此目前国内尚未大量采用.对于压边力的加载方法, 主要包括钢性加载和弹性加载2种手段:钢性加载是通过保持压边滑块与模具之间的距离为定值来实现压边, 压边力的控制不够精确, 主要应用于双动压力机上;弹性加载主要用弹簧、气垫或液压垫作为弹性元件来进行压边力控制, 一般应用在单动压力机上, 其压边效果优于钢性加载[7].
液压垫是目前最常用的弹性加载装置, 从20世纪80年代开始应用于大型多工位压力机的拉深工位中, 极大地提高了板料冲压成形的产品质量[8-9].液压垫采用比例溢流阀或者伺服阀来对冲压成形过程中压边液压缸内的压力进行调节, 从而起到调节压边力的作用;对于要求较高的系统, 通常需要对压边液压缸内的压力进行闭环控制.现有研究多采用PID控制器[10-11]对压力进行闭环控制;PID控制器虽然结构简单、易于实现, 但是不能很好地应对电液系统的强非线性特性, 使其很难在大的控制范围内得到令人满意的控制效果.为了克服电液系统固有的强非线性特性, 提高控制性能, 在传统PID控制器的基础上引入某种非线性调节机制对其控制参数进行在线调节是一种比较合理的策略, 例如:模糊PID控制器[12-14].此外, 也有研究采用经典状态空间控制理论[15]、积分滑模控制[16]等方法对冲压成形中的压边力进行闭环控制.
本文设计一种基于开/闭环切换的软溢流PID(soft relief PID, SPID)控制器, 并在SPID控制器的基础上进一步引入模糊控制器提出一种软溢流模糊PID(soft relief fuzzy PID, SFPID)控制器, 解决比例溢流阀控式液压垫在冲压成形过程中存在的压力超调大及调整时间长的问题.建立比例溢流阀控式液压垫的数学模型, 并通过仿真与实验相结合的手段验证所提SFPID控制器的有效性.
1 工作原理介绍及数学建模 1.1 工作原理介绍本文所研究的比例溢流阀控式液压垫的原理如图 1所示, 有4个工作模式:“慢速主动顶出”、“快速主动顶出”、“主动退回”及“被动压边”.在“慢速主动顶出”模式下, 电磁阀SV1、电磁阀SV3的a端以及电磁阀SV5得电, 来自泵源的液压油进入柱塞缸及活塞缸的无杆腔, 驱动液压垫慢速顶出.在“慢速主动顶出”模式下如果进一步使电磁阀SV4得电, 则进入“快速主动顶出”模式, 来自泵源的液压油仅进入活塞缸的无杆腔, 驱动液压垫快速顶出.在“主动退回”模式下, 电磁阀SV1、电磁阀SV2以及电磁阀SV3的b端得电, 来自泵源的液压油进入活塞缸的有杆腔, 驱动液压垫主动退回.在“被动压边”模式下, 电磁阀SV6的a端得电, 通过控制比例溢流阀PV1的输入电流就可以对柱塞缸以及活塞缸无杆腔内的压力进行调节, 从而控制工件的压边力.
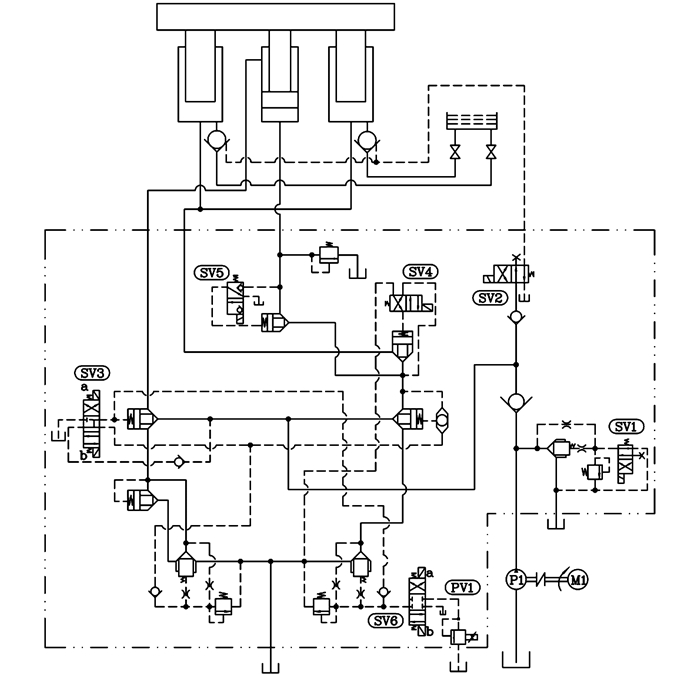
|
图 1 比例溢流阀控式液压垫的原理图 Fig. 1 Schematic of proportional relief valve-controlled hydraulic cushion |
从上面的分析可知, 在冲压成形中对压边力进行控制, 就是在“被动压边”模式下通过比例溢流阀对柱塞缸及活塞缸无杆腔内的压力进行调节, 使压边力满足冲压成形工艺要求.为了便于接下去的数学建模和分析, “被动压边”模式下的液压垫原理可以进一步简化, 如图 2所示.
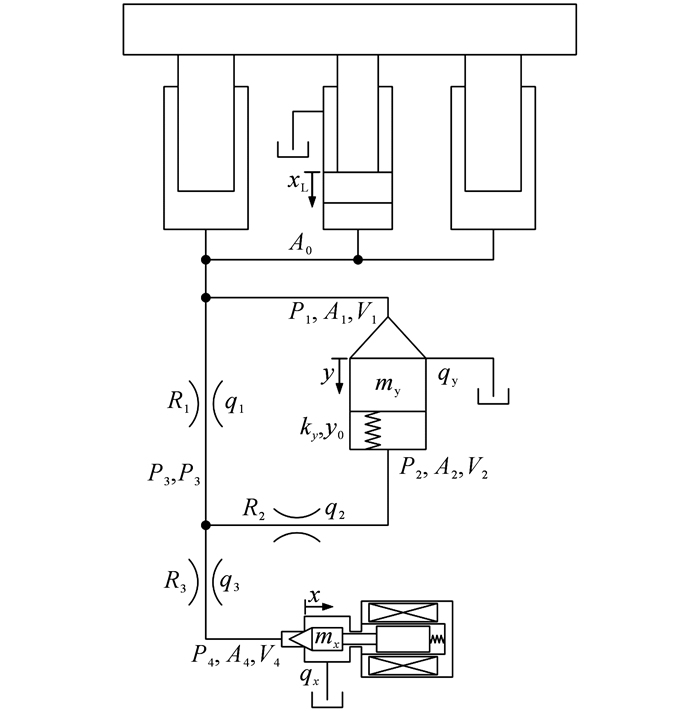
|
图 2 比例溢流阀控式液压垫的简化原理图 Fig. 2 Simplified schematic of proportional relief valve-controlled hydraulic cushion |
本节将建立如图 2所示的比例溢流阀控式液压垫在“被动压边”模式下的数学模型.
根据牛顿第二定律, 先导阀芯的力平衡方程[17]可以表示为
| $ \begin{array}{l} {m_x}\ddot x = {P_4}{A_4} - {b_x}\dot x - {F_x} - \\ \;\;\;\;\;\;\;\;{C_{{\rm{d}}x}}{C_{vx}}{\rm{\pi }}\left( {{d_x} - x{\rm{sin}}\;\alpha \;{\rm{cos}}\;\alpha } \right){\rm{sin}}\left( {2\alpha } \right)x{P_4}. \end{array} $ | (1) |
式中:mx为先导阀芯质量, x为先导阀芯开度, P4、A4分别为先导阀口前腔压力及作用面积, bx为先导阀芯黏性阻尼系数, Fx为比例电磁铁的输出力, Cdx、Cvx分别为先导阀口流量系数和流速系数, dx为先导阀口直径, α为先导阀芯半锥角.
比例电磁铁的“输出力-输入电压”特性包含了放大器的特性, 可用一阶惯性环节描述为
| $ {\tau _{\rm{v}}}{{\dot F}_x} = - {F_x} + {k_{\rm{v}}}u. $ | (2) |
式中:τv为比例电磁铁的时间常数, kv为比例电磁铁的输出力增益, u为比例电磁铁的输入电压.
根据牛顿第二定律, 主阀芯的力平衡方程[17]可以表示为
| $ \begin{array}{l} {m_y}\ddot y = {P_1}{A_1} - {P_2}{A_2} - {b_y}\dot y - {k_y}\left( {y + {y_0}} \right) - \\ \;\;\;\;\;\;\;{C_{{\rm{d}}y}}{C_{{\rm{v}}y}}{\rm{\pi }}\left( {{d_y} + y{\rm{sin}}\beta {\rm{cos}}\beta } \right){\rm{sin}}\left( {2\beta } \right)y{P_1}. \end{array} $ | (3) |
式中:my为主阀芯质量, y为主阀芯开度, P1、A1分别为主阀口前腔压力及作用面积, P2、A2分别为主阀弹簧腔压力及作用面积, by为主阀芯黏性阻尼系数, ky、y0分别为主阀复位弹簧刚度及预压缩量, Cdy、Cvy分别为主阀口流量系数及流速系数, dy为主阀口直径, β为主阀口半锥角.
根据压力容腔的压力公式, 主阀口前腔、主阀弹簧腔、先导阀口前腔以及液阻R1、R2、R3之间密闭容腔的压力动态可以表示为
| $ \left. \begin{array}{l} {{\dot p}_1} = \frac{{{\beta _{\rm{e}}}}}{{{V_1}}}({A_0}{v_{\rm{L}}} - {q_1} - {q_y} - {A_1}\dot y),\\ {{\dot p}_2} = \frac{{{\beta _{\rm{e}}}}}{{{V_2}}}({A_2}\dot y - {q_2}),\\ {{\dot p}_3} = \frac{{{\beta _{\rm{e}}}}}{{{V_3}}}({q_1} + {q_2} - {q_3}),\\ {{\dot p}_4} = \frac{{{\beta _{\rm{e}}}}}{{{V_4}}}({q_3} - {q_x} - {A_4}\dot x). \end{array} \right\} $ | (4) |
式中:βe为油液的体积弹性模量, A0为柱塞缸及活塞缸无杆腔的总作用面积, vL=ẋL为液压垫的冲压速度, V1=V1d-A0xL+A1y为主阀口前腔容积, 其中V1d为液压垫处于最高点, 且主阀关闭状态下的主阀口前腔容积, V2=V2d-A2y为主阀弹簧腔容积, 其中V2d为主阀关闭状态下的弹簧腔容积, V3为液阻R1、R2、R3之间密闭容腔的容积, V4=V4d+A4x为先导阀口前腔容积, 其中V4d为先导阀关闭状态下的先导阀口前腔容积.
根据薄壁小孔流量公式[17], 通过先导阀口的流量qx、通过主阀口的流量qy, 以及通过液阻R1、R2、R3的流量q1、q2、q3可表示为
| $ \left. \begin{array}{l} {q_x} = {\rm{sgn}}\left( {{P_4}} \right){C_{{\rm{d}}x}}{\rm{\pi }}\left( {{d_x} - x{\rm{sin}}\;\alpha \;{\rm{cos}}\;\alpha } \right)x\;{\rm{sin}}\;\alpha \sqrt {\frac{{2\left| {{P_4}} \right|}}{\rho }} ,\\ {q_y} = {\rm{sgn}}\left( {{P_1}} \right){C_{{\rm{dy}}}}{\rm{\pi }}\left( {{{\rm{d}}_y} + y{\rm{sin}}\;\beta \;{\rm{cos}}\beta } \right)y\;{\rm{sin}}\beta \sqrt {\frac{{2\left| {{P_1}} \right|}}{\rho },} \\ {q_1} = \frac{{{\rm{sgn}}\left( {{P_1} - {P_3}} \right){C_{{\rm{d1}}}}{\rm{\pi }}d_1^2}}{4}\sqrt {\frac{{2\left| {{P_1} - {P_3}} \right|}}{\rho }} ,\\ {q_2} = \frac{{{\rm{sgn}}\left( {{P_2} - {P_3}} \right){C_{{\rm{d2}}}}{\rm{\pi }}d_2^2}}{4}\sqrt {\frac{{2\left| {{P_2} - {P_3}} \right|}}{\rho }} ,\\ {q_3} = \frac{{{\rm{sgn}}\left( {{P_3} - {P_4}} \right){C_{{\rm{d3}}}}{\rm{\pi }}d_3^3}}{4}\sqrt {\frac{{2\left| {{P_3} - {P_4}} \right|}}{\rho }} . \end{array} \right\} $ | (5) |
式中:Cd1、Cd2、Cd3分别为液阻R1、R2、R3处流量系数, d1、d2、d3分别为液阻R1、R2、R3的直径.
式(1)~(5) 完整地描述了本文所研究的比例溢流阀控式液压垫在“被动压边”模式下的模型.定义状态变量
| $ \begin{array}{l} \boldsymbol{X} = {\left[ {{x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8},{x_9}} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;\;{\left[ {x,\dot x,y,\dot y,{P_1},{P_2},{P_3},{P_4},{F_x}} \right]^{\rm{T}}}, \end{array} $ |
则模型(1)~(5) 可用一个9阶的状态空间方程重述为
| $ \left. \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = \frac{1}{{{m_x}}}\left[ {{A_4}{x_8} - {b_x}{x_2} - {x_9} - } \right.\\ \;\;\;\;\;\;\left. {{C_{{\rm{d}}x}}{C_{{\rm{v}}x}}{\rm{\pi }}\left( {{d_x} - {x_1}{\rm{sin}}\;\alpha \;{\rm{cos}}\;\alpha } \right){\rm{sin}}\left( {2\alpha } \right){x_1}{x_8}} \right],\\ {{\dot x}_3} = {x_4},\\ {{\dot x}_4} = \frac{1}{{{m_y}}}\left[ {{A_1}{x_5} - {A_2}{x_6} - {b_y}{x_4} - {k_y}\left( {{x_3} + {y_0}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {{C_{{\rm{d}}y}}{C_{{\rm{v}}y}}{\rm{\pi }}\left( {{d_y} + {x_3}\;{\rm{sin}}\;\beta {\rm{cos}}\;\beta } \right){\rm{sin}}\left( {2\beta } \right){x_3}{x_5}} \right],\\ {{\dot x}_5} = \frac{{{\beta _{\rm{e}}}}}{{{V_1}}}({A_0}{v_{\rm{L}}} - {q_1} - {q_y} - {A_1}{x_4}),\\ {{\dot x}_6} = \frac{{{\beta _{\rm{e}}}}}{{{V_2}}}({A_2}{x_4} - {q_2}),\\ {{\dot x}_7} = \frac{{{\beta _{\rm{e}}}}}{{{V_3}}}({q_1} + {q_2} - {q_3}),\\ {{\dot x}_8} = \frac{{{\beta _{\rm{e}}}}}{{{V_4}}}({q_3} - {q_x} - {A_4}{x_2}),\\ {{\dot x}_9} = - \frac{1}{{{\tau _{\rm{v}}}}}{x_9} + \frac{{{k_v}}}{{{\tau _{\rm{v}}}}}u. \end{array} \right\} $ | (6) |
为了保证液压垫在不同的压力指令和冲压速度下都具有良好的动静态响应, 提出一种SFPID控制器, 其原理如图 3所示(屏蔽模糊控制器即为SPID控制器).从图 3可知, 该控制器主要包括3个子控制器, 即软溢流控制器、PID控制器和模糊控制器.
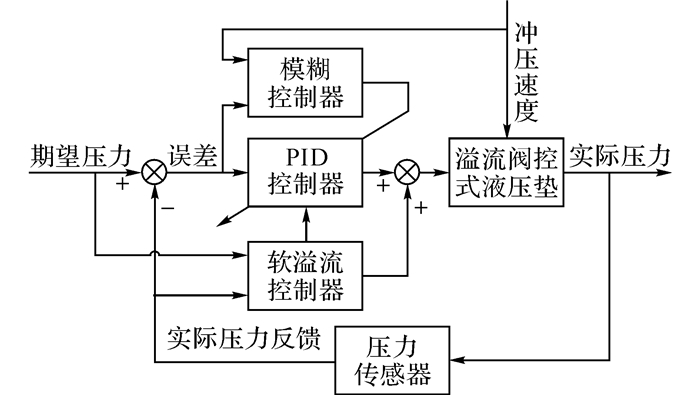
|
图 3 软溢流模糊PID(SFPID)控制器的原理图 Fig. 3 Schematic of soft relief fuzzy PID (SFPID)controller |
为了避免给控制器引入大的噪声干扰, 不采用微分控制, 而是采用如式(7) 所示的比例-积分控制.此外, 该PID控制器的输出还受到软溢流控制器及模糊控制器的调节:
| $ {u_{{\rm{PID}}}} = \left\{ \begin{array}{l} {k_{{\rm{p0}}}}{K_{\rm{p}}}e + {k_{{\rm{i0}}}}{K_{\rm{i}}}\int\limits_0^t {edt} ,\;\;\;\;\;\;{E_{\rm{s}}} = 1;\\ \;\;\;\;\;\;\;\;\;\;\;0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{E_{\rm{s}}} = 0. \end{array} \right. $ | (7) |
式中:uPID为PID控制器的输出, kp0为PID控制器的初始比例增益, Kp为模糊控制器输出的比例增益调节因子, ki0为PID控制器的初始积分增益, Ki为模糊控制器输出的积分增益调节因子, e为压力误差, Es为软溢流控制器输出的使能信号.
2.2 软溢流控制器设计软溢流控制器的核心思想是随着系统压力的升高进行开/闭环切换, 从而达到减小压力超调的目的.所设计的软溢流控制器如下式:
| $ {u_{{\rm{soft}}}} = \left\{ {\begin{array}{*{20}{c}} {{k_{{\rm{q1}}}}{P_{{\rm{1d}}}},}&{{E_{\rm{s}}} = 0,}&{{P_1} < {k_{{\rm{q}}3}}{P_{1d}};}\\ {{k_{{\rm{q2}}}}{P_{{\rm{1d}}}},}&{{E_{\rm{s}}} = 1,}&{{P_1} \ge {k_{{\rm{q}}3}}{P_{1d}}.} \end{array}} \right. $ | (8) |
式中:usoft为软溢流控制器的输出, P1d为溢流阀的期望压力, kq1为开环状态下的前馈增益, kq2为闭环状态下的前馈增益, kq3为开/闭环切换的分界点.
2.3 模糊控制器设计典型的模糊控制器包含如图 4所示的4个部分, 即知识库、模糊化、模糊推理和清晰化.知识库包含了具体应用领域的知识, 通常由数据库和模糊控制规则库两部分组成:数据库包括各语言变量的隶属函数、尺度变换因子以及模糊空间的划分等;模糊规则库则包括了用模糊语言变量表示的一系列控制规则, 反映了本领域控制专家的经验和知识, 是模糊推理的依据[18].
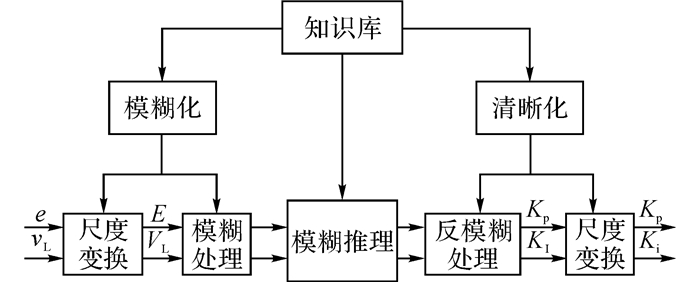
|
图 4 典型模糊控制器的结构 Fig. 4 Structure of classical fuzzy controller |
模糊化的作用是把输入的精确量转化为模糊量:采用如下式所示的线性变换进行尺度变换;考虑到采集到的数据经过处理后噪声较小, 在模糊处理中采用单点模糊集合[18]:
| $ \left. \begin{array}{l} E = \frac{{{E_{{\rm{max}}}}{\rm{ + }}{E_{{\rm{min}}}}}}{{\rm{2}}}{\rm{ + }}\frac{{{E_{{\rm{max}}}} - {E_{{\rm{min}}}}}}{{{e_{{\rm{max}}}} - {e_{{\rm{min}}}}}}\left( {e - \frac{{{e_{{\rm{max}}}}{\rm{ + }}{e_{{\rm{min}}}}}}{{\rm{2}}}} \right){\rm{,}}\\ {V_{\rm{L}}} = \frac{{{V_{\rm{L}}}_{{\rm{max}}}{\rm{ + }}{V_{\rm{L}}}_{{\rm{min}}}}}{{\rm{2}}}{\rm{ + }}\frac{{{V_{\rm{L}}}_{{\rm{max}}} - {V_{\rm{L}}}_{{\rm{min}}}}}{{{v_{\rm{L}}}_{{\rm{max}}} - {v_{\rm{L}}}_{{\rm{min}}}}}\left( {{v_{\rm{L}}} - \frac{{{v_{\rm{L}}}_{{\rm{max}}}{\rm{ + }}{v_{\rm{L}}}_{{\rm{min}}}}}{{\rm{2}}}} \right). \end{array} \right\} $ | (9) |
式中:emin、emax分别为压力误差的最小及最大值, [Emin, Emax]=[-1.00, 1.00]为尺度变换后压力误差的范围, E为尺度变换后的压力误差, vLmin、vLmax分别为液压垫的最小及最大冲压速度, [VLmin, VLmax]=[0, 1.00]为尺度变换后冲压速度的范围, VL为尺度变换后的冲压速度.
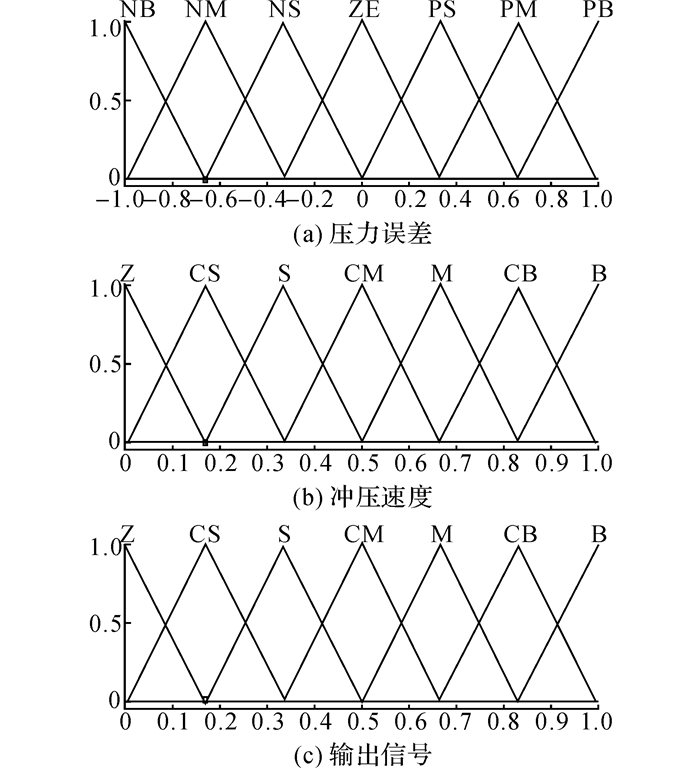
模糊推理是模糊控制器的核心, 能根据模糊逻辑中的蕴涵关系及推理规则从输入模糊量推导出输出模糊量[18].本文采用的输入/输出信号的模糊集合及相应的隶属函数如图 5所示, 模糊推理规则如表 1~2所示.
|
图 5 输入/输出信号的模糊集合及隶属函数 Fig. 5 Fuzzy sets and membership functions of input/output signals |
| 表 1 比例增益调节因子的模糊规则 Table 1 Fuzzy rules of proportional gain tuner |
| 表 2 积分增益调节因子的模糊规则 Table 2 Fuzzy rules of integral gain tuner |
清晰化的作用是将模糊推理得到的模糊控制量转换为实际的清晰控制量对PID控制器的参数进行调节, 改善其控制特性:采用“加权平均法”[18]作为反模糊处理的方法;经反模糊处理后的清晰控制量还需要进行尺度变换, 才能得到最终的控制量对PID控制器的控制参数进行在线调节, 本文采用如下式所示的线性变换进行尺度变换:
| $ {K_{\rm{p}}} = {k_{{\rm{fp}}}} \times {K_{\rm{P}}},{K_{\rm{i}}} = {k_{{\rm{fi}}}} \times {K_{\rm{I}}}. $ | (10) |
式中:KP、KI分别为反模糊后的比例及积分增益调节因子, kfp、kfi分别为尺度变换因子.
3 仿真研究 3.1 仿真设置为了验证本文所提控制策略的有效性, 在Matlab/Simulink仿真环境中利用S函数建立如式(6) 所示的溢流阀控式液压垫在“被动压边”模式下的仿真模型, 仿真模型相关参数的取值见表 3.在仿真过程中, 每一个节流口的流量系数和流速系数都取相同的值, 分别为Cdx=Cdy=Cd1=Cd2=Cd3=0.68, Cvx=Cvy=1.软溢流控制器和PID控制器通过S函数来实现, 模糊控制器则通过Matlab/Simulink的模糊工具箱来实现.在仿真中, 3个不同的控制器进行对比分析:第1个是式(11) 所示的带有前馈的参照PID控制器:
| $ {u_{{\rm{RPID}}}} = 0.02{P_{{\rm{1d}}}} + 0.01e + 0.06\int\limits_0^t {e{\rm{d}}t} . $ | (11) |
| 表 3 仿真模型的参数值 Table 3 Parameters of simulation model |
式中:uRPID为参照PID控制器的输出.第2个为本文中提到的SPID控制器;第3个为本文提出的SFPID控制器.SPID控制器及SFPID控制器的参数如表 4所示.
| 表 4 仿真过程中的控制器参数 Table 4 Parameters of controllers in simulations |
为了便于接下去的仿真和实验中定量分析每一个控制器的性能, 定义如下3个指标:1) 稳态误差es, 稳定压力与指令之间的偏差;2) 超调量σs, 压力响应曲线的第一个峰值与指令的差(为了对比无超调情况下的性能, 该指标允许出现负值);3) 调节时间ts, 压力响应曲线达到并一直保持在1 bar误差范围内的时间(对于考察时间内不能达到1 bar误差范围内的情况, 调节时间取为考察结束时刻的时间, 稳态误差则取为考察结束时刻的误差).
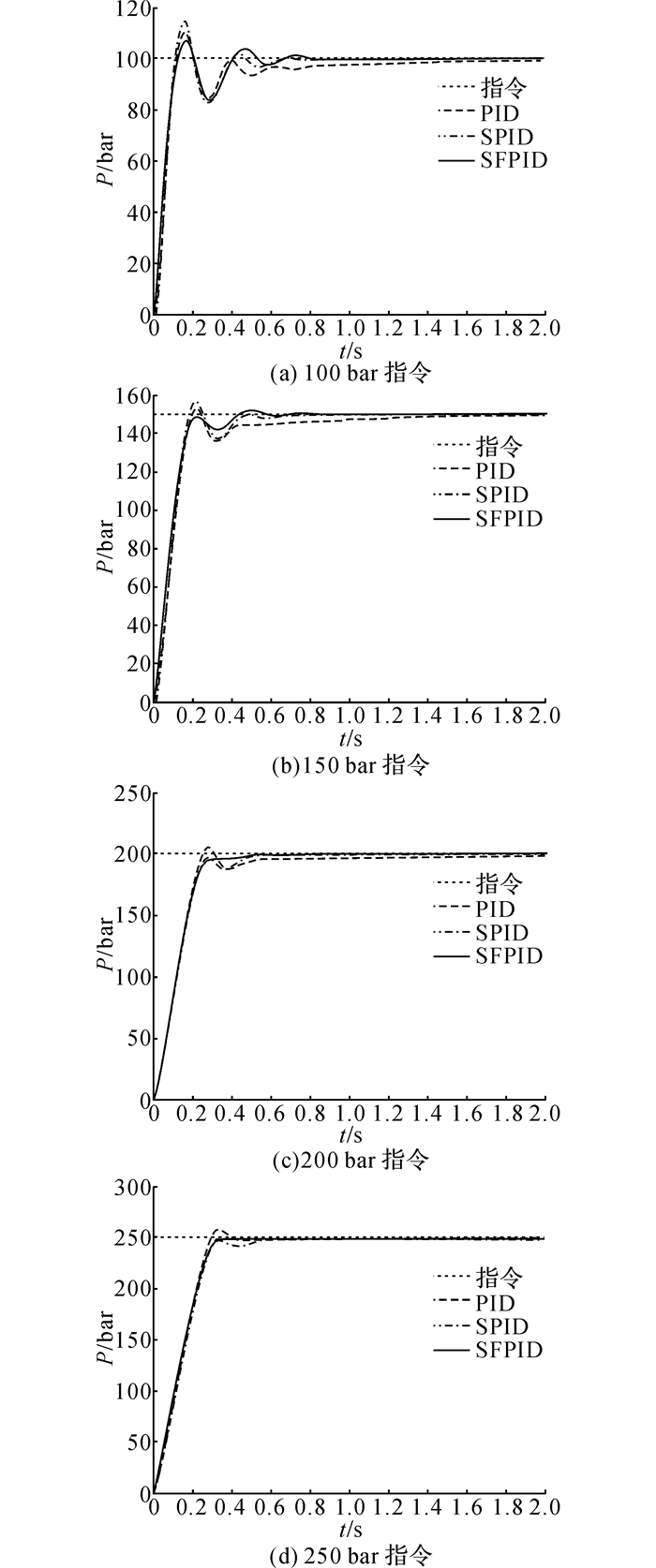
3.2 变压力指令仿真结果在变压力指令仿真中, 液压垫的冲压速度固定为vL=30 mm/s.上述3个控制器在不同压力指令下的响应曲线如图 6所示.由图 6可知:从稳态误差es来看, SFPID控制器与SPID控制器相近, 都比PID控制器要小;从超调量σs来看, SPID控制器(相对于PID控制器的超调减小量Δσs的4次平均值为4.01%)小于PID控制器, SFPID控制器进一步减小(超调减小量Δσs的4次平均值为5.31%);从调节时间ts来看, SPID控制器要远小于PID控制器(调节时间减小量Δts的4次平均值为46.18%), 而SFPID控制器更短(调节时间减小量Δts的4次平均值为57.25%).
|
图 6 变压力指令仿真中不同控制器的压力响应 Fig. 6 Pressure responses of different controllers in variable pressure instruction simulation |
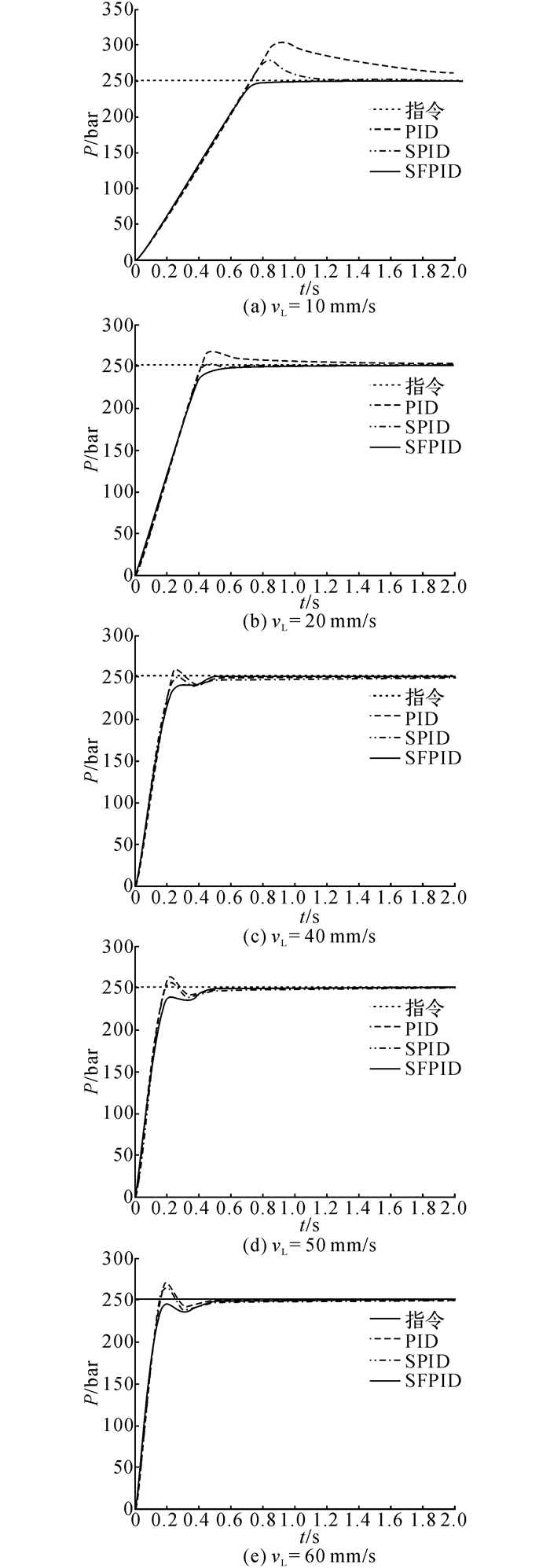
在变冲压速度仿真中, 压力指令固定为P1d=250 bar.上述3个控制器在不同冲压速度下的压力响应如图 7所示.由图 7结合图 6(d)可知:在稳态误差es方面, SFPID控制器的性能与SPID控制器相近, 均优于PID控制器;在超调量σs方面, SPID控制器的性能(相对于PID控制器的超调减小量Δσs的6次平均值为4.80%)优于PID控制器, SFPID控制器的性能更优(超调减小量Δσs的6次平均值为9.10%);在调节时间ts方面, 同样也是SPID控制器的性能(相对于PID控制器的调节时间减小量Δts的6次平均值为40.75%)优于PID控制器, SFPID控制器的调节时间ts则在SPID控制器的基础上进一步缩短(调节时间减小量Δts的6次平均值为53.73%).
|
图 7 变冲压速度仿真中不同控制器的压力响应 Fig. 7 Pressure responses of different controllers in variable stamping speed simulation |
为了进一步验证本文所提控制策略的有效性, 搭建如图 8、9所示的比例溢流阀控式液压垫实验平台:2个高频响伺服比例阀HPSV-1和HPSV-2(Rexroth, 4WRREH6VB40L-1X/G24K0/B5M)控制驱动缸带着滑块在固定框架内作上下运动, 模拟液压机的压制和回程;驱动缸的有杆腔配有溢流阀(Rexroth, DBDS6P1X/315) 来保证系统安全;电磁球阀(Rexroth, M-3SED10CK1X/350CG24N9K4) 保证滑块在停机情况下不会下滑;加载缸的无杆腔通过一个球阀(ROTELMANN, DN12) 连接到加载阀组, 模拟液压垫的压边液压缸;加载阀组中的比例溢流阀(Rexroth, DBE6-2X/200YG24K4M)用于实验平台压制过程中的加载, 减压阀(Rexroth, DR6DP2-5X/75YM)和液控单向阀(Rexroth, Z2S6A1-6X/)的组合用于回程过程中给加载缸的无杆腔补充低压油液;轴向柱塞泵(Rexroth, A10VSO28DFLR/31R-PSC61N00) 提供给实验平台一个恒压油源;实验平台的压力(泵源压力、驱动缸无杆腔/有杆腔压力和加载缸无杆腔压力)由压力传感器(Rexroth, HM20-20/400-C-K35) 来检测;滑块的位移由磁栅尺(上海迈信诺自动化科技有限公司, MS200-30+MR200c-3) 来检测.

|
图 8 比例溢流阀控式液压垫实验平台原理图 Fig. 8 Principle of proportional relief valve-controlled hydraulic cushion test bench |

|
图 9 比例溢流阀控式液压垫实验平台照片 Fig. 9 Photograph of proportional relief valve-controlled hydraulic cushion test bench |
整个模拟实验平台的控制系统基于Simulink Real-time实时控制系统来实现, 主要由上位机、下位机和数据采集卡所组成:上位机(联想, 拯救者14) 装有Matlab/Simulink软件用于编写和编译控制程序, 所得编译码通过TCP/IP总线下载到下位机(研华, IPC6606) 中执行;下位机通过数据采集卡(NI, PCI-6229) 采集反馈信号并生成相应的控制信号.在实验中, Simulink Real-time实时控制系统的采样周期设定在1 ms, 即控制频率为1 kHz.与仿真类似, 实验中用到的控制器分别是如下式所示的带有前馈的参照PID控制器以及本文的SPID控制器和SFPID控制器, 后两者的控制参数如表 5所示.
| $ {u_{{\rm{RPID}}}} = 0.05{P_{{\rm{1d}}}} + 0.01e + 0.03\int\limits_0^t {e{\rm{d}}t} . $ | (12) |
| 表 5 实验中的控制器参数 Table 5 Parameters of controllers in experiments |
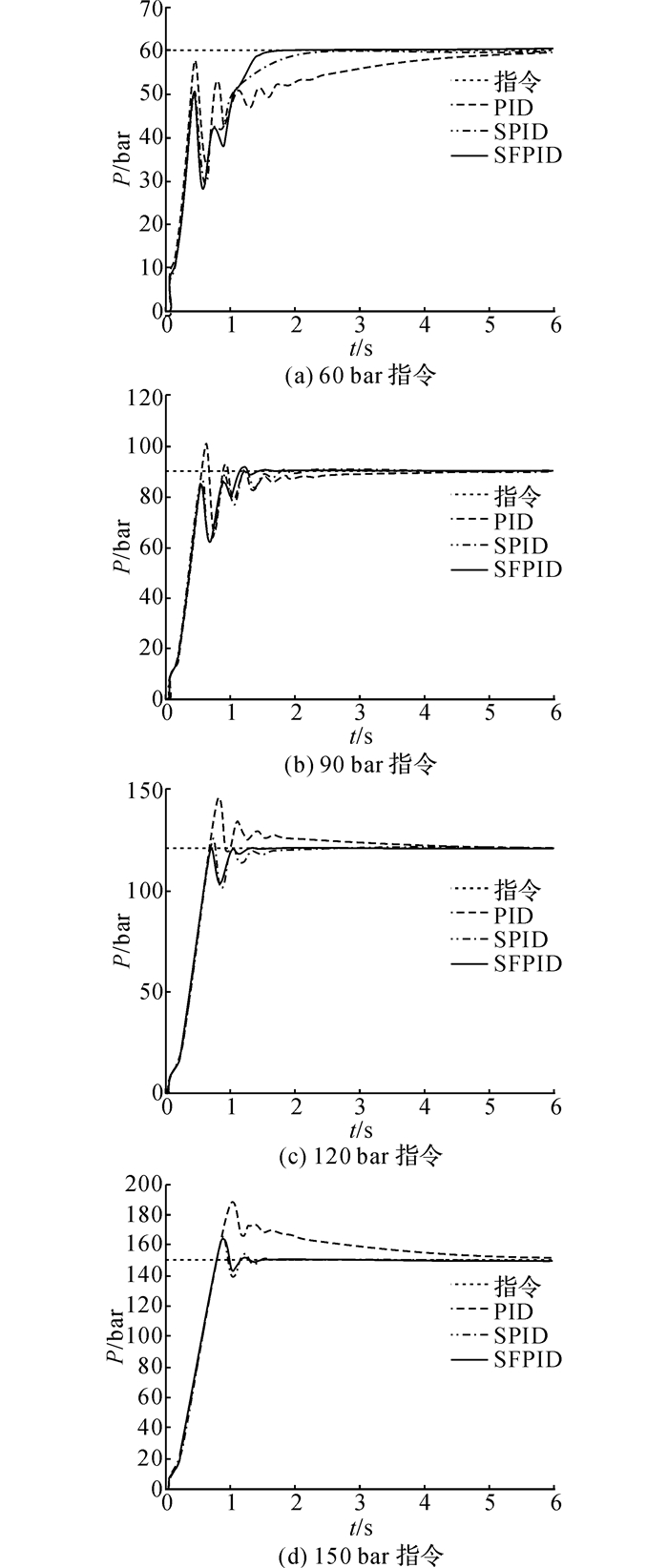
在变压力指令实验中, 滑块的冲压速度固定为vL=8 mm/s.上述3个控制器在不同压力指令下的响应曲线如图 10所示.由图 10可知, 实验结果与变压力指令仿真结果类似:即无论是从稳态误差es、超调量σs还是调节时间ts来看, SFPID控制器的性能都是最优的(稳态误差es=0, 相对于PID控制器的超调减小量Δσs的4次平均值为17.63%, 相对于PID控制器的调节时间减小量Δts的4次平均值为72.36%), SPID控制器次之(稳态误差es为0, 相对于PID控制器的超调减小量Δσs的4次平均值为15.17%, 相对于PID控制器的调节时间减小量Δts的4次平均值为61.07%), PID控制器在3个被比较的控制器中表现最差.
|
图 10 变压力指令实验中不同控制器的压力响应 Fig. 10 Pressure responses of different controllers in variable pressure instruction experiment |
考察本次实验结果, 并且注意变压力指令仿真结果, 可以得出以下基本结论:对于比例溢流阀控式液压垫的压力控制, 本文所提出的SFPID控制器在不同的压力指令下都能表现出良好的控制效果, 远远优于传统的PID控制器;此外, 得益于模糊控制器对控制参数的在线调整, SFPID控制器的控制性能也要比SPID控制器更优.
4.3 变冲压速度实验结果在变冲压速度实验中, 压力指令固定为P1d=150 bar.3个控制器在不同冲压速度下的压力响应如图 11所示.考察本次实验结果及变冲压速度仿真结果, 可知:在不同的冲压速度下, SFPID控制器从稳态误差es、超调量σs和调节时间ts等各项指标来看都是最优的(本次实验中, 稳态误差es=0, 相对于PID控制器的超调减小量Δσs的6次平均值为18.57%, 相对于PID控制器的调节时间减小量Δts的6次平均值为76.08%);SPID控制器次之(本次实验中, 稳态误差es=0, 相对于PID控制器的超调减小量Δσs的6次平均值为14.13%, 相对于PID控制器的调节时间减小量Δts的6次平均值为71.81%), PID控制器表现最差.
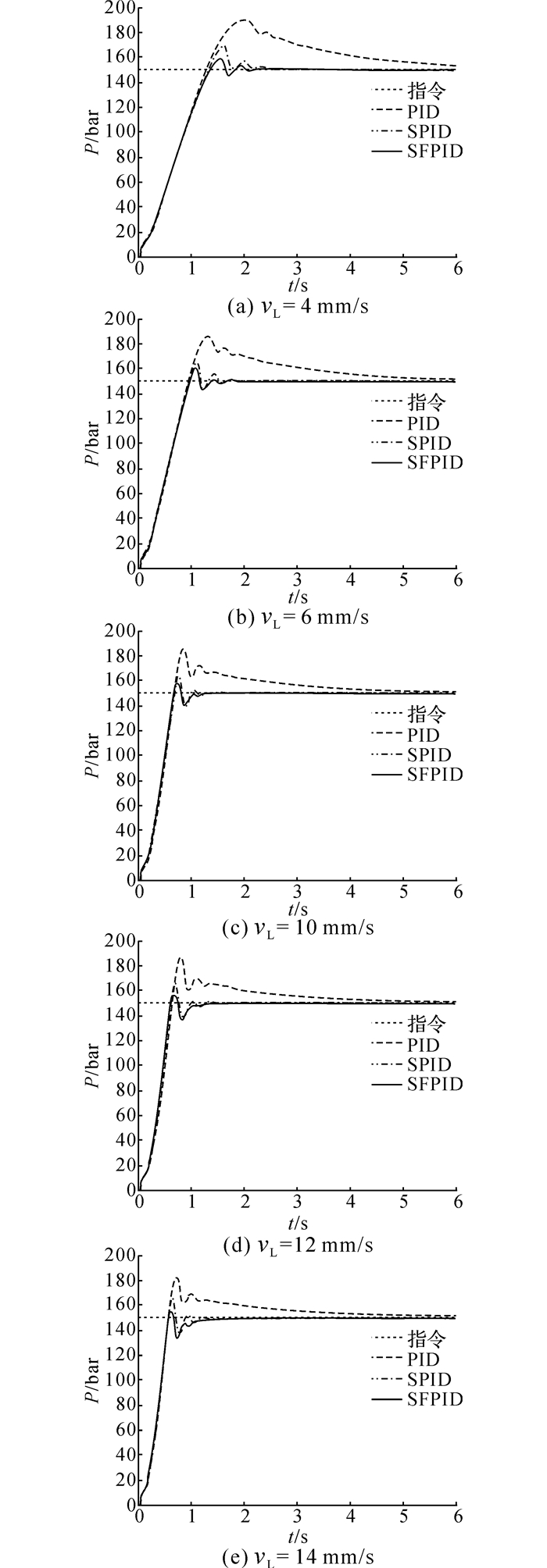
|
图 11 变冲压速度实验中不同控制器的压力响应 Fig. 11 Pressure responses of different controllers in variable stamping speed experiment |
仿真结果表明:在不同的压力指令下, SFPID控制器可以在保证稳态精度的前提下, 较PID控制器减小超调5.31%, 并且缩短57.25%的调节时间;在不同的冲压速度下, SFPID控制器可以在保证稳态精度的前提下, 较PID控制器减小超调9.10%, 并且缩短53.73%的调节时间.
实验结果表明:在不同的压力指令下, SFPID控制器可以在保证稳态精度的前提下, 较PID控制器减小超调17.63%, 并且缩短72.36%的调节时间;在不同的冲压速度下, SFPID控制器可以在保证稳态精度的前提下, 较PID控制器减小超调18.57%, 并且缩短76.08%的调节时间.
所提出的SFPID控制器适用于比例溢流阀控式液压垫的高性能压力控制, 并且为其他比例溢流阀控系统压力场合提供了控制策略上的借鉴.
| [1] |
秦泗吉. 压边力控制技术研究现状及伺服数控压边方法可行性探讨[J].
中国机械工程, 2007, 18(1): 120–125.
QIN Si-ji. State-of-the-art of blank holding force control technology and feasibility of numerical servo-control holding[J]. China Mechanical Engineering, 2007, 18(1): 120–125. |
| [2] |
张晓斌, 孙宇, 樊红梅, 等. 板料成形压边力控制技术研究现状及发展趋势[J].
锻压技术, 2007, 32(6): 6–12.
ZHANG Xiao-bin, SUN Yu, FAN Hong-mei, et al. Recent research and development trend of blank holder force control technology for sheet metal forming[J]. Forging and Stamping Technology, 2007, 32(6): 6–12. |
| [3] | YOSSIFON S, SWEENEY K, AHMETOGLU M, et al. On the acceptable blank-holder force range in the deep-drawing process[J]. Journal of Materials Processing Technology, 1992, 33(1/2): 175–194. |
| [4] | CHOI H, KOC M, NI J. Determination of optimal loading profiles in warm hydroforming of lightweight materials[J]. Journal of Materials Processing Technology, 2007, 190(1-3): 230–242. DOI:10.1016/j.jmatprotec.2007.02.040 |
| [5] | KITAYAMA S, NATSUME S, YAMAZAKI K, et al. Numerical optimization of blank shape considering flatness and variable blank holder force for cylindrical cup deep drawing[J]. International Journal of Advanced Manufacturing Technology, 2016, 85(9-12): 2389–2400. DOI:10.1007/s00170-015-8087-x |
| [6] | ÖZTVRK E, TVRKÖZ M, HALKACI H, et al. Determination of optimal loading profiles in hydromechanical deep drawing process using integrated adaptive finite element analysis and fuzzy control approach[J]. International Journal of Advanced Manufacturing Technology, 2017, 88(9-12): 2443–2459. DOI:10.1007/s00170-016-8912-x |
| [7] |
王健伟. 多工位压力机数控液压垫液压系统的研究[D]. 杭州: 浙江大学, 2008.
WANG Jian-wei. The research of hydraulic system on NC control multi-point die-cushion[D]. Hangzhou: Zhejiang University, 2008. |
| [8] | WAGENER H. New developments in sheet metal forming: Sheet materials, tools and machinery[J]. Journal of Materials Processing Technology, 1997, 72(3): 342–357. DOI:10.1016/S0924-0136(97)00193-3 |
| [9] | YAGAMI T, MANABE K, YANG M, et al. Intelligent sheet stamping process using segment blankholder modules[J]. Journal of Materials Processing Technology, 2004, 155/156(1/3): 2099–2105. |
| [10] | SIEGERT K, DANNENMANN E, WAGNER S, et al. Closed-loop control system for blank holder forces in deep drawing[J]. CIRP Annals-Manufacturing Technology, 1995, 44(1): 251–254. DOI:10.1016/S0007-8506(07)62319-1 |
| [11] | SIEGERT K, ZIEGLER M, WAGNER S. Closed loop control of the friction force deep drawing process[J]. Journal of Materials Processing Technology, 1997, 71(1): 126–133. DOI:10.1016/S0924-0136(97)00158-1 |
| [12] | SU C, ZHAO J. VBHF system research basing on the technology of fuzzy PID control[J]. Open Mechanical Engineering Journal, 2015, 9(1): 514–520. DOI:10.2174/1874155X01509010514 |
| [13] |
彭雄斌, 龚国芳, 陈馈, 等. 管片拼装机提升缸模糊PID同步控制[J].
浙江大学学报:工学版, 2014, 48(11): 2002–2008.
PENG Xiong-bin, GONG Guo-fang, CHEN Kui, et al. Synchronization fuzzy PID control oflifting hydraulic cylinders for segment erector[J]. Journal of Zhejiang University: Engineering Science, 2014, 48(11): 2002–2008. |
| [14] | MENG D, ZHAO S, LI L, et al. A servo-motor driven active blank holder control system for deep drawing process[J]. International Journal of Advanced Manufacturing Technology, 2016, 87(9-12): 3185–3193. DOI:10.1007/s00170-016-8723-0 |
| [15] | ENDELT B, TOMMERUP S, DANCKERT J. A novel feedback control system-controlling the material flow in deep drawing using distributed blank-holder force[J]. Journal of Materials Processing Technology, 2013, 213(1): 36–50. DOI:10.1016/j.jmatprotec.2012.08.003 |
| [16] | KOMSTA J, VAN OIJEN N, ANTOSZKIEWICZ P. Integral sliding mode compensator for load pressure control of die-cushion cylinder drive[J]. Control Engineering Practice, 2013, 21(5): 708–718. DOI:10.1016/j.conengprac.2011.12.006 |
| [17] | 李壮云. 液压元件与系统:第3版[M]. 北京: 机械工业出版社, 2011: 176-180. |
| [18] | 李国勇, 杨丽娟. 神经·模糊·预测控制及其MATLAB实现:第3版[M]. 北京: 电子工业出版社, 2013: 205-215. |



