2. 航空机电系统综合航空科技重点实验室, 江苏 南京 211100
2. Aviation Key Laboratory of Science and Technology on Aero Electromechanical System Integration, Nanjing 211100, China
传统飞机通过升降舵、副翼、襟翼、起落架、刹车系统等液压用户来完成飞行姿态的控制, 液压能源系统的特性对负载控制起着至关重要的影响[1].当系统压力不足, 负载会出现控制精度下降、响应变慢等现象.同时, 负载控制性能的优劣又将直接影响到飞机的机动性、安全可靠性及战伤生存率等整体性能[2].
绝大多数飞机能源系统在初期方案讨论时会采用流量负载模拟器对其特性进行研究, 从而测试出液压系统的可靠性以及稳定性, 因而流量负载模拟器的研制具有重大意义[3].根据检索文件, 目前对于流量负载模拟器可参考的资料较少.夏鹤鸣等[4]仿真分析了各用户在不同飞行剖面下的可用压力.谭路遥[5]基于某型飞机液压系统试验台, 利用伺服阀作为系统的负载来实现对流量负载模拟器的控制.笔者等[6]采用了非对称负载模拟器实现大载荷加载.袁朝辉等[7]对飞机液压系统流量压力负载模拟器进行了研究, 通过控制比例节流阀的开口大小, 从而控制系统的压力或流量.
常规PID控制广泛地应用在流量负载模拟器中, 但由于其参数固定, 很难同时满足动态响应和静态响应要求.为了克服快速性和稳定性之间的矛盾, 谭路遥等[5-9]采用了模糊PID控制, 但这类方法需要准确地定义量化因子和比例因子, 否则很难得到良好的动静态特性.谷俊杰等[10]根据系统非线性特性, 提出了非线性PID控制器, 但该方法需要准确的系统模型和参数.Chern等[11]提出了线性变速积分PID控制器, 基于偏差线性调整积分参数, 虽然该方法在一定程度上克服了动态和静态特性之间的矛盾, 但是调整参数变化率为固定值, 仍存在不足.
针对以上问题, 由于飞机液压系统常用伺服阀作为作动器的控制元件, 本文在分析飞机完整飞行剖面的泵源工作状态和流量变化的基础上, 为了更真实地模拟出在不同飞行剖面下飞机液压系统压力流量变化情况, 采用伺服阀作为流量负载模拟器, 并分析该流量负载模拟器的优缺点.设计新型变速积分PI控制器, 在完成快速跟踪的前提下, 有效地抑制流量阶跃过程带来的压力波动.
1 典型飞机飞行剖面分析 1.1 典型飞机液压系统配置一般液压驱动飞机的舵面主要通过液压系统来驱动, 典型大型飞机液压系统原理图如图 1所示.从图中可以看出,大型飞机液压系统包括3套系统.其中1#、2#系统泵源各由一个发动机驱动变量泵(engine-driven pump, EDP)和一个电动机驱动泵(electric-motor driven pump, EMP)组成.3#系统以2个EMP作为系统泵源.每套系统都设置了独立的自增压油箱, 并且对于关键执行机构的能源系统进行了余度配置, 从而使飞机在2套液压系统失效的极限情况下, 关键执行机构仍能正常工作, 保证飞机能够安全飞行和着陆.此外, 1#、2#系统之间还安装有单向动力传递单元(power transfer unit, PTU), 当一套液压系统出现故障时, 正常工作系统通过PTU向故障系统传输功率, 而不必切换或关闭执行机构.
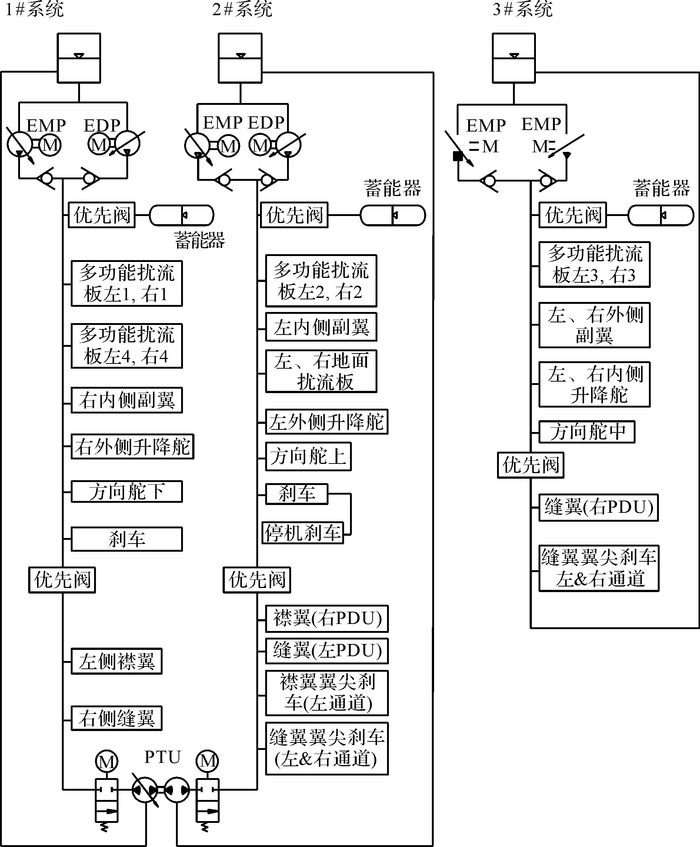
|
图 1 典型飞机液压系统配置图 Fig. 1 Configuration of typical aircraft hydraulic system |
飞机的完整飞行剖面组成如表 1所示, 在不同的飞行剖面下, EDP转速发生变化, EMP运行状态改变, 液压系统的主要用户会变化, 系统最大供应流量和需求均会发生改变[13].
| 表 1 飞机完整飞行剖面组成 Table 1 Constitue of full flight phases of aircraft |
某型飞机在正常工况下, 主系统在不同飞行剖面下泵源的运行状态和系统流量需求如图 2所示.从图中可以知道, 在飞行过程中, 在不同的飞行高度和飞行速度下, 飞机的EDP转速会随着发动机的转速变化而变.在F1、F2、F4、F5、F7、F8、F10飞行剖面下, 前轮转弯, 方向舵、升降舵、副翼、多功能扰流板等作动器作为主要工作舵机, 处于微动调整或静止状态来驱动飞机完成飞行任务, 液压系统处于小流量工作场合.在F3、F6、F9、F11、F12、F13场合, 系统需要完成起落架收放、飞机升降、急转、快速降速等任务, 主起落架、升降舵、扰流板以及反推力装置等作动器作为主要工作舵机, 处于高速、高频运行状态, 系统处于大流量工作状态.此时系统流量安全余度较低, 可能导致系统压力降低, 部分舵机工作不正常.在下降等重要的大流量飞行剖面下, 虽然EDP提供容量已经远大于系统需求流量, 但EMP仍会打开, 提高系统的最大输出流量, 减小液压系统由于EDP突然失效带来的泵源瞬变和压力延迟, 并提高液压系统的可靠性.
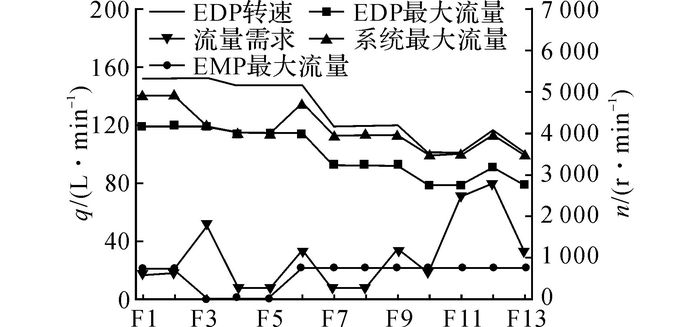
|
图 2 正常飞行剖面下液压系统状态 Fig. 2 Hydraulic system state at normal flight phases |
流量负载模拟器系统原理如图 3所示.系统包括2个泵源、1个溢流阀、1个流量负载模拟器以及1个流量计, 2个电动机分别带动EDP、EMP作为系统泵源, 通过调节流量负载模拟器完成系统的流量控制, 溢流阀安装在泵源与油箱之间, 作为安全阀使用.
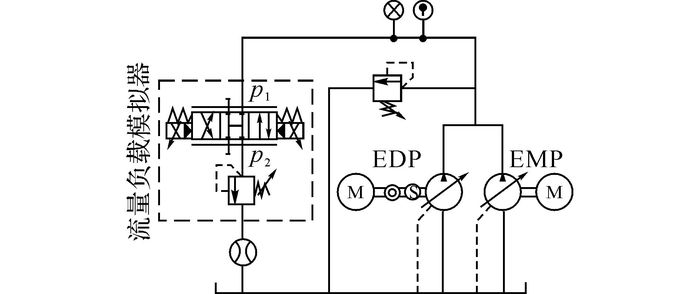
|
图 3 流量负载模拟器系统原理图 Fig. 3 Schematic diagram of flow load simulator |
根据飞机液压系统设计, 泵源采用斜盘式轴向柱塞泵EDP和EMP协同工作的方式, 正常状态下, EDP全程开启, EMP在一些特定的飞行剖面下开启.在稳态情况下, 泵出口压力取决于系统流量、泵转速、泵排量.由于系统研究恒压变量泵的输出特性, 可认为其为一阶系统[14-15]:
| $\left. {\begin{array}{*{20}{c}} {q = \frac{{n \times v}}{{1000}},}\\ {\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \frac{1}{t}\left( {\frac{{{q_{{\rm{nom}}}} \cdot 1000}}{{{n_{{\rm{nom}}}}}} - v} \right),}\\ {{q_{{\rm{nom}}}} = {\rm{min}}\left( {\frac{{n \times {v_{{\rm{max}}}}}}{{1000}} - {k_{{\rm{p}}1}}p,{q_0} - {k_{{\rm{p}}2}}p} \right).} \end{array}} \right\}$ | (1) |
式中:q为恒压变量泵的实际输出流量,n为恒压变量泵实际转速,v为恒压变量泵实际排量,p为恒压变量泵实际工作压力;qnom为恒压变量泵压力p下额定流量;nnom为恒压变量泵额定转速,q0为恒压变量泵恒压段流量坐标轴交点,kp1、kp2分别为恒压变量泵非恒压段和恒压段压力系数,vmax为恒压变量泵最大排量,t为排量变化时间.
2.2.2 流量负载模拟器流量负载模拟器, 包括伺服阀与一个溢流阀.伺服阀作为流量控制器, 溢流阀与恒压变量泵协同工作保障流量控制器前、后压差稳定.当考虑伺服阀动态特性时, 可以认为其为二阶振荡环节:
| $\left. {\begin{array}{*{20}{c}} {\frac{{{q_{\rm{s}}}}}{i} = {K_{{\rm{sv}}}}{{\left( {\frac{{{s^2}}}{{\omega _{{\rm{sv}}}^2}} + \frac{{2{\zeta _{{\rm{sv}}}}}}{{{\omega _{{\rm{sv}}}}}}s + 1} \right)}^{ - 1}},}\\ {{K_{{\rm{sv}}}} = \frac{{{q_{{\rm{smax}}}}}}{{{i_{{\rm{max}}}}}}\sqrt {\frac{{{p_1} - {p_2}}}{2}\Delta {p_n}} .} \end{array}} \right\}$ | (2) |
式中:qs为伺服阀流量负载模拟器实际输出流量,i为伺服阀控制信号,ωsv为伺服阀固有频率,ζsv为伺服阀阻尼比,qsmax为伺服阀流量负载模拟器额定压降下最大输出流量,imax为伺服阀最大控制信号,p1为伺服阀前端压力,p2为伺服阀后端压力,Δpn为伺服阀流量负载模拟器额定压降,Ksv为伺服阀额定流量增益.
2.2.3 系统数学模型泵源与流量负载模拟器之间通过管路连接, 根据容腔压缩性公式:
| $q - {q_{\rm{s}}} = \frac{{60V}}{\beta }\frac{{{\rm{d}}p}}{{{\rm{d}}t}}.$ | (3) |
式中:V为管路等效体积, β为系统油液弹性模量,qs为伺服阀流量负载模拟器实际输出流量.
根据式(1)~(3) 建立系统模型如图 4所示.从图中可以看出, 当系统处于恒压变量泵恒压段工作时, 流量负载模拟器系统流量主要取决于流量负载模拟器阀口开度的控制, 系统流量控制通过压力的变换反馈给泵源, 从而调整其摆角, 改变排量.
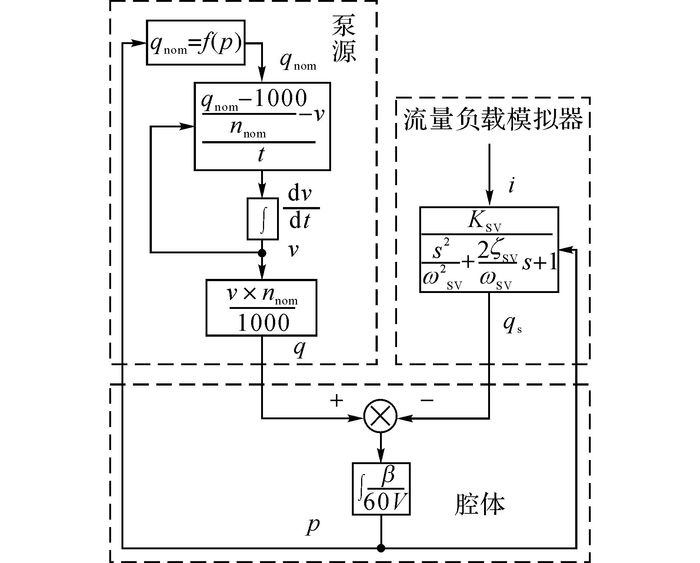
|
图 4 流量负载模拟器系统数学模型 Fig. 4 Mathematical models of flow load simulator system |
对于流量负载模拟器, 控制器需要在完成流量跟踪的要求下, 尽量减小由于流量的变化而导致的泵出口压力波动, 防止泵源受到压力波动而发生损坏.通过系统模型可以看出, 当流量负载模拟器快速变化时, 由于泵源斜盘摆角的改变是滞后环节, 导致泵源在跟踪不同流量需求的变化时产生较大的压力波动.由于所研究的流量控制系统具有动态响应快、纯滞后时间接近零、测量噪声大等特点, PID控制器在这种应用场合已经取得了广泛的应用, 但是传统PID在整个过程中保持控制器参数值不变, 导致控制器很难同时满足动态和静态响应要求.当系统追求高响应速度时将导致较大的系统压力波动, 而在系统追求稳定性时将导致跟踪性能变差[16-17].
3.1 变速积分PI控制器为了同时实现快速性并减小压力波动, 控制器需要在大偏差时缓慢增加, 而在小偏差时快速完成偏差消除.由于指数函数具有当底数大于1时函数单调递增的性质,在指数接近于0时函数值变化较慢, 而当指数较大时, 函数值会迅速变化的特点.设计基于指数调整的新型变积分控制器, 根据系统偏差, 实时调整积分参数Ki, 使系统在大偏差时积分累加速度较慢, 在小偏差时快速累加误差, 消除偏差.变速控制器如下式:
| $\left. {\begin{array}{*{20}{c}} {f(e) = {a^ \wedge }\left\{ {b \times \left[ {{e_{\rm{h}}}(k) - e} \right]/{e_{\rm{h}}}(k);} \right.}\\ {{e_{\rm{h}}}(k) = \left\{ {\begin{array}{*{20}{l}} {{e_{\rm{h}}}\left( {k - 1} \right),} & {{q_{1{\rm{c}}}} = {q_{2{\rm{c}}}};}\\ {\left| {{q_{1{\rm{c}}}} - {q_{2{\rm{c}}}}} \right|,} & {{q_{1{\rm{c}}}} \ne {q_{2{\rm{c}}}}.} \end{array}} \right.} \end{array}} \right\}$ | (4) |
式中:f(e)为变速系数, eh(k)第k次指令变化值, a为变速底数, b为变速指数, q1c为原始流量目标值, q2c为最新流量目标值.
变速积分PI控制器如图 5所示, 在传统的增量式PI控制器基础上, 利用变速控制器, 根据偏差e的大小, 不断地改变积分项的参数KI.变速积分PI控制器表达式[18]如下:
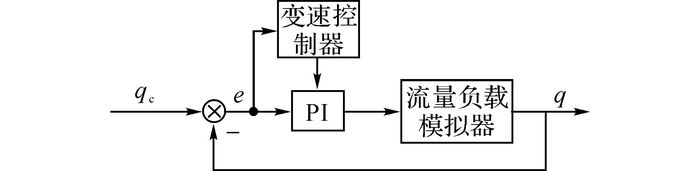
|
图 5 变速积分PI控制器 Fig. 5 Variable integral PI controller |
| $\Delta u\left( k \right) = {K_{\rm{P}}}\left[ {e\left( k \right) - e\left( {k - 1} \right)} \right] + f\left( e \right) \times {K_{\rm{I}}}e\left( k \right).$ | (5) |
式中:KP、KI分别为控制器比例、积分参数值, e(k)为第k次偏差计算值, Δu(k)为第k次控制量增值.
3.2 稳定性分析当系统在恒压变量泵恒压段工作时, 负载模拟器流量增益系数Ksv变化可忽略, 根据系统数学模型和控制器可得如图 6所示的系统传递函数框图.

|
图 6 流量负载模拟器系统传递函数框图 Fig. 6 Block diagram of flow load simulator transferfunction |
由传递函数可知, 系统特征方程如下:
| $\begin{array}{l} \frac{{{K_{\rm{P}}}}}{{{K_{\rm{I}}}}}{s^3} + 2\frac{{{K_{\rm{P}}}}}{{{K_{\rm{I}}}}}{\xi _{{\rm{sv}}}}{\omega _{{\rm{sv}}}}{s^2} + ({K_{\rm{P}}}{K_{{\rm{sv}}}} + 1)\frac{{{K_{\rm{P}}}}}{{{K_{\rm{I}}}}}{\xi _{{\rm{sv}}}}\omega _{{\rm{sv}}}^2s + \\ \quad {K_{\rm{P}}}{K_{{\rm{sv}}}}\omega _{{\rm{sv}}}^2 = 0. \end{array}$ | (6) |
根据特征方程可得劳斯列阵为
| $\begin{array}{*{20}{c}} {{s^3}}\\ {{s^2}}\\ {{s^1}}\\ {{s^0}} \end{array}\left| {\begin{array}{*{20}{c}} {\frac{{{K_{\rm{P}}}}}{{{K_{\rm{I}}}}}} & {\left( {{K_{\rm{P}}}{K_{{\rm{sv}}}} + 1} \right)\frac{{{K_{\rm{P}}}}}{{{K_{\rm{I}}}}}\omega _{{\rm{sv}}}^2}\\ {2\frac{{{K_{\rm{P}}}}}{{{K_{\rm{I}}}}}{\xi _{{\rm{sv}}}}{\omega _{{\rm{sv}}}}} & {{K_{\rm{P}}}{K_{{\rm{sv}}}}\omega _{{\rm{sv}}}^2}\\ {\frac{{2{K_{\rm{P}}}{\xi _{{\rm{sv}}}}\omega _{{\rm{sv}}}^2 - {K_{\rm{P}}}{K_{\rm{I}}}{K_{{\rm{sv}}}}{\omega _{{\rm{sv}}}}}}{{2{K_{\rm{I}}}{\xi _{{\rm{sv}}}}}}} & 0\\ {{K_{\rm{P}}}{K_{{\rm{sv}}}}\omega _{{\rm{sv}}}^2} & 0 \end{array}} \right.$ |
根据劳斯稳定性判据, 系统稳定的充分条件为劳斯列阵第一列系数全部大于0[19], 又因为KP、KI、ζsv、ωsv一定大于0, 可得系统稳定性条件为
| $\frac{{2{\xi _{{\rm{sv}}}}{\omega _{{\rm{sv}}}}}}{{{K_{{\rm{sv}}}}}} > {K_{\rm{I}}}.$ | (7) |
基于AMESim软件平台, 根据如图 4所示的系统数学模型搭建仿真模型, 模型参数如表 2所示.PI控制器比例参数KP和积分参数KI在符合系统稳定性条件下, 通过齐格勒-尼柯尔斯法则整定.变速积分PI控制器KP与增量式PI控制器相同, 取值2×10-6.根据系统时间响应要求, 整定得系统积分常数KI1=1.6×10-6.根据压力波动要求, 整定得系统积分常数KI2=8×10-7.为了保证参数整定的快速性和系统稳定性, 将KI2设置为变速积分PI控制器KI, 将KI1/KI2设置为a, 在系统稳定的条件下将b从1逐步提升从而使系统满足时间响应要求.根据上述方法整定得a=2、b=2.根据表 2可以得出流量负载模拟器稳定性条件为KI<20.28.
| 表 2 流量负载模拟器系统模型参数 Table 2 Model parameters of flow load simulator system |
飞行剖面流量跟踪就是在不同的飞行剖面下, 流量发生阶跃变化, 系统输出流量需要在指定时间内完成变化, 从而测试出系统的供流能力.为了测试控制方法的有效性, 根据图 2可知, 完整飞行剖面下的最大需求流量为79 L/min, 最小需求流量为7.3 L/min, 故测试10~80 L/min的阶跃响应;为了测量系统在完整飞行剖面下的供流能力, 根据图 2数据调整EDP和EMP工作状态以及系统流量需求.
流量负载模拟器阶跃响应曲线如图 7所示.从图(a)中可以看出, 变速积分PI控制器和PI控制器在系统流量从10 L/min到80 L/min变化时,两种控制器的响应时间均为1 s时, 均能完成流量跟踪要求.变速积分PI控制器在启动时偏差较大, 流量增速较慢, 而在偏差较小时, 流量增速较快.从图(b)显示的系统压力波动可以发现, 基于变速积分PI控制器压力波动只有0.14 MPa, 而基于PI控制器的压力波动达到了0.37 MPa.在流量响应时间相同的情况下, 变速积分PI控制器的压力波动相比于PI控制器降低了62.2%.
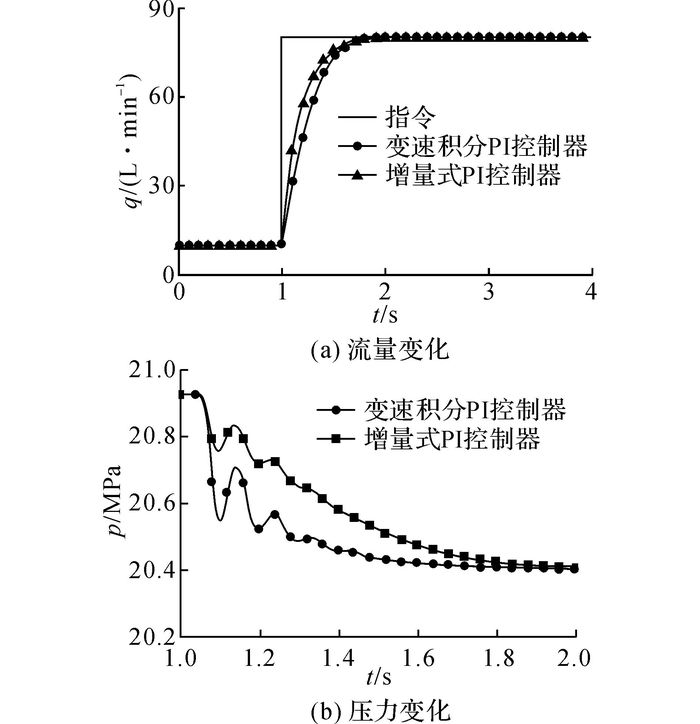
|
图 7 流量负载模拟器阶跃仿真曲线 Fig. 7 Step simulation results of flow load simulator |
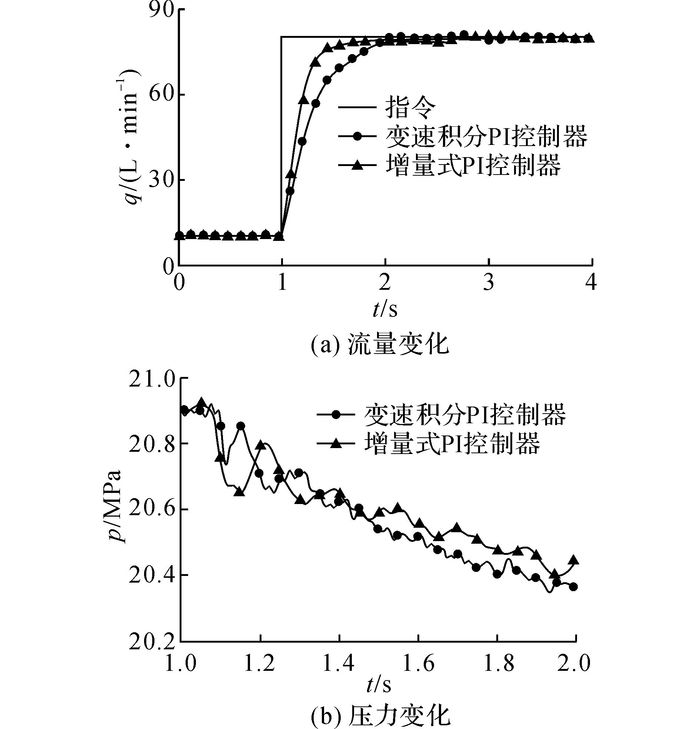
流量负载模拟器正常飞行剖面跟踪曲线如图 8所示.从图中可以看出, 在整个正常飞行剖面跟踪过程中, 在不同的阶跃变化时, 在变速积分PI控制器控制下, 流量响应时间稳定在1 s左右, 满足控制要求.在整个飞行阶段, 系统压力基本稳定在21 MPa左右, 当最大流量需求为79 L/min时, 系统压力最小为20.42 MPa, 此时液压系统稳定可靠.
|
图 8 正常飞行剖面下流量负载模拟器仿真曲线 Fig. 8 Simulation results at normal flight phases of flow load simulator |
试验台如图 9所示, 采用115 kW变频电机驱动EDP, 采用15 kW变频电机驱动EMP, 在试验台中安装流量负载模拟器作为系统负载.此外, 系统中还安装了温度传感器、压力传感器和转速传感器,用于完成系统工况监测,并使用工控机来实现数据测量以及人机交互控制.系统元件参数如表 2所示, 系统信号采样频率为1 kHz.系统采用测量范围为0~120 L/min的KEM涡轮流量计, 通过测量流量负载模拟器的流量, 实现系统流量闭环控制.

|
图 9 流量负载模拟器试验台 Fig. 9 Test rig of flow load simulator |
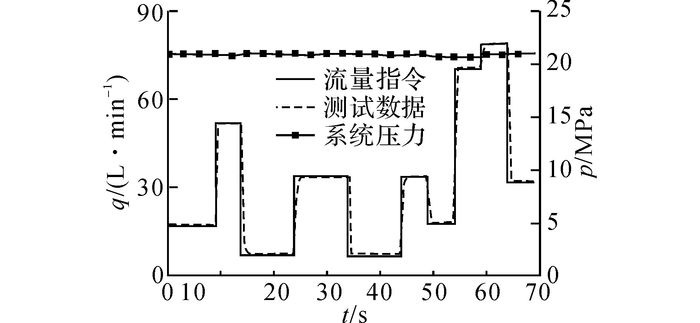
为了测试控制效果的有效性和泵源特性, 共进行2组试验, 试验结果如图 10、11所示.
|
图 10 流量负载模拟器阶跃试验曲线 Fig. 10 Step test results of flow load simulator |
|
图 11 正常飞行剖面下流量负载模拟器试验曲线 Fig. 11 Test results at normal flight phases of flow load simulator |
流量负载模拟器阶跃响应曲线如图 10所示.可知,图 10(a)的流量变化结果同图 7(a).从图 10(b)的系统压力波动可以发现, 基于变速积分PI控制器的压力波动只有0.14 MPa而基于PI控制器的压力波动达到了0.31 MPa.在流量响应时间相同的情况下, 变速积分PI控制器的压力波动相比于PI控制器降低了54.8%.
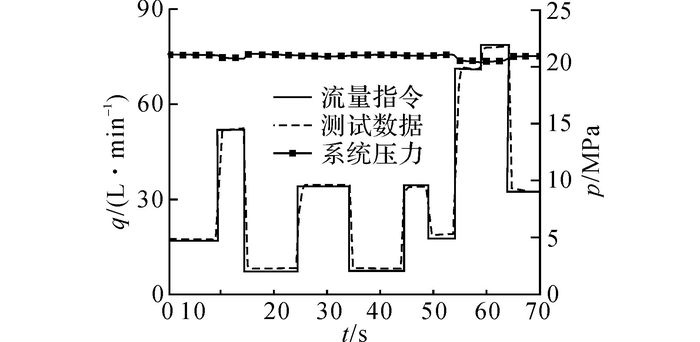
流量负载模拟器正常飞行剖面跟踪曲线如图 11所示.从图中可以看出, 在整个正常飞行剖面跟踪过程中, 在不同的阶跃响应过程中, 采用变速积分PI控制器的响应时间稳定在1 s左右, 满足系统控制要求.在整个飞行阶段, 系统压力基本稳定在21 MPa左右, 当最大流量需求为79 L/min时, 系统压力最小为20.41 MPa, 此时液压系统稳定可靠
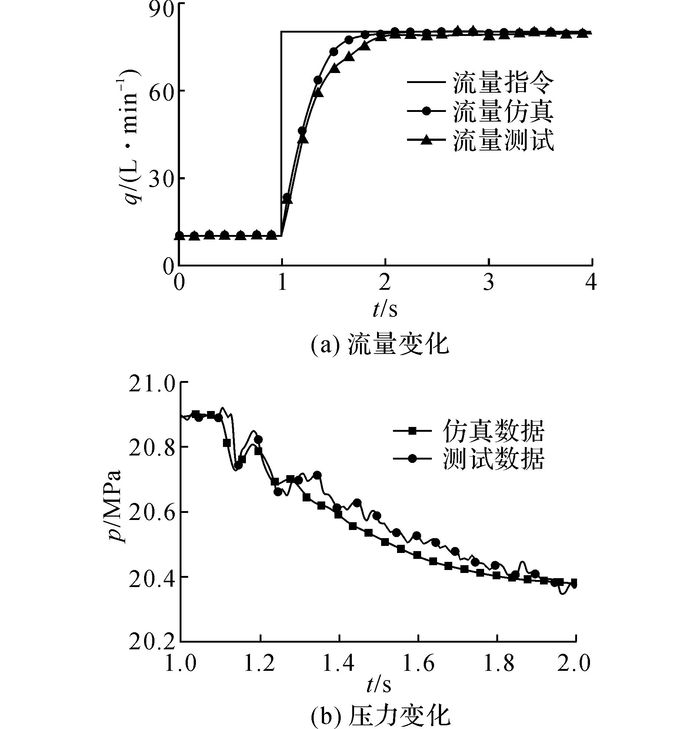
5.2.2 试验和仿真对比分析流量负载模拟器阶跃响应仿真和试验曲线如图 12所示.从图 12(a)中可以看出, 试验结果和仿真结果的流量跟踪基本吻合;当系统稳定在80 L/min时, 由于信号噪声的影响, 试验结果出现了1 L/min左右的波动.此外, 从图 12(b)的系统压力波动可以发现, 由于存在流量波动, 导致在稳定状态时系统也有一定程度的压力波动.
|
图 12 阶跃仿真试验对比曲线 Fig. 12 Comparison between steep simulation and test |
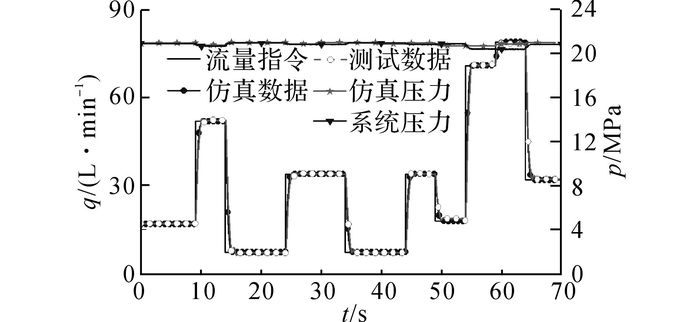
流量负载模拟器正常飞行阶段试验和仿真对比曲线如图 13所示.从图中可以看出, 试验结果与仿真结果的流量和压力变化规律接近, 但是存在一定的波动, 主要是由于流量控制本身是一个受噪声干扰较大的场合,同时也受到忽略电机转速的动态变化所引起的存在误差等的影响.
|
图 13 正常飞行剖面仿真试验对比曲线 Fig. 13 Comparison between simulation and test results at normal flight phases |
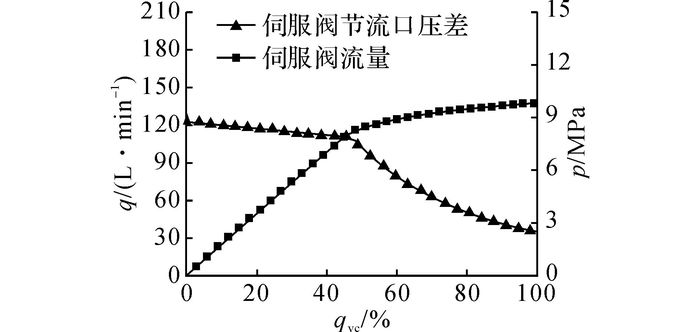
流量负载模拟器开环特性曲线如图 14所示.在不同的指令信号qvc下, 由于流量负载模拟器伺服阀压差由恒压变量泵和溢流阀系统工作来保证.当处于恒压变量泵恒压段工作时, 伺服阀前、后压差只存在小范围波动, 零流量控制线性度较好;但当系统处于恒压变量泵非恒压段工作时, 伺服阀前、后压力出现较大波动, 流量控制出现非线性特性.
|
图 14 流量负载模拟器开环特性 Fig. 14 Open loop characteristics of flow load simulator |
流量负载模拟器飞行剖面跟踪曲线如图 11所示.从图中可以看出, 由于系统处于恒压变量泵恒压段工作, 伺服阀流量负载模拟器跟踪精度高、响应速度快、以及不同流量指令响应下的重复精度较高等优势.
此外, 根据系统组成可知, 流量负载模拟器溢流阀和伺服阀分离, 结构复杂, 同时最低工作压力受到溢流阀的限制且调整麻烦, 难以在压力变化很大的范围应用.
6 结论(1) 本研究提出了新的流量负载模拟器, 为分析飞机液压系统的流量供给和控制提供了重要依据.通过流量负载模拟器的开环特性及正常飞行剖面下的曲线分析,发现其具有跟踪精度高、响应速度快等优点.
(2) 分析了完整飞行剖面下液压系统的工作状态, 利用流量负载模拟器模拟了系统的流量需求.仿真和试验结果均表明, 液压系统在完整飞行剖面的可用压力在20.4 MPa以上, 液压系统稳定可靠, 同时验证了泵源设计的合理性.
(3) 针对目前常规PI控制器不能适应系统变化过程中状态改变的不足, 设计了新型变速积分PI控制器.试验和仿真结果均表明, 在相同的流量阶跃响应时间下,相比于增量式PI控制器,新型变速积分PI控制器的最大压力波动至少减小了40 %, 明显降低了不同飞行剖面切换过程中的压力波动.
(4) 本文研究的流量负载模拟系统仅为正常工况下最大负载系统的工作状态, 对于故障工况状态下的系统流量模拟还不够完善, 未来可增加在故障工况下的系统工作状态的研究.
| [1] | SHANG Y X, JIAO Z X, YAO N. Influence of aerocraft actuator on ultimate performance of hydraulic load simulator [C] // International Conference on Fluid Power and Mechatronics. Beijing: IEEE, 2011: 850-856. |
| [2] |
杨华勇, 丁斐, 欧阳小平, 等. 大型客机液压能源系统[J].
中国机械工程, 2009, 20(18): 2152–2159.
YANG Hua-yong, DING Fei, OUYANG Xiao-ping, et al. Hydraulic power systems for trunk line aircrafts[J]. China Mechanical Engineering, 2009, 20(18): 2152–2159. DOI:10.3321/j.issn:1004-132X.2009.18.003 |
| [3] | PEI R, YUAN Z, JIANG H.Study on flow/pressure simulation subsystem for aircraft hydraulic energy system based on Fuzzy-PID control [C] // International Conference on Electronic Measurement and Instruments. Chengdu: IEEE, 2011: 181-185. |
| [4] |
夏鹤鸣, 王鸿鑫. 基于AMESim飞机液压能源系统用户可用压力仿真计算[J].
机械设计与制造工程, 2014, 43(7): 20–23.
XIA He-ming, WANG Hong-xin. The simulation of pressure available to the user in aircraft hydraulic energy system based on AMESim[J]. Machine Design and Manufacturing Engineering, 2014, 43(7): 20–23. |
| [5] |
谭路遥. 某型民用飞机液压原理试验系统设计及关键部件仿真分析[D]. 杭州: 浙江大学, 2014.
TAN Lu-yao.Development of the hydraulic system test rig(HSTR) for the civil aircraft and simulation of its key components [D].Hangzhou: Zhejiang University, 2014. |
| [6] |
欧阳小平, 李锋, 朱莹, 等. 重载航空负载模拟器非线性最优前馈补偿控制[J].
航空学报, 2016, 37(2): 669–679.
OUYANG Xiao-ping, LI Feng, ZHU Yi, et al. Nonlinear optimal feedforward compensation controller for heavy load aviation load simulator[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 669–679. |
| [7] |
袁朝辉, 马科, 江辉军, 等. 某型飞机液压能源系统原理验证试验系统设计[J].
测控技术, 2010, 29(6): 48–53.
YUAN Chao-hui, MA Ke, JIANG Hui-jun, et al. Design of principle verification test system with a certain type of aircraft hydraulic energy systems[J]. Measurement and Control Technology, 2010, 29(6): 48–53. |
| [8] | AHN K K, TRUONG D Q, THANH T Q, et al. Online self-tuning fuzzy proportional—integral—derivative control for hydraulic load simulator[J]. Proceedings of the Institution of Mechanical Engineers-Part Ⅰ: Journal of Systems and Control Engineering, 2008, 222(2): 81–95. DOI:10.1243/13506501JET301 |
| [9] | FAN B Q, LEE K M, OUYANG X P, et al. Soft-switchable dual-PI controlled axial loading system for high-speed EMU axle-box bearing test rig[J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7370–7381. DOI:10.1109/TIE.2015.2458303 |
| [10] |
谷俊杰, 张艳娟, 赵兴楼. 非线性PID控制器在主蒸汽温度控制中的应用[J].
热力发电, 2009, 38(7): 92–95.
GU Jun-jie, ZHANH Yan-juan, ZHAO Xing-lou. Application of non-linear PID controller in the main steam temperature control[J]. Power Equipment, 2009, 38(7): 92–95. |
| [11] | CHERN T L, WU Y C. Integral variable structure control approach for robot manipulators[J]. Control Theory and Applications, IEE Proceedings, 1992, 139(2): 161–166. DOI:10.1049/ip-d.1992.0022 |
| [12] | 欧阳小平, 杨华勇, 郭生荣, 等. 现代飞机液压技术[M]. 杭州: 浙江大学出版社, 2016: 1-24. |
| [13] | 刘星. 飞行原理[M]. 北京: 科学出版社, 2011: 68-90. |
| [14] |
莫波, 雷明, 曹泛. 恒功率恒压泵变量机构的调节原理[J].
液压与气动, 2002, 2002(6): 5–6.
MO Bo, LEI Ming, CAO Fan. A principle to adjust the volume control of constant power and constant pressure pump[J]. Chinese Hydraulics and Pneumatics, 2002, 2002(6): 5–6. |
| [15] | 李艳军. 飞机液压传动与控制[M]. 北京: 科学出版社, 2009: 65-85. |
| [16] |
许秀, 黄金华. 新型连续变速积分控制算法研究及应用[J].
工业仪表与自动化装置, 2006, 2006(6): 40–42.
XU Xiu, HUANG Jin-hua. Study and application ofa new PID algorithm-continues speed change integral[J]. Industrial Instrumentation and Automation, 2006, 2006(6): 40–42. |
| [17] |
肖磊, 谢菊芳. 一种基于PLC的PID流量控制设计[J].
湖北大学学报:自然科学版, 2007, 29(1): 44–46.
XIAO Lei, XIE Ju-fang. Design of PID flow control based on PLC[J]. Journal of Hubei University: Natural Science, 2007, 29(1): 44–46. |
| [18] |
李锋. 飞机液压系统负载模拟研究[D]. 杭州: 浙江大学, 2016.
LI Feng.Research on load simulation of the aircraft hydraulic system [D].Hangzhou: Zhejiang University, 2016. |
| [19] | 高铁红, 曲云霞. 控制工程基础:第2版[M]. 北京: 中国计量出版社, 2016: 82-89. |


