2. 浙江科技学院 机械与汽车工程学院, 浙江 杭州 310012
2. School of Mechanical and Automotive Engineering, Zhejiang University of Science and Technology, Hangzhou 310012, China
公共自行车系统(public bike system, PBS)已成为许多城市越来越重要的公共交通方式之一[1-2].但是, PBS在实际运行过程中还存在着不少问题[3-4], 其中最突出的是服务点规划不合理[5]及“租还车难”.服务点规划不合理加剧了“租还车难”, 降低了PBS的使用效率.
关于PBS服务点布设的研究主要包括以下内容.Lin等[6-8]综合考虑总成本和服务水平下得出PBS中服务点设置的最佳位置和数量.Garracía-Palomares等[9-10]提出了一种基于地理信息系统的方法来确定服务点的容量.Vogel等[11]通过研究高峰时段租还信息和服务点位置, 进行了服务点的位置优化.Martine等[12]提出了能同时解决服务点选址和服务点规模问题的优化模型.Li等[13]提出了城市公共自行车服务点的复杂网络构建方法.Dai等[14]根据公共自行车系统规划的实践, 提出了系统规划的基本原则和思路.耿雪等[15]在将公共自行车系统分区的基础上, 测算各区日均出行次数, 进而确定公共自行车服务点的数量和规模.李黎辉等[16]提出了“总量调控、分类分块、平衡规模、灵活调整”的布局总体思路.陈景旭等[17]提出了分层分级布设公共自行车服务点的布局方法.这些工作推动了PBS的科学布设研究, 但是也比较明显地受到了经验与主观因素的限制.
有限元方法是一种客观分析分布式数据的有效方法, 用于解决工程中平面薄板的力学问题, 根据相邻子域间的相互作用机制进行求解.有限元方法与交通流的空间分布特征不谋而合, 但目前用有限元方法解决交通问题的研究比较少, 主要有李福祥等[18]基于流体有限元的思想对交通流的研究.该研究证明了有限元流体分析系统ANSYS-FLOTR AN可以较好地模拟交通流状况.
PBS相邻服务点的服务区域之间的区域租还平衡, 具有与有限元中相邻子域间的类似相互作用机制.运用有限元思想建立PBS单元供需不平衡度的估算模型, 有助于合理布设公共自行车服务点, 缓解“租还车难”问题.本文借鉴有限元法原理, 提出一种公共自行车系统服务点布设的有限元估算方法.
1 PBS服务点布设的单元特性与有限元估算参数根据杭州城市公共自行车系统7年来的实践经验, 服务点布设需要分布密度较高且尽量均匀, 这样, 在PBS无车可租或者无空位可还车时, 用户可以较方便地步行到相邻各服务点或者更远的服务点租还车[19], PBS租还需求量通过相互邻接的区域实现了空间的传递与扩散.PBS交通出行的实际调查发现, 某区域中用户选择步行到相邻或者更远的各服务点租还车的可能性大致相等, 也就是每个单元租还需求的传递扩散能力基本相同, 因此公共自行车系统的微区域单元具有统计意义上的连续性、均匀性等特征, 符合运用有限元方法对单元特性的要求.
在PBS运营过程中, 需要有各种参数描述系统运行性能及服务质量.在应用有限元估算方法分析PBS单元供需不平衡度时, 用到的参数定义如下:
1) 单元:PBS覆盖区域通过虚拟网格划分离散出的虚拟矩形小片区, 包含若干服务点.
2) 节点:由租还需求量拟合成的租还函数在单元上的插值点, 即虚拟矩形单元上的4个顶点.
3) 单元需求强度:用于衡量在某时间段内, PBS覆盖的某区域采用公共自行车交通模式的租还需求差异的大小, 用该区域单位面积的租车数与还车数的差值来计算, 用Fui表示, 正、负符号分别表示租车和还车.
4) 单元服务能力:用于衡量PBS覆盖的某区域内各服务点为该服务点所服务的范围可以提供随租随还公共自行车的能力, 用该服务点某时刻的公共自行车数m与服务面积S的比值Focp和空锁桩数n与服务面积S的比值Femp表示.
5) 单元供需不平衡度:PBS单元需求强度与该单元服务能力的差值, 用某时刻该区域单位面积的租车数与还车数的差值与在该区域单位面积上Focp或Femp的差值, 用p表示, p<0.121e8, p位于小值区间;0.121 e8<p<0.242 e8, p所在的区间适中;0.242 e8<p, p位于大值区间.
若需求强度为正, 则有:当Focp-Fui<0.121e8时, p位于小值区间, 且p随着Focp-Fui的减小而减小;当Focp-Fui>0.242e8时, p位于大值区间, 且p随着Focp-Fui的增大而增大;当0.121e8<Focp-Fui<0.242e8时, p所在的区间适中, 且p随着Focp-Fui的增大而增大.
若需求强度为负, 则有:当Femp+Fui<0.121 e8时, p位于小值区间, 且p随着Femp+Fui的减小而减小;当Femp+Fui>0.242 e8时, p位于大值区间, 且p随着Femp+Fui的增大而增大;当0.121 e8<Femp+Fui<0.242 e8时, p所在的区间适中, 且p随着Femp+Fui的增大而增大.
6) 车锁比:某服务点公共自行车数量与该服务点锁桩数量的比值, 用α表示.
7) 需求增度:PBS的单元需求强度和车锁比的比值.需求增度矩阵为单元需求增度的集合, 用K表示.
8) 车变比:在采用PBS交通模式的一定需求量作用下, 公共自行车服务点车锁比的变化系数, 即需求量作用前、后的车锁比之差与作用前的车锁比之比, 用于仿真实验.
2 PBS服务点布设的有限元估算方法将PBS覆盖区域作为研究平面, 通过虚拟网格划分离散成各个虚拟矩形小片区为单元, 根据区域中的租还需求量[20], 求解计算出单元需求强度、服务点的车锁比、空缺数及满位数.有限元估算方法具体步骤如下.
1) 虚拟网格划分.
考虑估算的精度, 在PBS服务覆盖区域中选择一个能完全包含研究区域的最小矩形, 将矩形的长宽按比例划分, 形成各个小矩形, 依次对这些小矩形进行虚拟网格划分, 离散获得的这些虚拟矩形(设长为2a, 宽为2b)小片区为一个单元, 设虚拟矩形单元为i-j-m-k(逆时针顺序编号), i、j、m、k为4个节点, 坐标分别为(xi, yi)、(xj, yj)、(xm, ym)、(xk, yk), x为纬度方向, y为经度方向.
2) 虚拟矩形单元的插值租还函数.
插值租还函数是单元节点上的租还需求量拟合成的租还函数, 表达式为
| $\left. {\begin{array}{*{20}{l}} {s = {a_1} + {a_2}x + {a_3}y + {a_4}xy,}\\ {t = {b_1} + {b_2}x + {b_3}y + {b_4}xy.} \end{array}} \right\}$ | (1) |
式中:s、t分别为节点的租、还需求量.
将4个节点代入式(1), 解出a1、a2、a3、a4和b1、b2、b3、b4, 并将单元内的需求量表示成由4个节点的需求量为待定系数的近似展开式, 矩阵形式为
| $\begin{array}{l} \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{l}} {{N_i}} & 0 & {{N_j}} & 0 & {{N_m}} & 0 & {{N_k}} & 0\\ 0 & {{N_i}} & 0 & {{N_j}} & 0 & {{N_m}} & 0 & {{N_k}} \end{array}} \right] \times \\ \quad \quad {\left[ {\begin{array}{*{20}{l}} {{s_i}} & {{t_i}} & {{s_j}} & {{t_j}} & {{s_m}} & {{t_m}} & {{s_k}} & {{t_k}} \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{N\delta }} \end{array}$ | (2) |
式中:N为单元上租还基函数列阵, 即
| $\left. \begin{array}{*{35}{l}} {{N}_{i}}=\frac{1}{4}\left( 1-\xi \right)\left( 1-\eta \right), \\ {{N}_{j}}=\frac{1}{4}\left( 1+\xi \right)\left( 1-\eta \right), \\ {{N}_{m}}=\frac{1}{4}\left( 1+\xi \right)\left( 1+\eta \right), \\ {{N}_{k}}=\frac{1}{4}\left( 1-\xi \right)\left( 1+\eta \right). \\ \end{array} \right\}$ |
其中,
| $\xi = \frac{x}{a},\eta = \frac{y}{b},$ |
δ为i、j、m、k这4个节点租还量组成的列阵.
3) 分析求解车锁比α、单元需求强度Fui.
由于相邻服务点的服务区域之间租还需求具有相互作用机制, 推算可得出某一公共自行车服务点车锁比由沿纬度方向车锁比εx、经度方向车锁比εy和纬度与经度2个方向之间的车锁比γxy的列阵表示:
| $\mathit{\boldsymbol{\alpha }}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\gamma _{xy}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial s}}{{\partial x}}}\\ {\frac{{\partial t}}{{\partial y}}}\\ {\frac{{\partial s}}{{\partial y}} + \frac{{\partial t}}{{\partial x}}} \end{array}} \right] = \frac{1}{{ab}}\left[ {\begin{array}{*{20}{c}} {b\frac{{\partial s}}{{\partial \xi }}}\\ {a\frac{{\partial t}}{{\partial \eta }}}\\ {a\frac{{\partial t}}{{\partial \eta }} + b\frac{{\partial s}}{{\partial \xi }}} \end{array}} \right].$ | (3) |
记
| $\mathit{\boldsymbol{\alpha }} = \mathit{\boldsymbol{B\delta }}.$ | (4) |
令单元车锁比状态矩阵:
| $\mathit{\boldsymbol{B}} = \left[ {{B_i}\quad {B_j}\quad {B_m}\quad {B_k}} \right].$ | (5) |
其中,
| ${\mathit{\boldsymbol{B}}_i} = \left[ {\begin{array}{*{20}{c}} {b\frac{{\partial {N_i}}}{{\partial \xi }}} & 0\\ 0 & {a\frac{{\partial {N_i}}}{{\partial \eta }}}\\ {a\frac{{\partial {N_i}}}{{\partial \eta }}} & {b\frac{{\partial {N_i}}}{{\partial \xi }}} \end{array}} \right].$ | (6) |
相应地, 需求量来自服务点附近的所有方向, 单元需求强度即为由沿纬度方向单元需求强度σx、沿经度方向单元需求强度σy和垂直于纬度方向的平面上且沿经度方向的单元需求强度τxy的列阵表示.
| ${\mathit{\boldsymbol{F}}_{{\rm{ui}}}}{\rm{ = }}\left[ {\begin{array}{*{20}{l}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\tau _{xy}}} \end{array}} \right]{\rm{ = }}\frac{E}{{1 - {\mu ^2}}}\left[ {\begin{array}{*{20}{c}} 1 & \mu & 0\\ \mu & 1 & 0\\ 0 & 0 & {\frac{{1 - \mu }}{2}} \end{array}} \right]\alpha .$ | (7) |
式中:E为各单元需求强度与相应车锁比的比值的平均值;μ为横向车锁比与纵向车锁比的绝对值的比值, 由于公共自行车的需求只有租和还2种可能, 且在同一平面上, μ=0.即:
| ${\mathit{\boldsymbol{F}}_{{\rm{ui}}}}{\rm{ = }}\frac{1}{n}\sum\limits_{\omega = 1}^n {\frac{{{\mathit{\boldsymbol{F}}_{{\rm{ui}}\omega }}}}{{{\mathit{\boldsymbol{\alpha }}_\omega }}}} \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & {1/2} \end{array}} \right]\alpha .$ | (8) |
其中, Fuiω为每个单元的单元需求强度, αω为每个单元的车锁比, ω为第ω个矩形单元, n为研究区域的总单元数.
令单元需求强度状态矩阵:
| $\mathit{\boldsymbol{D}}{\rm{ = }}\frac{1}{n}\sum\limits_{\omega = 1}^n {\frac{{{\mathit{\boldsymbol{F}}_{{\rm{ui}}\omega }}}}{{{\mathit{\boldsymbol{\alpha }}_\omega }}}} \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & {1/2} \end{array}} \right].$ | (9) |
当α<0时, 表示某服务点的公共自行车在某段时间内无法满足自行车租借的需求;当α>1时, 表示某服务点的锁桩设施在某段时间内无法满足自行车归还的需求.当出现以上2种情况时, 短时间内不能通过PBS用户的租还自动调节到合理状态, 此服务点需要上架(或下架)公共自行车.
4) PBS单元需求增度矩阵K计算:
| $\mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{ }}.$ | (10) |
5) 系统综合并引入边界条件.
单元节点租还需求量列阵叠加后的系统方程为
| $\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{K}}\prime \mathit{\boldsymbol{\eta }}\prime .$ | (11) |
式中:F为叠加后各单元节点租还需求量列阵, K′叠加后需求增度矩阵, η′为叠加后区域内所有节点的车锁比列阵.
边界条件为
| ${C_i} = {C_a}.$ | (12) |
式中:Ci(i=1, 2, 3, 4) 分别表示研究区域平面的4个边, Ca为研究区域平面4个边的车锁比约束.
6) 求解方程组.
将式(12) 边界条件代入系统方程(11), 可求出区域内每个虚拟矩形节点的租还需求量.将节点的租还需求量s1、t1、s2、t2、s3、t3、…、si、ti代入式(3), 即可求出各单元的近似车锁比;利用式(8), 即可得到单元需求强度的近似解.
7) PBS服务点布设.
求解方程组得出PBS覆盖范围内所有的单元需求强度, 进而求得单元需求强度与单元服务能力之差, 判断单元供需不平衡度p的大小.在p位于大值区间的区域内设置新服务点或增加该区域内原服务点的锁桩数, 科学布设服务点, 有效解决“租还车难”的问题.
3 杭州市区域PBS服务点布设的有限元估算实践 3.1 服务点布设的有限元估算模型与边界条件根据数学计算步骤在ANSYS软件上实践杭州市区域PBS服务点布设的有限元估算.杭州是国内最先施行公共自行车的城市, 已经拥有7年的历史运行数据, 这可以为有限元估算方法的验证提供充实的数据支撑.取杭州市拱墅区30.300 0°N~30.306 0°N和120.150 0°E~120.157 0°E区域为研究对象, 该区域内共有8个公共自行车服务点.从历史运营数据分析可以得出公共自行车系统出行时间分布特性, 公共自行车“租还车难”的问题在早晚高峰开始和结束时段特别突出, 以某日7:00~7:30的实际租还量历史统计数据为例进行有限元法估算, 服务点相关数据如表 1所示.
| 表 1 公共自行车系统(PBS)服务点租还量数据(7:00—7:30) Table 1 Rent and return data of service station of public bike system (PBS) during 7:00 to 7:30 |
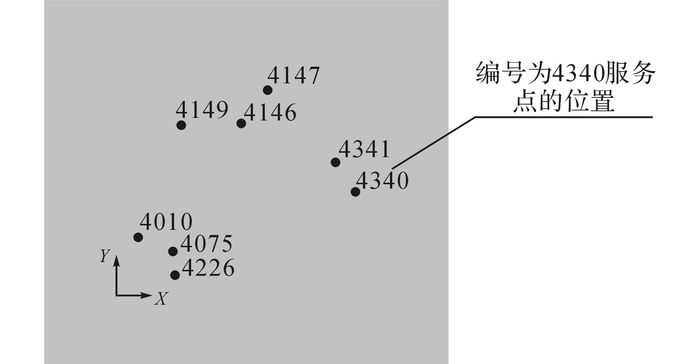
在此需要说明的是, 表中7:00~7:30时间段内租借的车辆数多于该服务点7:00的公共自行车数量和该时间段内归还的车辆数之和, 这是采用人工或机动车方法对自行车进行调度产生的结果.将选取的研究区域及8个服务点在ANSYS中建模, 根据“1 m=0.01”将研究区域转化为长1 m、宽1 m的矩形平面.公共自行车服务点位置如图 1所示.
|
图 1 ANSYS软件中的公共自行车服务(PBS)区域服务点位置建模 Fig. 1 Location modeling of public bicycle service (PBS) regional service station in ANSYSsoftware |
按照ANSYS建模要求和PBS的简化运行特性建立边界条件, 约束模型四边的单元服务能力, 即使有租还需求, 边界不提供租还服务.设置租借公共自行车为正方向, 归还公共自行车为反方向, 由于租还需求量来自于服务点各个方向, 租还需求量为以相应服务点为圆心, 100 m为半径的圆面均匀需求量.
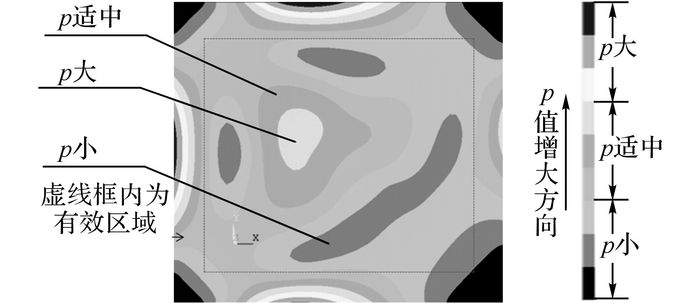
首先输入仿真的基本参数, 设置有限元估算仿真的需求增度为2.06e8, 车变比为0.3.在服务点香积寺路247号(编号为4146, 简称“服务点4146”)建立之前, 对该区域已建成的7个服务点在相应需求量作用下进行ANSYS有限元估算, 得到的单元供需不平衡度分析结果如图 2所示.
|
图 2 PBS的单元供需不平衡度有限元分析结果(未建4146点之前) Fig. 2 Finite element analysis results of PBS supply and demand imbalance degree (before No.4146 station was built) |
从图 2中可以看出, 在有限元估算模型的有效范围内, 公共自行车单元供需不平衡度最大的位置为图中白色区域, 该位置位于120.151 275°E~120.152 55°E和30.302 04°N~30.303 774°N.未建的服务点4146位置为120.153 44°E、30.304 72°N, 纬度误差为0.000 946(0.047 3%), 经度误差为0.000 89(0.044 5%).从模型分析估算值与实际设点的情况看, 两者虽然不完全一致, 但经、纬度平均相对误差均已小于0.05%, 基本能够反映出公共自行车供需不平衡度大的区域位置及范围.
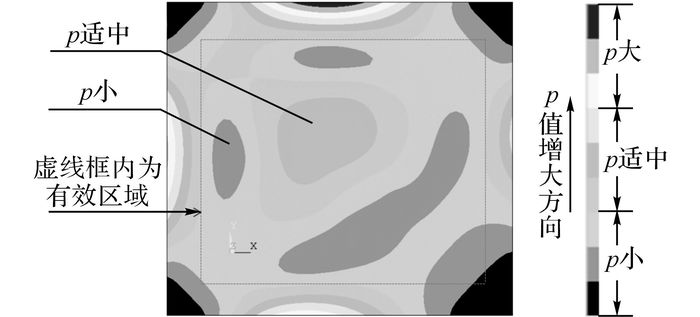
3.2 服务点布设的有限元估算仿真与结果分析在建立服务点4 146之后, 相同参数下对该区域8个服务点在相应需求量作用下再次进行ANSYS有限元估算, 得到的单元供需不平衡度分析结果如图 3所示.在有限元估算模型的有效范围内, 该范围内公共自行车单元供需不平衡度适中.在服务点4 416未建之前, 该位置出现了局部单元供需不平衡度较大, 服务点供需不平衡的现象;而在该服务点建成之后, 单元供需不平衡度适中, 供需基本平衡.这与目前杭州PBS的实际运行状况比较吻合, 说明了有限元估算方法的有效性, 能够评估PBS的单元供需不平衡度.
|
图 3 PBS的单元供需不平衡度有限元分析结果(建立4146点之后) Fig. 3 Finite element analysis results of PBS supply and demand imbalance degree (after No.4146 station was built) |
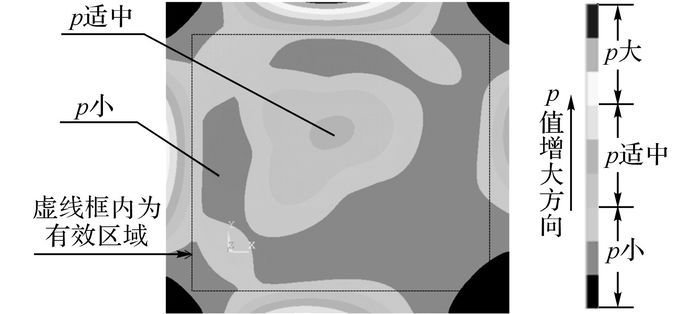
若把服务点4 146布设到图 2白色中间位置, 相同参数下对8个服务点在相应需求量作用下再次进行ANSYS有限元估算, 得到的单元供需不平衡度分析结果如图 4所示.在有限元估算模型的有效范围内, 该范围内大部分区域公共自行车单元供需不平衡度小.与图 3相比, 单元供需不平衡度明显减缓, 这进一步说明了有限元估算方法用于PBS服务点的布设的有效性.
|
图 4 PBS的单元供需不平衡度有限元分析结果(服务点4146布设于白色区域中间位置) Fig. 4 Finite element analysis results of PBS supply and demand imbalance degree (No.4146 station was located at center of white color area) |
需要指出的是, 该方法也有局限性.在仿真实验过程中, 由于PBS有限元估算的边界约束与公共自行车系统特性有差异, 仿真实验发现估算模型边界20%区域的相互作用机制受到了边界约束影响, 只能判断为无效区域, 不作有限元估算讨论;而中间80%的范围, 主要受到PBS区域租还平衡的相互作用机制影响, 因此是有效区域, 可以用于PBS单元供需不平衡度估算.
4 结语根据PBS的运行特性, 提出了PBS单元供需不平衡度的有限元估算模型, 建立了PBS服务点布设的有限元估算方法.以杭州市部分区域为例, 采用有限元分析软件ANSYS对方法的可行性予以验证, 实验结果显示, 未建服务点4 146前在120.151 275°E~120.152 55°E和30.302 04°N~30.303 774°N范围内出现公共自行车单元供需不平衡度位于大值区间的现象, 而在建立服务点4146后, 该位置的供需不平衡度明显缓解.若把服务点4 146布设到白色中间区域, 有效范围内大部分区域公共自行车单元供需不平衡度位于小值区间, 研究区域的公共自行车供需基本平衡.对比在该区域增加服务点4 146前、后及将4 146布设到单元供需不平衡度最大的位置的单元供需不平衡度分析结果, 证明此估算方法较为可靠, 能够分析PBS覆盖区域的供需不平衡度, 从而指导公共自行车系统服务点的布设.
PBS服务点布设的有限元估算方法还停留在小规模区域的研究阶段, 关于扩大到杭州区域更大范围的方法适用性以及如何通过改进边界条件的设置增加有效区域的比例等方面还需要进行深入研究.
| [1] | CHEN J X, CHEN X W, JIANG H, et al. Determining the optimal layout design for public bicycle system within the attractive scope of a metro station[J]. Mathematical Problems in Engineering, 2015, 2015(2134): 1–8. |
| [2] | VOGELA P, GREISERA T, MATTFELDA D C. Understanding bike-sharing systems using data mining:exploring activity patterns[J]. Procedia Social and Behavioral Sciences, 2011, 20(6): 514–523. |
| [3] | CHEMLA D, MEUNIER F, CALVO W R, et al. Bike sharing systems: solving the static rebalancing problem[J]. Discrete Optimiz, 2013, 10(2): 120–146. DOI:10.1016/j.disopt.2012.11.005 |
| [4] | RAVIV T, TZUR M, FORMA I A. Static repositioning in a bike-sharing system: models and solution approaches[J]. EURO Journal on Trans portation and Logistics, 2013, 2(3): 187–229. DOI:10.1007/s13676-012-0017-6 |
| [5] | RAINER-HARBACH M, PAPAZEK P, RAIDL G R, et al. PILOT, GRASP, and VNS approaches for the static balancing of bicycle sharing systems[J]. Journal of Global Optimization, 2015, 63(3): 1–33. |
| [6] | LIN J R, YANG T H, CHANG Y C. A hub location inventory model for bicycle sharing system design: formulation and solution[J]. Computers and Industrial Engineering, 2013, 1(65): 77–86. |
| [7] | LIN J R, YANG T H. Strategic design of public bicycle sharing systems with service level constraints[J]. Transportation Research Part E, 2011, 2(47): 284–294. |
| [8] |
王懿. 小城市公共自行车选址及需求优化设计[J].
交通科学与工程, 2016, 32(1): 96–100.
WANG Yi. Research on public bicycle rental sites selection and stock demand forecasting of a small city[J]. Journal of Transport Science and Engin eering, 2016, 32(1): 96–100. |
| [9] | GARRACÍA-PALOMARES J C, GUTIÉRREZ J, LATORRE M. Optimizing the location of stations in bike-sharing programs: a GIS approach[J]. Applied Geography, 2012, 1-2(35): 235–246. |
| [10] | ZHOU Y L, LU J M, XU S, et al. Research on the site selection of the public bicycle system[J]. Advanced Materials Research, 2014, 8(1030-1032): 229–2295. |
| [11] | VOGEL P, MATTFELD D C. Modeling of repositioning activities in bike-sharing systems [C] // 12th World Conference on Transport Research. Portugal:[s.n.], 2010: 1-13. |
| [12] | MARTINE L M, CAETANO L, EIRO T, et al. An optimisation algorithm to establish the location of stations of a mixed fleet biking system an application to the city of Lisbon[J]. Procedia-Social and Behavioral Sciences, 2012, 54(1): 513–524. |
| [13] | LI C, WANG Z F. Method on layout optimizing of public bicycle rental stations based on complex network theory [C] // International Conference on Transportation Engineering. Miami: [s.n.], 2011: 247-252. |
| [14] | DAI J F, ZHAO X L, LIN J X. Public bicycle system station deployment and scale prediction[J]. Advanced Materials Research, 2013, 3(790): 510–514. |
| [15] |
耿雪, 田凯, 张宇, 等. 巴黎公共自行车租赁点规划设计[J].
城市交通, 2009, 7(4): 21–29.
GENG Xue, TIAN Kai, ZHANG Yu, et al. Bike rental station planning and design in Paris[J]. Urban Transport of China, 2009, 7(4): 21–29. |
| [16] |
李黎辉, 陈华, 孙小丽. 武汉市公共自行车租赁点布局规划[J].
城市交通, 2009, 7(4): 30–38.
LI Li-hui, CHEN Hua, SUN Xiao-li. Bike rental station deployment planning in Wuhan[J]. Urban Transport of China, 2009, 7(4): 30–38. |
| [17] |
陈景旭, 王炜. 轨道交通站点公共自行车租赁点布局研究[J].
武汉理工大学学报:交通科学与工程版, 2013, 37(6): 1206–1210.
CHEN Jing-xu, WANG Wei. Research on the layout of bike rental station around a railway station[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering, 2013, 37(6): 1206–1210. |
| [18] |
李福祥, 李文勇, 李长军, 等. 基于有限元分析的交通流理论与技术研究[J].
武汉理工大学学报:交通科学与工程版, 2012, 1(36): 124–128.
LI Fu-xiang, LI Wen-yong, LI Chang-jun, et al. Traffic flow theory and technology research based on finite element analysis[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering, 2012, 1(36): 124–128. |
| [19] |
董红召, 史彩霞, 陈宁, 等. 基于关联规则的公共自行车调度区域聚类划分[J].
科技通报, 2013, 29(9): 209–216.
DONG Hong-zhao, SHI Cai-xia, CHEN Ning, et al. Clustering division of public bicycle scheduling regional based on association rules[J]. Bullet in of science and technology, 2013, 29(9): 209–216. |
| [20] |
董红召, 吴满金, 刘冬旭, 等. 城市公共自行车系统自然租赁需求的估算方法[J].
浙江大学学报:工学版, 2016, 50(2): 265–270.
DONG Hong-zhao, WU Man-jin, LIU Dong-xu, et al. Estimation method of natural demand of urban public bicycle system[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(2): 265–270. |


