2. 浙江省电力设计院, 浙江 杭州 310007
2. Electric Power Design Institute of Zhejiang Province, Hangzhou 310007, China
风荷载是输电塔的主要控制荷载, 通常基于输电塔的有限元模型进行风致响应计算.目前常见的输电塔有限元建模方法有3种, 即空间桁架模型、空间钢架模型[1]以及桁梁混合计算模型[2].以上3种建模方法均假定节点为完全刚接或完全铰接, 而实际上输电塔杆件之间的连接介于刚接和铰接之间, 为半刚性连接.
对于节点半刚性连接, 目前的研究主要集中在半刚性的转动刚度(弯矩-转角曲线)本身, 采用的方法有模型试验、有限元模拟和理论推导.在模型试验方面, Raul等[3]采用试验方法研究桁架T型件的转动刚度, 毛军朋[4]针对K型节点采用试验方法获得偏心距等参数对节点弯矩-转角特性的影响.在有限元模拟方面, Shi等[5]针对刚框架螺栓端板连接进行有限元模拟, 胡习兵等[6-8]对钢结构节点进行有限元建模并获得节点的弯矩-转角曲线.在理论推导方面, Ihaddoudène等[9]推导出了梁杆件两端存在半刚性节点时的梁单元刚度矩阵, 王振宇等[10]利用组件法研究了某半刚性节点的初始刚度, 焦安亮等[11]针对螺栓受剪K形节点理论推导出了其弯矩-转角曲线, 刘海峰等[12]根据后验误差估计理论推导出了考虑节点转动刚度的节点力-位移公式.
目前针对节点半刚性对网壳产生的影响研究较多[13-15];对结构受力产生的影响研究较少; 而对输电塔产生的影响研究则更少, 安利强等[16]研究了半刚性节点对输电塔轴力和位移的影响.实际上, 节点半刚性对输电塔弯矩和应力的影响比对轴力和位移的影响更大, 但目前仍缺乏关于节点刚度数值范围对结构响应影响的研究.
本文在通用有限元软件ANSYS中利用弹簧单元模拟节点的半刚性连接, 并以此建立考虑节点半刚性连接的输电塔有限元模型, 计算并分析节点半刚性对输电塔自振特性和风致响应的影响, 研究节点初始转动刚度对最大内力、主材内力和斜材内力的影响, 并给出基于输电塔不同响应的半刚性节点量化指标, 最后针对输电塔常见节点的初始转动刚度进行半刚性特性的评价.
1 节点半刚性连接的力学定义目前输电塔的节点连接有各种方式, 如相贯焊接、插板连接、法兰连接等, 这些连接方式的连接刚度介于铰接和刚接之间, 被定义为半刚性连接.半刚性连接相当于在铰接基础上有一定的初始转动刚度K, 当K=0时为铰接, 当K为无穷大时为刚接.转动刚度的定义为
| $K = \frac{M}{\theta }.$ | (1) |
式中:M为节点处弯矩, θ为与M对应的节点转角.
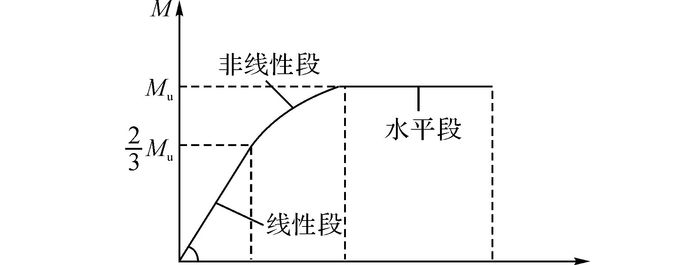
节点转动刚度可通过荷载试验[3-4]、有限元计算[5-8]和理论推导[9-12]等方式得到.欧洲规范EUROCODE3[17]提出了用于半刚性连接的M-θ曲线, 如图 1所示, 该曲线由线性段、非线性段和水平段组成, 图中Mu为极限弯矩承载力, 线性段的斜率即为初始转动刚度.
|
图 1 典型半刚性连接的弯矩-转角关系 Fig. 1 Moment versus rotation angle relation of typical semi-rigid connection |
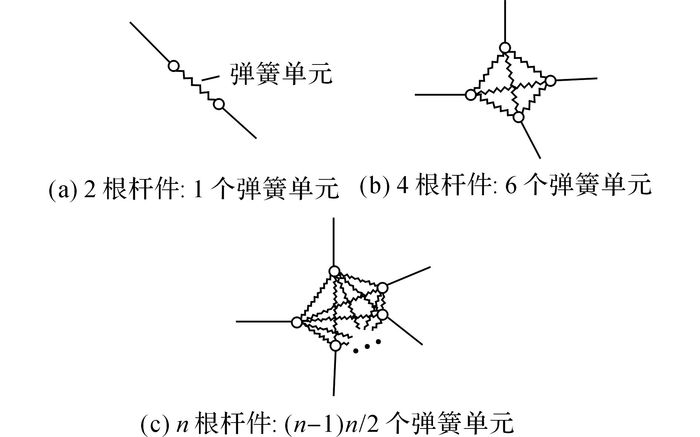
节点半刚性连接的有限元建模方法是在现有的输电塔有限元模型(如:梁单元模型、梁杆混合单元模型等)的基础上, 将某节点位置的连接(假设与该节点连接的杆件有n根)改成半刚性连接, 方法如下:1) 在某节点基础上新增与该节点具有完全相同位置的n-1个节点.2) 利用新增节点替换原节点重建输电塔模型的梁单元, 即重新建立n根梁单元.3) 在重合节点两两之间建立零长度的弹簧单元, 则n个重合节点间共需建立(n-1)n/2个弹簧单元, 如图 2所示.4) 耦合n个节点在总体笛卡尔坐标下X、Y、Z这3个方向上的平动位移.5) 根据实际结构的各杆件之间的转动刚度, 对(n-1)n/2个弹簧的转动刚度取不同数据, 如果2根杆在空间上没有联系, 将K置0.
|
图 2 利用弹簧单元对半刚性连接的有限元模拟 Fig. 2 Finite element simulation of semi-rigid connections by spring element |
在通用有限元软件ANSYS中, 弹簧单元可采用Combin14(线性)和Combin39(非线性)等来表达.由于节点的轴向刚度远大于杆件的轴向刚度, 在计算中只考虑节点的转动刚度, 而忽略节点的轴向刚度.
3 含半刚性节点的某输电塔有限元模型某输电塔高115 m, 塔身平面形状为正方形, 基底根开为22.3 m, 塔头由3条横担组成, 塔头高43 m.输电塔各层主材和斜材均采用薄壁钢管, 塔头中的连杆采用角钢.采用ANSYS软件进行建模, 选用BEAM188单元来模拟主力杆及横隔面外围杆件, 在横担桁架及横隔面内部则采用杆单位LINK8进行模拟, 用MASS21单元模拟节点板和螺栓等质量, 有限元模型如图 3所示, 以横线方向为X轴, 顺线方向为Y轴, 竖直方向为Z轴.

|
图 3 含半刚性节点的某输电塔有限元模型及分析计算时所选取的主、斜材 Fig. 3 Finite element model of transmission tower with semi-rigid connection, and selected primary members and diagonal members for analysis and calculation |
对主要受力构件处的124个节点(如图 3(a)所示框内节点)实现半刚性连接, 为考察节点转动刚度对结构动力特性和风致响应的影响, 将K分别赋值为1015、1014、1013……101、1 N·m/rad.本文着重研究转动刚度对输电塔风致响应的影响, 因此只考虑初始转动刚度(即如图 1所示的线性段斜率);各半刚性节点的3个转动方向均采用相同的转动刚度.
4 半刚性连接对输电塔自振特性的影响针对不同半刚性连接的转动刚度进行输电塔的自振特性计算, 发现在所有不同K值情况下, 前5阶振型不变, 均为输电塔的整体振型, 如图 4所示, 分别为X轴方向的一阶弯曲、二阶弯曲以及Y轴方向的一阶弯曲、一阶扭转、二阶弯曲.

|
图 4 含半刚性节点输电塔的前5阶振型 Fig. 4 First five vibration modes of transmission tower with semi-rigid connection |
如图 5所示为在不同K值情况下的自振频率f, 其中横坐标为K0, K0=ln K.由图 5可知:1) 一阶横线向、顺线向和扭转方向的频率随着K的增加而增加, 在K≤105时接近铰接, 在K≥108时接近固接;2) 对于二阶的横线向、顺线向振型, 在K≤103时接近铰接情况, 在K≥108时接近刚接情况;3) 总体而言, 半刚性节点的转动刚度对其振型频率有一定影响, 但影响相对较小, 铰接下与刚接下的振型频率相差不超过4%.

|
图 5 输电塔自振频率随半刚性节点刚度的变化曲线 Fig. 5 Curves of natural frequencies changing with stiffness of semi-rigid connection for transmission tower |
在输电塔Y方向施加水平风荷载, 地貌粗糙度为B类地貌, 地貌粗糙度系数取0.15, 基本风速为30 m/s, 风压高度变化系数按建筑结构荷载规范[18]取值, 体型系数根据杆塔结构设计规程[19]取值.同时, 根据杆塔结构设计规程[19]要求, 风振系数应按现行的荷载规范计算, 但考虑到本例中长塔臂和多塔臂的特殊性, 采用荷载规范计算风振系数时所要达到的“迎风面宽度和质量沿高度直线连续变化”的要求难以满足, 因此只考虑平均风荷载的作用, 即风振系数取1.
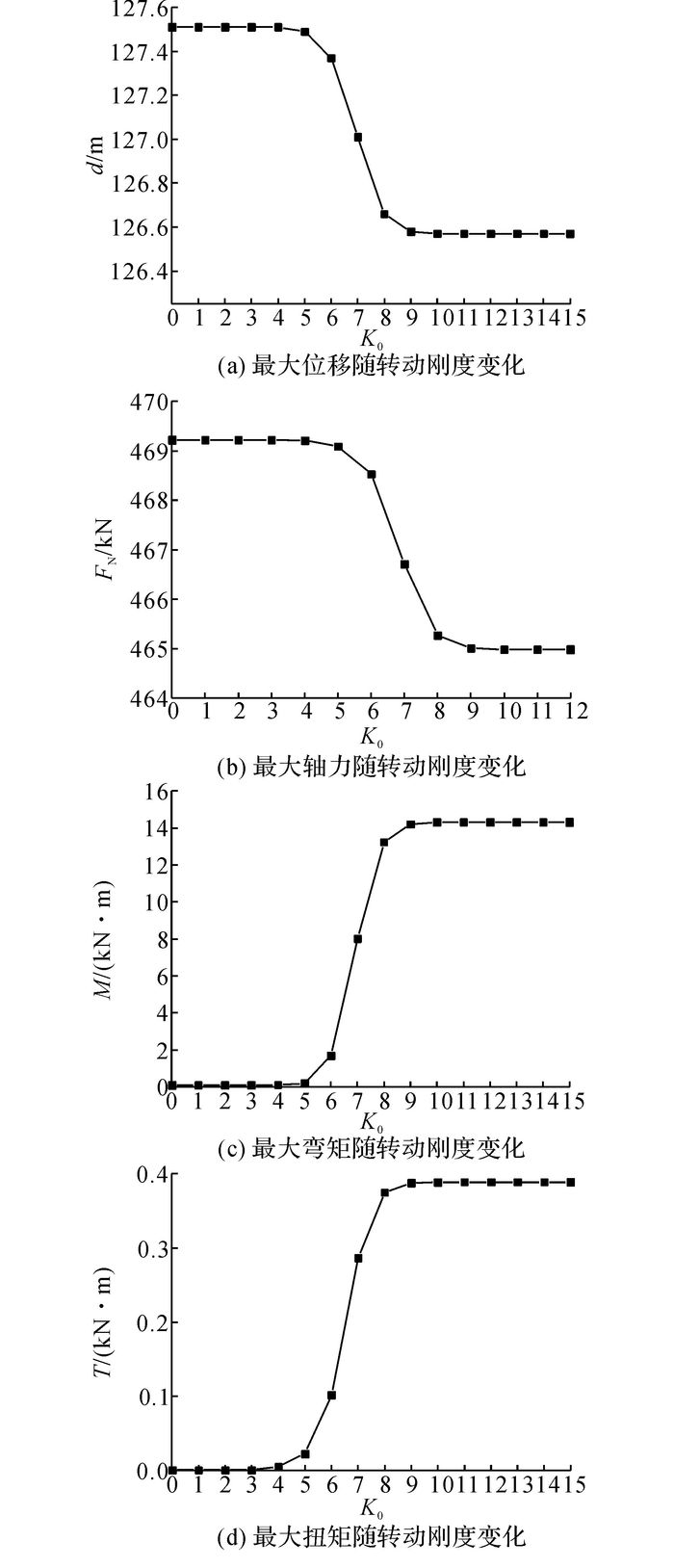
5.1 最大响应不同K值情况下的输电塔最大节点位移d、轴力FN、弯矩M和扭矩T如图 6所示, 各数据均取绝对值.由图 6可知:1) 对于最大位移和最大轴力, 半刚性连接的影响非常小, 即铰接体系和刚接体系的位移和轴力几乎不变;2) 对于最大弯矩和最大扭矩, 在铰接体系时为0, 对于刚接体系时最大, 可见节点的转动刚度对杆件的弯矩和扭矩有很大的影响;3) 从最大位移、轴力、弯矩和扭矩角度看, 当K≤105时可以视为铰接;当K≥109时, 节点可以视为刚性连接;当105<K<109时为半刚性连接.
|
图 6 风荷载作用下输电塔各最大响应(最大位移、最大轴力、最大弯矩、最大扭矩)随半刚性节点刚度的变化曲线 Fig. 6 Curves of maximum responses (maximum displacement, axial force, bending moment and torsion) of transmission tower changing with stiffness of semi-rigid connection under wind load |
如图 7所示为上述输电塔各响应最大值(处于刚接体系时)出现的位置, 可知当各节点均为刚接时:1) 最大位移出现在输电塔最上端;2) 最大轴力出现在输电塔背风面支座处;3) 最大弯矩出现在输电塔背风面处支座的靠上位置;4) 最大扭矩出现在输电塔中部位置.

|
图 7 节点为刚接时输电塔各最大响应(最大位移、最大轴力、最大弯矩、最大扭矩)出现的位置 Fig. 7 Positions of maximum responses (maximum displacement, axial force, bending moment and torsion) of transmission tower with rigid connections |
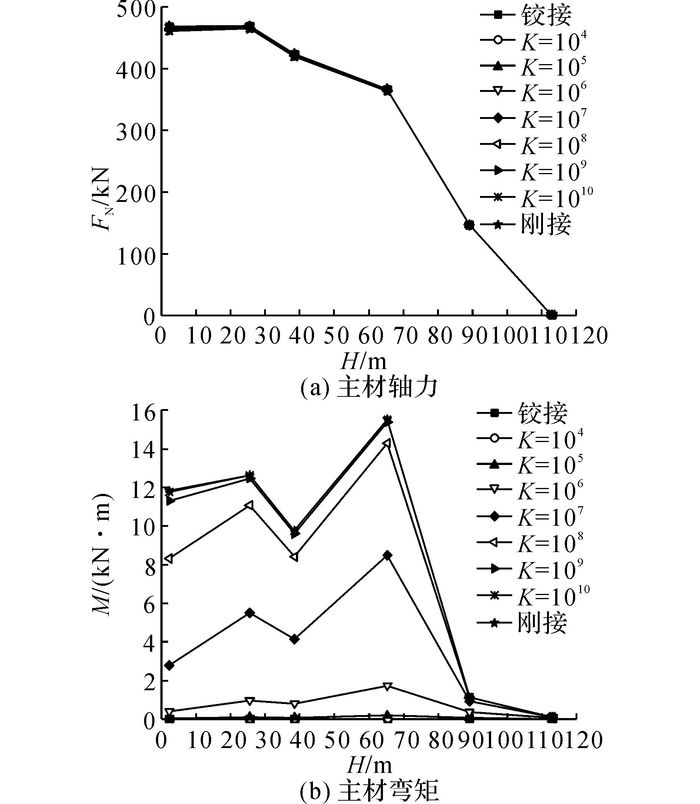
取典型主杆进行分析, 杆件选择如图 3(b)所示, 如图 8所示为主杆轴力FN、主杆弯矩M随转动刚度的变化, 图中H为从输电塔塔腿底部起算的高度.由图 8可知:1)K对轴力的影响较小;2)K对弯矩的影响较大, 且K越大, 弯矩M越大;3) 当K≤105时接近铰接, 在K≥109时接近固接, 当105<K<109时为半刚性连接.
|
图 8 不同转动刚度下主材内力(轴力和弯矩)随高度的变化曲线 Fig. 8 Curves of primary member's force (axial force and bending moment) changing with height under different stiffness |
根据图 8的杆件轴力和弯矩, 计算各杆的弯曲和轴向应力σ, 如图 9所示为在转动刚度取刚接情况下主力杆的弯曲应力、总应力及弯曲应力占总应力的比例(标于柱状图顶部).由图 9可知, 在较大应力情况下弯曲应力总体上占总应力的10%~25%, 说明在输电塔的设计中, 应充分考虑在荷载作用下杆件中由于节点存在半刚性而引起的弯曲应力.

|
图 9 节点为刚接时输电塔主力杆总应力以及主力杆中弯曲应力占总应力的比例 Fig. 9 Total stress of primary member of transmission tower with rigid connections and ratio between bending stress and total stress of primary member |
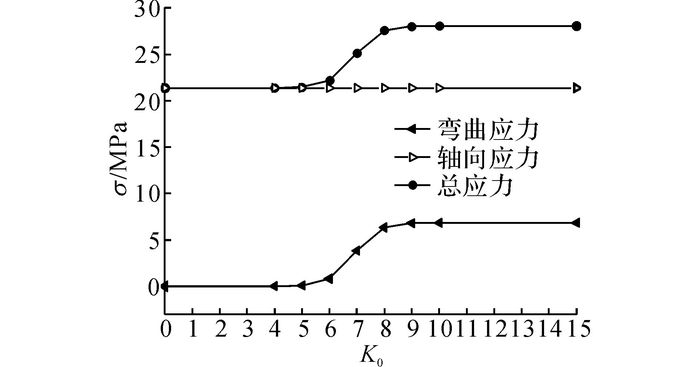
根据图 9, 位于65 m高度处主杆的弯曲应力及占比均较大, 如图 10所示为该杆在不同转动刚度时的弯曲应力、轴向应力和总应力.由图 10可知:1) 随着K的增加, 弯曲应力和总应力呈增大趋势, 而轴向应力几乎不变;2) 当K≤105时接近铰接, 在K≥108时接近固接, 当105<K<108时为半刚性连接;3) 在半刚性和刚性连接情况下, 由弯矩产生的应力占据较大比重(最大为24.4%), 因此对于具有半刚性和刚性连接的节点, 在对主杆进行应力计算时应考虑节点半刚性的影响;4) 本文提出的考虑半刚性节点的有限元建模方法可准确模拟节点的连接刚度从铰接变化至固接时的全过程, 相比于空间桁架模型、空间钢架模型[1]和桁梁混合计算模型[2]的建模方法更合理.
|
图 10 65 m高度处主杆的弯曲应力、轴向应力和总应力 Fig. 10 Bending stress, axial stress and total stress of primary member at height of 65 meters |
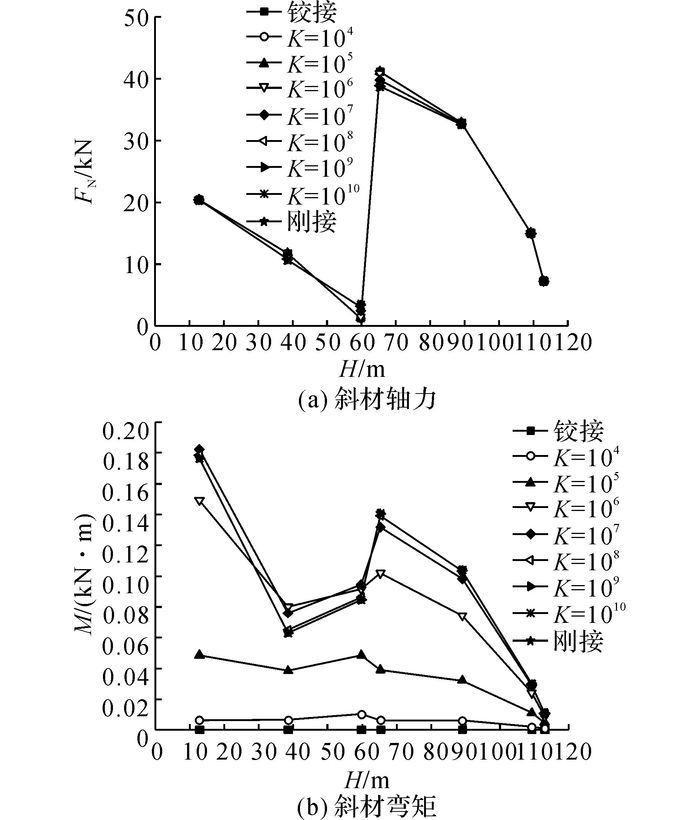
取典型斜材进行分析, 杆件选择如图 3(c)所示, 如图 11所示为斜杆轴力、弯矩随转动刚度的变化.由图 11可知:1)K对斜材轴力的影响较小;2)K对杆件弯矩的影响较大, 随着K的增大, 杆件弯矩总体呈增大趋势, 但也存在当转动刚度大于106时, 杆件弯矩随K的增大反而减小的情况, 如位于39 m和60 m高度处斜杆的弯矩.
|
图 11 各转动刚度下斜材内力随高度变化曲线 Fig. 11 Curves of diagonal member's force changing with height under different stiffness |
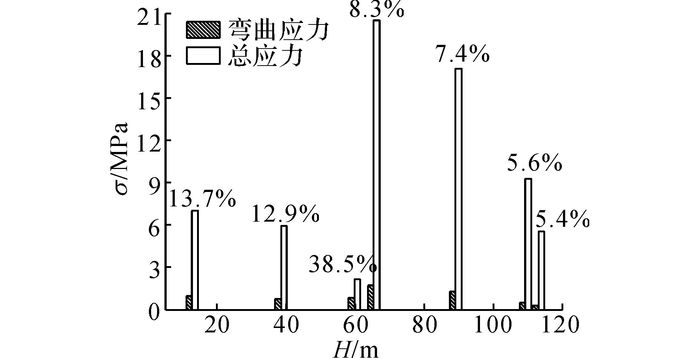
根据图 11所示的杆件轴力和弯矩, 计算各杆的弯曲应力和轴向应力, 如图 12所示为转动刚度取刚接情况下主力杆的弯曲应力、总应力及弯曲应力占总应力的比例.由图 12可知:在较大应力情况下, 弯曲应力总体上占总应力的5%~15%, 说明弯曲应力不可忽略.
|
图 12 当节点为刚接时输电塔斜杆总应力以及斜杆中弯曲应力占总应力比例 Fig. 12 Total stress of diagonal member of transmission tower with rigid connections, and ratio between bending stress and total stress of primary member |
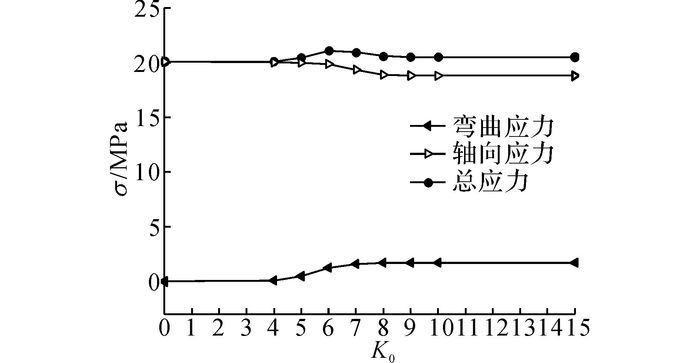
从图 12中还可以发现, 位于65 m高度处斜杆的弯曲应力及占比均较大, 如图 13所示为该杆在不同转动刚度情况下的弯曲应力和总应力.由图 13可知:1) 随着K的增加, 弯曲应力呈增大趋势, 轴向应力呈减小趋势;2) 当K≤104时接近铰接, 在K≥107时接近固接, 当104<K<107时为半刚性连接;3) 在半刚性和刚性连接情况下, 由弯矩产生的应力占据一定比重(约10%), 因此对于具有半刚性和刚性连接的节点, 在对斜杆进行应力计算时需要考虑节点半刚性的影响.
|
图 13 65 m高度处斜杆的弯曲应力、轴向应力和总应力 Fig. 13 Bending stress, axial stress and total stress of diagonal member at height of 65 meters |
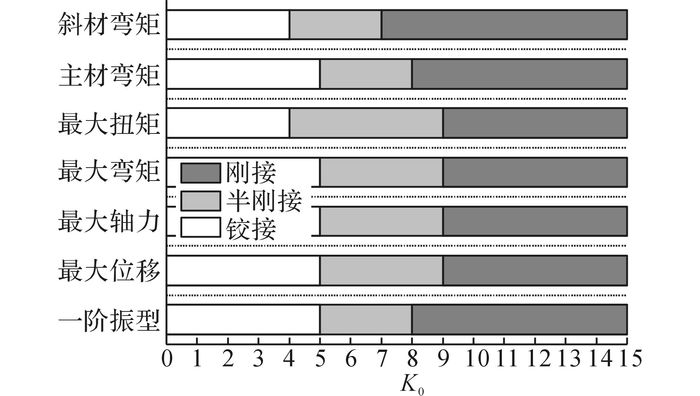
基于以上计算结果, 如图 14所示为基于输电塔不同响应的半刚性节点量化指标.由图 14可知:总体而言, 当K≤105时接近铰接, 在K≥109时接近刚接, 当105<K<109时为半刚性连接.当节点的转动刚度在105<K<109时, 需要考虑半刚性的影响.
|
图 14 基于输电塔不同响应的半刚性量化指标 Fig. 14 Quantitative indicators of semi-rigid connection with respect to different responses of transmission tower |
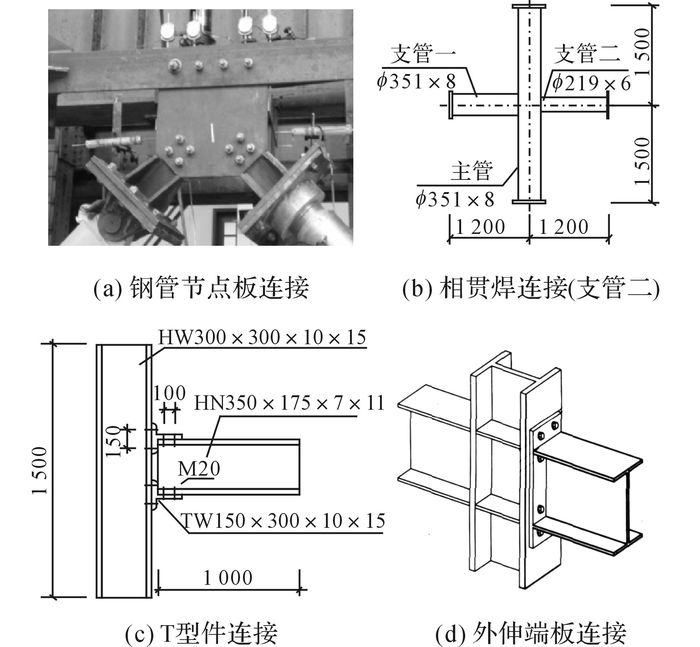
根据相关文献[6, 11, 20-21]可知, 用于输电塔节点连接的各种连接方式中, 已有节点弯矩-转角曲线数据的有K型节点板螺栓连接、钢管相关焊连接形式等.这些节点基于某实际尺寸获得的初始转动刚度如表 1所示, 节点类型图示如图 15所示, 节点的详细尺寸参数见对应的参考文献.另外, 除特殊说明外, 表 1中给出的初始转动刚度均指平面内.表 1中还增加了钢结构常见的外伸端板连接和T型件连接的相应初始转动刚度, 以供对比.
| 表 1 各种节点连接形式下典型构件的初始转动刚度 Table 1 Initial rotation stiffness of typical components under various connections |
|
图 15 输电塔及钢结构的常见连接 Fig. 15 Common connections of transmission towers and steel structures |
由表 1和图 15可知:1) 常见钢结构连接节点的初始转动刚度在106~108 N·m/rad, 根据图 14, 这些节点均属于半刚性连接;2) 输电塔的连接节点(如:相贯焊连接(平面外)、K形节点板螺栓连接等)的转动刚度较小, 偏铰接形式, 简化情况下可按铰接计算, 而相贯焊连接(平面内)的初始转动刚度为4×106 N·m/rad, 处于半刚性连接范围, 应按半刚性连接进行计算;3) T型件连接节点的初始转动刚度为1.9×107 N·m/rad, 处于半刚性连接范围, 也应按半刚性连接进行计算;4) 外伸端板连接节点的初始转动刚度为1.3×108 N·m/rad, 偏刚接形式, 简化情况下可按刚接计算;5) 根据以上结果, 在输电塔的有限元建模中, 应根据节点转动刚度的所处范围来确定该节点适用的连接方式.
7 结论(1) 本文提出考虑节点半刚性连接的输电塔有限元建模方法, 通过该方法计算得到的结果合理,说明该方法是合理、有效的, 同时该方法可以准确模拟节点连接刚度从铰接变化至固接的全过程, 比空间桁架模型、空间钢架模型和桁梁混合计算模型更合理.
(2) 半刚性节点的转动刚度对输电塔的振型频率影响较小, 不同刚度下频率的最大差异在小于4%.
(3) 半刚性节点的转动刚度对输电塔的位移和轴力影响非常小, 但对杆件的弯矩和扭矩影响较大, 杆件的弯矩随着转动刚度的增大而显著增大.当转动刚度增大至刚接情况时, 主材的弯曲应力占总应力(弯曲应力和拉伸应力之和)的10%~25%, 斜材的弯曲应力占总应力的5%~15%, 该部分应力对杆件的强度和稳定有较大影响.
(4) 本研究提出了基于输电塔响应类型的半刚性节点量化指标, 就本文实例而言, 当K≤105时为铰接, 当K≥109时为刚接, 当105<K<109时为半刚性连接.根据该半刚性节点量化指标, 发现常见的输电塔和钢结构的节点连接均属于半刚性连接范畴, 因此在输电塔的有限元建模中, 建议依照本文方法对节点进行半刚性连接的建模, 以提高计算结果的精确性.
| [1] | SHEN G H, CAI C S, SUN B N, et al. Study of dynamic impacts on transmission-line systems attributable to conductor breakage using the finite element method[J]. ASCE, Journal of Performance of Constructed Facilities, 2011, 25(2): 130–137. DOI:10.1061/(ASCE)CF.1943-5509.0000133 |
| [2] | LIU C C, XU Q S. Finite element model of high-voltage transmission tower cinfirmed[J]. Applied Mechanics and Materials, 2014, 459: 625–630. |
| [3] | RAUL Z, DAN D. Stiffness of joints in bolt connected cold-formed steel trusses[J]. Journal of Constructional Steel Research, 2006, 62(3): 240–249. DOI:10.1016/j.jcsr.2005.07.002 |
| [4] |
毛军朋. 特高压输电塔半刚性K型节点受力性能分析[D]. 重庆: 重庆大学, 2012: 21-38.
MAO Jun-peng. Behaviors analysis of semi-rigid K-joints in UHV transmission tower [D]. Chongqing: Chongqing University, 2012: 21-38. |
| [5] | SHI G, SHI Y J, WANG Y Q, et al. Finite elementanalysis and tests on bolted end-plate connections in steel portal frames[J]. Advances in Structural Engineering, 2004, 7(3): 45–56. |
| [6] |
胡习兵. T型钢半刚性连接节点的性能研究[D]. 湖南: 湖南大学, 2004: 33-53.
HU Xi-bing. The research on the behavior of T-stub semi-rigid connections [D]. Hunan: Hunan University, 2004: 33-53. |
| [7] |
刘超. 基于ANSYS的半刚性连接特高压输电塔结构非线性分析[D]. 重庆: 重庆大学, 2015: 9-19.
LIU Chao. Nonlinear analysis of semi-rigid UHV transmission tower based on ANSYS [D]. Chongqing: Chongqing University, 2015: 9-19. |
| [8] |
石永久, 王萌, 王元清, 等. 钢框架端板连接半刚性节点受力性能分析[J].
工程力学, 2011, 28(9): 51–58.
SHI Yong-jiu, WANG Meng, WANG Yuan-qing, et al. Analysis on the behavior of steel frame end-plate conne-ctions[J]. Engineering Mechanics, 2011, 28(9): 51–58. |
| [9] | IHADDOUDÈNE A N T, SAIDANI M, CHEMROUK M, et al. Mechanical model for the analysis of steel frames with semi rigid joints[J]. Journal of Constructional Steel Research, 2009, 65: 631–640. DOI:10.1016/j.jcsr.2008.08.010 |
| [10] |
王振宇, 张劲帆, 方成, 等. 半刚性节点初始刚度的组件式计算模型[J].
浙江大学学报:工学版, 2012, 46(11): 1998–2006.
WANG Zhen-yu, ZHANG Jing-fan, FANG Cheng, et al. Study on the component-based model of semi-rigid beam-to-column joints initial stiffness[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(11): 1998–2006. |
| [11] |
焦安亮, 李正良, 刘红军, 等. 特高压输电塔半刚性连接K形节点受力性能研究[J].
建筑结构学报, 2014, 35(7): 53–60.
JIAO An-liang, LI Zheng-liang, LIU Hong-jun, et al. Study on ultimate strength of semi-rigid K-type joints in UHV transmission tower[J]. Journal of Building Structures, 2014, 35(7): 53–60. |
| [12] |
刘海峰, 韩军科, 李清华, 等. 考虑节点转动刚度的圆管杆件结构自适应有限元分析方法[J].
工程力学, 2013, 30(10): 19–27.
LIU Hai-feng, HAN Jun-ke, LI Qing-hua, et al. Adaptive finite element procedure for circular bar structures considering rotating stiffness of joints[J]. Engineering Mechanics, 2013, 30(10): 19–27. |
| [13] |
张艺达, 朱楠, 忻之巍, 等. 半刚性节点对单层球面网壳的影响[J].
江苏建筑, 2014, 4: 36–40.
ZHANG Yi-da, ZHU Nan, XIN Zhi-wei, et al. Effect of semi-rigid joints on the single-layer spherical reticulated shell[J]. Jiangsu Construction, 2014, 4: 36–40. DOI:10.3969/j.issn.1005-6270.2014.04.011 |
| [14] |
刘才玮, 张毅刚, 吴金志. 考虑螺栓球节点半刚性的网格结构有限元模型修正研究[J].
振动与冲击, 2014, 33(6): 35–43.
LIU Cai-wei, ZHANG Yi-gang, WU Jin-zhi. Finite element model updating of single-layer latticed cylindrical shell in consideration of the semi-rigid characters of bolt-ball joint[J]. Journal of Vibration and Shock, 2014, 33(6): 35–43. |
| [15] | ZHAO Z W, CHEN Z H, YAN X Y, et al. Simplified numerical method for latticed shells that considers member geometric imperfection and semi-rigid joints[J]. Advances in Structural Engineering, 2016, 19(4): 689–702. DOI:10.1177/1369433216630123 |
| [16] |
安利强, 朱登杰, 武文玲, 等. 节点半刚性对特高压钢管塔静力特性的影响[J].
应用力学学报, 2015, 32(6): 1019–1024.
AN Li-qiang, ZHU Deng-jie, WU Wen-ling, et al. Influence of joint semi-rigidity on the static characteristic for UHV transmission steel tubular tower[J]. Chinese Journal of Applied Mechanics, 2015, 32(6): 1019–1024. |
| [17] | European Committee for Standardization. Eurocode 3: Design of steel structures, part 1-8 Design of joints [S], Berlin: Ernst and Sohn, A wiley company, 1993. |
| [18] | 中华人民共和国住房和城乡建设部. 建筑结构荷载规范: GB 50009-2012[S]. 北京: 中国建筑工业出版社, 2012. |
| [19] | 邱国志. 圆钢管X型相贯节点刚度及其对结构整体性能的影响[D]. 上海: 上海交通大学, 2008: 15-34. |
| [20] | QIU Guo-zhi. Rigidity of unstiffened circular tubular X-joints and its effects on global performance of steel tubular structures [D]. Shanghai: Shanghai Jiao Tong University, 2008: 15-34. |
| [21] |
吴兆旗, 张素梅, 姜绍飞. 梁柱外伸端板连接弯矩—转角性能有限元分析[J].
应用基础与工程科学学报, 2010, 18(6): 922–932.
WU Zhao-qi, ZHANG Su-mei, JIANG Shao-fei. Finite element analysis of moment-rotation behavior of beam-to-column extended endplate connetions[J]. Journal of Basic Science and Engineering, 2010, 18(6): 922–932. |



