2. 东南大学 交通学院, 江苏 南京 210096;
3. 美国华盛顿Catholic大学 土木工程系, 美国 华盛顿 20064
2. School of Transportation, Southeast University, Nanjing 210096, China;
3. Department of Civil Engineering, The Catholic University of America, Washington DC 20064, USA
在低温环境下, 混凝土孔隙内部由于冻胀力与孔隙水压力的作用导致材料微裂纹不断萌生、扩展而引起冻融损伤, 进而引起服役于冻融环境下的混凝土结构产生冻融破坏[1].近年来, 世界各地桥梁、路面、无砟轨道及海岸工程等大量混凝土结构广泛遭受的冻融损害事故屡见报道, 但目前缺乏一种可靠的方法来预测和评估受冻融损伤混凝土的承载能力和剩余服务寿命, 难以为混凝土结构的设计、维护、维修提供指导意见.要解决这个问题, 首先需要对受冻融损伤混凝土在静荷载和疲劳荷载下的力学性能进行系统研究.已有研究表明:冻融损伤常引起混凝土抗压和抗拉强度、刚度明显下降[2-4].有关冻融损伤混凝土在疲劳荷载作用下的性能研究还寥寥无几, 且这些研究主要关注冻融损伤对混凝土疲劳损伤的机理[5-8].
目前对受冻融损伤混凝土的研究主要集中在冻融损伤机理[9-11]和静力荷载作用下的力学性能, 如:拉压强度、模量[2-4]、应力应变关系[12-15]等方面.这些研究大多通过试验手段对混凝土受冻融循环作用的过程以及受冻后混凝土的力学性能变化规律进行探索.Hasan等[14]对疲劳荷载作用下受冻融损伤的混凝土抗压应力-应变关系进行了研究.洪锦祥等[4]对受冻融损伤后的混凝土弯曲疲劳寿命进行了初步研究.也有少数人对遭受冻融循环作用和力学疲劳作用后的混凝土机理、性能进行了研究.李文婷等[8, 15]对冻融循环和疲劳荷载共同作用下的混凝土性能进行了初步试验, 并通过有限元仿真来分析这种相互作用的组合损伤效应.对疲劳荷载作用下受冻融损伤混凝土疲劳寿命分布规律、疲劳寿命可靠性概率及疲劳寿命方程的研究鲜有报道.
本文通过试验对遭受不同冻融损伤程度的混凝土小梁弯曲疲劳寿命进行研究.引进概率模型对不同应力水平下受冻融损伤混凝土弯曲疲劳寿命的分布规律进行分析;研究受冻融损伤混凝土弯曲疲劳寿命的可靠性概率及具有不同概率水平的疲劳寿命方程, 为工程的设计和维修评估提供参考.
1 试验过程 1.1 混凝土试件制作制作尺寸为100 mm×100 mm×400 mm的混凝土小梁试件共96根, 用于冻融循环、静弯曲强度及弯曲疲劳试验研究.尺寸为150 mm×150 mm×150 mm的试件6组共计18个, 用于同条件下的混凝土抗压强度.所有试件采用相同的配比和制作工艺一次成型, 以减小试验结果的分散性.
试验采用混凝土的强度等级为C50.原材料如下:水泥为江宁水泥厂生产的P.O42.5R普通硅酸盐水泥;细度模数为2.8的赣江中砂;5~25 mm连续级配的龙潭碎石;减水剂为FDN高效减水粉剂;拌合水为符合JGJ 63-89《混凝土拌和用水标准》的自来水.混凝土配合比如下:减水剂水:水泥:砂:石=2.88:48:411:727:1 133, 含气量为1.5%~2.0%, 坍落度为120~160 mm.采用100 L自落式搅拌机拌合, 模筑振动成型后在标准养护室养护28 d, 在自然环境下养护不少于5 m后再进行试验, 以减小养护龄期对混凝土强度试验结果产生干扰.
1.2 混凝土小梁冻融试验按照《普通混凝土中长期性能和耐久性能试验方法标准》水泥混凝土抗冻试验方法(快冻法)进行混凝土试件的冻融循环试验[16].本研究仅采用液体介质为水的水冻试验.每20根小梁为1个大组, 3大组共60根, 分别进行50次、100次和150次的冻融循环试验各1个大组, 冻融试验后用于相对动弹性模量、静弯曲强度和弯曲疲劳强度测试试验;另外取2根小梁为1个小组, 5组共10根, 分别进行25、75、125、175、200次的冻融循环试验各一小组, 冻融试验后用于相对动弹性模量、静弯曲强度测试, 具体的试件数量及计划安排如表 1所示, 表中:ns为试件数量, n为冻融循环次数, Smax为最大应力水平, R为应力比, Pmax为最大荷载, σmax为应力上限.
| 表 1 试验试件数量及计划安排概述 Table 1 Outline of specimens preparation and experimental plan |
测量各组试件在冻融前的质量损失和相对动弹性模量并记录作为原始数据, 试验过程中每隔25次冻融循环测1次混凝土试件的质量损失和相对动弹性模量, 以表征混凝土所遭受的冻融损伤, 各组试件直至达到试验设计所需的总冻融循环次数后取出, 完成各组的冻融循环试验以用于力学性能试验.不同冻融循环次数后各组混凝土小梁相对动弹模量(RME, %)、质量损失(SS, %)的变化如表 2所示.
| 表 2 冻融循环后的混凝土物理性能结果 Table 2 Physical properties for various frost-damagedconcrete specimens |
混凝土小梁疲劳试验采用三点弯曲加载方式, 无间歇时间的正弦波荷载, 荷载频率为15 Hz, 低高应力比R=0.05, 以应力控制式模式进行循环加载.疲劳试验采用UTM-25伺服液压多功能材料试验系统, 最大动荷载为20 kN, 其一体化多轴控制系统可提供卓越的控制水平和高效的数据采集功能.试验梁的有效跨径为37.5 cm, 加载压头在梁跨中集中加载, 并通过加载压头上的位移计测量梁跨中挠度.
从遭受冻融循环次数为0、25、50、75、100、125、150、175、200次的冻融损伤后的混凝土小梁中各选取2根, 进行小梁弯曲静强度试验, 采用相同的加载设备所得到的混凝土弯曲强度如表 2所示.其余试件用于弯曲疲劳试验.
2 疲劳试验结果 2.1 未冻融损伤混凝土将未冻融循环试验的24根混凝土小梁分成4组进行弯曲疲劳试验, 采用应力水平Smax=0.55、0.65、0.75、0.85共4种疲劳荷载进行加载, 所得疲劳寿命数据见表 3所示, 表中*为在进行应力水平Smax=0.55的混凝土疲劳试验时, 3根小梁在疲劳荷载加载2×106个循环后都没有破坏, 此时停止加载, 故Smax=0.55应力水平下仅进行了3根小梁的疲劳试验, 且Smax=0.55应力水平下的疲劳寿命没有用于小梁弯曲疲劳寿命方程的回归分析.
| 表 3 未冻融损伤混凝土小梁弯曲疲劳寿命数据 Table 3 Results of flexural fatigue life for un-frost concrete |
通过研究疲劳试验研究结果得到混凝土疲劳加载应力水平S与疲劳寿命N之间的S-N曲线关系, 也称为Wöhler曲线.Tepfers[17]曾提出用如下方程来表示混凝土受拉疲劳寿命, 这个方程在Oh[18]进行混凝土弯曲疲劳试验的研究中进一步得到了验证和应用:
| ${S_{{\rm{max}}}} = \frac{{{\sigma _{{\rm{max}}}}}}{{{f_{\rm{t}}}}} = 1 - C\left( {1 - R} \right){\rm{lo}}{{\rm{g}}_{10}}N.$ | (1) |
式中:ft是混凝土的静弯曲强度;N为疲劳寿命;C为系数;R=σmin/σmax为疲劳应力比, 取R=0.05;σmin为疲劳加载的最小应力.
式(1) 可进一步简化为如下的表达形式:
| ${S_{{\rm{max}}}} = \frac{{{\sigma _{{\rm{max}}}}}}{{{f_{\rm{t}}}}}{\rm{ = }}A + B{\rm{lo}}{{\rm{g}}_{10}}N.$ | (2) |
式中:A、B为系数.
通过对前述试验结果平均值回归可得到式(2) 中常数A、B的值, 得到未冻融损伤混凝土小梁弯曲疲劳的S-N关系如图 1所示.图中,“没有破坏”代表当疲劳试验加载次数超过2×106次时终止试验, 这个次数并不代表混凝土在应力水平Smax=0.55下的疲劳寿命, 此数据也没有用于疲劳方程的分析.

|
图 1 未冻融损伤混凝土疲劳寿命方程拟合曲线 Fig. 1 Stress-fatigue life curves for un-frost concrete |
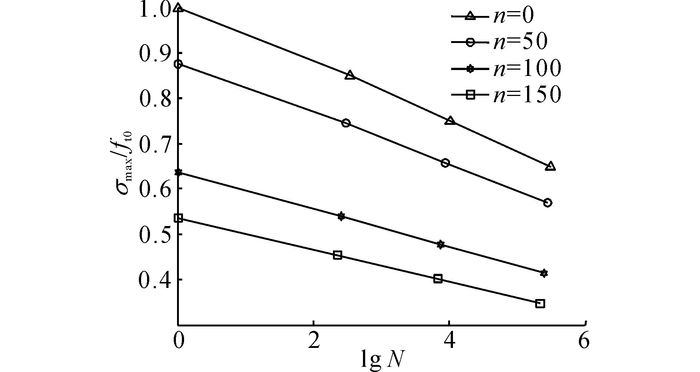
将冻融循环次数=50、100、150次小梁试件, 分成3组每组各6根混凝土小梁进行=0.65、0.75、0.85共3种应力水平的弯曲疲劳试验;前述冻融损伤混凝土小梁疲劳试验的应力水平为疲劳荷载的最大值与相应冻融损伤程度混凝土静载弯曲荷载的比值.各种冻融损伤后的混凝土弯曲疲劳试验的疲劳寿命结果见表 4和图 2所示.如图 2所示为不同冻融损伤程度混凝土疲劳加载的应力与未冻融损伤混凝土的静弯曲强度(ft0)的比值.
| 表 4 冻融损伤混凝土小梁弯曲疲劳寿命试验结果 Table 4 Test results of flexural fatigue life for frost-damaged concrete beam |
|
图 2 不同冻融损伤程度混凝土弯曲疲劳寿命变化趋势 Fig. 2 Flexural fatigue life trend for various frost-damaged concrete |
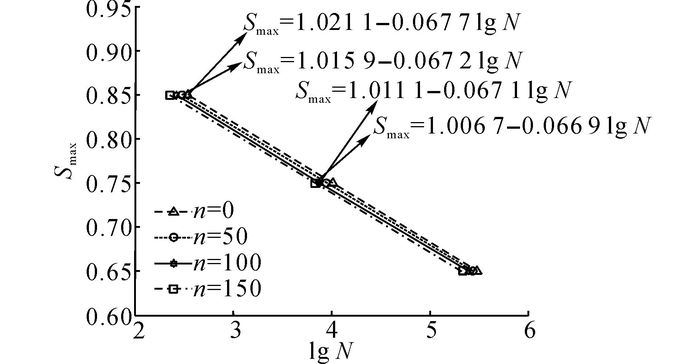
从表 4可以看出, 相同应力水平(真实应力水平)下不同冻融损伤程度的混凝土弯曲疲劳寿命相差不大, 基本处于一个等级, 并且随应力水平的增大而减小, 这表明混凝土的弯曲疲劳寿命与其应力水平有关, 其疲劳寿命分布的总体变化趋势基本一致.通过回归分析可得到如图 3所示的不同冻融损伤程度混凝土弯曲疲劳寿命方程.
|
图 3 不同冻融损伤程度混凝土疲劳寿命方程拟合图 Fig. 3 Stress-fatigue life curves for various frost-damaged concrete |
从表 2的结果可知, 受冻融循环作用后的混凝土静弯曲强度随冻融循环次数的增加而快速衰减(相对于未受冻融损伤混凝土的静弯曲强度), 因而由混凝土疲劳加载过程中真实应力水平所决定的混凝土疲劳强度也大大降低;在相同应力水平下混凝土弯曲疲劳强度随冻融循环次数的增加而减小;表明在相同的疲劳荷载作用下, 混凝土抵抗弯曲疲劳荷载作用的次数随冻融循环作用次数的增加而减小, 即遭受冻融循环作用后的混凝土疲劳强度相比未冻融混凝土要小.图 3的结果表明,受冻融循环作用后的混凝土弯曲疲劳寿命方程与未冻融损伤混凝土的弯曲疲劳寿命方程基本平行, 但受冻融循环次数越多的混凝土的疲劳寿命S-N曲线越靠左, 反映了受冻融损伤混凝土的弯曲疲劳寿命随冻融损伤程度的增加而减小的趋势.
3 疲劳分布拟合实际上,前述疲劳方程(1) 和(2) 中的N是由疲劳试验寿命数据的均值回归后得到的, S-N曲线也称为均值疲劳方程, 其失效概率接近50%, 显然对工程应用是不安全的.由于诸如材料强度、应用荷载等设计因素的变异性, 加之分析所采用的假设和材料构成的差异, 导致疲劳设计过程中的不确定性大大增加, 因而设计时必须确定一个合适的疲劳强度(疲劳寿命)以保证疲劳抗力, 这个疲劳强度必须能够反映疲劳行为的不确定性, 而概率可靠性理论是处理这种不确定性的一种有效方法[18].采用可靠性理论来进行疲劳分析首先需要确定一种合适的数学模型.用于描述结构疲劳寿命数据的概率模型包括:ASTM[19]提出的正态分布模型, 对数正态分布模型, 以及威布尔分布模型[18].在这几种模型中, 很多研究人员认为威布尔分布是最适合于描述疲劳寿命分布规律的一种模型[18, 20].
3.1 威布尔分布模型根据威布尔概率分布函数的定义, 可得在单幅重复荷载作用下各试件疲劳寿命Nx的概率密度函数f(Nx)和累计分布函数F(Nx)[17, 20-21]分别为
| $f({N_x}) = \frac{\alpha }{{u - {N_0}}}{\left( {\frac{{{N_x} - {N_0}}}{{u - {N_0}}}} \right)^{\alpha - 1}}{\rm{exp}}\left[ { - {{\left( {\frac{{{N_x} - {N_0}}}{{u - {N_0}}}} \right)}^\alpha }} \right],$ | (3) |
| $F({N_x}) = 1 - {\rm{exp}}\left[ { - {{\left( {\frac{{{N_x} - {N_0}}}{{u - {N_0}}}} \right)}^\alpha }} \right].$ | (4) |
式中:Nx为随机变量, α为威布尔形状参数, u为尺度参数或特征寿命参数, N0为位置参数或最小寿命参数.其中, Nx≥N0, α>0, u>N0.
累计分布函数F(Nx)表示疲劳寿命变量小于某一数值Nx概率, 相当于构件的破坏概率函数, 则构件在给定的时间间隔(荷载作用次数)内的安全概率(也称可靠性概率、存活概率)pr(Nx)可表示为
| ${p_{\rm{r}}}({N_x}) = 1 - F({N_x}).$ | (5) |
把式(4) 代入式(5) 可得存活概率函数表达式:
| ${p_{\rm{r}}}({N_x}) = {\rm{exp}}\left[ { - {{\left( {\frac{{{N_x} - {N_0}}}{{u - {N_0}}}} \right)}^\alpha }} \right].$ | (6) |
从安全、可靠的角度出发, 可假设混凝土材料强度的离散性以及所施加荷载的变异性对混凝土材料的最小寿命趋近于0, 因而在混凝土疲劳寿命概率分布函数中可取最小寿命参数N0=0, 则试件疲劳寿命的概率密度函数f(Nx)和存活概率函数pr(Nx)可简化为如下形式:
| $f({N_x}) = \frac{\alpha }{u}{\left( {\frac{{{N_x}}}{u}} \right)^{\alpha - 1}}{\rm{exp}}\left[ { - {{\left( {\frac{{{N_x}}}{u}} \right)}^\alpha }} \right].$ | (7) |
| ${p_{\rm{r}}}({N_x}) = {\rm{exp}}\left[ { - {{\left( {\frac{{{N_x}}}{u}} \right)}^\alpha }} \right].$ | (8) |
用矩估计法估计威布尔分布的特征寿命参数u和形状参数α, 需要先求出样本均值和样本方差之类的样本矩.两参数威布尔分布函数中的参数与样本一阶原点矩和二阶原点矩的关系[18, 20]可表示如下:
| $E({N_x}) = u\mathit{\Gamma }\left( {1 + \frac{1}{\alpha }} \right),$ | (9) |
| $E(N_x^2) = {u^2}\mathit{\Gamma }\left( {1 + \frac{2}{\alpha }} \right).$ | (10) |
式中:Γ()为伽玛函数, E(Nx)、E(Nx2)分别为某一应力水平下疲劳寿命数据样本的一阶原点矩和二阶原点矩.
由于样本一阶、二阶原点矩与其均值μ=E(Nx)和样本方差σ2=E(Nx2)-μ2有关, 通过这种关系可把式(9) 和(10) 进一步改写为
| $f_{{\rm{cov}}}^2 = {\left( {\frac{\sigma }{\mu }} \right)^2} = \frac{{\mathit{\Gamma }\left( {\frac{2}{\alpha } + 1} \right)}}{{{\mathit{\Gamma }^2}\left( {\frac{1}{\alpha } + 1} \right)}} - 1.$ | (11) |
式中:fcov为某一应力水平下疲劳寿命变异系数.
在式(11) 中, 因为难以提前获知形状参数α的值, 所以只能通过假设来求解, 但这种方法效率低.因此可用如下简便方法来近似求解α[18, 20-21]:
| $\alpha = f_{{\rm{cov}}}^{ - 1.08}.$ | (12) |
特征寿命参数则可表示如下:
| $u = \frac{\mu }{{\mathit{\Gamma }\left( {\frac{1}{\alpha } + 1} \right)}}.$ | (13) |
通过矩估计法可求解两参数威布尔分布函数的参数.对未冻融损伤混凝土及冻融循环次数为50、100、150次的混凝土, 其在各种应力水平下的弯曲疲劳寿命分布函数的参数估计值分别如表 5所示.威布尔分布函数的特征参数在一定程度上反映了疲劳寿命数据的分散性:特征参数愈大, 表示疲劳寿命数据愈分散.可知, 混凝土疲劳寿命的分散性随应力水平的增大而减小, 随冻融次数的增加而增大.
| 表 5 不同应力水平下不同冻融损伤程度混凝土小梁弯曲疲劳寿命威布尔分布参数估计值 Table 5 Evaluated Weibull parameters of fatigue life atdifferent stress levels for various frost-damagedconcrete |
采用单个样本分布的K-S(kolmogorov-smirnov)检验方法, 对冻融前、后混凝土疲劳寿命样本的拟合分布与实测分布进行比较, 以判断由矩估计方法确定的分布参数及由采用样本所来自的总体分布是否服从估计参数的威布尔分布.
K-S检验是基于将理论分布F(Ni)下的累计频数分布与观察到的累计频数分布Fk(Ni)相比较, 找出它们之间的最大偏差D作为统计量[22]:
| $D = \mathop {{\rm{max}}}\limits_i^k \left\{ {\left| {F({N_i}) - {F_k}({N_i})} \right|} \right\}.$ | (14) |
式中:D为理论分布的累计频数与观察值的累计频数的最大差值, F(Ni)表示理论分布的累计概率分布函数, F(Ni)=i/k, i为k个观察数据由小到大排列的顺序数, Fk(Ni)表示样本观测值的累计概率分布函数.
对本检验对象的原假设可表述为H0:来自混凝土弯曲疲劳寿命总体分布的样本服从威布尔分布.采用K-S法对各种应力水平下混凝土弯曲疲劳寿命分布拟合进行检验.查单样本K-S检验统计量表得当显著水平为0.05, 样本容量k=6的拒绝临界值Dc(6, 0.05)=0.519, 而实际观测的绝对差值最大值:当n=0时,D*=0.169 4<0.519;当n=50时,D*=0.151 8<0.519;当n=100时, D*=0.172 2<0.519;当n=150时, D*=0.212 3<0.519.因此, 接受原假设, 认为来自混凝土疲劳寿命总体分布的样本服从相应估计参数的威布尔分布.K-S检验的结果表明, 对冻融前、后的混凝土疲劳寿命威布尔分布, 采用矩估计法确定的参数, 能够满足混凝土弯曲疲劳寿命分布函数计算的需要.
4 混凝土弯曲疲劳可靠性分析前述通过疲劳试验数据均值回归得到的弯曲疲劳寿命方程是均值寿命, 其可靠性概率近似等于50%, 在进行混凝土构件疲劳寿命设计验算时, 这个可靠性概率的适用范围有限, 需要选用具有其他可靠性概率的设计疲劳寿命, 因此需要确定具有不同可靠性概率的设计疲劳寿命-强度关系.
4.1 混凝土弯曲疲劳P-S-N曲线根据式(5) 和(8) 可获得具有不同可靠性概率(保证概率或存活率)pr的疲劳寿命表达式为
| ${N_{{p_{\rm{r}}}}} = u{\left( {{\rm{ln}}\frac{1}{{{p_{\rm{r}}}}}} \right)^{1/\alpha }}.$ | (15) |
式中:Npr为具有可靠性概率pr的混凝土疲劳寿命.
从式(13) 可知,具有不同可靠性概率pr的疲劳寿命Npr与其疲劳寿命的数学期望E(Nx)有关, 则混凝土疲劳寿命Npr可表示为
| ${N_{{p_{\rm{r}}}}} = \frac{{E({N_x})}}{{\mathit{\Gamma }\left( {1 + \frac{1}{\alpha }} \right)}}{\left( {{\rm{ln}}\frac{1}{{{p_{\rm{r}}}}}} \right)^{1/\alpha }}.$ | (16) |
利用式(16) 可计算在给定可靠性概率pr下不同应力水平的混凝土疲劳寿命Npr.选取6种可靠性概率水平pr=5%、36.8%、50%、90%、95%、99%, 利用混凝土疲劳寿命分布估计参数, 可得到各级应力水平下具有规定可靠性概率的弯曲疲劳寿命计算值, 部分混凝土的疲劳寿命次数与可靠性概率关系如图 4所示.结果表明, 弯曲疲劳寿命可靠性概率随冻融循环作用次数的增加和概率水平的增大而减小, 这与材料的物理特性是一致的.

|
图 4 不同冻融损伤混凝土的疲劳寿命次数与可靠性概率关系 Fig. 4 Relationship of fatigue life and reliability probability for various frost-damaged concrete |
规定可靠性概率的弯曲疲劳寿命计算值进行回归计算, 可得到不同冻融损伤程度混凝土弯曲疲劳寿命具有不同概率的疲劳寿命方程, 以此结果绘制的部分P-S-N曲线如图 5所示.

|
图 5 具有不同可靠性概率的冻融损伤混凝土疲劳寿命方程图 Fig. 5 P-S-N curves for frosted concree in differentprobebilities |
根据式(16) 中Npr和E(Nx)的关系,令
| ${\gamma _{{p_{\rm{r}}}}} = \mathit{\Gamma }\left( {1 + \frac{1}{\alpha }} \right)/{\left( {{\rm{ln}}\frac{1}{{{p_{\rm{r}}}}}} \right)^{1/\alpha }},$ |
则上式可表示为
| ${N_{{p_{\rm{r}}}}} = \frac{{E({N_x})}}{{{\gamma _{{p_{\rm{r}}}}}}}.$ | (17) |
式中:γpr可视为具有可靠性概率pr的混凝土疲劳寿命安全系数.
对经不同冻融循环次数作用后的混凝土设计弯曲疲劳寿命, 具有不同可靠性概率的安全系数γpr的计算结果如表 6所示.由表 6可以看出, 随着冻融循环次数的增加, 具有相同概率水平的混凝土弯曲疲劳寿命所须的安全系数不断增大;这表明对经受较多次冻融循环作用的混凝土, 其弯曲疲劳寿命须采用较大的安全系数才能满足概率要求;在混凝土弯曲疲劳寿命设计时, 对可能遭受冻融损伤较严重的混凝土构件, 应适当增加其弯曲疲劳寿命的安全系数, 才能满足可靠性概率要求.另外,考虑到混凝土的力学性能与其类型、级配、等级及尺寸等多种因素有关, 本文所确定的疲劳寿命安全系数γpr仅适用研究中所采用混的凝土, 对其他类型混凝土可结合本文采用的方法经具体试验后确定.同时, 考虑本研究采用的试件是素混凝土小梁, 其结果主要适用于素混凝土梁板弯拉疲劳或不允许弯拉开裂的钢筋混凝土梁板结构.
| 表 6 不同应力水平冻融损伤前、后混凝土具有不同可靠性概率的安全系数 Table 6 Safety factor of flexural fatigue life with different probability for various frost-damaged concrete at different given stress levels |
(1) 试验研究结果表明:遭受冻融损伤作用的混凝土的动弹性模量、静弯曲强度和弯曲疲劳强度和寿命的平均值都随着冻融作用次数的增加而急剧减小;在相同荷载作用下, 混凝土的弯曲疲劳寿命随冻融作用次数的增加而明显减小.
(2) K-S检验结果表明:不同冻融损伤程度的混凝土的弯曲疲劳寿命都服从两参数威布尔分布;利用矩估计法获得的威布尔分布参数结果表明, 混凝土弯曲疲劳寿命的分散性随着应力水平的增大而减小, 随着冻融作用次数的增加而增大.
(3) 不同应力水平作用下的混凝土弯曲疲劳寿命的可靠性概率随着冻融循环作用次数的增加而有所降低, 这表明对遭受越多冻融循环作用次数作用的混凝土, 其弯曲疲劳寿命(强度)可靠性概率越低.可知, 在进行混凝土构件弯曲疲劳寿命(强度)设计验算时, 对可能会遭受较严重冻融损伤作用的构件, 应适当提高其可靠性概率, 或增加疲劳寿命(强度)的安全系数.
| [1] |
李钧, 王宗林. 冻融循环作用对混凝土毛细孔结构的劣化机制及改善措施[J].
建筑技术, 2016, 47(6): 491–494.
LI Jun, WANG Zong-lin. Freeze-thaw cycle effect on degradation mechanism of concrete pore structure and improvement measures[J]. Architecture Technology, 2016, 47(6): 491–494. |
| [2] | SUN W, ZHANG Y M, YAN H D, et al. Damage and damage resistance of high strength concrete under the action of load and freeze-thaw cycles[J]. Cement and Concrete Research, 1999, 29(9): 1519–1523. DOI:10.1016/S0008-8846(99)00097-6 |
| [3] |
邹超英, 赵娟, 梁锋, 等. 冻融作用后混凝土力学性能的衰减规律[J].
建筑结构学报, 2008, 29(1): 117–123.
ZOU Chao-ying, ZHAO Juan, LIANG Feng, et al. Degradation of mechanical properties of concrete caused by freeze-thaw action[J]. Journal of Building Structures, 2008, 29(1): 117–123. |
| [4] |
洪锦详, 缪昌文, 刘加平, 等. 冻融损伤混凝土力学性能衰减规律[J].
建筑材料学报, 2012, 15(2): 173–178.
HONG Jin-xiang, MIAO Chang-wen, LIU Jia-ping, et al. Degradation law of mechanical properties of concrete subjected to freeze-thaw cycles[J]. Journal of Building Materials, 2012, 15(2): 173–178. |
| [5] | BEAUDOIN J J, MACINNIS C. The mechanism of frost damage in hardened cement paste[J]. Cement and Concrete Research, 1974, 4(2): 139–147. DOI:10.1016/0008-8846(74)90128-8 |
| [6] | FAGERLUND G. The international cooperative test of the critical degree of saturation method of assessing the freeze/thaw resistance of concrete[J]. Matériauxet Construction, 1977, 10(4): 231–253. DOI:10.1007/BF02478694 |
| [7] |
郭寅川, 申爱琴, 何天钦, 等. 疲劳荷载与冻融循环耦合作用下季冻区路面水泥混凝土孔结构研究[J].
中国公路学报, 2016, 29(8): 29–35.
GUO Yin-chuan, SHEN Ai-qin, HE Tian-qin, et al. Pore structure research on pavement cement concrete subjected to coupling effect of fatigue load and cyclic freeze-thaw in seasonally frozen ground region[J]. China Journal of Highway and Transport, 2016, 29(8): 29–35. |
| [8] | LI W, SUN W, JIANG J. Damage of concrete experiencing flexural fatigue load and closed freeze/thaw cycles simultaneously[J]. Construction and Building Materials, 2011, 25(5): 2604–2610. DOI:10.1016/j.conbuildmat.2010.12.007 |
| [9] |
田威, 邢凯, 谢永利. 冻融环境下混凝土损伤劣化机制的力学试验研究[J].
实验力学, 2015, 30(3): 299–304.
TIAN Wei, XING Kai, XIE Yong-li. Experimental study of damage degradation mechanism of concrete in freeze-thaw environment[J]. Journal of Experimental Mechanics, 2015, 30(3): 299–304. DOI:10.7520/1001-4888-14-127 |
| [10] |
关虓, 牛荻涛, 沈可欣, 等.气冻气融环境下钢筋混凝土梁抗冻性研究[J].建筑材料学报, 2016, 19(3):461-466. GUAN Xiao, NIU Di-tao, SHEN Ke-xin, ZHANG Yong-li. Frost-resistance of RC beam under atmospheric freeze-thaw cycles [J]. Journal of Building Materials, 2016, 19(3): 461-466. http://www.cnki.com.cn/Article/CJFDTOTAL-JZCX201603008.htm |
| [11] | PENTTALA V, Al-NESHAWY F. Stress and strain state of concrete during freezing and thawing cycles[J]. Cement and Concrete Research, 2002, 32(9): 1407–1420. DOI:10.1016/S0008-8846(02)00785-8 |
| [12] |
徐善华, 王友德, 李安邦, 等. 冻融损伤混凝土重复受压本构关系[J].
哈尔滨工业大学学报, 2015, 47(4): 104–110.
XU Shan-hua, WANG You-de, LI An-bang, et al. Dynamic constitutive relation of concrete with freeze-thaw damage under repeated loading[J]. Journal of Harbin Institute of Technology, 2015, 47(4): 104–110. DOI:10.11918/j.issn.0367-6234.2015.04.018 |
| [13] | HANJARI K Z, KETTIL P, LUNDGREN K. Modelling the structural behaviour of frost-damaged reinforced concrete structures[J]. Structure and Infrastructure Engineering, 2013, 9(5): 416–431. DOI:10.1080/15732479.2011.552916 |
| [14] | HASAN M, UEDA T, SATO Y. Stress-strain relationship of frost-damaged concrete subjected to fatigue loading[J]. Journal of Materials in Civil Engineering, 2008, 20(1): 37–45. DOI:10.1061/(ASCE)0899-1561(2008)20:1(37) |
| [15] | LI W, JIANG Z, YANG Z, et al. Interactive effect of mechanical fatigue load and the fatigue effect of freeze-thaw on combined damage of concrete[J]. Journal of Materials in Civil Engineering, 2015, 27(8): 1–13. |
| [16] | 中华人民共和国国家标准. 普通混凝土长期性能和耐久性能试验方法标准: GB/T 50082-2009 [S]. 北京: 中国建筑工业出版社, 2009. |
| [17] | TEPFERS R. Tensile fatigue strength of plain concrete[J]. Journal of the American Concrete Institute, 1979, 76(8): 919–934. |
| [18] | OH B. Fatigue analysis of plain concrete in flexure[J]. Journal of Structural Engineering, 1986, 112(2): 273–288. DOI:10.1061/(ASCE)0733-9445(1986)112:2(273) |
| [19] | American Society for Testing. A guide for fatigue testing and the statistical analysis of fatigue data[M]. Philadelphia: American Society for Testing and Materials, 1963. |
| [20] | MOHAMMADI Y, KAUSHIK S K. Flexural fatigue-life distributions of plain and fibrous concrete at various stress levels[J]. Journal of materials in civil engineering, 2005, 17(6): 650–658. DOI:10.1061/(ASCE)0899-1561(2005)17:6(650) |
| [21] | WEIBULL W. Fatigue testing and analysis of results[M]. Amsterdam: Elsevier, 2013: 184-249. |
| [22] | 南京大学金陵学院大学数学教研室. 概率论与数理统计简明教程[M]. 南京: 东南大学出版社, 2014: 36-68. |



