2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024
2. State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology Dalian 116024, China
高分辨率格式在计算流体力学领域中已经得到了广泛的应用, 如数值模拟溃坝[1-2]、环境污染[3-4]、孤立水波[5], 激波捕捉[6]等实际问题.控制方程中的对流项看似简单, 但伪数值耗散和非物理振荡导致在数值求解上十分困难.计算流体力学中低阶格式(如一阶迎风格式)具有有界性、稳定性, 而且在间断附近不会产生数值震荡, 却会带来严重的数值耗散而导致局部的大梯度和间断抹平, 这是由于数值计算带来的而并非真实的物理现象[7-8];而高阶格式(如SOU格式, QUICK格式)虽然能够改进数值计算的准确性和减少数值耗散[9], 但是在陡坡和间断附近却会产生数值振荡[10-11].
因此, Harten[12]提出了一种高分辨率格式, 即最小变差递减(total variation diminishing, TVD)格式.该方法能够克服上述计算格式的缺陷, 并继承了计算流体力学中的迎风特性.TVD格式通过引入流通量限制器实现在低阶格式与高阶格式之间的转换保证TVD特性.之后, 各种各样的流通量限制器(Superbee[13], Van Leer[14], Minmod[12])被提出.Juntasaro等[15]在结构网格下比较了不同限制器的性质.对于结构网格, 流通量限制器的因数r是一致的.但实际中, 特别是溃坝, 孤立波爬坡等问题, 计算域往往较为复杂的问题, 非结构网格能够快速、灵活地对计算域进行网格划分.而对于非结构网格, 通常无法直接定义迎风点, 给TVD格式的实施带来困难.
近年来, 一种源于无网格方法并采用梯度光滑技术的梯度光滑法(gradient smoothing method, GSM)被提出, 应用于求解流体问题[16].由于有多种光滑函数与积分格式作为备选, 此方法具有更加优秀的通用性和灵活性.大量的数值实验证明了GSM能提供稳定、精确的数值解, 而且具有计算结果对网格畸变不敏感的性质[17-19].GSM方法已经成功被用于求解非结构网格下的可压缩/不可压缩和黏性/无黏流动, 但目前尚未引入高分辨率计算格式.引入TVD格式将有助于避免应用GSM方法求解间断问题时所产生的数值振荡与耗散, 对于求解复杂工程实际问题非常重要.相对于经典的基于非结构网格的TVD格式, GSM方法中能够形成多种光滑域, 在光滑域上可以灵活、准确地定义迎风点来构造TVD格式.
在Li等[20]构造非结构网格TVD格式的基础上, 本文提出了改进的TVD格式并用于非结构网格下求解对流方程.利用梯度光滑技术, 在3种不同的光滑域上分别定义迎风信息来构造TVD格式, 并将该方法应用到不同类型的对流方程, 进行数值实验.通过与现有的基于非结构网格TVD方法进行对比, 验证所提出的方法.
1 梯度光滑法Liu等[21]提出了广义梯度光滑技术, 并应用于固体力学中提出了基于G空间理论和双重弱形式的光滑点插值法.Liu等[16]将梯度光滑技术应用于直接求解偏微分方程提出了应用于流体求解的梯度光滑法.梯度光滑法利用散布在计算域与域边界上的节点形成背景网格来表示该问题计算域及其边界, 场变量信息存储在背景网格的节点上.计算域在不同位置(如节点、边中点、单元中心点)的梯度可以在相应的光滑域上利用光滑技术求解.
1.1 梯度光滑技术计算域Ω中任意一点Xi处场变量U的梯度可近似为
| $ \nabla {U_i} \equiv \nabla U\left( {{X_i}} \right) \approx \int_\mathit{\Omega } {\nabla U\left( X \right)\hat \omega \left( {X - {X_i}} \right){\rm{d}}\mathit{\Omega }} \cdot $ | (1) |
式中:
对式(1)分部积分并采用散度定理
| $ \begin{array}{*{20}{l}}{\nabla U\left( {{X_i}} \right) \approx \int_\mathit{\Gamma } {U\left( X \right)\hat \omega \left( {X - {X_i}} \right)\mathit{\boldsymbol{n}}{\rm{d}}\mathit{\Gamma }} - }\\{\;\;\;\int_\Omega {U\left( X \right)\nabla \hat \omega \left( {X - {X_i}} \right){\rm{d}}} \mathit{\Omega } \cdot }\end{array} $ | (2) |
式中:Γ为域的边界;n为边界的外法向向量;如图 1所示.
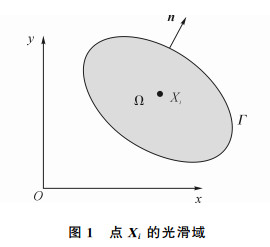
|
图 1 点Xi的光滑域 Fig. 1 Smoothing domain on point Xi |
光滑函数选取如下形式的分段函数:
| $ \hat \omega \left( {X - {X_i}} \right) = \left\{ \begin{array}{l} 1/{A_i}, X \in \mathit{\Omega };\\ \;\;\;0\;{\rm{ }}\;\;\;, X \notin \mathit{\Omega } \cdot \end{array} \right.{\rm{ }} $ | (3) |
式中:Ai为光滑域Ω的面积.将式(3)代入式(2)中, 化简为
| $ \nabla U\left( {{X_i}} \right) \approx \frac{1}{{{A_i}}}\int_\mathit{\Gamma } {U\left( X \right)\mathit{\boldsymbol{n}}{\rm{d}}\mathit{\Gamma }} \cdot $ | (4) |
在GSM方法中, 计算域及其边界用分布节点加以表示, 这些节点是场变量的载体.节点的分布一般为非均匀的, 节点分布密度取决计算精度的要求.通过连结这些节点来构成初始单元(背景网格).在GSM方法中提出了3种光滑域, 分别为:节点光滑域(node-based gradient smoothing domain, nGSD), 中点光滑域(midpoint-based gradient smoothing domain, mGSD)和中心点光滑域(centroid-based gradient smoothing domain, cGSD).节点光滑域的构成是通过连结相关单元中心点及其关联的边中点;中点光滑域是连结中点所在边的2个端点与边相邻的2个单元中点;中点光滑域就是计算域的初始单元, 3种光滑域如图 2所示.
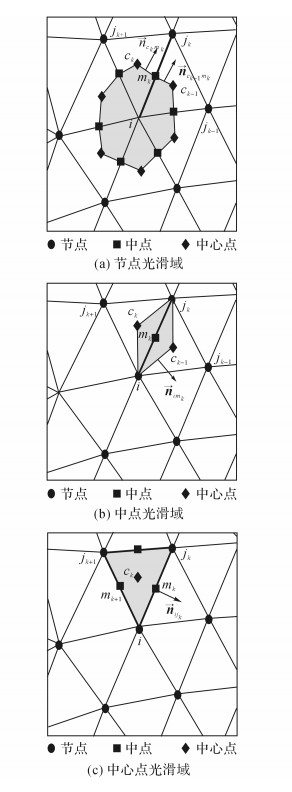
|
图 2 光滑域示意图[16] Fig. 2 Illustration of gradient smoothing domains |
计算节点一阶导数时采用一点积分格式, 并假设:
| $ {U_{{c_k}}} = {U_{{c_{k - 1}}}} = {U_{{m_k}}} \cdot $ | (5) |
式中:Uck, Uck-1分别为单元中心点ck, ck-1的场变量值, Umk为边中点mk的场变量值.
在节点光滑域上应用式(4), 节点处的一阶梯度可近似为
| $ \left. \begin{array}{l} \frac{{\partial {U_i}}}{{{\partial _x}}} \approx \frac{1}{{A_i^{nGSD}}}\sum\nolimits_{k = 1}^{{n_i}} {{{\left( {\Delta {\mathit{\boldsymbol{S}}_x}} \right)}_{i{j_k}}}{U_{{m_k}}}}, \\ \frac{{\partial {U_i}}}{{{\partial _y}}} \approx \frac{1}{{A_i^{nGSD}}}\sum\nolimits_{k = 1}^{{n_i}} {{{\left( {\Delta {\mathit{\boldsymbol{S}}_y}} \right)}_{i{j_k}}}{U_{{m_k}}}} \cdot \end{array} \right\} $ | (6) |
| $ \left. \begin{array}{l} {\left( {\Delta {\mathit{\boldsymbol{S}}_x}} \right)_{i{j_k}}} = \left( {\Delta {\mathit{\boldsymbol{S}}_x}} \right)_{i{j_k}}^{\left( L \right)} + \left( {\Delta {\mathit{\boldsymbol{S}}_x}} \right)_{_{i{j_k}}}^{\left( R \right)}, \\ {\left( {\Delta {\mathit{\boldsymbol{S}}_y}} \right)_{i{j_k}}} = \left( {\Delta {\mathit{\boldsymbol{S}}_y}} \right)_{i{j_k}}^{\left( L \right)} + \left( {\Delta {\mathit{\boldsymbol{S}}_y}} \right)_{_{i{j_k}}}^{\left( R \right)} \cdot \end{array} \right\} $ | (7) |
式中:AinGSD为节点光滑域的面积, ni为与节点i相连的节点总数, (ΔSx)ijk和(ΔSy)ijk为边界mkck的外法向向量, 上标(L)和(R)为原始单元的边ijk相关联的两侧的光滑域边界, 如图 2(a)所示.
| $ \;\;\;\left. \begin{array}{l} \;\;\;\;\left( {\Delta {\mathit{\boldsymbol{S}}_x}} \right)_{i{j_k}}^{\left( L \right)} = {r_{{m_k}{c_k}}}{\left( {{\mathit{\boldsymbol{n}}_x}} \right)_{{m_k}{c_k}}}\\ \;\;\;\;\left( {\Delta {\mathit{\boldsymbol{S}}_y}} \right)_{i{j_k}}^{\left( L \right)} = {r_{{m_k}{c_k}}}{\left( {{\mathit{\boldsymbol{n}}_y}} \right)_{{m_k}{c_k}}}\\ \;\left( {\Delta {\mathit{\boldsymbol{S}}_x}} \right)i{j_k}\left( R \right) = {r_{{m_k}{c_{k - 1}}}}{\left( {{\mathit{\boldsymbol{n}}_x}} \right)_{{m_k}{c_{k - 1}}}}\\ \;\left( {\Delta {\mathit{\boldsymbol{S}}_y}} \right)i{j_k}\left( R \right) = {r_{{m_k}{c_{k - 1}}}}{\left( {{\mathit{\boldsymbol{n}}_y}} \right)_{{m_k}{c_{k - 1}}}} \end{array} \right\} \cdot $ | (8) |
式中:rmkck、rmkck-1分别为光滑域边界mkck和mkck-1的长度, nx和ny为边界mkck和mkck-1的单位外法向向量.
边中点处的变量值利用线性插值计算,
| $ {U_{{m_k}}} \approx \frac{{{U_i} + {U_j}_k}}{2} \cdot $ | (9) |
可以在中点光滑域上利用式(4)来近似计算, 表达形式如下:
| $ \begin{array}{l} \frac{{\partial {U_{{m_k}}}}}{{{\partial _x}}} \approx \left[{\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_m^x} \right)}_{i{c_{k-1}}}}\left( {{U_i} + {U_{{c_{k-1}}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\Delta \mathit{\boldsymbol{S}}_m^x} \right)_{{c_{k-1}}{j_k}}}\left( {{U_{_{{c_{k - 1}}}}} + {U_{_{{j_k}}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\Delta \mathit{\boldsymbol{S}}_m^x} \right)_{{j_k}{c_k}}}\left( {{U_{_{{j_k}}}} + {U_{{c_k}}}} \right) + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_m^x} \right)}_{{c_k}i}}\left( {{U_{{c_k}}} + {U_i}} \right)} \right]\frac{1}{{A_i^{mGSD}}} \cdot \end{array} $ | (10) |
| $ \begin{array}{l} \frac{{\partial {U_{{m_k}}}}}{{{\partial _y}}} \approx \left[{\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_m^y} \right)}_{i{c_{k-1}}}}\left( {{U_i} + {U_{{c_{k-1}}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\Delta \mathit{\boldsymbol{S}}_m^y} \right)_{{c_{k-1}}{j_k}}}\left( {{U_{_{{c_{k - 1}}}}} + {U_{_{{j_k}}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\Delta \mathit{\boldsymbol{S}}_m^y} \right)_{{j_k}{c_k}}}\left( {{U_{_{{j_k}}}} + {U_{{c_k}}}} \right) + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_m^y} \right)}_{{c_k}i}}\left( {{U_{{c_k}}} + {U_i}} \right)} \right]\frac{1}{{A_i^{mGSD}}} \cdot \end{array} $ | (11) |
式中:Ui, Ujk为节点的场变量, AimGSD为中点光滑域的面积, ΔSmx和ΔSmy为中点光滑域界面的外法向矢量, 计算方式与节点光滑域界面的外法向矢量相似.中心点处的场变量Uck利用单元节点Ui, Ujk和Ujk+1的变量采用线性插值计算
| $ {U_{{c_k}}} \approx \frac{{{U_i} + {U_{{j_k}}} + {U_{{j_{k + 1}}}}}}{3} \cdot $ | (12) |
中心点一阶梯度的离散格式可近似为如下形式
| $ \begin{array}{l} \frac{{\partial {U_{{c_k}}}}}{{{\partial _x}}} \approx \left[{\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_c^x} \right)}_{i{j_k}}}\left( {{U_i} + {U_{{j_k}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\Delta \mathit{\boldsymbol{S}}_c^x} \right)_{{j_k}{j_{k + 1}}}}\left( {{U_{_{{j_k}}}} + {U_{_{{j_{k + 1}}}}}} \right) + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_c^x} \right)}_{{j_{k + 1}}i}}\left( {{U_{{j_{k + 1}}}} + {U_i}} \right)} \right]\frac{1}{{A_i^{cGSD}}} \cdot \end{array} $ | (13) |
| $ \begin{array}{l} \frac{{\partial {U_{{c_k}}}}}{{{\partial _y}}} \approx \left[{\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_c^y} \right)}_{i{j_k}}}\left( {{U_i} + {U_{{j_k}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\left( {\Delta \mathit{\boldsymbol{S}}_c^y} \right)_{{j_k}{j_{k + 1}}}}\left( {{U_{_{{j_k}}}} + {U_{_{{j_{k + 1}}}}}} \right) + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{{\left( {\Delta \mathit{\boldsymbol{S}}_c^y} \right)}_{{j_{k + 1}}i}}\left( {{U_{{j_{k + 1}}}} + {U_i}} \right)} \right]\frac{1}{{A_i^{cGSD}}} \cdot \end{array} $ | (14) |
式中:ΔScx和ΔScy为相应的中心点光滑域边界外法向向量, AicGSD为中心点光滑域的面积.
2 基于非结构网格的TVD格式光滑域边界上的流通量
| $ {\phi _{i + \frac{1}{2}}} = {\phi _i} + \frac{1}{2}\psi \left( {{r_{i + \frac{1}{2}}}} \right)\left( {{\phi _{i + 1}} - {\phi _i}} \right), $ | (15) |
| $ {r_{i + \frac{1}{2}}} = \frac{{{\phi _i} - {\phi _{i - 1}}}}{{{\phi _{i + 1}} - {\phi _i}}} \cdot $ | (16) |
式中:ψ(r)为流通量限制器.ψ(r)需要满足在r-ψ关系图中其图像落在二阶精度TVD单调区间内[24].在本文中采用了3种常见的限制器:Superbee限制器ψ(r)=max (0, min (1, 2r), min (2, r)), Van Leer限制器
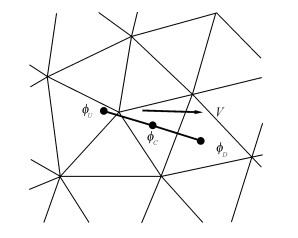
|
图 3 非结构网格的TVD符号示意图 Fig. 3 Illustration of node notation of TVD on unstructured mesh |
| $ {\phi _f} = {\phi _C} + \frac{1}{2}\psi \left( r \right)\left( {{\phi _D} - {\phi _C}} \right) \cdot $ | (17) |
| $ r = \frac{{{\phi _C} - {\phi _U}}}{{{\phi _D} - {\phi _C}}} \cdot $ | (18) |
式中:ϕD, ϕC和ϕU分别为下风点, 中心点和迎风点的变量值.可以看出在非结构网格上应用TVD格式, 迎风点U的变量信息无法直接得到.因此, 很多学者提出了不同的方法在非结构网格下构造TVD格式.
2.1 现有非结构网格的TVD格式在构造非结构网格的TVD格式中, 主要在于计算迎风点处的变量信息和因数r.Darwish等[25]假设在线段UD上, 变量梯度为
可以看出, 非结构网格下迎风点的变量直接影响到整个计算结果的准确性.
Darwish等[25]通过节点C的梯度及节点D值外插计算ϕU.
| $ {\phi _U} = {\phi _D} - 2{\mathit{\boldsymbol{d}}_{CD}} \cdot {\left( {\nabla \phi } \right)_C} \cdot $ | (19) |
式中:
| $ {r_{{\rm{Darwish}}}} = \frac{{2{{(\nabla \phi )}_C} \cdot {\mathit{\boldsymbol{d}}_{CD}}}}{{{\phi _D} - {\phi _C}}} - 1 \cdot $ | (20) |
Li等[20]在研究中发现Darwish方法对ϕU的插值计算并不准确.当变量ϕ呈抛物线分布时, 根据公式(19)计算上风点的变量ϕU是精确的;而当ϕ呈指数分布时, 会导致了对ϕU计算的误差较大.
与Darwish通过外插方式计算迎风点的变量值不同, Li提出了因数r的改进算法.假设lCD=lDU来确定上风点U在计算域中所位于的单元, 在单元内通过内插值的方式计算迎风点的变量值[20], 表达式如下:
| $ {\phi _U} = {\phi _{{U_r}}} - 2{\mathit{\boldsymbol{d}}_{U{U_r}}} \cdot {(\nabla \phi )_U}_r \cdot $ | (21) |
在Li关于r的计算格式中应用了更多的迎风信息, 将式(21)代入到公式(18)中, 可得
| $ {r_{Li}} = - \frac{{2{\mathit{\boldsymbol{d}}_{U{U_r}}}\cdot{{(\nabla \phi )}_{{U_r}}}}}{{{\phi _D} - {\phi _C}}} + \frac{{{\phi _C} - {\phi _{{U_r}}}}}{{{\phi _D} - {\phi _C}}} \cdot $ | (22) |
式中: Ur为点U所在单元的中心点变量,
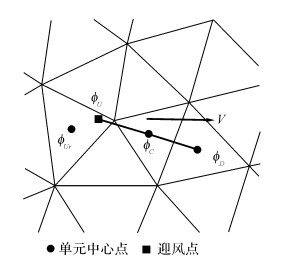
|
图 4 Li提出的非结构网格TVD格式[20] Fig. 4 Li’s TVD scheme on unstructured mesh |
与上述的2种方法通过梯度插值计算得到迎风点的变量信息不同, Barth等[29]通过满足单调性准则的方式来构造TVD格式.Speikreijse单调性准则被改进来重构控制体上的 ϕ, 要求控制体上的变量ϕ必须在周围相邻单元ϕ的最大值与最小值范围内.构造出了不同表达形式的TVD格式并且被成功地应用到实际问题[30, 31].
Speikreijse单调性准则被改写成如下形式:
| $ \begin{array}{l} {\rm{min}}\left( {{\phi _N}, {\phi _P}} \right) \le {R_P}\left( {{r_j}} \right) \le {\rm{max}}\left( {{\phi _N}, {\phi _P}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\forall N \in {\rm{Neighbors}}\left( P \right) \cdot \end{array} $ | (23) |
式中:j为控制体P内的任意点, R为重构多项式,
| $ {R_P}\left( {{r_j}} \right) = {\phi _P} + \psi {\left( {\nabla \phi } \right)_P} \cdot \left( {{\mathit{\boldsymbol{d}}_f} - {\mathit{\boldsymbol{d}}_P}} \right) \cdot $ | (24) |
式中:ψ为流通量限制器, df和dP为坐标向量.控制体界f面积分点处的变量为
| $ {R_P}\left( {{\phi _f}} \right) = {\phi _P} + \psi {\left( {\nabla \phi } \right)_P} \cdot \left( {{\mathit{\boldsymbol{d}}_f} - {\mathit{\boldsymbol{d}}_P}} \right) \cdot $ | (25) |
满足条件:min(ϕN, ϕP)≤RP(rf)≤max(ϕN, ϕP)
式(25)中的流通量限制器ψ表达式为[29]
| $ {\psi _f} = \left\{ \begin{array}{l} \mathit{\Phi }\left( {\frac{{({\rm{max}}\left( {{\phi _N}, {\phi _P}} \right) - {\phi _P}}}{{{{\left( {\nabla \phi } \right)}_P} \cdot \left( {{\mathit{\boldsymbol{d}}_f} - {\mathit{\boldsymbol{d}}_P}} \right)}}} \right), \;\;\;{\phi _f} > {\phi _P};\\ \mathit{\Phi }\left( {\frac{{{\phi _P} - {\rm{min}}\left( {{\phi _N}, {\phi _P}} \right)}}{{{{\left( {\nabla \phi } \right)}_P} \cdot \left( {{\mathit{\boldsymbol{d}}_f} - {\mathit{\boldsymbol{d}}_P}} \right)}}} \right)\;\;\;\;\;{\phi _f} < {\phi _P};\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;1, \;\;\;\;\;\;\;\;\;\;\;\;\;{\phi _f} = {\phi _P} \cdot \end{array} \right. \cdot $ | (26) |
式中:Φ(x)=min(x, 1).定义控制体上所有界面的ψf中的最小值作为流通量限制器ψP=min(ψf).
TVD格式应用于传统的有限体积法时, 变量值存储和计算都是在单元的中心点;而在GSM中, 存储和计算都是在节点上实施同时需要在初始单元上形成节点光滑域.因此, 应用到GSM中时都需要一定的修改.类似地, 针对于这一点Zhang等[32]对比分析了非结构网格下不同TVD格式利用单元顶点方式和单元中心点方式有限体积法求解输运方程计的算结果.
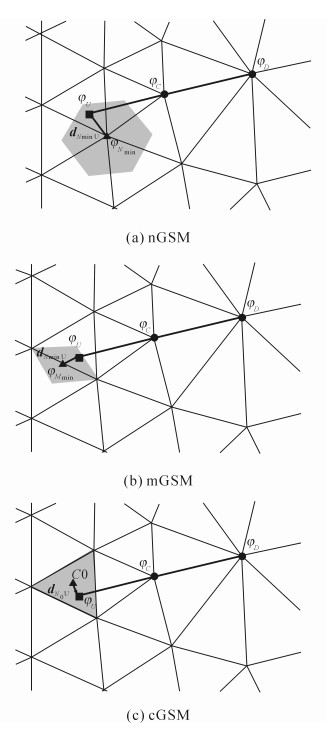
2.2 基于光滑技术改进的非结构网格TVD格式在Li方法基础上, 提出了不同对上风点U的插值计算格式.在3种不同的光滑域上计算迎风点上的变量, 计算步骤如下:
1)延长边DC到点U, 使lCD=lDU, 可得U点坐标(xU, yU), 由此确定U点在计算域中所在的单元.
2)在U点所在的单元分别根据建立的节点光滑域、中点光滑域、中心点光滑域提出nGSM、mGSM、cGSM3种方案来插值计算U点的变量值.
nGSM (node gradient smoothed method):计算U点到单元3个节点的距离, 选择距U最近的节点Nmin, 根据节点光滑域计算该节点梯度来插值计算ϕU, 如图 5(a)所示.
|
图 5 3种基于GSM的改进TVD格式 Fig. 5 Three improved TVD schemes based on GSM |
| $ {\phi _U} = {\phi _{{N_{{\rm{mim}}}}}} + {{\boldsymbol{d}}_{{N_{{\rm{mim}}}}U}} \cdot {(\nabla \phi )_{{N_{{\rm{mim}}}}}} \cdot $ | (27) |
式中:dNmimU为NmimU的矢径.
mGSM (midpoint gradient smoothed method):计算U点到单元3条边中点的距离, 选择距U最近的边中点Mmin, 根据中点光滑域计算该中点梯度来插值计算ϕU, 如图 5(b)所示.
| $ {\phi _U} = {\phi _{{M_{{\rm{mim}}}}}} + {{\boldsymbol{d}}_{{M_{{\rm{mim}}}}U}} \cdot {(\nabla \phi )_{{M_{{\rm{mim}}}}}} \cdot $ | (28) |
式中:dMmimU为MmimU的矢径.
cGSM (centre gradient smoothed method):计算U点到单元中心点C0距离, 根据中心点光滑域计算节点梯度来插值计算ϕU, 如图 5(c)所示.
| $ {\phi _U} = {\phi _{_{{C_0}}}} + {\mathit{\boldsymbol{d}}_{{C_0}U}} \cdot {(\nabla \phi )_{{C_0}}} \cdot $ | (29) |
式中:dC0U为C0U的矢径.
(3)根据上面3种方案算出了迎风点ϕU, 利用式(17)、(18)计算光滑域边界上积分点的流通量, 利用式(6)在节点上建立节点光滑域进行空间离散.
可以看出在3种光滑域上插值计算迎风点ϕU方法是相似的.但由于在插值计算ϕU时所应用的光滑域不同, 在实例计算中的数值振荡与耗散也是不同的.在计算公式上, 步骤(2.3)中cGSM的ϕU的计算方法与Li的方法是基本相同的, 但2种方法计算
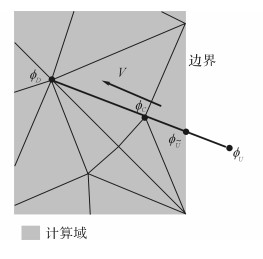
当迎风点U落在计算域之外时, 计算线段UD与边界的交点
|
图 6 边界处理 Fig. 6 Boundary treatment |
为了验证本文提出的基于非结构网格的改进TVD格式, 通过经典算例来与应用Darwish, Li和BJ方法进行对比.算例中既包括间断问题和连续问题, 也包括稳态问题和瞬态问题.在数值计算中分别采用Superbee, Van Leer和Minmod3种常见的流通量限制器.数值计算的误差为
| $ E = \frac{1}{N}\sqrt {\sum\nolimits_{i = 1}^N {{{\left( {\phi _i^n - \phi _i^e} \right)}^2}} } \cdot $ | (30) |
式中:N为计算域节点总数, ϕin为数值解, ϕie为解析解.
3.1 单阶梯对流该问题可以检验不同TVD构造方案在横风方向上的数值耗散与振荡, 控制方程如下:
| $ \frac{{\partial \phi }}{{\partial t}} + \frac{{\partial u\phi }}{{\partial x}} + \frac{{\partial v\phi }}{{\partial y}} = 0 \cdot $ | (31) |
式中:ϕ为输运变量, 速度场为V=(1, 1), 计算模型如图 7(a)所示.

|
图 7 单阶梯对流的计算域 Fig. 7 Computational field of advection of step profile |
计算域几何形状为1×1的正方形, 在计算域内任意布置7 481个节点、14 640个三角形单元, 如图 7(b)所示.
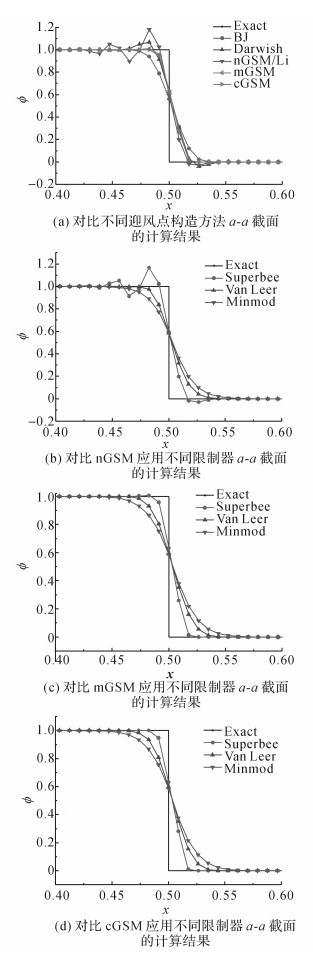
为了验证提出的改进TVD格式, 将数值结果与前人构造的TVD格式进行对比分析, 在计算中所有TVD格式均采用了Superbee流通量限制器(除BJ格式以外), 如图 8(a)所示.
|
图 8 单阶梯对流的计算结果 Fig. 8 Result of convection of step profile |
图 8(a)表明Darwish和nGSM/Li的比值构造方案均在阶梯附近产生了较大的数值振荡.BJ的计算结果并未产生任何数值振荡, 但在横风方向上数值耗散最大的方法.Darwish方法在数值耗散不严重, 但存在数值振荡.基于梯度光滑技术提出的mGSM和cGSM 2种方案基本没有产生数值振荡, 在数值耗散方面也优于之前的方法.
对提出的3种不同的改进方案应用不同的流通量限制器, 计算结果如图 8(b)~(d)所示.Superbee限制器能够最大程度地保证结果的间断性, 最接近真实解, 而应用于nGSM时会产生较大的数值振荡;Minmod限制器会产生了最大的数值耗散;而Van Leer限制器则介于两者之间.此外, 提出的3种方案应用不同的限制器对流场完成初始化后, 收敛误差εcon均能随着时间步数N快速地达到收敛, 如图 9所示.

|
图 9 单阶梯对流的3种方案的收敛性 Fig. 9 Convergence of convective of a step profilefor three schemes |
此计算模型与单阶梯对流基本相同, 但是在计算域中具有双阶梯, 计算模型如图 10所示.网格布置与时间步长和上一个算例的参数相同.控制方程与上节相同, 边界条件如下:
|
图 10 双阶梯对流的计算模型 Fig. 10 Computational model of convective of double-step profile |
| $ \left. \begin{array}{l} \phi = 1\;\;\;x = 0, {\rm{ }}\;\;\;0 \le y \le 0.3;\\ \phi = 0\;\;\;\;x = 0, {\rm{ }}\;\;0.3 \le y \le 1 \cdot \end{array} \right\} $ | (32) |
双阶梯对流对于TVD格式提出了更为严格的要求, 进一步检验改进的TVD格式.与单阶梯对流算例相似, 将数值结果与前人构造的TVD格式进行对比分析, 如图 11(a)所示.
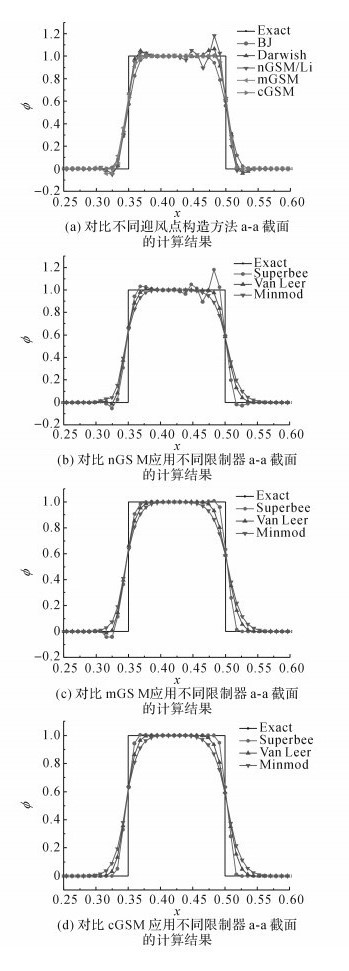
|
图 11 双阶梯对流的计算结果 Fig. 11 Result of convection of double-step profile |
从图 11的计算结果中可以看出, 与单梯度对流的计算结果相似, 所有的方法中nGSM/Li在2个间断附件产生了最为严重的数值振荡, BJ方法的数值耗散最大, Darwish方法产生了数值振荡, mGSM在双阶梯的一侧产生了轻微的振荡, cGSM依然能够得到令人满意的结果.应用其他替他限制器代替Superbee限制器, nGSM和mGSM能够消除数值振荡.Minmod限制器会带来最大的数值耗散.计算收敛性如图 12所示.
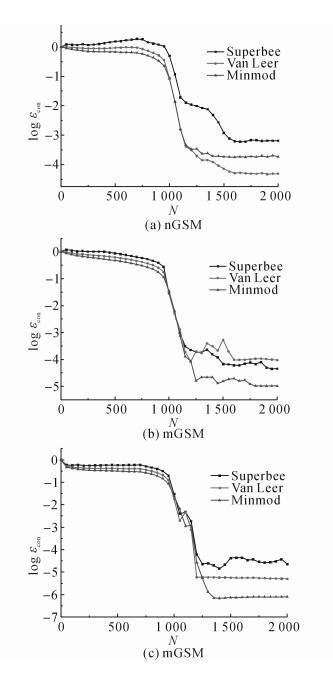
|
图 12 双阶梯对流的3种方案的收敛性 Fig. 12 Convergence of double-step profilefor threeschemes |
为了验证改进TVD方法对于计算连续场问题的准确性, 以计算风暴形成旋转流场过程为例.初始状态(t=0)为场变量从计算域顶端正值逐渐过渡到低端的负值, 如图 13(a)所示.场变量随时间变化的解析解表达式如下:
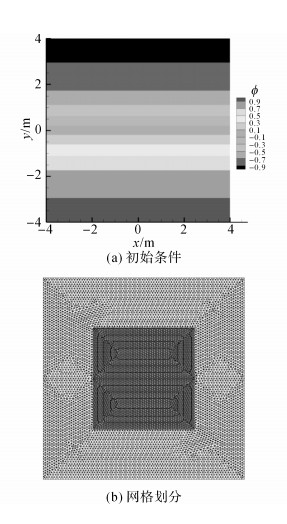
|
图 13 风暴对流的计算模型 Fig. 13 Computational model of convective of cyclogenesis flow field |
| $ \phi = - {\rm{tanh}}\left( {0.5\left[{y{\rm{cos}}\left( {\omega t} \right)-x{\rm{sin}}\left( {\omega t} \right)} \right]} \right) \cdot $ | (33) |
式中:速度场为V=(-ωy, ωx), 角速度为ω=Q/dmax (Q), 距风暴中心的距离为
计算域为一个8 m×8 m的正方形.在计算域的中心处设置为细网格, 单元大小为0.05 m;而远离中心处选择粗网格, 单元大小为0.1 m, 如图 13(b)所示.计算时间步长为0.01 s, 初始条件由ϕt=0计算得到.
在旋转流场的作用下, 计算域中心处场变量的梯度随着时间推移而增大.当t=9 s时, 对比截面(y=0)上, 应用不同TVD方法的计算结果如图 14(a)所示.除了BJ方法, 与解析解对比其他方法均能够得到令人满意的计算结果.BJ方法产生了较大的数值耗散.其他的方法在远离中心处的梯度变化较大的位置造成了轻微的振荡, 随着靠近中心的位置存在一定的数值耗散.综合来看cGSM是最为接近解析解.应用不同限制器的计算结果如图 14(b)~(d)所示, 与之前的计算结果相似, Superbee限制器更加接近解析解, 而其他2种限制器却产生了不同程度的较大数值耗散.此例证明了本文基于光滑技术改进的非结构网格的TVD格式能够解决连续场变量的问题, 其中3种改进格式中cGSM依旧最为出色.
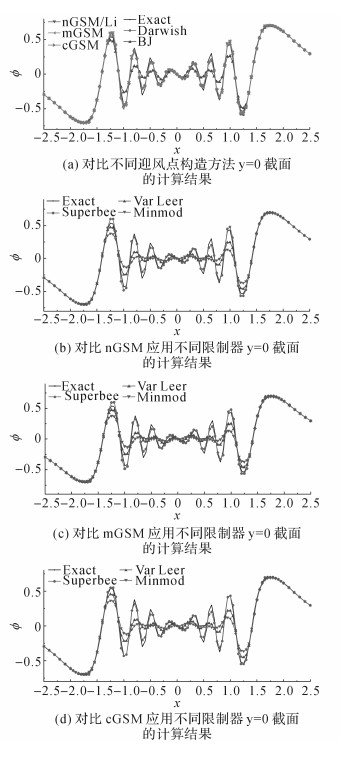
|
图 14 风暴形成流域的对流的计算结果 Fig. 14 Result of convection of cyclogenesis flow field |
根据式(30)对本文提出的3种改进TVD格式对3个数值算例进行准确性对比, 如表 1所示(表中S, V, M分别表示Superbee, Van Leer, Minmod这3种流通量限制器).可以看出mGSM和cGSM这2种改进格式在所有的算例中都具有较高的精度, 其中cGSM改进格式采用Superbee流通量限制器时计算结果最为优秀.
| 表 1 非结构网格下不同方法应用3种限制器的计算精度比较 Table 1 Accuracy comparison of various algorithms for three flux-limiters on unstructured meshes10-4 |
在提出的3种改进TVD格式中, cGSM格式在上面的3个算例中表现最为优秀, 能够准确模拟数值间断.对cGSM格式在相对非均匀的非结构网格下的计算精度进行验证.
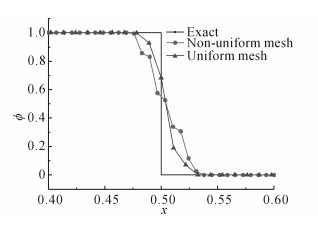
以3.1节的单阶梯对流为例, cGSM格式采用Superbee限制器进行非均匀网格的验证及分析.本文选取了2种网格.网格A采用大小为0.15的相对均匀网格, 节点总数为5 023, 如图 15(a)所示.网格B将计算域分为3部分, 上部和下部处采用的网格尺寸为0.04, 而计算域中间的网格大小为0.01, 网格节点总数为4 527, 网格尺寸具有明显差别, 如图 15(b)所示.对比数值结果, 可以看出在相对非均匀网格B下计算结果并未产生任何数值振荡;但受网格非均匀性的影响, 在间断附近结果不如网格A结果光顺, 准确性略也差于网格A, 如图 16所示.总体上, cGSM在非均匀网格下依然能够保证在间断附近避免产生数值振荡.

|
图 15 相对均匀和和非均匀的非结构网格 Fig. 15 Uniform mesh and Non-uniform mesh |
|
图 16 非均匀网和均匀网格的计算结果对比 Fig. 16 Results comparison of convection of step profile by using non-uniform mesh and uniformmesh |
根据梯度光滑技术, 在3种不同的光滑域上分别构造了非结构网格TVD格式, 灵活地定义迎风点, 讨论了3种构造方法的准确性.之前多数方法都是通过外插方式定义迎风点, 而本文首先确定迎风点所在的单元, 之后计算单元节点、边中点和单元中心点的梯度, 分别通过梯度插值计算迎风点的变量.在数值实验中对比了本文提出的基于nGSM、mGSM和cGSM构造的3种改进TVD格式和传统TVD格式在非结构网格下的计算结果.nGSM在3种格式中结果最差, 表现为采用Superbee限制器时在间断附近产生了数值振荡, 采用其他两种限制器时会带来较大的数值耗散.mGSM和cGSM利用Superbee限制器在计算无论间断问题还是连续问题中均优于之前的方法, 其中mGSM在能够基本不产生数值振荡或轻微数值的情况下依然保持较小的数值耗散, cGSM在不带来数值振荡的同时保证了间断解的锐利性.综合来看, cGSM要略优于mGSM.在应用Var Leer与Minmod限制器时, cGSM相对于其他的方法也能够取得较高的精度.通过对cGSM格式进行了网格非均匀性的验证, 发现对比相对均匀的非结构网格, 非均匀网格的计算结果精度略差, 但仍能够保证在间断处避免产生数值振荡.
根据以上的讨论可以看出, 通过合理的插值格式计算迎风点变量ϕU对于非结构网格的TVD格式非常重要.本文提出的TVD构造格式同样可用于基于非结构网格的其他高阶计算格式, 将在后续工作中深入研究.
| [1] |
黄师化, 汪继文, 李付鹏. 二维非结构网格的一个TVD型有限体积方法[J].
合肥工业大学学报:自然科学版, 2004, 27(5): 522–525.
HUANG Shi-hua, WANG Ji-wen, LI Fu-peng. A finitevolume TVD scheme on the unstructured meshes[J]. Journal of Hefei University of Technology: NaturalScience Edition, 2004, 27(5): 522–525. |
| [2] |
朱华君, 宋松和. 二维浅水波方程的非结构网格TVD型有限体积法[J].
系统仿真学报, 2009, 21(6): 1575–1578.
ZHU Hua-jun, SONG Song-he. TVD-style finite volumemethod on unstructured meshes for two-dimensionalshallow water equations[J]. Journal of SystemSimulation, 2009, 21(6): 1575–1578. |
| [3] |
刘玉玲. 浅水流动与污染物输运的高分辨率计算模型[J].
水动力学研究与进展, 2007, 22(2): 249–253.
LIU Yu-ling. High-resolution numerical model forshallow water flows and pollutant diffusions[J]. Chinese Journalof Hydrodynamics, 2007, 22(2): 249–253. |
| [4] |
王嘉松, 何友声. 浅水流动与污染物扩散的高分辨率计算模型[J].
应用数学和力学, 2002, 7(7): 661–666.
WANG Jia-song, HE You-sheng. High-resolutionnumerical model for shallow water flows and pollutantdispersion[J]. Applied Mathematics and Mechanics, 2002, 7(7): 661–666. |
| [5] |
陈同庆, 张庆河. 不同TVD格式对内孤立波数值模拟结果影响研究[J].
海洋科学, 2013, 37(6): 102–107.
CHENG Tong-qing, ZHANG Qing-he. The research ofthe influence of internal solitary waves for different TVDschemes[J]. Marine Sciences, 2013, 37(6): 102–107. |
| [6] |
王文龙, 李桦, 刘枫, 等. 基于TVD思想的高阶迎风紧致格式[J].
国防科技大学学报, 2013, 35(6): 9–14.
WANG Wen-long, LI Ye, LIU Feng, et al. High orderupwind compact schemes based on TVDalgorithm[J]. Journal National University of DefenseTechnology, 2013, 35(6): 9–14. |
| [7] | LEONARD B. A survey of finite differences with upwinding for numerical modelling of the incompressible convective diffusion equation[J]. Computational Techniques in Transient and Turbulent Flow, 1981, 2: 1–35. |
| [8] | DE VAHL DAVIS G, MALLINSON G. An evaluation of upwind and central difference approximations by a study of recirculating flow[J]. Computers & Fluids, 1976, 4(1): 29–43. |
| [9] | CHEN Y, FALCONER R A. Advection-diffusion modelling using the modified QUICK scheme[J]. International Journal for Numerical Methods in Fluids, 1992, 15(10): 1171–1196. |
| [10] | II S, SHIMUTA M, XIAO F. A 4th-order and single-cell-based advection scheme on unstructured grids using multi-moments[J]. Computer Physics Communications, 2005, 173(1): 17–33. |
| [11] | GERLINGER P. Multi-dimensional limiting for high-order schemes including turbulence and combustion[J]. Journal of Computational Physics, 2012, 231(5): 2199–2228. |
| [12] | HARTEN A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 49(3): 357–393. |
| [13] | ROE P L. Some contributions to the modelling of discontinuous flows[C]//Large-scale Computations in Fluid Mechanics. San Diego: [s.n.]. 1985: 163-193. |
| [14] | VAN LEER B. Towards the ultimate conservative difference scheme[J]. Journal of Computational Physics, 1997, 135(2): 229–248. |
| [15] | JUNTASARO V, MARQUIS† A. Comparative study of flux-limiters based on MUST differencing scheme[J]. International Journal of Computational Fluid Dynamics, 2004, 18(7): 569–576. |
| [16] | LIU G, XU G X. A gradient smoothing method (GSM) for fluid dynamics problems[J]. International Journal for Numerical Methods in Fluids, 2008, 58(10): 1101–1133. |
| [17] | XU G X, LI E, TAN V, et al. Simulation of steady and unsteady incompressible flow using gradient smoothing method (GSM)[J]. Computers & Structures, 2012, 90-91(1): 131–144. |
| [18] | YAO J, LIU G, QIAN D, et al. A moving-mesh gradient smoothing method for compressible CFD problems[J]. Mathematical Models and Methods in Applied Sciences, 2013, 23(2): 273–305. |
| [19] | YAO J, LIN T, LIU G R, et al. An adaptive GSM-CFD solver and its application to shock-wave boundary layer interaction[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2015, 25(6): 1282–1310. |
| [20] | LI L X, LIAO H S, QI L J. An improved r-factor algorithm for TVD schemes[J]. International Journal of Heat and Mass Transfer, 2008, 51(3): 610–617. |
| [21] | LIU G R, ZHANG G Y. Smoothed point interpolation methods: G space theory and weakened weak forms[M]. Singapore: World Scientific Publishing Co. Pte.Ltd, 2013: 174-182. |
| [22] | LIU G R, LIU M B. Smoothed particle hydrodynamics: a meshfree particle method[M]. Singapore: World Scientific publishing, Lo.Pte Ltd, 2003: 58-60. |
| [23] | SONG S H, CHEN M Z. TVD-style finite volume method on unstructured meshes in two dimensions[J]. Acta Aeronautica Et Astronautica Sinica, 2001, 22(3): 244–246. |
| [24] | SWEBY P K. High resolution schemes using flux limiters for hyperbolic conservation laws[J]. SIAM Journal On Numerical Analysis, 1984, 21(5): 995–1011. |
| [25] | DARWISH M, MOUKALLED F. TVD schemes for unstructured grids[J]. International Journal of heat and mass transfer, 2003, 46(4): 599–611. |
| [26] | ZHANG Z, SONG Z Y, KONG J, et al. A new r-ratio formulation for TVD schemes for vertex-centered FVM on an unstructured mesh[J]. International Journal for Numerical Methods in Fluids, 2015. |
| [27] | HOU J, SIMONS F, HINKELMANN R. A new TVD method for advection simulation on 2D unstructured grids[J]. International Journal for Numerical Methods in Fluids, 2013, 71(10): 1260–1281. |
| [28] | ZHANG D, JIANG C, CHENG L, et al. A refined r-factor algorithm for TVD schemes on arbitrary unstructured meshes[J]. International Journal for Numerical Methods in Fluids, 2016, 80(2): 105–139. |
| [29] | BARTH T J, JESPERSEN D C. The design and application of upwind schemes on unstructured meshes[C]//Proc., AIAA, 27th Aerospace Sciences Meeting American Institute of Aeronautics and Astronautics. Reston. VA: [s.n.]. 1989: 366. |
| [30] |
高二, 宋松和. 一种TVD方法在三维非结构网格中的应用[J].
航空计算技术, 2008, 38(5): 14–17.
GAO Er, SONG Song-he. The apply of a TVD algorithmon three-dimensional unstructured mesh[J]. AeronauticalComputing Technique, 2008, 38(5): 14–17. |
| [31] |
宋松和, 陈矛章. 二维非结构网格的一个TVD型有限体积方法[J].
航空学报, 2001, 22(3): 244–246.
SONG Song-he, CHEN Mao-zhang. TVD-style finitevolume method on unstructured meshes in twodimensions[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(3): 244–246. |
| [32] | ZHUO Z, ZHI-YAO S, FEI G, et al. Comparison and Modification: TVD schemes for scalar transport on an unstructured Grid[J]. China Ocean Engineering, 2016, 30(4): 615–626. |



