随着项目调度在工程及制造系统中的应用愈加广泛, 如何高效解决资源约束项目调度问题(resource constrained project scheduling problem, RCPSP)已成为企业运营过程中日益关心的问题.构成企业项目的一系列复杂且相互关联的活动可看作项目调度中的作业, 执行不同作业所需求的人力资源可视为项目调度中的可更新资源.由于个体差异性及学习能力, 实际上每种人力资源又具备不同的能力, 即不同水平的多种技能.此时, 对于拥有复合型人力资源且资源能力不同的企业, 将运营中的调度问题抽象成带有技能水平的多技能资源约束项目调度问题更加贴切.在考虑技能水平条件下, 通过对作业及资源的合理调度与分配, 可以缩短作业执行时间以及整个项目工期.因此, 对该问题的研究具备重要的理论和现实意义.
鉴于带有技能水平的多技能资源约束项目调度问题在实际工程运用中具有重要的作用, 国内外许多学者已经对相关问题进行了研究.Bellenguez等[1]对带有技能水平的基本多技能资源约束问题进行了研究, 认为可看成多模式资源约束项目调度问题的扩展, 证明了该问题是NP-hard问题, 并以最小化项目工期为目标, 提出了2种求解该问题低界的方法.Barz等[2]以电信行业中具备不同技能水平的多技能资源分配问题为研究对象, 以最小化平均惩罚和等待费用为优化目标, 建立了相应的决策模型.Fırat等[6]又在Hurkens[3]基础上作了进一步扩展, 认为项目中一个资源可以执行同一项作业所需的多种技能.喻小光等[7]研究了多技能资源约束项目调度条件下的资源水平问题并利用最大流算法解决资源分配问题.陈君兰等[8]采用混沌粒子群算法对多技能资源受限项目调度问题有效地实现资源分配和工作时间安排.以上研究均认为作业的执行时间是固定的, 事实上, 在很多实际问题中, 不同资源具备的技能水平不尽相同, 因而作业执行时间随分配资源的技能水平而变化.对于单一资源需求作业, Valls等[9]以服务中心人力资源分配为研究对象, 将资源分为3个等级, 作业执行时间由为其分配的资源等级决定.Heimerl等[10]将资源分为内外2部分, 内部资源在使用不同技能时效率不同, 即作业执行时间不同.在作业执行具有多资源需求假设方面, Chen等[11]认为作业执行时间应由为其分配的资源平均效率决定, Naber等[12]将资源分为主要、依赖和非依赖3类并认为作业执行时间随分配资源数量增加而减小.Fernandez-Viagas等[13]认为作业执行时间与分配的资源数是非线性关系并存在最优分配资源数.周辅疆等[14]将可再生资源进一步扩展为具有能力差异的资源并建立考虑能力差异的资源受限的多模式项目调度问题模型.以上研究考虑了作业执行时间与资源间的关系, 但没有充分考虑资源的多技能性或技能水平的分级.
综合分析, 现有研究中针对资源技能水平不同对作业执行时间影响的研究较少.另外, 实际工程中, 不同资源或技能在作业执行过程中所扮演的角色不尽相同, 而现有文献对资源和技能进行分类和分级的研究较为鲜见.故而, 本文在Bellenguez[1]研究问题的基础上, 统筹考虑资源和技能的分类分级以及资源对作业实际执行时间的影响.
1 问题描述及数学模型 1.1 问题描述项目P由若干项作业构成, 记作业集合为J={1, 2, …, j}, j∈J为作业编号, 其标准作业时间为tj.全部作业所需要的S种不同水平的技能由R个可更新资源提供, 资源集合、技能集合及技能水平集合分别记为R={1, 2, …, r}, S={1, 2, …, s}, L={1, 2, 3}, k∈R为资源编号, s∈S为技能编号, l∈L为技能水平编号.作业只有在其需求的技能种类和数量得到满足且符合作业间时序时才能开始执行, 其实际执行时间记为taj, 作业执行不可中断.记Pj为第j项作业的紧前作业集合, i∈Pj为j的紧前作业, rjsl表示第j项作业对l水平下技能s的需求量.资源k具备l水平的技能s记为hskl=1, 否则为0.若hskl′=1且任意l < l′, 则hskl=1.
由于不同种类技能在作业执行过程中所起的作用不同, 故而定义S*为关键技能集, S*由对作业集的执行具有关键作用的技能构成, s*∈S*为关键技能.资源k具备多种技能且只有在具备的技能水平不低于作业需求的该技能水平时, 方可执行该作业.规定资源k在某时刻只能使用一种技能s, 若s为关键技能s*, 则此时k称为关键资源.msk和ηskl分别表示资源k具备技能s的最高水平以及其执行l水平的技能s时的效率.作业j所需l水平技能s由资源k执行的效率可表示为ηskl=1-0.25(msk-l), taj由为其分配的关键资源平均效率与的乘积决定.tSTj和tFTj分别为作业j的开始时间和结束时间, tT为项目实际总完工时间.本文对时间进行离散化处理, 记D={1, 2, …, tz}为时间集合, tz为所有作业串行执行时间之和, d∈D为离散时间节点.
假设:作业j需求且仅需求一类关键技能.
求解目标是获得满足各种约束的最小项目工期T.决策变量如下:
xjd 0, 1变量, 若作业j在d时刻处于执行状态则为1;否则为0.
yjkd 0, 1变量, 资源k在d时刻执行作业j则为1;否则为0.
zjskl 0, 1变量, 作业j所需l水平技能s由资源k提供则为1;否则为0.
δij 0, 1变量, 作业j在作业i结束后开始则为1;否则为0.
1.2 数学模型| $ {\rm{min}}\;\;{t_T} = \mathop {{\rm{max}}}\limits_{j \in J, d \in D} \left\{ {d{x_{jd}}} \right\}, $ | (1) |
| $ \begin{array}{l} {\rm{S}}{\rm{.t}}{\rm{.}}\\ \sum\limits_{d \in D} {{x_{jd}} = {t_{aj}}, \;\;\;\;\;\;\;\;\;\;\forall j \in J;} \end{array} $ | (2) |
| $ {t_{S{T_j}}} + {t_{aj}} \ge d{x_{jd}}, \;\;\;\;\;\;\;\;\;\;\forall j \in J, \forall d \in D; $ | (3) |
| $ {t_{S{T_j}}} \le d{x_{jd}} + M(1 - {x_{jd}}), \;\forall j \in J, \forall d \in D; $ | (4) |
| $ {t_{S{T_i}}} \ge {t_{S{T_j}}} + {t_{aj}} - M(1 - {\delta _{ji}}), {\rm{ }}\;\;\;\;\;\forall i, j \in J; $ | (5) |
| $ \sum\limits_{k \in R} {{z_{jsk}}^l = {r_{js}}^l, {\rm{ }}\;\;\;\;\;\forall j \in J, \forall l \in L, \forall s \in S;} $ | (6) |
| $ \sum\limits_{k \in R} {{y_{jkd}} = \sum\limits_{l \in L} {\sum\limits_{s \in S} {{r_{js}}^l{x_{jd}}, \;\;\;\;\;\;\;\;\forall j \in J, \forall d \in D;} } } $ | (7) |
| $ \begin{array}{l} {z_{jsk}}^l \le {h_{sk}}^l, {\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall j \in J, \forall l \in L, \forall s \in S, \forall k \in R; \end{array} $ | (8) |
| $ \sum\limits_{j \in J} {\sum\limits_{k \in R} {{y_{jkd}} \le R, \;\;\;\;\;\;\;\;\;\;\;\;\forall d \in D;} } $ | (9) |
| $ \sum\limits_{l \in L} {\sum\limits_{s \in S} {{z_{jsk}}^l \le 1, {\rm{ }}\;\;\;\;\;\;\;\;\;\;\forall j \in J, \forall k \in R;} } $ | (10) |
| $ \sum\limits_{j \in J} {{y_{jkd}} \le 1, \;\;\;\;\;\;\;\;\;\;\forall d \in D, \forall k \in R;} $ | (11) |
| $ {\delta _{ij}} + {\delta _{ji}} \le 1, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall i, j \in J; $ | (12) |
| $ {t_{S{T_j}}} + {t_{aj}} \le {t_T}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall j \in J; $ | (13) |
| $ \begin{array}{l} {t_{aj}} = \left\lceil {{t_j}\sum\limits_{k \in R} {{\eta _{{s^*}k}}^l{z_{j{s^*}k}}^l/{r_{j{s^*}}}^l} } \right\rceil, {\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall j \in J, \forall l \in L, \forall s \in S, \forall k \in R; \end{array} $ | (14) |
| $ \begin{array}{l} q{x_{jq}} - d{x_{jd}} - M(1 - {x_{jd}}) \le {t_{aj}} - 1, \\ \forall j \in J, \forall d, q \in D; \end{array} $ | (15) |
| $ \begin{array}{l} \sum\limits_{d \in D} {{y_{jkd}} + M(1 - \sum\limits_{l \in L} {\sum\limits_{s \in S} {{z_{jsk}}^l} } ) \ge {t_{aj}}, } \\ \forall j \in J, \forall k \in R; \end{array} $ | (16) |
| $ \begin{array}{l} {x_{jd}}, {y_{jkd}}, {z_{jsk}}^l, {\delta _{ij}} \in \left\{ {0, 1} \right\}, \\ \forall j \in J, \forall l \in L, \forall s \in S, \forall k \in R, \forall d \in D; \end{array} $ | (17) |
模型中各式含义如下:式(1) 是目标函数, 表示本研究问题目标是最小化项目工期;式(2) 表示作业必须被执行完;式(3) 和(4) 确保作业的开始时间为该作业第一次被执行时间, 其中M是正无穷大的数;式(5) 表示作业间应满足的时序关系;式(6) 表示作业所需某水平技能数量应被满足;式(7) 表示作业所需资源总量应被满足, 同时也表示决策变量xjd与yjkd之间的关系;式(8) 表示资源只有在具备相应技能水平时方可使用该水平技能;式(9) 表示在某时刻执行的作业对资源总需求量应不大于总资源供应量;式(10) 表示资源只能执行某作业的一种技能;式(11) 表示资源在某时刻只能执行一项作业;式(12) 表示两作业不能同时在对方开始之前完成;式(13) 表示作业实际结束时间与项目工期tT之间的关系;式(14) 表示作业的实际执行时间, 由该公式向上取整得到;式(15) 表示作业不可中断;式(16) 表示资源为非抢占式;式(17) 表示决策变量的可行域.
2 算法构建本文研究问题引入带有技能水平的多技能资源使得传统资源约束项目调度问题的决策因素和约束数量增多, 从而导致问题模型和解的分布情况更加复杂(见2.1节).
2.1 问题复杂性解析本文研究与作业执行时间固定的相关研究的区别, 主要在于执行时间的可变性, 这使得资源分配时面临的选择更加多元, 问题变得复杂.相较于执行时间可变的相关研究, 本文研究考虑了作业的多资源需求以及资源和技能的分类和分级, 这都为作业的调度带来了一定的困难.本文研究虽区别于上述现有研究, 但由于文中作业执行时间可变, 相当于作业有多个执行“模式”, 因此读者很可能将本文问题理解为一般的多模式调度问题.
本文研究与多模式调度问题的区别, 体现在模式数量的不同[1], 前者中作业模式数量很可能远大于后者的.本研究问题中, 若作业对关键技能的需求量rjsl=2及可满足该需求的技能水平|L′| =3(L′={l′|l′≥l}), 则作业可选择“模式”数为6;若作业的资源需求量增加, 如rjsl=3, 则“模式”数变为10.对于一般的多模式项目调度问题, 作业模式数一般较少, 如一些研究中的模式数为2.模式数量的增加, 导致整个项目中各作业间的模式组合数急剧膨胀, 从而给传统的采用模式搜索的算法带来了极大的挑战.
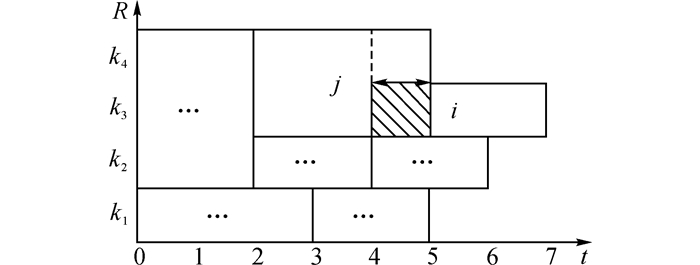
作业实际执行时间只有在确定分配的关键资源后才能确定, 这也是本文研究与多模式调度问题的不同之处.若事先确定其执行时间, 即作业的模式, 则可能会出现图 1所示的困境.对作业j进行调度, 按照现有多模式方法确定其执行时间为3个时间单位, 但j所需要的资源k3在时间段[4, 5]内被作业i占用(如图阴影斜线所示), 导致作业j无法在t=2时刻开始.实际情况可能是, 作业的实际执行时间和分配的资源有关, 资源k3的技能水平较高, 使得作业j的实际执行时间缩短为2个时间单位或者更小, 故作业j实际上可以在t=2时刻开始.这种情况会使得传统求解方法如模式搜索[15-17]在解码得到作业调度顺序和作业实际执行时间时, 很可能造成资源技能水平的浪费或者对作业的可开始执行时间产生误判, 从而使得解码质量欠佳.
|
图 1 作业执行时间可变示意图 Fig. 1 Modification duration of job's makespan |
因此, 针对多模式资源约束项目调度问题常用的求解方法, 直接用于求解本文研究问题很难得到较优的解.为解决本文研究问题带来的上述困难, 本文只对作业优先级进行搜索, 从而减少搜索空间提高搜索质量.在确定作业实际执行时间并进行调度时, 采用基于优先规则的关键资源决策启发式算法, 在避免资源技能水平被浪费的同时能够准确判断调度作业在某时刻是否可行.此外, 为进一步提高求解质量, 本文算法采用基于关键链的局域搜索算法对求解结果进行深度优化.
2.2 整体框架本文中作业优先级列表由遗传算法得到, 采用自然数编码方式, 两点交叉, 种群规模为50, 迭代次数为N=100.x(wλ)表示第λ代种群中第w个染色体, T(xwλ)和F(xwλ)分别表示相应调度方案目标函数值和个体xwλ的适应值, 当个体适应值取得最大值时, 目标函数值取得最小值, 即最优解;xbestλ表示第λ代群体中的最优解, 即当代最优解;xbestG表示算法运行至第λ代得到的全局最优解.算法步骤如下:
Step1:令λ=0, 最优解未变化代数M=0, 初始化染色体种群, 除2条染色体按照最迟结束和最早开始时间外, 其余染色体均随机生成.
Step2:将染色体xwλ转换为作业优先级列表AL, 作业的排列顺序即表示其优先级顺序.
Step3:调用关键资源决策启发式算法模块和局域搜索模块进行解码, 求得各染色体对应的调度方案的目标函数值T(xwλ)以及个体适应值F(xwλ), 此时xbestλ=minT(xwλ).若T(xbestλ≤T(xbestG, 则xbestG←xbestλ;否则, M←M+1.
Step4:若M=15, 则重新生成种群, M←0;若M < 15, 转step5.
Step5:依据适应值对种群中的个体采用轮盘赌方式进行选择操作, 选出所需个体.
Step6:对选出个体采用王万良[15]自适应方式进行交叉和变异操作, 得到新的种群, λ←λ+1.
Step7:若λ≤N, 则转step2;否则, 输出T(xbestG), 即为整个项目最小工期tT.
2.3 关键资源决策启发式算法在对作业进行调度时, 只有在确定作业的实际执行时间后, 才能得到在该时段内空闲的资源, 从而判断调度作业在该调度时刻是否可行.由于作业实际执行时间随为其分配的资源而变化, 故而需要先确定作业的关键资源分配.本文通过基于优先规则的串行调度方法来确定作业关键资源分配, 采用的4种优先规则分别为最小执行时间LDT(为作业分配最高效率的关键资源)、最小后续需求LSR(为作业分配后续未调度作业需求量最小的关键资源)、最长空闲时间LST(为作业分配在该作业标准时间段内空闲时间最大的资源)、随机需求ROD(为作业随机分配关键资源).通过关键路径法按照作业的标准执行时间tj求得作业j的tESTj和tLFTj.
Step1:从优先级列表AL中取出符合时序约束的作业j, 确定其关键资源需求rjs*l.
Step2:得到tESTj时的空闲资源集, Rs*={k|hs*kl=1}.若|Rs*| < rjs*l, 则转step3;若|Rs*|=rjs*l, 则转step5;若|Rs*| > rjs*l, 则转step4.
Step3:tESTj←tESTj+1, 转step2.
Step4:分别采用4种优先规则为作业j分配关键资源, 确定作业j相应的执行时间, 若分配的关键资源在该时段内空闲, 则该分配方式可行;否则, 该分配方式不可行.若4种分配方式中, 至少有一种可行, 则转step6;否则, 转step3.
Step5:由Rs*中所有关键资源确定作业j的实际执行时间, 若Rs*中关键资源在该时段内均空闲, 则step6;否则, 转step3.
Step6:由为作业j分配的关键资源确定taj, 调用最小费用—最大流[7]判断作业j是否可执行, 若是则转step7;否则, 转step3.
Step7:令tSTj=tESTj, 更新tFTj=tSTj+taj, tT=max{tT, tFTj}, AL=AL/j, 若|AL|≠0, 转step1;否则, 转step8.
Step8:输出项目工期, 算法终止.
2.4 局域搜索模块为提高2.2中算法的求解质量, 本文在其基础上结合局域搜索算法对得到的可能解作进一步的优化, 算法步骤如下:
Step1:初始化迭代次数iter=0, 禁忌集TL=ϕ, 输入可行调度FS以及相应目标值UB.
Step2:初始化重组集RC=ϕ, 调整集RA=ϕ, 由FS得到处在由关键路径法得到的关键链上的作业, 将执行时间可以缩短的关键作业加入到作业集CJ.
Step3:若|CJ|=0, 转step10;否则, 从CJ中取出执行时间缩短量, 即Δtaj最大的(若多个作业Δtaj相同, 则随机选取)作业j且j∉TL, 得到j所需的关键技能s*以及为其分配用于执行该技能的资源集R*.
Step4:以作业j为基准, 将在[tSTj, tFTj]范围内执行的作业加入重组集RC, 构建资源重组作业集.
Step6:得到k∉R*且mks* > mk*s*, k*∈R*, 将mks*作为作业j对技能s*的水平需求, 若RC包含其他关键作业j′, 则用当前为j′分配的关键资源水平作为j′对其关键技能的水平需求.
Step7:对重组集RC中作业按照更改技能水平需求后进行重新调度, 若RC中作业均可行, 记录a=tSTj及b=tFTj, 则更新作业的开始、结束、实际执行时间以及资源分配, 转step8;否则, FS不变, 将作业j加入禁忌集TL, 转step2.
Step8:若任意作业j″满足tSTj″∈[a, b]且j″∉RC或者tSTj″ > b, 则将j″加入调整集RA.
Step9:在保证原调度顺序条件下, 更新RA中作业的开始和结束时间, 得到新的调度FS′目标值UB′, iter←iter+1.若UB′ < UB, 则FS←FS′;否则, FS不变.
Step9:若iter未达到规定代数N, 转step2;否则, 转step10.
step10:输入得到的可行调度, 算法终止.
3 数值实验为验证算法的有效性, 本文采用对标准问题库PSPLIB改造后的算例进行测试.改造主要包括:1) 设定资源集R、技能集S、技能水平集L、资源柔性程度F, 其中F为所有资源具备的技能数之和与资源数和技能数乘积的比值, 即F=
| 表 1 20 jobs测试结果 Table 1 Results of 20 jobs |
| 表 2 30 jobs测试结果 Table 2 Results of 30 jobs |
| 表 3 60 jobs测试结果 Table 3 Results of 60 jobs |
| 表 4 90 jobs测试结果 Table 4 Results of 90 jobs |
| 表 5 120 jobs测试结果 Table 5 Results of 120 jobs |
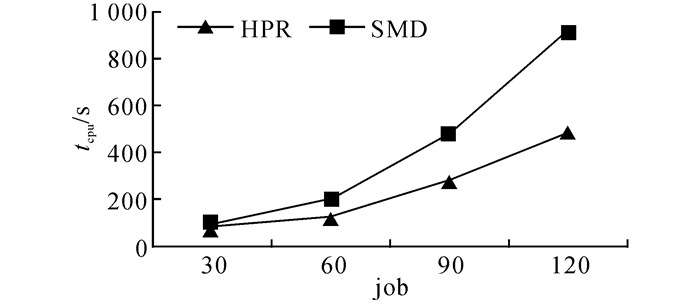
当小规模(20 jobs)算例时, 由表 1可知:在求解质量方面, 本文所采用算法HPR与CPLEX求得最优解或可行解的GHC=3.7%左右, 而多模式项目调度相关文献采用的模式搜索算法SMD与CPLEX所得最优解或可行解的差距甚大(GSC=12.5%左右);在CPU时间方面, HPR时间基本在23 s左右, 而CPLEX求解时间在6 000 s左右, 前者远优于后者.分析可知, HPR求解质量与CPLEX的差距在可接受范围, 但CPU时间远优于后者.大规模(30~120 jobs)算例时, CPLEX无法求出测试算例的可行解, HPR却可以求得较优解.由表 2~5可知, 在0.4、0.6、0.8任意资源柔性程度及30、60、90、120任意规模算例条件下, HPR求解质量均优于SMD, 且两者求解质量间的GSH随着问题规模增加而明显增大.SMD求解质量较差的原因, 一方面在于本文研究问题中作业可选“模式”明显多于一般多模式项目调度, 这降低了算法的搜索效率;另一方面, SMD解码时采用的指定模式的方式并不利于本文研究问题的解决, 本文研究问题中作业实际执行时间因分配的关键资源水平而变, 这有别于现有的多模式方式(如图 1分析).大规模算例条件下, 各算法运算时间如图 2所示, 综合可知, 本文采用的HPR算法在求解质量和求解速度方面均具有良好的性能.
|
图 2 各算法CPU时间 Fig. 2 CPU time of algorithms |
本文以带有技能水平的多技能资源约束项目调度问题为研究对象, 充分考虑了资源技能水平不同对作业实际执行时间的影响, 建立了相应的数学模型.针对该问题, 提出了基于遗传算法、启发式解码和局域搜索算法的混合算法.遗传算法以及基于优先规则的启发式解码提供了该问题的可行解, 局域搜索算法在可行解的基础上进一步提高了求解的质量.下一步研究可以针对资源均衡使用或者资源差异对作业质量造成的影响进行深入研究.
| [1] | BELLENGUEZ O, NETON E. Lower bounds for the multi-skill project scheduling problem with hierarchical levels of skills[M]. Berlin: Springer Berlin Heidelberg, 2005: 229-243. |
| [2] | BARZ C, KOLISCH R. Hierarchical multi-skill resource assignment in the telecommunications industry[J]. Production and Operations Management, 2014, 23(3): 489–503. DOI:10.1111/poms.12053 |
| [3] | HURKENS C A J. Incorporating the strength of MIP modeling in schedule construction[J]. RAIRO-Operations Research, 2009, 43(4): 409–420. DOI:10.1051/ro/2009026 |
| [4] | ESTELLON B, GARDI F, NOUIOUA K. High-performance local search for task scheduling with human resource allocation[C]//International Workshop on Enigneering Stochastic Local Search Algorithms. Berlin: Springer Berlin Heidelberg, 2009: 1-15. |
| [5] | CORDEAU J F, LAPORTE G, PASIN F, et al. Scheduling technicians and tasks in a telecommunications company[J]. Journal of Scheduling, 2010, 13(4): 393–409. DOI:10.1007/s10951-010-0188-7 |
| [6] | FIRAT M, HURKENS C A J. An improved MIP-based approach for a multi-skill workforce scheduling problem[J]. Journal of Scheduling, 2012, 15(3): 363–380. DOI:10.1007/s10951-011-0245-x |
| [7] |
喻小光, 战德臣, 聂兰顺, 等. 柔性资源约束的资源水平项目调度问题[J].
计算机集成制造系统, 2010, 16(9): 1967–1976.
YU Xiao-guang, ZHAN De-chen, NIE Lan-shun, et al. Flexible resource constrained resource leveling project scheduling problem[J]. Computer Integrated Manufacturing Systems, 2010, 16(9): 1967–1976. |
| [8] |
陈君兰, 叶春明. 柔性资源受限多项目调度的混沌粒子群算法研究[J].
计算机应用研究, 2013, 30(1): 117–120.
CHEN Jun-lan, YE Chun-ming. Chaos particle swarm optimization on flexible-resource constrained multi-project scheduling research[J]. Application Research of Computers, 2013, 30(1): 117–120. |
| [9] | VALLS V, PÉREZ Á, QUINTANILLA S. Skilled workforce scheduling in service centres[J]. European Journal of Operational Research, 2009, 193(3): 791–804. DOI:10.1016/j.ejor.2007.11.008 |
| [10] | HEIMERL C, KOLISCH R. Scheduling and staffing multiple projects with a multi-skilled workforce[J]. OR Spectrum, 2010, 32(2): 343–368. DOI:10.1007/s00291-009-0169-4 |
| [11] | CHEN J, ZHU J, ZHANG D. Multi-project scheduling problem with human resources based on dynamic programming and staff time coefficient[C]//Management Science & Engineering (ICMSE), 2014 International Conference on. Helsinki: IEEE, 2014: 1012-1018. |
| [12] | NABER A, KOLISCH R. MIP Models for resource-constrained project scheduling with flexible resource profiles[J]. European Journal of Operational Research, 2014, 239(2): 335–348. DOI:10.1016/j.ejor.2014.05.036 |
| [13] | FERNANDEZ V V, FRAMINAN J M. Integrated project scheduling and staff assignment with controllable processing times[J]. The Scientific World Journal, 2014, 2014(1): 1–16. |
| [14] |
周辅疆, 陈宏文, 王斌, 等. 改进柔性资源约束项目调度模型与粒子群算法[J].
火力与指挥控制, 2016, 41(1): 62–66.
ZHOU Fu-jiang, CHEN Hong-wen, WANG Bin, et al. Modified model of flexible resource-constrained multi-mode project scheduling problem and particle swarm optimization[J]. Fire Control & Command Control, 2016, 41(1): 62–66. |
| [15] | JARBOUI B, DAMAK N, SIARRY P, et al. A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems[J]. Applied Mathematics & Computation, 2008, 195(1): 299–308. |
| [16] | PETEGHEM V V, VANHOUCKE M. A genetic algorithm for the preemptive and non-preemptive multi-mode resource-constrained project scheduling problem[J]. European Journal of Operational Research, 2010, 201(2): 409–418. DOI:10.1016/j.ejor.2009.03.034 |
| [17] | PETEGHEM V V, VANHOUCKE M. An experimental investigation of metaheuristics for the multi-mode resource-constrained project scheduling problem on new dataset instances[J]. European Journal of Operational Research, 2014, 235(1): 62–72. DOI:10.1016/j.ejor.2013.10.012 |
| [18] | 王万良, 吴启迪. 生产调度智能算法及其应用[M]. 北京: 科学出版社, 2007: 15-21. |



