2. 展讯科技(杭州)有限公司, 浙江 杭州 310052
2. Spreadtrum Technology(Hangzhou) limited company, Hangzhou 310052, China
图像处理技术得到广泛应用, 图像的实时处理依赖于硬件加速的支持.一些实时性处理的应用对实时性的要求非常严格, 必须采用硬件加速的方法才可满足其需求[1-3].使用硬件方法来实现图像处理, 传统方式常采用数字信号处理器(digital signal processors, DSP)或专用集成电路(application specificintegrated circuits, ASIC), 但是综合考虑速度要求与设计灵活性使得采用现场可编程门阵列(field programmable gate array, FPGA)进行硬件加速的方法得到广泛使用[4-5].与DSP的指令串行处理方式相比, FPGA内部可以对信号并行处理, 得到更高的处理速度.ASIC处理方式难以适应算法的变动, 一旦算法发生改变, 芯片需要重新设计生产, 灵活性较差;FPGA的可配置性为设计提供更好的灵活性.也有研究者使用专用指令集处理器(application special instruction processor, ASIP)的矢量化处理方式, 来实现多个图像处理算法的功能.ASIP方式的灵活性与并行度均介于DSP与ASIC之间, 但是ASIP的设计难度大, 对设计者的综合要求高, 设计周期长.
在图像处理中, 通常需要对输入图像进行高斯滤波、中值滤波、顺序滤波或卷积运算等预处理, 其中对高斯滤波与中值滤波方法的选用最为广泛.例如, 杨帆等[6]将快速中值滤波算法与Sobel算子边缘检测算法相结合对图像处理系统进行了建模, 并将FPGA实现结果与DSP的实现结果进行了性能的对比.Kalomiros等[4]将基于3×3模板的高斯滤波器模块和基于Prewitt算子或Sobel算子的图像边缘检测模块相结合, 对基于FPGA的硬件/软件系统进行了设计和评估, 同时对硬件架构进行了分析, 并对处理效果进行了比对.付昱强[7]则对多种图像处理的预处理算法:中值滤波、快速中值滤波、顺序滤波、卷积运算和高斯滤波算法进行了统一建模与对比分析.
传统的高斯滤波器设计方法, 需要3个模块的设计:方形窗产生模块、行列计算模块和高斯滤波算法模块.杨帆等[6-7]对方形窗产生模块的设计方法和硬件架构进行了介绍, 付昱强等[7]对行列计数器的功能和设计方法进行了研究.Kalomiros等[4, 7]提出了高斯滤波算法模块的硬件设计方法.在滤波算法模块, 需要先计算乘法, 再进行累加求和, 最后进行除法计算.付昱强[7]采用移位操作替代乘法、除法计算, 再对加数进行相加求和.相加过程中使用8个全加器, 同时采用4层加法逻辑来完成9个加数的累加.但全加器的进位链较长[8-12], 产生较大的逻辑延时, 4个层次的加法逻辑将产生更大的逻辑延时.
针对以上设计的局限性, 本文引入保留进位加法器(carry save adder, CSA)结构[13-14]、基于多路选择器(MUX)的4-2压缩器[13-14]、加数压缩的树型结构[13-14]对9个加数进行压缩.最后只需采用1个全加器来完成最终求和, 降低了逻辑延时.
1 高斯滤波器原理图像在传输过程与获取过程中, 容易受到干扰而引入噪声, 2种典型的噪声如椒盐噪声和高斯噪声.椒盐噪声表现为幅值大小相同, 且随机分布于图像中不同的点;高斯噪声表现为整个图像中都存在, 幅值强度按照高斯分布函数进行分布.因此需要通过平滑处理对图像进行噪声抑制, 增强图像质量.常用的平滑处理方法分为线性平滑处理(如高斯滤波, 均值滤波等)与非线性平滑处理(如中值滤波, 顺序滤波等).线性平滑滤波方法是一种使用中心点及其邻域的线性组合来取代中心点像素值的方法.高斯滤波器也是一种低通滤波器, 可以对表现为高频特点的噪声产生很好的滤波效果.
1.1 高斯滤波定义与性质在图像处理中, 一般采用二维高斯分布来对高斯滤波器进行定义.在二维平面上高斯分布函数的数学定义式与高斯滤波算法定义式分别为
| $ G\left( {x,y} \right) = \frac{1}{{2{\rm{\pi }}{\sigma ^2}}}{\rm{exp}}\left( {\frac{{ - {x^2} + {y^2}}}{{2{\sigma ^2}}}} \right). $ | (1) |
式中:σ为高斯函数的标准差, x, y为二维坐标系中横坐标与纵坐标;
| $ {{f}_{\text{out}}}\left( x, y \right)=G\left( x, y \right)*{{f}_{\text{in}}}\left( x, y \right). $ | (2) |
式中:G(x, y)用式(1) 替换, fin(x, y)为输入图像, fout(x, y)为滤波后输出图像, *为卷积运算符.
二维高斯函数具备2个重要的特性.首先, 二维高斯函数具有旋转对称性.这保证了高斯滤波对任何一个方向的平滑程度相同.由于一幅图像的边缘方向事先不确定, 滤波过程中不能确定哪一个方向需要比另一个方向有更多的平滑.旋转对称性保证了滤波后的结果不会使后续边缘检测偏向于某一个方向.其次, 高斯函数是单值函数, 高斯函数的函数值随着邻域像素点与中心点的距离单调递减, 邻域像素点离中心点越远, 其权值就越小.这样的性质可以保证平滑运算图像的失真小.
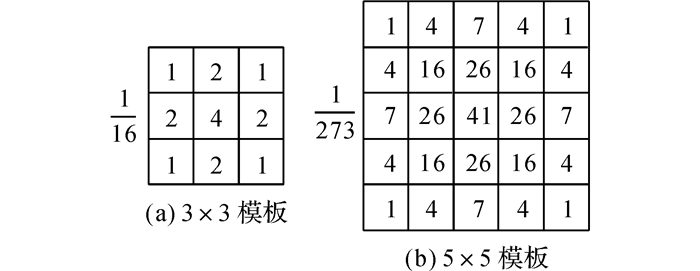
1.2 高斯滤波计算流程在实际处理中, 为了便于硬件计算和处理, 采用高斯模板来简化计算, 使用中心点以及中心点的邻域进行相应的卷积计算.常用的卷积模板包含3×3模板、5×5模板, 模板参数也各有差异, 如图 1所示列出2种常用的模板以作参考.
|
图 1 2种常用的高斯滤波模板 Fig. 1 2 kinds of commonly used Gaussian filter kernel |
杨帆等[6-7, 15]都采用3×3模板对中值滤波进行处理.付昱强[7]指出采用3×3模板进行高斯处理不仅可以获得与采用5×5模板相当的效果, 同时可以节省更多的硬件资源.所以传统的高斯滤波器[4, 7]硬件设计中均选用3×3模板, 本文以3×3模板作为核心来进行优化改进.经过简化后, 对输入图像进行高斯滤波的运算示意图如图 2所示.

|
图 2 基于3×3模板的高斯滤波算法 Fig. 2 Gaussian filter algorithm based on 3×3 kernel |
算法过程需要进行9次乘法运算, 再对9个乘积进行求和, 最后作除法得到输出结果.对于5×5的模板, 需要进行25次乘法运算, 计算25个数的和, 最后进行除法运算.在设计过程中, 还需要考虑发生在图像边缘上的情况.对于1个M×N(M行, N列)的图像而言, 由于第1列(或最后1列)没有左邻域(或右邻域), 取不到3×3窗, 无法进行滤波运算.为了使输出图像大小与输入图像大小保持一致, 付昱强[7]直接将输出设为0.同理, 第一行(或最后一行)没有上邻域(或下邻域), 因此第一行(或最后一行)的输出直接设为0.中间各点的输出值, 按照图 2方式计算得到.
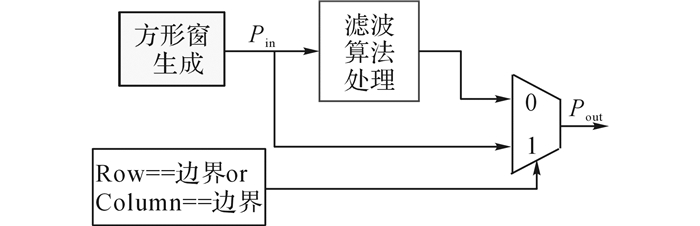
2 传统高斯滤波器结构对于高斯滤波器, 设计时包含3个模块:方形窗生成模块、滤波算法模块和行列计算控制模块, 整体硬件结构如图 3所示.
|
图 3 高斯滤波器整体硬件流程 Fig. 3 Overall hardware structure of Gaussian filter |
随着滤波处理中心点的移动, 模板需要跟随一起滑动.因此设计一个方形窗生成模块, 以达成同一时刻取到方形窗中的3×3个像素值, 杨帆等[6]提出了一种方形窗生成模块的硬件架构图.方形窗中数据通路的流程示意如图 4所示, 需要设计2个深度为M的同步时钟先进先出(first in first out, FIFO).

|
图 4 基于3×3模板的高斯滤波算法处理硬件流程 Fig. 4 Hardware structure of Gaussian filter calculations based on 3×3 kernel |
行列计算控制模块用来判断当前处理状态是否处在行或列的边缘, 起到控制作用.滤波算法模块完成图 2所示的运算功能.在3个模块中, 在滤波算法模块[4, 7]是整个滤波器的核心模块.在滤波运算模块中, 共使用了9个乘法器、8个全加器和一个移位寄存器.信号在关键路径上需要经过1个乘法器、4个全加器、1个移位寄存器(完成除法运算)才可得出最终输出信号Pout.
由于乘法器占用的面积较大, 消耗的路径延时较多.本文结合3×3模板的特点, 依次采用移位寄存器替换乘法器.模板值为1对应于原始数据, 模板值为2对应于左移1位, 模板值为4对应于左移2位.输入为无符号数8位像素值, 可以将左移后的输出结果处理为10位(避免移位后的溢出)来做后续加法运算处理.经过移位处理后仍然将产生9个加数, 依次累加求和得到12位的输出, 再经过移位寄存器右移4位(忽略低4位的影响)得到滤波结果.
对于5×5模板, 共有1、4、7、16、26、41共6种不同的数.为避免使用乘法器, 可以将7拆分为4+2+1, 对应于2个移位操作与一个原始数据, 分别为左移2、1位, 产生3个加数.26可以拆分为16+8+2, 对应于3个移位操作, 分别为左移4、3、1位, 产生3个加数.对于数值41可以拆分为32+8+1, 对应产生3个加数.最终得到43个加数, 再做后续处理得到累加结果.在进行除以273操作时, 不适合采用移位操作来实现除法器.可以对除数进行直接等效转换, 再采用乘法和移位操作来实现.本例中, 除以273操作可以通过被除数乘上240, 再除以65 536(右移16位)来实现.由于乘法器的逻辑延时较长, 此时可以在乘法器之前插入一级流水线以减小关键路径.
3 改进高斯滤波器 3.1 CSA结构CSA又称为3-2压缩器, 按照3:2的压缩比对加数的个数进行压缩.CSA的基本单元是1个1 bit的单元, 输入为3个权值(20)一致的1 bit数.输出分别为2个1 bit的数:1个1 bit的伪和Sum, 权重与输入一致;另一个为1 bit的进位Carry, 权值(21)比输入大.计算的布尔表达式为
| $ \text{Sum}={{A}_{1}}\oplus {{A}_{2}}\oplus {{A}_{3}}, $ | (3) |
| $ \text{Carry}={{A}_{1}}{{A}_{2}}+{{A}_{1}}{{A}_{3}}+{{A}_{2}}{{A}_{3}}. $ | (4) |
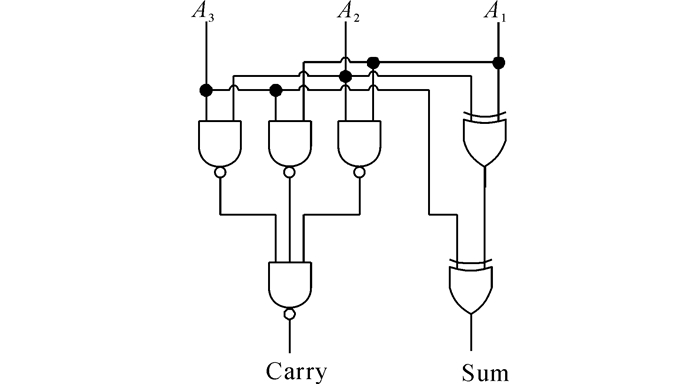
式中:A1、A2、A3为3个1 bit的输入数.其中, 1 bit的CSA电路结构如图 5所示.
|
图 5 基于逻辑门的1 bit CSA电路结构 Fig. 5 CSA structure of 1 bit based on logic gates |
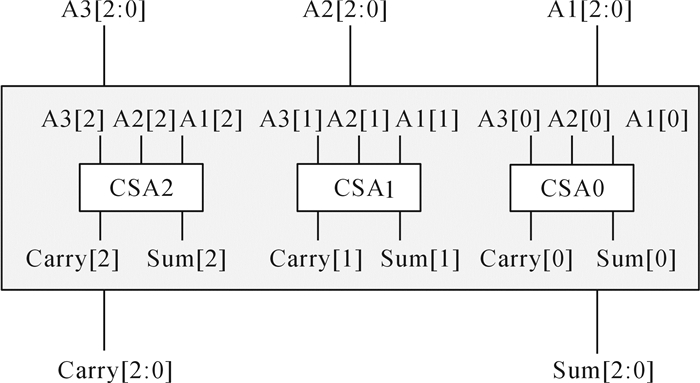
以1 bit的CSA为基本单元可以实现多位宽的CSA电路.以3 bits的CSA电路为例, 采用3个1 bit的CSA基本单元, 并行计算即可得到2个位宽分别为3 bits的Sum和Carry, 电路结构如图 6所示.
|
图 6 基于1 bit CSA的3 bits CSA电路结构 Fig. 6 CSA structure of 3 bits based on CSA structure of 1 bit |
一个多位的CSA电路只需占用2个逻辑门的延时, 比一个多位的全加器进位链上的延时小得多.同时CSA结构的电路结构规整, 使用的逻辑门少, 节省硬件资源.
3.2 4-2压缩器结构运用4-2压缩器可以达到4:2的压缩比, 将4个输入加数压缩为2个输出结果.4-2压缩器又称为(5, 3) 计数器, 5个输入分别为A4、A3、A2、A1和Cin, 输出为伪和Sum、进位Carry和进位输出Cout.5个输入与输出Sum权值(20)相同, 输出Carry的权值(21)比输入高, 进位输出Cout的权值与Carry相同.
一种启发式的方法是直接采用2个CSA基本单元级联来实现4-2压缩器.计算的布尔表达式如下:
| $ \text{Cout}={{A}_{4}}{{A}_{3}}+{{A}_{4}}{{A}_{2}}+{{A}_{3}}{{A}_{2}}, $ | (5) |
| $ \text{Sum}=({{A}_{4}}\oplus {{A}_{3}}\oplus {{A}_{2}})\oplus {{A}_{1}}\oplus \text{Cin}, $ | (6) |
| $ \text{Carry}=({{A}_{4}}\oplus {{A}_{3}}\oplus {{A}_{2}}){{A}_{1}}+({{A}_{4}}\oplus {{A}_{3}}\oplus {{A}_{2}})\text{Cin}+{{A}_{1}}\text{Cin}. $ | (7) |
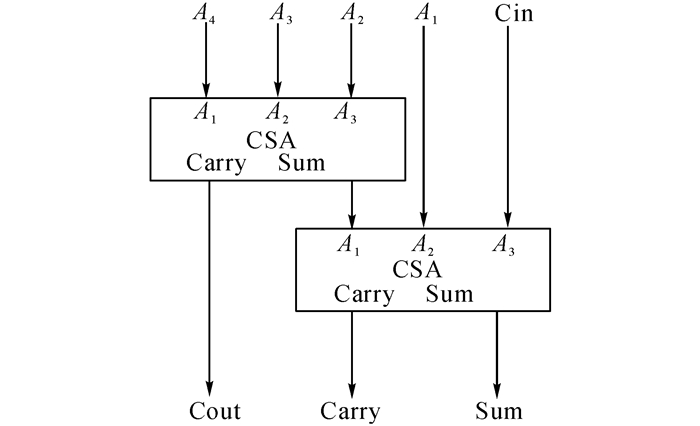
采用2个CSA基本单元级联来实现的4-2压缩器电路结构如图 7所示.
|
图 7 2级1 bit CSA级联的1 bit 4-2压缩器 Fig. 7 4-2 compressor of 1 bit based on cascade of CSA |
另一种实现方法是基于MUX的4-2压缩器.对布尔表达式(5-7) 进行等价性变换可以得到基于MUX的4-2压缩器的布尔表达式:
| $ \text{Cout}=({{A}_{4}}\oplus {{A}_{3}}){{A}_{2}}+(\overline{{{A}_{4}}\oplus {{A}_{3}}}){{A}_{4}}, $ | (8) |
| $ \text{Sum}=({{A}_{4}}\oplus {{A}_{3}}\oplus {{A}_{2}})\oplus {{A}_{1}}\oplus \text{Cin}, $ | (9) |
| $ \begin{align} &\mathit{C}\text{arry}=({{A}_{4}}\oplus {{A}_{3}}\oplus {{A}_{2}}\oplus {{A}_{1}})\text{Cin}+ \\ &(\overline{{{A}_{4}}\oplus {{A}_{3}}\oplus {{A}_{2}}\oplus {{A}_{1}}}){{A}_{1}}. \\ \end{align} $ | (10) |
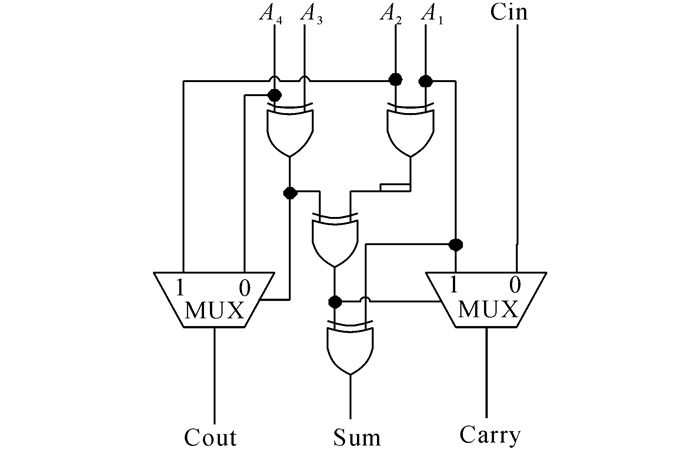
基于MUX的4-2压缩器电路结构如图 8所示.
|
图 8 基于MUX的1 bit4-2压缩器 Fig. 8 4-2 compressor of 1 bit based on 2 MUX |
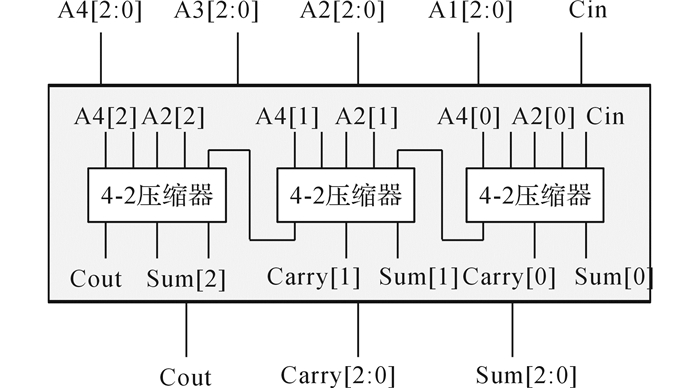
采用1位的4-2压缩器基本单元可以构建多位4-2压缩器.以3 bits的4-2压缩器为例, 其电路结构如图 9所示.设计过程中需要注意Cout的权值与Carry[2]的权值相同.
|
图 9 基于1 bit 4-2压缩器的3 bits 4-2压缩器 Fig. 9 4-2 compressor of 3 bits based on 4-2 compressor of 1 bit |
设计1个1 bit的CSA需要采用6个逻辑门, 采用2个CSA级联设计的4-2压缩器共需要12个逻辑门.而基于MUX的4-2压缩器使用了4个逻辑门和2个2选1的MUX, 共使用了6个逻辑单元.基于MUX的4-2压缩器与基于CSA级联的4-2压缩器相比, 基于MUX的4-2压缩器可以得到更短的路径延迟, 缩短关键路径上的延时.因此在设计中将选用基于MUX的4-2压缩器作为多位4-2压缩器设计中的基本单元.
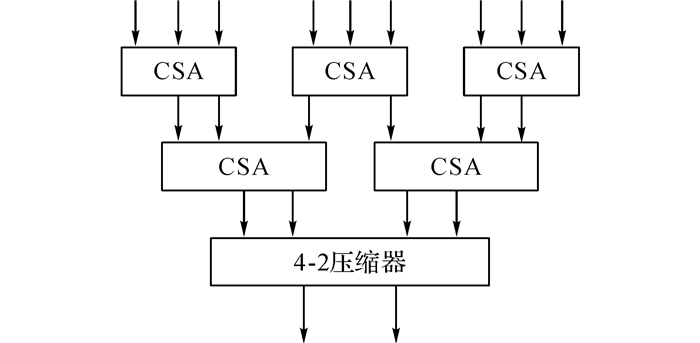
3.3 树型压缩结构在传统的高斯滤波器设计中, 高斯滤波算法模块中组合逻辑电路部分C2(见图 4), 使用了7个全加器.这种设计方法不仅消耗了较多的硬件资源, 同时C2电路部分的组合逻辑延时将是3个全加器的延时之和.考虑到CSA结构和4-2压缩器的逻辑延时较短, 电路逻辑简单, 非常适合用来进行加数的压缩, 因此采用CSA与基于MUX的4-2压缩器来构建如图 10所示的树型压缩结构.
|
图 10 CSA与4-2压缩器相结合的加数压缩树型结构 Fig. 10 Tree structure for compressing attends based on CSA structure and 4-2 compressor structure |
采用该树型结构替换C2电路部分, 由于该树型结构简单、对称性好且易于实现, 与只采用CSA结构的Wallace Tree(华莱士树)型[16]结构相比, 这种混合树型结构可以获得更小的逻辑延时.
4 实验结果与分析采用matlab工具对高斯滤波的模板参数进行仿真, 如图 11所示.
|
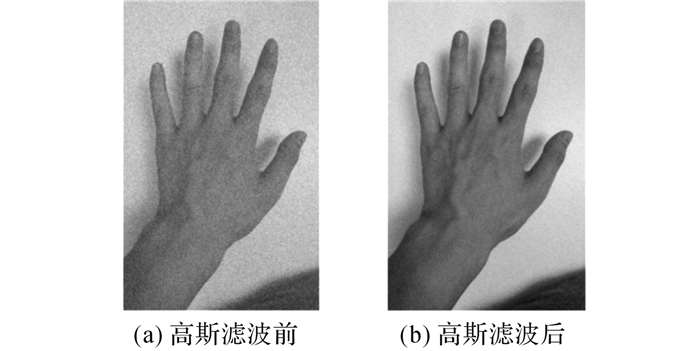
图 11 高斯滤波前后人手图像对比 Fig. 11 Comparison of hand images before and after Gaussian filter |
左图是经过对原始灰度图像添加均值为0, 方差为20的高斯白噪声后得到, 右图是采用3×3模板的高斯滤波器对包含噪声的图像进行滤波后得到的结果.高斯滤波器模板大小由纹理的尺度决定, 尺度较小的适合选择较小的模板, 尺度较大的适合选择较大的模板.由于人手的纹理比较多且尺度较小, 因此可以选用3×3模板.滤波前图像的峰值信噪比(peak signal to noise ratio, PSNR)为22.11, 滤波后图像PSNR=30.42.实验表明, 经过高斯滤波处理后, 可以有效降低噪声, 并使手上的纹理更加清晰可见, 将有利于进行人手识别.
不同的全加器实现方法消耗的逻辑延时与占用的面积各有不同, 表 1中给出5种全加器设计方法的逻辑延时复杂度、消耗面积复杂度与加数位宽的关系.对于n位的全加器, 采用行波进位加法器(carry ripple adder[8], CRA, )面积占用复杂度为O(n), 逻辑延时复杂度为O(n).采用超前进位加法器(carry look-ahead Adder[9], CLA)结构可以有效地缩短进位链, 获得更小的逻辑延时O(log (n));但是电路结构规整性下降, 使电路的面积消耗增大为O(n·log (n)).如果将Brent-Kung[10]结构(brent-kung adder, BKA)插入到全加器中, 可以进一步优化, 获得逻辑延时与面积消耗分别为2log (n)、nlog (n)的全加器电路结构.另外进位选择加法器(carry-select adder[11], CSA_SEL)和, 进位跳位加法器(carry-skip adder[12], CSA_SKIP)两者均占用面积O(n), 逻辑延时O(
| 表 1 5种全加器逻辑延时与面积消耗复杂度比较 Table 1 Comparison complexity of logic delay and area consumption between 5 kinds of full adders |
本次实验采用Verilog语言进行硬件电路描述, 并使用ISE14.3进行逻辑综合.选用Xilinx公司的Virtex-7进行综合, Target Device设置为xc7vx330v-3-ffg1157.并调用Macro Statistics(静态宏单元)中的Adders/Subtractors(加法器/减法器)来实现加法.对于全加器的调用与综合方法, 不同的综合工具选用的实现方法也有区别.例如, Synopsys公司的Design Compiler工具, 在电路综合时可以设置是否调用Design Ware中的全加器电路结构.而Cadence公司的RTL Compiler工具在综合时可以设置是否调用Chip Ware中全加器电路结构.综合策略的差异, 也会带来全加器性能与面积的差异.
实验结果(如表 2所示)表明, 在使用3×3模板的情况下:与中值滤波[6]相比, 本文结构有更小的逻辑延时, 中值滤波使用了21个比较器(本质上比较器就是全加器), 而本文结构只使用1个全加器, 节省了宏单元;与传统高斯滤波结构[7]相比, 传统结构逻辑延时为1.441 ns, 本文电路结构只需0.973 ns, 逻辑延时缩小了32.48%, 同时将加法器宏单元调用数目从8个降为1个.节省下来的宏单元, 可以为预处理设计之后的边缘检测模块及其他图像处理模块提供更大的设计自由度.在FPGA中, 加法器、乘法器等宏单元的数量有限, 在综合时一般会优先使用宏单元, 在宏单元不足的情况下使用LUT配置乘法器.从设计者的角度考虑, 宏单元相较于LUT资源更为宝贵.
| 表 2 在2种模板尺度下中值滤波、高斯滤波与本文方法硬件实现结果比较 Table 2 Hardware implementation results comparison between median filter, Gauss filter and this paper's method under 2 kinds of kernel |
结合乘法拆分替换乘法器、除数直接等效转换设计除法器的方法, 可以很好地将本文提出的加数压缩电路结构应用到5×5模板的情形.但3×3模板比5×5模板占用更少的硬件资源, 有更小的逻辑延时, 从硬件设计的角度考虑, 应优先选择3×3模板完成设计.
5 结语本文通过分析传统高斯滤波器结构中存在的局限性, 最终确定由CSA结构、基于MUX的4-2压缩器和混合型加数压缩树型结构替换传统设计中的3层全加器逻辑, 从电路速度和占用资源2方面对传统滤波器进行了优化, 同时对该方法的适应性进行了简要讨论.在有高并行度要求的目标检测算法中, 预处理的高斯滤波模块需要设计多份以满足并行要求, 因此对宏单元的节省与复用就显得尤其重要.采用新的架构设计方法之后, 加快了高斯滤波算法模块的计算速度.实验表明, 新的电路设计方法可以将逻辑延时缩小32.48%.同时将调用的加法器宏单元数目从8个降为1个, 可以为后续图像处理模块提供更大的设计自由度.
| [1] | DRAPER B A, BEVERIDGE J R, BOHM A P W, ROSS C, et al. Accelerated image processing on FPGAs[J]. IEEE Transactions on Image Processing, 2003, 12(12): 1543–1551. DOI:10.1109/TIP.2003.819226 |
| [2] | VEGA-RODRIGUEZ M A, SANCHEZ-PEREZ J M, GOMEZ-PULIDO J.A. Real time image processing with reconfigurable hardware[C]//8th IEEE International Conference on Electronics, Circuits and Systems. Malta: IEEE, 2001: 213-216. |
| [3] | LEESER M L, MILLER S, YU H. Smart camera based on reconfigurable hardware enables diverse real time applications[C]// Proceedings of the 12th Annual IEEE Symposium on Field-Programmable Custom Computing Machines. Napa: IEEE, 2004: 147-155. |
| [4] | KALOMIROS J A, LYGOURAS J. Design and evaluation of a hardware/software FPGA-based system for fast image processing[J]. Microprocessors and Microsystems, 2008, 32(2): 95–106. DOI:10.1016/j.micpro.2007.09.001 |
| [5] | LEE P S, LEE C S, JU H L. Development of FPGA-based digital signal processing system for radiation spectroscopy[J]. Radiation Measurements, 2013, 48(1): 12–17. |
| [6] |
杨帆, 张皓, 马新文, 等. 基于FPGA的图像处理系统[J]. 华中科技大学学报: 自然科学版, 2015, 43(2): 119-123.
YANG Fan, ZHANG Hao, MA Xin-wen, JIANG Yong, et al. Image processing system based on FPGA[J]. Journal of Huazhong University of Science & Technology :Natural Science Edition, 2015, 43(2): 119-123. http://www.cqvip.com/QK/90344A/201502/665303299.html |
| [7] |
付昱强. 基于FPGA的图像算法的研究与硬件实现[D]. 南昌: 南昌大学, 2006.
FU Yu-qiang. Research and hardware design of image processing algorithms based on FPGA[D]. Nanchang: Nanchang University, 2006. |
| [8] | NIDHI, GURINDERPAL S. Efficient design of ripple carry adder and carry skip adder with low quantum cost and low power consumption[J]. International Journal of Engineering Research and Applications, 2014, 4(7): 247–251. |
| [9] | EFSTATHIOU C, OWDA Z, TSIATOUHAS Y. New high-speed multioutput carry look-ahead adders[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2013, 60(10): 667–671. DOI:10.1109/TCSII.2013.2278088 |
| [10] | ANAND V, VIJAYAKUMAR V. Optimizing area of vedic multiplier using Brent-Kung adder[J]. Research Journal of Pharmaceutical, Biological and Chemical Sciences, 2016, 7(3): 1178–1185. |
| [11] | PRIYADHARSHINI M, THIRUVENI M. Performance evaluation of carry select adder-review[J]. International Journal of Engineering Sciences & Research Technology, 2014, 3(11): 469–475. |
| [12] | VARUN P S, SHIV D, MANISH R. Efficient carry skip Adder design using full adder and carry skip block based on reversible Logic[J]. American Journal of Engineering Research, 2015, 4(12): 95–100. |
| [13] |
赵忠明, 林正浩. 一种改进的Wallace树型乘法器的设计[J].
电子设计应用, 2006(8): 113–116.
ZHAO Zhong-ming, LIN Zheng-hao. Optimizing multiplier design and implementation based on optimizing Wallace tree[J]. Electronic Design & Application, 2006(8): 113–116. |
| [14] |
李军强, 李东生, 李奕磊, 等. 32×32高速乘法器的设计与实现[J].
微电子学与计算机, 2009, 26(12): 23–26.
LI Jun-qiang, LI Dong-sheng, LI Yi-lei, et al. 32×32 High-speed Multiplier Design and Implementation[J]. Microelectronics & Computer, 2009, 26(12): 23–26. |
| [15] |
王红君, 施楠, 赵辉, 等. 改进中值滤波方法的图像预处理技术[J].
计算机系统应用, 2015, 24(5): 237–240.
WANG Hong-jun, SHI Nan, ZHAO Hui, et al. Image preprocessing technology based on improved median filter[J]. Computer Systems & Applications, 2015, 24(5): 237–240. |
| [16] | ITOH N, NAEMURA Y, MAKINO H. A 600-MHz 54×54-bit multiplier with rectangular-styled Wallace tree[J]. IEEE Journal of Solid-State Circuits, 2001, 36(2): 249–257. DOI:10.1109/4.902765 |



