2. 南京林业大学 机械电子工程学院, 江苏 南京 210094
2. College of Electronic and Mechanical Engineering, Nanjing Forestry University, Nanjing 210094, China
传统的火炮反后坐装置是利用制退机实现被动的后坐缓冲, 以保证火炮射击稳定性及提高射击精度.火炮制退机多采用节制杆式, 以制退液为缓冲介质, 当节制杆和液流孔的结构尺寸以及制退液型号确定后, 所产生的输出阻尼力也随之确定下来[1], 无法满足现代战争对火炮技术性能所提出的要求.
基于磁流变液为工作介质的磁流变缓冲器, 具有输出阻尼力可调的优势, 使之广泛应用于车辆悬架、起落架、舰船隔振、建筑桥梁抗震等缓冲减振工程应用领域中[2-8], 同时, 磁流变缓冲器在武器系统中, 尤其是在反后坐系统中的应用具有广阔的前景[9-10].其中, 美国弗吉尼亚理工大学[11]将磁流变缓冲器用于舰炮反后坐系统中并进行了靶场试验, 得到了满意的后坐缓冲效果;Bajkowski等[12-13]研究磁流变缓冲器用于AKMS卡宾枪的后坐系统中的缓冲性能;Singh等[14]对火炮反后坐系统的磁流变缓冲器进行优化分析.Mao等[15-16]对高冲击载荷下的磁流变缓冲器的动态特性及控制策略进行了研究分析.
上述研究为磁流变缓冲器用于反后坐装置等工程问题提供了宝贵的借鉴, 但这些缓冲器大多是采用单级线圈或者多级串联线圈形式, 阻尼通道内的磁场强度随同一电流一致变化.虽有Yang等[17-18]出于减小响应时间考虑而采用并联式线圈结构磁流变缓冲器, 但在缓冲器工作时仍对各线圈施加等值电流, 并未真正发挥出并联式磁流变缓冲器各线圈独立可控的优势:不同工作线圈的组合、各线圈不同电流大小、不同加载时间等都会在阻尼通道中产生灵活多变的磁场分布, 从而得到不同的阻尼特性.
本文以磁流变缓冲器在火炮反后坐缓冲系统中的应用为研究背景, 设计了长行程多阶并联式磁流变缓冲器, 并通过试验比较不同线圈组合工作模式下缓冲器的缓冲特性, 旨在得到在阻尼通道轴向几何维度上不同分布规律下的磁场对缓冲性能的影响, 分析比较了传统串联形式与并联结构的缓冲特性.同时利用电流逐级加载方式分析时间维度上磁场的变化对输出阻尼力的影响, 并从可调系数角度分析了磁流变缓冲器的可控性.
1 缓冲系统动力学分析 1.1 多阶并联式缓冲器结构火炮在发射时膛压能在几个毫秒内达到几百兆帕.磁流变缓冲器在发射瞬间承受很大的后坐冲击力, 因此要求缓冲器能够提供与之相当的阻尼力来减缓发射冲击力.采用多级线圈可以增加磁流变液工作间隙的有效长度, 使磁流变缓冲器的输出阻尼力调节范围得以提高.为便于冲击试验研究, 简化了真实火炮系统中的复进弹簧等装置, 且根据试验台冲击条件, 所设计的缓冲器在后坐速度达5 m/s时, 其最大目标阻尼力为8 kN.设计的四级并联式磁流变缓冲器试验样机, 如图 1所示, 其主要尺寸和相关参数如表 1所示.选用的磁流变液体为宁波杉工集团生产的SG-MRF2305液体, 活塞采用四级线圈并联的方式, 每级线圈500匝, 其中相邻线圈的绕向必须为相反, 以保证产生的磁场不会因为磁场方向相反而抵消, 允许通过的最大电流值为2 A.
| 表 1 磁流变缓冲器及磁流变液的主要参数 Table 1 Main parameters of MR damper and MR fluid |

|
图 1 四级并联式磁流变缓冲器结构图 Fig. 1 Schematic diagram of four-stage MR damper |
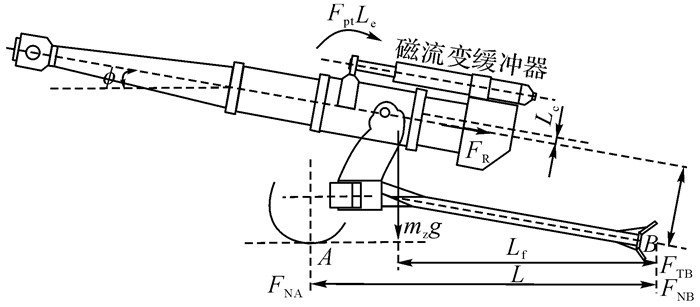
选取火炮后坐部分为研究对象, 对发射时后坐部分进行受力分析, 如图 2所示.反后坐装置所提供的后坐阻力FR主要包括驻退机阻力Fh、复进机阻力Ff、运动部件之间的摩擦力Fμ以及后坐部分重力分力所构成.
| $ {{F}_{\text{R}}}={{F}_{\text{h}}}+{{F}_{\text{f}}}+\left( {{F}_{\mu }}-{{m}_{\text{z}}}g\sin \varphi \right). $ | (1) |
|
图 2 火炮后坐缓冲系统结构图 Fig. 2 Structural diagram of recoil system |
式中:mz为后坐部分质量, g为重力加速度, φ为火炮射角.
阻尼弹簧式的反后坐过程可用单自由度系统进行描述, 其运动微分方程为
| $ {{m}_{\text{z}}}\ddot{x}=-{{F}_{\text{MR}}}\left( x, \dot{x} \right)-\mu {{m}_{\text{z}}}g\text{cos}\varphi +{{m}_{\text{z}}}g\text{sin}\varphi +{{F}_{\text{pt}}}\left( t \right). $ | (2) |
式中:FMR为磁流变缓冲器所提供的阻力, μ为炮身与摇架之间的摩擦系数, Fpt(t)为火药燃烧所产生的随时间t变化的冲击力.
不考虑火炮复进过程, 且根据后坐过程火药燃烧的瞬时性, 冲击力对后坐部分的作用可以用阶跃为vs的速度阶跃冲击来近似,则运动方程为
| $ {{m}_{\text{z}}}\ddot{x}=-{{F}_{\text{MR}}}\left( x, \dot{x} \right)-\mu {{m}_{\text{z}}}g\text{cos}\varphi +{{m}_{\text{z}}}g\text{sin}\varphi =-{{F}_{\text{R}}}\left( x, \dot{x} \right).~ $ | (3) |
初始条件:
| $ x\left( 0 \right)=0, \text{ }\dot{x}\left( 0 \right)={{v}_{s}}. $ | (4) |
在对缓冲系统的抗冲击性能进行研究时, 通常以2个泛函指标J1和J2来评价系统性能:最大后坐位移、最大后坐加速度或者阻尼力.
| $ \left. \begin{align} &{{J}_{1}}=\underset{t}{\mathop{\text{max}}}\, |x\left( t \right)|, \\ &{{J}_{2}}=\underset{t}{\mathop{\text{max}}}\, |\ddot{x}\left( t \right)|. \\ \end{align} \right\} $ | (5) |
以后坐位移为约束条件, 则应保证后坐阻尼力最小.控制后坐阻尼力在后坐过程中达到峰值点后继续维持恒定值, 力值变化曲线呈“平台效应”, 则可在后坐位移约束下获取最佳冲击缓冲效果.
2 磁流变缓冲器冲击试验分析 2.1 冲击试验装置为了证实新结构形式的火炮磁流变缓冲器的可控性, 利用已搭建的含磁流变缓冲器的冲击试验台架[19], 进行缓冲器的抗冲击试验, 如图 3所示.

|
图 3 冲击试验平台 Fig. 3 Impact test platform |
该冲击试验台以火药在密闭腔内燃烧产生瞬间压力作为冲击源, 推动磁流变缓冲器沿光滑导轨作后坐运动.为了更好地模拟火炮发射时的后坐冲击速度, 将磁流变缓冲器与运动质量块相固连, 在冲击载荷下一同沿导轨运动.由于火炮的不同射角对于磁流变缓冲器的可控性能分析没有太大影响, 其所引起的附加后坐阻力可以与后坐系统的摩擦力项一并考虑, 因此, 该试验平台仅进行水平冲击载荷的试验.试验系统主要由工控机、dSPACE实时仿真系统、电流控制器及冲击试验台架组成.测试数据包括阻尼力信号、后坐速度信号以及后坐位移信号.
2.2 冲击试验结果为保证每组试验方案的冲击能量相同, 统一采用6 g火药量.对并联式磁流变缓冲器各线圈施加不同电流值, 分别进行等值电流加载、组合电流加载及延时加载试验.
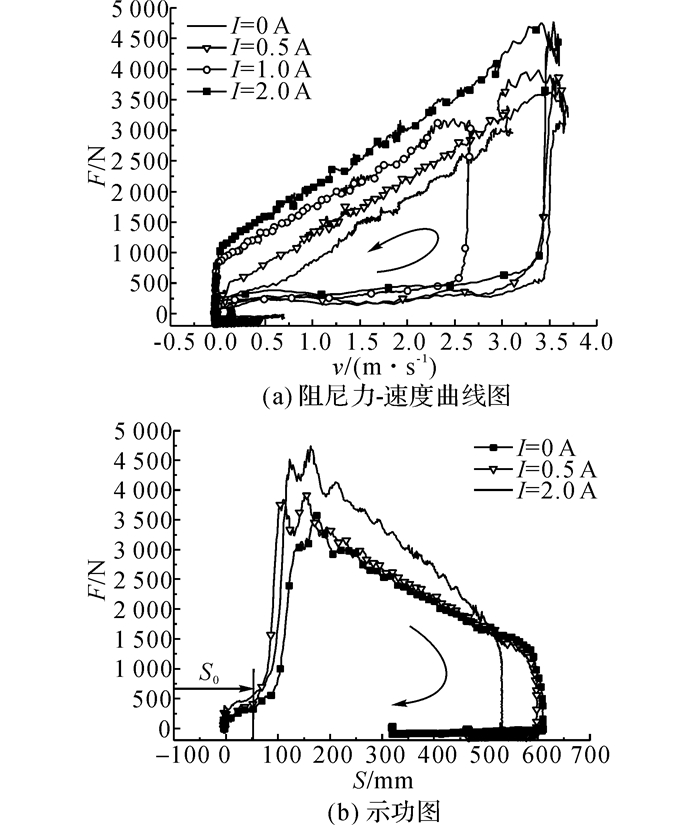
2.2.1 等值电流加载为了比较并联式与传统串联式线圈结构的磁流变缓冲器的缓冲特性, 设置了对照组.由于传统串联式线圈结构的磁流变缓冲器, 其多级线圈的电流输入值皆相同, 因此在本试验中分别对四级线圈输入相同的电流值来模拟串联式线圈结构的磁流变缓冲器, 试验分别对电流I为0、0.5、1.0、2.0 A进行冲击试验研究, 结果如图 4所示.图中F为阻尼力, v为后坐运动速度, S为后坐位移.
|
图 4 串联模式下磁流变缓冲器的阻尼特性 Fig. 4 Dynamic characteristics of MRD in traditional working mode |
图 4(a)为缓冲器在不同电流情况下的力-速度特性曲线.冲击速度和激励电流分别决定了磁流变液的黏滞阻力和库仑阻力的大小.后坐冲击速度、激励电流越大, 则缓冲器的输出阻尼力也越大.在加载0、0.5、2.0 A电流, 最大冲击速度一致时(3.5 m/s), 磁流变缓冲器的最大阻尼力与输入电流大小呈正相关关系.而当输入电流为1.0 A时, 因为其最大速度相对较小(2.5 m/s), 与速度相关的最大的黏滞阻尼力也相对较小, 导致最大输出阻尼力不及其他电流加载的情况.
各电流加载下缓冲器的库仑阻尼力为在相同后坐速度下其相对于零场(0 A)时阻尼力的增值.电流越大, 所产生的库仑力也随之越大.由图 4(a)可知, 施加2.0 A电流时所产生库仑阻尼力达1 086 N.在速度下降沿段, 阻尼力与速度呈线性关系.值得注意的是, 在力-速度特性曲线上升沿水平段, 输出阻尼力的变化与后坐速度及输入电流的变化之间具有显著滞后现象, 并未显现出明显的库仑阻尼力、黏滞阻尼力的作用, 而当后坐速度接近最大值时, 阻尼力才急剧上升至最高值.经分析, 由于缺乏补偿腔的单筒单杆式磁流变缓冲器在运行中会造成真空区, 但在实际试验过程中, 缓冲器的绝对气密性难以保证, 空气的吸入会使得在冲击开始瞬间, 缓冲器压缩腔中的液体呈不完全充满状态, 导致冲击起始阶段其阻尼力的变化不明显, 而当缓冲器移动一段距离后, 磁流变液开始被大量挤入阻尼通道, 继而产生库仑阻尼力和黏滞阻尼力等.
磁流变液挤入点发在后坐位移S0=50 mm左右, 如图 4(b).阻尼力-位移曲线所围面积表示磁流变缓冲器所消耗的功, 在最大后坐速度一致, 即初始冲击能量相同的情况下, 后坐输出阻尼力越大其相应的后坐位移越小.
2.2.2 各级组合电流加载电流加载方案如表 2所示, 以加载线圈数目可分为4种加载形式, 分别为单级加载I1、双级加载I2、三级加载I3以及四级加载I4, 且各组试验所施加的总电流为2 A.研究了并联式磁流变缓冲器在不同线圈电流组合工作情况下的缓冲性能, 如图 5所示.由图可知, 不同线圈组合工作方式下的阻尼力-速度曲线(F-v)的变化趋势与之前分析的串联模式的特性曲线相同, 不同的是在各加载电流情况下, 不同工作线圈组合方式引起阻尼通道间磁场分布不同, 从而导致磁流变效应强弱不一, 即库仑阻尼力不同.
| 表 2 冲击试验电流加载方案 Table 2 Current loading case |

|
图 5 并联组合模式下磁流变缓冲器的阻尼特性 Fig. 5 Dynamic characteristics of MRD in combination working mode |
图 5(a)为单线圈工作的情况, 所产生的最大库仑阻尼力为第三级线圈通电时的495 N.第一级线圈工作所产生的库仑阻尼力值最小, 其阻尼力-速度特性曲线几乎与零场情况下特性曲线重合.而第二、四级线圈所产生的磁流变效应介于上面两者之间.图 5(b)为双级线圈同时施加1 A电流的情况, 其中产生的最大库仑阻尼力的为第二、三级线圈组合, 达673 N.当工作线圈有三级, 各级线圈输入电流0.67 A时, 如图 5(c), 最大的库仑阻尼力为610 N, 含第一、二两级的组合2组阻尼特性情况相似, 其产生的库仑阻尼力比含有三、四级线圈的组合要大.在图 5(d)中, 四级线圈全部施加电流, 所产生的库仑阻尼力相差不大, 约500 N左右, 但与零场情况的阻尼力-速度特性曲线相比, 四级线圈同时工作所产生的磁流变效应明显.
总体而言, 在输入电流总和相同的情况下, 单级线圈工作时的库仑阻尼力较其他组合加载形式小, 线圈磁场分布集中导致产生磁流变效应的范围有限;而双级线圈组合加载情况产生的库仑阻尼相对较大, 由于双级线圈产生的磁场分布范围较广, 因此阻尼通道内的磁流变效应更显著;但是随着级数进一步增加, 电流进一步被分散在多个线圈时, 所产生的库仑阻尼力相较于双级线圈情况有所下降, 并且在四级线圈工作状态下, 在总电流有限情况下, 电流分配的过于分散导致各加载情况下的特性曲线差异不大.阻尼间隙轴向几何维度上的磁场分布变化对缓冲性能的影响有助于下一步进行动力学建模及控制算法设计.
2.2.3 延时加载通过对各级线圈逐级延时加载电流如表 3所示, 考察阻尼间隙内磁场分布在时间维度上的变化对阻尼器缓冲性能的影响, 尤其是对阻尼峰值Fp的影响.分别从第四级线圈至第一级线圈每隔10 ms逐级施加0.5、1.0、2.0 A电流值, 则延时加载所产生的最大阻尼峰值Fpd与各级线圈同时加载电流所得到的最大阻尼峰值Fpg相比, 阻尼力峰值分别减少了12.3 %、10.47 %和8.3 %.这说明多级线圈结构阻尼器可在时间维度上变化磁场从而对输出阻尼力进行控制.在冲击过程中, 先加载阻尼通道末端线圈可一定程度上缓解“液体阻塞”现象, 降低阻尼力峰值.
| 表 3 延时加载试验 Table 3 Delay current loading experiment |
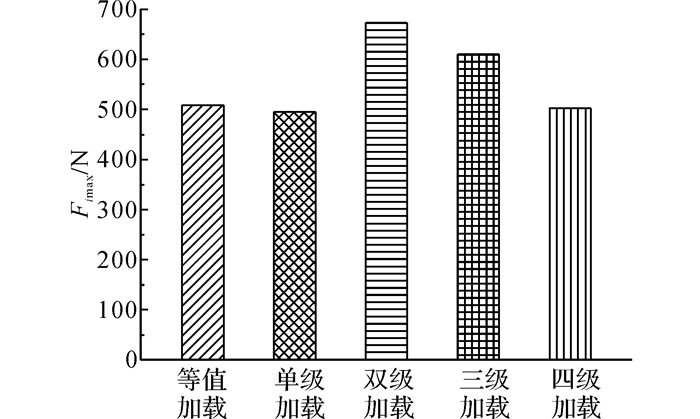
比较等值加载的串联模式及组合加载的并联模式下的阻尼输出特性.以总输入电流2 A为例, 在2种不同模式下的最大输出库仑阻尼力Fimax如图 6所示.在各线圈等值加载0.5 A电流时, 所产生的库仑阻尼力为508 N, 与组合加载模式下单级、四级加载所产生的库仑阻尼力495和502 N相接近.而双级加载和三级加载所产生的可控库仑阻尼力大于等值加载情形.根据Koo等[20]可知, 线圈施加电流值越大, 其磁流变液产生的阻尼力响应速度越快.因此, 为提高缓冲器的响应速度, 可将等值加载模式转换成较少工作线圈、较大输入电流的组合加载模式.例如, 在单级加载2 A电流时可基本实现0.5 A等值加载串联模式下的可控库仑阻力输出, 并且提高了响应速度.若需同时考虑耗电功率, 则三级线圈加载下既能实现串联模式下的阻尼输出, 提高缓冲器的响应时间, 同时其耗电功率较单级、双级加载时小.
|
图 6 不同工作模式下的最大库仑阻尼力 Fig. 6 Maximum coulomb damping force under different working mode |
因此, 并联式磁流变缓冲器可实现传统串联式缓冲器的阻尼输出, 同时由于各级独立可控的特点, 能根据控制目标进行工作线圈优化配置.
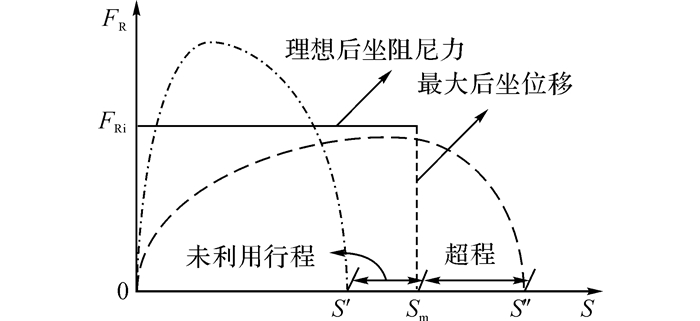
3 缓冲器可控性分析根据1.2节的分析可知, 磁流变缓冲器在反后坐系统中的理想阻力应保持恒定输出, 最有效地耗散冲击能量, 如图 7所示.
|
图 7 理想后坐阻尼力变化示意图 Fig. 7 Schematic diagram of ideal recoil damping force |
在火炮后坐运动过程中, 后坐速度在极短时间内上升至峰值, 而后逐渐下降直至最终停止.在自由后坐阶段, 黏滞阻尼力随后坐速度下降而逐渐减小.为保证后坐过程的理想平缓, 即实现阻尼力的“平台效应”, 则库仑阻尼力应在后坐过程中逐渐增大以弥补黏滞阻尼力下降导, 使缓冲器总输出阻力维持稳定.因此, 磁流变缓冲器的黏滞阻尼力及库仑阻尼力需满足约束:
| $ {{F}_{\text{off}}}={{F}_{\eta }}+{{F}_{\text{m}}}+{{F}_{\text{i}}}+{{F}_{\text{f}}}\le {{F}_{\text{Ri}}}, $ | (6) |
| $ {{F}_{\tau }}\ge {{F}_{\text{Ri}}}. $ | (7) |
式中:Foff为零场阻尼力;FRi为理想的后坐阻尼力;Fη、Fm、Fi及Ff分别为黏滞阻尼力、节流阻尼力、流体惯性力及摩擦力等.Fτ为磁流变效应所引起的库仑阻尼力.
理想后坐阻尼力FRi与最大后坐位移及后坐速度相关:
| $ {{F}_{\text{Ri}}}=\frac{m{{v}^{2}}_{\text{max}}}{2{{S}_{\text{max}}}}. $ | (8) |
试验台架最大后坐位移Smax=600 mm, 运动质量块与磁流变缓冲器总质量m=270 kg, 则可求得本次试验的最大后坐速度vmax=3.5 m/s时的理想后坐阻尼力FRi=2 838 N.
通过图 4、5可知, 当Vmax=3.5 m/s时, 缓冲器的Foff=3 500 N > FRi;而最大库仑阻尼力Fτ=1 086 N < FRi, 皆不满足式(6)、(7) 的要求.即缓冲器在该后坐冲击速度下无法输出理想的后坐曲线.
为求得可输出理想后坐阻力的后坐冲击速度, 根据式(6)~(8) 得
| $ {{F}_{\eta }}+{{F}_{\text{m}}}+{{F}_{\text{i}}}+{{F}_{\text{f}}}=c{{v}_{0}}+300\le \frac{m{{v}_{0}}^{2}}{2{{S}_{\text{max}}}}. $ | (9) |
| $ {{F}_{\tau }}=1\ 086\ge \frac{m{{v}_{0}}^{2}}{2{{S}_{\text{max}}}}. $ | (10) |
为简便处理, 不单独考虑Fm、Fi和Ff的影响, 根据图(4)、(5) 的F-v曲线初始阶段平均阻尼力在300 N左右;黏滞阻尼系数取c=914.则同时满足式(9)、(10) 所对应的后坐速度范围为
| $ {{v}_{0}}\ge 4.30\text{ m/s}且{{v}_{0}}\le 2.16\text{ m/s}. $ | (11) |
无法通过式(11) 找到一个合理的v0, 使之同时满足理想后坐所需的约束条件(9)、(10).即所设计的并联式磁流变缓冲器阻尼力输出无法实现全后坐过程的平台效应.
究其原因是由于所设计的缓冲器的非可控阻尼力过大, 导致缓冲器在冲击后坐过程中可控库仑阻尼力所占比重过低, 影响缓冲器的可控性.定义磁流变缓冲器可控系数β为磁流变效应所引起的库仑阻尼力Fτ与零场下非可控阻尼力Foff之比.可控系数β越大, 即意味着缓冲器的可控性能越佳, 缓冲器能够通过控制输入电流大小来输出较大变化范围的可调阻尼力.
| $ \beta =\frac{{{F}_{\tau }}}{{{F}_{\text{off}}}}=\frac{1\ 086}{3\ 500}=0.31. $ | (12) |
缓冲器可调系数β < 1, 与一般磁流变缓冲器的可调系数范围2~6[14-16]有一定差距, 需通过结构优化设计来改善缓冲器在冲击载荷下的可控性.
在该既定结构的缓冲器中, 虽由于结构设计问题而无法在整个后坐过程实现恒定的阻尼输出, 但可在某一速度范围内实现部分后坐的恒定阻尼输出.当满足式(11) 中v0≤2.16 m/s的条件时, 缓冲器的输出阻尼力曲线示意图如图 8所示.

|
图 8 后坐阻尼力控制示意图 Fig. 8 Schematic diagram of recoil damping force control |
其中, 不可控区Ⅰ是由于冲击载荷在极短时间内加载于磁流变缓冲器上, 此时阻尼力的峰值很大程度上与液体压缩相关, 而磁流变效应未能有效发挥[21-22].而区域Ⅱ因非可控阻尼力大于理想后坐阻尼力FRi, 因此该区域不需通过库仑阻尼进行可控调节.随着后坐位移进一步增大, 非可控阻尼力随之逐渐下降并小于FRi, 此时, 可通过调节库仑阻尼力来使得后坐阻尼维持在一个恒定值.
4 结论通过对应用于反后坐系统中的多阶并联式磁流变缓冲器的冲击试验研究, 得到该缓冲器在后坐冲击试验环境下的性能, 并分析了其可控性.
(1) 试验表明, 并联式结构的磁流变缓冲器不仅可以通过给各线圈施加等值电流实现传统串联式线圈缓冲器所能达到的阻尼特性, 还能给各线圈施加不同电流, 不同的组合加载方式产生多变的阻尼特性.在线圈总电流固定情况下, 单级线圈工作时, 由于磁场分布集中导致阻尼力偏小;而双级线圈工作时磁场分布相对均匀, 产生的可调库仑力较为明显;然而当有限总电流过于分散于各级线圈中, 则阻尼特性有趋同现象.并通过对比分析可知并联式磁流变缓冲器相比于传统串联式缓冲器能利用各级独立可控特点, 根据不同控制目标进行工作线圈优化配置.
(2) 通过延时加载电流试验表明, 多阶并联式磁流变缓冲器不仅能通过改变阻尼通道几何维度上的分布规律来获得灵活多变的阻尼特性, 并且能在时间维度上通过合理布置各级线圈的加载时间而输出理想的阻尼力, 体现多阶并联式磁流变缓冲器的独特优势.
(3) 通过对反后坐系统中磁流变缓冲器的可控性分析可知, 该缓冲器的可调系数较小需通过结构优化设计进行完善改进.对已加工设计的缓冲器在临界后坐速度小于2.16m/s时可实现部分后坐阻尼的“平台效应”.
| [1] | HAJIHOSSEINLOO M A, HOOKE C J, WALTON D. Gun recoil system performance measurement and prediction[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1989, 203(2): 85–92. DOI:10.1243/PIME_PROC_1989_203_091_02 |
| [2] | WANG D H, LIAO W H. Magnetorheological fluid dampers: a review of parametric modeling[J]. Smart materials and structures, 2011, 20(2): 023001. DOI:10.1088/0964-1726/20/2/023001 |
| [3] | ZONG L H, GONG X L, XUAN S H, et al. Semi-active H∞ control of high-speed railway vehicle suspension with magnetorheological dampers[J]. Vehicle System Dynamics, 2013, 51(5): 600–626. DOI:10.1080/00423114.2012.758858 |
| [4] | POWELL L A, HU W, WERELEY N M. Magnetorheological fluid composites synthesized for helicopter landing gear applications[J]. Journal of Intelligent Material Systems and Structures, 2013, 24(9): 1043–1048. DOI:10.1177/1045389X13476153 |
| [5] | ATABAY E, OZKOL I. Application of a magnetorheological damper modeled using the current-dependent Bouc-Wen model for shimmy suppression in a torsional nose landing gear with and without freeplay[J]. Journal of Vibration and Control, 2014, 20(11): 1622–1644. DOI:10.1177/1077546312468925 |
| [6] | PHU D X, CHOI S B, LEE Y S, et al. Design of a new engine mount for vertical and horizontal vibration control using magnetorheological fluid[J]. Smart Materials and Structures, 2014, 23(11): 117001. DOI:10.1088/0964-1726/23/11/117001 |
| [7] | OZBULUT O E, HURLEBAUS S. Optimal design of superelastic-friction base isolators for seismic protection of highway bridges against near-field earthquakes[J]. Earthquake Engineering & Structural Dynamics, 2011, 40(3): 273–291. |
| [8] |
董小闵, 余淼, 廖昌荣, 等. 飞行器磁流变自适应半主动冲击缓冲器[J].
西南交通大学学报, 2009, 44(5): 748–752.
DONG Xiao-min, YU Miao, LIAO Chang-rong, et al. Adaptive semiactive bumper for aircraft[J]. Journal of Southwest Jiaotong University, 2009, 44(5): 748–752. |
| [9] |
胡红生, 王炅, 蒋学争, 等. 火炮磁流变后坐阻尼器的设计与可控性分析[J].
振动与冲击, 2010, 29(2): 184–188.
HU Hong-sheng, WANG Jiong, JIANG Xue-zheng, et al. Design and controllability analysis of a gun magnetorheological recoil damper[J]. Journal of Vibration and Shock, 2010, 29(2): 184–188. |
| [10] | LI Z C, WANG J. A gun recoil system employing a magnetorheological fluid damper[J]. Smart Materials and Structures, 2012, 21(10): 105003. DOI:10.1088/0964-1726/21/10/105003 |
| [11] | AHMADIAN M, POYNOR J C. An evaluation of magneto rheological dampers for controlling gun recoil dynamics[J]. Shock and Vibration, 2001, 8(3/4): 147–155. |
| [12] | BAJKOWSKI M, BAJKOWSKI J M. Design of the magnetorheological damper for the recoil damping of the special object 7.62 mm calibre[J]. Machine Dynamics Research,, 2012, 36(1): 15–23. |
| [13] | BAJKOWSKI M, MAKUCH A, LINDEMANN Z. Determining parameters of recoil reduction system with spring and magnetorheological damper intended for special object[J]. Machine Dynamics Research, 2015, 38(3): 87–96. |
| [14] | SINGH H J, WERELEY N M. Optimal control of gun recoil in direct fire using magnetorheological absorbers[J]. Smart materials and Structures, 2014, 23(5): 055009. DOI:10.1088/0964-1726/23/5/055009 |
| [15] | MAO M, CHOI Y T, WERELEY N M. Effective design strategy for a magneto-rheological damper using a nonlinear flow model[C]//Smart Structures and Materials 2005: Damping and Isolation. San Diego: Intermational Society for Optics and Photonics, 2005: 446-455. |
| [16] | BAI X X, WERELEY N M, HU W, et al. A bidirectional-controllable magnetorheological energy absorber for shock and vibration isolation systems[C]//Adaptive Structures and Intelligent Systems. Philadelphia: American Society of Mechanical Engineers, 2012: 485-495. |
| [17] | YANG G, SPENCER B F, CARLSON J D, et al. Large-scale MR fluid dampers: modeling and dynamic performance considerations[J]. Engineering structures, 2002, 24(3): 309–323. DOI:10.1016/S0141-0296(01)00097-9 |
| [18] | GUAN X, LI J, OU J. Experiment study of large-scale magnetorheological fluid damper[C]//Smart Structures and Materials 2005: Damping and Isolation. San Diego: Intermational Society for Optics and Photonics, 2005: 588-595. |
| [19] |
李延成. 冲击载荷下磁流变缓冲器半主动控制研究[D]. 南京: 南京理工大学, 2007.
LI Yan-cheng. Semi-active control of magnetorheological shock absorber subjected to impact Load[D]. Nanjing: Nanjing University of Science and Technology, 2007. |
| [20] | KOO J H, GONCALVES F D, AHMADIAN M. A comprehensive analysis of the response time of MR dampers[J]. Smart Materials and Structures, 2006, 15(2): 351. DOI:10.1088/0964-1726/15/2/015 |
| [21] |
张莉洁, 王炅, 钱林方. 冲击载荷下磁流变阻尼器动态特性试验分析[J].
兵工学报, 2008, 29(5): 532–536.
ZHANG Li-jie, WANG Jiong, QIAN Lin-fang. Experimental analysis of the dynamic performance of magneto-rheological dampers under impact loads[J]. Acta Armamentarii, 2008, 29(5): 532–536. |
| [22] | AHMADIAN M, NORRIS J A. Experimental analysis of magnetorheological dampers when subjected to impact and shock loading[J]. Communications in Nonlinear Science and Numerical Simulation, 2008, 13(9): 1978–1985. DOI:10.1016/j.cnsns.2007.03.028 |



