2. 浙江大学 宁波理工学院, 浙江 宁波 315100;
3. 浙江大学 软弱土与环境土工教育部重点实验室, 浙江 杭州 310058
2. Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China;
3. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China
滨海软土在固结过程中渗透系数随孔隙比的降低而变化, 强非线性的渗透规律长期以来受到了国内外学者的广泛关注[1-9].针对软黏土渗透系数与孔隙比的非线性关系, Samarasinghe等[10]、Mesri等[11]、Narasimha等[6]以及谢康和等[12]提出土的对数及幂指数渗透模型, 为预测孔隙比及渗透性等的发展规律提供了指导, 然而模型参数的选取却需要针对特定研究对象进行试验得到, 限制了模型的适用性.齐添等[13]基于非达西渗流理论, 对萧山黏土进行GDS固结渗透联合试验, 研究了渗透速度与水力梯度的关系, 拟合了试验结果的三参数模型、幂指数模型及非线性分段模型, 并得到萧山黏土的折线模型;张明等[14]采用GDS固结仪对深圳前湾吹填淤泥高含水率重塑样进行固结渗透试验, 回归拟合4种软黏土非线性渗透模型, 认为4种渗透系数-孔隙比非线性关系都适用于所选土样, 当固结压力较小(≤50 kPa)时, 各试样的渗透系数差异较大;李西斌等[15]考虑软土的流变性以及应力历史, 采用GDS高级固结仪对萧山软土进行常规渗透试验, 得到萧山软土的压缩指数、回弹指数、渗透指数和次固结系数;齐添等[16]建立了考虑非线性压缩系数、渗透系数、荷载、自重等变化的一维固结控制方程, 利用GDS试验得到了不同试验条件下的相应固结系数, 验证了压缩和渗透非线性, 认为萧山软黏土的渗透系数值在10-9~10-8 cm/s, 且随着固结压力的增加该值不断减小.对比前人的研究结果可发现, 对于软黏土的渗透特性虽有大量试验研究成果, 但对不同水力梯度、渗透围压以及含水率下的软黏土渗透特性研究缺乏统一性, 研究成果往往随地域、土性等不同而发生变化, 几种常用渗透模型的适用性也尚需试验验证.
本文利用GDS渗透仪对宁波地区淤泥质粉质黏土原状样和重塑样进行多组常水头渗透试验, 对不同孔隙比、围压作用下的滨海软黏土非线性渗透规律进行研究, 验证经典渗透模型对宁波软土的适用性, 并得到拟合参数.基于试验结果提出一种新的非线性渗透模型, 并通过既有文献中10种土样的渗透试验数据验证本文模型的适用性.
1 土体非线性渗透模型渗透模型是用于表征土体渗透特性与自身物理参数及外界作用之间关系的重要工具.对软土渗透系数的模型研究由来已久:1927年Kozeny[17]和Carman[18]首先提出了多孔介质材料渗透系数的求解公式:
| $ {\mathit{k}_{\rm{v}}}{\rm{ = }}\frac{{\rm{1}}}{{{\mathit{K}_{\rm{0}}}{\mathit{T}^{\rm{2}}}\mathit{S}_{\rm{0}}^{\rm{2}}}}\frac{\gamma }{\mu }\frac{{{\mathit{n}^{\rm{3}}}}}{{{{{\rm{(1 - }}\mathit{n}{\rm{)}}}^{\rm{2}}}}}. $ | (1) |
式中:kv为竖向渗透系数, K0为孔隙形状参数, T为流体渗透路径弯曲度, S0为土颗粒比表面, n为孔隙率, γ为流体重度, μ为流体黏度系数.
随后, Taylor[19]在1948年提出式(1) 只适用于砂土, 并建议采用e~lg kv线性经验公式描述黏土的渗透特性:
| $ {\rm{lg}}\;{k_{\rm{v}}}{\rm{ = lg}}\;{k_\mathit{w}}{\rm{ - }}\frac{{{e_{\rm{0}}}{\rm{ - }}e}}{{{C_{\rm{k}}}}}. $ | (2) |
式中:Ck为渗透指数, kw、e0分别为土体初始渗透系数及初始孔隙比,e为孔隙比.由于对工程范围内的土体孔隙比适用, 该公式被广泛用于揭示渗透系数随孔隙比变化的发展规律.
然而, 当孔隙比变化区间超出一定范围时, 式(2) 也不再适用, 因此Mesri[11]将其推广为适用于孔隙比在更大范围内变化时的渗透系数关系表达式, 如下:
| $ {\rm{lg}}\;{\mathit{k}_{\rm{v}}}{\rm{ = }}{\mathit{A}_{\rm{1}}}{\rm{lg}}\;\mathit{e}{\rm{ + }}{\mathit{B}_{\rm{1}}}{\rm{.}} $ | (3) |
式中:A1、B1均为渗透性参数.
Samarasinghe等[10]在1982年对式(1) 进行修正, 使其能够描述正常固结黏土的渗透特性, 得到
| $ {\rm{lg [}}{\mathit{k}_{\rm{v}}}{\rm{(1 + }}\mathit{e}{\rm{)] = lg}}\;\mathit{C}{\rm{ + }}\mathit{m}{\rm{lg}}\;\mathit{e}{\rm{.}} $ | (4) |
式中:C为标准土体渗透特性的参考渗透系数, m为土体材料参数, 一般取4~5.
以上学者所给渗透系数经验式都是基于室内重塑或扰动土样进行的.Tavenas[4-5]取加拿大Quebec等地原状土样进行室内变、常水头渗透试验, 验证试样尺寸、各向异性、孔隙对土样渗透性能的影响并得到e~kv关系, 认为式(2) 将渗透系数的测定转嫁为对初始渗透系数kw和渗透指数Ck的测定, 并且对于初始孔隙比e0≤2.5、固结过程中体应变小于20%的条件下具有很好的效果.
谢康和等[12]在求解以超静孔压为变量的一维非线性大应变固结方程时提出软土的幂指数渗透模型(5), 随后利用GDS渗透仪对萧山黏土渗透非线性进行试验研究, 进一步对式(5) 进行改进得到了对数模型式(6).
| $ {\mathit{k}_{\rm{v}}}{\rm{ = }}{\mathit{k}_{{\rm{v0}}}}{{\rm{(}}\frac{{{\rm{1 + }}\mathit{e}}}{{{\rm{1 + }}{\mathit{e}_{\rm{0}}}}}{\rm{)}}^{\rm{2}}}{\rm{.}} $ | (5) |
| $ {\rm{lg}}\;{\mathit{k}_{\rm{v}}}{\rm{(1 + }}\mathit{e}{\rm{) = }}\alpha {\rm{lg}}\;{\mathit{k}_{\rm{v}}} + \beta . $ | (6) |
式中:α、β为土性参数, 可通过分析试验数据得到.
为验证以上各经验模型对描述滨海软土渗透规律的适用性, 本文将通过对宁波淤泥质粉质黏土的试验结果对各模型公式进行拟合研究.
2 试验方案与结果 2.1 试验内容试验土样取自宁波地铁某工程地下15~20 m处淤泥质粉质黏土.原状土样密度ρ=1.781 g/cm3, 土粒比重Gs=2.66, 含水率w=41.21%.采用切土架切取原状标准样, 并取足量原状土碾碎、烘干配制目标含水率重塑样.通过固结仪进行50、100、200、400 kPa一维固结, 至压缩稳定卸荷待其回弹稳定, 得到8组不同孔隙比渗透样.
安装试样于渗透仪基座上, 施加围压并进行多组常水头渗透试验至渗流稳定.进行常水头渗透试验的压力设置及土样参数如表 1、2所示, 表中p1、p2及Δp分别表示试验过程中的围压、反压及渗透压差值.
| 表 1 原状样渗透试验参数 Table 1 Seepage parameters of undisturbed samples |
| 表 2 重塑样渗透试验参数 Table 2 Seepage parameters of remolded samples |
宁波软土的渗透系数较小, 达到渗流稳定需时较长.对常水头渗透试验过程中软土试样顶部和底部渗透系数实时监测, 至渗流稳定选取试样顶部渗透系数、底部渗透系数均值作为该级试验下的土样渗透系数.
表 3、4分别列出了各级试验完成后所得原状土样和重塑土样在特定水力梯度作用下的渗透系数值.表中kv1、kv2分别为渗透试样顶部和底部渗透系数值, 分别由GDS先进渗透系统中的部件反压压力体积控制器和底部压力体积控制器通过其内部流体的渗出、渗入量变化得到.kv3、和kv4分别为土样在同一级和同一组渗透水头下的试验均值.
| 表 3 原状土样渗透系数 Table 3 Seepage coefficients of undisturbed soil samples |
| 表 4 重塑土样渗透系数 Table 4 Seepage coefficients of remolded soil samples |
由表 3、4绘制原状、重塑土样渗透系数随孔隙比的变化关系如图 1所示, 由图可得土样在不同渗透压差的作用下, 体现出较规律的渗透特性:1) 随土样孔隙比的减小, 土颗粒间孔隙逐渐密实, 原状和重塑试样渗透系数均显著减小;2) 原状土样在孔隙比由1.11降至0.80的过程中渗透系数降低了68.7%, 重塑土样随着孔隙比自0.98降为0.68, 渗透系数降低了77.6%, 降幅大于原状土样, 在孔隙比相同时, 重塑试样渗透系数值大于原状样.

|
图 1 试样渗透系数~孔隙比变化关系 Fig. 1 Sketch of permeability changed with void ratio in seepage tests |
采用本文试验数据作为拟合对象, 对不同经验公式的拟合结果如图 2~5所示.需要说明的是, 由于未考虑土中孔隙形状及渗透路径弯曲度等影响因素, 且考虑到研究对象为黏土, 故此处只对土体非线性渗透模型中的(2)、(3)、(4)、(6) 等进行了拟合研究.
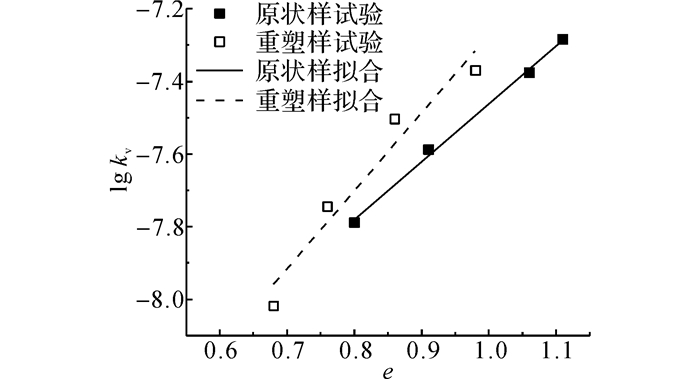
|
图 2 式(2) 拟合结果(lg kv~e) Fig. 2 Fitting results for Formula (2) (lg kv~e) |
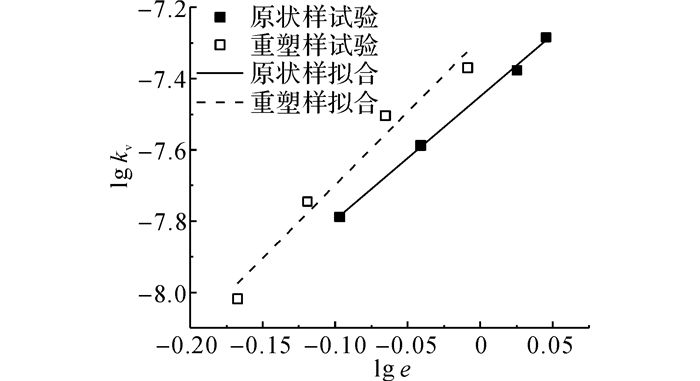
|
图 3 式(3) 拟合结果(lg kv~lg e) Fig. 3 Fitting results for Formula (3) (lg kv~lg e) |
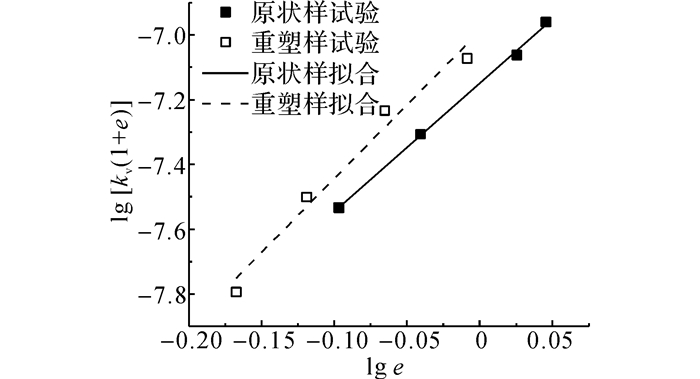
|
图 4 式(4) 拟合结果(lg [kv(1+e)]~lg e) Fig. 4 Fitting results for Formula (4) (lg [kv(1+e)]~lg e) |

|
图 5 式(6) 拟合结果(lg kv~lg (1+e)) Fig. 5 Fitting results for Formula (6) (lg kv~lg (1+e)) |
通过以上对宁波软土渗透试验结果的分析, 在4种经典模型的基础上, 本文提出了基于lg [kv(1+e)]~e关系的渗透模型如式(7):
| $ {\rm{lg [}}{\mathit{k}_{\rm{v}}}{\rm{(1 + }}\mathit{e}{\rm{)] = }}{\mathit{A}_{\rm{2}}}\mathit{e}{\rm{ + }}{\mathit{B}_{\rm{2}}}{\rm{.}} $ | (7) |
式中:A2、B2为土性参数, 可通过选取代表性土样, 进行试验分析得到.原状和重塑样试验数据对式(7) 的拟合结果如图 6所示.
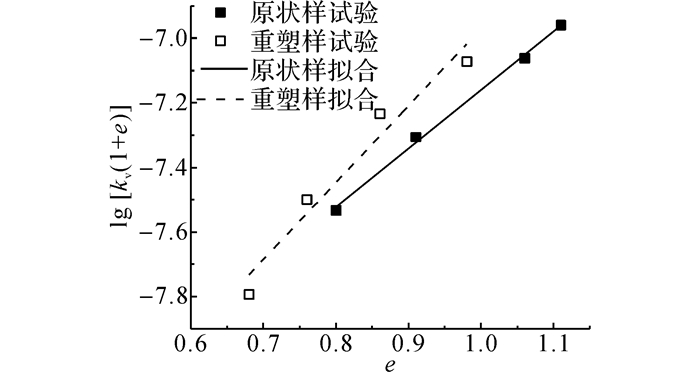
|
图 6 式(7) 拟合结果(lg [kv(1+e)]~e) Fig. 6 Fitting results for Formula (7) (lg [kv(1+e)]~e) |
渗透结果对各经验公式的拟合参数如表 5所示, 表中R为拟合所得相关系数.由表可知, 各渗透模型的拟合相关系数均在0.921以上, 基于lg [kv(1+e)]~e关系的式(7) 相关系数位于0.933~0.997之间, 此即表明包含本文所提出的渗透模型在内的五种渗透模型均适用于宁波软土.
| 表 5 渗透经验模型的拟合参数及相关系数 Table 5 Fitting parameters and correlation coefficients for classical seepage formulas |
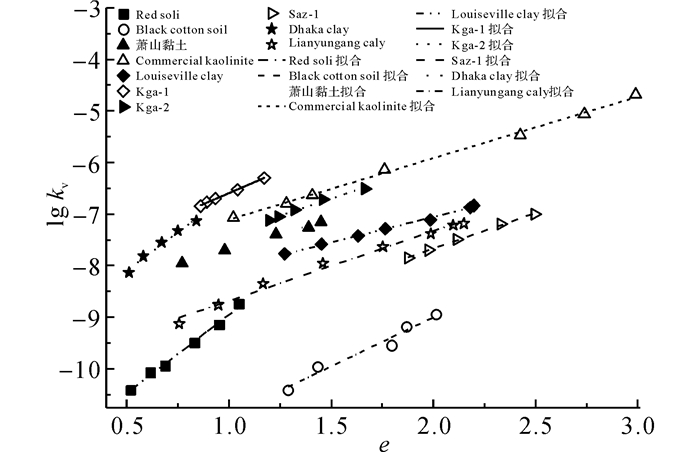
为验证本文模型的适用性, 收集既有文献中十组土样的渗透试验数据如表 6所示, 所列数据均为来自引用文献中的原始试验数据, 试验土包含印度班加罗尔红黏土、中国杭州萧山黏土等多地区不同类别土样.对以上试验数据采用经典非线性渗透模型(2)、(3)、(4)、(6) 以及本文模型(7) 进行拟合分析, 以验证本文基于宁波软土所提出渗透模型的适用性, 拟合结果如图 7~11所示.
| 表 6 既有文献中的渗透试验数据 Table 6 Seepage test data from published works |
|
图 7 式(2) 拟合结果(lg kv~e) Fig. 7 Fitting results for formula (2) (lg kv~e) |
|
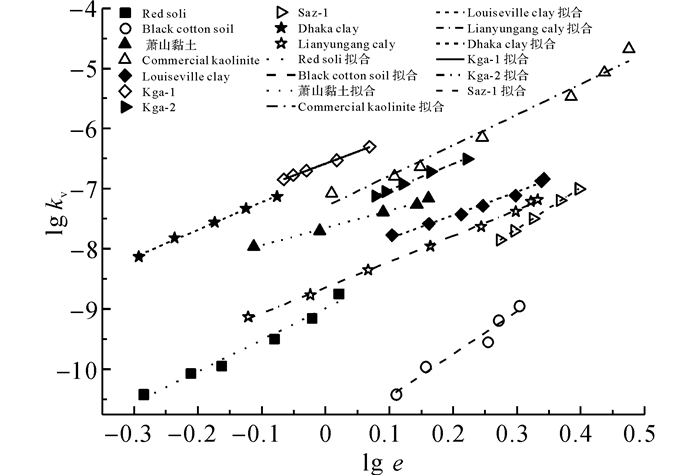
图 8 式(3) 拟合结果(lg kv~lg e) Fig. 8 Fitting results for Formula (3) (lg kv~lg e) |
|
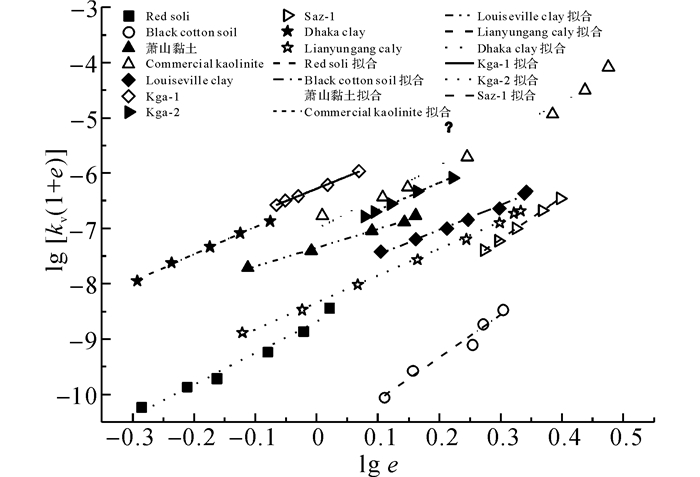
图 9 式(4) 拟合结果(lg [kv(1+e)]~lg e) Fig. 9 Fitting results for Formula (4) (lg [kv(1+e)]~lg e) |

|
图 10 式(6) 拟合结果(lg kv~lg (1+e)) Fig. 10 Fitting results for Formula (6) (lg kv~lg (1+e)) |

|
图 11 本文模型拟合结果(lg [kv(1+e)]~e) Fig. 11 Fitting results for proposed model (lg [kv(1+e)]~e) |
由图 7~11可知, 本文模型和4种已有模型能较好吻合于10组文献试验数据.各模型拟合结果的相关系数如表 7所示.
| 表 7 渗透模型对既有文献数据的拟合相关系数 Table 7 Fitting correlation coefficients for published data |
由表 7可知, 5种渗透模型对10种土的拟合效果均较好, 其中本文模型拟合的相关系数在0.961~0.998之间, 并对Red soil、Black cotton soil、Commercial kaolinite、Louisiseville clay和Kga-1等5种土的拟合效果最优, 表明该模型能够较好揭示10种土样渗透系数与孔隙比之间的非线性关系.
4 结论本文采用GDS渗透仪对宁波淤泥质粉质黏土进行了常水头渗透试验, 系统研究了不同孔隙比状态的宁波软土重塑样和原状样的渗透特性, 得到了以下结论:
(1) 宁波软土渗透系数随孔隙比的减小而减小, 重塑试样减小更为明显;重塑样和原状样的试验结果均基本符合几种目前广泛使用的渗透经验模型.
(2) 基于本文试验结果提出的lg [kv(1+e)]~e渗透模型, 能较好地描述宁波软土渗透系数与孔隙比之间的非线性变化关系.
(3) 对10组土样的拟合结果显示本文模型能更好地揭示土体的渗透特性, 适用性相对已有模型更优, 为进一步开展软土渗透性研究工作提供了参考.
| [1] | DAVIS E H, RAYMOND G P. A non-linear theory of consolidation[J]. Geotechnique, 1965, 15(2): 161–173. DOI:10.1680/geot.1965.15.2.161 |
| [2] | LEI H, WU Y, YU Y, et al. Influence of shear on permeability of clayey soil[J]. International Journal of Geomechanics, 2016, 16(5): 0401–6010. |
| [3] | MESRI G, ROKHSAR A. Theory of Consolidation for Clays[J]. Journal of the Geotechnical Engineering, 1974, 100(8): 889–904. |
| [4] | TAVENAS F, LEBLOND P, JEAN P, et al. The permeability of natural soft clays. Part I: Methods of laboratory measurement[J]. Canadian Geotechnical Journal, 1983, 20(4): 629–644. DOI:10.1139/t83-072 |
| [5] | TAVENAS F, JEAN P, LEBLOND P, et al. The permeability of natural soft clays. Part Ⅱ: Permeability characteristics[J]. Canadian Geotechnical Journal, 1983, 20(4): 645–660. DOI:10.1139/t83-073 |
| [6] | NARASIMHA RAJU P S R, PANDIAN N S, NAGARAJ T S. Determination of the coefficient of consolidation from independent measurements of permeability and compressibility[J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 1997, 12(54): 224–229. |
| [7] |
谢康和, 庄迎春, 李西斌. 萧山饱和软黏土的渗透性试验研究[J].
岩土工程学报, 2005, 27(5): 591–594.
XIE Kang-he, ZHUANG Ying-chun, LI Xi-bin. Laboratory investigation of permeability characteristics of Xiaoshan clay[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(5): 591–594. |
| [8] |
胡安峰, 黄杰卿, 谢新宇, 等. 考虑自重影响的饱和土体一维复杂非线性固结研究[J].
浙江大学学报:工学版, 2012, 46(3): 441–447.
HU An-feng, Huang Jie-qing, Xie Xin-yu, et al. Study on properties of one-dimensional complex nonlinear consolidation considering self-weight of saturated soils[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(3): 441–447. |
| [9] | DENG Y, YUE X, LIU S, et al. Hydraulic conductivity of cement-stabilized marine clay with metakaolin and its correlation with pore size distribution[J]. Engineering Geology, 2015, 193: 146–152. DOI:10.1016/j.enggeo.2015.04.018 |
| [10] | SAMARASINGHE A M, HUANG Y H, DRNEVICH V P. Permeability and consolidation of normally consolidated soils[J]. Journal of the Geotechnical Engineering Division, 1982, 1086: 835–850. |
| [11] | MESRI G. Mechanisms controlling the permeability of clays[J]. Clays and Clay Minerals, 1971, 19: 151–158. DOI:10.1346/CCMN |
| [12] |
谢康和, 齐添, 胡安峰, 等. 基于GDS的黏土非线性渗透特性试验研究[J].
岩土力学, 2008, 49(2): 420–424.
XIE Kang-he, QI Tian, HU An-feng, et al. Experimental study on nonlinear permeability characteristics of Xiaoshan clay[J]. Rock and Soil Mechanics, 2008, 49(2): 420–424. |
| [13] |
齐添, 谢康和, 胡安峰, 等. 萧山黏土非达西渗流性状的试验研究[J].
浙江大学学报:工学版, 2007, 41(6): 1023–1028.
QI Tian, XIE Kang-he, HU An-feng, et al. Laboratorial study on non-Darcy seepage in Xiaoshan clay[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(6): 1023–1028. |
| [14] |
张明, 蒋敏敏, 赵有明. 基于GDS固结仪的吹填淤泥非线性渗透性及参数测定[J].
岩石力学与工程学报, 2013(3): 625–632.
ZHANG Ming, JIANG Ming-ming, ZHAO You-ming. Nonlinear permeability and parameter determination for dredged fill based on gds consolidation apparatus[J]. Chinese Journal of Rock Mechanics and Engineering, 2013(3): 625–632. |
| [15] |
李西斌, 谢康和, 陈福全. 考虑软土流变特性和应力历史的一维固结与渗透试验[J].
水利学报, 2013, 44(1): 18–25.
LI Xi-bin, XIE Kang-he, CHEN Fu-quan. One dimensional consolidation and permeability tests considering stress history and rheological characteristic of soft soils[J]. Journal of Hydraulic Engineering, 2013, 44(1): 18–25. |
| [16] |
齐添, 谢康和, 李西斌. 软土的一维非线性固结计算参数及其测定[J].
浙江大学学报:工学版, 2006, 40(8): 1388–1392.
QI Tian, XIE Kang-he, LI Xi-bin. Laboratory determination of one-dimensional nonlinear consolidation computational parameters of soft soil[J]. Journal of Zhejiang University: Engineering Science, 2006, 40(8): 1388–1392. |
| [17] | KOZENY J. Über kapillare Leitung des Wassers im Boden, Sitz. Der Wien[J]. Akad.der wissenschafen, 1927, 136: 271–306. |
| [18] | CARMAN P C. Flow of gases through porous media[M]. [S.l.] Academic press, 1956. |
| [19] | TAYLOR D W. Fundamentals of soil mechanics[J]. Soil Science, 1948, 66(2): 161. |
| [20] | NAGARAJ T S, PANDIAN N S, RAJU P S R N. Stress state-permeability relationships for fine-grained soils[J]. Géotechnique, 1993, 43(2): 333–336. DOI:10.1680/geot.1993.43.2.333 |
| [21] | PANE V, CROCE P, ZNIDARCIC D, et al. Effects of consolidation on permeability measurements for soft clay[J]. Géotechnique, 1983, 23(1): 67–72. |
| [22] | DOLINAR B. Predicting the hydraulic conductivity of saturated clays using plasticity-value correlations[J]. Applied Clay Science, 2009, 45(1): 90–94. |
| [23] | SIDDIQUE A, SAFIULLAH A. Permeability characteristics of reconstituted Dhaka clay[J]. Journal of the Civil Engineering Division, the Institution of Engineers, Bangladesh, Vol, CE, 1995, 23(1): 103–108. |
| [24] | ZENG L L, HONG Z S, CAI Y Q, et al. Change of hydraulic conductivity during compression of undisturbed and remolded clays[J]. Applied Clay Science, 2011, 51(1): 86–93. |



