混凝土作为常见的建筑材料, 多应用于海洋和港口工程、高层建筑结构、核反应堆高压容器、水坝和地下及隧道工程等领域.这些结构物中的混凝土大多都处在复杂的二轴或者三轴受力状态.复杂受力状态下混凝土的力学特性与单轴差异性很大, 因此对混凝土进行多轴试验研究很有实际意义.

混凝土的双轴试验通常是平面应力试验, 国内外相关学者对此进行了研究.Kupfer等^[1]第一次真正考虑压头和混凝土试块之间的摩擦对双轴试验的影响, 得到了正确和有效的试验结果.覃丽坤等^[2-3]对普通混凝土进行4种定侧应力等级的非比例加载双轴压试验, 定侧压等级分别为0、0.2f_c、0.4f_c和0.6f_c.开展5种比例加载双轴压缩试验, 加载应力比分别为0、0.25、0.5、0.75和1.0.测得两种加载方式下混凝土的强度和应变, 得到了轴向应力和应变的变化规律, 并将两种条件下的应力和应变进行对比分析.王浩等^[4]对饱和大骨料混凝土进行动态双轴压的试验, 设定了4个数量级的应变率(10^-5、10^-4、10^-3、10^-2、10^-1)和5种应力比(0:1、0.25:1、0.5:1、0.75:1、1:1), 给出不同条件下的混凝土强度以及动态受压破坏准则.试验结果表明, 在相同应变速率下, 与单轴相比, 双轴极限抗压强度在应力比0.5:1时最大.杨健辉等^[5]对高强混凝土和复合高强混凝土进行了不同应力比条件下的二轴受压对比试验, 得到了极限应力和峰值应变等其他参数, 建立了本构模型, 并将该模型与宋玉普的模型进行了对比分析.这些研究主要都侧重于混凝土强度的性能, 对变形性能的研究只停留在对应力应变曲线的分析上.几乎没有对各个轴向应变之间的关系进行深入的研究.

Jan等^[6]在对混凝土进行真三轴加载的文章中, 简单介绍了加载位移成比例的试验方法(u₁/u₂=1/α, σ₁/σ₃=1/β, du₁/dt=c).Ren等^[7]对高性能混凝土进行应变比分别为0.1、0.3和1.0的等比例压缩试验；余自若等^[8]对RPC混凝土进行应变比为0、0.1、0.3和1.0的双轴压缩试验.这三种加载方式与本文较类似.该试验维持一个方向力恒定, 另外两个方向按应变速率比恒定进行压缩试验.该加载方式在以往的文献中还未发现.本文重点分析了加载后半部分3个轴向应变之间的关系, 这种关系与破坏形态有关, 它包含了剪切面几何特征方面的信息.

表 1给出混凝土的配合比.

表 1

表 1 混凝土配合比 Table 1 Mix proportion of concrete 原材料名称 类型 质量/(kg·m-3) 水泥 PII42.5 182 水泥 PO42.5 182 细骨料 机制砂 229 细骨料 细黄砂 459 粗骨料 碎石 1 123 水 自来水 225 外加剂 消泡剂 2.4

表 1 混凝土配合比 Table 1 Mix proportion of concrete

1) 水泥：采用强度等级为42.5的普通硅酸盐水泥.

2) 砂子:因配合比设计需要, 结合拌和物和易性, 考虑采用人工砂和天然砂两种砂子.人工砂为石粉砂, 颗粒级配属于级配Ⅱ区, 经测量可知, 砂子的细度模数为2.5, 故为中砂.天然砂为普通河砂, 细度模数较小, 属于特细砂.使用特细砂能够提高拌和物浆体的局部流动性以及试件的外表面质量、并能够增加拌合物的黏聚性能.人工砂可以确保所用砂在正常级配范围, 并且保证混凝土的强度.

3) 石子：5~10 mm粒径的石灰岩碎石.

4) 外加剂：采用北京建筑工程研究院生产的ANX-Ⅲ型固体消泡剂.

试件制备：试验采用额定搅拌量为30 L的强制式搅拌机, 制作时每次拌和25 L料, 投料顺序为先将砂子与混入消泡剂的水泥干拌1 min, 让消泡剂与水泥充分接触并拌均；投入石子拌和1 min, 将水放入拌和1分30秒.按规范要求, 正式制作前先用相同配合比的7 L料对搅拌机进行涮膛.将拌和料分两次装入100 mm的立方体钢模中, 并人工插捣两次, 插捣按螺旋方向从边缘向中心进行, 插捣时插捣棒保持垂直, 每层插捣次数不少于10次.人工插捣完毕后, 拿到磁性振动台上振捣密实.每联振捣时间为2 min.

在试件制作完成后, 在恒温室静置16 h之后脱模, 到24 h放入恒温40 ℃的水中养护28 d, 之后在室内存放.选取3块混凝土试块, 测得混凝土的单轴抗压强度为35.1 MPa, 劈裂强度为5.5 MPa.

对于受压试件, 首先要涂贴三层塑料薄膜, 各层间涂硫化钼油膏, 以消除试块和压头之间的摩擦力.

加载设备采用大连理工大学“海岸和近海工程”国家重点实验室的电液伺服系统试验机, 3个方向均可以分别采用位移反馈控制和荷载反馈控制, 详细信息见文献[9].

为了测量试块的受力和变形, 在设备的每个轴向安装有一个荷载传感器和一对型号相同的LVDT位移传感器.荷载传感器出厂设计量程为2 500 kN, 整个测力系统在250 kN时重复性误差小于4 kN；荷载在0~1 000 kN下, 非线性误差小于40 kN；荷载在0~1 400 kN下变化时, 非线形误差小于60 kN.每个轴向测得的荷载除以垂直于该轴向的试块截面面积认为是相应轴向的正应力.

位移传感器量程为20 mm, 出厂非线性度为千分之一.详细布置图见图 1.测量同一轴向位移的两个传感器固定在压头侧面, 关于轴线对称.二者测得量的平均值是两个压头在该轴向的相对位移, 近似认为是试块长度的变化值.该值除以试块在该方向上的长度, 认为是试块的应变.

图 1

图 1 真三轴试验设备 Fig. 1 Ture triaxial experimental machine

约定压应力和压应变为正.记σ_x、σ_y、σ_z和ε_x、ε_y、ε_z分别为X、Y、Z轴向的应力和应变.

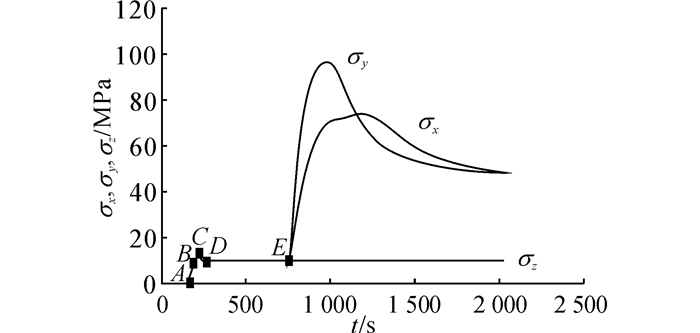
选择一个试块为例, 用实测原始数据来描述加载过程.加载方法如图 2、3所示.整个过程分为两个阶段：第一阶段对应于图 2中A到E, 第二阶段对应于E点之后.

图 2

图 2 3个轴向应力随时间的变化图 Fig. 2 Relationships between three axial stresses and time

图 3

图 3 3个轴向应变随时间的变化图 Fig. 3 Relationships between three axial strains and time

第一阶段, 在3个方向保持应力比为1:1:1的条件下进行加载.从A点开始, 应力第一次到达设计值σ_x=σ_y=σ_z=p时, 对应于图 2中B点；之后施加一个应力增量2.5 MPa, 到达C点；再施加一个应力增量-2.5 MPa, 到达D点；从D点开始一直到E点, 应力保持恒定, 应力为σ_x=σ_y=σ_z=p.BC-CD-DE的加载过程是为了消除试块和减摩层的黏塑性应变, 详细解释见文献[10].

第二阶段, 保持Z轴向压力σ_z恒定, 同时保持X轴应变速率${\dot \varepsilon _x} $和Y轴应变速率${\dot \varepsilon _y} $之比$\alpha = {\dot \varepsilon _x}/{\dot \varepsilon _y}$恒定.在该条件下, 单调地增加Y轴应变.

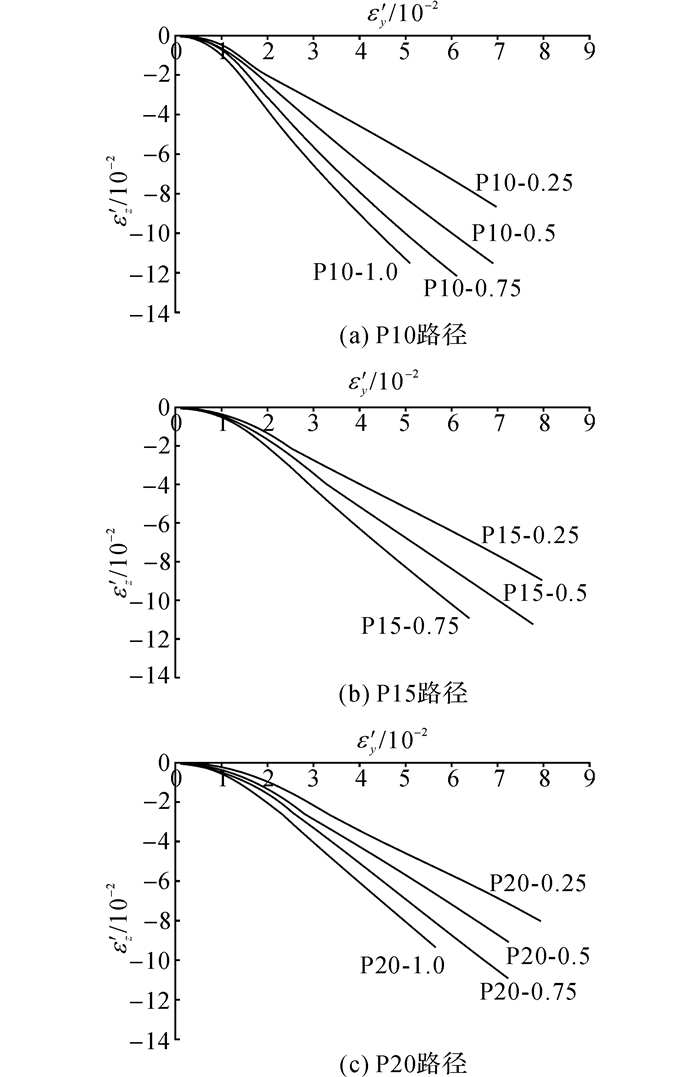
整个试验的加载路径有11条, 对应于p与α的取值组合, 试验中p的取值有3档：10 MPa、15 MPa、20 MPa.每档p对应的应变速率比α的取值有3到4档, 分别在0.25、0.5、0.75、1.0中选取.用p与α的组合来定义加载路径的代号, 例如, 应力路径的符号P10-0.25, 表示第二阶段的起点应力为10 MPa, 加载应变速率比为0.25, 如图 4和表 2中的符号所示.

图 4

图 4 不同加载路径下ε′z-ε′y关系曲线 Fig. 4 Relationship between ε′z and ε′y under different load paths

表 2

表 2 ε′z-ε′y曲线中从不同起点到终点的曲线(N1N2)按照直线拟合得到的斜率 Table 2 Slope of fitting straight line (N1N2) of ε′z-ε′y from different starting points to end 加载路径 试块编号 拟合直线方程斜率和方差 近似斜直线起点N1横坐标的选择 K1(j)之间最大相对误差/% ε′y(1)=2ε′y(p) ε′y(l)=2.5ε′y(p) ε′yl=3ε′y(p) ε′y(l)=3.5ε′y(p) P10-0.25 P10-0.25-1 K1(j) 1.322 6 1.335 9 1.351 8 1.369 8 3.445 759 R2 0.999 5 0.999 6 0.999 7 0.999 8 0.030 006 P10-0.25-2 K1(j) 1.302 2 1.316 1 1.330 9 1.347 7 3.376 122 R2 0.999 7 0.999 8 0.999 9 0.999 9 0.020 002 P10-0.5 P10-0.5-1 K1(j) 1.806 5 1.792 6 1.773 1.752 2 3.005 812 R2 0.999 9 0.999 9 0.999 9 0.999 9 0 P10-0.5-2 K1(j) 1.775 8 1.782 8 1.779 8 1.764 9 1.004 039 R2 1 1 1 1 0 P10-0.5-3 K1(j) 1.784 7 1.743 1 1.710 1 1.683 7 5.659 214 R2 0.999 0.999 5 0.999 8 0.999 9 0.090 009 P10-0.75 P10-0.75-1 K1(j) 2.051 6 2.022 3 2.001 1.983 4 3.324 235 R2 0.999 5 0.999 8 0.999 9 1 0.05 P10-0.75-2 K1(j) 2.102 4 2.042 5 1.999 6 1.976 4 5.993 151 R2 0.998 7 0.999 5 0.999 8 0.999 9 0.120 012 P10-1.0 P10-1.0-1 K1(j) 2.417 3 2.358 2 2.316 4 2.288 4 5.332 396 R2 0.999 0.999 6 0.999 9 1 0.1 P10-1.0-2 K1(j) 2.414 7 2.343 3 2.295 2.268 7 6.046 3 R2 0.998 8 0.999 6 0.999 9 1 0.12 P15-0.25 P15-0.25-1 K1(j) 1.243 7 1.253 3 1.266 1.280 8 2.896 627 R2 0.999 9 0.999 9 1 1 0.01 P15-0.25-2 K1(j) 1.254 3 1.268 3 1.281 1 1.294 1 3.075 496 R2 0.999 8 0.999 9 0.999 9 1 0.02 P15-0.5 P15-0.5-1 K1(j) 1.610 9 1.608 9 1.607 4 1.605 3 0.347 632 R2 1 1 1 1 0 P15-0.5-2 K1(j) 1.61 1.616 2 1.621 9 1.624 3 0.880 379 R2 1 1 1 1 0 P15-0.75 P10-0.75-1 K1(j) 1.870 6 1.854 4 1.839 3 1.833 5 1.983 321 R2 0.999 9 1 1 1 0.01 P10-0.75-2 K1(j) 1.929 4 1.902 8 1.887 1.874 2 2.860 993 R2 0.999 8 1 1 1 0.02 P20-0.25 P20-0.25-1 K1(j) 1.004 3 0.994 6 0.992 9 - 1.135 119 R2 0.999 9 1 1 - 0.01 P20-0.25-2 K1(j) 1.017 1.009 6 1.003 9 0.999 6 1.710 914 R2 1 1 1 1 0 P20-0.5 P20-0.5-1 K1(j) 1.009 5 0.997 6 0.990 7 0.988 2.129 767 R2 0.999 8 0.999 9 0.999 9 0.999 7 0.020 002 P20-0.5-2 K1(j) 1.185 1 1.202 1.2231 - 3.106 86 R2 0.999 8 0.999 8 0.999 4 - 0.040 008 P20-0.75 P20-0.75-1 K1(j) 1.164 2 1.180 7 1.195 4 - 2.610 005 R2 0.999 8 0.999 7 0.998 6 - 0.120 024 P20-0.75-2 K1(j) 1.498 1 1.500 8 1.505 1 - 0.465 085 R2 1 1 1 - 0 P20-1.0 P20-1.0-1 K1(j) 1.466 1 1.477 4 1.486 9 1.495 8 1.985 56 R2 0.999 9 1 1 1 0.01 P20-1.0-2 K1(j) 1.796 1 1.788 7 1.790 8 - 0.412 004 R2 0.999 9 0.999 9 0.999 7 - 0.020 002

表 2 ε′z-ε′y曲线中从不同起点到终点的曲线(N1N2)按照直线拟合得到的斜率 Table 2 Slope of fitting straight line (N1N2) of ε′z-ε′y from different starting points to end

引入符号：

ε′_i=ε_i-ε_{i, E}；i=x, y, z.

式中：ε_{i, E}为图 2中E点对应的i轴向的应变.在对加载第二阶段的数据进行分析处理时, 使用ε′_i可以消除之前各轴向应变误差的影响.图 3给出加载过程中ε′_i与时间t的关系曲线.当强调主应力的大小顺序时, 用σ₁、σ₂、σ₃来表示应力, 它们满足约束关系σ₁≥σ₂≥σ₃.

从每种加载路径中选取一个试块的数据为代表, 绘制不同最小主应力下ε′_z-ε′_y的曲线图, 如图 4所示.图中, 不同加载应变速率比对应的ε′_z-ε′_y的后半部分虽然近似直线, 但不是相互平行的.

图 4中所有ε′_z-ε′_y曲线的后半部分都近似呈直线, 定义N₁N₂为曲线中近似直线段, 其中N₁为近似直线段的起点, N₂为近似直线段的终点, 如图 5所示.

图 5

图 5 ε′z-ε′y曲线特征点标示图 Fig. 5 Feature points of ε′z-ε′y

1) 不同起点对应的K_1(j).

近似直线段的直线程度与起点N₁的位置选取有关.为了研究起点的影响, 选取4档ε′_y(1)(N₁点的横坐标)的取值, 分别按照直线拟合.依次取ε′_y(1)等于2ε′_y(p)、2.5ε′_y(p)、3ε′_y(p)、3.5ε′_y(p), 其中ε′_y(p)为Y轴强度峰值点N₀对应的应变ε′_y, 如图 5所示；然后在近似直线段N₁N₂所在的区间内, 对ε′_y-ε′_z曲线按照以下方程来回归：

式中：j依次取为2、2.5、3和3.5, 分别对应于N₁点横坐标ε′_y(1), 取2ε′_y(p)、2.5ε′_y(p)、3ε′_y(p)和3.5ε′_y(p).

将回归得到的K_1(j)和R²列于表 2.可知, 无论ε′_y(1)在2ε′_y(p)、2.5ε′_y(p)、3ε′_y(p)、3.5ε′_y(p)中取何值, 对应的R²都相差无几, 说明在该范围内选取ε′_y(1)时, 似直线段都非常接近直线.对于最小主应力为10 MPa, 加载应变速率比α=1.0的试块, K₁₍₂₎、K_1(2.5)、K₁₍₃₎和K_1(3.5)之间的相对误差最大, 但其中的最大值仅为6.05%.这说明对于每一条ε′_z-ε′_y曲线的近似直线段N₁N₂, 起点N₁的横坐标ε′_y(1)在2ε′_y(p)、2.5ε′_y(p)、3ε′_y(p)和3.5ε′_y(p)中取值时, 无论取何值, 对拟合直线斜率的影响都不大.

2)K_1(j)~α关系.

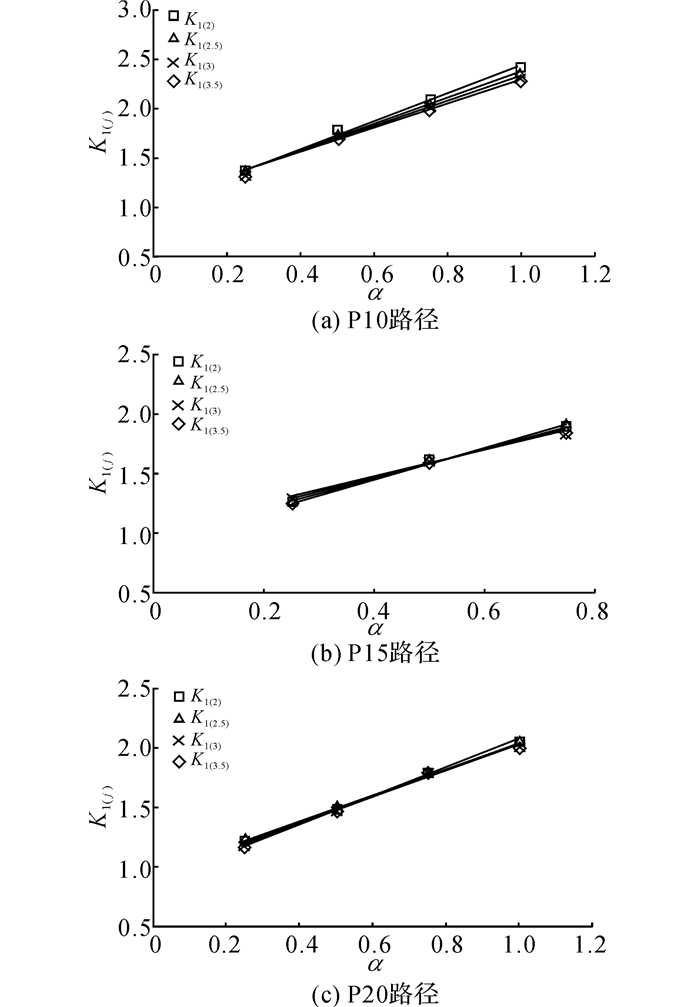
根据表 2的数据, 分别绘制各档σ_z取值对应的K_1(j)和α之间的关系曲线于图 6中, 再按照线性公式

图 6

图 6 不同加载路径下K1(j)-α关系图 Fig. 6 Relationship between K1(j) and α under different load paths

对图 6的曲线进行拟合.在加载路径为P20-0.25和P20-1.0的曲线中(加载路径符号的说明详见1.3节), 当曲线结束时, ε′_y的数据小于ε′_y(1)=3.5ε′_y(p), 这两种加载路径下没有K_1(3.5)和K_2(3.5), 参见图 6(c).由图 6可以看出, 在相同的最小主应力下, K_1(j)=K_2(j)α+H_2(j)拟合直线几乎重合在一起.

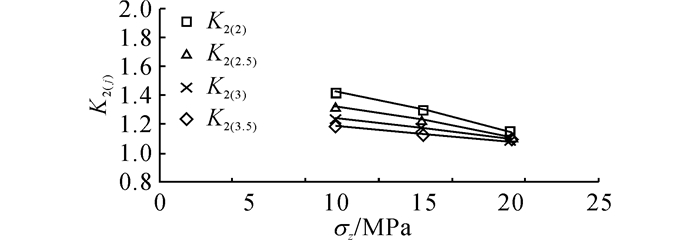
选取式(2) 中每一档σ_z的取值与对应的回归系数K_2(j)来绘制K_2(j)-σ_z曲线, 详见图 7.不论是K₂₍₂₎、K_2(2.5)、K₂₍₃₎还是K_2(3.5), 都随着σ_z的增加而减小.

图 7

图 7 不同加载路径下K2(j)-σz关系图 Fig. 7 Relationships between K2(j) and σz under different load paths

根据定义$\alpha = {\dot \varepsilon _x}/{\dot \varepsilon _y} $, 可得α=dε_x/dε_y.由1.4节可知, ε′_i=ε_i-ε_{i, E}, 其中ε_{i, E}为常数, 所以α=dε_x/dε_y=dε′_x/dε′_y, 进一步得到

在加载的第二阶段, α为已知的常数, 加载路径存在约束关系dε′_x=αdε′_y和dσ_z=0.当给出一个dε′_y时, 相当于dε′_x、dε′_y和dσ_z全部已知, 可将dε′_x、dε′_y和dσ_z视为作用量, 相应地, 将dσ_x、dσ_y和dε_z视为响应量.因此有,

由于dσ_z=0, 式(4) 简化为

将式(3) 代入式(5), 可得

写成导数形式, 则

由式(1) 可得, K_1(j)=-dε′_z/dε′_y.将其代入式(2), 再与式(6) 比较, 可得

代入式(6), 写成微分形式, 则

由2.1节的分析可知, 初始起点的选择对拟合直线斜率影响不大, 并且K_1(j)=K_2(j)α+H_2(j)拟合直线几乎重合在一起, 所以任意选取图 6中的K₂₍₃₎与式(7) 进行比较, 如表 3所示.

表 3

表 3 不同σz对应的∂ε′z/∂ε′x和∂ε′z/∂ε′y的值 Table 3 Values of ∂ε′z/∂ε′x and ∂ε′z/∂ε′y for different σz σz/MPa $\frac{{\partial \varepsilon {'_z}}}{{\partial \varepsilon {'_x}}} =-{K_{2\left( 3 \right)}} $ $\frac{{\partial \varepsilon {'_z}}}{{\partial \varepsilon {'_y}}} =-{H_{2\left( 3 \right)}} $ 10 -1.245 -1.080 15 -1.179 -0.994 20 -1.095 -0.945

表 3 不同σz对应的∂ε′z/∂ε′x和∂ε′z/∂ε′y的值 Table 3 Values of ∂ε′z/∂ε′x and ∂ε′z/∂ε′y for different σz

∂ε′_z/∂ε′_x和∂ε′_z/∂ε′_y的绝对值随着最小主应力的增加而减小, 这一现象与剪切带的变形特性有关.剪切带两侧块体发生错动时, 剪切带上的颗粒会随之转动, 并产生一定的膨胀量.当剪切带上压应力较大时, 剪切带的颗粒在转动时被压碎成更小颗粒的概率较大, 颗粒转动产生的膨胀量较小；反之, 当压应力较小时, 颗粒转动时被压碎的概率较小, 产生的膨胀量较大.

ε′_z-ε′_y曲线的后一部分出现直线段, 是与破坏模式相关的.当Y轴应力达到峰值强度时, 试块发生剪切破坏, 当剪切带两侧块体发生相对的滑动时, ε′_z和ε′_y呈线性关系.试块的变形包含3个部分：剪切带两侧块体的刚性滑移、块体内部的变形以及剪切面附近的剪切带的膨胀和收缩.虽然∂ε′_z/∂ε′_x和∂ε′_z/∂ε′_y的具体数值不能用来直接计算剪切面的倾角, 但是它对分析破坏形态, 以及估算剪切面的倾角具有重要的意义和参考价值.

(1) 当最小主应力相同而加载应变速率不同时, ε′_z-ε′_y曲线的后半部分近似成斜直线, 但是彼此之间不平行.这种线性关系与破坏形态有关, 也表明剪切带两侧块体发生了刚性滑移.

(2) 经过数据分析和公式的推导, 可以将最小主应力相同而应变速率比不同的∂ε′_z/∂ε′_x和∂ε′_z/∂ε′_y, 回归出相同的数值.∂ε′_z/∂ε′_x和∂ε′_z/∂ε′_y的绝对值随着最小主应力的增加而减小, 这一现象与剪切带两侧块体发生相对滑动时, 剪切带内部颗粒的滚动有关.

(3) 试块的变形包含3个部分：剪切带两侧块体的刚性滑移、块体内部的变形以及剪切面附近的剪切带的膨胀和收缩.∂ε′_z/∂ε′_x和∂ε′_z/∂ε′_y可以用来估算剪切带的倾角.