2. 浙江大学 唐仲英传感材料及应用研究中心, 浙江 杭州 310058
2. Cyrus Tang Center for Sensor Materials and Applications, Zhejiang University, Hangzhou 310058, China
钢-混组合梁将钢与混凝土组合在一起协同工作, 充分发挥钢材和混凝土的材料特性, 从而具有重量轻、强度高、建筑高度小、抗震性能好等优点.预应力钢-混组合梁能够克服非预应力钢-混组合梁挠度大、易开裂、耐久性差等缺点.笔者等在前期的研究中, 提出采用横向预应力提高多梁式组合小箱梁桥桥面结构横向整体性的方法, 并获国家的发明专利授权[1], 该结构在桥面板抗裂、耐久性等方面具有一定的优势.
一般来讲, 钢-混组合梁的钢梁与混凝土桥面板是通过剪力连接件和界面粘结作用组合而共同受力.目前应用较广泛的是栓钉柔性剪力连接件, 其在竖向荷载作用下, 钢梁与混凝土板的界面出现滑移将不可避免, 并导致组合梁刚度降低、变形增大, 截面承载力减小[2];同时, 由于预应力及混凝土收缩徐变, 将会引起组合结构内力和应力的重分布, 进一步增加界面滑移.在研究组合梁界面滑移时, 不仅需要考虑短期荷载效应, 还需考虑桥梁服役期桥面板混凝土的长期效应及引起结构内力重分布对滑移产生的影响.
国内外对一般的钢-混组合梁桥已展开了深入的研究, 如Angelo等[3]构建了考虑滑移和收缩徐变影响的组合梁截面内力微分方程, Gjelsvik[4]提出在组合梁交界面有一假想的剪切层来模拟组合梁界面相对滑移的方法.聂建国等[5-6]推导组合梁交界面相对滑移的计算公式, 研究考虑界面滑移的预应力组合梁的变形性能.蒋丽忠[7]利用Goodman弹性夹层假设及弹性体变形理论推导了均布荷载下组合梁界面滑移的理论计算公式.王刚[8]研究双层钢-混凝土组合梁上下层界面滑移的微分方程, 由于形式过于繁琐, 没有给出解析解.笔者等之前对横向预应力下多梁式组合小箱梁长期性能进行分析探讨[9].
目前, 对预应力钢-混组合梁桥界面的滑移及考虑混凝土长期性能影响的组合梁桥滑移计算几乎未见报道.国内现行规范[10]中有关组合梁滑移效应, 采用折减刚度法计算滑移引起的附加挠度, 尚未考虑混凝土长期效应对滑移的影响, 这样是偏不安全的.本文针对施加体外预应力的钢-混组合梁, 考虑预应力施加和混凝土长期性能对组合梁界面滑移的影响, 研究界面滑移时变的计算公式, 探讨混凝土长期效应作用下的组合梁滑移变化规律.
1 体外预应力组合梁一般粘结滑移效应的理论推导Gara等[2-5]的实验和数值分析表明, 钢-混凝土组合梁在使用荷载作用下, 钢梁处于弹性工作阶段, 混凝土翼缘的最大压应变位于应力-应变曲线的上升段.为了简化分析模型, 在分析滑移效应时, 近似地将组合梁作为弹性体来考虑, 参照文献[5-6], 作如下假设.
1) 忽略组合梁的掀起效应, 认为钢梁和混凝土翼缘板具有相同的曲率.
2) 组合梁交界面上的水平剪切应力与相对滑移成正比.
3) 混凝土桥面板与钢梁分别符合平截面假定, 如图 1所示.

|
图 1 组合梁滑移分析模型及横截面应力分布图 Fig. 1 Analysis model of slip and cross-sectional stress distribution in steel-concrete composite bridge |
考虑跨中承受一集中荷载的情况, 设剪力连接键的间距为d, 钢与混凝土交接面单位距离的水平切应力为τ, 连接件刚度系数为K, 相对滑移为S, 由假设2) 可得
| $ d \cdot \tau = K \cdot S. $ | (1) |
截取梁微段模型如图 2所示, 由水平方向受力平衡
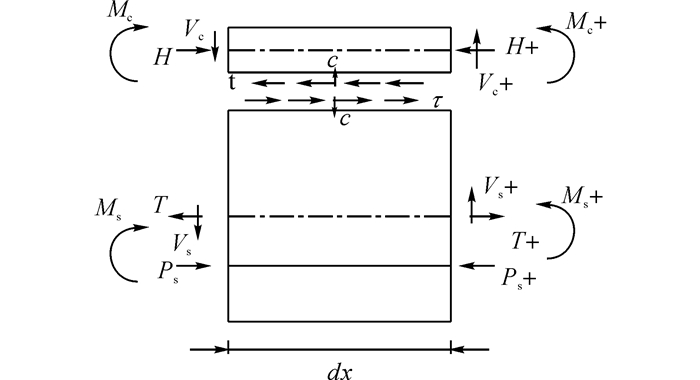
|
图 2 梁微段及作用的力示意图 Fig. 2 Micro-segment beam & forces acted on it |
| $ \frac{{{\rm{d}}H}}{{{\rm{d}}x}} = - \tau , $ | (2) |
| $ \frac{{{\rm{d}}T - {\rm{d}}{P_s}}}{{{\rm{d}}x}} = - \tau . $ | (3) |
式中:H为混凝土梁的轴力, T为钢梁的轴力, Ps为体外预应力.
对混凝土和钢梁截面右侧形心分别取矩, dc为混凝土桥面板截面形心到钢梁截面形心的距离, dc=d1-d2, 其中d1、d2分别为体外预应力筋距离混凝土桥面板形心和钢梁形心的距离, 化简可得
| $ \frac{{{\rm{d}}{M_{\rm{c}}}}}{{{\rm{d}}x}} + {V_{\rm{c}}} = \tau \cdot {h_{\rm{c}}}/2 + c \cdot {\rm{d}}x/2, $ | (4) |
| $ \frac{{{\rm{d}}{M_{\rm{s}}}}}{{{\rm{d}}x}} + {V_{\rm{s}}} = \tau \cdot {h_{\rm{s}}}/2 - c \cdot {\rm{d}}x/2 + \frac{{{\rm{d}}{M_{\rm{p}}}}}{{{\rm{d}}x}}. $ | (5) |
式中:Mc为混凝土翼缘板截面绕自身形心轴的弯矩, Vc为混凝土翼缘板截面剪力, Ms为钢梁截面绕自身形心轴的弯矩, Vs为钢梁截面剪力, c为钢混梁之间的竖向作用力与反作用力, hc为混凝土翼缘板截面高度, hs为钢梁截面高度.
当组合梁跨中作用集中荷载F, 有Vc+Vs=F/2, 则由式(4)、(5) 以及hc+hs=h, 可以得到
| $ \frac{{{\rm{d}}{M_{\rm{c}}}}}{{{\rm{d}}x}} + \frac{{{\rm{d}}{M_{\rm{s}}}}}{{{\rm{d}}x}} + F/2 = \tau \cdot h/2 + \frac{{{\rm{d}}{M_{\rm{p}}}}}{{{\rm{d}}x}}. $ | (6) |
由混凝土板及钢梁的曲率相同(假设1), 可得
| $ {\varphi _1} = \frac{{{M_{\rm{c}}}}}{{{E_{\rm{c}}}{I_{\rm{c}}}}} = \frac{{{\alpha _{\rm{E}}} \cdot {M_{\rm{c}}}}}{{{E_{\rm{s}}}{I_{\rm{c}}}}} = \frac{{{M_{\rm{s}}} - {M_{\rm{p}}}}}{{{E_{\rm{s}}}{I_{\rm{s}}}}}. $ | (7) |
式中:αE为钢与混凝土材料弹性模量之比, αE=Es/Ec.
混凝土板底部拉应变εtc和钢梁顶部拉应变εts分别为
| $ {\varepsilon _{{\rm{tc}}}} = \frac{{{\varphi _1} \cdot {h_{\rm{c}}}}}{2} - \frac{{{\alpha _{\rm{E}}} \cdot H}}{{{E_{\rm{s}}}{A_{\rm{c}}}}}, $ | (8) |
| $ {\varepsilon _{{\rm{ts}}}} = \frac{{T - {P_{\rm{s}}}}}{{{E_{\rm{s}}}{A_{\rm{s}}}}} - \frac{{{\varphi _1} \cdot {h_{\rm{s}}}}}{2}. $ | (9) |
交界面相对滑移应变εs为
| $ {\varepsilon _{\rm{s}}} = S' = {\varepsilon _{{\rm{tc}}}} - {\varepsilon _{{\rm{ts}}}} = \frac{{{\varphi _1} \cdot h}}{2} - \frac{{{\alpha _{\rm{E}}}H}}{{{E_{\rm{s}}}{A_{\rm{c}}}}} - \frac{{T - {P_{\rm{s}}}}}{{{E_{\rm{s}}}{A_{\rm{s}}}}}. $ | (10) |
由式(7) 可得
| $ {M_{\rm{s}}} - {M_{\rm{p}}} = {E_{\rm{s}}}{I_{\rm{s}}} \cdot {\varphi _1}, $ | (11) |
| $ {M_{\rm{c}}} = {E_{\rm{s}}}{I_{\rm{c}}} \cdot {\varphi _1}/{\alpha _{\rm{E}}}. $ | (12) |
将式(11)、(12) 代入式(6), 同时根据式(1), 并令I0=Is+Ic/αE, 化简可得
| $ \frac{{{\rm{d}}{\varphi _1}}}{{{\rm{d}}x}} = \frac{{\left( {K \cdot S \cdot h/\left( {2d} \right) - F/2} \right)}}{{{E_{\rm{s}}}{I_{\rm{0}}}}}. $ | (13) |
对式(10) 求一次导, 并将式(1)~(3) 和(13) 代入并化简可得
| $ S'' = {m^2}S - \frac{{{m^2}nF}}{2}. $ | (14) |
式中:
| $ \begin{array}{l} {m^2} = \frac{{K \cdot A'}}{{{E_{\rm{s}}}{I_0} \cdot d}},n = \frac{{h \cdot d}}{{2K \cdot A'}},A' = {I_0}/{A_0} + {\left( {h/2} \right)^2},\\ \frac{1}{{{A_0}}} = \frac{1}{{{A_{\rm{s}}}}} + \frac{{{\alpha _{\rm{E}}}}}{{{A_{\rm{c}}}}}, \end{array} $ |
其中As、Ac分别为钢梁和混凝土板截面面积.
m2和m2nF/2为常数, 求解该常系数二阶微分方程可知, 通解为S=C1exp (mx)+C2exp (-mx), S=nF/2为方程一特解.由边界条件, S(x=0)=0, S′(x=l/2)=Psd2dc/(EsI0), 可得C1和C2, 化简得到考虑施加预应力影响的组合梁滑移量计算表达式:
| $ {C_1} = \frac{1}{{\exp \left( {ml} \right) + 1}}\left( {\frac{{\exp \left( {ml/2} \right)}}{m} \cdot \frac{{{P_{\rm{s}}}{d_2}{d_{\rm{c}}}}}{{{E_{\rm{s}}}{I_0}}} - nF/2} \right), $ | (15) |
| $ \begin{array}{l} {C_2} = \frac{{ - 1}}{{\exp \left( {ml} \right) + 1}}\left( {\frac{{\exp \left( {ml/2} \right)}}{m} \cdot \frac{{{P_{\rm{s}}}{d_2}{d_{\rm{c}}}}}{{{E_{\rm{s}}}{I_0}}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\exp \left( {ml} \right) \cdot nF/2} \right), \end{array} $ | (16) |
| $ S = {C_1}\exp \left( {mx} \right) + {C_2}\exp \left( { - mx} \right) + nF/2. $ | (17) |
相应地, 可得滑移应变的计算公式:
| $ {\varepsilon _{\rm{s}}} = S' = m\left[ {{C_1}\exp \left( {mx} \right) - {C_2}\exp \left( { - mx} \right)} \right]. $ | (18) |
在有体外预应力的钢-混组合桥梁中, 随着使用年龄的增长, 桥面板混凝土会发生收缩徐变和预应力钢筋的松弛等, 将使组合截面发生内力和应力的重分布.这种效应会导致组合梁的界面滑移随着时间发生变化.我国现行的《公路钢筋混凝土及预应力混凝土桥涵设计规范》对混凝土徐变的影响采用有效弹性模量法近似计算.结合已有的研究成果[11-16], 可以推导考虑混凝土收缩徐变影响下的预应力组合梁滑移计算公式.
沿用前面提出的假设, 考虑跨中仅承受一集中荷载的情况, 其中右下角的小标表示考虑长期效应随时间的变化值.由假设(2), 可得
| $ d \cdot {\tau _t} = K \cdot {S_t}, $ | (19) |
| $ \frac{{{\rm{d}}{H_t}}}{{{\rm{d}}x}} = - {\tau _t}, $ | (20) |
| $ \frac{{{\rm{d}}{T_t} - {\rm{d}}{P_{st}}}}{{{\rm{d}}x}} = - {\tau _t}, $ | (21) |
| $ \frac{{{\rm{d}}{M_{{\rm{c}}t}}}}{{{\rm{d}}x}} + \frac{{{\rm{d}}{M_{{\rm{s}}t}}}}{{{\rm{d}}x}} + F/2 = {\tau _t}h/2 + \frac{{{\rm{d}}{M_{{\rm{p}}t}}}}{{{\rm{d}}x}}. $ | (22) |
由假设(1), 采用龄期调整的有效弹性模量法考虑混凝土收缩徐变, 可得
| $ \begin{array}{l} {\varphi _t} = \frac{{{M_{{\rm{s}}t}} - {M_{{\rm{p}}t}}}}{{{E_{\rm{s}}}{I_{\rm{s}}}}} = \frac{{{M_{{\rm{c}}0}}}}{{{I_c}}} \cdot \frac{{\phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}}}\left[ {1 - {\rm{\chi }}\left( {t,{t_0}} \right)} \right] + \\ \;\;\;\;\;\;\;\frac{{{M_{{\rm{c}}t}}}}{{{I_{\rm{c}}}}}\left[ {\frac{1}{{{E_{\rm{c}}}\left( {{t_0}} \right)}} + \frac{{{\rm{\chi }}\left( {t,{t_0}} \right) \cdot \phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}}}} \right]. \end{array} $ | (23) |
式中:χ(t, t0)为混凝土老化系数;ϕ(t, t0)为混凝土徐变系数, 可以按CEB-FIP1990模型计算;Ec(t0)为初始加载时刻t0时的混凝土弹性模量, Ec为混凝土28天龄期弹性模量;Mc0为未考虑长期作用时的初期结构弯矩.
考虑收缩应变εtsh, 交界面相对滑移应变εst为
| $ \begin{array}{l} {\varepsilon _{{\rm{s}}t}} = {{S'}_t} = \varepsilon _t^{{\rm{sh}}} - \frac{{{T_t} - {P_{{\rm{s}}t}}}}{{{E_{\rm{s}}}{A_{\rm{s}}}}} + \frac{{{M_{{\rm{s}}t}} - {M_{{\rm{p}}t}}}}{{{E_{\rm{s}}}{I_{\rm{s}}}}} \cdot {h_{\rm{s}}} - \\ \;\;\;\;\;\left[ {\frac{{{N_0}}}{{{A_{\rm{c}}}}} - \frac{{{M_{{\rm{c}}0}}}}{{{I_{\rm{c}}}}} \cdot {h_{\rm{c}}}} \right] \cdot \frac{{\phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}}} \cdot \left[ {1 - {\rm{\chi }}\left( {t,{t_0}} \right)} \right] - \\ \;\;\;\;\;\left[ {\frac{{{N_t}}}{{{A_{\rm{c}}}}} - \frac{{{M_{{\rm{c}}t}}}}{{{I_{\rm{c}}}}} \cdot {h_{\rm{c}}}} \right] \cdot \left[ {\frac{1}{{{E_{\rm{c}}}\left( {{t_0}} \right)}} + \frac{{{\rm{\chi }}\left( {t,{t_0}} \right) \cdot \phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}}}} \right]. \end{array} $ | (24) |
将式(23) 代入式(24), 可得
| $ \begin{array}{l} {\varepsilon _{{\rm{s}}t}} = {{S'}_t} = \varepsilon _t^{{\rm{sh}}} - \frac{{{T_t} - {P_{{\rm{s}}t}}}}{{{E_{\rm{s}}}{A_{\rm{s}}}}} + \frac{{{M_{{\rm{s}}t}} - {M_{{\rm{p}}t}}}}{{{E_{\rm{s}}}{I_{\rm{s}}}}} \cdot \frac{h}{2} - \frac{{{H_t}}}{{{A_{\rm{c}}}}} \times \\ \;\;\;\;\;\frac{{\phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}}} \cdot \left[ {1 - {\rm{\chi }}\left( {t,{t_0}} \right)} \right] - \frac{{{H_t}}}{{{A_{\rm{c}}}}} \times \\ \;\;\;\;\;\left[ {\frac{1}{{{E_{\rm{c}}}\left( {{t_0}} \right)}} + \frac{{{\rm{\chi }}\left( {t,{t_0}} \right) \cdot \phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}}}} \right]. \end{array} $ | (25) |
将式(13)、(17) 和(23) 代入式(22), 令C=[EsIs+1/B], 整理化简可得
| $ \begin{array}{l} \frac{{{\rm{d}}{\varphi _t}}}{{{\rm{d}}x}} = \frac{{Kh}}{{2dC}} \cdot {S_t} - \frac{F}{{2C}} + \frac{{A{E_{\rm{c}}}{I_{\rm{c}}}}}{{BC{E_{\rm{s}}}{I_0}}} \times \\ \left[ {\frac{{Kh}}{{2d}}\left( {{C_1}\exp \left( {mx} \right) + {C_2}\exp \left( { - mx} \right) + {\alpha _{\rm{E}}}F/2} \right) - F/2} \right]. \end{array} $ | (26) |
对式(25) 求一次导, 考虑到收缩应变沿梁长均匀分布, 同时将式(26) 代入, 整理化简为
| $ \begin{array}{l} {{S''}_t} = Q \cdot {L_t} + Y \cdot F/2 + \\ \;\;\;\;\;\;\;R\left( {{C_1}\exp \left( {mx} \right) + {C_2}\exp \left( { - mx} \right)} \right). \end{array} $ | (27) |
式中:
| $ Q = D + \frac{{K{h^2}}}{{4dC}}, $ |
| $ \begin{array}{l} R = \frac{{A \cdot {E_{\rm{c}}}{I_{\rm{c}}}}}{{B \cdot C \cdot {E_{\rm{s}}}{I_0}}} \cdot \frac{{K \cdot {h^2}}}{{4d}} + \frac{{\phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}{A_{\rm{c}}}}} \cdot \frac{K}{d} \times \\ \;\;\;\;\;\;\left[ {1 - {\rm{\chi }}\left( {t,{t_0}} \right)} \right], \end{array} $ |
| $ Y = R \cdot n - \frac{{A \cdot {E_{\rm{c}}}{I_{\rm{c}}} \cdot h}}{{2B \cdot {E_{\rm{s}}}{I_0} \cdot C}} - \frac{h}{{2C}}, $ |
| $ A = \frac{{\phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}{I_{\rm{c}}}}}\left[ {1 - {\rm{\chi }}\left( {t,{t_0}} \right)} \right], $ |
| $ B = \frac{1}{{{E_{\rm{c}}}\left( {{t_0}} \right){I_{\rm{c}}}}} + \frac{{{\rm{\chi }}\left( {t,{t_0}} \right) \cdot \phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}{I_{\rm{c}}}}}, $ |
| $ D = \left[ {\frac{1}{{{E_{\rm{c}}}\left( {{t_0}} \right){A_{\rm{c}}}}} + \frac{{{\rm{\chi }}\left( {t,{t_0}} \right) \cdot \phi \left( {t,{t_0}} \right)}}{{{E_{\rm{c}}}{A_{\rm{c}}}}} + \frac{1}{{{E_{\rm{s}}}{A_{\rm{s}}}}}} \right] \cdot \frac{K}{d}. $ |
其中, Q、R、Y三个系数仅与时间有关, 对于某一特定的时刻都是一个确定的常数.求解该二阶常系数非齐次微分方程可知, 通解为
| $ \begin{array}{l} S\left( {x,t} \right) = {C_3}\exp \left( {\sqrt Q x} \right) + {C_4}\exp \left( { - \sqrt Q x} \right) + \\ \frac{{R{C_1}}}{{{m^2} - Q}} \cdot \exp \left( {mx} \right) + \frac{{R{C_2}}}{{{m^2} - Q}}\exp \left( { - mx} \right) - YF/\left( {2Q} \right). \end{array} $ | (28) |
边界条件为S(0, t)=0, S′(l/2, t)=Pt·d2dc/(EsI0t), 其中Pt为t时刻扣除预应力损失后的预应力有效值, 详细的计算方法可见文献[17, 18].可得
| $ \begin{array}{l} {C_3} = \frac{1}{{\sqrt Q \cdot \left( {\exp \left( {l\sqrt Q /2} \right) + \exp \left( { - l\sqrt Q /2} \right)} \right)}} \times \\ \;\;\;\left[ {\frac{{YF}}{{2\sqrt Q }} \cdot \exp \left( { - l\sqrt Q /2} \right) - \frac{{R\left( {{C_1} + {C_2}} \right)}}{{{m^2} - Q}} \cdot \sqrt Q \times } \right.\\ \;\;\;\exp \left( { - l\sqrt Q /2} \right) + \frac{{{P_t}{d_2}{d_{\rm{c}}}}}{{{E_{\rm{s}}}{I_{0t}}}} - \frac{{R{C_1}m}}{{{m^2} - Q}}\exp \left( {lm/2} \right) + \\ \;\;\;\left. {\frac{{R{C_2}m}}{{{m^2} - Q}} \cdot \exp \left( { - lm/2} \right)} \right]. \end{array} $ | (29) |
| $ \begin{array}{l} {C_4} = \frac{1}{{\sqrt Q \cdot \left( {\exp \left( {l\sqrt Q /2} \right) + \exp \left( { - l\sqrt Q /2} \right)} \right)}} \times \\ \;\;\;\left[ {\frac{{YF}}{{2\sqrt Q }} \cdot \exp \left( {l\sqrt Q /2} \right) - \frac{{R\left( {{C_1} + {C_2}} \right)}}{{{m^2} - Q}} \cdot \sqrt Q \times } \right.\\ \;\;\;\exp \left( {l\sqrt Q /2} \right) + \frac{{{P_t}{d_2}{d_{\rm{c}}}}}{{{E_{\rm{s}}}{I_{0t}}}} - \frac{{R{C_1}m}}{{{m^2} - Q}}\exp \left( {lm/2} \right) - \\ \;\;\;\left. {\frac{{R{C_2}m}}{{{m^2} - Q}} \cdot \exp \left( { - lm/2} \right)} \right]. \end{array} $ | (30) |
考虑混凝土收缩徐变和预应力松弛影响的体外预应力钢-混组合梁滑移计算公式推导完毕.式(28) 是根据跨中承受集中荷载的简支组合梁推得的, 对于其他形式荷载作用下简支组合梁的滑移计算公式推导同理.
3 工程实例验证为了验证理论公式的正确性, 以某工程跨越高速公路的简支钢-混组合小箱梁桥为算例进行研究.结构形式采用40 m体外预应力钢-混组合小箱梁, 钢结构部分采用全焊接钢梁, 钢梁由U型主梁, 横隔梁及加劲肋组成, 钢梁上翼缘板顶面设置剪力键与混凝土桥面板连为整体.单跨为四片钢混组合小箱梁, 桥宽为19.8 m.梁高2.5 m, 栓钉间距采用100 mm, 钢束采用抗拉强度标准值为1 860 MPa的高强度低松弛钢绞线.单梁横纵断示意图如图 3所示.

|
图 3 单梁纵横断面示意图 Fig. 3 Section of single-beam |
图 4给出采用提出的理论及方法对跨中施加集中荷载800 kN的上述钢-混组合小箱梁沿着梁长滑移量的计算结果, 无预应力的计算结果为式(28) 预应力取为零的特例.将文献[6, 7]公式的计算滑移量结果一并列入图 4, 通过比较发现本文公式的合理性.图 4进一步给出有、无体外预应力的组合梁在初始时刻滑移量沿跨径的分布对比.可以看出, 施加体外预应力会增大组合梁的初始界面滑移, 与不施加体外预应力相比, 初始滑移量增大约14%.

|
图 4 典型简支钢-混组合小箱梁粘结滑移计算结果及比较 Fig. 4 Bond-slip calculation results and comparison of typical simply-supported steel and concrete combination small box girder |
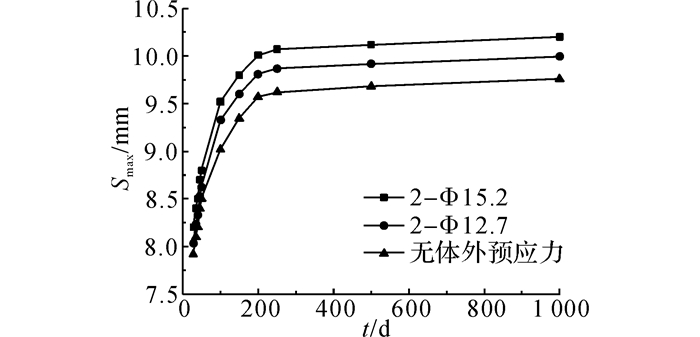
如图 5所示为不同时刻简支钢-混组合小箱梁滑移量沿梁长的分布图.如图 6所示为不同预应力下考虑混凝土收缩徐变的钢-混组合小箱梁端最大滑移量随时间的变化.

|
图 5 不同时期简支钢-混组合小箱梁滑移量沿梁长的分布 Fig. 5 Distribution of slippage along beam length at different time in simply-supported steel and concrete combination small box girder |
|
图 6 不同预应力对钢-混组合小箱梁滑移的影响 Fig. 6 Effect of prestressing on slippage at end in simply-supported steel and concrete combination small box girder |
从图 5可以看出, 在长期荷载作用下, 组合梁的滑移量由中间向梁两端逐渐增大, 在梁两端滑移量达到最大值;滑移量随时间的增加而不断增加.其中前期增长较明显, 前100 d滑移量增长几乎完成最终增长量的90%, 到500 d以后滑移量基本达到稳定.由图 6可得, 在钢梁上施加体外预应力会增大组合梁的滑移量, 施加的有效预应力越大, 组合梁的最终滑移越大;考虑混凝土长期效应的影响, 不同预应力水平下的组合梁长期滑移量均增长了18%左右, 可见改变有效预应力不会对组合梁考虑长期效应引起的滑移增量产生显著影响.
4 结论(1) 本文采用龄期调整有效弹性模量法, 考虑混凝土收缩徐变, 推导了考虑桥面板混凝土长期性能的钢-混组合梁界面滑移计算公式.通过算例分析对比验证, 证明所推导公式的正确性, 且更具一般性和适用性.
(2) 施加体外预应力会增大钢-混组合梁加载初期的界面滑移, 相比不施加体外预应力的组合梁, 初始滑移量增加约14%.在长期荷载作用下, 由于混凝土的收缩徐变, 钢-混组合梁的滑移量随时间不断增长.值得注意的是, 该滑移量前期增长较明显, 前100 d几乎完成增长量的90%, 到500 d以后基本达到稳定, 算例的滑移最终增长量约为初期滑移的18%.
(3) 考虑桥面板混凝土的收缩徐变长期效应会导致组合梁界面滑移量增加.有体外预应力筋的钢-混组合梁, 随着施加预应力的增加, 梁体的界面滑移量会随着预应力的加大而增加.在体外预应力钢-混组合梁的设计中, 除考虑预应力对组合梁桥变形性能有利的方面外, 应注意和控制预应力对组合梁界面滑移不利的影响.
| [1] |
浙江大学. 一种提高多梁式组合小箱梁桥桥面结构横向整体性的方法: 中国, CN201110356879. X[P]. 2012-04-11.
Zhejiang University. Method for improving cross integrity of bridge deck structure of multi-girder type combined small box girder bridge: China, CN20111035 6879. X[P]. 2012-04-11. |
| [2] | GARA F, RANZI G, LEONI G. Short-and long-term analytical solutions for composite beams with partial interaction and shear-lag effects[J]. International Journal of Steel Structures, 2010, 10(4): 359–372. DOI:10.1007/BF03215844 |
| [3] | ANGELO M T, LUIGINO D. Creep effects in composite beams with flexible shear connectors[J]. Journal of Structural Engineering, 1992, 118(8): 2063–2080. DOI:10.1061/(ASCE)0733-9445(1992)118:8(2063) |
| [4] | GJELSVIK A. Analog-beam method for determining shear-lag effect[J]. Journal of Engineering Mechanics, 1991, 117(7): 1575–1595. DOI:10.1061/(ASCE)0733-9399(1991)117:7(1575) |
| [5] | NIE J G, CAI C S, ZHOU T R, et al. Experimental and analytical study of prestressed steel-concrete composite beams considering slip effect[J]. Journal of Structural Engineering, 2007, 133(4): 530–540. DOI:10.1061/(ASCE)0733-9445(2007)133:4(530) |
| [6] |
聂建国, 沈聚敏, 袁彦声. 钢-混凝土简支组合梁变形计算的一般公式[J].
工程力学, 1994, 11(1): 21–27.
NIE Jian-guo, SHEN Ju-min, YUAN Yan-sheng. A general formula for predicting the deflection of simply supported composite steel-concrete beams with consideration of slip effect[J]. Engineering Mechanics, 1994, 11(1): 21–27. |
| [7] |
蒋丽忠, 余志武, 李佳. 均布荷载作用下钢-混凝土组合梁滑移及变形的理论计算[J].
工程力学, 2003, 20(2): 133–137.
JIANG Li-zhong, YU Zhi-wu, LI jia. Theoretical analysis of slip and deformation of steel-concrete composite beam under uniformly distributed loads[J]. Engineering Mechanics, 2003, 20(2): 133–137. |
| [8] |
王刚, 王福建, 申永刚, 等. 双层连续组合梁弹塑性状态的界面滑移[J].
浙江大学学报:工学版, 2008, 42(11): 2023–2027.
WANG Gang, WANG Fu-jian, SHEN Yong-gang, et al. Interface slip of double continuous composite beam in inelastic state[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(11): 2023–2027. |
| [9] |
项贻强, 李少骏, 刘丽思. 横向预应力下多梁式组合小箱梁长期性能[J].
浙江大学学报:工学版, 2015, 49(5): 956–962.
XIANG Yi-qiang, LI Shao-jun, LIU Li-si. Long-term performance of multi-box composite bridges under transverse prestressing[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(5): 956–962. |
| [10] | GB 50917-2013, 钢-混凝土组合桥梁设计规范[S]. 北京: 中国计划出版社, 2013. |
| [11] | DEZI L, GARA F, LEONI G, et al. Time-dependent analysis of shear-lag effect in composite beams[J]. Journal of Engineering Mechanics, 2001, 127(1): 71–79. DOI:10.1061/(ASCE)0733-9399(2001)127:1(71) |
| [12] |
王玉强, 张宽地, 陈晓东. 胶黏钢-混凝土组合梁的界面行为数值分析[J].
浙江大学学报:工学版, 2013, 43(9): 2023–2027.
WANG Yu-qiang, ZHANG Kuan-di, CHEN Xiao-dong. Numerical analysis on interface behavior of adhesive bonded steel-concrete composite beams[J]. Journal of Zhejiang University: Engineering Science, 2013, 43(9): 2023–2027. |
| [13] |
何余良. 多梁式钢混组合小箱梁桥受力特性及试验研究[D]. 杭州: 浙江大学, 2014.
HE Yu-liang. Mechanism properties and experimental investigation of multi-beam steel concrete composite girder bridge[D]. Hangzhou: Zhejiang University, 2014. |
| [14] | NIE J G, CAI C S. Steel-concrete composite beams considering shear slip effects[J]. Journal of Structural Engineering, 2003, 129(4): 495–506. DOI:10.1061/(ASCE)0733-9445(2003)129:4(495) |
| [15] | GARA F, LEONI G, DEZI L. A beam finite element including shear lag effect for the time-dependent analysis of steel-concrete composite decks[J]. Engineering Structures, 2009, 31(8): 1888–1902. DOI:10.1016/j.engstruct.2009.03.017 |
| [16] | DEZI L, IANNI C, TARANTINO A M. Simplified creep analysis of composite beams with flexible connectors[J]. Journal of Structural Engineering, 1993, 119(5): 1484–1497. DOI:10.1061/(ASCE)0733-9445(1993)119:5(1484) |
| [17] |
丁敏, 蒋秀根, 剧锦三. 体外预应力钢-混凝土组合梁长期挠度分析[J].
工程力学, 2010, 27(9): 94–101.
DING Min, JIANG Xiu-gen, JU Jin-san. Analysis of long-term deflection of externally prestressed steel-concrete composite beams[J]. Engineering Mechanics, 2010, 27(9): 94–101. |
| [18] | 叶见曙. 结构设计原理[M]. 北京: 人民交通出版社, 2009. |


