作为一种微创手术技术, 针穿刺广泛应用于活检、脊柱硬膜外注射、近距放射治疗、麻醉和消融等临床实践^[1-2].通常情况下, 如近距放射治疗、麻醉和活检等手术要求mm级的针穿刺精度, 当手术涉及婴儿、眼睛和耳朵等时, 要求针穿刺精度达到mm级^[3].此外, 穿刺针在穿刺过程中需要绕开血管和骨骼等障碍物而到达靶点^[4], 否则导致严重的并发症, 因此需要严格控制针穿刺的路径.传统的刚性穿刺针由于难以发生较大弯曲, 不能绕过障碍物到达靶点；斜尖柔性穿刺针具有很好的可操控性, 能够绕过障碍物到达靶点^[5].医生依靠自身的感觉以及三维解剖结构经验, 操控超柔性穿刺针沿特定路径进针极具挑战.最具潜力的机器人辅助针穿刺操控技术由于能够精确控制进针量和针尖方向, 成为近年来研究的热点^[6-7].路径规划和避障技术是机器人辅助针穿刺操控技术的两大核心问题, 多年来, 虽然有大量的相关文献对针刺路径规划问题展开了研究, 但是由于柔性穿刺针是一个非完整系统以及存在组织变形导致靶点偏移和组织结构复杂等诸多因素^[8], 柔性穿刺针路径规划和避障技术一直没有得到解决.Webster等^[8-9]通过实验证明, 在理想条件下, 斜尖柔性针沿着固定半径的圆弧路径进行穿刺, 通过改变斜尖的方向可以改变圆弧曲线的方位.此后, 大量的相关文献都基于Webster等^{[8, 10-13]}的结论来进行斜尖柔性穿刺针运动学、路径规划和避障技术研究.Webster等^{[8, 11]}基于自行车模型, 给出斜尖柔性针的正向运动学模型, 但没有给出逆向运动学模型.Park等^[13]利用随机路径(path-of-probability, POP)算法对柔性穿刺针的路径规划算法进行研究, 但是所存在的局限性将整个穿刺路径进行了等量分段处理.Duindam等^[10]利用几何学方法对柔性穿刺针的逆向运动学进行分析, 但是提供的模型都是针对特定分段数的路径, 并且为了减少自由度, 易于计算, 规定了少数操控量(旋转角度)的值.现有方法只能求出部分可行路径, 现有方法的局限性在一定程度上限制了路径规划和避障技术的研究和与应用.

相对上述方法, 本文的几何逼近法由于没有对穿刺针进行等分段、固定分段数和指定某些操控量等特殊处理, 能够遍及所有逆解.提供的运动学模型虽然是基于斜尖柔性穿刺针的特性所建立的, 但是很容易拓展到其他具有类似特点的路径规划问题中.

斜尖柔性针进行穿刺时, 针尖运动完全受控于针体在针座处的运动, 且针座与针尖运动之间无扭转迟滞效应.Duindam等^[10]将三维条件下的穿刺针比作固定速率、常俯仰率、零偏转角和回转角可控的飞机.如图 1所示, 建立针尖坐标系, 坐标原点O建立在针轴线与针尖斜面的交点处, Z轴为进针方向, X轴位于针尖偏转平面内且指向偏转方向, Y轴根据右手法则确定.图中, v_t为针尖进针速度(等于针体在基座处的进针速度)；ω_t为针尖旋转速度(通常小于针体在基座处的旋转速度)；α为回转角；β为俯仰角；γ(等于0) 为偏转角；r为圆弧路径固定半径.

图 1

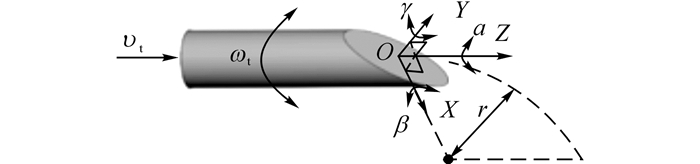
图 1 针尖坐标系 Fig. 1 Coordinate frame of needle tip

传统刚性针穿刺将针夹持在针座上, 通过针座的进给和旋转运动带动穿刺针进行穿刺^[14-17].采用该穿刺方法进行柔性穿刺针穿刺, 会使得柔性针在体外发生折曲, 无法刺入体内.与传统的刚性针穿刺过程不同, 如图 2所示, 柔性穿刺针在非常靠近针座处的驱动力作用下以及在针座的支撑下刺入组织内部^{[8-9, 18]}.图 2中, v_b为针体在针座处的进针速度, ω_b为针体在针座处的旋转速度.这种穿刺过程由于驱动力作用点非常靠近针座, 且针座在整个穿刺过程中不运动, 可以将非常柔性的穿刺针刺入组织内.根据柔性穿刺针穿刺过程的特点可知, 整个穿刺路径由多段同面或异面圆弧曲线相切形成^[19].假定整个穿刺路径由n(n为正整数)段圆弧组成, 第i(i=1, …, n)段圆弧路径长度为Δl_i.整个针穿刺过程如下：首先将针尖以特定的姿态定位于皮肤表面, 其次将针尖绕针轴线旋转α₁, 最后进针深度Δl₁, 重复进行后两步动作到刺中目标靶点T^[8-11].在针穿刺过程中, 针尖的坐标系是一个动态的更替建立过程, 即针尖在每段路径的始端时留下针尖坐标系, 到达末端时产生新的针尖坐标系, 这样不断的重复下去, 形成了如图 2所示的坐标系统.动态建立坐标系统的最大优点是可以实时地捕获针尖的位姿信息.

图 2

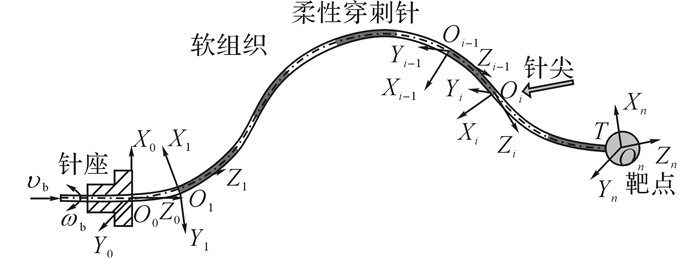
图 2 柔性穿刺针穿刺路径的离散化及坐标系统的建立 Fig. 2 Discretization of insertion path of flexible needle and establishment of its coordinate system

正向运动学是已知操控量(穿刺针初始位姿、绕针轴旋转的角度α_i和进针量Δl_i), 求取针穿刺路径.首先, 穿刺针绕针轴旋转α_i, 即坐标系O_i-1-X_i-1Y_i-1Z_i-1绕Z_i-1轴旋转α_i形成坐标系O_i-1′-X_i-1′Y_i-1′Z_i-1′；其次, 穿刺针进针深度Δl_i, 这时由于穿刺针发生了弯曲变形, 将坐标变换分两步进行，如图 3所示.1) 坐标系O_i-1′-X_i-1′Y_i-1′Z_i-1′平移(h_i, 0, d_i)形成坐标系O_i-1″-X_i-1″Y_i-1″Z_i-1″；2) 坐标系O_i-1″-X_i-1″Y_i-1″Z_i-1″绕Y_i-1″轴旋转β_i形成新的坐标系O_i-X_iY_iZ_i；不断地重复这两步, 形成了整个针穿刺过程的坐标描述.对于给定的均匀假体及穿刺针, r是确定的, 有β_i=Δl_i/r, h_i= r(1-cos β_i), d_i=rsin β_i.

图 3

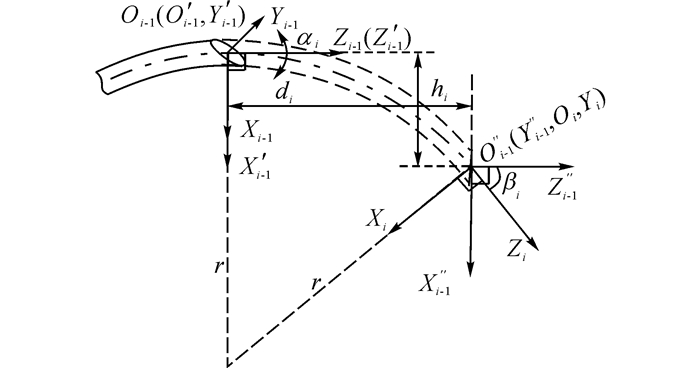
图 3 第i段路径的坐标变换 Fig. 3 Frame transformation of ith segment

综上所述, 第i段路径的齐次坐标变换矩阵如下式所示(s代表sin, c代表cos)：

在初始时刻, 针尖坐标系O₀-X₀Y₀Z₀相对于全局坐标系O-XYZ的齐次变换矩阵记为₀^gT.在针尖穿刺完第i段路径后, 针尖相对于全局坐标系的位姿可用下式表示：

当_i^i-1Tα_i, Δl_i的Δl_i用小于Δl_i的相应进针量Δl_im代替时, 可以求得针穿刺轨迹上第i段路径上的任意一点处针尖的位姿.

式(2) 中, 当i=n时, _n^gT表示针尖刺到目标靶点时的位姿, 假设_n^gT用下式表示：

在临床应用中, 往往已知病灶点在病人体中的位置以及人体解剖结构, 需要得到一组操控量, 以使穿刺针绕过障碍物精确地到达病灶点.本文不考虑穿刺避障问题, 即在已知靶点的位置而没有障碍物的情况下来求取针穿刺的逆向运动学(操控量).通常, 病灶点是一个体积元, 为了提高针穿刺的容许误差, 选择的靶点位置应该尽量靠近病灶点的中心位置.在靶点T的位置已知, 即_n^gT中的t_x、t_y和t_z已知的情况下, 式(2)(i=n时)是一个非线性的不定方程组, 直接求解运动学逆解非常困难；随着n的增加, 求解更加困难.通常情况下, 式(2)(i=n时)的逆解是一个多解的情况, 即因为多解, 路径规划有开展的可能性.本文不直接求解逆解, 通过保证针穿刺过程中的针尖对靶点的可达性来确保针尖可以到达目标靶点.如图 4所示, 在针穿刺过程中, 针尖在穿刺路径上的每一点处, 相对靶点都有一个可达空间；当靶点T超出可达空间后, 针尖无法到达靶点.为了使针尖刺中靶点, 只需要保证靶点在穿刺过程中的每一步都在可达空间内即可.如图 4所示, 随着针尖从S_i点运动到S_i+1点, 可达空间由A_i缩小为A_i+1.在保证针尖实时可达性的前提下, 随着针穿刺的进行, 针尖的可达空间将收敛于靶点, 即针尖刺中了靶点.于是, 穿刺针逆向运动学问题转化成针尖的实时可达性问题.从图 4可以看出, 随着针尖旋转位置S_i+1点向右移动, 可达空间A_i+1逐渐缩小并逼近靶点.因为可能使得靶点离开可达空间, 为了保证针尖的可达性, 需要确定每一次进针的最大进针量(临界值), 即每一次进针量都基于当前针尖的状态存在一个最大值.只要针穿刺过程中的每一次进针量都基于当前针尖状态取不超过进针临界值, 均可以使得靶点位于针尖的可达空间内.综上所述, 本文中针穿刺逆向运动学的求解过程是一个实时保证针尖可达性的过程, 从而使得针尖逐渐逼近靶点.根据可达空间逐渐收敛于靶点的特点, 将该逆向运动学求解的方法称为几何逼近法, 该逆向运动学模型称为几何逼近模型.

图 4

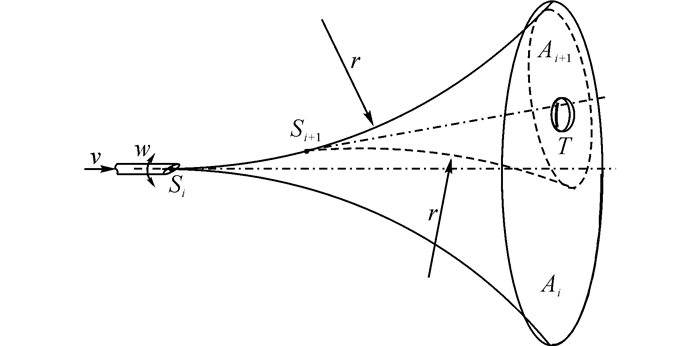
图 4 针穿刺过程中针尖的可达性图解 Fig. 4 Reachability diagram of needle tip in needleinsertion procedure

进针前, 首先将针尖以特定的姿态定位于组织表面上的进针点处(简称进针点), 该过程称为定位针尖初始姿态.在利用几何逼近法求取逆向运动学时, 对定位针尖初始姿态和进针两个过程分别进行研究.其中, 对定位针尖初始姿态过程的研究将得到针尖定位于进针点处时的初始坐标系O₀-X₀Y₀Z₀相对于全局坐标系O-XYZ的齐次坐标变换矩阵₀^gT, 进针过程的研究将得到针尖坐标系O_i-X_iY_iZ_i相对于针尖初始坐标系O₀-X₀Y₀Z₀的齐次坐标变换矩阵_i⁰T.由于针尖与靶点的距离超过2r, 针尖坐标系处于任何位姿状态, 靶点都位于针尖可达空间内, 即任意进针都能够保证针尖对靶点的可达性, 仅仅通过可达性条件不能约束针尖逐渐逼近靶点.本文主要针对进针点与靶点之间的距离小于等于2r的情况进行研究, 这通常是符合大多数临床应用实践的.当针尖从距离靶点2r外经过任意路径穿刺到距离靶点2r处时, 通过几何分析可知, 此时针尖坐标系Z轴的方向与靶点所成角度都一定不超过π/2, 因此针尖从距离靶点2r外, 经过任意路径穿刺到距离靶点2r处时, 都满足针尖对靶点的可达性要求.

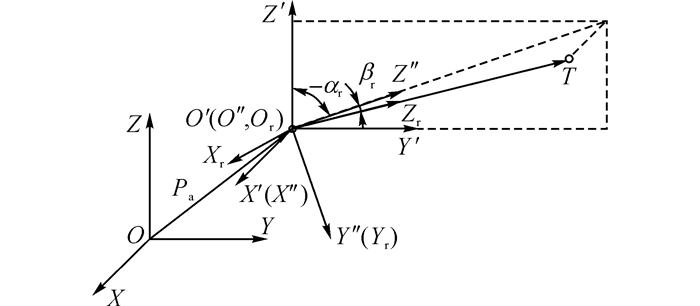
通常情况下, 进针点位置不受几何逼近法的约束, 需要根据实际情况进行路径规划确定, 因此直接将进针点位置作为已知量.如图 5所示, 在全局坐标系O-XYZ下, 进针点O_r的位置P_a: (a, b, c)和靶点T的位置P_T: (t_x, t_y, t_z)已知.如图 5所示, 建立参考坐标系O_r-X_rY_rZ_r, Z_r轴由进针点指向靶点.首先将全局坐标系O-XYZ的原点平移至点O′得到坐标系O′-X′Y′Z′；其次将坐标系O′-X′Y′Z′绕X′轴旋转α_r得到坐标系O″-X″Y″Z″；最后将坐标系O″-X″Y″Z″绕Y″轴旋转β_r, 得到参考坐标系O_r-X_rY_rZ_r.靶点T在参考坐标系O_r-X_rY_rZ_r中的位置P_Tr为(0, 0, $\sqrt {{{\left( {{t_x}-a} \right)}^2} + {{\left( {{t_y}-b} \right)}^2} + {{\left( {{t_z}-c} \right)}^2}} $).全局坐标系与参考坐标系之间的齐次变换矩阵_r^gT可以用下式表示.

图 5

图 5 全局坐标系O-XYZ与参考坐标系Or-XrYrZr之间的变换关系 Fig. 5 Transformation relation between global frame O-XYZ and reference frame Or-XrYrZr

式中：

约定：所有的Atan2(y, x)取值为[0, 2π).

如图 6所示, 给出针尖初始坐标系O₀-X₀Y₀Z₀与参考坐标系O_r-X_rY_rZ_r之间的变换关系.参考坐标系O_r-X_rY_rZ_r绕着Z_r轴旋转γ_s得到坐标系O_r′-X_r′Y_r′Z_r′, 坐标系O_r′-X_r′Y_r′Z_r′绕Y_r′轴旋转β_s, 得到针尖初始坐标系O₀-X₀Y₀Z₀.针尖初始坐标系O₀-X₀Y₀Z₀与参考坐标系O_r-X_rY_rZ_r之间的齐次变换矩阵如下式所示(s代表sin, c代表cos)：

图 6

图 6 针尖初始坐标系O0-X0Y0Z0与参考坐标系Or-XrYrZr之间的变换关系 Fig. 6 Transformation relation between needle tip initial frame O0-X0Y0Z0 and reference frame Or-XrYrZr

结合式(4)、(5), 可以得到针尖初始坐标系O₀-X₀Y₀Z₀与全局坐标系O-XYZ之间的齐次变换矩阵, 如下所示：

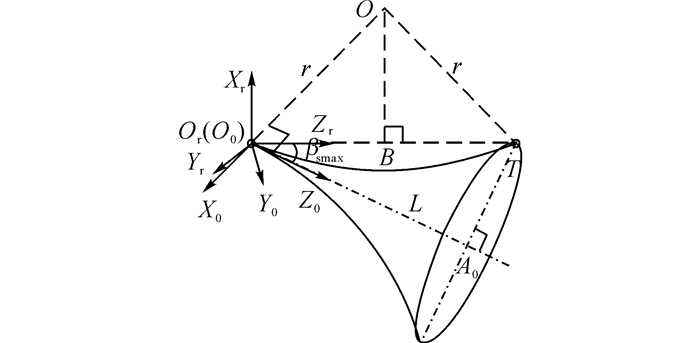
针尖的可达性不受γ_s取值的影响, 即γ_s∈[0, 2π).对于β_s来说, 随着β_s的增大, 靶点逐渐靠近针尖可达空间的边界, 因此需要控制β_s的取值.当靶点位于针尖可达空间A₀的边界上时, β_s取得最大值, 如图 7所示, β_smax为β_s能够取得的最大值, 故β_s∈[0, β_smax].图 7中, 靶点T位于针尖可达空间的边界上.可达空间的轴线L是针尖初始坐标系O₀-X₀Y₀Z₀的Z₀轴方向, 相切于穿刺圆弧轨迹$\overset\frown{{{O}_{0}}T} $.点O是圆弧轨迹$\overset\frown{{{O}_{0}}T} $的圆心, 点B是线段O₀T的中点.可以得到β_smax=∠O₀OB.因为$ \left| {{O}_{0}}B \right|=\frac{1}{2}\left| {{O}_{0}}T \right|=\frac{1}{2}\sqrt{{{\left( {{t}_{x}}-a \right)}^{2}}+{{\left( {{t}_{y}}-b \right)}^{2}}+{{\left( {{t}_{z}}-c \right)}^{2}}}, \left| {{O}_{0}}O \right|=r$, 可得

图 7

图 7 βs取最大临界值βsmax时的示意图 Fig. 7 Explanation of βs obtaining its maximum value βsmax

1) n=1, 此时β_s=β_smax.

当β_s=β_smax时, 靶点T在针尖可达空间的边界上, 因此只有当针尖沿着如图 7所示的$\overset\frown{{{O}_{0}}T} $圆弧轨迹进针时, 才能到达靶点.根据针尖初始坐标系O₀-X₀Y₀Z₀与参考坐标系O_r-X_rY_rZ_r之间的变换关系可知, 图 7中X₀轴的方向由点O指向点O_r.要使得针尖沿着$\overset\frown{{{O}_{0}}T} $圆弧轨迹进针, 穿刺针需要绕Z₀轴旋转π角度, 即α₁=π.可得进针量如下所示：

综上所述, 当n=1时, 穿刺路径只有一段圆弧, 此时逆向运动学可以用下式表示：

2) n>1, 此时β_s < β_smax.

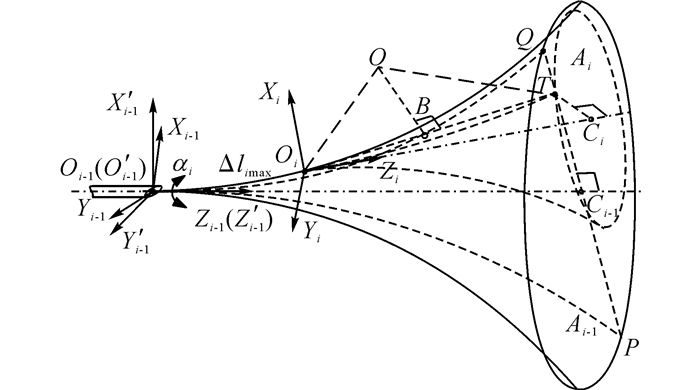
当Δl_i-1 < Δl_i-1max(Δl_i-1max是第i-1次进针量Δl_i-1能取的最大值)时, 即如图 8所示的第i-1次进针后针尖坐标系O_i-1-X_i-1Y_i-1Z_i-1所处的状态.第i-1次进针后靶点T在针尖的可达空间A_i-1的内部, 所以α_i∈[0, 2π), 即α_i可以在[0, 2π)上任意取值.第i次进针极限情况如下：首先针尖绕Z_i-1轴旋转α_i, 然后进针Δl_imax使针尖坐标系变成图 8所示的坐标系O_i-X_iY_iZ_i.在第i次进针Δl_imax后, 靶点T位于针尖可达空间A_i的边界上.

图 8

图 8 当前第i-1次进针后状态下最大最小允许进针量路径($\overbrace{{O}_{i-1}Q} $和$\overbrace{{O}_{i-1}P} $)以及第i次进针量临界值情况 Fig. 8 Maximum or minimum insertion depth allowed path at state of (i-1) th insertion performed ($\overbrace{{O}_{i-1}Q} $or $\overbrace{{O}_{i-1}P} $) and explanation of ith critical insertion depth

图 8中, 向量$\overrightarrow{{{C}_{i-1}}T} $垂直于Z_i-1轴, 点Q和点P是线段C_i-1T延长线与针尖可达空间边界的交点.穿刺针沿着圆弧路径$\overbrace{{O}_{i-1}Q} $进针, 可以得到最大的进针量临界值Δl_imax；沿着圆弧路径$\overbrace{{O}_{i-1}P} $进针, 可以得到最小的进针量临界值Δl_imax.Δl_imax的取值与α_i相关, 下面详细讨论α_i对Δl_imax取值情况的影响.

针尖刺中靶点时的针尖坐标系O_n-X_nY_nZ_n相对于坐标系O_i-1-X_i-1Y_i-1Z_i-1的位置和姿态可以用以下齐次矩阵表示：

由式(10) 可得, 靶点T在针尖坐标系O_i-1-X_i-1Y_i-1Z_i-1中的位置P_Ti-1为(t_xi-1, t_yi-1, t_zi-1).

要使得穿刺针沿着圆弧路径$ \overbrace{{O}_{i-1}Q}$进针, 只需要使X_i-1′轴与向量$\overrightarrow{{{C}_{i-1}}T} $在X_i-1Y_i-1平面内的投影同向, 此时α_i的取值记为α_i-max；穿刺针沿着圆弧路径$\overbrace{{O}_{i-1}Q} $进针时, X_i-1′轴与向量$\overrightarrow{{{C}_{i-1}}T} $在X_i-1Y_i-1平面内的投影反向, 此时α_i的取值记为α_i-min.很容易得到$\overrightarrow{{{C}_{i-1}}T} $=(t_xi-1, t_yi-1, 0), 因此,

当α_i的取值向α_i-max靠近时, Δl_imax越大, 因此, 第i次进针允许量越大；相反, 当α_i的取值向α_i-min靠近时, Δl_imax越小, 因此, 第i次进针允许量越小.为了使得第i次进针允许量较大, 通常α_i在α_i-max附近取值较合适.

如图 8所示, 在Δl_i=Δl_imax的情况下, 针尖坐标系O_i-X_iY_iZ_i相对于坐标系O_i-1-X_i-1Y_i-1Z_i-1的位置和姿态可以用下面的齐次矩阵表示(s代表sin, c代表cos)：

图 8中, 点O是圆弧轨迹$\overset\frown{{{O}_{i}}T} $的圆心, 点B是线段O_iT的中点.根据几何学的知识, 可得∠C_iO_iT=∠O_iOB, 因此在针尖坐标系O_i-1-X_i-1Y_i-1Z_i-1中, 有

式中：

将式(13) 化简, 可得

式中：

可得

式中：

当Δl_imax=max{Δl_imax1, Δl_imax2}时, Z_i轴与图 8所示的方向相反, 即针尖背离靶点, 不合要求, 因此,

当i=n时, 针尖刺中靶点, 所以Δl_n-1=Δl_n-1max；当i < n-1时, Δl_i < Δl_imax.由式(10) 可得, 靶点T在针尖坐标系O_n-1-X_n-1Y_n-1Z_n-1中的位置P_Tn-1为(t_xn-1, t_yn-1, t_zn-1).如图 8所示, 第n次进针时, 穿刺针只能沿着圆弧路径$\overbrace{{O}_{i-1}T} $进针, 才能到达靶点, 因此需要使X_n-1′轴与向量$\overrightarrow{{{C}_{i-1}}T} $同向, 可得

圆弧$\overbrace{{O}_{i-1}T} $的长度为第n次进针量, 故

综上所述, 当n>1时, 逆向运动学如下所示：

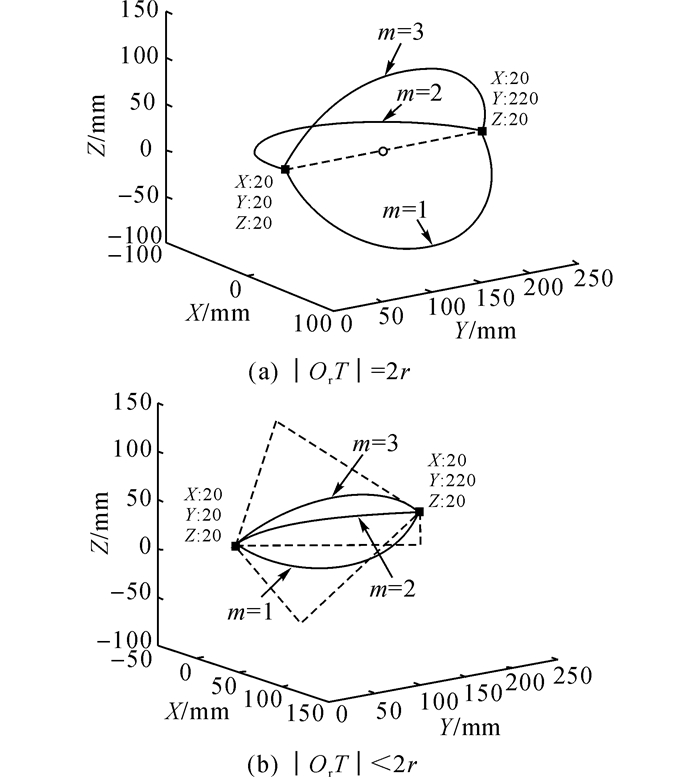
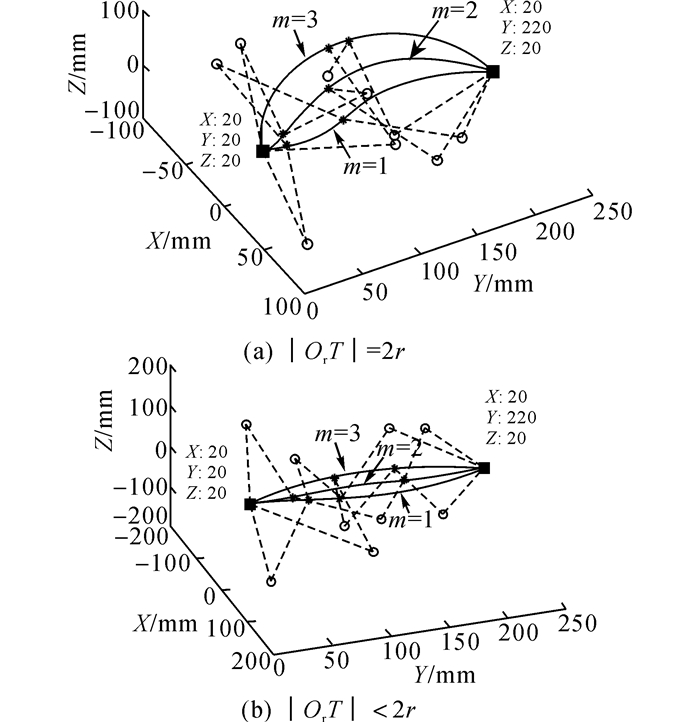
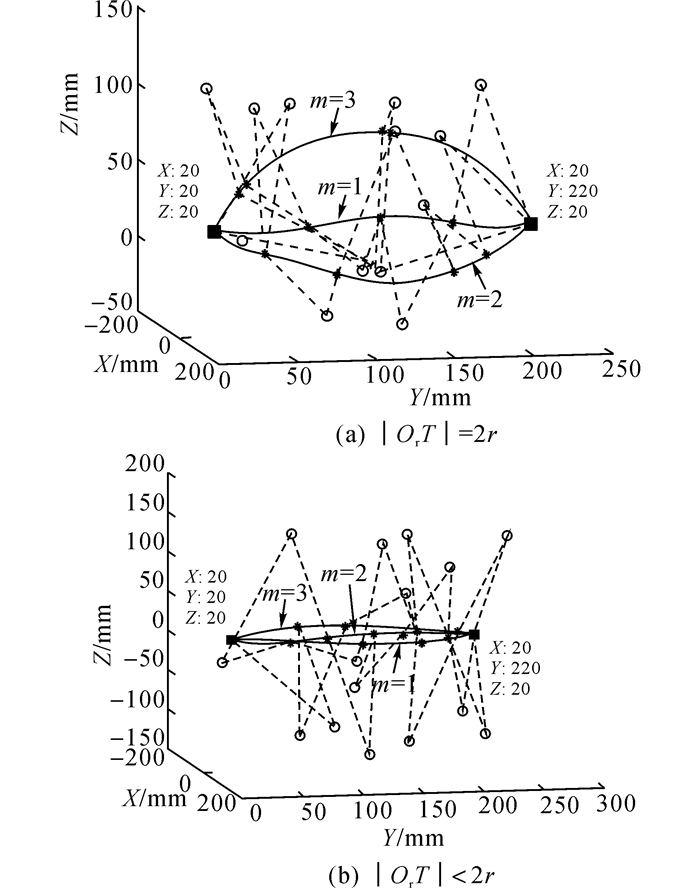
为了验证正逆向运动学模型的有效性, 开展仿真实验对该模型进行验证.实验研究表明, 弯曲半径r与穿刺速度、穿刺力、组织材料特性、穿刺针的材料特性、穿刺针的直径和穿刺针针尖形状等因素相关^[20].依据所测的实验数据, 将表 1列出的r、P_a和P_T等参数作为仿真参数.如表 1所示, 进针点和靶点的位置不变, r分别取100和150 mm, 分别对进针点与靶点之间的距离|O_rT|等于2r和小于2r的情况进行验证.

表 1

表 1 针穿刺系统参数 Table 1 Needle insertion system parameters 弯曲半径/mm 进针点位置 靶点位置 100/150 (20, 20, 20) (20, 220, 20)

表 1 针穿刺系统参数 Table 1 Needle insertion system parameters

如图 9~11所示, 分别对n=1, 3, 5三种情况进行验证, 每种情况进行了m=3次验证.图中, 小圆圈表示每段圆弧路径的圆心, 星号表示每段圆弧路径的端点.如表 2所示, 给出|O_rT| < 2r, n=3和m=2时, 根据逆向运动学模型得到的操控量.表中, ‘-’表示不存在对应的变量取值.

图 9

图 9 1段圆弧路径下的针穿刺轨迹 Fig. 9 Needle insertion path including one circular arc

图 10

图 10 3段圆弧路径下的针穿刺轨迹 Fig. 10 Needle insertion path including three circular arcs

图 11

图 11 5段圆弧路径下的针穿刺轨迹 Fig. 11 Needle insertion path including five circular arcs

表 2

表 2 针穿刺操控量 Table 2 Needle insertion manipulation variables i βsmax γs βs Δlimax/mm αi Δli/mm 0 0.729 728 2.000 000 0.300 000 - - - 1 - - - 61.398 993 2.000 000 40.000 000 2 - - - 96.800 845 2.000 000 96.800 845 3 - - - - 3.341 616 67.623 962

表 2 针穿刺操控量 Table 2 Needle insertion manipulation variables

从图 9~11可以看出, 在给定进针点位置、靶点位置和穿刺针弯曲半径的条件下, 通过正逆向运动学模型都能够精确地生成针穿刺路径, 以刺中靶点.运动学模型求解的是从进针点到靶点的所有可行路径.通过以上理论推导过程可知, 模型得到的是进针过程中操控量的取值范围, 对应取值范围中操控量的所有取值都符合, 采用运动学模型能够求出从进针点到靶点的所有可行路径.虽然上面只分别对|O_rT|=2r和O_rT < 2r两种情况进行了3组实验数据验证, 但是根据需要, 可以采用所提供的几何逼近模型遍及所有满足条件的逆解, 因此利用本文提供的正逆向运动学模型能够准确地实现三维空间针穿刺轨迹预测.

本文利用D-H参数法, 建立斜角柔性穿刺针的正向和逆向运动学模型, 提出几何逼近法来计算从进针点到靶点的所有可行路径.传统机器人学中的解析法和投影法难以解决柔性穿刺针的逆向运动学问题, 相比之下, 几何逼近模型不仅求解简单, 而且能够求出所有逆解, 这为机器人辅助针穿刺路径规划及操控技术研究提供了理论基础.