2. 扬州大学 信息工程学院, 江苏 扬州 225009
2. College of Information Science and Technology, Yangzhou University, Yangzhou 225009, China
在现实社会的生物和信息系统中, 从神经系统到生态系统, 从道路交通到互联网, 从蚁群结构到人类社会关系, 都可以自然地描述为网络, 其中网络顶点代表实体, 而链接表示顶点之间的相互作用或者存在的关系.作为复杂系统的拓扑近似, 由于时间、空间或实验条件的限制, 复杂网络在构建过程中不可避免地会出现错误或冗余链路以及一些未被发现的潜在链接.此外, 由于复杂网络随着时间的推移, 动态发生着变化, 需要网络链接预测来根据已知的网络信息预测丢失和潜在的链接[1].链接预测问题在很多领域都有着广泛的应用.例如, 在生物网络中存在着的蛋白质-蛋白质相互作用网络、代谢网络和疾病基因网络[2].链接预测的结果可以直接用来设计生物实验, 以降低成本, 提高实验的成功率.在社会网络分析中, 链接预测也可以用来分析社会网络结构.对于在线社交网络, 用户可以通过链接预测找出潜在的友谊, 并推荐给用户[3-4].通过分析社会关系, 可以发现潜在的人际关系[5-7].链接预测也可以用在学术网络中对论文的学术类型和合作伙伴进行预测[8].链接预测方法还可以直接用于信息建议[9], 如将商品推荐给客户[10-11].在监控电子邮件通信时, 链接预测被应用于检测异常电子邮件[12].金融公司可以通过链接预测来检测欺诈行为, 以监控交易网络.链接预测不仅具有广泛的实用价值, 而且具有重要的理论意义, 例如, 链接预测有助于理解复杂网络演化的机制[13].
近年来, 出现了许多链接预测算法.最常用的链接预测算法是基于相似度的算法, 在这种算法中, 每个节点对被分配一个指标, 即2个节点之间的相似度.当观察到的两链接越相似, 认为两者之间有更高的链接存在可能.结构相似性指标被划分为3类:局部指标、全局指标以及准本地指标.局部指标仅适用于节点的邻居信息, 典型的局部指标有常见邻居(common neighbors, CN)算法、Salton指标、Jaccard指标、Sorensen指标、Hub Depressed指标(Hub Depressed index, HDI)以及Adamic-Adar系数算法等[14].全局指标需要全部的拓扑特征信息, 经典的全局指标有Katz指标、Leicht-Holme-Newman指标以及森林指数矩阵等.准本地指标不需要全局的拓扑特征, 但是所需要的信息比局部指标要多.Liu等[15]提出2种新的局部指标, 资源分配指标和局部路径指标.研究了基于局部随机游走(local random walk, LRW)和叠加随机游走(superposed random walk, SRW)链路预测问题, 从中发现使用有限的步骤可能会得到比全局随机游走更好的预测.Wang等[16]提出一种在有向网络中使用局部定向路径预测链路方向的方法.还存在一些网络链接预测方法是以概率模型为基础的, 如Popescul等[17]提出了一种基于统计关系学习的链接预测方法;Hanneke等[18]提出了一种将指数型随机图模型推广到社会网络链接预测的统计模型;Hu等[19]提出了一种概率模型, 用来对社会网络中的人体运动进行检测, 并采用基于约束的遗传算法标记人体运动, 以便对这个模型进行优化.
在现实世界的许多网络应用中, 只需要预测给定顶点最可能存在的链接.需要回答的问题可能是:“网络中最可能与节点v相连的链接是哪几个?”;“哪5位作者做的研究与约翰逊教授的研究兴趣最相似?”;“哪10个客户的购物习惯与客户史密斯最相似?”等.这些实际上是给定顶点的链接预测问题.
根据全局参数的性质, 若要使用全局参数准确地得出给定顶点v的链接预测结果, 需要计算网络中所有节点对之间的参数, 这种方法耗费时间大, 显然不适合解决给定顶点上的链接预测问题.
本文提出一种基于抽样的方法来预测与用户感兴趣的节点相关的链接.采用随机游走的方法生成样本路径集并进行抽样, 将这些路径集组成一个子图;为有效控制子图的大小和准确率, 通过实验找出合理的容错阈值ε.在这个子图上对给定的顶点进行链接预测, 并对链接预测的结果进行检验.
1 Katz指标及其随机游走抽样 1.1 链接预测的Katz指标Katz指标是连接预测中最常使用的一种全局指标.顶点对vx和vy之间的Katz相似度指标定义为
| $ {s_{xy}} = \sum\limits_{i = 1}^\infty {{\alpha ^i}} \left| {p_{xy}^{\left( i \right)}} \right|. $ | (1) |
式中:pxy(i)表示连接顶点vx和vy的长度为i的路径集合;α为路径权重的系数, 且α∈(0, 1), 当α较小时, 高阶路径对指标的影响变小.
由于较长路径的影响较小, 可取正整数L, 定义Katz指标为
| $ {s_{xy}} = \sum\limits_{i = 1}^L {{\alpha ^i}} \left| {p_{xy}^{\left( i \right)}} \right|. $ | (2) |
设x为所给定的顶点, 为了预测与顶点x相关的链接, 考虑从顶点x出发的所有长度不超过L的路径集合为PL(x).设某一路径p∈PL(x), p=(x, x1, x2,…,xL), 将路径p中以节点x开头、节点y结束、长度为k的最短子路径表示为
| $ {l_x}\left( {p, y} \right) = \mathop {\min }\limits_{{x_k} = y} k, $ |
则式(2) 改写为
| $ {s_{xy}} = \sum\limits_{p \in {P_L}\left( x \right)} {{\alpha ^{{l_x}\left( {p, y} \right)}}} . $ | (3) |
PL(x)中的路径可能很多, 完全枚举出PL(x)中的路径花费时间较多, 为此, 提出一个基于随机游走的抽样方法, 在PL(x)中取出R条路径, 组成样本路径集QL(x), |QL(x)|=R, 则式(3) 改写为
| $ {{\bar s}_{xy}} = \sum\limits_{p \in {Q_L}\left( x \right)} {{\alpha ^{{l_x}\left( {p, y} \right)}}} . $ | (4) |
以sxy近似代替式(3) 中的sxy作为预测的评分.
1.2 随机游走的方法用随机游走的方法生成样本路径集QL(x).若网络G为非带权图, 设邻接矩阵为W=[wij];若G为带权图, 或为顶点具有属性的图, 设边上的权重或属性相似度矩阵为W=[wij], 由定义顶点vi到vj游走的转移概率为
| $ {t_{ij}} = \frac{{{w_{ij}}}}{{\sum\limits_{{v_k} \in \tau \left( {{v_i}} \right)} {{w_{ik}}} }}. $ | (5) |
式中:τ(vi)为vi的直接邻居节点的集合.
由给定顶点x出发, 随机游走产生R条长度为L的路径集合QL(x)的算法如下:
算法1: GeneratePaths (x, L, R)
输入:x:查询的顶点;
L:路径长度;
R:样本路径的系数;
W:邻接矩阵或权重矩阵;
输出:QL(x):样本路径集;
Begin
根据式(5) 计算样本转移矩阵T=[tij];QL(x)=ϕ;
For k=1 to R do
Pk=ϕ(Pk为第k条路径)
根据转移概率在τ(x)中选择一顶点x1;
将x1加入Pk;
For j=1 to L do
根据转移概率在τ(xj)中选择一顶点;
将此顶点记为xj+1;
将xj+1加入Pk;
End for j;
QL(x)=QL(x)∪{Pk};
End for k;
End
显然, 算法GeneratePaths (x, L, R)的时间复杂度为O(L·R).
2 基于抽样的链接预测算法PL(x)与样本集合QL(x)的不一致会产生估计上的误差, 如果样本较多, 则误差较小.对于给定的误差范围ε, 需要确定合适的样本大小R, 使得误差不超过ε.为此, 可以借助VC(Vepnit-Chervankis)维的概念进行分析.
定义1(打散shatter):1个实例集S被空间集H打散, 当且仅当S的每一种划分, 在H中都能找到1个与之一致的假设;
定义2(VC维):为可被空间集H打散的实例集S的最大有限集的大小, 记为VC(H).
定义1中的实例集S在上述的路径抽样问题中即为PL(x), 空间集H即为路径抽样问题中的集合Hx, 记作:
Hx={px, v|v∈V, |px, v|≤L}.
即长度小于L的以节点x开头的路径的集合, 其中V为所有顶点的集合.
设px, v∈Hx, p∈PL(x), 若px, v为p的一个子路径, 则记px, v∈p, 若对于路径集合, p∈PL(x), 路径集P中的所有路径p, 均有px, v∈p, 则称px, v∈p, 或称p含有px, v.设有px, v∈Hx, 可将PL(x)分为2部分:p和p.对P中的所有路径p, 均有px, v∈p, 对于p中所有路径均有px, v∉p, 则称px, v对应划分PL(x)=p∪p.若对于P(v)的一个子集Q的任意一种划分, 皆有Hx中的一个px, v与之对应, 则称Q可以被Hx打散.
设有数据集D, 记S={x1, x2, …, xm}为数据集D上按照分布ϕ抽样出的样本集合, 对于集合A⊆D, 记ϕ(A)为根据分布ϕ抽出的样本属于A的概率.记ϕS(A)为在S中对ϕ(A)的实验估计值, 且有
| $ {\phi _S}\left( A \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{I_A}\left( {{x_i}} \right)} . $ | (6) |
式中:指示函数IA(xi)定义为
| $ {I_A}\left( {{x_i}} \right) = \left\{ \begin{array}{l} 1, \;\;\;{x_i} \in A;\\ 0, \;\;\;其他. \end{array} \right. $ |
定义3(ε近似):设H为D上的一个空间集, ϕ为D上的概率分布, 设ε∈(0, 1), 则(H, ϕ)中的ε近似值, 就可以是满足下列条件的S:
| $ {\rm{su}}{{\rm{p}}_{A \in H}}\left| {\phi \left( A \right)-{\phi _s}\left( A \right)} \right| \le {\rm{\varepsilon }}{\rm{.}} $ | (7) |
式中:sup为取“上确界”, 即最小上界.VC维学习理论[20]说明, 如果能够估计出H的VC维大小, 就可以根据ϕ的分布来计算出抽样的个数, 构造(H, ϕ)的ε近似.
定理1[21]:记H为D上的空间集, VC(H)≤d, ϕ为D上的一个分布, 设ε, σ∈(0, 1), 且
| $ \left| S \right| = \frac{1}{{{{\rm{\varepsilon }}^2} \cdot C}}\left( {d\ln \frac{1}{C} + \ln \frac{1}{\delta }} \right). $ | (8) |
式中:|S|为集合S中包含的样本数目, C为一个正常数, 则S以1-δ的概率成为(H, ϕ)的ε近似.
由定理1可知, 只要估计出VC(H)的大小, 就能按照式(8) 估计出样本QL(x)的大小R, 以保证QL(x)以1-δ的概率成为PL(x)的ε近似.
为此, 可以给出的定理如下.
定理2:设H为PL(x)上的空间集, x为G的某一顶点, H={px, v|v∈V, |px, v|≤L}, 则
VC(H)≤log2(L+1).
证明:设VC(H)=l, 则必有PL(x)的子集W, |W|=l, 且W能被H打散.根据打散的定义, 对任一Wi⊆W, 存在px, vi使得W中所有含有px, vi为子路径的子集合恰好为Wi, 记W中其余路径构成的集合为Wi, 则PL(x)被px, vi划分为Wi和Wi.不同的子集Wi⊆W, 对应的px, vi也不相同.而W的所有子集个数为2|W|=2l.
对于W中的任一元素p, 可以将W分为2部分:含有p的和不含有p的.记含有p的部分为Wp, 则Wp中有2l-1个子集合, 则Wp也应该有2l-1个相应的子空间px, v, 将其打散.另一方面, 设Wp中的一条路径为p=(x, u1, u2, …, uL), 由于Wp中每一个子集均含p, 对其进行划分的子空间必有px, ui的形式(i=1, 2, …, L).因此, 至多有L个子空间, 即有2l-1≤L, 则l≤log2 (L+1).证毕.
由定理2可知, 使用H={px, v|v∈V, |px, v|≤L}的VC维最多为log2 (L+1).将此值带入式(8) 中的d, 得到所需样本个数R的取值范围为
| $ R \ge \frac{1}{{{\varepsilon ^2} \cdot C}}\left[{{{\log }_2}\left( {L + 1} \right)\ln \frac{1}{C} + \ln \frac{1}{\delta }} \right]. $ | (9) |
只要取大小满足式(9) 的R, 就可以保证QL(x)以1-δ的概率成为PL(x)的ε近似.
根据上述分析, 对给定的顶点x以及误差界ε, 对与x相关的连接预测算法框架描述如下.
算法2: Node_LPS(x, ε)
输入:x:被查询顶点;
ε:误差界;
δ:概率;
L:路径长度;
输出:x近邻的相似Katz值
Begin:
根据式(9) 计算样本个数R;
GeneratePaths(x, L, R, );
结果存在QL(x);
For each path p in QL(x) do
设p=(x, v1, v2, …, vL);
For i=1 to L do
S(x, vi)=S(x, vi)+αi
End for i
End for
End
从以上分析可知, 算法Node_LPS(x, ε)可以在O(L·R)的时间为顶点x预测相关的连接, 其中L和R为和网络中节点的个数n无关的常数.如果要对整个网络的所有顶点对进行连接预测, 可对网络的所有顶点调用算法Node_LPS, 那么该算法在网络中进行链接预测的时间复杂度为O(n).
3 实验结果及分析 3.1 实验环境为了验证Node_LPS算法在复杂网络中进行链接预测的准确性, 本研究将其和其他相关算法进行比较.实验环境是Windows XP, 内存为1.7 G, 编程语言为VC++ 6.0, 画图工具为Origin 8软件.
3.2 数据集实验主要使用不同领域的5个数据集[22]:蛋白质相互作用网络(protein-protein interaction, PPI)、科学家合作网络(scientific collaboration networks NS)、美国政治博客网(American politician blogs, PB)、因特网(internet, INT)以及美国航空网络(US airways, USAir).对于每个数据集, 都对其最大连通分量进行测试.如表 1所示为这些网络中最大连通分量具备的拓扑特征.N为节点的总数;M为连接的总数;NC为网络中连接组件的数量以及最大的规模, 如1 222/2代表的是该网络中有2个连接分量, 而最大的那个含有1 222个节点;e为网络的性能;C为聚类系数;a为相关系数.
| 表 1 5个数据集中最大连通分量具备的拓扑特征 Table 1 Topological features of the largest connected component in five data sets |
本节对链接预测的算法Node_LPS(x, ε)进行测试, 并使用曲线下面积(area under curve, AUC)指标衡量预测结果的准确性.将90%的数据集作为训练集, 而剩余的10%的链接作为测试集.根据训练集建立基于节点x的子图Gx(r)=(Vx, Ex).将和节点x直接相连的节点作为x的第一阶邻居.设定Nr(x)是x对应的第r阶邻居的集合, 而
| $ {N_{1, r}}\left( x \right) = \mathop \cup \limits_{i = 1}^r {N_i}\left( x \right). $ |
为了检测子图Gx(r)=(Vx, Ex)在原图G=(V, E)中所占的百分比, 设定Gx(r)=(Vx, Ex)的覆盖率为
| $ {c_{\rm{g}}}\left( {x, r} \right) = \frac{{\left| {{V_x}} \right|}}{{\left| {{N_{1, r}}\left( x \right)} \right|}}, $ |
称为r阶覆盖.当cg(x, r)的值低时, 表示使用Gx(r)只能预测有限个目标, 则该值对于检测目标者没有意义.在网络预测中, 对于目标检测者来说, 覆盖率越大越能预测出更多的目标.
本实验在5个数据集中使用不同的ε值检测算法Node_LPS(x, ε)的覆盖率.全局覆盖率被定义为所有测试节点的平均覆盖率.如图 1(b)所示为平均搜索半径r, 以及在不同ε值下对应子图节点和链路的平均数目.当节点和链接的搜索半径r和百分比较小时, 说明算法Node_LPS(x, ε)可以在规模较小的子图中获得高质量的链接预测结果.
如图 1所示, 当ε值增加时, 所有测试结果呈现下降趋势, 其中, Pn为预测到的节点与真实节点的百分比, Pe为预测到的边和真实边的百分比.例如, 对于数据集USAir, 当ε=0.035时, 覆盖率为0.932, 当平均搜索半径为1.92时, 子图中边的百分比为48.2%, 而链接的百分比为44.3%.而对于数据集INT, 当ε=0.003 2时, 覆盖率为0.891, 平均搜索半径为2, 边的百分比为1.92%, 而链接的百分比为2.31%.从图中可以发现, 算法Node_LPS在子图规模不大时可以获得较高的覆盖率.
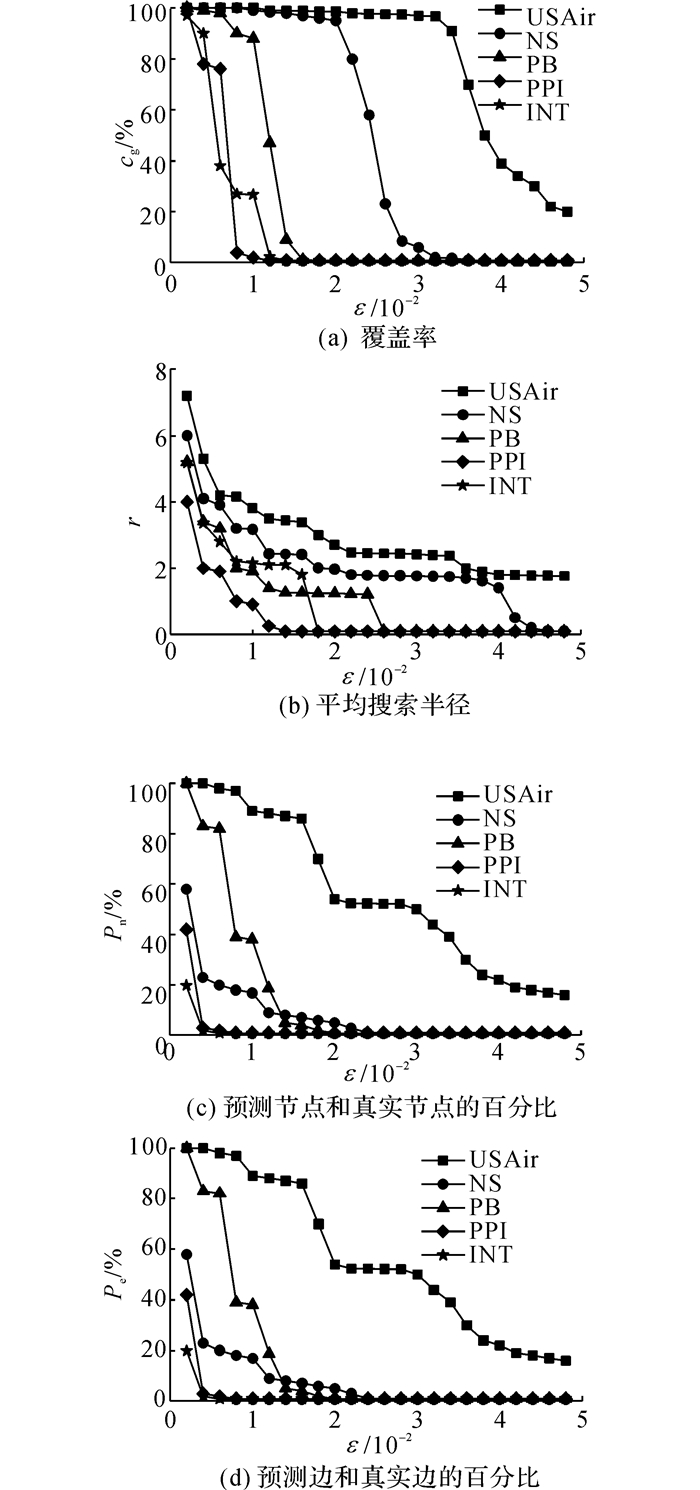
|
图 1 当容错阈值变化时, 覆盖率、平均搜索半径、预测节点与真实节点的百分比以及预测边与真实边的百分比的变化图 Fig. 1 Variation diagram of coverage rate, average search radius, percentage of predicted nodes and real nodes, percentage of predicted edges and real edges with changing fault tolerance value |
在覆盖率变化时对Node_LPS算法的性能进行测试.对于一个r步覆盖率δ, 某个给定节点x的子图Gx=(Vx, Ex)的建立步骤如下:设N1r(x)是训练集中节点x的第一到第r阶邻居的集合;自由选择δ·|N1, r(x)|个节点组成集合Vx, 在训练集中选择包含Vx的所有链接组成集合Ex.
通过设定不同覆盖值, 测试使用Node_LPS算法所找出的子图中第一、第二阶邻居的平均数, 如表 2所示, 同时还比较了通过整个网络所获得的第一、第二阶邻居的平均数目.如表 2和3所示, 当覆盖率大于0.9时, 子图中每个顶点的第一、第二邻居的平均数是大于整个网络的.这是因为Node_LPS算法忽略了非观察到的发生概率很低的链接, 只保留有丰富拓扑信息的节点对, 而Node_LPS算法推荐的潜在链接比在整个网络中检测到的链接更可能存在.因此, 算法Node_LPS的链接预测结果准确可靠.
| 表 2 不同覆盖率下5种数据集第一阶邻居的平均数目 Table 2 Average numbers of first order neighbors of five data sets under different coverages |
| 表 3 不同覆盖率下5种数据集第二阶邻居的平均数目 Table 3 Average numbers of second order neighbors of five data sets under different coverage |
设定覆盖率为0.9, 并选择每个数据集的最佳ε值, 然后通过Node_LPS(x, ε)算法计算子图Gx(r)的拓扑特征, 如表 4所示.与图 1(a)中所示的原始网络的拓扑特征相比, 缩小每个数据集的范围后, 每个节点x所产生的子图Gx(r)所具有的顶点和边数的平均值显著下降, 网络效率e也是显著的改进, 如
| 表 4 5种数据集通过Node_LPS算法计算检得到的子图平均拓扑特征 Table 4 Average topological features of sub graphs extracted from five data sets by Node_LPS algorithm |
如表 4所示.网络聚类系数C变化不明显, 由表 1和表 4所示, 随着ε的减小, 网络平均度M/N也在减小, 表明通过Node_LPS算法实验得到的子图仍保持原有网络的拓扑特征.
通过设置覆盖值为0.9、0.8、0.7、0.6和0.5, 测试Node_LPS算法的AUC结果及其与覆盖率之间的关系.实验结果如表 5所示, 每个数据集在不同覆盖率下得到的最高AUC值用粗体标示.当覆盖率降低时, AUC值随之减小.当覆盖率超过0.8时, Node_LPS算法的AUC得分大于0.9.而覆盖率的值在很大程度上取决于误差值ε.如图 1所示, 当设置ε值为0.01时, 覆盖率超过85%;如果把ε的值设为0.005, 在大多数的数据集中, 覆盖率超过90%.如表 5所示, 如果覆盖率大于90%, Node_LPS算法可以得到大于0.95的高AUC值.这表明, 在误差小于ε时, Node_LPS算法可以获得高质量的结果.
| 表 5 不同覆盖率下5种数据集的曲线下面积(AUC)得分 Table 5 Area under curve (AUC) scores of five data sets under different coverage |
在实验中, 将算法Node_LPS与基于指标的Jaccard、LP算法(local path)、Katz、PA(preferencial attachment)以及CN (common neighbors)的结果的AUC值进行比较, 如表 6所示为在各个数据集上各种算法预测结果的AUC值, 其中最大的值用加黑表示. Node_LPS算法与CN、Jaccard以及PA相比具有较高的AUC值.与LP和Katz算法相比, Node_LPS算法在大部分数据集上具有较高的AUC值, 在少数数据集上, 其AUC值略小一些, 但总体上比较接近.
| 表 6 不同算法在5种数据集上的预测精度比较 Table 6 Prediction accuracy comparison by different algorithms on five data sets |
时间复杂度是链接预测算法设计中的重要问题.在实验中, 将Node_LPS算法与基于指标的算法Jaccard、LP、Katz、PA以及CN的时间复杂度进行比较.如图 2所示为不同算法所需的平均计算时间tag.可以看出,Node_LPS算法与其他算法相比消耗的计算时间更少.

|
图 2 不同算法在5种数据集上的运行时间对比 Fig. 2 Running time comparisons of different algorithms on five kinds data sets |
设网络中节点的个数为n, 则使用Node_LPS算法在网络中进行链接预测的时间复杂度为O(n).设网络中节点的平均度为k, 对于局部指标CN、Jaccard和PA算法, 计算每个节点对(vi, vj)共同邻居的时间复杂度均为O(k).因此, 计算所有节点对CN、Jaccard和PA指标的时间复杂度均为O(n2k).由于局部指标仅使用一阶邻居的拓扑信息, 其预测结果的质量比Node_LPS算法低很多.因此这些算法与Node_LPS算法相比, 需要更多的时间.Katz算法是以全局拓扑路径为基础的指标, 时间复杂度为O(n3).和其他基于相似度的算法相比, Node_LPS算法可以在更短的时间内获得较好的预测结果.Node_LPS算法只抽样考虑了部分随机游走的结构信息, 但又同时保留了全局的结构信息, 因此, 与基于全局随机游走以及其他基于局部随机游走的指标方法相比, Node_LPS算法可以在更少的步数内获得较理想的预测结果.
4 结语本文提出了一种基于抽样的方法来预测与用户感兴趣的节点相关的链接.实验结果表明, 本文算法时间复杂度为O(n), 而其他同类算法, 比如基于局部指标的算法CN、Jaccard以及PA的时间复杂度为O(n2k), 以全局拓扑路径为基础的算法Katz, 时间复杂度为O(n3).与其他同类算法相比, 该算法能够在保持预测精度的基础上使复杂度降低.
对于较小的ε值, 本文方法虽然预测精度较高, 但计算时间会随之增加.这就需要在计算时间和预测精度之间取得较好的平衡.如何根据具体问题确定合适的ε值, 以使得算法取得较好的鲁棒性, 这是需要进一步研究的问题.此外, 本文仅考虑了网络中的顶点不带有属性的静态网络, 即假设网络中的顶点和连接都是不变的, 但现实世界中更多的是动态网络, 即顶点及其连接随时间在变化, 而且顶点所代表的实体具有一定的属性, 这些属性信息有助于提高连接预测的精度.如何将本文的方法应用到顶点带属性的网络、动态网络中, 也是进一步要研究的问题.
| [1] | LU L Y, ZHOU T. Link prediction in complex networks: a survey[J]. Physica A, 2011, 390(6): 1150–1170. DOI:10.1016/j.physa.2010.11.027 |
| [2] | KAYA B, POYRAZ M. Age-series based link prediction in evolving disease networks[J]. Computers in Biology and Medicine, 2015, 63: 1–10. DOI:10.1016/j.compbiomed.2015.05.003 |
| [3] | BAO Z F, ZENG Y, TAY Y C. sonLP: social network link prediction by principal component regression [C] // Proceedings of the 2013 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. Canada: ACM, 2013: 364-371. |
| [4] | PAPADIMITRIOU A, SYMEONIDIS P, YANNIS M. Fast and accurate link prediction in social networking systems[J]. Journal of Systems and Software, 2012, 85(9): 2119–2132. DOI:10.1016/j.jss.2012.04.019 |
| [5] | FOURNET J, BARRAT A. Contact patterns among high school students[J]. PLoS One, 2014, 9(9). |
| [6] | BUCCAFURRI F, LAX G, NOCERA A, et al. Discovering missing me edges across social networks[J]. Information Sciences, 2015, 319: 18–37. DOI:10.1016/j.ins.2015.05.014 |
| [7] | JAHANBAKHSH K, KING V, SHOJA G C. Predicting missing contacts in mobile social networks[J]. Pervasive and Mobile Computing, 2012, 8(5): 698–716. DOI:10.1016/j.pmcj.2012.07.007 |
| [8] | SUN Y, BARBERY R, GUPTA M., AGGARWAL C C, et al. Co-author relationship prediction in heterogeneous bibliographic networks [C] // Proceedings of 2011 International Conference on Advances in Social Networks Analysis and Mining. Taiwan: IEEE, 2011: 121-128. |
| [9] | XIE F, CHEN Z, SHANG J X, et al. A link prediction approach for item recommendation with complex number[J]. Knowledge-Based Systems, 2015, 81: 148–158. DOI:10.1016/j.knosys.2015.02.013 |
| [10] | VIDMER A, ZENG A, MEDO M, et al. Prediction in complex systems: the case of the international trade network[J]. Physica A: Statistical Mechanics and its Applications, 2015, 436: 188–199. DOI:10.1016/j.physa.2015.05.057 |
| [11] | LI X, CHEN H C. Recommendation as link prediction in bipartite graphs: a graph kernel-based machine learning approach[J]. Decision Support Systems, 2013, 54(2): 880–890. DOI:10.1016/j.dss.2012.09.019 |
| [12] | HUANG Z, LIN D K J. The time-series link prediction problem with applications in communication surveillance[J]. INFORMS J on Computing, 2009, 21(2): 286–303. DOI:10.1287/ijoc.1080.0292 |
| [13] | LIU H. Uncovering the network evolution mechanism by link prediction[J]. Scientia Sinica Physica, Mechanica and Astronomica, 2011, 41: 816–823. DOI:10.1360/132010-922 |
| [14] | LV L, JIN C H, ZHOU T. Similarity index based on local paths for link prediction of complex networks[J]. Physical Review E-Statistical, Nonlinear, and Soft Matter Physics, 2009, 80(4): 046122. DOI:10.1103/PhysRevE.80.046122 |
| [15] | LIU W P, LV L. Linkprediction based on local random walk[J]. European Physics Letter, 2010, 89(5): 58007. DOI:10.1209/0295-5075/89/58007 |
| [16] | WANG X J, ZHANG X, ZHAO C L, et al. Predicting link directions using local directed path[J]. Physica A: Statistical Mechanics and its Applications, 2015, 419: 260–267. DOI:10.1016/j.physa.2014.10.007 |
| [17] | POPESCUL A, UNGAR L. Statistical relational learning for link prediction [C] // In Proceedings of the International Workshop on Learning Statistical Models from Relational Data. Mexico: IJCAI, 2003: 172-179. |
| [18] | HANNEKE S, FU W J, XING E P. Discrete temporal models of social Networks[J]. Electronic Journal of Statistics, 2010, 4: 585–605. DOI:10.1214/09-EJS548 |
| [19] | HU F, WONG H S. Labeling of human moion based on CBGA and probabilistic model[J]. International Journal on Smart Sensing and Intelligent Systems, 2013, 6(2): 583–609. |
| [20] | MUNARO A. The VC-dimension of graphs with respect to K-connected subgraphs[J]. Discrete Applied Mathematics, 2016, 211: 163–174. DOI:10.1016/j.dam.2016.04.016 |
| [21] | LI Y, LONG P M. Improved bounds on the sample complexity of learning[J]. Journal of Computer and System Sciences, 2001, 62(1): 516–527. |
| [22] | Link Prediction Group. Resources [EB/OL]. [2013-05-25].http://www.linkprediction.org/index.php/link/resource/data. |



