近年来, 新能源电动汽车凭借节能与环保的优势逐步获得广泛应用.动力电池系统作为电动汽车关键零部件之一, 尤其需要先进的管理技术来保障系统安全、可靠、高效地运行, 而先进的电池模型是电池管理系统的基础.目前, 主流的电池模型主要分为2种:等效电路模型[1-7]以及电化学机理模型[8-26].等效电路模型因具有形式简单、精度较高、计算量小等优势而被更多用于实际工程, 不过其缺点是不能给出电池内部电化学反应的详细信息, 制约了有关对电池系统进行更高级控制的应用, 比如最优充电技术和在线故障诊断等.电化学机理模型能够有效描述电池内部电化学反应发生的状况, 包括锂离子浓度分布、内部电位势空间分布、过电位分布等信息;其缺点是模型控制方程多为偏微分方程组, 且电池内部分为负极、隔膜和正极三区域, 电化学模型空间离散化以及繁重的计算量制约其在实时控制场景的应用.
电化学模型是一种描述锂离子电池内部电化学反应发生过程和状态的机理模型.该模型最早由Doyle等[10-12]提出, 是基于多孔电极理论和溶液浓度理论的准二维通用电池模型.采用Butler-Volmer方程来描述电极与电解液界面间的电化学过程, 使用Fick定律描述固相颗粒内部锂离子的嵌入与迁出, 电解液相的锂离子浓度分布问题采用扩散方程进行描述.
由于电化学模型的计算复杂性较高, 随后很多学者开展一系列模型降阶和简化工作.美国密西根大学Forman等[13-14]采用Pade近似逼近技术来描述锂离子电池电化学模型中的固相离子扩散方程.研究结果显示, Pade逼近在低频段的近似直流区域展示出良好的拟合特性, 不过在更高频率段的拟合效果却很不理想.宾夕法尼亚州立大学Smith等[15-18]对于严格广义二维模型进行了线性化, 并推导出固相浓度扩散方程的传递函数形式.但是, 他们未能推导出电解液相锂离子扩散方程的传递函数解析形式, 而是采用有限元的方法进行离散化计算求解.科罗拉多大学Lee等[19]基于电化学机理模型简化得到一维离散时间状态空间模型, 该模型可以预测全部电化学内部变量.该方法首先将复杂的电化学模型进行线性化, 经过拉普拉斯变换技术由线性方程导出封闭形式传递函数, 再使用离散时间实现算法(discrete-time realization algorithm, DRA)将传递函数转换成最佳离散时间状态空间实现形式.其优点是采用离散时间实现算法技术可以避免非线性优化问题并给出直接选取阶次的降阶模型.美国俄亥俄州立大学Marcicki等[20]对于电化学模型进行拉普拉斯变换而得到电解液相和固相浓度与外部应用电流的传递函数, 然后采用Pade近似逼近的方法得到电解液相和固相浓度与电流的简化传递函数.另外, 有学者分别将电化学模型应用于锂离子电池的模型参数估计[21]、状态估计[22-23]、充电优化[24]、老化分析[25]以及电池组热分析[26]等领域.
为了保持电化学模型的物理表征能力的同时增加其实时性, 本文提出一种基于修正边界条件和Pade逼近技术的分子分母传递函数型的简化电化学模型.本文创新点有以下2个方面:1) 提出电解液相浓度扩散方程的修正边界条件, 大大简化模型解析解的求解;2) 采用Pade逼近近似方法得到描述固相和电解液相浓度分布函数与电流密度的分子分母型传递函数, 该简化形式有利于实时性计算.
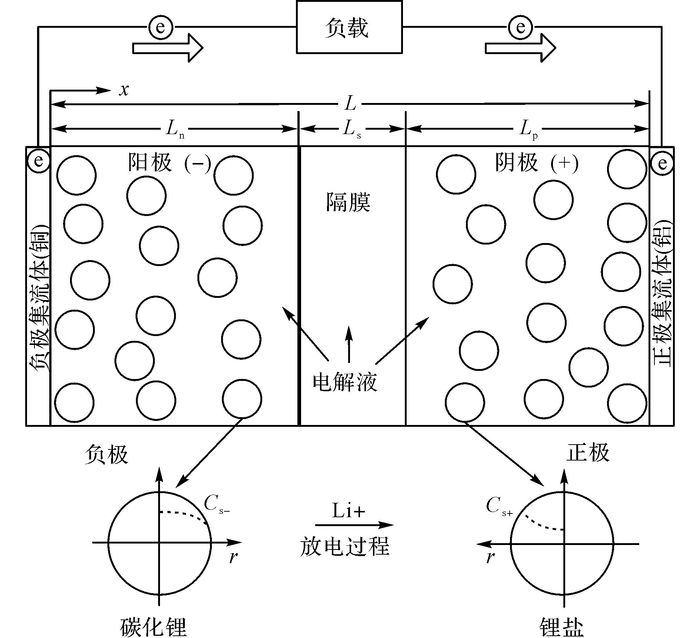
1 电化学模型简介锂离子电池单体的基本结构如图 1所示, 主要包含负极集流体(铜)、负极材料、隔膜、正极材料以及正极集流体(铝)等.图中,Ln为负极厚度,Ls为隔膜厚度, LP为正极厚度,L为单体总厚度,x为电池正、负极间横向维度,r为电极粒子的球坐标径向维度.其中, 负极材料为层状碳化锂(LixC6)活性物质, 正极材料为锂盐(比如磷酸铁锂或钴酸锂等).正负极活性材料分别包覆在正负集流体上, 且被微孔绝缘聚合物隔膜所分割.隔膜具有允许离子通过但阻隔电子通过的特性.电解液相分布于正极、负极和隔膜之中, 其存在能使锂离子在正负极之间扩散移动.
|
图 1 锂离子电池单体模型示意图 Fig. 1 Schematic diagram of lithium-ion battery cell model |
电化学模型[10, 15-18]中所涉及到的描述方程介绍如下.
1) 正/负极固相浓度守恒方程:
| $ \frac{{\partial {c_s}\left( {x,r,t} \right)}}{{\partial t}} = \frac{{{D_{\rm{s}}}}}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}\frac{{\partial {c_s}\left( {x,r,t} \right)}}{{\partial r}}} \right). $ | (1) |
式中:r为球坐标下的径向维度, r∈(0, Rs);cs(x, r, t)为在x位置处锂离子在正、负极活性材料粒子内部关于球坐标径向位置r和时间t的浓度函数;Ds为固相锂离子扩散系数;Rs为正/负极粒子半径.
2) 正/负极固相电荷守恒方程:
| $ \frac{\partial }{{\partial x}}\left( {{\sigma ^{{\rm{eff}}}}\frac{\partial }{{\partial x}}{\phi _{\rm{s}}}} \right) - {j^{{\rm{Li}}}} = 0. $ | (2) |
式中:φs为正/负极固相区域的电位势分布函数, jLi为反应电流密度,σeff为多孔状态下的固相电极等效电导率, 可由Bruggeman介电常数理论计算得到:
| $ {\sigma ^{{\rm{eff}}}} = \sigma {\left( {1 - \varepsilon } \right)^{1.5}}. $ |
其中, σ为活性物质参考电导率, ε为多孔固相电极的孔隙率.
3) 电解液相离子浓度守恒方程:
| $ \frac{{\partial \left( {{\varepsilon _{\rm{e}}}{c_{\rm{e}}}} \right)}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D_{\rm{e}}^{{\rm{eff}}}\frac{\partial }{{\partial x}}{c_{\rm{e}}}} \right) + \frac{{1 - t_ + ^0}}{F}{j^{{\rm{Li}}}}. $ | (3) |
式中:ce为电解液相的锂离子浓度, εe为电解液相的孔隙率, t+0为锂离子相对于溶液速率的迁移数.Deeff为电解液相的等效扩散系数, 可以根据Bruggeman关系式和锂离子的参考扩散系数De计算得到:
| $ D_{\rm{e}}^{{\rm{eff}}} = {D_{\rm{e}}}\varepsilon _{\rm{e}}^{1.5}. $ |
4) 电解液相电荷守恒方程:
| $ \begin{array}{*{20}{l}} {\frac{\partial }{{\partial x}}\left( {{\kappa ^{{\rm{eff}}}}\frac{\partial }{{\partial x}}{\phi _{\rm{e}}}} \right) + \frac{\partial }{{\partial x}}\left( {\kappa _{\rm{D}}^{{\rm{eff}}}\frac{\partial }{{\partial x}}\ln {c_{\rm{e}}}} \right) + {j^{{\rm{Li}}}} = 0}\\ {\kappa _{\rm{D}}^{{\rm{eff}}} = \frac{{2RT{\kappa ^{{\rm{eff}}}}}}{F}\left( {t_ + ^0 - 1} \right)\left( {1 + \frac{{d\ln {f_ \pm }}}{{d\ln {c_{\rm{e}}}}}} \right).} \end{array} $ | (4) |
式中:φe为电解液相的电位势函数;κeff为等效离子电导率, 可通过Bruggeman关系式κeff=κεe1.5计算得到;κDeff表示等效离子扩散电导率;R为通用气体常数, R=8.314 J/mol.K;T为温度;且
| $ \frac{{{\rm{d}}\ln {f_ \pm }}}{{{\rm{d}}\ln {c_{\rm{e}}}}} \approx 0. $ |
5) 描述反应过程的Bulter-Volmer方程:
| $ {j^{{\rm{Li}}}} = {a_{\rm{s}}}{i_{\rm{o}}}\left\{ {\exp \left[ {\frac{{{\alpha _{\rm{a}}}F}}{{RT}}\eta } \right] - \exp - \left[ { - \frac{{{\alpha _{\rm{c}}}F}}{{RT}}\eta } \right]} \right\}. $ | (5) |
式中:as为固相比表面积;io为交换电流密度;η表示反应过电势, η=φs-φe-U, 表示固相与电解液相电位势之差减去固相热动力学平衡电位U.αa和αc分别为阳极和阴极传递系数, 通常αa=αc=0.5.
6) 电流电压关系描述方程:
| $ V\left( t \right) = {\phi _{\rm{s}}}\left( {L,t} \right) - {\phi _{\rm{s}}}\left( {0,t} \right) - \frac{{{R_{\rm{f}}}}}{A}I\left( t \right). $ | (6) |
式中:同式中Rf为接触电阻, I(t)为电池应用电流输入, A为正/负极区域的反应面积.
锰酸锂(LiyMn2O4|LixC6)电池单体电化学模型参数[19]参见表 1.
| 表 1 锂离子电池单体电化学模型参数 Table 1 Parameters for lithium-ion battery cell electrochemical model |
假定在正/负电极处的锂活性物质为一个球形粒子, 关于锂物质守恒的描述遵从Fick第二扩散定律:
| $ \frac{{\partial {c_s}\left( {x,r,t} \right)}}{{\partial t}} = \frac{{{D_{\rm{s}}}}}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}\frac{{\partial {c_s}\left( {x,r,t} \right)}}{{\partial r}}} \right). $ | (7) |
其中, 边界条件为
| $ \begin{array}{l} \frac{{\partial {c_s}\left( {x,r,t} \right)}}{{\partial r}}\left| {_{r = 0}} \right. = 0,{D_{\rm{s}}}\frac{{\partial {c_s}\left( {x,r,t} \right)}}{{\partial r}}\left| {_{r = {R_{\rm{s}}}}} \right. = \\ \;\;\;\;\;\frac{{ - {j^{{\rm{Li}}}}\left( {x,t} \right)}}{{{a_{\rm{s}}}F}}. \end{array} $ | (8) |
式中:jLi(x, t)为在正负极粒子表面的电化学反应电流密度(jLi(x, t)>0表示放电);F为法拉第常数, F=96 487 C/mol;as表示固相物质比接触面积.对于球形活性物质粒子来说, 其电极容积率εs满足as=3εs/Rs.
上述描述固相浓度扩散的方程式(式(7))属于在球形结构下的抛物线型偏微分方程.为了更有效地求解方程, 采用拉普拉斯变换方法进行如下转换:
| $ {D_{\rm{s}}}\frac{{{{\rm{d}}^2}{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{\rm{d}}{r^2}}} + \frac{{2{D_{\rm{s}}}}}{r}\frac{{{\rm{d}}{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{\rm{d}}r}} - s{C_{\rm{s}}}\left( {x,r,s} \right) = 0. $ | (9) |
边界条件经拉普拉斯变换之后为
| $ \begin{array}{l} \frac{{{\rm{d}}{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{\rm{d}}r}}\left| {_{r = 0}} \right. = 0,{D_{\rm{s}}}\frac{{{\rm{d}}{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{\rm{d}}r}}\left| {_{r = {R_{\rm{s}}}}} \right. = \\ \;\;\;\;\;\frac{{ - {j^{{\rm{Li}}}}\left( {x,s} \right)}}{{{a_{\rm{s}}}F}}. \end{array} $ | (10) |
式(9) 为一般常微分方程, 通解形式为
| $ {C_{\rm{s}}}\left( {x,r,s} \right) = \frac{A}{r}\sinh \left( {r\sqrt {\frac{s}{{{D_{\rm{s}}}}}} } \right) + \frac{B}{r}\cosh \left( {r\sqrt {\frac{s}{{{D_{\rm{s}}}}}} } \right). $ | (11) |
其中, 未知系数A和B可以通过联合2个边界条件方程式(式(10) 和(11))求解得到:
| $ \begin{array}{l} A = \frac{{{J^{{\rm{Li}}}}\left( {x,s} \right) \cdot R_{\rm{s}}^2}}{{{a_{\rm{s}}}{D_{\rm{s}}}F\left( { - \sqrt {\frac{s}{{{D_{\rm{s}}}}}} \cosh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right){R_{\rm{s}}} + \sinh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right)} \right)}},B = 0,\\ \frac{{{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{J^{{\rm{Li}}}}\left( {x,s} \right)}} = \frac{{R_{\rm{s}}^2\sinh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} r} \right)}}{{{a_{\rm{s}}}{D_{\rm{s}}}F\left( { - \sqrt {\frac{s}{{{D_{\rm{s}}}}}} \cosh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right){R_{\rm{s}}} + \sinh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right)} \right)r}}. \end{array} $ | (12) |
要求解固相粒子表面的锂离子浓度Cs(x, Rs, s), 只需要将r=Rs代入式(12) 即可.最终计算得到的固相粒子表面浓度函数Cs(x, Rs, s)与电流密度的传递函数如下:
| $ \begin{array}{l} \frac{{{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{J^{{\rm{Li}}}}\left( {x,s} \right)}} = \\ \frac{{ - \frac{{{R_{\rm{s}}}}}{{{a_{\rm{s}}}F{D_{\rm{s}}}}}\sinh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right)}}{{\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}\cosh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right) - \sinh \left( {\sqrt {\frac{s}{{{D_{\rm{s}}}}}} {R_{\rm{s}}}} \right)}}. \end{array} $ | (13) |
上述方程式是描述电池内部的扩散传质过程, 该行为可以通过使用低通滤波器来近似模拟.这里采用Pade近似逼近方法来实现, 具体公式如下:
| $ \frac{{{C_{\rm{s}}}\left( {x,r,s} \right)}}{{{J^{{\rm{Li}}}}\left( {x,s} \right)}} \approx {G_{\rm{s}}}\left( s \right) = \frac{{{a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_m}{x^m}}}{{1 + {b_1}x + {b_2}{x^2} + \cdots + {b_n}{x^n}}}. $ | (14) |
对于负极固相粒子表面浓度与电流密度的传递函数方程式(式(13)), 采用Pade逼近方法得到的不同阶次的计算结果如下.
1) Pade-1阶([m, n]=[0, 1]):
| $ \frac{{{C_{\rm{s}}}\left( {x,{R_{\rm{s}}},s} \right)}}{{{J^{{\rm{Li}}}}\left( {x,s} \right)}} = - \frac{3}{{s{a_{\rm{s}}}F{R_{\rm{s}}}}}. $ | (15) |
2) Pade-2阶([m, n]=[1, 2]):
| $ \frac{{{C_{\rm{s}}}\left( {x,{R_{\rm{s}}},s} \right)}}{{{J^{{\rm{Li}}}}\left( {x,s} \right)}} = - \frac{{\frac{3}{{F{R_{\rm{s}}}}} + \frac{{2{R_{\rm{s}}}s}}{{7{D_{\rm{s}}}F}}}}{{{a_{\rm{s}}}\left( {s + \frac{{R_{\rm{s}}^2{s^2}}}{{35{D_{\rm{s}}}}}} \right)}}. $ | (16) |
3) Pade-3阶([m, n]=[2, 3]):
| $ \frac{{{C_{\rm{s}}}\left( {x,{R_{\rm{s}}},s} \right)}}{{{J^{{\rm{Li}}}}\left( {x,s} \right)}} = - \frac{{\frac{3}{{F{R_{\rm{s}}}}} + \frac{{4{R_{\rm{s}}}s}}{{11{D_{\rm{s}}}F}} + \frac{{R_{\rm{s}}^3{s^2}}}{{165D_{\rm{s}}^2F}}}}{{{a_{\rm{s}}}\left( {s + \frac{{3R_{\rm{s}}^2{s^2}}}{{55{D_{\rm{s}}}}} + \frac{{R_{\rm{s}}^4{s^3}}}{{3465D_{\rm{s}}^2}}} \right)}}. $ | (17) |
对于正极固相粒子表面浓度与电流密度的传递函数方程式来说, 其Pade逼近表达式与负极部分相同, 只需要将参数转换成对应正极参数即可.
2.3 仿真实验对比 2.3.1 时域仿真对比关于电化学模型中的负极固相浓度扩散方程的时域求解, 这里采用20阶次有限差分方法(finite difference method, FDM)的计算结果作为参考标准.然后, 通过仿真计算Pade近似逼近3种结果(Pade-1阶, Pade-2阶和Pade-3阶)的精度差异.在仿真中, 应用电流序列假定为4段:16.148 A, 持续时间0.5 h;静置, 持续时间1 h;-16.148 A, 持续时间0.5 h;静置, 持续时间1 h.负极粒子表面浓度的仿真结果如图 2所示, 从图中可以看出, Pade-1阶近似结果的精度最差, 特别是在动态激励时, Pade-1阶无法反映出动态变动趋势.经统计, Pade-1阶, Pade-2阶和Pade-3阶的最大误差分别为7.48%, 1.48%和0.60%.

|
图 2 3种Pade近似模型的表面浓度结果与参考值对比 Fig. 2 Surface concentration comparisons for three Pade approximation models and reference standard |
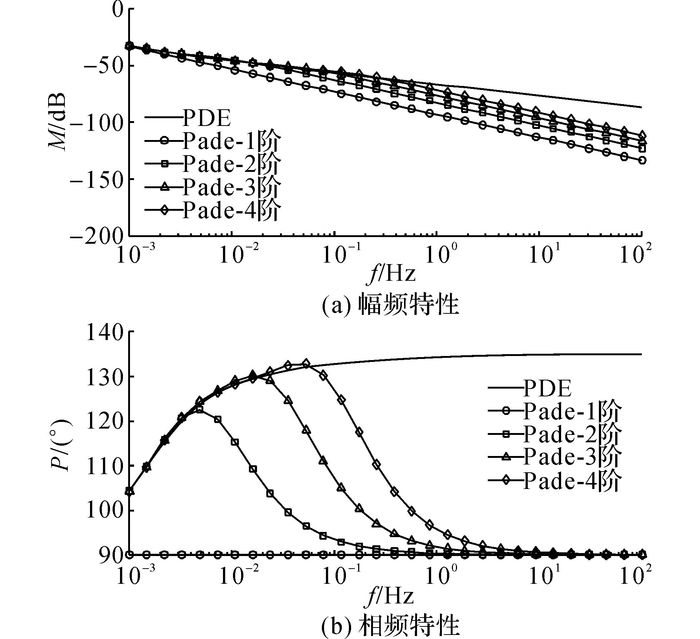
对固相粒子表面浓度与电流密度的传递函数进行Pade逼近, 得到的4种近似结果与偏微分方程(partial differential equation, PDE)解析结果的对比如图 3所示.可以看出, 在幅频特性上,随着Pade阶次的增加, Pade近似结果的幅值逐渐接近于PDE解析结果.不过, 随着频率的增大, Pade逼近结果与PDE解析结果之间的误差也相应增加.
|
图 3 固相粒子表面浓度与电流密度传递函数与Pade近似模型的频域特性对比 Fig. 3 Comparison of frequency domain characteristic for transfer function of solid particles surface concentration to the current density and its Pade approximations |
从相频特性来看, 随着Pade阶次的提升, Pade逼近结果与PDE解析结果更加接近,但仍存在2个问题:随着Pade逼近阶次的提高, 最优拟合频率点有所提高, 不过仍处于较低水平, 以Pade-3阶逼近结果为例, 最优的相频拟合区域为10-3~10-1 Hz.为了提高系统的频带覆盖范围, 需要增加Pade逼近的阶次, 这会造成计算复杂度的提升, 因此系统设计时需要综合考虑计算复杂度与模型精度之间的平衡关系.从相频曲线可以看出, PDE解析结果在高频时相位趋向于135°, 而Pade逼近结果趋向于90°, 因此两者之间存在不可调和的结构性矛盾.
3 电解液相浓度简化由于电解液相存在于正极、隔膜和负极3区域, 因此需要对于3个区域进行分段考虑, 得到的电解液相锂离子扩散方程如下.
1) 负极:
| $ {\varepsilon _{{\rm{e}},{\rm{n}}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D_{{\rm{e}},{\rm{n}}}^{{\rm{eff}}}\frac{\partial }{{\partial x}}{c_{\rm{e}}}} \right) + \frac{{1 - t_ + ^0}}{F}{j^{{\rm{Li}}}},\;\;\;\;0 \le x \le {L_{\rm{n}}}. $ | (18) |
2) 隔膜:
| $ {\varepsilon _{{\rm{e,s}}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D_{{\rm{e,s}}}^{{\rm{eff}}}\frac{\partial }{{\partial x}}{c_{\rm{e}}}} \right),{L_{\rm{n}}} \le x \le {L_{\rm{n}}} + {L_{\rm{s}}}. $ | (19) |
3) 正极:
| $ {\varepsilon _{{\rm{e,p}}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D_{{\rm{e,p}}}^{{\rm{eff}}}\frac{\partial }{{\partial x}}{c_{\rm{e}}}} \right) - \frac{{1 - t_ + ^0}}{F}{j^{{\rm{Li}}}},{L_{\rm{n}}} + {L_{\rm{s}}} \le x \le L. $ | (20) |
式中:ce为电解液相的锂离子浓度, εe为电解液相的孔隙率, t+0为锂离子相对于溶液速率的迁移数, Deeff为电解液相的等效扩散系数.
电解液相液浓度扩散方程组的原始边界条件如下.
1) 在正、负极集流体处, 锂离子空间扩散速度为0, 满足
| $ \frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = 0}} \right. = \frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = L}} \right. = 0. $ | (21) |
2) 根据流体的二次连续性, 锂离子浓度在负极/隔膜边界处应该满足二次连续条件:
| $ {c_{\rm{e}}}\left| {_{x = L_{\rm{n}}^ - }} \right. = {c_{\rm{e}}}\left| {_{x = L_{\rm{n}}^ + }} \right., $ | (22) |
| $ D_{{\rm{e,n}}}^{{\rm{eff}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = L_{\rm{n}}^ - }} \right. = D_{{\rm{e,s}}}^{{\rm{eff}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = L_{\rm{n}}^ + }} \right., $ | (23) |
3) 根据流体的二次连续性, 锂离子浓度在隔膜/正极边界处应该满足二次连续条件:
| $ {c_{\rm{e}}}\left| {_{x = {{\left( {{L_n} + {L_s}} \right)}^ - }}} \right. = {c_{\rm{e}}}\left| {_{x = {{\left( {{L_n} + {L_s}} \right)}^ + }}} \right., $ | (24) |
| $ D_{{\rm{e,s}}}^{{\rm{eff}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = {{\left( {{L_n} + {L_s}} \right)}^ - }}} \right. = D_{{\rm{e,p}}}^{{\rm{eff}}}\frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = {{\left( {{L_n} + {L_s}} \right)}^ + }}} \right.. $ | (25) |
4) 初始状态, 电解液相中锂离子浓度为一常数, 满足
| $ {c_{\rm{e}}}\left| {_{t = 0}} \right. = {c_{{\rm{e}},0}}. $ | (26) |
以上即为电解液相锂离子浓度函数ce(x, t)的边界条件和初始条件.不过由于上述3个方程耦合在一起, 且6个边界条件也是共同耦合在一起才能求解, 形成的偏微分方程组不利于解析解的求解.通过对于上述方程和边界条件耦合问题的分析, 尝试提出新的非耦合边界条件.
3.1 修正边界条件本文提出新的边界条件的出发点包括:1) 解耦负极/隔膜/正极边界处的浓度扩散耦合条件, 使得在任一区域的浓度扩散方程求解得到简化;2) 隔膜处没有外界激励, 只有隔膜两端边界处的浓度差异, 并且, 隔膜区域的浓度扩散基本满足准线性的扩散规律.出于以上考虑, 本文希望寻找到隔膜区域处的电解液相浓度扩散基本平衡点P, 进而以平衡点P为依据, 重新给出新的负极/隔膜处边界条件和隔膜/正极处的边界条件.下面以负极/隔膜边界处为例分析新的边界条件给出的过程.
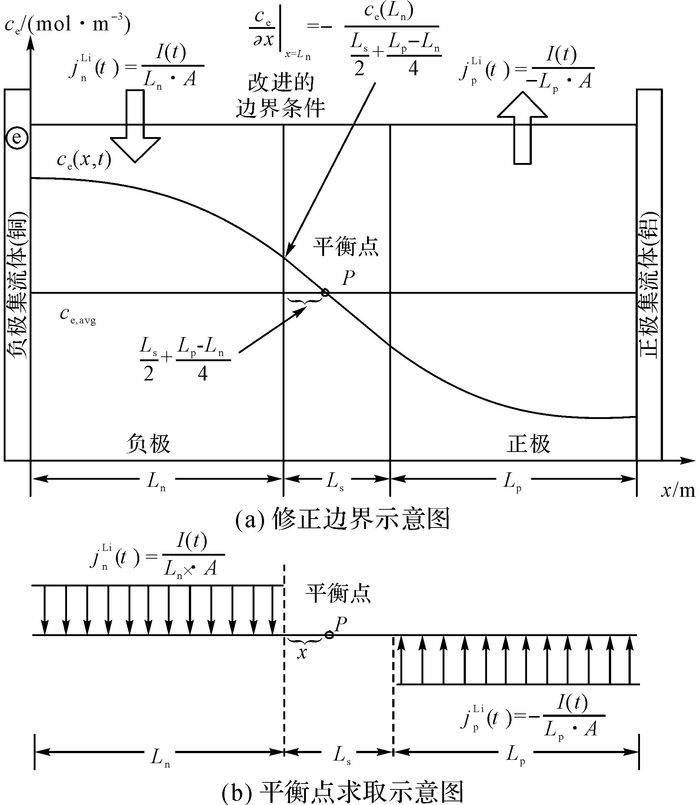
修正边界条件的示意图如图 4所示, 在负极和正极处施加的外界电流密度jnLi和jpLi是方向相反的.假设正负极处的电流密度符合均匀分布, 则根据机械学上的准平衡原理可以计算出平衡点P的位置, 所服从的类转矩平衡方程如下:
|
图 4 电解液相扩散方程的修正边界条件示意图 Fig. 4 Schematic diagram of modified boundary conditions for electrolyte diffusion equations |
| $ \begin{array}{l} j_{\rm{n}}^{{\rm{Li}}}\left( t \right) \cdot {L_{\rm{n}}} \times \left( {\frac{{{L_{\rm{n}}}}}{2} + x} \right) = - j_{\rm{p}}^{{\rm{Li}}}\left( t \right) \cdot {L_{\rm{p}}} \times \\ \;\;\;\;\;\;\;\;\left( {\frac{{{L_{\rm{p}}}}}{2} + {L_{\rm{s}}} - x} \right). \end{array} $ | (27) |
式中:
| $ j_{\rm{n}}^{{\rm{Li}}}\left( t \right) = \frac{{I\left( t \right)}}{{{L_{\rm{n}}} \cdot A}},\;\;\;\;j_{\rm{p}}^{{\rm{Li}}}\left( t \right) = - \frac{{I\left( t \right)}}{{{L_{\rm{p}}} \cdot A}}. $ |
求解上述方程能够得到x的结果如下:
| $ x = \frac{{{L_{\rm{s}}}}}{2} + \frac{{{L_{\rm{p}}} - {L_{\rm{n}}}}}{4}. $ | (28) |
考虑到隔膜区域的锂离子浓度扩散基本上呈现近似线性的趋势, 引入新的负极/隔膜边界处的条件:
| $ \frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = 0}} \right. = 0,\frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = {L_{\rm{n}}}}} \right. = - {c_{\rm{e}}}\left( {{L_{\rm{n}}}} \right){\left( {\frac{{{L_{\rm{s}}}}}{2} + \frac{{{L_{\rm{p}}} - {L_{\rm{n}}}}}{4}} \right)^{ - 1}}. $ | (29) |
同理, 定义新的隔膜/正极边界处的条件:
| $ \begin{array}{l} \frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = L}} \right. = 0,\frac{{\partial {c_{\rm{e}}}}}{{\partial x}}\left| {_{x = {L_{\rm{n}}} + {L_{\rm{s}}}}} \right. = \\ \;\;\;\; - {c_{\rm{e}}}\left( {{L_{\rm{n}}} + {L_{\rm{s}}}} \right){\left( {\frac{{{L_{\rm{s}}}}}{2} - \frac{{{L_{\rm{p}}} - {L_{\rm{n}}}}}{4}} \right)^{ - 1}}. \end{array} $ | (30) |
对于负极, 联合电解液相浓度扩散方程(式(18))和新提出的边界条件(式(29)), 最终可以计算得到的负极电解液相浓度函数Cen(x, s)与电流密度JnLi(x, s)的传递函数如下所示:
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F}\frac{{{s^{1/2}}{\varepsilon ^{1/2}}K\sinh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{n}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}}}{{{s^{3/2}}{\varepsilon ^{3/2}}K\sinh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{n}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }} - 4\cosh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{n}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}\sqrt {D_{\rm{e}}^{{\rm{eff}}}} s\varepsilon }} + \\ \;\;\;\;\frac{{1 - t_ + ^0}}{F}\frac{{4\sqrt {D_{\rm{e}}^{{\rm{eff}}}} \left( {\cosh \frac{{\sqrt \varepsilon \sqrt s x}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }} - \cosh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{n}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}} \right)}}{{{s^{3/2}}{\varepsilon ^{3/2}}K\sinh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{n}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }} - 4\cosh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{n}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}\sqrt {D_{\rm{e}}^{{\rm{eff}}}} s\varepsilon }}. \end{array} $ | (31) |
式中:K=-2Ls-Lp+Ln,ε=εe.
将负极处x=0、1/4Ln、1/2Ln、3/4Ln和Ln的传递函数进行Pade逼近简化的结果如下.
1) 负极位置x=0, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \;\;\;\;\frac{{ - 3{L_{\rm{n}}}{{\left( {K - 2{L_{\rm{n}}}} \right)}^2}}}{{{L_{\rm{n}}} \cdot \varepsilon \left( { - 3{K^2} + 10K{L_{\rm{n}}} - 10L_{\rm{n}}^2} \right)s + \left( {12K - 24{L_{\rm{n}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (32) |
2) 负极位置x=1/4Ln, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \;\;\;\;\frac{{ - 6{L_{\rm{n}}}{{\left( {8K - 15{L_{\rm{n}}}} \right)}^2}}}{{{L_{\rm{n}}} \cdot \varepsilon \left( { - 384{K^2} + 1232K{L_{\rm{n}}} - 1185L_{\rm{n}}^2} \right)s + \left( {1536K - 2880{L_{\rm{n}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (33) |
3) 负极位置x=1/2Ln, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \;\;\;\;\frac{{ - 6{L_{\rm{n}}}{{\left( {2K - 3{L_{\rm{n}}}} \right)}^2}}}{{{L_{\rm{n}}} \cdot \varepsilon \left( { - 24{K^2} + 68K{L_{\rm{n}}} - 57L_{\rm{n}}^2} \right)s + \left( {96K - 144{L_{\rm{n}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (34) |
4) 负极位置x=3/4Ln, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \;\;\;\;\frac{{ - 6{L_{\rm{n}}}{{\left( {8K - 7{L_{\rm{n}}}} \right)}^2}}}{{{L_{\rm{n}}} \cdot \varepsilon \left( { - 384{K^2} + 848K{L_{\rm{n}}} - 497L_{\rm{n}}^2} \right)s + \left( {1536K - 1344{L_{\rm{n}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (35) |
5) 负极位置x=Ln, 简化后的传递函数为
| $ \frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \frac{{ - 3K{L_{\rm{n}}}}}{{{L_{\rm{n}}} \cdot \varepsilon \left( { - 3K + 4{L_{\rm{n}}}} \right)s + 12D_{\rm{e}}^{{\rm{eff}}}}}. $ | (36) |
正极浓度传递函数如下:
| $ \begin{array}{*{20}{c}} {\frac{{C_{\rm{e}}^{\rm{n}}\left( {x,s} \right)}}{{J_{\rm{n}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F}\left\{ {\frac{{ - {s^{1/2}}{\varepsilon ^{1/2}}K'\sinh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{p}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}}}{{{s^{3/2}}{\varepsilon ^{3/2}}K'\sinh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{p}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }} + 4\cosh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{p}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}\sqrt {D_{\rm{e}}^{{\rm{eff}}}} s\varepsilon }} + } \right.}\\ {\left. {\frac{{4\sqrt {D_{\rm{e}}^{{\rm{eff}}}} \left( {\cosh \frac{{\sqrt \varepsilon \sqrt s \left( {{L_{\rm{n}}} + {L_{\rm{s}}} + {L_{\rm{p}}} - x} \right)}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }} - \cosh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{p}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}} \right)}}{{{s^{3/2}}{\varepsilon ^{3/2}}K'\sinh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{p}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }} + 4\cosh \frac{{\sqrt \varepsilon \sqrt s {L_{\rm{p}}}}}{{\sqrt {D_{\rm{e}}^{{\rm{eff}}}} }}\sqrt {D_{\rm{e}}^{{\rm{eff}}}} s\varepsilon }}} \right\}.} \end{array} $ | (37) |
式中:K′=2Ls+Ln-Lp,ε=εe.
同样地, 将正极处x=Ln+Ls、Ln+Ls+1/4Lp、Ln+Ls+1/2Lp、Ln+Ls+3/4Lp和Ln+Ls+Lp的传递函数进行Pade逼近简化结果如下.
1) 正极位置x=Ln+Ls, 简化后的传递函数为
| $ \frac{{C_{\rm{e}}^{\rm{p}}\left( {x,s} \right)}}{{J_{\rm{p}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F}\frac{{ - 3K'{L_{\rm{p}}}}}{{{L_{\rm{p}}} \cdot \varepsilon \left( {3K' + 4{L_{\rm{p}}}} \right)s + 12D_{\rm{e}}^{{\rm{eff}}}}}. $ | (38) |
2) 正极位置x=Ln+Ls+1/4Lp, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{p}}\left( {x,s} \right)}}{{J_{\rm{p}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \frac{{ - 6{L_{\rm{p}}}{{\left( {8K' + 7{L_{\rm{p}}}} \right)}^2}}}{{{L_{\rm{p}}} \cdot \varepsilon \left( {384{K^{'2}} + 848K'{L_{\rm{p}}} + 497L_{\rm{p}}^2} \right)s + \left( {1536K' + 1344{L_{\rm{p}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (39) |
3) 正极位置x=Ln+Ls+1/2Lp, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{p}}\left( {x,s} \right)}}{{J_{\rm{p}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \frac{{ - 6{L_{\rm{p}}}{{\left( {2K' + 3{L_{\rm{p}}}} \right)}^2}}}{{{L_{\rm{p}}} \cdot \varepsilon \left( {24{K^{'2}} + 68K'{L_{\rm{p}}} + 57L_{\rm{p}}^2} \right)s + \left( {96K' + 144{L_{\rm{p}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (40) |
4) 正极位置x=Ln+Ls+3/4Lp, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{p}}\left( {x,s} \right)}}{{J_{\rm{p}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \frac{{ - 6{L_{\rm{p}}}{{\left( {8K' + 15{L_{\rm{p}}}} \right)}^2}}}{{{L_{\rm{p}}} \cdot \varepsilon \left( {384{K^{'2}} + 1232K'{L_{\rm{p}}} + 1185L_{\rm{p}}^2} \right)s + \left( {1536K' + 2880{L_{\rm{p}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (41) |
5) 正极位置x=Ln+Ls+Lp, 简化后的传递函数为
| $ \begin{array}{l} \frac{{C_{\rm{e}}^{\rm{p}}\left( {x,s} \right)}}{{J_{\rm{p}}^{{\rm{Li}}}\left( {x,s} \right)}} = \frac{{1 - t_ + ^0}}{F} \times \\ \frac{{ - 3{L_{\rm{p}}}{{\left( {K' + 2{L_{\rm{p}}}} \right)}^2}}}{{{L_{\rm{p}}} \cdot \varepsilon \left( {3{K^{'2}} + 10K'{L_{\rm{p}}} + 10L_{\rm{p}}^2} \right)s + \left( {12K' + 24{L_{\rm{p}}}} \right)D_{\rm{e}}^{{\rm{eff}}}}}. \end{array} $ | (42) |
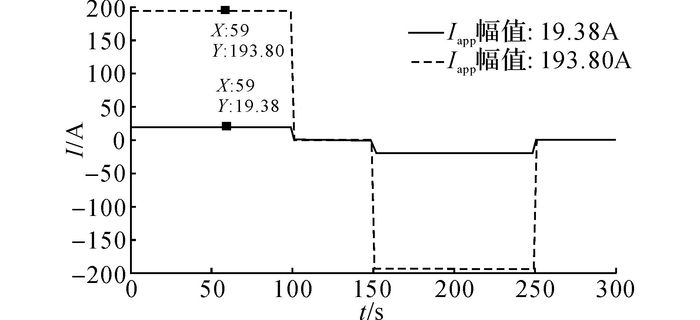
PDE模型采用有限元商业软件COMSOL进行计算, 而Pade逼近结果根据公式进行计算.仿真中的输入条件如图 5所示(Iapp为应用电流激励), 分别为电流19.38 A(~1 C)和193.80 A(~10 C)的脉冲充放电序列.
|
图 5 幅值为19.38 A和193.80 A的仿真输入电流信号 Fig. 5 Two simulation input current signals with magnitudes of 19.38 A and 193.80 A |
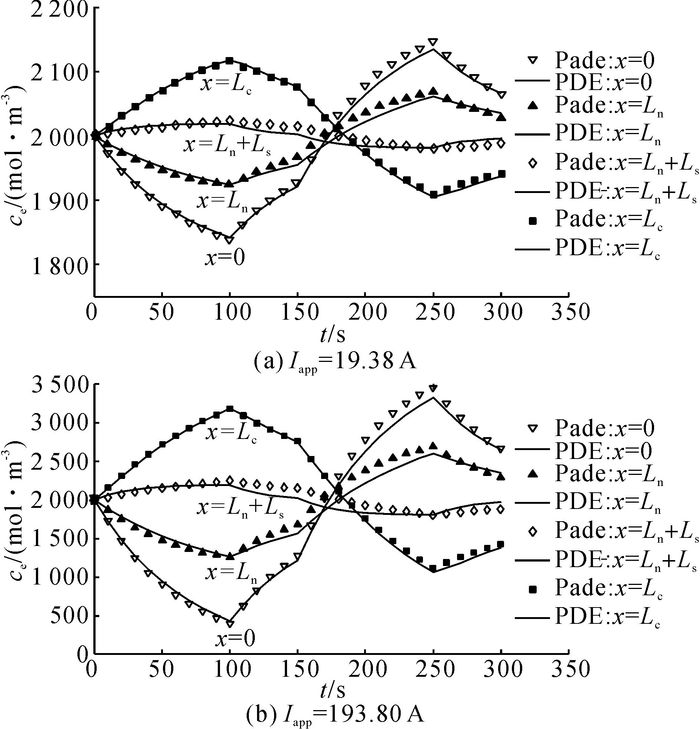
为了详细对比PDE计算结果与Pade逼近结果的差异性, 选用4个特征点, 其位置分别为x=0, x=Ln, x=Ln+Ls, x=Lc= Ln+Ls+Lp.当激励电流为19.38 A时, PDE计算结果与Pade逼近结果对比如图 6 (a)所示.可以看出, 当恒流充电时负极电解液相锂离子浓度会逐渐降低, 而正极电解液相锂离子浓度会不断提高, 以达到将锂离子从正极输送至负极的目的.2种模型的计算结果具有较好的一致性, 计算误差统计结果如表 2所示.表中, eavg为平均误差, emax为最大误差.
|
图 6 不同激励电流时PDE模型和Pade逼近计算电解液相浓度对比 Fig. 6 Comparison of electrolyte concentration with PDE model and Pade approximation under different excitation currents |
| 表 2 PDE模型和Pade近似模型误差对比 Table 2 Error comparison between PDE model and Pade approximation-based model |
当激励电流为193.80 A时, PDE计算结果与Pade逼近结果对比如图 6(b)所示.从图中可知, 当激励电流增大时负极和正极的电解液相浓度会产生剧烈的浓度差异.过大的浓度差异会对电池工作性能和寿命产生不良的影响.2种模型的计算误差统计结果如表 2所示.
从表 2可知, 当激励电流为19.38 A(~1C)时, 4个特征点处的平均误差为7.777 mol/m3, 最大误差为17.351 mol/m3.假定电解液相初始浓度为2 000 mol/m3, 此时相对最大误差为0.867%, 能够满足实际精度要求.当激励电流增大为193.80 A(~10C)时, 4个特征点处的平均误差为77.775 mol/m3, 最大误差为173.514 mol/m3.假定电解液相初始浓度为2 000 mol/m3, 此时相对最大误差为8.670%, 基本满足实际精度要求.
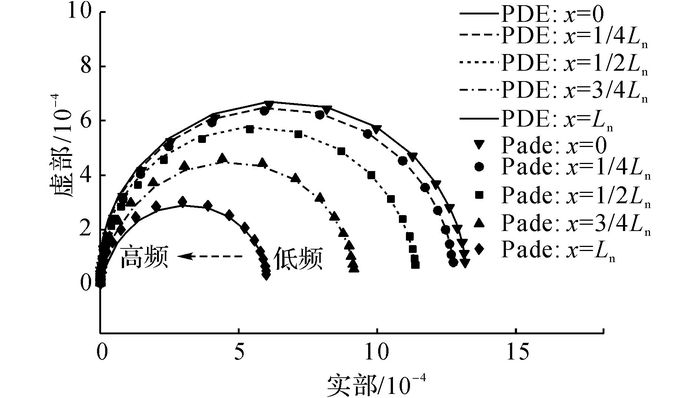
3.3.2 频域对比对于负极电解液相浓度与电流密度的传递函数关系式, 进行Pade近似逼近, 可以作出PDE解析结果和Pade逼近结果的奈奎斯特图,如图 7所示.可以看出, 在负极左边界处(x=0), 传递函数的幅值最大;随着位置向隔膜方向移动, 传递函数的幅值逐步降低, 传递函数的频域响应差不多为半圆形状.当频率较低时, 阻抗较大;随着频率增加, 阻抗会沿着半圆曲线向0靠近.经统计, 5个特征点(x=0, 1/4Ln, 1/2Ln, 3/4Ln, Ln)在频率范围内的平均误差分别为6.12%, 4.70%, 0.82%, 8.26%, 12.58%.该结果也验证了所提出的简化结果具有较高的精度水平.
|
图 7 负极电解液相浓度/电流密度传递函数奈奎斯特图 Fig. 7 Nyquist plotting figure for transfer function ofelectrolyte concentration to current density in negative electrode |
(1) 推导出正/负极固相浓度扩散动力方程解析解, 并利用Pade近似逼近给出简化结果.在16.148 A充放电倍率, 持续放电时间0.5 h的情况下, 3种Pade近似结果的最大误差分别为7.48%, 1.48%和0.60%, 该仿真结果验证了固相浓度简化模型的有效性.
(2) 关于电解液相浓度扩散问题, 本文提出了修正边界条件以简化电化学方程组求解难度.利用Pade逼近方法给出电解液相(负极和正极区域)10个特征点的简化传递函数.采用~1C和~10C倍率的脉冲充放电工况进行仿真, 结果表明所提出简化模型的最大相对误差约为0.867%和8.670%.该仿真结果验证了简化模型的有效性, 能够极大降低传统电化学模型的求解时间, 有利于实时化工程应用.
未来研究可依据简化浓度模型进一步推导得到描述电流-电压关系的简化电化学模型.另外, 可以开展基于电化学模型的参数辨识和电池故障诊断工作.
| [1] | WU H, YUAN S, ZHANG X, et al. Model parameter estimation approach based on incremental analysis for lithium-ion batteries without using open circuit voltage[J]. Journal of Power Sources, 2015, 287: 108–118. DOI:10.1016/j.jpowsour.2015.04.037 |
| [2] | YUAN S, WU H, YIN C. State of charge estimationusing the extended Kalman filter for battery management systems based on the ARX battery model[J]. Energies, 2013, 6(1): 444–470. DOI:10.3390/en6010444 |
| [3] | YUAN S, WU H, MA X, et al. Stability analysis for li-ion battery model parameters and state of charge estimation by measurement uncertainty consideration[J]. Energies, 2015, 8(8): 7729–7751. DOI:10.3390/en8087729 |
| [4] | PEI L, ZHU C, WANG T, et al. Online peak power prediction based on a parameter and state estimator for lithium-ion batteries in electric vehicles[J]. Energy, 2014, 66: 766–778. DOI:10.1016/j.energy.2014.02.009 |
| [5] | LIU X, CHEN Z, ZHANG C, et al. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation[J]. Applied Energy, 2014, 123: 263–272. DOI:10.1016/j.apenergy.2014.02.072 |
| [6] |
戴海峰, 魏学哲, 孙泽昌. 基于等效电路的内阻自适应锂离子电池模型[J].
同济大学学报:自然科学版, 2010, 38(1): 98–102.
DAI Hai-feng, WEI Xue-zhe, SUN Ze-chang. An inner resistance adaptive model based on equivalent circuit of lithium-ion batteries[J]. Journal of Tongji University: Natural Science, 2010, 38(1): 98–102. |
| [7] |
杨阳, 汤桃峰, 秦大同, 等. 电动汽车锂电池PNGV等效电路模型与SOC估算方法[J].
系统仿真学报, 2012, 24(4): 938–942.
YANG Yang, TANG Tao-feng, QIN Da-tong, et al. PNGV Equivalent Circuit Model and SOC Estimation Algorithm of Lithium Batteries for Electric Vehicle[J]. Journal of System Simulation, 2012, 24(4): 938–942. |
| [8] |
汤依伟. 基于电化学—热耦合模型的锂离子动力电池放电行为研究[D]. 长沙: 中南大学, 2013.
TANG Yi-wei. Discharge behavior research of the lithium ion power battery based on the electrochemical-thermal coupling model [D]. Changsha: Central South University, 2013. |
| [9] |
徐蒙. 磷酸铁锂动力电池放电过程电化学—热耦合模型研究[D]. 北京: 北京交通大学, 2014.
XU Meng. Study on electrochemical and heat transfer model of LiFePO4 power battery during discharge process [D]. Beijing: Beijing Jiao Tong University, 2014. |
| [10] | DOYLE M, FULLER T F, NEWMAN J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell[J]. Journal of the Electrochemical Society, 1993, 140(6): 1526–1533. DOI:10.1149/1.2221597 |
| [11] | FULLER T F, DOYLE M, NEWMAN J. Simulation and optimization of the dual lithium ion insertion cell[J]. Journal of the Electrochemical Society, 1994, 141(1): 1–10. DOI:10.1149/1.2054684 |
| [12] | NEWMAN J, TIEDEMANN W. Porous-electrode theory with battery applications[J]. AIChE Journal, 1975, 21(1): 25–41. DOI:10.1002/(ISSN)1547-5905 |
| [13] | FORMAN J C, BASHASH S, STEIN J L, et al. Reduction of an electrochemistry-based Li-ion battery model via quasi-linearization and Padé approximation[J]. Journal of the Electrochemical Society, 2011, 158(2): A93–A101. DOI:10.1149/1.3519059 |
| [14] | FORMAN J C, BASHASH S, STEIN J L, et al. Reduction of an electrochemistry-based Li-ion battery health degradation model via constraint linearization and Padé approximation [C] // ASME 2010 Dynamic Systems and Control Conference. Cambridge: American Society of Mechanical Engineers, 2010: 173-183. |
| [15] | SMITH K A. Electrochemical modeling, estimation and control of lithium ion batteries [D]. University Park: The Pennsylvania State University, 2006. |
| [16] | SMITH K A, WANG C Y. Solid-state diffusion limitations on pulse operation of a lithium ion cell for hybrid electric vehicles[J]. Journal of Power Sources, 2006, 161(1): 628–639. DOI:10.1016/j.jpowsour.2006.03.050 |
| [17] | SMITH K A, RAHN C D, WANG C Y. Control oriented 1D electrochemical model of lithium ion battery[J]. Energy Conversion and Management, 2007, 48(9): 2565–2578. DOI:10.1016/j.enconman.2007.03.015 |
| [18] | SMITH K A, RAHN C D, WANG C Y. Model order reduction of 1D diffusion systems via residue grouping[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(1): 011012. DOI:10.1115/1.2807068 |
| [19] | LEE J L, CHEMISTRUCK A, PLETT G L. One-dimensional physics-based reduced-order model of lithium-ion dynamics[J]. Journal of Power Sources, 2012, 220: 430–448. DOI:10.1016/j.jpowsour.2012.07.075 |
| [20] | MARCICKI J, CANOVA M, CONLISK A T, et al. Design and parametrization analysis of a reduced-order electrochemical model of graphite/LiFePO 4 cells for SOC/SOH estimation[J]. Journal of Power Sources, 2013, 237: 310–324. DOI:10.1016/j.jpowsour.2012.12.120 |
| [21] | RAHMAN M A, ANWAR S, IZADIAN A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method[J]. Journal of Power Sources, 2016, 307: 86–97. DOI:10.1016/j.jpowsour.2015.12.083 |
| [22] | STETZEL K D, ALDRICH L L, TRIMBOLI M S, et al. Electrochemical state and internal variables estimation using a reduced-order physics-based model of a lithium-ion cell and an extended Kalman filter[J]. Journal of Power Sources, 2015, 278: 490–505. DOI:10.1016/j.jpowsour.2014.11.135 |
| [23] | OUYANG M, LIU G, LU L, et al. Enhancing the estimation accuracy in low state-of-charge area: a novel onboard battery model through surface state of charge determination[J]. Journal of Power Sources, 2014, 270: 221–237. DOI:10.1016/j.jpowsour.2014.07.090 |
| [24] | PRAMANIK S, ANWAR S. Electrochemical model based charge optimization for lithium-ion batteries[J]. Journal of Power Sources, 2016, 313: 164–177. DOI:10.1016/j.jpowsour.2016.01.096 |
| [25] | EDOUARD C, PETIT M, FORGEZ C, et al. Parameter sensitivity analysis of a simplified electrochemical and thermal model for Li-ion batteries aging[J]. Journal of Power Sources, 2016, 325: 482–494. DOI:10.1016/j.jpowsour.2016.06.030 |
| [26] | GANESAN N, BASU S, HARIHARAN K S, et al. Physics based modeling of a series parallel battery pack for asymmetry analysis, predictive control and life extension[J]. Journal of Power Sources, 2016, 322: 57–67. DOI:10.1016/j.jpowsour.2016.05.005 |



