当流体流经空腔结构时, 腔体附近流场会产生强烈的振荡, 引起结构振动和噪声.空腔自持振荡由于涉及到湍流和声的复杂耦合作用, 至今没有一个广泛接受的物理解释, 但普遍认为腔内存在从导边至随边的反馈作用, 这种反馈作用就是自持振荡产生的原因.在空气动力学领域Rossiter[1]最早给出了空腔自持振荡的频率预估公式, 但Rossiter公式对介质为水的问题预报并不准确, 这是因为流场不可压缩性及低马赫数特性使水下空腔的声反馈效应很小.对于不可压缩空腔流问题, 主要采用粒子图像测速法(PIV)进行试验研究, 国外Basley[2], Cicca[3]、国内方涛等[4]都采用了这种方法, 着重对腔内涡结构、振荡模式等进行描述, 但并没有对Rossiter公式进行修正.何作镛[5]采用水洞试验进行模拟, 给出了凹陷圆柱腔的振荡频率预报公式.戴绍仕等[6]则采用拖曳试验的手段, 给出了方形陷落腔的振荡频率公式.数值计算方面, Arunajatesan等[7]用混合方法预报了水下航行器表面开孔部位发生的亥姆霍兹共振现象, 通过详细的参数化分析, 检查了计算流体动力学(CFD)预报中的有关数值问题.刘聪尉等[8]采用大涡模拟法对空腔不可压缩流动特征进行仿真, 并与试验结果进行对比, 验证了计算方法的可靠性.
目前大多采用水洞实验对水下流激空腔问题进行研究, 研究对象均为陷落式空腔, 而大腔体小开孔形式的水下流激孔腔振荡问题还没有类似的研究成果发表.本文在深湖中对大腔体开孔模型进行自由上浮试验, 测得了一系列振动加速度线谱, 分析发现振动线谱频率和空腔自持振荡频率一致.研究结果证明了振动线谱是由空腔自持振荡强迫结构振动产生的, 同时通过分析实测振荡频率, 进一步研究了空腔流场振荡的规律.
1 试验及数值模拟为了研究开孔的流激振荡特性, 对无开孔围壳模型和开孔围壳模型分别进行无动力上浮试验, 开孔在围壳顶部, 如图 1所示, 大小为50 mm × 55 mm, 板厚1.5 mm.开孔模型于回转体上, 首先将回转体艉部挂载重物沉入深水区, 当抵达一定深度后, 再将艉部重物释放, 之后开孔模型与回转体同时自由上浮, 上浮过程示意图如图 2所示.

|
图 1 无开孔围壳模型和开孔围壳模型 Fig. 1 Normal fairwater model and opening fairwater model |
|
图 2 上浮过程示意图 Fig. 2 Diagram of floating process |
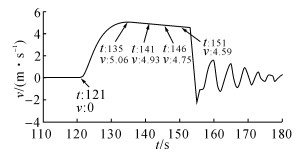
上浮模型内部安装了压力传感器, 通过伯努利公式p-p0=ρgh0-ρgh可换算为模型所处深度, 进一步换算为实时速度.式中:p0、h0分别为参考的压力和深度,p、h分别为目标的压力和深度,g为重力加速度,ρ为质量密度.以开孔围壳为例, 做出速度v随时间t变化曲线如图 3所示, 曲线显示模型在t=121 s时模型开始上浮, 经过短暂的加速后, 在t=135 s达到最大速度5.06 m/s, 之后在t=141、146 s和t=151 s时速度降为4.93, 4.75和4.59 m/s.最终模型浮出水面, 并在净浮力和惯性作用下上下起伏.
|
图 3 开孔围壳模型上浮速度曲线 Fig. 3 Velocity curve of floating opening fairwater |
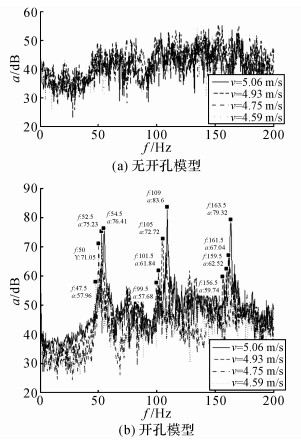
在模型指定部位布置振动传感器, 分别用于测试模型艏部、艉部、舯部及顶部的振动, 如图 4所示, 为避免传感器对流场的影响, 选用的传感器模型很小, 且均放置于模型内部.当模型上浮后, 对每一速度下4个振动加速度求取均值, 分别做出无开孔模型(如图 5(a)所示)和开孔模型的a(加速度)-f(频率)谱图(图 5(b)), 从频谱图对比中可知, 围壳开孔后产生三阶线谱.同时对上浮模型进行水下锤击试验, 试验结果表明这些线谱频率和结构湿模态并无重合.开孔围壳产生的线谱频率呈现随着速度减小而降低的性质, 符合空腔自持振荡频率的特性, 因此振动传感器测得的线谱频率, 推测是空腔流场的自持振荡引起的.
|
图 4 上浮围壳模型测点布置示意图 Fig. 4 Layout of monitor points in buoyant fairwater model |
|
图 5 自浮模型振动加速度频谱 Fig. 5 Acceleration frequency spectrum of buoyant model |
对空腔模型进行精细的流场仿真以验证试验中出现的加速度线谱频率来自空腔的自持振荡.建立与试验开孔尺寸相同的2种模型:围壳开孔模型和简化了的平板开孔模型, 如图 6所示, 网格如图 7所示.为了能够很好地捕捉壁面的涡流信息, 网格在壁面进行了加密处理, 保证壁面y+值在1附近, 壁厚方向进行了50层网格划分.计算过程中湍流模拟使用大涡模拟(LES)方法, 并且采用动态Smagorinsky-Lilly亚格子模型.大涡模拟的中心思想为:用瞬时的N-S方程直接模拟大尺度涡, 但不计算小尺度涡, 小涡对大涡的影响通过近似模型来考虑.其中, 小尺度涡判断通过滤波函数来实现.在流场计算过程中, 首先进行定常计算, 待计算稳定后, 再将定常计算结果作为非定常计算的输入, 非定常计算时间步长取2×10-4 s.进行非定常计算的同时, 为获取流场的脉动压力的信息, 在空腔附近设置如图 6所示的监测点p1和p2(2种模型监测点相对位置相同).
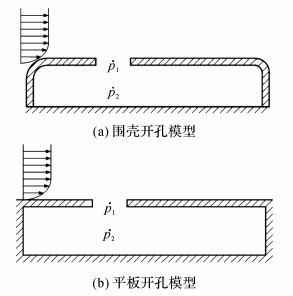
|
图 6 开孔仿真模型示意图 Fig. 6 Diagram of simulation model of opening |
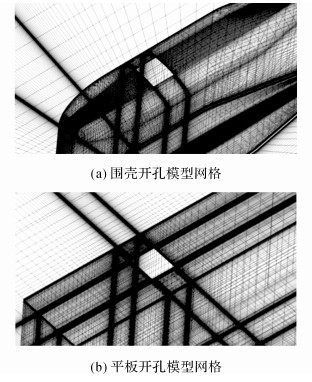
|
图 7 开孔流场计算网格 Fig. 7 Mesh of opening on fairwater and opening on plate |
设置来流速度为5.06 m/s, 提取围壳开孔和空腔开孔模型在监测点p1、p2处的脉动压力, 脉动压力功率谱密度PPSD随频率f变化的曲线如图 8所示.从图 8中可以看出, 2种模型的压力脉动变化基本一致, 说明对于围壳开孔模型, 其空腔周围流场的脉动和平板开孔模型基本相同, 2种计算模型都能捕捉到空腔的自持振荡频率.2种模型模拟的脉动压力频率、幅值以及流场分布相似.
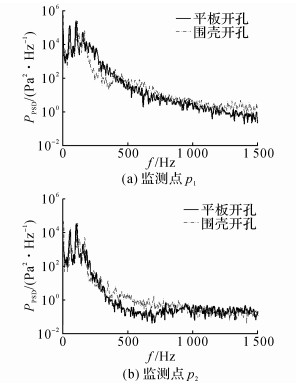
|
图 8 空腔附近脉动压力PSD曲线(v=5.06 m/s) Fig. 8 PSD curve of fluctuating pressure around cavity while v=5.06 m/s |
改变来流速度, 计算振荡频率.引入无量纲频率斯特劳哈尔数Sr, Sr数表达式如式(1) 所示, L为物体的特征长度, 本例中特指来流方向孔长.
| $ Sr = \frac{{fL}}{v}. $ | (1) |
将不同速度下的空腔自持振荡频率预报结果转换为Sr数, 并与试验对比, 如表 1所示.Sr_1st, Sr_2nd, Sr_3rd分别代表一、二、三阶Sr数, Exp为试验值, Case1为平板开孔仿真值, Case2为围壳开孔仿真值, δ1case1、δ1case2、δ2case1、δ2case2、δ3case1、δ3case2分别为平板开孔和的围壳开孔一、二、三阶的误差.从表中的结果可以看出, 试验测得的第1阶Sr数约为0.53, 而何作镛给出的空腔振荡频率预报公式结果为0.55, 二者较为接近.同时数值模拟的频率与试验结果的最大误差在3%以内, 证明了试验测得的振动线谱是由流场的自持振荡引起的.
| 表 1 试验和预报的自持振荡频率对比表 Table 1 Comparison of self-sustained oscillation frequencies in numerical prediction and experiment |
试验中出现的线谱频率, 被证实是由流体流经空腔的自持振荡产生的.空腔自持振荡的机理, 空气动力学最早用“声反馈”的机制进行解释.Rossiter[1]认为, 从上游产生的不稳定流运动至空腔随边时, 与随边产生碰撞, 并生成一个向上游传播的声波;这个声波会对上游的自由剪切层造成干扰, 使流场的不稳定作用放大, 最终形成一个向下游运动的漩涡, 漩涡会再次碰撞随边并产生声波反馈, 这就完成了一个自持振荡的循环过程.水下空腔的自持振荡和空气动力学领域有所不同:水下空腔的研究介质是不可压缩流, 不存在声波的反馈作用;且水下空腔流动的马赫数极低, 即使是考虑流体的可压缩性, 声波对流场的作用也很小.
如图 9所示为一周期内空腔自持振荡的涡量变化过程, T为周期从图 9中可以看出, 剪切层在导边生成, 逐渐发展形成大尺度涡, 随后大尺度涡向下运动, 最终与空腔随边碰撞.腔体内部流动极不稳定, 腔体后部产生大尺度涡从壁面脱离, 并且可以观察到从随边被抛射出腔外的现象, 同时也有大尺度涡被挤压进入腔内, 此时空腔尾流流场与钝体绕流的尾流非常相似.当流场产生周期性振荡时, 涡结构不断拍打空腔随边薄板, 相当于对结构进行周期性激励, 从而出现了试验中的振动加速度线谱.
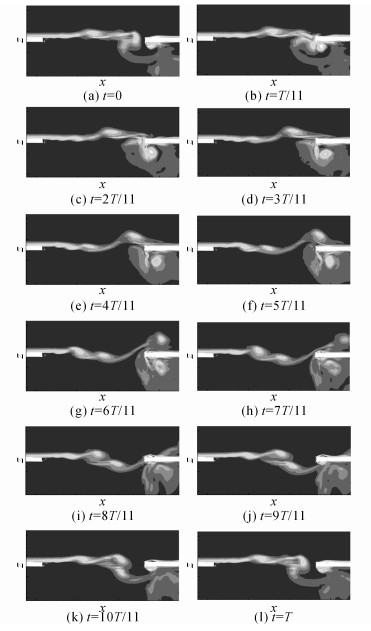
|
图 9 空腔附近流向截面涡量一周期变化云图 Fig. 9 Vorticity of flow section around cavity in a cycle |
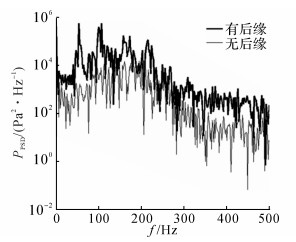
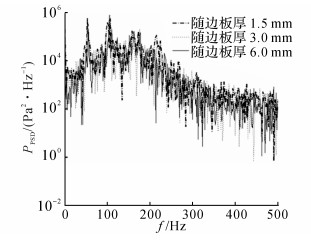
水下空腔自持振荡产生的原因, 如果只和空腔的导边有关, 则流体流经无后缘的模型时, 仍会发生自持振荡的现象.通过对无后缘的腔模型进行建模仿真, 作出PPSD-f曲线如图 10所示, 流场的压力频谱图中并没有出现明显的线谱频率, 所以仅靠导边的作用不会产生流体的自持振荡的.如果是由随边钝体绕流引起的振荡作用, 则如果改变随边的厚度, 自持振荡的频率会有所改变.通过建立随边厚度分别为1.5、3.0和6.0 mm的的模型, 提取流场振荡频率并做出PPSD-f曲线如图 11所示, 对比可知3种模型的流场振荡频率基本一致, 说明空腔振动频率并非随边的涡脱落特性.
|
图 10 有/无后缘模型脉动压力PSD曲线(v=0.56 m/s) Fig. 10 Fluctuating pressure PSD curve of with/without trailing edge models while v=5.06 m/s |
|
图 11 随边厚度改变模型脉动压力PSD曲线(v=0.56 m/s) Fig. 11 Fluctuating pressure PSD curve of varied-trailing edge thickness models while v=5.06 m/s |
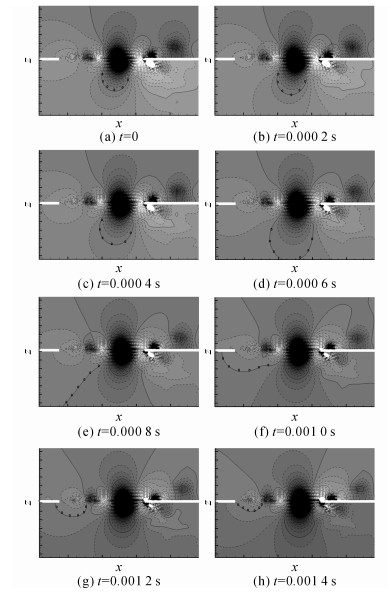
提取流场的脉动压力值.做出流场的脉动压力随时间变化云图, 如图 12所示.图片时间间隔dt=0.000 2 s.图中的深色区域对应的是流场中的漩涡区域, 因为漩涡处的流场扰动大, 相应的压力脉动也非常剧烈, 所以脉动压力大的区域, 也即漩涡所在的区域.图中的开始时刻漩涡接近空腔后缘, 随着时间的推移, 漩涡向空腔后缘移动, 而其下缘的脉动压力则开始向前缘移动, 如图中标示的0 Pa压力等值线正逐渐向空腔导边运动, 当漩涡撞击空腔随边时, 脉动压力急剧向导边传播, 影响导边的自由剪切层, 完成自持振荡过程.
|
图 12 空腔附近流场脉动压力随时间变化云图 Fig. 12 Time-varying fluctuating pressure contours around cavity |
图 12的脉动压力变化云图证实了空腔自持振荡是由导边和随边的反馈作用引起的.这种反馈作用可以理解为, 当漩涡运动至随边时, 会对空腔形成一个挤压或者抽吸的作用, 而由于流体的连续性和不可压缩性, 在随边处的挤压作用必然会引起导边处的反作用, 反作用通过流体静压脉动的形式体现出来.空腔的反馈作用加剧了导边自由剪切层的不稳定性, 导致漩涡在导边产生, 从而形成空腔的自持振荡.
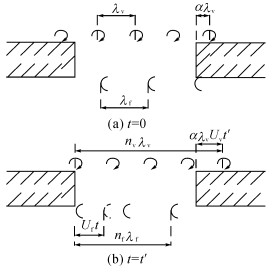
3 频率特性空腔自持振荡的简化过程如图 13所示, 上下两图分别代表t=0随边压力反馈产生的时刻和t=t′反馈到达导边的时刻.λf为反馈压力传播波长, λv为涡流运动的波长.Rossiter等[1, 9, 5-6]认为, 涡从上游撞击空腔随边, 但并没有立刻产生反馈作用, 而是在反馈产生和涡撞击导边之间存在时间为α的相位迟滞.所以在t=0时刻, 此时空腔随边产生反馈, 涡已经向下游运动了αλv的距离.经过了t′时, 最上游的反馈压力抵达导边, 使导边的涡产生, Uv为涡流运动的速度, Uf为反馈压力传播速度.如果空腔内有nv(nv≥1) 个涡, 同时反馈波有nf(nf≥0) 个, 同时, 反馈波向上游运动了Uft′距离, 有联立方程:
|
图 13 空腔自持振荡的反馈过程示意图 Fig. 13 Feedback process of self-sustained oscillation in cavity |
| $ \left. \begin{array}{l} {n_{\rm{v}}}{\lambda _{\rm{v}}} = L + \alpha {\lambda _{\rm{v}}} + {U_{\rm{v}}}t', \\ L = {n_{\rm{f}}}{\lambda _{\rm{f}}} + {U_{\rm{f}}}t'. \end{array} \right\} $ | (2) |
消除两式中的t′, 可以得到
| $ \frac{{{U_{\rm{v}}}}}{{{U_{\rm{f}}}}}{n_{\rm{f}}}{\lambda _{\rm{f}}} + ({n_{\rm{v}}}-\alpha ){\lambda _{\rm{v}}}{\rm{ = }}L\left( {1 + \frac{{{U_{\rm{v}}}}}{{{U_{\rm{f}}}}}} \right). $ | (3) |
进一步, 将λf=Uf/f和λv=Uv/f代入式(2), 可得
| $ {n_{\rm{f}}} + ({n_{\rm{v}}}-\alpha ){\rm{ = }}fL\left( {\frac{1}{{{U_{\rm{v}}}}} + \frac{1}{{{U_{\rm{f}}}}}} \right). $ | (4) |
| $ \begin{array}{l} Sr = \frac{{fL}}{{{U_\infty }}} = ({n_{\rm{v}}} + {n_{\rm{f}}}-\alpha )/\left( {\frac{{{U_\infty }}}{{{U_{\rm{v}}}}} + \frac{{{U_\infty }}}{{{U_{\rm{f}}}}}} \right) = \\ \;\;\;\;\;\;\;(n-\alpha )/\left( {\frac{1}{\kappa } + \frac{{{U_\infty }}}{{{U_{\rm{f}}}}}} \right).(n = 1, 2, 3 \cdots ). \end{array} $ | (5) |
式中:n为空腔自持振荡的阶数, κ=Uv/U∞为腔内涡的对流运动速度与来流速度的比值, α为空腔涡碰撞随边与反馈产生之间的相位迟滞.
式(5) 表明空腔自持振荡无量纲频率Sr数是与空腔尺寸无关的常数.Rossiter对介质为空气的高速流激空腔模型进行了风洞试验, 通过这些试验数据, Rossiter拟合得到的κ和α值分别为0.57和0.25.Rossiter公式能够在空气动力学领域有较好的适用性, 但水下的空腔流动和Rossiter的模型完全不同, 如在速度为5.06 m/s下试验频率为55 Hz, 用Rossiter公式预估的频率为45.09 Hz, 误差高达22%.原因是水介质和空气介质的差异以及马赫数不同, 这表明要对水中流激空腔振荡频率进行预估, 必须修正Rossiter公式.
从脉动压力输运变化图可知, 脉动压力反馈的传播速度远大于远场流动的速度, 所以U∞/Ua可近似取为0, Sr数和自持振荡阶数的关系为:Sr=κn-κα.这是一个一次多项式, 将试验测得的每个速度下的Sr数求出, 并与对应的阶数进行最小二乘拟合, 得到拟合的κ和α值如表 2所示.从拟合得到的κ和α值可知, 水下空腔流动的值远小于Rossiter给出的0.25的取值, 何祚镛[5]给出的水下圆柱形空腔频率估算公式中, α值只取0.08, 同样远小于Rossiter的值, 说明在水中低速流动的条件下, 导边漩涡冲击与水动力反馈之间的相位迟滞很小.从表 2的结果可以看出, 这种相位迟滞在0~0.055之间(v=5.06 m/s时出现负值, 应是实验误差).试验拟合的κ值也在0.547左右, 稍小于Rossiter给出的0.57的值.通过以上的分析, 可认为对于水下空腔自持振荡时, 公式(5) 中的α值远小于0.25, 应取0~0.055之间, 本文推荐取0.028 6, κ值取0.547 4, 得到适合于水下低速空腔自持振荡频率的预估公式:
| 表 2 上浮试验数据最小二乘拟合得到的κ和α Table 2 Least square fitting values of κ and αfrom data in buoyant model experiment |
| $ Sr = \frac{{{f_n}L}}{V} = \frac{{n-0.028\;6}}{{1/0.547\;4}}.(n = 1, 2, 3 \cdots ) $ | (6) |
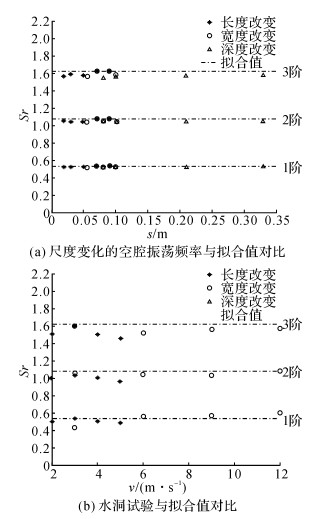
为了验证式(6) 的有效性, 对原孔高50 mm、孔宽55 mm、腔深330 mm的空腔进行尺寸修改, 计算其自持振荡频率, 将数值模拟结果与拟合公式对比, 得到的对比结果如图 14(a)所示, s为单一变化的尺寸, 如孔宽改变, 则s代表孔宽, 并且保持其他变量不变.从图中可以看出经验公式与数值模拟结果非常接近.另外, 中国船舶科学研究中心[10]对空腔自持振荡也进行了一系列水洞试验, 中国船舶科学研究中心试验结果与拟合公式对比如图 14(b)所示.从图 14(b)的比较结果来看, 频率预报公式(6) 误差较小, 与水洞试验结果和数值仿真结果均比较接近, 证明了本文的修正公式能够精确的预报水下空腔流激振荡的频率.
|
图 14 本文修正的水下空腔自持振荡频率预估公式验证 Fig. 14 Verification of formula to predict frequencies of self-sustained oscillation of underwater cavity |
本文对空腔模型进行自由上浮试验和数值模拟分析.在试验中测得一系列振动加速度线谱, 建立了流场仿真模型, 采用大涡模拟结合动态Smagorinsky-Lilly亚格子模型的方法进行精细的流场模拟, 同时通过对流场脉动压力的监测, 对流场的涡量以及脉动压力变化的观察, 研究了空腔自持振荡的规律.得出结论如下.
(1) 在上浮试验过程中, 在结构表面的振动传感器能够监测到一系列加速度线谱, 振荡频率呈现随速度减小而降低的性质, 通过流场仿真分析认为线谱是由流场自持振荡冲击结构引起振动产生.
(2) 水下空腔自持振荡机制是由水动力静压脉动引起的反馈作用, 这种反馈作用可以理解为, 当漩涡运动至随边时, 会对空腔形成一个挤压或者抽吸的作用, 而由于流体的连续性和不可压缩性, 在随边处的挤压作用必然会引起导边处的反作用, 这种反作用通过流体静压脉动的形式体现了出来.
(3) 对空腔自持振荡的线谱频率研究发现, 在水中低马赫数条件下, 漩涡撞击随边与水动力反馈产生之间的相位迟滞远低于Rossiter的取值.通过对实验数据的拟合, 本文修正了Rossiter公式, 使其更适用于水中低马赫数的情形, 修正的α值取0.028 6, κ取0.547 4, 得到频率预估公式如下:
| $ Sr = \frac{{n-0.028\;6}}{{1/0.547\;4}}.(n = 1, 2, 3 \cdots ) $ |
| [1] | ROSSITER J E. Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds [M]. [S.l.]: Hm Stalionery office, 1964: 68-91. |
| [2] | BASLEY J, PASTUR L R, LUSSEYRAN F, et al. Experimental investigation of global structures in an incompressible cavity flow using time-resolved PIV[J]. Experiments in Fluids, 2011, 50(4): 905–918. DOI:10.1007/s00348-010-0942-9 |
| [3] | CICCA G M D, MARTINEZ M, HAIGERMOSER C, et al. Three-dimensional flow features in a nominally two-dimensional rectangular cavity[J]. Physics of Fluids, 2013, 25(9): 708–709. |
| [4] |
方涛. 不可压缩空腔流振荡特性研究[D]. 武汉: 华中科技大学, 2013: 46-65.
FANG TAO. The oscillation characteristics of incompressible cavity flow[D].Wuhan: Huazhong University of Science and Technology, 2013: 46-65. |
| [5] | 何祚镛. 结构振动与声辐射[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001: 147-183. |
| [6] |
戴绍仕, 姚熊亮, 李卓, 等. 均匀流场中三维陷落腔流激振荡实验研究[J].
哈尔滨工程大学学报, 2010, 31(6): 693–700.
DAI Shao-shi, YAO Xiong-liang, LI Zhuo, et al. Experimental research on fluid induced oscillation of 3-D cave-in cavities in uniform shear layers[J]. Journal of Harbin Engineering University, 2010, 31(6): 693–700. |
| [7] | ARUNAJATESAN S, SINHA N. Hybrid RANS-LES modeling for cavity aeroacoutics predictions[J]. International Journal of Aeroacoustics, 2003, 2(1): 65–93. DOI:10.1260/147547203322436944 |
| [8] |
刘聪尉, 吴方良, 李环, 等. 空腔不可压缩流动特征及其声学特性研究[J].
水动力学研究与进展, 2014, 29(2): 218–224.
LIU Cong-wei, WU Fang-liang, LI Huan, et al. Investigation on the characteristics of incompressible flow and acoustics fields of cavity[J]. Chinese Journal of Hydrodynamices, 2014, 29(2): 218–224. |
| [9] | KEGERISE M, SPINA E, LOUIS CATTAFESTA I. An experimental investigation of flow-induced cavity oscillations[J]. Dissertation Abstracts International, 2013, 227(9): 1375–1388. |
| [10] |
沈琪, 高岩, 张晓伟, 等. 流激开口剪切振荡特性试验研究[C]//第十五届船舶水下噪声讨论会. 郑州: [s. n]2015: 283-287.
SHEN Qi, GAO Yan, ZHANG Xiao-wei, et al. Experimental research on property of shear layer oscillation[C]//15th underwater noise conference. Zhengzhou: [s.n], 2015: 283-287. |



