2. 洛阳理工学院 土木工程学院, 河南 洛阳 471023
2. College of Civil Engineering, Luoyang Institute of Science and Technology, Luoyang 471023, China
传统的栓焊梁柱连接节点在1995年日本阪神地震和1994年美国北岭地震中出现了许多不同程度的脆性破坏, 因此高强螺栓半刚性梁柱连接成为国内外专家研究的方向[1-5].
近30年来, 国内外专家对高强螺栓半刚性梁柱连接的研究主要集中在平面梁柱连接节点的初始刚度、变形能力、极限承载力、耗能特性等方面.特点主要包括:1) 现有的试验研究对象是框架结构中的平面边柱节点;2) 试验加载方式采用比较容易的梁端加载[6-7];3) 很少考虑框架柱承受的轴向压力对节点的受力影响.但是在实际框架体系中, 由于钢框架在承受地震作用过程中, 梁柱连接节点需要承受空间传来的多个方向内力, 受到的影响因素特别多, 特别是梁柱连接的空间效应不容忽略[8-11].
因此, 研究空间半刚性梁柱连接节点的受力特性具有很好的工程意义.本文选取空间角柱节点和对应的平面边柱节点为研究对象, 采用柱端双向交替受荷的加载方式进行拟静力试验, 通过拟静力试验研究空间角柱及平面边柱梁柱连接节点的抗震性能.
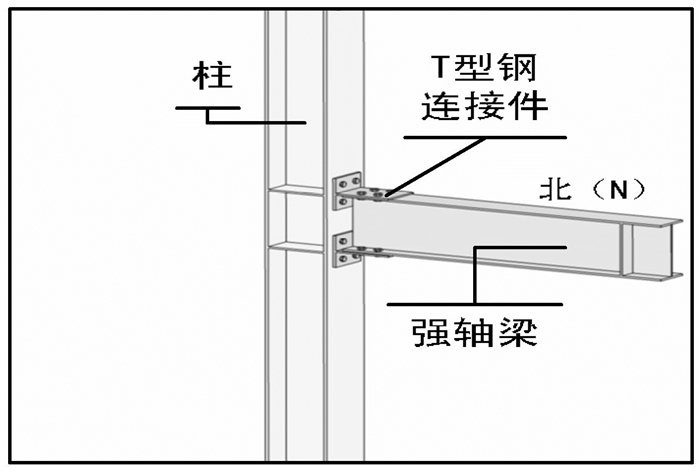
1 试件设计按照节点在空间钢框架中的位置主要包括空间角柱节点、空间边柱节点以及空间中柱节点, 见图 1.在现有的钢框架梁柱节点中按受力特点将节点分为刚性与半刚性节点, 而半刚性梁柱连接节点中, 剖分T型钢连接是比较典型的具有较大转动刚度和承载力的梁柱连接形式之一.本文根据空间节点在空间框架所在的相对位置, 选取角柱节点为研究对象.主要针对剖分T型钢连接的2个平面边柱半刚性节点(PBJD1和PBJD2)、2个空间角柱半刚性节点(KJJD1和KJJD2) 和1个空间刚性连接的角柱节点(KJGJD)为研究对象进行拟静力试验, 如图 2~4所示.

|
图 1 框架节点分类图 Fig. 1 Classification of frame joints |
|
图 2 PBJD1与PBJD 2节点示意图 Fig. 2 PBJD1 and PBJD 2 connection |
|
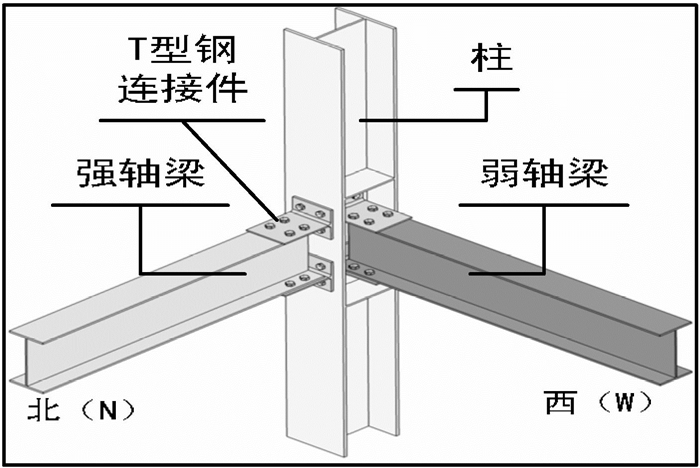
图 3 KJJD1与KJJD 2节点示意图 Fig. 3 KJJD1 and KJJD 2 connection |
|
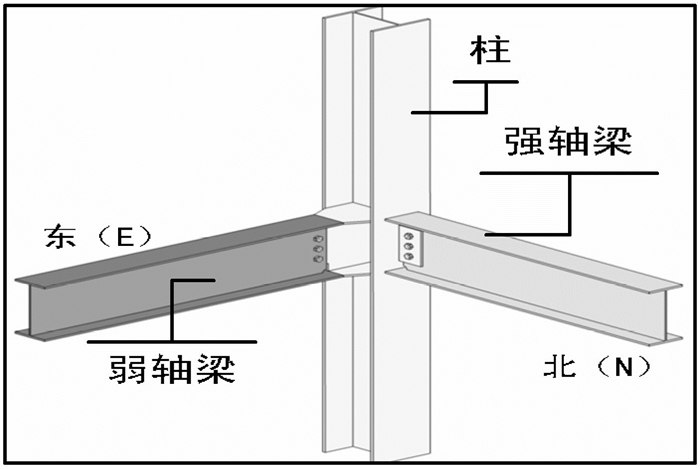
图 4 刚性节点KJGJD示意图 Fig. 4 Spatial rigid connection |
空间半刚性节点采用剖分T型钢梁柱连接形式.试件中的梁、柱均采用热轧H型钢, 柱型号为WH300×300×10×15, 梁型号为NH350×175×7×11.螺栓为10.9级M22高强螺栓.空间刚性节点连接为传统栓焊连接方式[12-13], 平面节点连接方式与空间半刚性连接方式相同, 但只考虑强轴所在的方向.梁柱连接均按照钢结构施工及验收规程(GB50205-2001) 要求安装, 节点试件中的构件尺寸见表 1.
| 表 1 节点试件参数表 Table 1 Basic parameters of specimens |
试验中所采用的梁、柱以及剖分T型钢采用同一批次的钢材, 钢材牌号为Q235B, 材料力学性能屈服强度fy、抗拉强度fu、收缩率A、伸长率δ和弹性模量E, 测试结果如表 2所示.
| 表 2 节点试件钢材力学性能 Table 2 Material properties of steels |
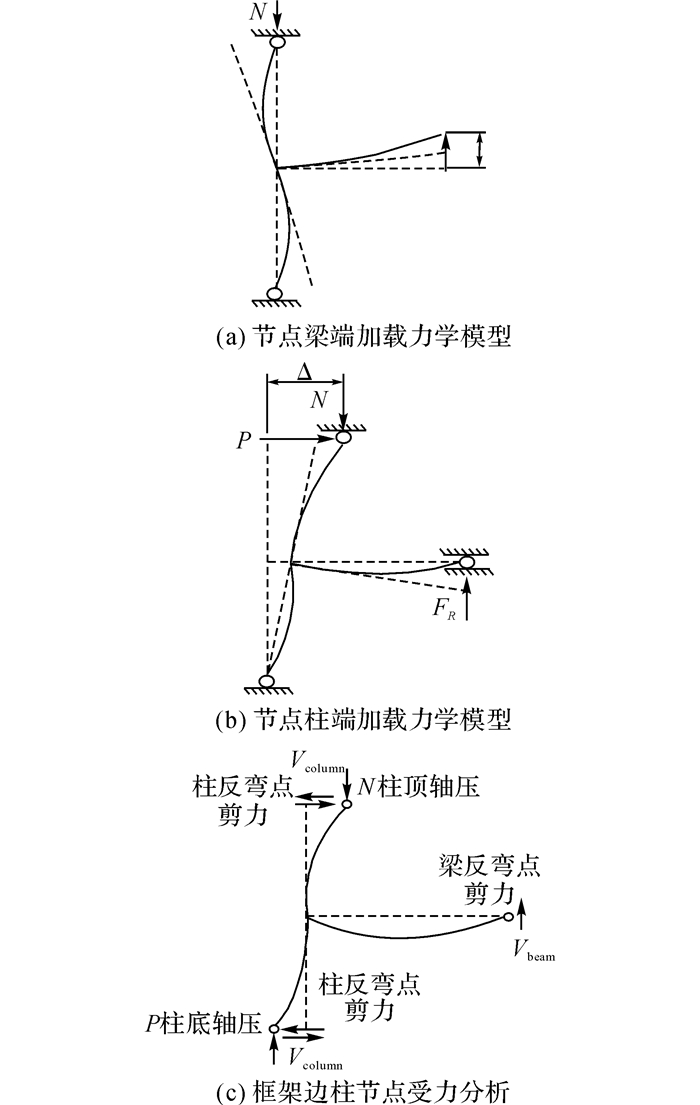
目前国内外在进行梁柱连接节点拟静力试验时, 大部分采用梁端加载方式, 少部分采用柱端加载方式, 如图 5(a)~(b)所示.梁端加载方式虽然能够使得节点的受力状态与实际的受力状态基本相吻合, 但其忽略了框架柱所具有的P-Δ二阶效应;柱端加载方式能够较全面的实现节点的受力状态, 因此本文选择柱端加载方式.对图 5(b)的力学模型进行受力分析如图 5(c)所示, 根据梁端和柱端的受力特性和空间梁柱连接节点的受力特性, 在节点的强轴轴线方向和弱轴轴线方向分别设置2组水平作动器, 作动器一端安装在L形反力墙上, 另一端与柱子的上下两端相连并交替施加水平荷载;柱顶端设置能够双向跟动的竖向作动器, 对柱顶施加轴向压力.以上5个作动器均由电液伺服试验系统控制加载, 南北向节点强轴轴线方向, 东西向为节点的弱轴轴线方向, 在柱下端设置自主设计的万向滑动铰支座, 确保试验时能够实现双向加载.在东(E)西(W)向和北(N)向的梁端同时设置可以实现双向跟动的滑动支座, 梁端部安装在四肢桁架柱上, 在每根梁端部上下翼缘分别设置饼状压力传感器来量测梁端的支座反力, 以空间角柱节点为例对试验装置进行说明如图 6所示, 空间角柱节点KJJD1和KJJD2试验现场如图 7(a)所示, 空间角柱刚性连接节点KJGJD试验现场如图 7(b)所示, 平面边柱节点PBJD1和PBJD2试验现场如图 7(c)所示.
|
图 5 梁柱节点拟静力试验力学模型 Fig. 5 Mechanical model of beam-column connection quasi-static test |
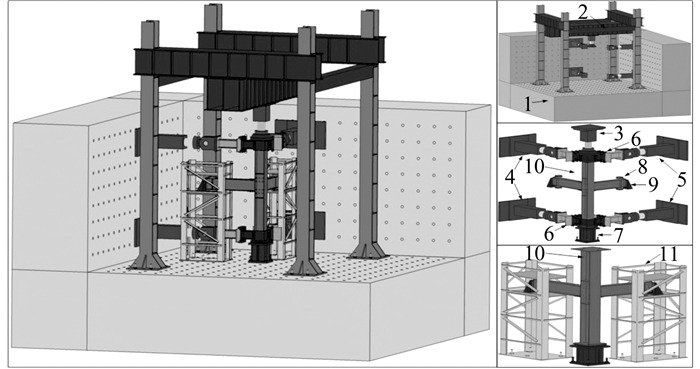
|
1-反应墙;2-反力架;3-柱轴压作动器;4-强轴作动器;5-弱轴作动器;6-双向加载装置;7-柱底支座;8-梁端力传感器;9-梁端侧向滑档;10-试件;11-梁支座桁架 图 6 空间框架角柱节点拟静力试验系统 Fig. 6 Spatial beam-column joint quasi-static test system |

|
图 7 节点试验现场 Fig. 7 Joints test site |
本次试验参考文献[14], 按照强弱轴正交交替循环加载的方式进行, 采用位移控制加载方式, 每级加载增量按照初估的屈服位移控制, 本次试验按照量测出的特殊部位应变达到屈服应变时对应的位移作为连接节点的初估屈服位移, 随后荷载位移量按屈服位移整数倍增加, 双向荷载步曲线图如图 8所示,图中:δy为屈服位移,n为屈服位移整数倍, 在试验过程中, 首先在柱子顶端通过竖向作动器施加200 kN的轴压, 在整个试验加载过程中始终保持这个数值;水平荷载按照图 8的荷载历程曲线进行施加, 作动器以推为正向荷载, 反之以拉为负向荷载.首先保证弱轴方向的作动器不动, 强轴方向的作动器同时对模型柱子顶端以及底端施加反向的水平荷载, 每个等级荷载循环3次, 然后强轴方向作动器归置零位, 并保持不动;接着, 在模型柱子上下两端弱轴方向施加反向的水平荷载.在试验过程中, 出现下列几种情况, 如节点连接部件断裂、局部发生明显的屈曲变形、试验得到的滞回曲线承载力有明显下降趋势, 则试验终止.
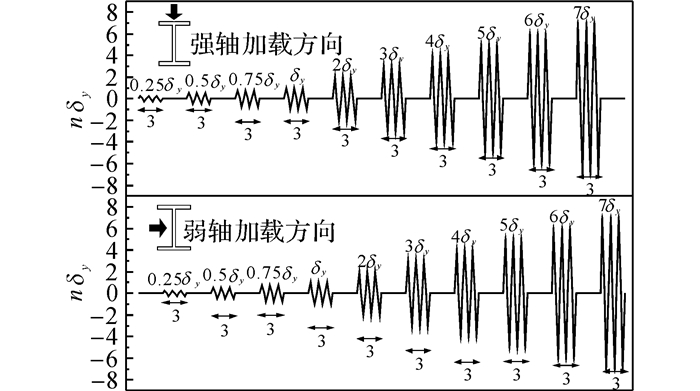
|
图 8 双向荷载步曲线图 Fig. 8 Test loading path |
为测出空间节点的梁端弯矩与梁柱之间相对转角, 在每根梁端上下各放置一个压力传感器采集梁端支座反力数据, 在每个方向梁与柱的夹角位置安放拉线式位移计, 用于测量梁与柱之间的相对位移, 将测得的相对位移δd利用公式换算成梁柱之间的相对转角[5], 如图 9所示.考虑节点区域在低周往复荷载作用下的塑性变形, 在T型件、梁和柱的腹板与翼缘上粘贴应变片及应变花监测节点区域的塑性变形.
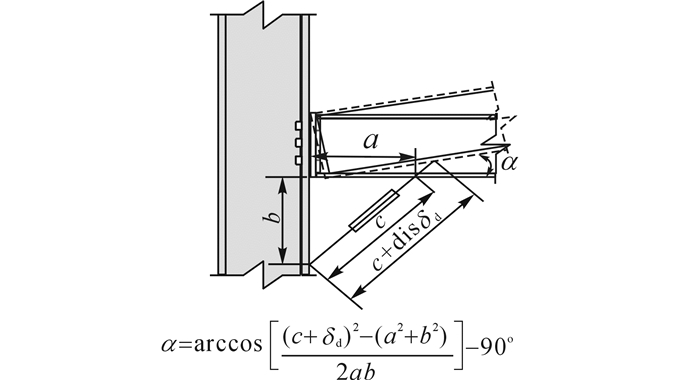
|
图 9 梁柱相对转角测量原理图 Fig. 9 Measurement method of relative rotation |
在试验过程中无论是半刚性平面节点还是空间节点, 由于节点核心区域在逐渐增大的加载过程中T型连接件、梁、柱和高强螺栓之间相互挤压摩擦, 导致在施加荷载的过程中伴随着响声, 当位移荷载处在平衡或最大位置时, 响声消失, 当剖分T型连接件发生断裂时产生较大的响声.采用剖分T型钢连接梁柱连接节点, 无论是平面节点还是空间节点均表现出延性较大的半刚性特性, 其破坏特征主要表现在首先T型连接件翼缘产生较大的弯曲变形, 接着T型件腹板与翼缘交界处断裂(如图 10、11、12和13所示).无论是平面节点还是空间节点经历了相似的破坏过程:T型件腹板与翼缘交界处屈服→T型件翼缘发生受拉弯曲→T型件腹板与翼缘交界处塑性区域扩大产生塑性铰→T型件腹板与翼缘交界处断裂.

|
图 10 T型连接件翼缘弯曲变形 Fig. 10 Flange bending of T-stub |

|
图 11 试件PBJD1节点破坏 Fig. 11 Failure phenomena of PBJD1 specimen |

|
图 12 试件KJJD1节点破坏 Fig. 12 Failure phenomena of KJJD1 specimen |

|
图 13 试件KJJD2节点破坏 Fig. 13 Failure phenomena of KJJD2 specimen |
由于平面节点PBJD2比PBJD1的T型件翼缘厚度厚2 mm, 经过了9倍屈服位移荷载循环后发生断裂, 而PBJD1节点只经过6倍屈服位移荷载循环就发生断裂, 空间节点中KJJD1的T型件比KJJD2的T型件薄了2 mm, 节点KJJD1与KJJD2破坏现象均发生在强轴平面, 表现为T型件被拉断. T连接型件较厚的KJJD2节点破经历了8倍屈服位移荷载循环后T型件断裂(如图 13所示), KJJD1节点破经历了6倍屈服位移荷载循环后T型件断裂(如图 12), 因此通过增加T型连接件的厚度可以提高了节点的承载能力能力.而空间刚性节点KJGJD由于焊缝缺陷在实际中不可避免, 在拟静力循环荷载作用下, 在强轴平面和弱轴平面均发生了脆性断裂, 受拉的梁柱交界焊缝处产生脆性断裂, 如图 14、15所示为节点KJGJD强轴和弱轴破坏现象.

|
图 14 试件KJGJD节点强轴破坏 Fig. 14 Failure phenomena of KJGJD specimen |

|
图 15 试件KJGJD节点弱轴破坏 Fig. 15 Failure phenomena of KJGJD specimen |
本次试验将各个梁端压力传感器采集的支座反力数据转化为节点区域的梁端弯矩, 将梁柱之间的拉线式位移传感器采集到的各个方向梁与中柱的相对位移数据经计算转化为梁与柱之间的相对转角, 从而可以得到空间梁柱连接节点弱轴方向和强轴方向的弯矩-转角滞回曲线, 如图 16所示.图中θ为转角,M为弯矩,从图中可以看出, 各个节点试件的滞回曲线呈现为梭形, 无捏缩, 表明剖分T型钢为连接的节点的耗能特性较好.以较弱T型件为连接的框架角柱节点KJJD1和PBJD1滞回曲线在强轴平面表现出明显的下降, 主要原因是T型件连接件在循环荷载作用下发生了断裂而导致节点失去了承载力.以较强T型件为连接的节点PBJD2和KJJD2体现出较好的延性, PJJD2经历了9倍屈服位移的循环荷载后滞回曲线才出现承载力下降的现象.KJJD2节点的滞回曲线无论是强轴(北侧)还是弱轴(西侧), 都比较饱满, 体现出较好的滞回特性.刚性节点KJGJD则表现出相对较差的延性, 分别在强轴平面经历3倍屈服位移以及弱轴平面经历2倍屈服位移的循环荷载后在焊缝处发生明显脆性断裂.除刚性节点外的半刚性节点, 在施加荷载的前4个荷载等级即2倍屈服位移之前, 弯矩-转角关系表现为线性阶段.在2倍屈服位移之后, 弯矩-转角关系具有明显的非线性特点, 在每一荷载等级弯矩承载力的弯矩数值基本相同, 认为节点承载力均无退化现象发生, 节点在发生破坏后承载力明显下降, 节点的承载力退化明显.
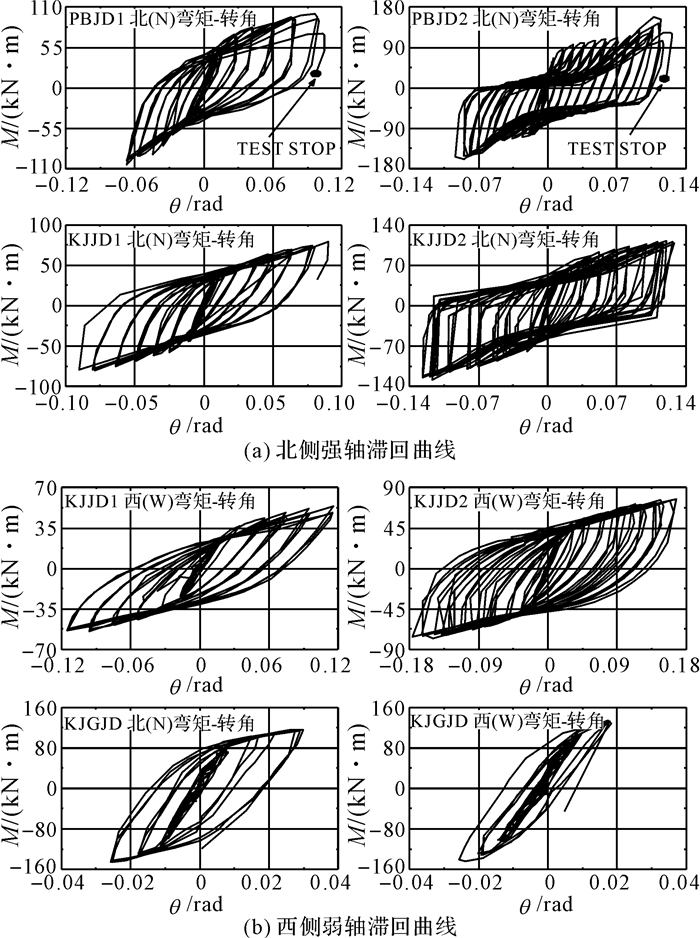
|
图 16 试验节点滞回曲线 Fig. 16 Hysteresis curves of specimens |
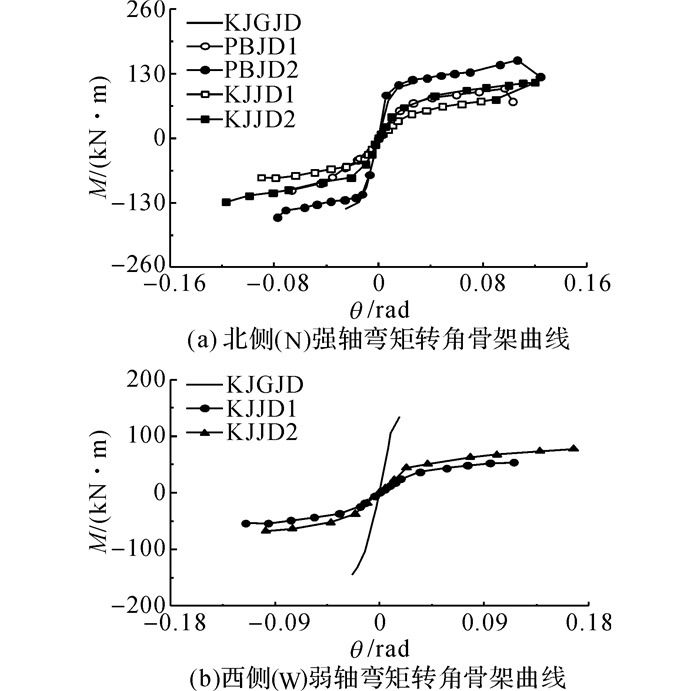
骨架曲线是每次循环加载达到的水平力最大峰值的轨迹, 反映了构件受力与变形的各个不同阶段及特性(强度、刚度、延性等), 也是确定恢复力模型中特征点的重要依据.由滞回曲线确定的各节点试件强轴(北侧)和弱轴(西侧)的骨架曲线如图 17所示, 根据骨架曲线获得试验每个节点模型各个方向的屈服转角(θy)、屈服弯矩(My)、极限转角(θu)、极限弯矩(Mu), 详见表 3.
|
图 17 梁端弯矩转角骨架曲线 Fig. 17 Skeleton curves of test specimens |
| 表 3 测试结果 Table 3 Test results |
节点试件在强轴平面与弱轴平面都经历了弹性阶段和塑性阶段.空间刚性节点KJGJD的强轴和弱轴承载弯矩最大, 强轴屈服承载弯矩最大为112.01 kN·m, 最大极限承载弯矩达到了145.17 kN·m, 极限承载力与屈服承载力比值在1.30~1.65倍之间;弱轴屈服承载弯矩最大为104.88 kN·m, 最大极限承载弯矩达到了141.35 kN·m, 极限承载力与屈服承载力比值在1.29~1.35倍之间, 说明从屈服到破坏承载力无较大的提升, 节点的破坏是脆性破坏.由于空间半刚性试件KJJD1的T型连接件要比KJJD2的连接件弱, 因此KJJD1的屈服弯矩和极限弯矩明显比KJJD2要低.KJJD1强轴屈服承载弯矩是KJJD2的55.39%~62.07%, 强轴极限承载弯矩之比为63.49%~71.42%, 弱轴屈服承载弯矩之比为52.86%~58.75%, 弱轴极限承载弯矩之比为69.48%~70.50%.可见连接T型件腹板与翼缘的厚度是影响节点承载力的因素之一.空间刚性节点KJGJD与空间半刚性节点KJJD2相比, KJGJD的强轴极限承载弯矩是KJJD2的1.05~1.17倍, KJGJD节点弱轴极限承载弯矩是KJJD2的1.75~1.85倍, 刚性节点KJGJD的强轴极限转角是KJJD2的20.31%~23.63%, 弱轴极限转角是半刚性的10.42%~14.59%, 这是由于刚性节点变形能力差, 滞回循环荷载等级远低于半刚性节点而造成.边柱平面节点(PBJD1和PBJD2) 与之相匹配的空间节点(KJJD1和KJJD2) 进行对比分析来看, 这种连接的梁柱空间节点和平面节点, 其屈服弯矩和极限弯矩、屈服转角和极限转角都和T型件腹板翼缘厚度有很大关系, 采用较厚的T型钢连接件, 可以明显提高这种连接方式空间梁柱连接节点和平面梁柱连接节点的承载能力和变形能力.但空间梁柱连接节点的强轴极限弯矩低于平面梁柱连接节点的极限弯矩, KJJD1只有PBJD1的75.21%~78.10%, KJJD2为PBJD2的69.91%~78.43%, 说明空间梁柱连接节点由于受到弱轴的影响, 其强轴的极限承载力有明显削弱.
4.4 转动刚度退化分析对于半刚性梁柱连接节点, 在节点屈服之前其初始转动刚度基本呈线性, 节点屈服后进入塑性状态, 弯矩与转角关系表现为非线性, 节点的转动刚度通常用割线刚度来表示.考虑到拟静力试验中往复施加荷载, 节点的弯矩承载力与相对应的节点转角有正负之分, 所以其割线刚度根据同一级荷载下正反方向弯矩承载力绝对值之和与对应峰值转角绝对值之和的比值来确定, 即由式(1) 计算来确定节点的转动刚度.
| $ {{K}_{i}}=\frac{|+{{M}_{i}}|+|-{{M}_{i}}|}{|+{{\theta }_{i}}|+|-{{\theta }_{i}}|}. $ | (1) |
式中:Mi为循环荷载任意一级荷载作用下的弯矩承载力峰值, θi为循环荷载任意一级荷载作用下弯矩承载力峰值对应的转角.空间刚性节点(KJGJD)初始转动刚度最大, 强轴为10 280.79 kN·m/rad, 弱轴为8 513.42kN·m/rad, 但其强轴与弱轴的转动刚度分别达到了初始转动刚度的46.28%和67.81%时, 节点断裂失去承载能力.对采用相同规格T型连接件的平面节点与空间节点进行分析, PBJD1与PBJD2的强轴初始转动刚度分别为3 188.01kN·m/rad和9 811.11 kN·m/rad, KJJD1与KJJD2的强轴初始刚度分别为2 837.99 kN·m/rad和3 014.79 kN·m/rad.KJJD1比PBJD1初始刚度降低了10.98%, KJJD2是PBJD2初始转动刚度的30.73%, 考虑空间的弱轴对强轴的影响, 空间角柱节点的强轴初始转动刚度比平面节点要低, 而且受T型连接件翼缘与腹板厚度的影响有较大的差异性.KJJD1弱轴西侧的初始转动刚度为1 419.65 kN·m/rad, KJJD2弱西侧的初始转动刚度为1 418.36 kN·m/rad, 可以看出T型连接件的腹板与翼缘厚度对角柱节点弱轴的初始转动刚度影响不大.将每个节点各个方向的刚度归一化后, 节点的转动刚度随荷载增加的退化关系曲线见图 18, 图中:DK为刚度退化率,随着荷载等级的增加, 刚性节点和半刚性节点的转动刚度退化率在前3个荷载等级的退化速率基本一致, KJJD1和KJJD2强轴与弱轴的转动刚度退化率基本一致, 即T型连接件的规格对空间角柱节点的刚度退化影响不大.当T型连接件断裂后强轴方向的转动刚度退化至初始的26%左右, 弱轴方向的初始转动刚度退化至初始的23%左右.平面节点PBJD1与PBJD2相比T型连接件较厚的PBJD2刚度退化速率比PBJD1要快, 节点PBJD1在破坏状态时的转动刚度是初始的30.98%, 节点PBJD2破坏时的转动刚度是初始的17.33%.以上分析可以认为, 空间半刚性角柱节点强轴转动刚度退化规律与平面半刚性节点相比基本一致差别不大.

|
图 18 割线转动刚度退化曲线 Fig. 18 Stiffness degradation curves of test specimens |
节点的延性采用极限转角θu与屈服转角θy的比值进行评价, 对判断节点的延性和耗能能力有一定的参考价值.试验节点各个方向的延性系数如表 4所示, 表中μmajor为强轴延性系数、μminor为弱轴延性系数、μaverage1为强轴平均延性系数;μaverage2为弱轴平均延性系数.节点PBJD2和KJJD2采用相同型号的T型连接件, 延性系数最大为节点PBJD2, 其平均值为15.46, 节点KJJD2的延性系数是5.70, 空间节点的延性系数明显低于平面节点, 降低了63.13%;空间节点KJJD1延性系数比平面节点PBJD1有所增加, 增幅为24.08%, 说明空间角柱节点强轴方向的延性系数在考虑弱轴受力与T型连接件规格这2个影响因素后延性系数存在较大的差异性.无论是平面梁柱节点还是空间梁柱节点, 从表 4可以看出, 通过增加T型连接件的厚度可以提高梁柱连接节点的延性系数, PBJD2节点的强轴平均延性系数是PBJD1节点的3倍多.而空间节点强轴与弱轴的延性系数随着T型连接件的增加延性系数略有下降, KJJD2节点的强轴与弱轴的平均延性系数分别是KJJD1节点的89.20%和87.11%.可见T型连接件腹板与翼缘的厚度对节点的延性系数有较大影响.空间刚性节点KJGJD与承载能力及刚度较大的KJJD2节点无论强轴平面还是弱轴平面, 空间半刚性节点的延性系数是空间刚性节点的1.8倍以上, 体现出半刚性节点具有很好的延性.
| 表 4 延性系数 Table 4 Ductility factor of specimens |
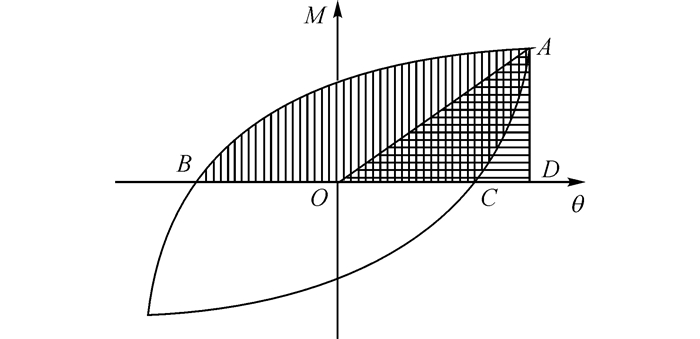
节点的耗能能力通常采用等效黏滞阻尼系数he来评定试件在循环往复荷载作用下吸收能量的大小, 其计算方法可按如图 19所示进行计算, 其计算表达式为
| $ {{h}_{\text{e}}}=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\frac{{{S}_{ABC}}}{{{S}_{AOD}}}. $ | (2) |
|
图 19 等效黏滞阻尼系数计算简图 Fig. 19 Calculation diagram of damp coefficient |
式中:SABC为图形AC面积,SAOD为图形AOD面积.
按式(2) 计算出节点的等效黏滞阻尼系数如表 5所示.
| 表 5 等效黏滞阻尼系数 Table 5 Equivalent viscous damp coefficient |
从表中看出, 平面半刚性节点与空间半刚性节点强轴方向的等效黏滞阻尼系数相差不大, 其数值在0.216~0.285范围之内.考虑弱轴受力对强轴耗能特性的影响不大, 弱轴平面内节点KJJD2比KJJD1等效黏滞阻尼系数高出43.44%, 即增加T连接件腹板与翼缘的厚度, 节点的等效黏滞阻尼系数具有明显的增加, 说明T型件腹板与翼缘厚度对节点等效黏滞阻尼系数在弱轴平面的影响要大于在强轴平面的影响.T型连接件较薄的空间半刚性节点KJJD1比空间刚性节点KJGJD强轴方向的等效黏滞阻尼系低了25%, 是由于其T型连接件承载力不足而导致.腹板翼缘厚的T型连接件角柱节点与刚性节点基本接近, 半刚性节点比刚性节点略大3%, 但在弱轴平面内半刚性节点KJJD1和KJJD2的等效黏滞阻尼系数分别是刚性节点的1.17倍和2.08倍.由此可见角柱半刚性节点采用腹板和翼缘较厚的T型连接件的耗能特性比刚性角柱节点好.
5 结论本文进行了剖分T型钢连接框架角柱空间节点的拟静力试验, 对比了这种节点与空间刚性梁柱连接节点和平面剖分T型钢梁柱连接节点的受力特点差异性.通过分析各种梁柱连接节点试件的试验破坏现象, 承载力、刚度特性、延性特性和耗能等力学特性, 得到以下结论.
(1) 空间半刚性梁柱剖分T型钢连接角柱节点由于采用高强螺栓连接, 避免了焊缝连接, 其延性、滞回性能以及耗能特性优于刚性节点.空间角柱刚性节点由于节点焊缝缺陷的不可规避性, 在往复循环荷载作用下受拉焊缝易出现脆性断裂, 不利于实现建筑钢结构发挥其自身的延性特性.
(2) 空间半刚性梁柱连接角柱节点在空间双向循环荷载作用下, 空间节点的强轴承载能力比平面节点平均降低接近17%, 空间节点的强轴相对转动刚度比平面节点平均降低至20%左右, 空间节点的延性系数同样和平面节点存在差异.这2种节点的等效黏滞阻尼系数相差不大, 说明考虑空间节点的复杂受力特性影响节点的抗震性能.
(3) 以剖分T型钢为连接形式的节点, 无论是空间节点还是平面节点均属典型的半刚性梁柱连接节点.节点的转动刚度相对刚性节点要低, 节点的塑性铰主要出现在T型件腹板与翼缘的交界处, 该处塑性应变发展最快最明显.
(4) T型连接件腹板与翼缘的厚度是空间节点受力特性不可忽略的影响因素, 无论是对采用T型钢连接的半刚性节点, 对其极限承载力、初始刚度及刚度退化率、延性系数、耗能特性都有不同程度的影响.在该类节点的设计中应尽量采用腹板与翼缘的厚度较大的T型连接件进行梁柱连接设计, 有利于提高节点的受力性能.
| [1] |
郝际平, 李文岭. 钢梁柱半刚性节点顶底角钢弱轴连接的有限元分析[J].
土木工程学报, 2007, 40(09): 36–42.
HAO Jip-ping, LI Wen-ling. Finite element analysis for the top-and-seat angle minor axis connection of semi-rigid steel beam-column joints[J]. China Civil Engineering Journal, 2007, 40(09): 36–42. DOI:10.3321/j.issn:1000-131x.2007.09.006 |
| [2] |
王湛, 王涛. 半刚性钢框架梁柱弱轴端板连接的试验研究和有限元分析[J].
土木工程学报, 2012, 45(8): 83–89.
WANG Zhan, WANG Tao. Experiment and finite element analysis for the end plate minor axis connection of semi-rigid steel frames[J]. China Civil Engineering Journal, 2012, 45(8): 83–89. |
| [3] |
王燕, 冯双, 王玉田. 钢框架刚性连接加强型节点滞回性能试验研究[J].
土木工程学报, 2011, 44(5): 57–68.
WANG Yan, FENG Shuang, WANG Yu-tian. Experimental study on hysteretic behavior for rigid-reinforced connections[J]. China Civil Engineering Journal, 2011, 44(5): 57–68. |
| [4] |
石文龙, 李国强, 肖勇, 等. 半刚性连接梁柱组合节点低周反复荷载试验研究[J].
建筑结构学报, 2008, 29(5): 57–66.
SHI Wen-long, LI Guo-qiang, XIAO Yong, et al. Cyclic loading tests on composite beam-to-column joints with semi-rigid connections[J]. Journal of Building Structures, 2008, 29(5): 57–66. |
| [5] |
李泽深, 李秀梅, 郑小伟, 等. T形钢连接梁柱半刚性节点滞回性能试验研究及数值分析[J].
建筑结构学报, 2014, 35(7): 61–68.
LI Ze-shen, LI Xiu-mei, ZHENG Xiao-wei, et al. Experimental study and numerical investigation on bysteretic behavior of T-stub semi-rigid beam-to -column connections[J]. Journal of Building Structures, 2014, 35(7): 61–68. |
| [6] |
李凤霞, 布欣, 王新武. 剖分T型钢梁柱连接滞回性能研究[J].
建筑科学, 2010, 26(5): 28–32.
LI Feng-xia, BU Xin, WANG Xin-wu. Research on hysteretic behavior of the slit T steel beam-column connections[J]. Building Science, 2010, 26(5): 28–32. |
| [7] |
王新武. 钢框架梁柱连接研究[D]. 武汉: 武汉理工大土木建筑工程学院, 2003.
WANG Xin-wu.Research on beam-to-column connections of steel frame[D]. Wuhan: Wuhan University of Technology, 2003. |
| [8] |
樊健生, 周慧, 聂建国. 空间钢-混凝土组合节点抗震性能试验研究[J].
土木工程学报, 2014, 32(12): 47–55.
FAN Jian-sheng, ZHOU Hui, NIE Jian-guo, et al. Experimental study on seismic performance of three-dimensional composite beam-to-column joints[J]. China Civil Engineering Journal, 2014, 32(12): 47–55. |
| [9] |
樊健生, 周慧, 聂建国. 空间钢-混凝土组合节点抗震性能试验研究进展[J].
建筑结构学报, 2011, 32(12): 37–45.
FAN Jian-sheng, ZHOU Hui, NIE Jian-guo. Experimental study on seismic performance of three-dimensional composite beam-to-column joints[J]. Journal of Building Structures, 2011, 32(12): 37–45. |
| [10] | KAWAGUCHI J, MORINO S, SUGIMOTO T. Elasto-plastic behavior of concrete-filled steel tubular three dimensional sub assemblages[C]//Proceedings of an Engineering Foundation Conference Reston. VA, USA: ASCE, 1992: 726-741. |
| [11] | NISHIYAMA I.Seismic test facility for three dimensional beam-to-column sub assemblages[D]. Tachihara: Building Research Institute. Department of Production Engineering, 1999. |
| [12] | FEMA.FEMA-350. Recommended seismic design criteria for new steel structural buildings[S]. Washington: Federal Emergency Management Agency, 2000. |
| [13] | FEMA.FEMA-351. Recommended seismic evaluation and upgrade criteria for existing welded steel moment-frame buildings[S]. Washington: Federal Emergency Management Agency, 2000. |
| [14] | FEMA.FEMA-461. Interim testing protocols for determining the seismic performance characteristics of structural and nonstructural components[S]. Redwood City: Applied Technology Council, 2007. |



