2. 地球空间信息技术协同创新中心,湖北 武汉 430079;
3. 中国科学院 遥感与数字地球研究所,北京 100094
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China
空间连接(spatial join)是空间数据库系统中最重要的一项操作, 即从两个或多个空间数据集中获取满足一定空间谓词(如相交、覆盖等)的空间对象[1-3].并行空间连接[4-8]需要对源数据进行划分, 再将划分结果放在不同的运算节点并行执行.数据划分的方式会影响节点间的数据通信传输, 划分结果会影响系统的运算负荷和整体负载均衡, 因此, 空间数据划分对于并行空间连接具有重要意义.
按照划分过程是否允许空间对象重复存储的标准, 空间数据划分方法可以分为以下两类.第一类划分方法如R树[9-12]、R*树[13]等不允许空间对象重复存储于不同的划分数据块中; 第二类划分方法允许同一空间对象重复存在于不同的数据块中, 如R+树[14-15]、网格划分[15-16]、空间填充曲线[17-18]等方法.前一种划分方式虽然不产生重复数据(冗余数据), 但是划分得到的各数据块的空间范围可能会出现覆盖、交叠等情况.在并行空间连接时, 各数据块不能独立完成连接操作, 运算节点之间需要进行数据通信和传输.这往往成为制约并行系统整体效率的瓶颈.第二类划分方法通常使用空间范围进行划分.按照这种划分方式得到的划分结果, 各数据块的空间范围不会有重叠区域, 可以充分保持独立性.在并行运算时, 各数据块可以作为一个独立单元, 在运算节点独立执行.对于并行运算系统, 第二类划分方式更适合分布式并行计算的需求.
在第二类划分方式中, 网格划分是一种常用的划分方法.现有的网格划分方法的划分结果中包含的冗余数据较多, 划分得到的数据块之间的数据量均衡度较低, 这会增加系统的工作负荷和影响系统的负载均衡.如文献[19]的数据划分方法在一定程度上可以减轻数据倾斜(data skew)的问题, 但是面对空间聚集性差异较大的数据, 划分结果的数据量均衡性较低; 文献[20]的划分算法虽然可以在一定程度上提高划分结果的数据量均衡性, 但会产生较多的冗余数据.
本文提出一种两轮映射数据划分算法, 允许空间对象重复存储, 以保证各划分数据块之间的独立性.此外, 在第一轮映射中通过充分利用划分对象的空间属性来减少冗余数据, 通过合理设置阈值来均衡划分数据.在第二轮映射中通过动态映射机制, 进一步对数据进行均衡划分.
1 基本原理 1.1 并行连接原理将数据集R和S的连接操作记为R⨝S, 并行化计算的基本原理如下:分别将R和S分割成n个数据块R1, R2, …, Rn和S1, S2, …, Sn, 并且对于任意1≤i、j≤n, Ri∩Rj=ϕ, Si∩Sj=ϕ(i≠j), 则R⨝S≡Ui=1n(Ri⨝Si).在该过程中, 将每一对Ri和Si组合放在不同的运算节点进行处理, 可以实现并行化连接操作.
1.2 网格划分原理网格划分的基本原理如下:将源数据的空间范围网格化, 得到N个网格(其中N为待划分的份数); 按照一定的规则比较空间对象与网格的空间关系, 将符合条件的空间对象划分到对应的网格中.对于线、面等具有空间范围属性的空间对象, 在允许同一空间对象可以重复存在于不同划分数据块的前提下, 一种常用的划分规则是将空间对象划分到所有与其最小外包矩形(minimum bounding rectangle, MBR)相交的网格中, 若同时存在多个网格满足条件, 则将空间对象复制并分别划分到对应的网格中.
由于空间数据分布的不规则性, 单一使用网格划分容易造成数据倾斜的情况.Dewitt等[21]提出virtual processor range partitioning方法, 可以有效控制数据倾斜的情况.基本原理是先使用细小网格将源数据集在空间上进行充分分割, 再整合到大的数据块中.如使用2n×2n的网格对源数据空间进行分割(2n×2n
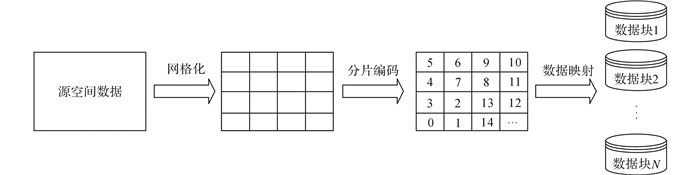
综上所述, 网格划分的基本流程包括空间网格化、分片编码和数据映射3个部分.基本流程如图 1所示.
|
图 1 网格划分基本流程图 Fig. 1 Flow charts of grid division |
提出的数据划分方法以网格划分方法为基础, 使用2n×2n的网格, 将源数据范围空间划分为22n个网格分片(2n×2n
|
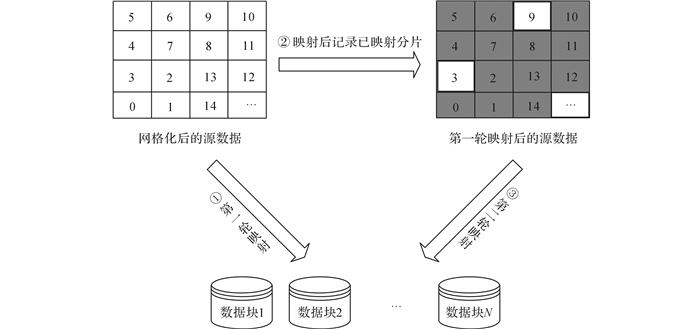
图 2 两轮映射示意图 Fig. 2 Sketch map of two-rounds-map |
两轮映射过程如图 2所示, 对原空间数据集首先执行① 第一轮映射, 将大部分数据映射到结果数据块中; 同时执行②, 对已经完成映射的网格分片进行标记.在第一轮映射完成后, 原空间数据集尚有少量网格分片未被映射, 如图 2所示, 灰色的分片表示已经被映射过的网格分片, 在第二轮映射中不再进行映射.此时, 进行③ 第二轮映射, 将未被标记的网格分片映射到数据块中, 当所有数据块完成映射后, 整个划分过程完成.
在映射过程中, 需要满足以下两点:1) 尽量减少划分过程产生的冗余数据; 2) 尽量提高划分结果的数据量均衡性.针对上述两点需求, 两轮映射方法的第一轮映射通过将空间上邻近的分片映射到相同的数据块中, 使不同分片中保存的相同空间对象出现合并的情况大大增加, 从而减少冗余数据的产生; 第二轮映射使用动态映射的方式, 动态调节结果的数据量均衡性.其中, 第一轮映射的完成条件是所有的待划分数据块均完成映射.设定阈值Mmean来判定每个数据块映射的完成情况.阈值的设定的依据如下:在理想状态下, 即完全不产生冗余数据且划分得到的所有数据块包含的数据量完全均衡时, 平均每个数据块所包含的数据量为一定值, 即M/N, 其中M为源数据集包含的空间对象的总量, N为要划分的数据块份数.由于空间对象的数量和划分份数均为自然数, 可能出现无法整除的情况, 将结果向下取整, 有M/N, 设定Mmean=M/N.当使用22n个分片将源数据空间网格化后, 平均每个分片包含的数据量为mmean=M/22n.当第一轮映射完成后, 设此时所有数据块包含的数据量之和为M′, 有M′≤(Mmean+mmean)×N≤M+(N/22n)M, 其中22n
具体而言, 该划分算法的流程如下.
1) 使用2n×2n的格网对数据集进行划分, 比较数据集中的空间对象与网格分片, 将空间对象划分到所有与其MBR相交或重合的网格分片中.在划分过程中, 同一空间对象可能会被划分到不同的网格分片中.
2) 使用n阶Hilbert曲线, 对1) 中划分得到的22n个网格分片进行编码, 将网格分片的编码数组记为H={H1, H2, …, H22n}, 并将所有的网格分片标记为未被映射状态.
3) 在编码完成后, 开始进行第一轮映射, 具体分为以下3个步骤.
a)从第1个数据块开始映射.遍历所有的网格分片, 找到包含空间对象最多的分片, 将包含的空间对象映射到当前数据块中.获取该分片的Hilbert编码, 记作种子编码, 并将分片映射状态标记为已映射.
b)查看此时数据块内包含的数据量是否超出阈值Mmean.若未超出阈值, 则遍历所有未被映射的网格分片的Hilbert编码值, 取出与种子编码值最相近的编码对应的网格分片, 并将分片包含的空间对象映射到当前数据块中(若同时存在两个网格分片满足条件, 则取包含空间对象较多的网格分片进行映射).映射后, 将种子编码替换为该网格分片的Hilbert编码, 同时将该网格分片的映射状态记为已映射; 若超出阈值, 则将数据块序号+1.此时, 若数据块序号大于目标划分的数据块份数, 则表示在第一轮映射中, 所有的数据块都已完成映射工作, 开始准备进行第二轮映射.若数据块序号小于等于目标划分的数据块份数, 则表示将对下一个数据块进行映射.遍历所有未被映射的网格分片, 取出其中包含空间对象最多的分片, 将其包含的空间对象映射到当前数据块中, 将种子编码值替换为该分片的Hilbert编码值, 并将该分片的映射状态记为已映射.
c)分片包含的空间对象映射完成后, 重复执行b), 直到待映射数据块序号大于划分数据块的份数, 表示所有的数据块均已完成第一轮映射.
4) 在第一轮映射完成后, 准备进行第二轮映射.由于存在冗余数据, 经过第一轮映射, 尚会有少量的冗余数据存在.第二轮映射分为以下2个步骤.
a)遍历所有未被映射的网格分片, 选取包含空间对象最多的分片, 将该网格分片所含空间对象映射到当前包含数据量最小的数据块中.在映射完成后, 将该分片的映射状态记为已映射.
b)重复执行a), 直到所有的网格分片都已经被映射.此时, 第二轮映射完成, 所有的数据划分工作完成.
3 实验与分析 3.1 实验数据与对比算法并行空间连接常用来处理数据量较大的空间数据, 因此实验数据选取大数据量的矢量数据进行验证.目前, 国内外大多数相关文献均采用美国统计局TIGER数据进行实验分析[4, 19-20].本文选用TIGER数据中的2014年德克萨斯州路网数据作为线要素实验数据.数据格式为Shape数据, 包含1 598 292个线对象, 大小为703 Mb; 选用TIGER数据中的2014年德州街区数据作为面要素实验数据.数据格式为Shape数据, 包含914 231个面空间对象, 大小为806 Mb.实验数据的具体情况如图 3、4所示.
|
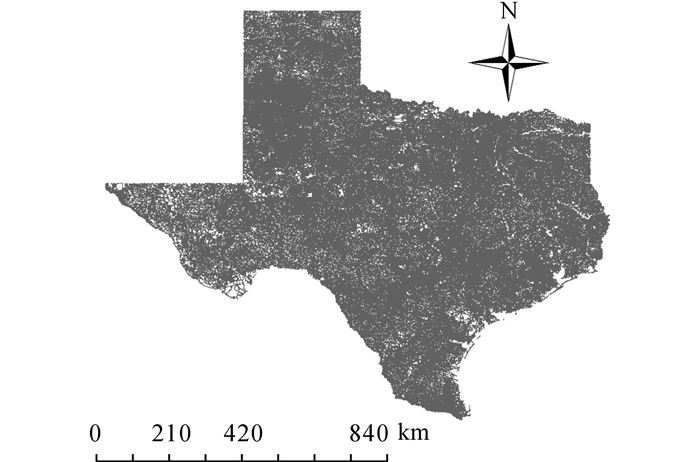
图 3 2014年德克萨斯州路网分布图 Fig. 3 Roads distribution of Texas, 2014 |
|
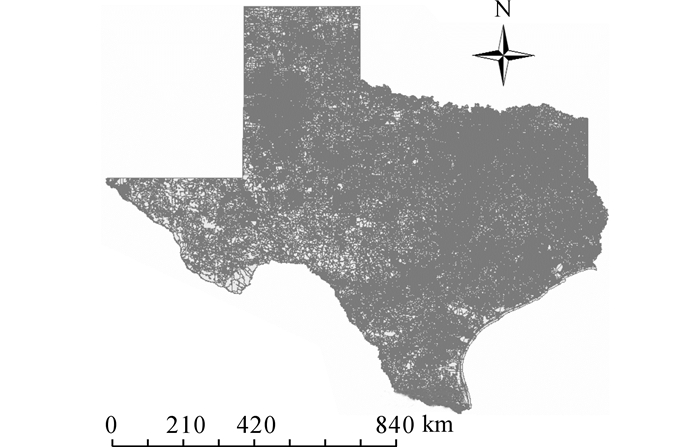
图 4 2014年德克萨斯州街区分布图 Fig. 4 Blocks distribution of Texas, 2014 |
如图 3所示为德州地区道路网数据.图中, 灰色线条表示道路.在东部地区, 道路网更稠密, 灰色线条更密集, 因而线条之间的显示层次比较混杂, 而在西部地区, 道路网较稀疏, 所以灰色线条显示更清晰.如图 4所示为德州地区街区分布图.图中, 灰色表示街区的面对像边框.在东部地区, 街区分布较密集, 单位街区面积较小, 所以面对象的边框色较突出, 呈现出灰色, 而在西部地区, 街区分布较稀疏, 单位街区面积较大, 街区的灰色边界比较清晰.从总体上而言, 德州地区的路网和街区空间对象在不同区域的空间聚集性差异较大, 大体呈现出西部稀疏、东部密集的情况.
3.2 算法有效性实验分别使用Oracle Spatial数据划分方法和两轮映射划分方法, 将线要素实验数据和面要素实验数据划分为4份.使用Oracle Spatial进行划分时, 调用PARTITION BY RANGE函数, 以X_VALUE和Y_VALUE为划分依据, 分别在X轴和Y轴方向上进行等分划分, 将空间范围划分为4个区域.4份数据块Part1、Part2、Part3和Part4的区域范围分别对应西南部、东南部、西北部和东北部.对于线要素, 使用SDO_GEOM. SDO_POINTONSURFACE函数来获取定位点, 对于面要素, 通过SDO_GEOM.SDO_CENTROID函数获得定位点, 并将空间对象划分到定位点所在空间区域对应的数据块.两轮映射方法先使用16×16的网格进行划分, 再将256个网格分片映射到4个数据块中.采用这两种划分方法得到的结果如表 1所示.
| 表 1 Oracle Spatial和本文划分方法划分路网数据结果数据量比较 Table 1 Comparison of roads data results partitioned byOracle Spatial and Two-Rounds-Map |
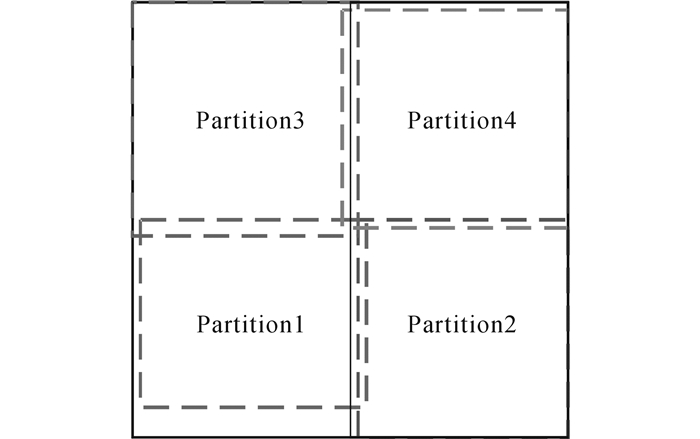
由表 1、2的划分结果数据量可得, 对于OracleSpatial划分方法, 无论是线数据还是面数据, 均不会产生冗余数据, 数据量冗余度为0.对于线数据划分结果的数据量倾斜度为227 701.3, 面数据划分结果的数据量倾斜度为144 584.8;对于线数据和面数据, 两轮映射法划分结果的数据量冗余度分别为0.242%、0.281%, 数据量倾斜度分别为14 470、7 995.8.可以看出, 在冗余数据方面, Oracle Spatial划分方法具有一定优势, 而在数据量均衡方面, 两轮映射划分方法大大优于Oracle Spatial.这是因为Oracle Spatial的划分方式不允许空间对象重复存储, 所有的空间对象只能被唯一划分到某个数据块中, 所以在划分过程中不会产生冗余数据.划分后, 各数据块的范围为数据块所包含的所有空间对象最小外包矩形的并集.在该划分方式下, 各数据块范围之间可能会存在重叠部分.如图 5所示为使用Oracle Spatial划分实验数据后, 各数据块最小外包矩形与划分边界的比较示意图.
| 表 2 Oracle Spatial和本文划分方法划分街区数据结果数据量比较 Table 2 Comparison of blocks data results partitioned byOracle Spatial and Two-Rounds-Map |
|
图 5 Oracle Spatial划分结果的最小外包矩形与划分边界比较示意图 Fig. 5 MBR and partition boundary of data blocks partitioned by Oracle Spatial |
图 5中, 黑色实线部分为划分边界, 灰色虚线部分为各数据块的范围边界.可以看出, Oracle Spatial的划分方式会存在空间重叠的情况, 在并行空间连接时, 各数据块无法独立完成连接运算.此外, 由图 3、4可以看出, 实验数据在空间分布上大体具有西部稀疏、东部稠密的特性, 并且西部区域具有较大部分的空白部分, Oracle Spatial划分结果的Part1(西南区域)和Part3(西北区域)数据块包含的数据量明显少于Part2(东南区域)和Part4(东北区域)数据块.这是因为Oracle Spatial的划分方式是基于空间范围的单一划分, 当空间数据的聚集性差异较大时或空间范围不规则时, 容易产生数据倾斜.在开展并行运算时, 数据倾斜会造成不同运算节点的工作负荷严重失衡, 影响整体效率.
提出的两轮映射数据划分方法允许空间对象重复存储, 各数据块可以独立完成空间连接任务, 更适合于并行化计算需求.同时, 可以将产生的冗余数据控制在一定范围内, 在数据量均衡性方面具有较大的优势.
3.3 算法优越性实验 3.3.1 实验评价指标允许空间对象重复存在的划分方法得到的不同数据块中, 可能会包含相同的空间对象.对于并行空间连接, 冗余数据越多, 系统整体的运算任务越重, 因此划分结果的数据冗余度是评价划分结果的指标之一.数据冗余度的计算公式如下:
| $ R = \frac{{\sum\nolimits_{i = 1}^N {\left( {{m_i} - M} \right)} }}{M}. $ | (1) |
式中:N为所划分的数据块份数, M为源数据包含的数据量, mi为第i个数据块所包含的数据量.
划分结果的数据量均衡性对系统的负载均衡影响较大.当划分结果的数据量倾斜度较大时, 系统整体的负载均衡度较低, 个别运算节点的工作负荷大, 影响整体的运算效率, 因此划分结果的数据量倾斜度是评价划分结果的指标.已知标准差可以用来反映一组统计数据的离散程度, 因此数据量倾斜度为
| $ S = \sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left( {{m_i} - \overline M } \right)} }^2}} . $ | (2) |
式中:M为各数据块包含数据量的均值.
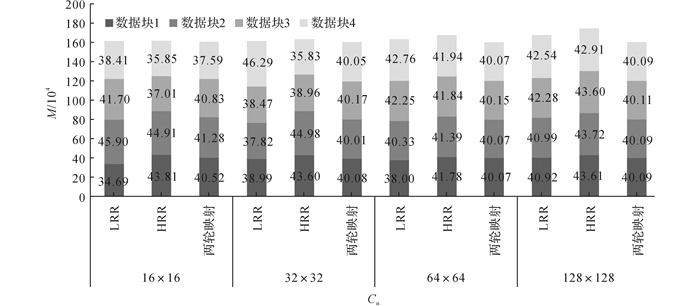
3.3.2 实验过程网格分片划分方式虽然更适合于并行化计算需求, 但是采用不同划分方法得到的划分结果的数据冗余度和数据量倾斜度差距较大.与线性编码轮询调度[19](linear-round-Robin, LRR)和Hilbert编码轮询调度[20](Hilbert-round-Robin, HRR)两种基于网格分片的划分方法进行比较, 具体分析两轮映射划分方法的特性和优势.对于网格分片划分方法, 对划分结果产生影响的变量主要有:1) 进行网格分片时, 所选择网格的大小; 2) 待划分的数据块的数目; 3) 分片映射时所选用的映射方法.该实验针对上述3种变量, 利用2套实验数据, 设计4组实验, 分别如下.A组实验采用16×16的网格分别对2套数据进行分片; B组实验采用32×32的网格分别对2套数据进行分片; C组实验采用64×64的网格分别对2套数据进行分片; D组实验采用128×128的网格分别对2套数据进行分片.在每组实验中, 均使用LRR、HRR和本文提出的两轮映射划分方法, 分别将2套实验数据划分为4个数据块和8个数据块.实验的具体结果如图 6~9所示.图中,M为数据量,Cn为不同划分算法的网格分片数.
|
图 6 线数据划分为4个数据块时的结果数据量 Fig. 6 Results data size of line data when division parts is 4 |
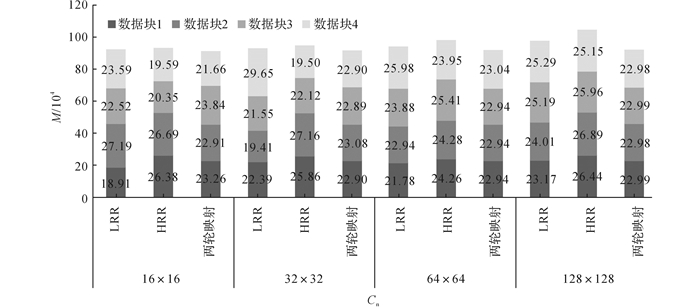
|
图 7 面数据划分为4个数据块时的结果数据量 Fig. 7 Results data size of polygon data when division parts is 4 |
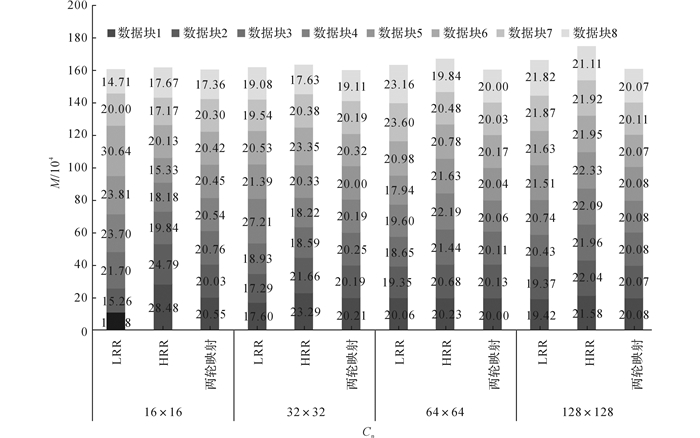
|
图 8 线数据划分为8个数据块时的结果数据量 Fig. 8 Results data size of line data when division parts is 8 |
|
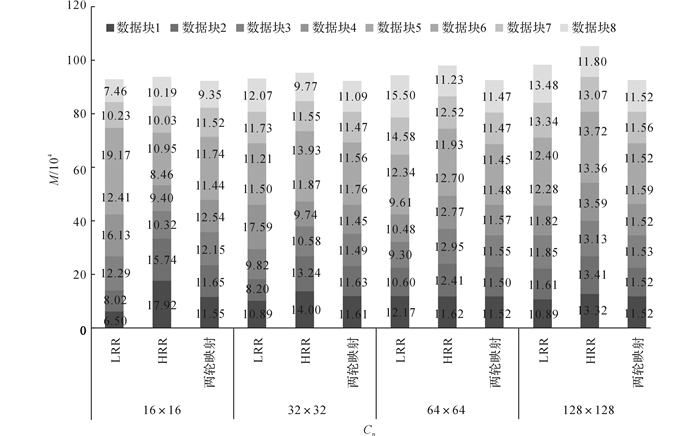
图 9 面数据划分为8个数据块时的结果数据量 Fig. 9 Results data size of polygon data when division parts is 8 |
图 6~9中, 不同灰度的色块代表划分得到的结果数据块, 色块高度表示数据块包含数据量的多少.图 6~9中, 柱状图的总体高度越高, 表示划分结果的数据总量越大, 划分过程产生的冗余数据越多; 在柱内, 各色块之间的高度越接近, 表明划分得到的数据块之间的数据量越均衡.
3.3.3 实验分析通过计算可得4组实验的数据冗余度和数据量倾斜度, 如表 3~6所示.
| 表 3 线数据4组实验结果数据冗余度 Table 3 Data redundancy degree of 4 sets of experiments towards line data |
| 表 4 面数据4组实验结果数据冗余度 Table 4 Data redundancy degree of 4 sets of experiments towards polygon data% |
| 表 5 线数据4组实验结果数据倾斜度 Table 5 Data skew degree of 4 sets of experiments towards line data |
| 表 6 面数据4组实验结果数据倾斜度 Table 6 Data skew degree of 4 sets of experiments towards polygon data |
将4组实验得到的数据冗余度R和数据倾斜度S统计后, 如图 10~13所示.
|
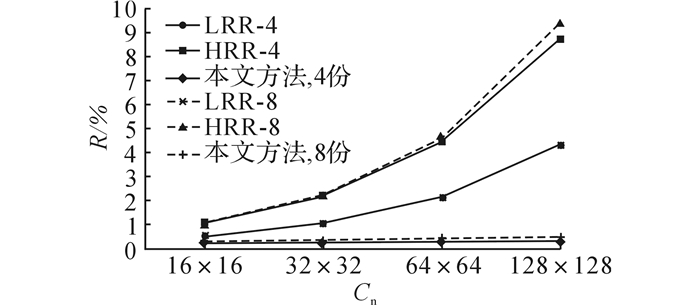
图 10 线数据数据冗余度随网格分片数的变化图 Fig. 10 Variation of data redundancy degree with different grid subdivision number |
|
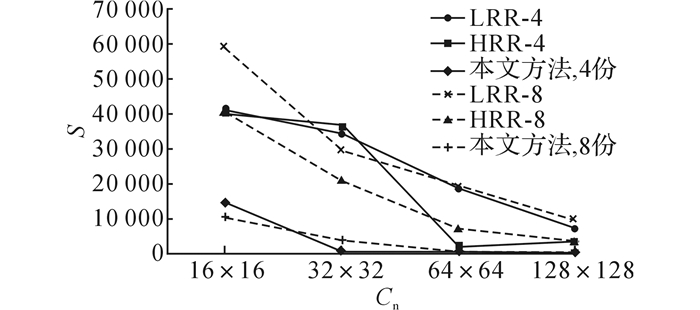
图 11 线数据数据倾斜度随网格分片数的变化图 Fig. 11 Variation of data skew degree with different grid subdivision number |
|
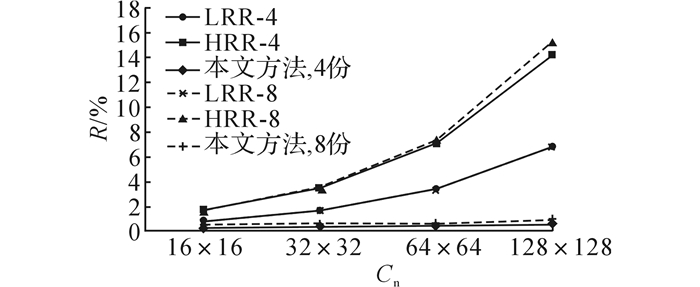
图 12 面数据数据冗余度随网格分片数的变化图 Fig. 12 Variation of data redundancy degree with different grid subdivision number |
|
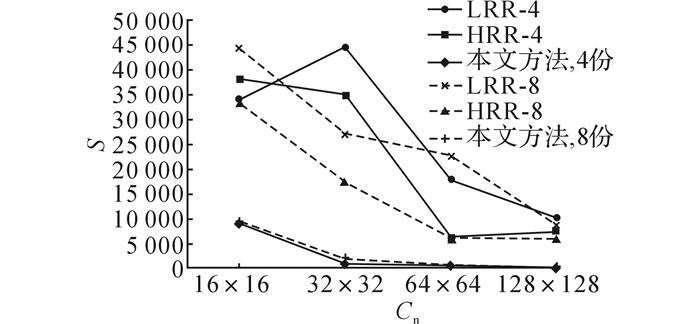
图 13 面数据数据倾斜度随网格分片数的变化图 Fig. 13 Variation of data skew degree with different grid subdivision number |
从图 10、12可以看出, 在4组实验中, 对于线数据和面数据, 不论是划分为4份或8份数据块, 随着网格分片数目的增加, 3种划分方法的数据冗余度均有所增加.当网格分片数目确定时, 划分数据块份数越多, 划分结果的数据冗余度越高.这是因为随着网格分片数目的增加, 同一空间对象可能会出现在更多的分片中, 因此最终映射后产生的冗余数据更多.当划分的数据块份数较多时, 平均每个数据块内包含的数据量较少, 同一数据块内包含的冗余数据较少, 能够消除的冗余数据较少.比较图 10、12可以看出, 对于同样的划分方式, 线数据划分结果的数据冗余度低于面数据划分结果.这是因为面对象往往具有较大的空间范围, 导致MBR相交或覆盖的网格分片数较多, 需要重复存储的数据份数较多, 最终使得划分产生的冗余数据较多.
由图 11、13可以看出, 从整体趋势而言, 在4组实验中, 不论是对于线数据还是面数据, 划分结果的数据倾斜度都随着网格分片数目的增加逐渐减少.这是因为随着网格分片数目的增加, 网格分片对空间的分割更彻底, 特别是空间对象聚集度较高的区域, 划分更充分, 这大大减少了由空间分布不均造成的数据倾斜的情况.
对比两种参照划分方法可以看出, 对于LRR, 划分结果的数据冗余度较低, 但数据倾斜度较高; HRR划分结果的数据倾斜度较低, 但数据冗余度较高.这是因为线性编码的方法按行或者列扫描网格分片进行编码, 按照编码顺序得到的空间对象之间的空间关系较弱, 按照Hilbert编码顺序得到的空间对象之间的空间关系较紧密.使用轮转循环的方式, HRR的划分方法使得距离较近的空间对象被划分到不同的数据块中.这一方面使得空间对象密集的区域被分配得更平均, 提高了整体划分结果的数据量均衡度; 另一方面, 容易使冗余数据分布到不同的数据块中, 降低了冗余数据的消除.
无论是对于线数据还是面数据, 本文提出两轮映射划分方法, 从数据冗余度和数据倾斜度两方面都明显优于LRR和HRR方法, 原因如下:1) 按照Hilbert编码顺序, 将空间距离较近的空间对象映射到同一数据块中, 可以有效地消除冗余数据, 降低划分结果的数据冗余度; 2) 通过设定数据量阈值和最后的动态映射过程, 有效地控制了各数据块中空间对象的数量, 达到了空间对象均匀划分的目的.
3.4 划分效率实验 3.4.1 实验平台该实验所用硬件平台的处理器为Intel Core i5-3330, 内存为DDR3规格的8 GB内存, 硬盘转速为7 200 r/min; 软件平台为Windows 7旗舰版64位操作系统, Visual Studio2010开发环境.
3.4.2 实验过程考虑到网格分片划分方法主要包含网格分片、分片编码和数据映射3个过程, 利用2套实验数据设计4组实验, 分别如下.A组实验采用16×16的网格, 分别对2套数据进行分片; B组实验采用32×32的网格, 分别对2套数据进行分片; C组实验采用64×64的网格, 分别对2套数据进行分片; D组实验采用128×128的网格, 分别对2套数据进行分片.在每组实验中, 均使用LRR、HRR和本文提出的两轮映射划分方法, 分别将2套实验数据划分为4个数据块和8个数据块.分别记录不同划分过程中网格分片、分片编码和数据映射的耗时情况.考虑到4组实验中网格分片使用的方法一致, 耗时仅与网格分片数目相关, 因此网格分片耗时单表列出.具体的实验情况如表 7~10所示.
| 表 7 4组实验中网格分片步骤耗时情况 Table 7 Time consuming situation of grid subdivision in 4 sets of experiments |
| 表 8 LRR划分算法4组实验耗时情况 Table 8 Time consuming situation of 4 sets of experiments when using LRR algorithm |
| 表 9 HRR划分算法4组实验耗时情况 Table 9 Time consuming situation of 4 sets of experiments when using HRR algorithm |
| 表 10 本文划分算法4组实验耗时情况 Table 10 Time consuming situation of 4 sets of experiments when using proposed algorithmms |
将4组实验得到的耗时数据统计后如图 14~16所示.图中,t为消耗时间.
|
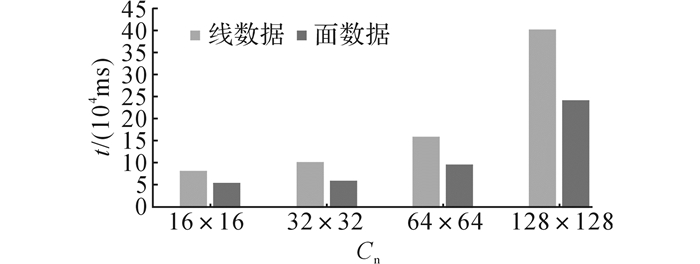
图 14 网格分片耗时情况图 Fig. 14 Time consuming situation of grid subdivision |
|
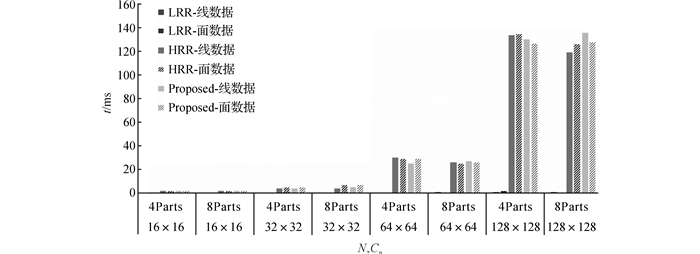
图 15 分片编码耗时情况图 Fig. 15 Time consuming situation of tile coding |
|
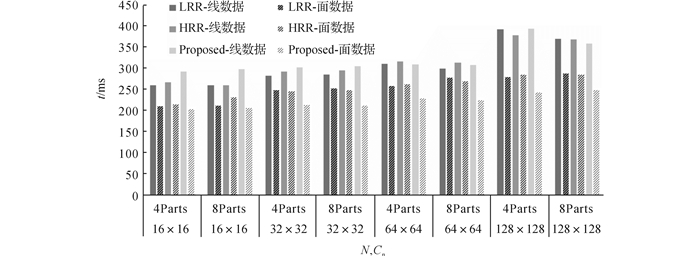
图 16 数据映射耗时情况图 Fig. 16 Time consuming situation of data mapping |
从图 14可以看出, 总体上, 无论是对于线数据还是面数据, 网格分片过程的耗时都随着划分网格数的增加而增加.这是因为划分的网格数越多, 与空间对象MBR比较的网格数越多, 需要消耗的时间越多.具体比较线数据和面数据可以看出, 在划分网格数一定的情况下, 线数据网格分片所消耗的时间多于面数据网格分片的时间.这是因为线数据集包含的空间对象数多于面数据集包含的空间对象数量, 在网格分片过程中, 需要较多的空间对象.虽然线数据和面数据的复杂度差异较大, 但是网格分片过程只需考虑空间对象的MBR与网格的空间位置关系, 不受数据类型的影响, 因此计算耗时与数据集数据量成正相关关系.通过计算可以得出, 在相同情况下, 线数据网格分片耗时比面数据网格分片耗时多70%左右, 线数据集包含空间对象的数据量比面数据集数据量多74%, 计算结果符合上述分析.综合以上分析可知, 对于网格分片过程, 划分数据集包含的数据量越多、划分的网格数越多, 计算耗时越大.
从图 15可以看出, 对于分片编码过程, 当划分网格数较少时, 线性编码(LRR划分算法的编码方式)和Hilbert编码(HRR划分算法和两轮映射划分算法的编码方式)耗时均较短; 当划分网格数较多时, 线性编码表现出明显的优势, Hilbert编码由于计算复杂度高, 耗时大大增加.同时, 由于编码过程是针对划分网格进行的, 编码过程耗时与数据集包含的数据量无关.
从图 16可以看出, 对于数据映射过程, 总体上, 网格分片数越多, 映射过程耗时越长.这是因为网格数越多, 映射过程需要遍历的网格数越多.比较线数据集和面数据集可知, 在相同的划分情况下, 线数据集映射过程耗时比面数据集映射耗时更多, 这是因为在数据映射过程中, 网格分片完成映射后, 需要对网格分片内包含的空间对象进行遍历、映射和存储, 而线数据集包含的空间对象数据量更大, 映射过程中需要处理的空间对象更多.比较数据块划分份数可知, 在相同的划分情况下, 不同的数据块划分份数下的数据映射过程耗时大致相同.比较3种数据划分算法可知, 在相同的划分情况下, 3种划分算法下的数据映射过程耗时大致相同.
综合对比图 14~16可以看出, 在整个数据划分过程中, 网格分片过程的耗时占用时间最多, 占用整体划分时间的99%以上, 而数据映射过程消耗的时间较短, 分片编码过程耗时最短.这是因为在网格分片过程中, 不仅要完成对空间范围的网格化, 而且需要比较空间对象MBR与网格的空间关系, 定位空间对象的存储网格, 而空间操作需要消耗的计算资源较多.数据映射过程需要对网格和数据进行处理, 不涉及空间操作, 耗时较短.分片编码过程仅需要对网格进行处理, 耗时最短.通过比较可以看出, 本文的两轮映射划分算法与LRR和HRR划分算法的耗时大致相当, 适用性强.
4 结语空间数据划分是并行空间连接的基础和关键技术.特别是对于大数据量, 空间分布聚集性差异较大的数据, 如何划分得到低数据冗余度, 高数据量均衡度的划分结果将直接影响到整个系统的运算效率和负载均衡.与经典的Oracle Spatial划分方法相比, 两轮映射划分方法可以充分满足并行计算的需求, 同时能够均衡划分数据; 与常用的的网格划分方法相比, 两轮映射划分方法的划分结果中包含的冗余数据更少, 数据块之间的数据均衡度更高.实验表明, 本文的两轮映射数据划分方法切实有效, 具有较大的优势, 对于并行空间的连接操作具有重要的意义.
| [1] | JACOX E H, SAMET H. Spatial join techniques[J]. ACM Transactions on Database Systems, 2007, 32(1): 14–23. |
| [2] | SIDLAUSKAS D, JENSEN C S. Spatial joins in main memory: implementation matters![J]. Proceedings of the VLDB Endowment, 2014, 8(1): 97–100. DOI:10.14778/2735461 |
| [3] |
付仲良, 刘思远, 俞志强. 一种双映射变换的空间索引及空间连接算法研究[J].
武汉大学学报:信息科学版, 2014, 39(10): 1248–1251.
FU Zhong-liang, LIU Si-yuan, YU Zhi-qiang. A novel spatial index with a high-performance spatial join[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1248–1251. |
| [4] | ZHOU X F, ABEL D J, TRUFFET D. Data partitioning for parallel spatial join processing[J]. Geoinformatica, 1998, 2(2): 175–204. DOI:10.1023/A:1009755931056 |
| [5] | HOEL E G, SAMET H. Data-parallel spatial join algorithms [C]//International Conference on Parallel Processing. Illinois: IEEE, 1994: 227-234. |
| [6] | ELDAWY A, MOKBEL M F. SpatialHadoop: a MapReduce framework for spatial data [C]// 2015 IEEE 31st International Conference on Data Engineering (ICDE). Seoul: IEEE, 2015: 1352-1363. |
| [7] | ZHANG J T, YOU S M, GRUENWALD L. Lightweight distributed execution engine for large-scale spatial join query processing [C]// 2015 IEEE International Congress on Big Data (BigData Congress). Santa Clara: IEEE, 2015: 150-157. |
| [8] |
陈勇旭, 陈梦杰, 刘雪冰, 等. 基于MapReduce的连接聚集查询算法研究[J].
计算机研究与发展, 2013, 50(supple.1): 306–311.
CHEN Yong-xu, CHEN Meng-jie, LIU Xue-bing, et al. MapReduce based aggregate-join query algorithms[J]. Journal of Computer Research and Development, 2013, 50(supple.1): 306–311. |
| [9] | GUTTMAN A. R-Trees: a dynamic index structure for spatial searching[J]. SIGMOD84, 1984, 14(2): 47–57. DOI:10.1145/971697 |
| [10] | BRINKHOFF T, KRIEGEL H P, SEEGER B. Parallel processing of spatial joins using R-trees [C]//Proceedings of the 12th International Conference on Data Engineering. New Orleans: IEEE, 1996: 258-265. |
| [11] | MUTENDA I, KITSUREGAWA M. Parallel R-tree spatial join for a shared-nothing architecture [C]//1999 International Symposium on Database Applications in Non-Traditional Environments. Kyoto: IEEE, 1999: 423-430. |
| [12] |
刘义, 陈荦, 景宁, 等. 基于R树索引的Map-Reduce空间连接聚集操作[J].
国防科技大学学报, 2013, 35(1): 136–141.
LIU Yi, CHEN Luo, JING Ning, et al. Processing spatial join aggregate in Map-Reduce based on R-tree[J]. Journal of National University of Defense Technology, 2013, 35(1): 136–141. |
| [13] | BECKMANN N, KRIEGEL H P, SCHNEIDER R, et al. The r*-tree: an efficient and robust access method for points and rectangles[J]. ACM SIGMOD Record, 1990, 19(2): 322–331. DOI:10.1145/93605 |
| [14] | SELLIS T K, ROUSSOPOULOS N, FALOUTSOS C. The R+Tree: a dynamic index for multi-dimensional objects [C]//International Conference on Very Large Data Bases. Brighton: Morgan Kaufmann, 1987: 507-518. |
| [15] | ELDAWY A, MOKBEL M F. A demonstration of SpatialHadoop: an efficient mapreduce framework for spatial data[J]. Proceedings of the Vldb Endowment, 2013, 6(12): 1230–1233. DOI:10.14778/2536274 |
| [16] |
张丽芬, 王晓华, 胡景松, 等. 基于网格划分的几种空间索引[J].
北京理工大学学报, 2004, 24(2): 140–144.
ZHANG Li-fen, WANG Xiao-hua, HU Jing-song, et al. Spatial indices based on grid partition[J]. Transactions of Beijing Institute of Technology, 2004, 24(2): 140–144. |
| [17] |
赵春宇, 孟令奎, 林志勇. 一种面向并行空间数据库的数据划分算法研究[J].
武汉大学学报:信息科学版, 2006, 31(11): 962–965.
ZHAO Chun-yu, MENG Ling-kui, LIN Zhi-yong. Spatial data partitioning towards parallel spatial database system[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11): 962–965. |
| [18] |
王永杰, 孟令奎, 赵春宇. 基于Hilbert空间排列码的海量空间数据划分算法研究[J].
武汉大学学报:信息科学版, 2007, 32(7): 650–653.
WANG Yong-jie, MENG Ling-kui, ZHAO Chun-yu. Spatial partitioning of massive data based on Hilbert spatial ordering code[J]. Geomatics and Information Science of Wuhan University, 2007, 32(7): 650–653. |
| [19] | PATEL J M, DEWITT D J. Partition based spatial-merge join [C]//ACM SIGMOD Record. Montreal: ACM, 1996, 25(2): 259-270. |
| [20] | ZHANG S B, HAN J Z, LIU Z Y, et al. Sjmr: parallelizing spatial join with mapreduce on clusters [C]//IEEE International Conference on Cluster Computing and Workshops. New Orleans: IEEE, 2009: 1-8. |
| [21] | DEWITT D J, NAUGHTON J F, SCHNEIDER D A, et al. Practical skew handling in parallel joins[C]//Proceedings of the 18th VLDB Conference. Vancouver: VLDB, 1992: 27-40. |
| [22] | LAM W M, SHAPIRO J M. A class of fast algorithms for the Peano-Hilbert space-filling curve [C]//IEEE International Conference on Image Processing. Austin: IEEE, 1994: 638-641. |



