2. 义乌工商职业技术学院 机电信息学院, 浙江 义乌 322000;
3. 华东交通大学 机电工程学院, 江西 南昌 330013
2. School of Electromechanical and Information Engineering, Yiwu Industrial and Commercial College, Yiwu 322000, China;
3. School of Mechanical and Electrical Engineering, East China Jiaotong University, Nanchang 330013, China
注射成型已广泛应用于汽车组件、家电外壳和电子产品外壳等聚合物产品的制造.流体辅助共注成型(fluid-assisted co-injection molding, FACIM)是流体辅助成型和共注成型这两种工艺的结合, 依次将2种以上的聚合物熔体注入模腔, 最后形成多层复合结构的聚合物制品.先注入的熔体为制品的表层, 后注入的熔体为制品的芯层[1-2].流体辅助共注成型工艺主要包括5个阶段:熔体短射、流体注射、流体保压、流体排出和制品顶出.FACIM兼顾流体辅助成型和共注成型工艺的优点, 可以将废旧聚合物作为芯层聚合物, 实现对废旧聚合物的回收利用, 也可以根据需要形成内部中空结构, 节省材料的使用量, 故在聚合物制品成型中被广泛使用.在流体辅助共注成型工艺中, 制品各层厚度和空心层厚度的精度影响着制品的品质, 有效地控制壁厚是流体辅助共注成型成熟的重要指标.目前, 国内外众多学者已针对流体辅助共注成型制品各层壁厚的形成机理进行大量的研究分析[3-5].研究表明, 流体辅助共注成型的各层壁厚主要与各聚合物熔体温度、各聚合物熔体预注射量(体积百分比)、延迟注射时间及辅助流体压力等工艺参数有关[5].目前, 各层壁厚的测量方法主要是将制品切开, 机械测量横截面; 该方法的最大缺点是破坏制品.利用超声波的测量方法具有快速、无损的优点, Ono等[6-7]将超声波用于监测注射成型过程并进行定性分析, Hsu等[8-9]将超声波应用于复合材料的辨识.RaiŠutis等[10-13]利用超声波方法表征多层聚合物厚度, 但计算过程复杂, 使用困难.
为了在成型过程中控制多层聚合物共注制品的各层壁厚, 需要优化调整流体辅助共注成型的工艺参数.为了便于参数实时调整, 本文提出一种相对简便的流体辅助共注成型制品层厚的超声无损测量方法.
1 超声波在界面处的反射透射行为超声波在介质中传播的一维波动方程[14]可以表示为
| $ \frac{{{\partial ^2}p}}{{\partial {t^2}}} = {c^2}\frac{{{\partial ^2}p}}{{\partial {x^2}}}. $ | (1) |
式中:x为超声传播方向; t为超声传播时间; c为超声波的传播速度; p为超声声压, 是x和t的函数.该波动方程的解如下:
| $ p = {A_1}\exp \left[ {{\rm{j}}\left( {wt - kx} \right)} \right] + {A_2}\exp \left[ {{\rm{j}}\left( {wt + kx} \right)} \right]. $ | (2) |
式中:A1、A2为常数, 由超声声源和边界条件决定; k表示波数, k=2π/λ.式(2) 中的第一项表示沿+x方向传播的超声波; 第二项表示反射波, 即为沿-x方向传播的超声波.
当超声波从一个介质传播到另一个介质时, 会在介质界面处发生反射和透射行为.假设超声波从介质1垂直入射进介质2, 介质1中的超声波声压为p1, 且由入射波pi和反射波pr组成; 介质2中的超声波声压为p2, 由透射波pt组成.p1和p2分别如下:
| $ \begin{array}{l} {p_1} = {p_{\rm{i}}} + {p_{\rm{r}}} = {p_{{\rm{ia}}}}\exp \left[ {{\rm{j}}\left( {wt - {k_1}x} \right)} \right] + \\ \;\;\;\;\;\;\;{p_{{\rm{ra}}}}\exp \left[ {{\rm{j}}\left( {wt + {k_1}x} \right)} \right], \end{array} $ | (3) |
| $ {p_2} = {p_{\rm{t}}} = {p_{{\rm{ta}}}}\exp \left[ {{\rm{j}}\left( {wt - {k_2}x} \right)} \right]. $ | (4) |
类似地, 介质1中的质点振动速度v1和介质2中的质点振动速度v2分别如下:
| $ {v_1} = {v_{{\rm{ia}}}}\exp \left[ {{\rm{j}}\left( {wt - {k_1}x} \right)} \right] + {v_{{\rm{ra}}}}\exp \left[ {{\rm{j}}\left( {wt + {k_1}x} \right)} \right], $ | (5) |
| $ {v_2} = {v_{{\rm{ta}}}}\exp \left[ {{\rm{j}}\left( {wt - {k_2}x} \right)} \right]. $ | (6) |
对于同一传播介质, 超声波声压与质点振动速度的比值为介质的声阻抗Z, 即Z=p/v=ρc, 有
| $ {v_{{\rm{ia}}}} = \frac{{{p_{{\rm{ia}}}}}}{{{\rho _1}{c_1}}},{v_{{\rm{ra}}}} = - \frac{{{p_{{\rm{ra}}}}}}{{{\rho _1}{c_1}}},{v_{{\rm{ta}}}} = \frac{{{p_{{\rm{ta}}}}}}{{{\rho _2}{c_2}}}. $ | (7) |
考虑到超声波声压和质点振动速度在介质界面处都是连续的, 即p1=p2, v1=v2, 可得
| $ {p_{{\rm{ra}}}} + {p_{{\rm{ra}}}} = {p_{{\rm{ta}}}}, $ | (8a) |
| $ {v_{{\rm{ia}}}} + {v_{{\rm{ra}}}} = {v_{{\rm{ta}}}}. $ | (8b) |
结合式(7)、(8) 可知, 在超声波从介质1垂直入射至介质2的过程中, 界面处的声压反射系数R和声压透射系数T[15]分别为
| $ R = \frac{{{p_{{\rm{ra}}}}}}{{{p_{{\rm{ia}}}}}} = \frac{{{\rho _2}{c_2} - {\rho _1}{c_1}}}{{{\rho _2}{c_2} + {\rho _1}{c_1}}} = \frac{{{Z_2} - {Z_1}}}{{{Z_2} + {Z_1}}}, $ | (9) |
| $ T = \frac{{{p_{{\rm{ta}}}}}}{{{p_{{\rm{ia}}}}}} = \frac{{2{\rho _2}{c_2}}}{{{\rho _2}{c_2} + {\rho _1}{c_1}}} = \frac{{2{Z_2}}}{{{Z_2} + {Z_1}}}. $ | (10) |
式中:Z1和Z2分别为介质1和介质2的声阻抗.
声压反射系数和透射系数之间有如下关系:
| $ T = 1 + R, $ | (11) |
| $ R' = - R. $ | (12) |
式中:R′为超声波从介质2垂直入射到介质1中时界面处的反射系数.
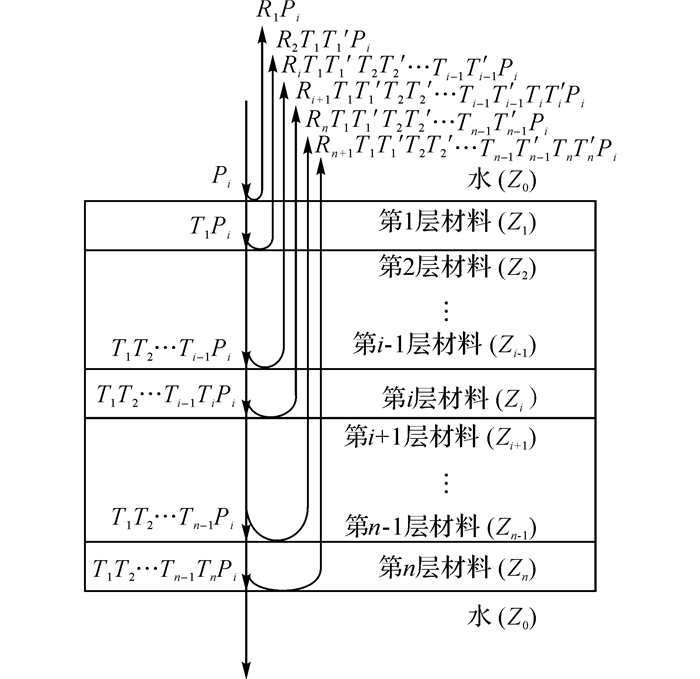
2 测量理论与方法 2.1 测量理论根据超声波在不同物质界面的反射和透射行为, 可以采用水浸法对多层材料进行超声波测量[16], 超声波在水及n层材料复合结构的试样中的传播过程如图 1所示.不考虑超声波在材料内部传播的衰减, 第i层材料上表面和下表面的反射波声压之间存在如下关系:
|
图 1 多层材料中超声波传播示意图 Fig. 1 Propagation of ultrasound in multilayer material |
| $ \begin{array}{l} \frac{{{R_i}{T_1}{{T'}_1}{T_2}{{T'}_2} \cdots {T_{i - 1}}{{T'}_{i - 1}}{p_i}}}{{{R_{i + 1}}{T_1}{{T'}_1}{T_2}{{T'}_2} \cdots {T_{i - 1}}{{T'}_{i - 1}}{T_i}{{T'}_i}{p_i}}} = \\ \;\;\;\;\;\;\;\frac{{{R_i}}}{{{R_{i + 1}}{T_i}{{T'}_i}}} = \frac{{{A_i}}}{{{A_{i + 1}}}};i = 1,2, \cdots ,n. \end{array} $ | (13) |
式中:Ri为从第i-1层到第i层的声压反射系数; Ti为从第i-1层到第i层的声压透射系数, T′i为第i层到第i-1层的声压透射系数; Ai为探头接收到的第i层材料上表面反射回波的声压幅值, Ai可由3.3节测量实验中超声探头接收到的回波信号测得.
根据式(9)、(10), 可得
| $ {R_i} = \frac{{{Z_i} - {Z_{i - 1}}}}{{{Z_i} + {Z_{i - 1}}}}, $ | (14) |
| $ {T_i} = \frac{{2{Z_i}}}{{{Z_i} + {Z_{i - 1}}}}. $ | (15) |
式中:Zi和Zi-1分别为第i层和第i-1层材料的声阻抗.将式(14)、(15) 代入式(13), 可得
| $ \frac{{Z_i^2 - Z_{i - 1}^2}}{{4{Z_i}{Z_{i - 1}}\left( {\frac{{{Z_{i + 1}} - {Z_i}}}{{{Z_{i + 1}} + {Z_i}}}} \right)}} = \frac{{{A_i}}}{{{A_{i + 1}}}}. $ | (16) |
式中:Zi-1、Zi、Zi+1分别为第i-1层、第i层和第i+1层材料的声阻抗, i=1~n.水在20 ℃时的声阻抗为1.48×106 N·S/m3, Ai(i=1~n)可由3.3节测量实验中超声探头接收到的回波信号测得.
式(16) 中, Zi(i=1~n)为未知数, 式(16) 有n个方程(i=1~n), 可以求解Zi(i=1~n).
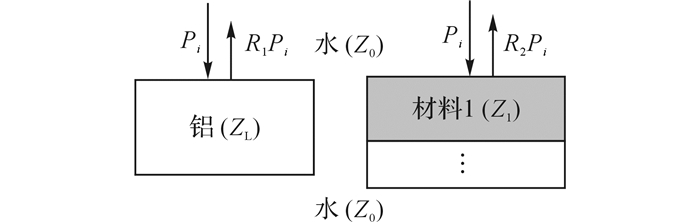
2.2 测量方法直接求解式(16) 较复杂, 在实际测量中, 为了简便计算, 先用试样与标准铝块的对比实验来求解材料1的声阻抗Z1, 再用式(16) 依次计算第2~n层材料的声阻抗Zi(i=2~n).试样与标准铝块反射波对比法测量声阻抗的示意图如图 2所示, 用同一超声探头发出同样的入射波Pi到铝块和试样的上表面, 分别测量它们上表面的反射回波Pr1和Pr2, 两者上表面反射回波的声压幅值比可由下式表示:
|
图 2 试样与标准铝块反射波对比 Fig. 2 Comparison of echo from top surface of aluminum and sample |
| $ A = \frac{{{P_{r1}}}}{{{P_{r2}}}} = \frac{{{R_1}{p_i}}}{{{R_2}{p_i}}} = \frac{{{R_1}}}{{{R_2}}} = \frac{{{Z_{\rm{L}}} - {Z_0}}}{{{Z_{\rm{L}}} + {Z_0}}} \cdot \frac{{{Z_{\rm{1}}} + {Z_0}}}{{{Z_{\rm{1}}} - {Z_0}}}. $ | (17) |
式中:A为铝和试样上表面反射波的幅值比; ZL、Z1、Z0分别为铝块、材料1和水的声阻抗, 其中ZL、Z0为已知值.
经变换求解Z1, 可得
| $ {Z_1} = \frac{{A\left( {{Z_{\rm{L}}} + {Z_{\rm{0}}}} \right) + \left( {{Z_{\rm{L}}} - {Z_{\rm{0}}}} \right)}}{{A\left( {{Z_{\rm{L}}} + {Z_{\rm{0}}}} \right) - \left( {{Z_{\rm{L}}} - {Z_{\rm{0}}}} \right)}}{Z_0}. $ | (18) |
求得Z1后, 代入式(16), 可得Zi(i=2~n).声阻抗与密度和声速的关系如下:
| $ c = z/\rho . $ | (19) |
式中:c为声速, z为材料的声阻抗, ρ为材料的密度.
若材料的密度已知, 则采用式(19) 可以计算超声波在各层材料中的声速ci(i=1~n), 从而可以根据下式计算各层材料的厚度:
| $ {h_i} = \frac{1}{2}{c_i} \cdot \Delta {t_i}. $ | (20) |
式中:Δti为探头分别接收到第i层材料上表面和下表面反射回波的时间间隔.
3 实验验证为了验证该方法, 对由2种材料气辅共注成型的试样进行超声波测量(n=2), 将超声波测量结果与扫描电镜的测量结果进行比较验证.
3.1 被测试样被测试样为气体辅助共注成型工艺制得的制品, 表层聚合物为高密度聚乙烯(HDPE, 牌号为DMDA-8008), 内层聚合物为聚丙烯(PP, 牌号为1102K), 成型工艺参数如表 1所示.试样是截面为矩形的管件.如图 3所示为试样的实物照片和截面形状尺寸, 超声探头在厚度方向上的位置如图 3所示, 超声探头在长度方向上的位置随机选择.
| 表 1 气辅共注成型工艺参数 Table 1 Process parameters for gas assisted co-injectionmolding |

|
图 3 试样的实物图和截面形状 Fig. 3 Photographs of products and its sectional view |
如表 1所示为制作试样时所用的气辅成型工艺参数.表中, p为注气压力, t1为注气延迟时间, Q为流率, θ为料温, t2为A、B料的延迟时间.
3.2 超声装置超声发射采集装置为广东汕头超声电子有限公司生产的多通道超声探伤仪, 型号为CTS-04PC.超声探头采用频率为5 MHz、晶片直径为8 mm的窄脉冲探头(型号为5N8), 既能够满足分辨率的要求, 又可以避免过大衰减.
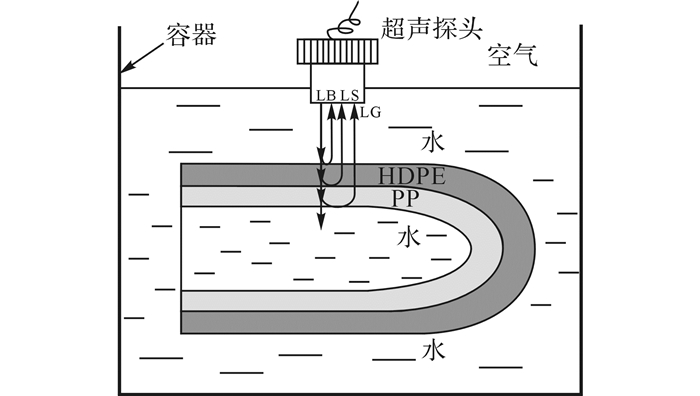
如图 4所示为采用水浸法测量得到气辅共注成型制品各层壁厚的示意图.图中, LB表示超声波在水与表层聚合物HDPE界面的反射回波, LS表示超声波在聚合物HDPE与聚合物PP分界面的反射回波, LG表示聚合物PP与水分界面的反射回波.对于中空层封闭的制品, 测量时中空层充满的只能是空气; 对于中空层与外界连通的制品, 测量时中空层可充水, 也可充空气, 在该实验中, 试样中空层充水.如图 3所示, 试样有9.2 mm层厚比较均匀的区域, 该实验采用晶片直径为8 mm的5N8超声探头, 可以测量气辅共注成型制品各层聚合物的平均壁厚.
|
图 4 超声脉冲反射法测量厚度示意图 Fig. 4 Measurement of wall thickness with pulse reflection method |
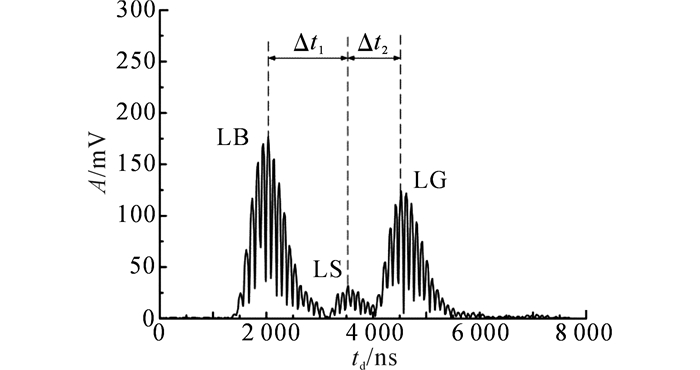
如图 5所示是超声波在两层聚合物试样的3个分界面上的反射回波信号, 测量时增益设置为50.在PP与水的分界面, 超声波有一部分透入水中, 这时LG的波幅比LB小; 若中空层充满空气, 则超声波在PP与空气分界面几乎发生全反射, 此时LG的波幅可能比LB大.
|
图 5 超声波在试样中各界面的发射回波信号 Fig. 5 Reflected wave from interfaces in sample |
通过测量各界面的反射回波幅值和时间间隔, 测量各层壁厚, 具体测量步骤如下.
1) 根据2.2节所述的测量方法, 先用与标准铝块对比的方法测量HDPE的声阻抗Z1.测量时, 增益设置为30, 超声波在标准铝块和试样上表面的反射回波信号分别如图 6(a)、(b)所示.选取各自的最大声压幅值来计算比值, 经多次实验采集数据, 求取平均值, 铝块的最大声压幅值为127 mV, 试样的最大声压幅值为28 mV, 它们的声压幅值比为A=4.54.
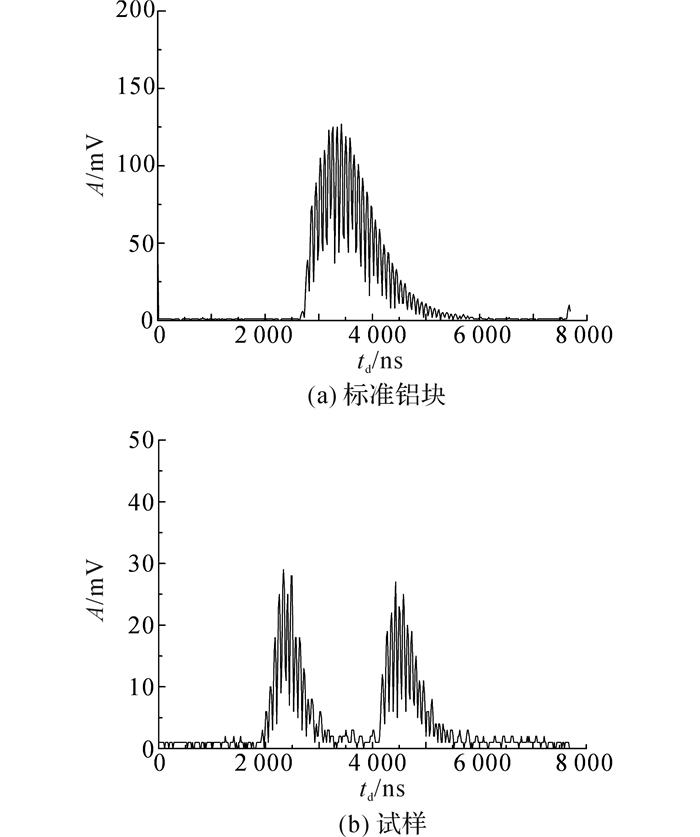
|
图 6 标准铝块和试样的上表面回波 Fig. 6 Echo from top surface of aluminum and specimen |
2) 标准铝块的声阻抗ZL=1.69×107 N·S/m3, 水的声阻抗Z0=1.48×106 N·S/m3, A=4.54, 代入式(17) 计算可得, HDPE的声阻抗Z1=2.15×106 N·S/m3.HDPE的密度为951 kg/m3, 代入式(19) 计算可得超声波在HDPE中的声速为c1=2 261.8 m/s.
3) 超声波在试样中传播, 各界面的反射回波信号如图 5所示.图中,A为信号幅值,td为延迟时间.经多次实验采集数据求取平均值, LB、LS、LG的最大幅值分别为A1=170 mV,A2=32 mV,A3=122 mV.将计算得到的HDPE声阻抗Z1=2.15×106 N·S/m3和水的声阻抗Z0=1.48×106 N·S/m3代入式(16), 可得PP的声阻抗Z2=2.31×106 N·S/m3, PP的密度为918 kg/m3, 因此超声波在PP中的声速为c2=2 516.3 m/s.
4) 图 5采样的数据中, Δt1=1 483.197 8 ns, Δt2=1 151.845 1 ns, 将c1、c2、Δt1、Δt2代入式(20) 计算, 可得h1=1.68 mm, h2=1.45 mm, 总厚度h=3.13 mm.
3.4 结果验证利用扫描电镜, 来验证超声测量结果的正确性.将超声测量位置的试样浸入液氮10 min后进行淬断, 喷金并拍摄截面的扫描电镜图片.扫描电镜的操作参数如下:加速电压为3 kV, 工作距离为8.9 mm, 放大倍数为40.截面的扫描电镜照片如图 7所示.可知, 同一截面左侧部分是淬断的, 右侧部分是锯断的.分别对两材料层进行厚度测量, HDPE层的厚度为h1*=1.76 mm, PP层的厚度为h2*=1.42 mm.超声波测量方法与扫描电镜测量结果相比, HDPE层厚度的测量结果偏小0.08 mm, 误差约为4.5%;PP层厚度的测量结果偏大0.03 mm, 误差约为2.1%;总厚度的结果仅偏小0.05 mm, 误差约为1.6%.分析其中的原因可知, 误差的主要影响因素如下:1) 在用与标准铝块对比的方法测量第一层材料HDPE的声阻抗Z1时, 幅值比存在误差; 2) 测量声速时, 材料的密度可能存在误差; 3) 测量时间间隔Δt1、Δt2存在误差.从测量结果来看, 采用超声波方法测量共注成型制品各层厚度是可行的, 而且它的无损测量特性具有极大的优越性, 为进一步研究流体辅助共注成型过程中各层聚合物厚度的实时在线测量奠定了基础.

|
图 7 试样的扫描电镜及壁厚测量 Fig. 7 SEM and thickness measurement of HDPE and PP |
本文基于超声波在异质界面发生反射和透射的规律, 建立超声波在多层复合材料的传播过程中各分界面反射声压比与各层材料声阻抗之间的关系.采用与标准铝块对比测量的方法, 建立被测试样表层材料的声阻抗与标准铝块声阻抗的关系, 得到表层材料的声阻抗, 并根据公式递推依次得到其他层材料的声阻抗.利用超声波对浸在水中的气辅共注成型制品进行测量, 得到各分界面反射波的声压幅值和时间间隔, 结合不同材料层的密度计算得到各个材料层的壁厚.
将超声波测量方法得到的结果与扫描电镜方法的测量结果进行比较, 结果表明, 两者的测量结果偏差在0.08 mm以内, 误差百分比为4.5%.总厚度的测量结果偏差仅为0.05 mm, 误差百分比约为1.6%, 说明利用超声波测量多层复合材料厚度的方法是有效的.分析了各层厚度测量误差的主要原因.超声波探头的工作频率、脉冲宽度和晶片直径等参数对测量结果会有影响, 下一步工作将研究这些因素对测量结果的影响.
| [1] |
匡唐清, 柳和生, 周国发, 等. 气体辅助共注成型的发展现状[J].
中国塑料, 2003(09): 36–40.
KUANG Tang-qing, LIU He-sheng, ZHOU Guo-fa, et al. Present situation of gas-assisted co-injection molding[J]. China Plastics, 2003(09): 36–40. DOI:10.3321/j.issn:1001-9278.2003.09.009 |
| [2] |
周国发, 孙懋, 柳和生, 等. 顺序共注成型的实验研究[J].
中国塑料, 2003(04): 55–59.
ZHOU Guo-fa, SUN Mao, LIU He-sheng, et al. Experimental study of sequential co-injection molding[J]. China Plastics, 2003(04): 55–59. |
| [3] | MULVANEY-JOHNSON L, CHENG C C, ONO Y, et al. Real time diagnostics of gas/water assisted injection moulding using integrated ultrasonic sensors[J]. Plastics, Rubber and Composites, 2013, 36(3): 111–121. |
| [4] | CHENG C, ONO Y, JEN C. Real-time diagnosis of co-injection molding using ultrasound[J]. Polymer Engineering and Science, 2007, 47(9): 1491–1500. DOI:10.1002/(ISSN)1548-2634 |
| [5] |
章凯, 柳和生, 匡唐清, 等. 注水延迟时间对水辅共注成型充填的影响[J].
高分子材料科学与工程, 2013(06): 173–177.
ZHANG Kai, LIU He-sheng, KUANG Tang-qing, et al. Influence of water injection delay time on water-assisted co-injection molding filling process[J]. Polymer Materials Science and Engineering, 2013(06): 173–177. |
| [6] | ONO Y, JEN C K, CHENG C C, et al. Real-time monitoring of injection molding for microfluidic devicesusing ultrasound[J]. Polymer Engineering and Science, 2005, 45(4): 606–612. DOI:10.1002/(ISSN)1548-2634 |
| [7] | ONO Y, WHITESIDE B R, BROWN E C, et al. Real-time process monitoring of micromoulding using integrated ultrasonic sensors[J]. Transactions of the Institute of Measurement and Control, 2007, 29(5): 383–401. DOI:10.1177/0142331207080153 |
| [8] | HSU D K, HUGHES M S. Simultaneous ultrasonic velocity and sample thickness measurement and application in composites[J]. Journal of the Acoustical Society ofAmerica, 1992, 92(2): 669–675. DOI:10.1121/1.405279 |
| [9] | WOOH S C, WEI C. A high-fidelity ultrasonic pulse-echo scheme for detecting delaminations in composite laminates[J]. Composites Part B Engineering, 1999, 30(5): 433–441. DOI:10.1016/S1359-8368(99)00017-7 |
| [10] | RAIŠUTIS R, KAŽYS R, MAŽEIKA L. Application of the ultrasonic pulse-echo technique for quality control of the multi-layered plastic materials[J]. NDT and E International, 2008, 41(4): 300–311. DOI:10.1016/j.ndteint.2007.10.008 |
| [11] | RAIŠUTIS R, KAŽYS R, MAŽEIKA L. Application of the ultrasonic characterization methods for highly attenuating plastic materials[J]. NDT and E International, 2007, 40(4): 324–332. DOI:10.1016/j.ndteint.2006.11.002 |
| [12] | HÄGGLUND F. Tools for ultrasonic characterization of layered media [D]. Luleå : Luleå University of Technology, 2007. https://www.researchgate.net/publication/253269213_Tools_for_Ultrasonic_Characterization_of_Layered_Media |
| [13] | LIONETTO F, MAFFEZZOLI A. Polymer characterization by ultrasonic wave propagation[J]. Advances in Polymer Technology, 2008, 27(2): 63–73. |
| [14] | 丁辉. 计算超声学:声场分析及应用[M]. 北京: 科学出版社, 2010: 10-13. |
| [15] | ZHAO P, WANG S, YING J, et al. Non-destructive measurement of cavity pressure during injection molding process based on ultrasonic technology and Gaussian process[J]. Polymer Testing, 2013, 32(8): 1436–1444. DOI:10.1016/j.polymertesting.2013.09.006 |
| [16] | ZHAO P, PENG Y, YANG W, et al. Crystallization measurements via ultrasonic velocity: study of poly(lactic acid) parts[J]. Journal of Polymer Science Part B-Polymer Physics, 2015, 53(10): 700–708. DOI:10.1002/polb.v53.10 |



