磁瓦是永磁体中的一种瓦状磁铁, 主要用在永磁电机上, 材料主要是铁氧体.磁瓦质量直接影响到电机性能和使用寿命, 但由于加工过程中不恰当的温度、压力或其他因素, 磁瓦可能会存在起级、裂纹、缺口、空隙、夹层、起层等多种表面缺陷或内部缺陷.目前, 针对磁瓦的表面检测, 机器视觉已经较成熟[1]; 由于内部缺陷形状不一、位置不定、缺陷严重度不同等因素限制, 相关检测方法未深入研究.在实际检测中, 磁瓦的内部缺陷检测主要采用人耳辨析音频的方法, 即依靠磁瓦与金属块撞击产生的声音来判断缺陷的有无.这种方法主要取决于工人的经验, 受到主观因素影响.
从最近的发展来看, 目前用于无损检测的手段主要有超声波检测[2]、磁粉检测[3]、涡流检测[4]、渗透检测[5]等.考虑到检测效率、成本、可靠性等多种因素, 本文提出基于音频共振的方法来检测磁瓦的内部缺陷.
在实际检测过程中, 由于收集的声音信号一般为非平稳信号, 加大了提取磁瓦内部缺陷特征的难度.黄沁元等[6]提出采用归一化双谱3切片的方法来提取磁瓦内部缺陷的特征, 识别准确率高于98.5%.双树复小波包变换作为一种新的信号处理方法, 能够同时划分高频信号和低频信号, 具有近似平移不变性、良好的方向选择性、完全重构性、有限的数据冗余性和高效的计算效率等优良性质[7].目前, 双树复小波包变换已经被用在图像处理[8]、故障诊断[9]、语音信号识别[10]等领域.考虑到双树复小波包分解良好的性能及应用的广泛性, 本文提出利用双树复小波包对声音信号进行分解, 选择包含频域信息丰富的频带, 然后计算相应频带的能量、峭度、偏度、模糊熵.考虑到各个特征存在一些相关性(线性或非线性)以及数据维度的冗余性, 本文提出利用邻域成分分析方法对数据降维[11].邻域成分分析方法利用训练数据来寻找最优的变换矩阵, 使数据维度降低、保留了特征的有效信息, 提高了分类的精度和效率.
支持向量机作为建立在统计学理论基础上的一种机器学习算法, 具有强大的非线性处理能力和良好的推广能力.与人工神经网络相比, 支持向量机克服了前者训练时间长、训练结果不确定等缺点.前者需要大量的样本数据.最小二乘支持向量机遵循结构风险最小化原则, 结构参数在训练过程中根据样本数据自动确定, 不存在过拟合的现象.它将标准的支持向量机的学习问题转化为求解线性方程问题, 具有更快的求解速度[12-13].
本文利用双树复小波包变换对声音信号进行分解, 得到不同频带分量; 对子带进行筛选, 求出筛选频带分量的能量、峭度、偏度、模糊熵, 将能量、峭度、偏度、模糊熵作为特征参数, 为了保留原始特征的有效信息, 提高分类精度和速度; 采用邻域成分分析方法对原始数据降维, 构造新的特征量, 将新的特征量输入最小二乘支持向量机来识别磁瓦内部缺陷.
1 理论背景 1.1 双树复小波包变换原理传统的离散小波包变换对信号进行分解时, 采用下抽样操作, 每一次分解之后信号的采样频率将下降一半, 时间分辨率也下降一半.一旦分解层数确定, 频带的频率分辨率确定, 分解的层数越多, 频率分辨率越高, 但是时间分辨率降低.下抽样操作不具有平移不变性的特点, 同时会引起较大的频率混叠问题, 并且对信号的奇异点敏感.
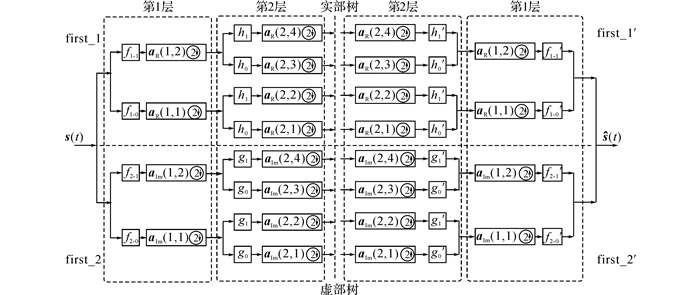
针对传统小波包变换的缺点, Bayram等[7]提出双树复小波包变换.双树复小波包变换是在双树复小波变换[14]的基础上提出的.双树复小波包变换对信号进行分解重构, 是由两个平行且使用不同的低通、高通滤波器的离散小波包构成, 可以看成实部树和虚部树.该分解方法可以使信息互补.如图 1所示为两层信号的分解与重构示意图.图中, s(t)表示分解原始信号,
|
图 1 双树复小波包变换的分解与重构过程 Fig. 1 Decomposition and reconstruction of DTCWT |
假设输入带标记样本集X=[x1, x2, …, xn]且xi∈Rd.相应的样本标签为{c1, c2, …, cn}.马氏距离通过下式定义:
| $ \begin{array}{l} d\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right) = \sqrt {{{\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_j}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_j}} \right)} = \\ \sqrt {{{\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_j}} \right)} . \end{array} $ | (1) |
式中:点xj是点xi随机选的邻域点, 可能性用pi, j表示, 点xi继承点xj的标签.pi, j用欧式距离在变换空间定义:
| $ \left. \begin{array}{l} {p_{i,j}} = \frac{{\exp \left( { - {{\left\| {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_j}} \right\|}^2}} \right)}}{{\sum {_{k \ne i}\exp \left( { - {{\left\| {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_k}} \right\|}^2}} \right)} }},j \ne i;\\ {p_{i,j}} = 0,j = i. \end{array} \right\} $ | (2) |
每个点均可被当成邻域点.
每个数据点均可被当作邻点, 输入的数据可以继承所有的类标签.数据点xi被正确分类的可能性可用下式表示(假设xi属于ci类):
| $ {p_i} = \sum\limits_{j \in {c_i}} {{p_{ij}}} . $ | (3) |
所有点被正确分类的可能性可用下式表示:
| $ f\left( \mathit{\boldsymbol{A}} \right) = \sum\limits_i {\sum\limits_{j \in {c_i}} {{p_{ij}}} } = \sum\limits_i {{p_i}} . $ | (4) |
邻域成分分析[11]的核心是通过寻找最合适的变换矩阵, 使尽量多的点被正确地分类.寻找最合适的变换矩阵, 可以采用梯度法[11]:
| $ \begin{array}{l} \frac{{\partial f\left( \mathit{\boldsymbol{A}} \right)}}{{\partial \mathit{\boldsymbol{A}}}} = \\ \;\;\; - 2\mathit{\boldsymbol{A}}\sum\limits_i {\sum\nolimits_{j \in {c_i}} {{p_{ij}} \cdots \left( {{\mathit{\boldsymbol{x}}_{ij}}\mathit{\boldsymbol{x}}_{ij}^{\rm{T}} - \sum\limits_k {{p_{ik}}{\mathit{\boldsymbol{x}}_{ik}}\mathit{\boldsymbol{x}}_{ik}^{\rm{T}}} } \right).} } \end{array} $ | (5) |
式中:xij为xi和xj的差.
1.3 最小二乘支持向量机最小二乘支持向量机[12-13]主要的思想如下:将输入数据映射到高维空间, 在高维空间建立线性回归方程.假设有一个线性可分样本集{xi, yi}, i=1, 2, 3, …, n.其中i表示样本的数量, xi∈R表示样本数据, yi∈{-1, 1}表示分类标签.线性可分函数可以表示为
| $ g\left( \mathit{\boldsymbol{X}} \right) = \mathit{\boldsymbol{wX + b}}. $ | (6) |
式中:w、b分别为权重矢量和偏差.
最小二乘支持向量机构成线性回归问题可以转化为求解最优问题:
| $ \mathop {\min }\limits_{w,b,e} J\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{e}}} \right) = \frac{1}{2}\left( {\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^{\rm{T}}} + \gamma \sum\limits_{i = 1}^n {e_i^2} } \right). $ | (7) |
服从于:
| $ g\left( {{\mathit{\boldsymbol{x}}_i}} \right) = \mathit{\boldsymbol{w}}{\mathit{\boldsymbol{x}}_i} + {b_i} + {e_i}. $ | (8) |
式中:γ为正规化参数, ei为残留误差.
因为权重矢量w具有高维特性, 不能直接求解, 引入核函数简化求解问题:
| $ g\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}} \right) = \sum\limits_{i = 1}^n {{\alpha _i}K\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}},{\mathit{\boldsymbol{x}}_i}} \right) + {b_i}} . $ | (9) |
式中:K为核函数, 理论上讲, 只要满足Mercer条件的函数都可以作为核函数; α为支持向量系数; xt为新输入的数据.目前使用的核函数有4种:线性核函数、p阶多项式核函数、多层感知器核函数和RBF核函数.由于RBF核函数的广义性和计算速度快的能力, 使得RBF核函数更受欢迎.RBF核函数可以表示为
| $ K\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}},{\mathit{\boldsymbol{x}}_i}} \right) = \exp \left( { - \frac{{{{\left\| {{\mathit{\boldsymbol{x}}_{\rm{t}}} - {\mathit{\boldsymbol{x}}_i}} \right\|}^2}}}{{{\sigma ^2}}}} \right). $ | (10) |
式中:σ为核参数.
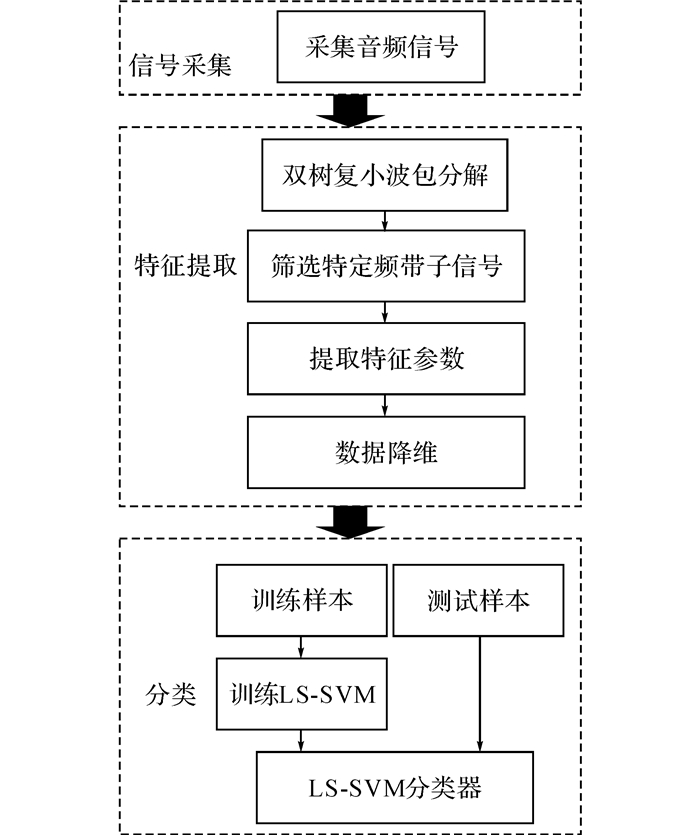
2 集成双树复小波包、邻域成分分析法和最小二乘支持向量机检测步骤利用双树复小波包变换, 对原始信号进行分解; 然后根据频带选择所需子信号, 对子信号提取特征, 利用邻域成分分析法对数据降维; 最后将降维后构造的特征集作为最小二乘支持向量机的输入, 进行内部缺陷识别.提出的磁瓦内部缺陷识别的流程图如图 2所示, 主要包含以下步骤.
|
图 2 磁瓦内部缺陷检测流程图 Fig. 2 Flow chart of detection of magnetic tile internaldefects |
1) 根据奈奎斯特原理设置一定的采样频率对合格磁瓦及含内部缺陷的磁瓦分别采集N次声音信号, 共获得2N个样本.
2) 对获取的样本信号进行双树复小波包分解.分解的层数为m, 获取到2m个不同频带的子信号.
3) 筛选所含信息量较大的频带的子信号.对这些子信号提取特征参数.
4) 利用邻域成分分析法对数据进行降维, 构造新的特征量.
5) 将构造的新特征量输入到最小二乘支持向量机, 利用这些参数训练好最小二乘支持向量机.
6) 收集测试信号.重复步骤2)~4), 以获取特征向量; 最后将获取的特征向量输入到训练好的最小二乘支持向量机, 识别缺陷磁瓦.
3 试验分析与分类 3.1 样本陈述检测对象为四川某厂家生产的铁氧体类型磁瓦, 由于磁瓦种类繁多, 收集了该厂生产较普遍的3种类型磁瓦作为实验对象, 将其划分为A、B、C三类.其中每类磁瓦共收集240片, 包含120片检测合格样本和120片含内部缺陷样本.为了保证收集样本的可靠性, 每片磁瓦均被经验丰富的工人检测多次.
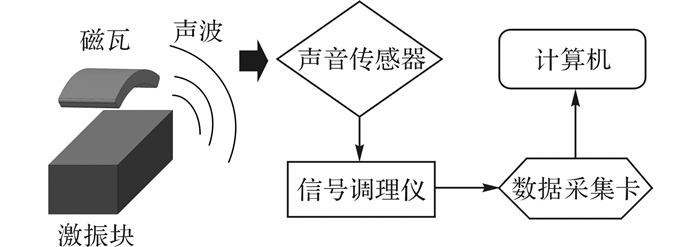
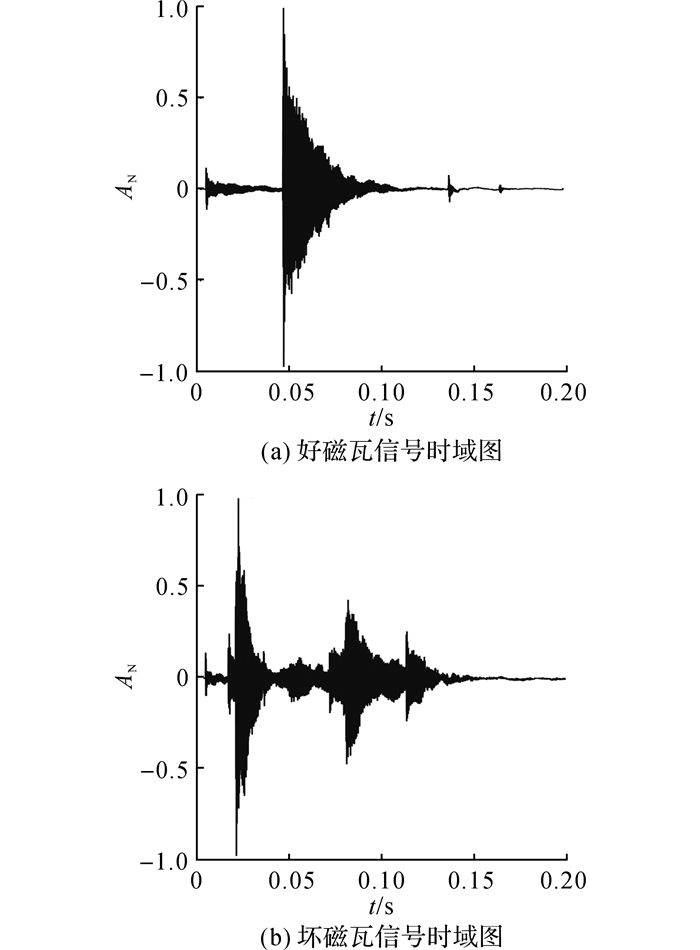
3.2 磁瓦内部缺陷特征提取检测系统示意图如图 3所示, 整个检测系统主要包括激振块、声音传感器、信号调理仪、数据采集卡、计算机.磁瓦从固定的高度(20 mm)跌落到激振块, 撞击产生声音, 利用声音传感器将声音信号转换为电信号, 通过信号调理仪对采集的声音信号做放大、滤波处理, 最后经过数据采集卡对信号进行采样率为40 000 Hz的量化.每次信号采集的时长为0.2 s, 这段时间包含了整个磁瓦从跌落到撞击结束的整个时长.图 4中,AN为电压信号的归一化幅值.如图 4所示为A类磁瓦中一片合格品与一片非合格品的时域波形图, 为了便于分析, 将时域信号通过傅里叶变换转换到频域信号.如图 5所示为图 4对应的频域转换.由于时域和频域信号存在幅值差异, 对时域和频域信号作归一化处理.归一化的原则是将每个点值除以所有点的最大值.
|
图 3 检测系统示意图 Fig. 3 Schematic diagram of detection system |
|
图 4 磁瓦声信号时域图 Fig. 4 Time history of impact sound from magnetic tile |
|
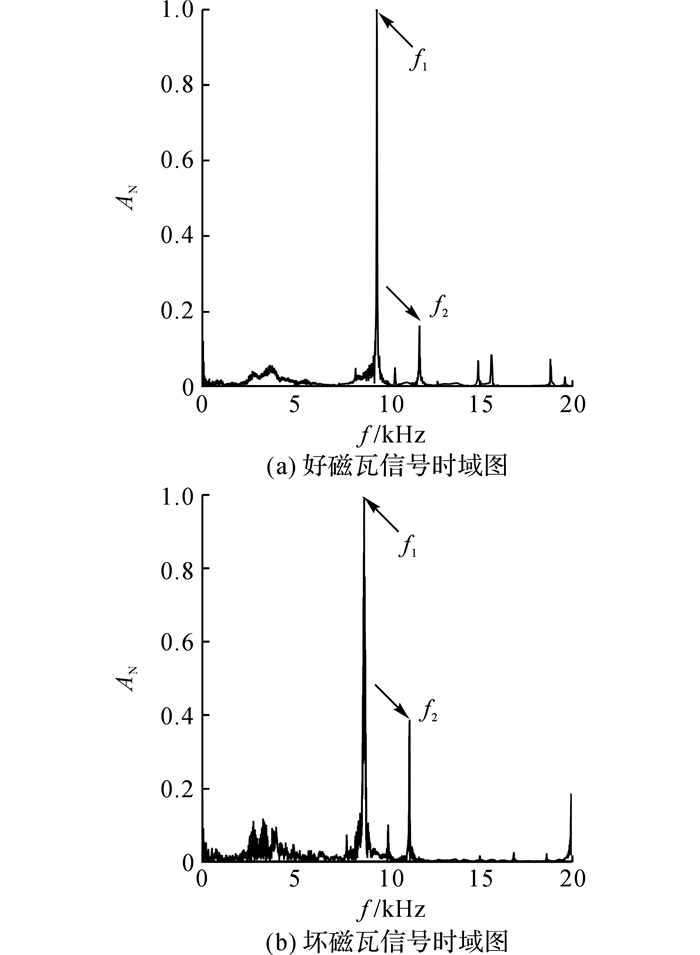
图 5 磁瓦声信号频域图 Fig. 5 Frequency domain of impact sound from magnetic tile |
分别对比图 4、5中的两幅图可知, 在时域和频域下, 合格磁瓦与含缺陷磁瓦的波形存在相似现象, 相应的内部缺陷特征不易提取.由于磁瓦内部缺陷大小未知, 位置不定, 严重度未知, 加大了提取磁瓦内部缺陷的难度.为了细化信号, 利用双树复小波包对信号进行分解.李辉等[9]利用3层双树复小波包分解, 成功获取了滚动轴承缺陷特征.由于所采集的磁瓦声音信号为衰减信号, 且内部缺陷位置不定、大小不一, 利用3层双树复小波包分解难以获取内部缺陷特征, 需要将原始信号分解更多的层数.通常不是所有的频带均包含缺陷信号, 缺陷信号一般只存在于部分频带.选择合适的频带更能有利于提取缺陷特征.胥永刚等[15]通过计算峭度和相关系数, 利用相关系数和峭度的最大值筛选所需频带.胥永刚等[16]通过分解原始信号, 计算每个子带的谱峭度, 利用谱峭度的滤波器作用, 计算最大峭度值对应分量信号的包络谱, 根据包络谱可以识别齿轮箱轴承的故障部位和类型.本文根据傅里叶频谱, 选择频域所含信息最丰富的频带来提取特征.由频谱图可知, 8 000~12 000 Hz这段频带所含有的信息最丰富, 包含两个共振点(f1和f2).本文利用双树复小波包变换将原始信号分解为6层, 共获得64个分解信号.由于8 000~12 000 Hz这段频带所含有的信息最丰富, 包含这段信息的频率的子信号被用来提取特征, 共获得13个子信号.双树复小波包采用下抽样操作, 存在频带混叠的特点, 所以选择的频带为(6, 16-19), (6, 21-23), (6, 48-51), (6, 54-55).
在信号处理领域中, 数据统计特征能够有效地反映信号特征.常见的数据特征包括平均值、标准差、峭度、能量、方差、偏度等.由于磁瓦内部缺陷位置随机, 缺陷严重度不定, 缺陷特征不存在于固定的所筛选的子带信号中.平均值不能很好地反映缺陷信息.标准差和方差所需的计算方法相似, 因此两者只需要选择一个.如图 6(a)~(d)所示分别为好磁瓦与坏磁瓦所计算的所选频带的峭度Ku、方差Va、能量En、偏度Sk.为了减少数值之间的差异, 所计算的数值均被归一化处理.从图 6可以看出, 统计量方差与能量值波动相似, 但能量波动更加明显, 因此选择峭度、能量、偏度作为分类特征.

|
图 6 特征曲线图 Fig. 6 Curves of features |
近年来, 模糊熵在故障诊断领域中得到了广泛的关注, 是一种衡量时间序列复杂性程度的参数, 属于非线性科学和信息论的范畴.序列越复杂, 自相似性越低, 熵越大, 当序列规整时, 自相似性越高, 熵越小.目前, 模糊熵已经成功用在滚动轴承的检测中[17].模糊熵被选为分类特征之一.所选频带的模糊熵Su如图 6(e)所示, 模糊熵被归一化处理.综上所述, 共提取4个特征参数作为磁瓦内部缺陷识别的依据.
直接将13个子信号提取的特征参数输入到分类器, 不但会增加计算时间, 而且会降低分类精度, 造成维数灾难.本文利用邻域成分分析方法对数据进行降维, 由于邻域降维具有卓越的降维能力, 将原始的52维数据降成两维数据.基于邻域降维方法的主要步骤如下.
1) 构造输入样本集X, 由60片合格样本和60片含缺陷样本组成, 每个样本包括52维数据.
2) 设置行数为2、列数为52的任意初始变换矩阵A.
3) 利用式(1)、(2) 计算变换域中的欧式距离.
4) 利用式(3)、(4) 计算所有点被正确分类的可能性.
5) 利用式(5) 寻找最合适的变换矩阵A, 尽量使式(4) 达到最大值, 利用该矩阵对数据降维.
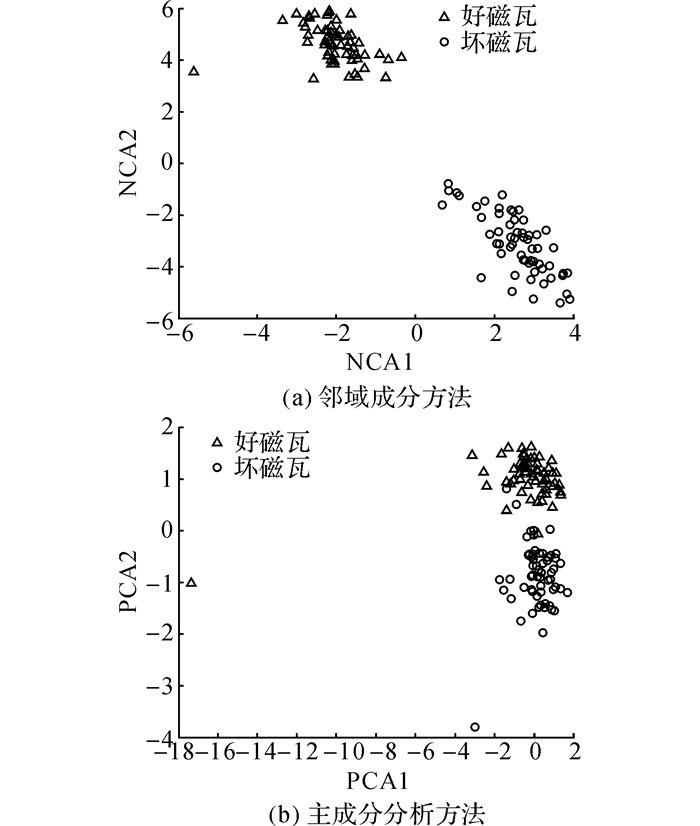
降维结果如图 7(a)所示.图中,NCA1、NCA2分别为邻域成分分量1和邻域成分分量2.为了验证邻域成分分析方法降维的卓越性, 将邻域成分分析方法与主成分分析作对比.主成分降维结果如图 7(b)所示.图中,PCA1、PCA2分别为主成分分量1和主成分分量2.可以看出, 主成分基本能够使数据聚成两类, 但在主成分聚类的结果中, 存在个别散点交叉的现象, 所以主成分降维结果不如邻域成分降维的效果好.
|
图 7 数据降维结果 Fig. 7 Results of data reduction |
所选的最小二乘支持向量机基于RBF核, 求解最优的参数σ和正规化参数γ是决定支持向量机分类优劣的关键.训练的实质是寻找出能够使分类精度最高的两个参数的组合.σ和γ对于支持向量机的分类有着非常重要的作用.对于如何选择合适的参数, 国内外学者已经作了很多研究, 这些优化方法包括网格寻优、遗传算法、粒子群算法等.最简单的方法是通过组合σ和γ, 然后利用网格寻优算法进行网络搜索, 将能够使精度最高的一个参数组合作为向量机的分类参数.该方法时以消耗时间为代价.后来学者提出梯度下降的方法来寻找最优的分类参数, 但该方法求导困难, 通用性不好.为了避免上述问题, 本文使用的最小二乘支持向量机对最优分类参数的寻找分为两步.1) 利用模拟退火算法[18]决定合适的参数集.2) 利用网格寻优算法对参数集寻找最合适的参数.模拟退火算法的效率已经被证实比多起点梯度下降算法高.在参数优化过程中, 利用训练样本集对该两种分类参数寻优, 交叉验证层数设为10, 相应的训练样本集被分为10组, 每组训练样本包含的合格磁瓦与含内部缺陷磁瓦的数量等同.分类器被训练10次, 保证了每个训练样本既作训练组, 又作测试组.由于邻域成分降维已经将数据类别分为较好的两类, 在第一步模拟退火算法中, 找出的网格寻优的初始值为σ=1, γ=2, 此时已经能够完全分类样本数据; 在进行第二步网格寻优算法时, 该初始值为最终优化值.由于该分类器只需要识别合格品与含内部缺陷样品, 合格磁瓦用+1标识, 含内部缺陷用-1标识.
为了测试提出方法的检测性能, 通常用受试者工件特性曲线(ROC)来评价某个分类方法的可靠性.ROC曲线通过构图法揭示敏感性(sensitivity)和特异性(specificity)的相互关系[19].通过连续的变量设定出多个不同的临界值, 计算出一系列敏感性和特异性, 以敏感性为纵坐标、特异性为横坐标, 绘制曲线.曲线面积越大, 诊断率越高.敏感性被称为真正率tpr(true positives rate), 特异性被称为假正率fpr(false positives rate).对于一个二分类问题, 将实例分为正类和负类, 如果一个实例是正类并且也被预测成正类, 即为真正类tp(true positive); 如果实例是负类被预测成正类, 称为假正类fp(false positive).相应地, 若实例是负类被预测成负类, 则称为真负类tn(true negative); 若正类被预测成负类, 则为假负类fn(false negative).
| $ {t_{{\rm{pr}}}} = \frac{{{t_{\rm{p}}}}}{{{t_{\rm{p}}} + {f_{\rm{n}}}}}, $ | (11) |
| $ {t_{{\rm{pr}}}} = \frac{{{f_{\rm{p}}}}}{{{f_{\rm{p}}} + {t_{\rm{n}}}}}. $ | (12) |
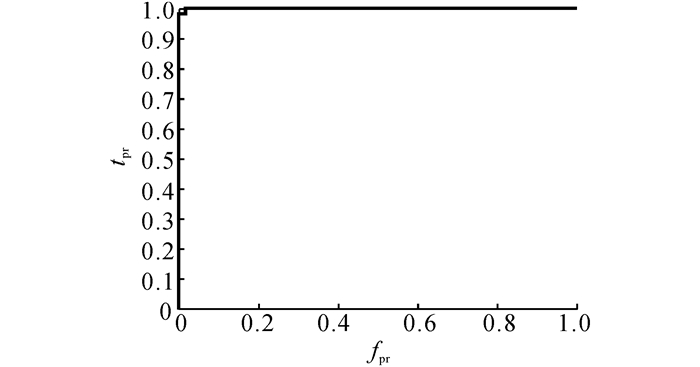
ROC曲线的结果如图 8所示.ROC曲线包含的面积越大, 越能表明该方法分类的可靠性.从图 8可以看出, 曲线包含的面积接近于1.提出的方法具有较高的可靠性, 能够应用于磁瓦内部缺陷检测.
|
图 8 ROC曲线图 Fig. 8 ROC curve |
为了验证该方法的可靠性与识别能力, 将提出的方法应用到另外两种类型的磁瓦中, 相应的识别率如表 1所示.可以看出, 该方法应用在3种类型的磁瓦上, 均可达到较高的准确率, 证实了提出方法的可靠性及分类的精确性.对比黄沁元等[6]提出的双谱分析方法可知, 双谱分析对磁瓦的几何尺寸敏感, 磁瓦几何尺寸越大, 分类精度越高, 检测结果如表 1所示.可知, 对A、B、C三种磁瓦内部缺陷的识别能力均不如提出方法.
| 表 1 2种算法的分类结果 Table 1 Classification results of two methods |
(1) 合格品与含内部缺陷磁瓦在归一化频谱下特征差异不明显, 不能够提取有效的特征参数.双树复小波包分解具有近似平移不变性、良好的方向选择性、完全重构性等特点, 利用该方法分解信号, 能够细化信号, 利于提取特征参数.
(2) 提取特定频段的能量、偏度、峭度、模糊熵作为特征, 能够有效地区别合格磁瓦与含内部缺陷磁瓦.
(3) 利用邻域成分分析方法降维, 能够保留原始特征信息, 提高分类精度和速度.
(4) 利用最小二乘支持向量机对磁瓦缺陷进行识别, 磁瓦分类准确率高于99%, 且分类速度快, 训练过程简单.
| [1] | LI X, JIANG H, YIN G. Detection of surface crack defects on ferrite magnetic tile[J]. NDT & E International, 2014, 62(2): 6–13. |
| [2] | WAGNER R, GONCALVES O, DEMMA A, et al. Guided wave testing performance studies: comparison with ultrasonic and magnetic flux leakage pigs[J]. Insight, 2013, 55(4): 187–196. DOI:10.1784/insi.2012.55.4.187 |
| [3] | MOHAMMAD R, AFZALNIA MR, HAMED F. Heat residual stress measurement of welded areas in steel pipes via magnetic particle testing[J]. Materials Evaluation, 2012, 70(6): 624–630. |
| [4] | SHKATOV P. Combining eddy-current and magnetic methods for the defectoscopy of ferromagnetic materials[J]. Nondestructive Testing and Evaluation, 2013, 28: 155–165. DOI:10.1080/10589759.2012.716436 |
| [5] | BAKNOV A S, KUROZAEV V P, KUDRYAVTSEV D A, et al. Increasing the reliability of magnetic-particle testing by means of a YMJIK-10 automated unit for magnetic fluorescent-penetrant inspection of pipe end faces[J]. Russian Journal of Nondestructive Testing, 2014, 40(5): 311–316. |
| [6] |
黄沁元, 殷鹰, 赵越, 等. 基于双谱分析的磁瓦内部缺陷音频检测方法[J].
四川大学学报:工程科学版, 2014, 46(5): 188–194.
HUANG Qin-yuan, YIN Ying, ZHAO Yue, et al. Acoustic inspection of internal defect in magnetic tile based on bispectrum analysis[J]. Journal of SichuanUniversity: Engineering Science, 2014, 46(5): 188–194. |
| [7] | BAYRAM I, SELESNICK I W. On the dual-Tree complex wavelet packet and M-Band transforms[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2298–2310. DOI:10.1109/TSP.2007.916129 |
| [8] | LO E H S, PICKERING M R, FRATER M R, et al. Image segmentation from scale and rotation invariant texture features from the double dyadic dual-tree complex wavelet transform[J]. Image and Vision Computing, 2011, 9(1): 15–28. |
| [9] |
李辉, 郑海起, 唐力伟. 基于双树复小波包峭度图的轴承故障诊断研究[J].
振动与冲击, 2012, 31(10): 13–18.
LI Hui, ZHANG Hai-qi, TANG Li-wei. Bearing fault diagnosis based on kurtogram of dual-tree complex wavelet packet transform[J]. Journal of Vibration and Shock, 2012, 31(10): 13–18. |
| [10] |
王娜, 郑德忠, 刘永红. 双树复小波包变换语音增强新算法[J].
传感技术学报, 2009, 22(7): 983–987.
WANG Na, ZHENG De-zhong, LIU Yong-hong. New method for speech enhancement based on dual tree complex wavelet packet transform[J]. Journal of Sensors and Actuators, 2009, 22(7): 983–987. |
| [11] | ZHOU H, CHEN J, DONG G, et al. Bearing fault recognition method based on neighbourhood component analysis and coupled hidden Markov model[J]. Mechanical Systems and Signal Processing, 2016, 66-67: 568–581. DOI:10.1016/j.ymssp.2015.04.037 |
| [12] | XU Q, WONG PK. Hysteresis modeling and compensation of a piezostage using least squares support vector machines[J]. Mechatronics, 2011, 21(7): 1239–1251. DOI:10.1016/j.mechatronics.2011.08.006 |
| [13] |
杨先勇, 周晓军, 张文斌, 等. 基于局域波法和KPCA-LSSVM的滚动轴承故障诊断[J].
浙江大学学报:工学版, 2010, 44(8): 1519–1524.
YANG Xian-yong, ZHOU Xiao-jun, ZHANG Wen-bin, et al. Rolling bearing fault diagnosis based on local wave method and KPCA-LSSVM[J]. Journal of Zhejiang University: Engineering Science, 2010, 44(8): 1519–1524. |
| [14] | SELESNICK I W, BARANIUK R G, KINGSBURY N G. The dual-tree complex wavelet transform[J]. IEEE Digital Signal Processing Magazine, 2005, 22(6): 123–151. DOI:10.1109/MSP.2005.1550194 |
| [15] |
胥永刚, 孟志鹏, 陆明. 基于双树复小波包变换的滚动轴承故障诊断[J].
农业工程学报, 2013, 29(10): 49–56.
XU Yong-gang, MENG Zhi-peng, LU Ming. Fault diagnosis of rolling bearing based on dual-tree complex wavelet packet transform[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(10): 49–56. |
| [16] |
胥永刚, 孟志鹏, 赵国亮, 等. 双树复小波包和谱峭度在齿轮故障诊断中的应用[J].
北京工业大学学报, 2014, 40(4): 488–494.
XU Yong-gang, MENG Zhi-peng, ZHAO Guo-liang, et al. Application of gear fault diagnosis based on dual-tree complex wavelet packet transform and spectral kurtosis[J]. Journal of Beijing University of Technology, 2014, 40(4): 488–494. |
| [17] |
郑近德, 程军圣, 杨宇. 基于改进的ITD和模糊熵的滚动轴承故障诊断方法[J].
中国机械工程, 2012, 23(19): 2372–2377.
ZHENG Jin-de, CHENG Jun-sheng, YANG Yu. A rolling bearing fault diagnosis method based on improved ITD and fuzzy entropy[J]. Chinese Mechanical Engineering, 2012, 23(19): 2372–2377. DOI:10.3969/j.issn.1004-132X.2012.19.021 |
| [18] | XAVIER-DE-SOUZA S, SUYKENS J A, VANDE-WALLE J, et al. Coupled simulated annealing[J]. IEEE Transactions on Systems, Man and Cybernetics: Part B, 2010, 40(2): 320–335. DOI:10.1109/TSMCB.2009.2020435 |
| [19] | FAWCETT T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861–874. DOI:10.1016/j.patrec.2005.10.010 |



