2. 浙江大学 信息与电子工程学院, 浙江 杭州 310027;
3. 浙江工业大学 计算机科学与技术学院, 浙江 杭州 310023;
4. University of California, Electrical Computer Engineering, CA Santa Barbara 93106, USA
2. College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou 310027, China;
3. College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China;
4. Electrical Computer Engineering, University of California, Santa Barbara, 93106, USA
片上网络(network-on-chip, NoC)在单一芯片中集成了数十、甚至数百个处理核心, 因此是解决不断增长的计算需求的有效方案之一[1-4].由于集成了大量的处理核心, 片上网络的硅片面积较大, 更易受到工艺偏差和制造缺陷的影响[5], 导致较低的良率[6].为了能在设计阶段优化片上网络的良率, 需要在早期设计阶段, 从系统层准确地评估片上网络的良率.
基于负二项分布[7]的良率评估方法可以用于绝大多数冗余单元较少的设计, 如MPSoCs(multi-processor system-on-chip).考虑到片上网络有较多的冗余单元, 可靠性较高, 评估片上网络时应当考虑设计中的冗余特性[8-11].换言之, 一个有缺陷器件的片上网络能够利用冗余单元正常工作, 因此片上网络的良率应该明显高于无缺陷片上网络的概率[12-16].
近年来的研究主要依靠蒙特卡洛(Monte Carlo, MC)仿真方法[17-19]来评估片上网络的良率或可靠性.由于单一器件的良率较高, 且片上网络设计中包含冗余单元, 使得片上网络的良率较高, 进而导致基于蒙特卡洛仿真方法[17]的良率评估仿真次数极大, 效率很低.
在蒙特卡洛仿真方法中, 各次仿真过程完全独立, 具有良好的并行性, 可以采用GPU并行执行的方法加速.GPU加速蒙特卡洛方法已经被广泛应用于不同的算法中, 如应用在医学图像处理[20]、物理模拟[21]、金融计算[21]、通信仿真[22]以及电路静态时序的统计分析[23]等.
本文将片上网络良率评估算法移植到GPU上, 利用GPU的并行计算能力, 加速蒙特卡洛仿真, 提高评估效率, 最终实现了10倍效率的提升.
本文提出的异构并行算法有以下两方面贡献.1) 本文完成了片上网络良率评估算法的GPU移植, 利用GPU的并行性, 极大地减小了评估算法的运行时间, 提升了评估效率.由于评估算法基于蒙特卡洛仿真方法, 该方法需要对大量、相互独立的随机样本进行仿真, 并行性较好, 因此利用GPU的并行特性, 能够获得较大的性能提升.2) 本文深入研究了蒙特卡洛方法中所需的随机数生成算法, 比较了CPU和GPU平台随机数生成的优劣, 总结出CPU更适合生成的随机数; 进一步挖掘了CPU和GPU之间的异构并行能力, 提出了异构并行算法.由于许多随机数生成算法, 前、后两个随机数之间具有依赖关系, 即后一个随机数的生成依赖于前一个随机数[24-25], 不具有并行性, 不利于GPU移植.本文提出的异构并行算法中, 随机数生成部分采用CPU平台, 确保了随机数的质量, 从而保证良率评估的准确度, 又不会影响算法的整体效率.
1 片上网络的良率模型以通用同构2D mesh拓扑的片上网络为例, 介绍良率模型, 如图 1所示.在该模型中, 一个片上网络由两类器件组成, 分别为:节点和互连.其中节点包含了一个处理核心及路由单元.每种器件有自身的良率, 记作Ynode和Ylink.各器件的无缺陷概率等于良率, 即Ynode或Ylink.

|
图 1 片上网络的良率模型 Fig. 1 Yield model of network-on-chip |
各器件只有两种可能的状态, 即有缺陷和无缺陷, 因此可以用伯努利(Bernoulli)分布描述器件的状态.对于任意一个器件, 器件状态可用随机变量Xi表示, 即Xi~B(1, Ydevice), 其中B()表示二项分布(伯努利分布的一般形式), Ydevice可以是Ynode或Ylink(取决于器件类型).Xi的概率质量函数f(Xi)的定义为
| $ f\left( {{X_i}} \right) = \left\{ \begin{array}{l} {Y_{{\rm{device}}}},{X_i} = 1;\\ 1 - {Y_{{\rm{device}}}},{X_i} = 0. \end{array} \right. $ | (1) |
对于整个片上网络中的所有p个器件, 可以使用多维随机变量X=[X1, X2, …, Xp]T描述p个器件的状态.f(X)=f(X1)·f(X2)…f(Xp)为X的概率质量函数.
由于片上网络具有较高的容错特性, Shamshiri等[17]将片上网络的良率定义为“有足够数量无缺陷节点的网络的概率”.其中, “足够数量”的具体数值由应用程序需求决定; “无缺陷节点”指节点和节点间的互连都需要“无缺陷”.满足这些条件的网络称为“连通”网络, 否则称为“不通连”网络.式(2) 定义了一个指示函数, 用于描述多维随机变量X的连通性.
| $ {I_\rm {f}}\left( \boldsymbol{X} \right) = \left\{ \begin{array}{l} 1,{\boldsymbol{X}}{\rm{对应连通网络}};\\ 0,{\boldsymbol{X}}{\rm{对应不连通网络}}. \end{array} \right. $ | (2) |
以图 1的片上网络为例, 解释连通性概念.如图 1所示, 片上网络的拓扑为3×4共12个节点, 假设应用程序需求9个无缺陷节点.网络中的各个器件会随机地出现缺陷, 如图 1(a)所示.图 1(b)~(d)分别表示3个不同的网络实例.图 1(b)中, 有多于9个无缺陷的节点, 因此是“连通”的; 图 1(c)中, 无缺陷节点的数量不足9个, 因此是“不连通”的; 图 1(d)中, 虽然有9个无缺陷节点, 但这些节点未连接在一起, 因此是“不连通”的.
如果能够穷举全部网络实例, 即穷举全部可能的多维随机变量X取值, 则片上网络的良率可以由下式计算:
| $ Y = \sum\limits_{\boldsymbol{X} = {{\left[ {0,0 \cdots ,0} \right]}^{\rm{T}}}}^{\boldsymbol{X} = {{\left[ {1,1 \cdots ,1} \right]}^{\rm{T}}}} {{I_{\rm{f}}}\left( \boldsymbol{X} \right)} f\left( \boldsymbol{X} \right). $ | (3) |
式中:Y为片上网络的良率, 从X=[0, 0, …, 0]T到X=[1, 1, …, 1]T的求和表示所有可能的X取值都需要计算.
2 片上网络良率评估算法按式(3) 穷举全部网络实例是不现实的, 通常情况下, 可以采用蒙特卡洛方法[26]计算式(3).蒙特卡洛方法的计算原理如下所示:
| $ {Y^{{\rm{MC}}}} = \frac{1}{N}\sum\limits_{n = 1}^N {{I_{\rm{f}}}\left( {{\boldsymbol{X}^{\left( n \right)}}} \right)} . $ | (4) |
式中:X(n)为f(X)的第n个样本.当样本总数N足够大时, If(X)的平均值YMC会收敛至实际的良率Y.
YMC的方差σ等于YMC(1-YMC)/N[27], 正比于1/N.根据数理统计理论[27]可知, 若需要95%的置信区间(即[YMC-1.96σ, YMC+1.96σ])和10%的置信度α=10%, 则样本容量N必须满足下式:
| $ N \ge \frac{{{{1.96}^2}}}{{{\alpha ^2}}}\frac{{\left( {1 - \sigma } \right)}}{\sigma }. $ | (5) |
式(5) 用作蒙特卡洛方法的停止条件.此外, 式(5) 可以用于估计完成蒙特卡洛方法所需的样本数量, 即N, 从而估计所需的运行时间.
2.1 异构并行评估算法分析式(4) 可知, 算法的实现需要解决2个环节:1) 生成随机样本X(n); 2) 分析样本X(n), 计算If(X(n)).前者生成样本需要用到随机数生成算法, 如LCG[24]、MT[25]算法, 算法复杂度为O(n)(n为样本X的维度); 后者分析样本, 可以将样本转化为图表示, 并遍历图, 得到最大无缺陷节点数量, 从而判断连通性, 算法复杂度为O(n2).由于后者分析样本是整个算法的性能瓶颈(算法复杂度高于前者), 本文提出的异构并行算法将分析样本部分移植到GPU实现加速.对于生成样本, 由于随机数生成算法的随机数之间具有一定依赖性, 即将前一个随机数作为种子, 产生下一个随机数, 如LCG[24]、MT[25]算法, 不利于GPU移植, 因此本文将随机数生成部分保留在CPU上执行.此外, 异构并行算法进一步挖掘CPU和GPU之间的并行性, 即本轮在GPU上执行的样本分析和下一轮在CPU上执行的生成样本没有数据依赖关系, 可以同时执行, 进一步提升算法效率.详细的算法如算法1所示.
算法1 片上网络良率评估算法-异构并行
1:初始化连通网络计数器cnt := 0
2:初始化样本容量N := 0
3:初始化样本数组sample[1…K] := 0
4:初始化连通性数组conn[1…K] := 0
5: for i = 1, 2, …, K do
6: sample[i] :=随机生成样本X
7: end for
8: repeat
9: 将sample数组从CPU传送到GPU
10: GPU for i = 1, 2, …, K do
11: 从sample[i]中取出样本X
12: 将样本X对应的网络实例转化为图表示, 并遍历此图, 记最大无缺陷节点数目为m
13: if m >=应用程序所需要节点数目
14: conn[i] := 1
15: end if
16: end for
17: CPU for i = 1, 2, …, K do
18: sample[i] :=随机生成样本X
19: end for
20: 等待GPU for和CPU for执行完成
21: 将conn数组从GPU传送到CPU
22: for i = 1, 2, …, K do
23: cnt := cnt + conn[i]
24: end for
25: N := N+K
26: 良率Y = cnt / N
27: until N满足式(5)
在算法1中, 步骤10)~16) 的GPU for部分实现了分析样本的GPU并行执行, 并行执行的线程数为K, 实现了评估算法的执行效率提升.另一方面, 步骤10)~16) 的GPU for和步骤17)~19) 的CPU for之间没有数据依赖, 因此可以同时执行, 仅需要在步骤20) 确定两者都完成执行.为了实现GPU for和CPU for两者的并行执行, 需要保证GPU for中分析的样本和CPU for中生成的样本不相同, 即没有数据依赖关系, 因此, 在算法最初的步骤5)~7) 预先生成了一组样本, 使得每次循环过程中, GPU for分析的是本轮迭代的样本, 而CPU for生成的是下一轮的样本.
该算法有以下三方面优势:1) 利用GPU的并行特性, 提升评估算法的效率; 2) 随机数生成在CPU上执行, 确保了随机数的质量; 3) GPU和CPU之间的异构并行, 保证了CPU上的随机数生成不会影响算法的整体效率.
2.2 CPU评估算法算法2给出CPU平台的评估算法.该算法与算法1在功能上完全等价, 因此两者结果的一致性会非常高.由于CPU平台的并行性较差, 该算法的运行时间远高于算法1, 效率非常低.
算法2 片上网络良率评估算法-CPU
1:初始化连通网络计数器cnt := 0
2:初始化样本容量N := 0
3: repeat
4: 随机生成样本X
5: 将样本X对应的网络实例转化为图表示, 并遍历此图, 记最大无缺陷节点数目为m
6: if m >=应用程序所需要节点数目
7: cnt := cnt+1
8: end if
9: N := N+1
10: 良率Y = cnt / N
11: until N满足式(5)
2.3 GPU评估算法给出完全使用GPU平台的评估算法.完全使用GPU平台的难点在于随机数生成算法不能直接并行化.针对该问题, 本节的算法使用多个随机数种子, 解决随机数生成并行化的问题.具体来说, 记GPU并行线程数为K, 在开始GPU计算之前, 预先准备K个随机数种子, 使K个并行线程能够同时执行.与之相比, 算法1中只需要1个随机数种子.详细算法如下.
算法3 片上网络良率评估算法-GPU
1:初始化连通网络计数器cnt := 0
2:初始化样本容量N := 0
3:初始化随机数种子数组seed[1…K] := 0
4:初始化连通性数组conn[1…K] := 0
5: repeat
6: for i = 1, 2, …, K do
7: seed[i] :=系统时间
8: end for
9: 将seed数组从CPU传送到GPU
10: GPU for i = 1, 2, …, K do
11: 以seed[i]为种子, 随机生成样本X
12: 将样本X对应的网络实例转化为图表示, 并遍历此图, 记最大无缺陷节点数目为m
13: if m >=应用程序所需要节点数目
14: conn[i] := 1
15: end if
16: end for
17: 将conn数组从GPU传送到CPU
18: for i = 1, 2, …, K do
19: cnt := cnt + conn[i]
20: end for
21: N := N+K
22: 良率Y = cnt / N
23: until N满足式(5)
算法3中的GPU并行部分为步骤10)~16), 即GPU for部分.与算法1相比, 算法3使用GPU生成随机数, 执行时间会略微增加, 但非常接近.另一方面, 算法3多次取系统时间作为随机数种子, 如步骤6)~8) 所示, 解决随机数算法难以并行化的问题.在多次取系统时间的过程中, 相邻两次之间的时间间隔不会有太大变化, 因此数组seed[1…K]的数据基本上是一个等差数列, 这会影响随机数的质量, 从而导致良率评估的准确度下降.
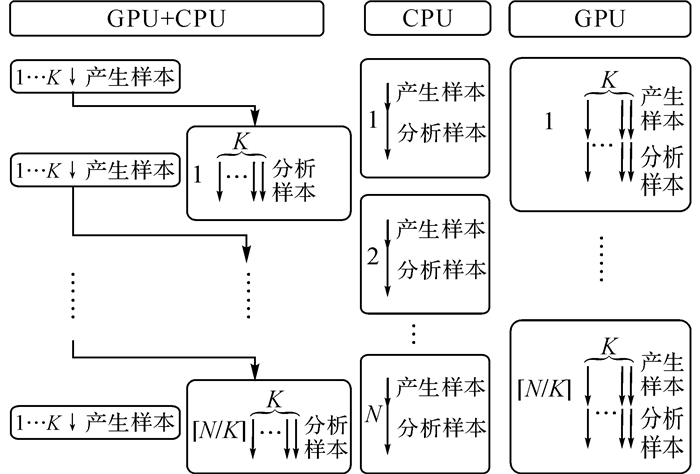
2.4 综合分析介绍了总共3种片上网络良率评估的算法, 分别是:CPU产生随机样本、GPU分析样本的异构并行算法(简记作GPU+CPU); CPU算法(简记作CPU); GPU算法(简记作GPU).3个算法的流程可以用图 2的示意图表示.
|
图 2 3种良率评估算法对比示意图 Fig. 2 Flow chart of three yield evaluation algorithms |
图 2中的左侧是异构并行GPU+CPU算法, 由于每次都有K个线程同时执行, 总共需要迭代
记在CPU上的单线程产生样本和分析样本的时间分别为TC_gen和TC_analy; 在GPU上的K线程产生样本和分析样本的时间分别为TG_gen和TG_analy.在图 2左侧的异构并行GPU+CPU算法中, 产生样本和分析样本分别同时运行在CPU和GPU上, 因此执行时间为max(KTC_gen, TG_analy); GPU算法或CPU算法执行时间分别为(TG_gen+TG_analy)和(TC_gen+TC_analy).3种算法的总时间可以用表 1描述.对于GPU+CPU算法中的额外开销KTC_gen, 由于
| 表 1 3种算法的运行时间比较 Table 1 Runtime comparison of three algorithms |
展示了3种不同算法的实验数据.实验平台使用的CPU为Intel i5 2.4 GHz; GPU为Intel Iris 5100 Graphics; GPU算法使用OpenCL实现, 并行执行线程数K=512, 该值与实验环境所使用的GPU最大并行线程数相等.假设应用程序所需求的节点数量为9.后文中的实验将使用不同的网络大小(拓扑大小)和不同的器件良率(Ynode和Ylink), 分析3种算法的优劣.
此外, 由于实验分析中片上网络的良率普遍较高, 能够达到99.9%以上, 实验中主要分析失效率, 即1-Y.
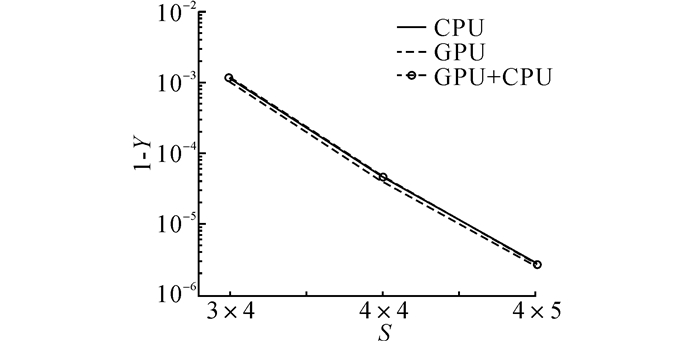
3.1 评估精确度分析首先将器件良率固定为0.98, 即Ynode=0.98, Ylink=0.98;然后改变网络大小, 观察3种算法的结果是否一致.实验结果如图 3所示, 图中,S为网络大小.
|
图 3 3种良率评估算法在不同网络大小下的准确度比较 Fig. 3 Accuracy comparison of different network size |
如图 3所示, 3种算法的评估结果总体来看比较一致, 3条线基本都紧靠在一起.其中GPU算法的结果偏差比较明显, 比另2种算法的结果偏小.以具体数据来说, 在4×4网络下, GPU算法的结果为3.936 768×10-5, 而CPU算法和GPU+CPU算法的结果分别为4.784×10-5和4.662 408×10-5, GPU算法的相对误差达到17.7%.可见, GPU产生的随机数质量较低的问题, 已经达到了影响蒙特卡洛评估结果的程度.
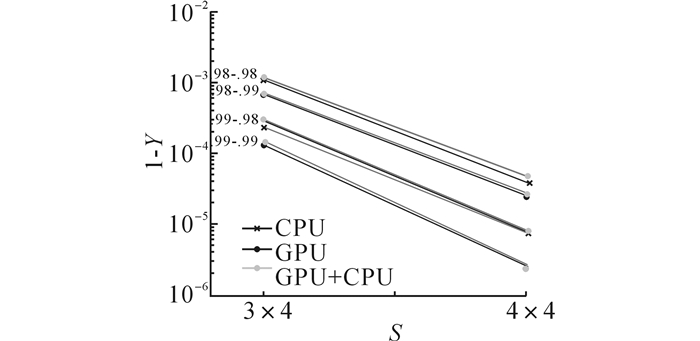
观察不同器件良率下的3种算法结果, 具体选择了4种Ynode和Ylink结合, 实验结果如图 4所示.图中, “.9x-.9y”的标记表示Ynode=0.9x, Ylink=0.9y, 例如“.98-.99”的标记表示Ynode=0.98, Ylink=0.99.
|
图 4 3种良率评估算法在不同器件良率下的准确度比较 Fig. 4 Accuracy comparison of different device yield |
如图 4所示, 在该组实验结果中, GPU算法结果的偏小显现更明显:在3×4网络下, “.99-.98”和“.99-.99”明显偏小; 在4×4网络下, “.99-.98”明显偏小.可以总结出:GPU不适合产生随机数, 特别是在用于蒙特卡洛分析这类对随机数质量有一定要求的环境.
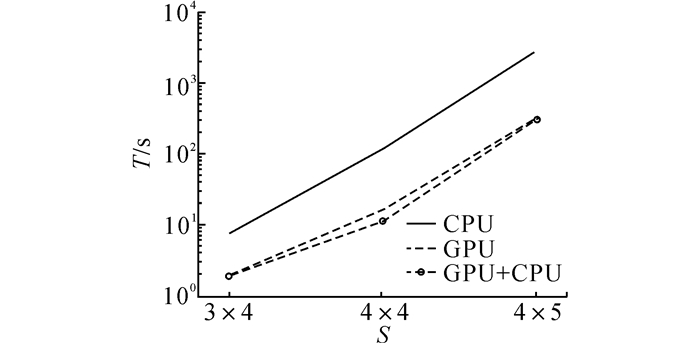
3.2 评估效率分析将器件良率固定为0.98, 即Ynode=0.98, Ylink=0.98;改变网络大小, 观察3种算法的运行时间T.实验结果如图 5所示.
|
图 5 3种良率评估算法在不同网络大小下的运行时间比较 Fig. 5 Runtime comparison of different network size by using three evaluation algorithms |
当网络较小时, 如3×4网络, 因为CPU算法的运行时间较小(约10 s), GPU和GPU+CPU的加速效果不是非常明显, 仅有5倍左右.当网络变大, 如4×5网络, CPU算法的时间需要近1 h.此时的GPU和GPU+CPU加速效果较显著, 仅需要5 min左右, 加速比大约为10倍.
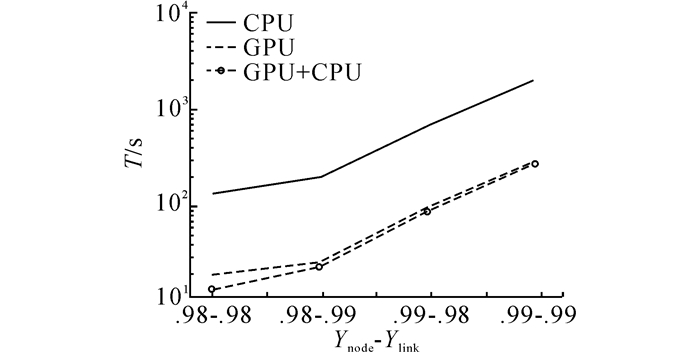
将网络大小固定为3×4, 观察不同器件良率下的3种算法结果, 具体选择了4种Ynode和Ylink结合, 实验结果如图 6所示.图 6中, “.9x-.9y”的标记与图 4相同, 表示Ynode=0.9x, Ylink=0.9y.
|
图 6 3种良率评估算法在不同器件良率下的运行时间比较 Fig. 6 Runtime comparison of different device yield by using three evaluation algorithms |
在不同器件良率下, GPU和GPU+CPU加速比基本上都保持在10倍左右, 无论是在网络良率较低时(即较小的Ynode和Ylink), 如“.98-.98”, 还是在网络良率较高时, 如“.99-.99”.
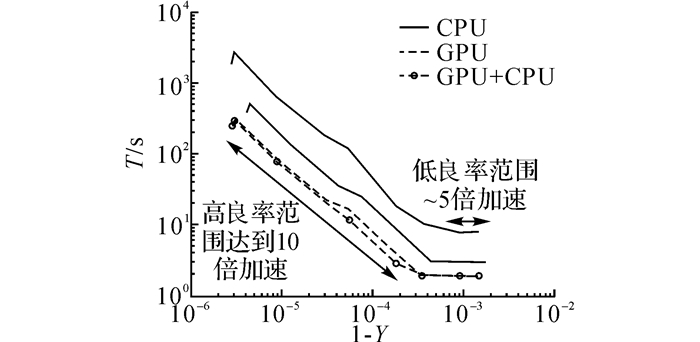
3.3 加速比分析综合图 5、6可以看出, 采用GPU算法和GPU+CPU算法的加速比似乎为一个定值.将全部数据样本点, 包括不同网络大小(3×4, 4×4, 4×5) 和不同器件良率(各种Ynode和Ylink的组合)的结果, 绘制在一张图上, 如图 7所示.
|
图 7 不同良率下的加速比分析 Fig. 7 Speedup under different scenarios |
分析图 7可见, CPU算法与GPU算法和GPU+CPU算法之间的间隔基本上是固定的, 大约为10倍, 因此GPU和GPU+CPU的加速比大约为10倍.在低良率下, 即1-Y=10-3附近, GPU和GPU+CPU的曲线变得平坦, 加速比略有降低, 约为5倍, 这一范围对应网络较小(3×4网络)的情形.加速比的降低不影响GPU和GPU+CPU的高效率, 因为在该范围内, 无论是CPU还是GPU或GPU+CPU都能在数秒内完成良率评估(GPU和GPU+CPU 2 s, CPU 8~10 s), 运行时间较短, 一般不需要担心评估效率的问题.
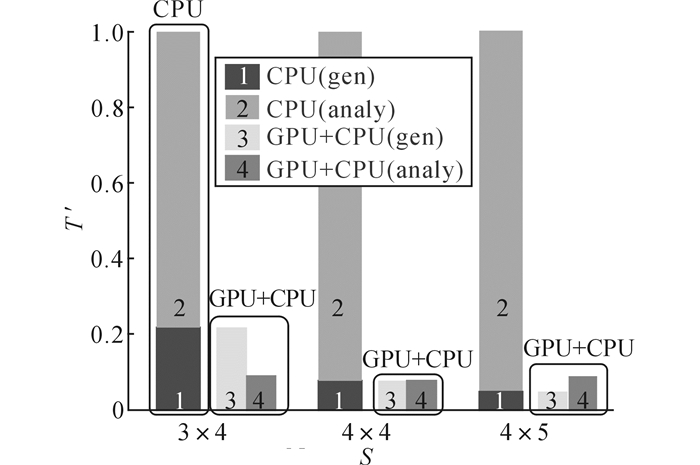
算法整体包含2个主要阶段:样本随机生成阶段和样本分析阶段.选用3种不同的网络(3×4, 4×4, 4×5), 将器件良率固定为0.98, 即Ynode=0.98, Ylink=0.98, 进一步分析整体加速比的瓶颈.首先将算法中的2个阶段, 样本生成阶段和样本分析阶段, 分别记作gen和analy; 然后将CPU+GPU算法中两个阶段的执行时间以CPU算法的总执行时间作归一化, 结果如图 8所示.图中,T′为归一化的运行时间.
|
图 8 异构并行算法中样本生成阶段和样本分析阶段 Fig. 8 Sample generation phase and sample analysis phase |
在GPU+CPU算法中, 生成阶段(gen)和分析阶段(analy)分别同时运行在CPU和GPU上, 瓶颈为两者中的时间较大者.如图 8所示, CPU算法的总运行时间为gen和analy的累加(如图 8中1与2所示), GPU+CPU算法的gen和analy是平行进行的(如图 8中3与4所示), 总时间为两者中的时间较大者.
分析图 8可知, GPU+CPU算法的瓶颈会随着网络大小的改变而变化.当网络较大时(如图 8的4×5网络所示, 对应片上网络的良率较高), 样本分析时间(analy)大于样本生成时间(gen), 即表 1公式max(KTC_gen, TG_analy)中TG_analy > KTC_gen, 此时的瓶颈是GPU上的样本分析, 因此加速比由GPU决定.当网络较小时(如图 8的3×4网络, 对应片上网络良率较低时), 样本分析时间(analy)小于样本生成时间(gen), 即表 1公式max(KTC_gen, TG_analy)中KTC_gen > TG_analy, 此时算法的瓶颈不再是GPU上的样本分析, 而是CPU上的样本生成, 因此降低了低良率范围内的整体加速比, 即图 7中的低良率范围加速比.
观察图 8中的4×4与4×5网络, 即性能瓶颈在GPU的情形可以发现, CPU+GPU算法都能够保持10倍左右的加速比.通过控制GPU上的并行线程数量, 观察加速比与GPU并行容量之间的关系.在本文的实现环境中, GPU的最大线程数量K=512, 使K=256、128, 观察4×4网络下, Ynode=0.98, Ylink=0.98的加速比变化, 结果如表 2所示.表中,T1为CPU算法的运行时间,T2为GPU+CPU算法的运行时间,P为加速比.
| 表 2 不同并行线程数量下的加速比 Table 2 Speedup under different number of parallel threads |
分析表 2可知, 随着K从512降至256和128, 加速比随之降至约1/2和1/4.可见, 加速比和GPU并行线程数量基本呈线性关系.表 1公式中, 当瓶颈在GPU, 且
本文以片上网络的良率评估为背景, 研究蒙特卡洛算法的GPU加速技术.在将该算法移植到GPU的过程中, 分析随机数生成算法GPU移植的优劣, 总结出CPU更适合随机数生成算法, 提出CPU与GPU异构并行的良率评估算法.实验数据显示, 采用异构并行算法能够在保证评估准确度的前提下, 减少10倍的运行时间, 极大地提升了良率评估的效率.
| [1] | MARCULESCU R, OGRAS U Y, PEH L S, et al. Outstanding research problems in NoC design: system, microarchitecture, and circuit perspectives[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2009, 28(1): 3–21. DOI:10.1109/TCAD.2008.2010691 |
| [2] | BELL S, EDWARDS B, AMANN J, et al. TILE64 processor: a 64-Core SoC with mesh Interconnect [C]//IEEE International Solid-State Circuits Conference-Digest of Technical Papers. San Francisco: IEEE, 2008. |
| [3] | VANGAL S, HOWARD J, RUHL G, et al. An 80-Tile 1.28TFLOPS network-on-chip in 65nm CMOS [C]//IEEE International Solid-State Circuits Conference-Digest of Technical Papers. San Francisco: IEEE, 2007. |
| [4] |
全励, 程爱莲, 潘赟, 等. 基于旁路通道的片上网络差别型服务实现方法[J].
浙江大学学报:工学版, 2013, 47(6): 957–968.
QUAN Li, CHENG Ai-lian, PAN Yun, et al. Bypassed channels based differentiated service implementation method for network-on-chip[J]. Journal of Zhejiang University: Engineering Science, 2013, 47(6): 957–968. |
| [5] | KOREN I, KOREN Z. Defect tolerance in VLSI circuits: techniques and yield analysis[J]. Proceedings of IEEE, 1998, 86(9): 1819–1838. DOI:10.1109/5.705525 |
| [6] | KAHLE J A, DAY M N, HOFSTEE H P, et al. Introduction to the cell multiprocessor[J]. IBM Journal of Research and Development, 2005, 40((4.5): 589–604. |
| [7] | YANG Y, SHI Z, YU J, et al. Evaluating performance of manycore processors with various granularities considering yield and lifetime reliability [C]//IEEE International Symposium on Circuits and Systems. Seoul: IEEE, 2012. |
| [8] | CHEN Y Y, UPADHYAYA S J. Yield analysis of reconfigurable array processors based on multiple-level redundancy[J]. IEEE Transactions on Computers, 1993, 42(9): 1136–1141. DOI:10.1109/12.241602 |
| [9] | MICHALKA T L, VARSHNEY R C, MEINDL J D. A discussion of yield modeling with defect clustering, circuit repair, and circuit redundancy[J]. IEEE Transactions on Semiconductor Manufacture, 1990, 3(3): 116–127. DOI:10.1109/66.56568 |
| [10] | BREUER M A. Trading off area, yield and performance via hybrid redundancy in multi-core architectures [C]//IEEE VLSI Test Symposium. Berkeley: IEEE, 2013. |
| [11] | PHAM D, ASANO S, BOLLIGER M, et al. The design and implementation of a first-generation CELL processor: a multi-core SoC [C]//International Conference on Integrated Circuit Design and Technology. Austin: IEEE, 2005. |
| [12] | CHOUDHURY A D, PALERMO G, SILVANO C, et al. Yield enhancement by robust application-specific mapping on network-on-chips [C]//NoCArc. New York: IEEE, 2009. |
| [13] | KHALILINEZHAD S H, REZA A, RESHADI M. Yield modeling and yield-aware mapping for application specific networks-on-chip [C]//NORCHIP. Lund: IEEE, 2011. |
| [14] | KOLOGESKI A, CONCATTO C, MATOS D, et al. Combining fault tolerance and serialization effort to improve yield in 3D Networks-on-Chip [C]//IEEE International Conference on Electronics, Circuits, and Systems. Abu Dhabi: IEEE, 2013. |
| [15] | PALESI M, KUMAR S, CATANIA V. Leveraging partially faulty links usage for enhancing yield and performance in networks-on-chip[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2010, 29(3): 426–440. DOI:10.1109/TCAD.2010.2041851 |
| [16] | RODRIGO S, HERNANDEZ C, FLICH J, et al. Yield-oriented evaluation methodology of network-on-chip routing implementations [C]//International Symposium on System-on-Chip. Tampere: IEEE, 2009. |
| [17] | SHAMSHIRI S, CHENG K T. Modeling yield, cost, and quality of a spare-enhanced multicore chip[J]. IEEE Transactions on Computers, 2011, 60(9): 1246–1259. DOI:10.1109/TC.2011.32 |
| [18] | SHAMSHIRI S, CHENG K T. Yield and cost analysis of a reliable NoC [C]//IEEE VLSI Test Symposium. Washington: IEEE, 2009. |
| [19] | SHAMSHIRI S, CHENG K T. Modeling yield, cost, and quality of an NoC with uniformly and non-uniformly distributed redundancy [C]//IEEE VLSI Test Symposium. Santa Cruz: IEEE, 2010. |
| [20] |
解聪, 雷辉, 徐星, 等. 基于并行欧式距离变换的三维障碍距离场计算[J].
浙江大学学报:工学版, 2014, 48(2): 360–367.
XIE Cong, LEI Hui, XU Xing, et al. Computing 3D distance fields with obstacles based on parallel Euclidean distance transform[J]. Journal of Zhejiang University: Engineering Science, 2014, 48(2): 360–367. |
| [21] |
巨涛, 朱正东, 董小社. 异构众核系统及其编程模型与性能优化技术研究综述[J].
电子学报, 2015, 43(1): 111–119.
JU Tao, ZHU Zheng-dong, DONG Xiao-she. The feature, programming model and performance optimization strategy of heterogeneous many-core system: a review[J]. Acta Electronica Sinica, 2015, 43(1): 111–119. |
| [22] |
党青青. 基于GPU的通信仿真加速方法研究[D]. 北京: 北京邮电大学, 2015.
DANG Qing-qing. The research of acceleration methods in communication simulation based on GPU [D]. Beijing: Beijing University of Posts and Telecommunications, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10013-1015585681.htm |
| [23] |
马海晨. 基于GPU的EDA加速技术[D]. 上海: 复旦大学, 2011.
MA Hai-chen. EDA acceleration techniques based on GPU [D]. Shanghai: Fudan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10246-1011194849.htm |
| [24] | KNUTH D E. Seminumerical algorithms, Vol. 2 of the art of computer programming[M]. 3rd ed. Boston: Wesley, 1981: 763-767. |
| [25] | MATSUMOTO M, NISHIMURA T. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator[J]. ACM Transactions on Modeling and Computer Simulation, 1998, 8(1): 3–30. DOI:10.1145/272991.272995 |
| [26] | ROBERT C, GEORGE C. Monte Carlo statistical methods[M]. 2nd ed. New York: Springer, 2004: 325-330. |
| [27] | SHAO J. Mathematical statistics[M]. 2nd ed. New York: Springer, 2003: 524-530. |



