潮流能作为一种清洁的可再生能源, 以其能流密度大、可预测性强等优点受到越来越多的重视.振荡式水翼是潮流能转换装置的一种, 核心为水翼, 水翼水动力性能直接影响系统的能量捕获效率.
McKinney等[1]首次提出应用振荡翼捕获流体动能的概念, 通过理论和实验证明了振荡翼具有较高的捕能效率; Plater等[2-3]通过数值和试验研究流体自诱导振荡翼发电装置; Zhu等[4-5]研究层流下需要控制俯仰运动的半自动系统模型和流体诱导的不稳定自维持系统模型; Simpson[6]通过对水翼施加正弦的俯仰运动和升沉运动来得到正弦的有效攻角, 并在试验槽中对NACA0012翼型进行试验, 结果表明, 当振荡频率标准化为折算频率时, 尾迹漩涡的结构与振荡幅值有关.Xiao等[7]通过改变参数β及Lu等[8]通过改变参数K, 研究非正弦的俯仰/升沉运动对系统捕能效率的影响.
Kinsey等[9-12]通过建立单水翼和并联配置的双水翼运动模型以及对模型进行二维和三维网格划分, 分析运动参数、几何参数和黏性参数对简谐振荡翼能量提取性能的影响; 将2 kW振荡水翼发电原型机的实验结果与数值模拟结果进行对比.
振荡式水翼捕获潮流能系统浅海优势明显, 振荡水翼技术的低速性能好、启动流速低, 能够获得较高的捕能效率, 适合我国海域平均流速较低的特点.本文基于双水翼耦合振荡模型, 应用Fluent进行CFD模拟, 分析不同参数下系统的水动力特性、捕能性能和稳定性, 给出系统设计参数的推荐值, 为以后的工程设计提供一定价值的参考.
1 双水翼理论概述 1.1 运动模型利用水翼在来流中的俯仰-升沉振荡捕获潮流能, 并通过液压式能量转化系统将升沉动能转化为液压马达的旋转动能, 再转化为电能, 实现利用潮流能发电[13].
双水翼耦合振荡为两个水翼按简谐规律作同步的俯仰运动θ(t)和升沉运动y(t), 如图 1所示, 建立数学模型如下.
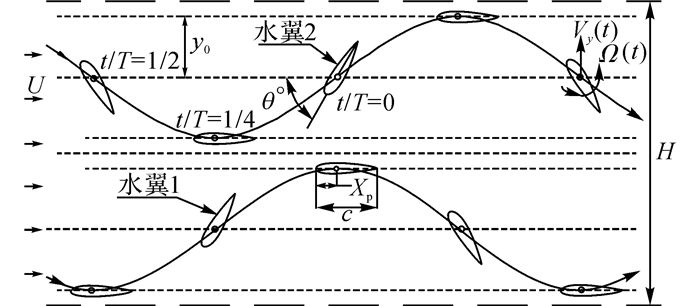
|
图 1 双水翼运动模型图 Fig. 1 Position relationship of dual-oscillating hydrofoils over one cycle (Φ=90°) |
| $ {\theta _1}\left( t \right) = {\theta _0}\sin \left( {\omega t} \right). $ | (1) |
| $ {y_1}\left( t \right) = {y_0}\sin \left( {\omega t + \frac{\phi }{{180}}\pi } \right). $ | (2) |
| $ {\theta _2}\left( t \right) = {\theta _0}\cos \left( {\omega t} \right). $ | (3) |
| $ {y_2}\left( t \right) = {y_0}\cos \left( {\omega t + \frac{\phi }{{180}}\pi } \right). $ | (4) |
式中:θ0和y0分别为水翼运动的俯仰振幅和升沉振幅, Ω(t)为水翼的俯仰角速度, Vy(t)为水翼的升沉运动速度, ω为角频率(2πf), ϕ为水翼升沉运动与俯仰运动的相位差.本文研究对称翼型, ϕ采用固定值90°, 稳定来流速度为U∞.
1.2 效率分析振荡水翼从来流捕获能量由升沉运动捕获功率PL(t)=L(t)Vy(t)和俯仰运动捕获功率PM(t)=M(t)Ω(t)两部分组成, 定义时均功率系数
| $ \overline {{C_\rm{P}}} = \overline {{C_{\rm{PL}}}} + \overline {{C_{\rm{PM}}}} = \frac{1}{T}\int_0^1 {\left\{ {{C_\rm{L}}\left( t \right)\frac{{{V_y}\left( t \right)}}{{{U_\infty }}} + {C_\rm{M}}\left( t \right)\frac{{\mathit{\Omega} \left( t \right)c}}{{{U_\infty }}}} \right\}} {\text{d}}t. $ | (5) |
式中:
在水翼运动过程中, 有效攻角影响水翼水动力特性和捕能效率, 计算攻角时的等效速度为来流流速与水翼升沉运动的和速度:
| $ {V_{\rm{e}}}\left( t \right){\rm{ = }}\sqrt {U_\infty ^2{\rm{ + }}V_y^2\left( t \right)} , $ |
即
| $ \alpha \left( t \right){\rm{ = }}\arctan ({\rm{ - }}{V_y}\left( t \right)/{U_\infty }){\rm{ - }}\theta \left( t \right). $ | (6) |
对于二维双振荡翼, 扫掠面积S为两水翼运动过程垂直方向运动的幅值H, 则水翼从来流捕获能量的总效率为
| $ \eta {\rm{ = }}\bar P{\rm{/}}\left( {\frac{1}{2}\rho U_\infty ^3S} \right){\rm{ = }}\overline {{C_{\rm{P}}}} \frac{c}{H}. $ | (7) |
为了综合评价振荡水翼的阻力特性对系统可靠性的影响及系统的能量捕获特性, 引入效率时均阻力系数比ψ, 即
| $ {\rm{\psi = \eta }}/\overline {{C_{\rm{D}}}} . $ | (8) |
式中:
采用有限体积法ANSYS Fluent求解绕二维振荡翼非定常雷诺-时均方程(URANS).
湍流模型:计算采用S-A湍流模型.该模型适用于墙壁束缚流动, 对模型网格粗糙带来的数值误差不敏感.
数值计算:采用PISO!方法进行压力速度耦合分析, 动量的离散为二阶迎风格式, 时间离散采用一阶隐式格式, 流场求解器采用基于压力的分离求解算法, 残差的绝对收敛标准为0.000 01.
网格模型:采用完全非结构化网格, 如图 2所示.圆形内部流体域与壁面作同步的升沉-俯仰运动, 核心计算区域网格单独加密, 外部流体域只受滑移交界面升沉运动的影响.
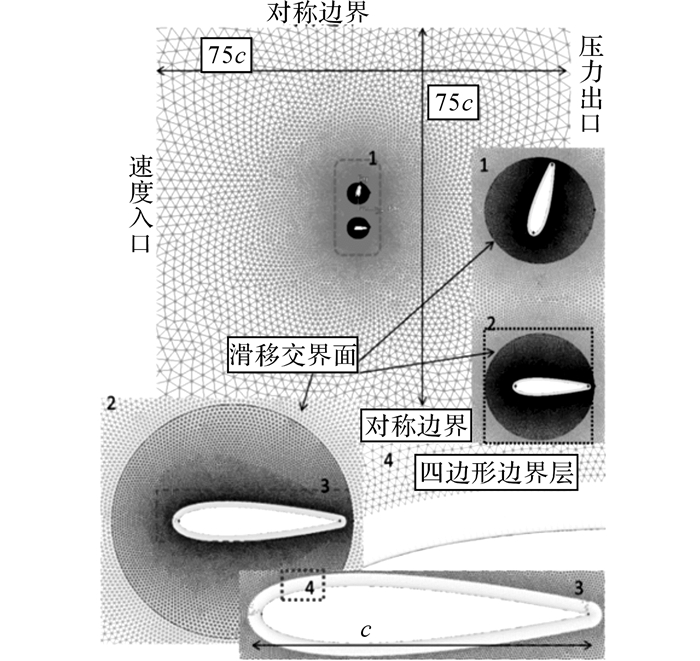
|
图 2 双水翼网格模型 Fig. 2 Mesh model of dual-hydrofoils |
通过改变翼型上的节点数量、边界层厚度、尺寸增长率等来保证网格质量[14].通过用户自定义函数(UDF)来控制网格边界的运动规律[15].
为了验证提出的运动模型及数值模拟方法的正确性, 在与文献[9]相同的参数条件下进行验证.如表 1所示为相应的数值计算结果.表中,
| 表 1 双水翼系统数值计算结果验证 Table 1 Comparison of dual-hydrofoils numerical resultsbetween reference and validation |
为了研究翼型的相对厚度对双水翼捕能性能的影响, 选用5种典型的对称水翼翼型(NACA0009、NACA0012、NACA0015、NACA0018和NACA0020) 进行对比.为了使翼型的相对厚度对系统捕能特性的影响具有广泛的适用性, 设置3组升沉振幅分别为y0/c=0.5、y0/c=1和y0/c=1.5, 以及两组折算频率和俯仰振幅方案1和方案2, 如表 2所示.
| 表 2 不同参数下双水翼系统时均功率系数的计算结果(方案1:f*=0.08, θ0=75°; 方案2:f*=0.16, θ0=60°) Table 2 Time-averaged power coefficient versus different parameters(Case1: f*=0.08, θ0=75°; Case2: f*=0.16, θ0=60°) |
在升沉振幅、折算频率和俯仰振幅一定的情况下, 双水翼系统的时均功率随着翼型厚度的增加而增大, 当翼型厚度为18%弦长时, 水翼的时均功率系数达到最大值.比较每种升沉振幅下的方案1和方案2可知, 当升沉振幅一定时, 水翼翼型对时均功率的影响随折算频率及俯仰振幅的改变而不同; 在方案1中, 翼型对时均功率的影响较大, 而在方案2中, 翼型的厚度对时均功率的影响较小.比较表 2的时均效率系数可知, 在各项运动参数下, NACA0018翼型的捕能性能较好.为了阐明翼型厚度对水动力特性的影响, 进一步分析不同水翼翼型在运动过程中的漩涡结构图及升力系数曲线.
不同翼型厚度下, 水翼1和水翼2的漩涡结构如图 3所示, 折算频率为0.16, 俯仰振幅为60°.NACA0018翼型的边界层均匀的分布在2个水翼的壁面, 随着水翼的俯仰运动向后绕流形成尾流, 逐渐与水翼分离, 且升力系数曲线比较平滑, 因此水动力特性较好.NACA0012和NACA0015与NACA0018翼型的漩涡特性相似, 因此升力系数曲线的趋势基本一致, 边界层厚度的差异导致升力系数曲线的极值不同; NACA0009翼型的水翼1和水翼2的壁面均发生漩涡的产生及脱落现象.水翼2的前缘漩涡在3T/8时重新附着在水翼的尾部, 造成水动力的突变, 升力系数曲线随之发生较大的改变(见图 4), 因此NACA0009翼型的水动力特性较差.在以后的研究中, 均采用捕能性能和水动力特性较好的NACA0018翼型.
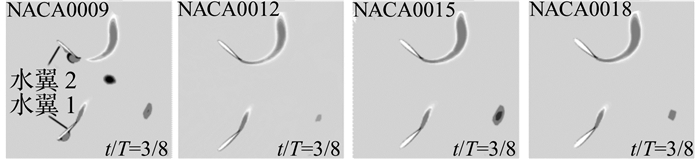
|
图 3 3T/8时刻不同水翼翼型的漩涡结构图(f*=0.16, θ0=60°) Fig. 3 Vortex structure of different foils at 3T/8 (f*=0.16, θ0=60°) |

|
图 4 不同翼型下水翼2的升力系数曲线(f*=0.16, θ0=60°) Fig. 4 Lift coefficient curve of foil 2 versus different foils (f*=0.16, θ0=60°) |
由式(7) 可知, 振荡水翼的捕能效率与时均功率系数呈正相关, 与升沉振幅呈负相关.如图 5所示为不同折算频率下, 水翼的时均功率系数与能量提取效率随着升沉振幅的变化折线图.当折算频率为0.04时, 水翼的时均功率系数随着升沉振幅的增大而增大, 能量提取效率随着升沉振幅的增加而增加, 但增加的幅度较小; 在相同的振荡频率和升沉振幅下, 水翼的时均功率系数和捕能效率随着俯仰振幅的增加而减小, 如图 5(a)所示.
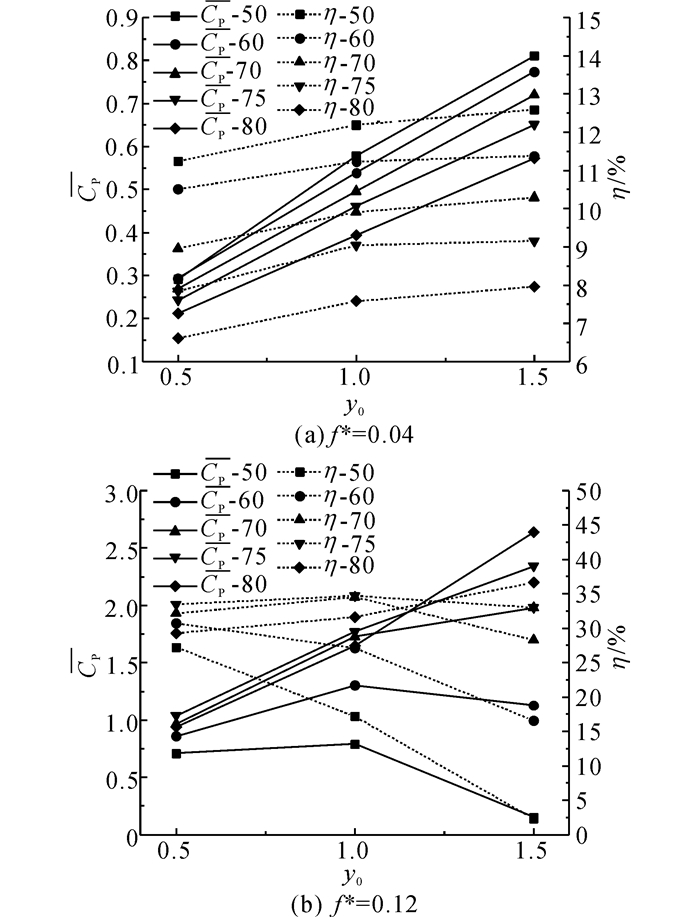
|
图 5 时均功率系数与捕能效率随升沉振幅变化折线图 Fig. 5 Time-averaged power coefficient and energy extraction efficiency versus heaving amplitude |
图 5(b)中, 当折算频率为0.12时, 在俯仰振幅为50°和60°时, 时均功率系数随升沉振幅的增加先小幅增加, 然后出现降低的趋势.水翼的能量提取效率随升沉振幅的增加而逐渐降低, 且降幅较大; 在大的俯仰振幅70°~80°下, 水翼的时均功率系数随升沉振幅的增加有较大的增幅, 与图 5(a)中时均功率系数的变化趋势相似, 但能量提取效率不再呈单一的变化趋势.图 5表明, 在不同的俯仰振幅和振荡频率下, 升沉振幅对水翼的能量提取性能影响不同.为了阐明升沉振幅对振荡水翼系统能量提取性能的影响机理, 进一步分析水翼在运动过程中攻角的变化.如图 6所示为不同运动参数下双水翼运动过程中攻角的变化曲线.
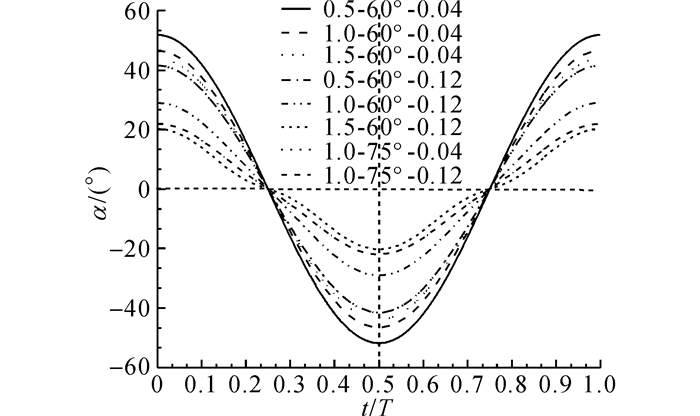
|
图 6 典型折算频率下不同升沉振幅攻角曲线变化曲线 Fig. 6 Angle of attack versus typical heaving amplitude and reduced frequency |
当折算频率为0.04时, 水翼的攻角极值较大.当水翼在运动过程中攻角超过失速角时, 会使水翼的升力特性变差, 水翼的能量提取效率降低.当水翼的振荡频率较小时, 水翼在运动过程中的速度较小, 升沉振幅所引起式(6) 中-Vy(t)/U∞的变化较小, 使得攻角的变化较小, 因此水翼的升沉振幅对攻角曲线的极值改变较小.增大升沉振幅降低了水翼攻角的极值, 改善了水翼的能量提取性能, 但由于水翼的捕能效率与升沉振幅成反比, 所以增大升沉振幅不能显著提高水翼的捕能效率.如图 6所示, 随着频率的增大, 升沉振幅的增加引起水翼运动的速度变化增大.当f*=0.12时, 增大升沉振幅, 使得式(10) 中-Vy(t)/U∞有较大的极值, 水翼在运动过程中攻角极值有较大幅度的降低, 相应条件下水翼的时均功率系数明显提高.此时, 时均功率系数和捕能效率不再随俯仰振幅的增大而呈递减的趋势.增大水翼的俯仰振幅不一定会降低系统能量提取效率.为了在获得较高的捕能效率的同时, 使双水翼系统具有良好的水动力性能, 应使振荡水翼在合适的升沉振幅下工作.
3.3 俯仰运动参数为了进一步分析俯仰运动参数对振荡水翼能量提取效率及水动力性能的影响, 在不同的升沉振幅下, 分析水翼俯仰振幅及振荡频率对双水翼系统的捕能特性的影响.如图 7所示为当y0=c时, 不同的俯仰振幅下, 水翼的捕能效率随折算频率变化的折线图.

|
图 7 捕能效率随折算频率变化折线图(y0=c) Fig. 7 Energy extraction efficiency versus reduced frequency(y0=c) |
在小的振荡频率下, 水翼的俯仰振幅对水翼的能量捕获效率影响较小, 且俯仰振幅越大, 水翼的能量捕获效率越小; 随着频率的增加, 俯仰振幅对捕能效率的影响增大.水翼在不同振幅下都对应一个最优频率, 最优频率下水翼的捕能效率最高.在折算频率达到最优频率之前, 水翼的能量提取性能随着折算频率的增加而提高, 当振荡频率超过最优频率后, 水翼的捕能效率随着频率的增加而下降, 较小的俯仰振幅对应的最优频率较低.当俯仰振幅为75°~80°, 0.16<f*<0.20时, 水翼的捕能性能较好, 最高捕能效率可达43.18 %.
在运动过程中, 水翼受力的变化是水翼水动力性能的直接体现.如图 8所示为当升沉振幅y0=c时, 部分运动参数下水翼的瞬时功率系数CP、俯仰力矩捕获的瞬时功率系数CPθ、升沉速度与来流速度的比值及瞬时升力系数与俯仰力矩系数曲线.
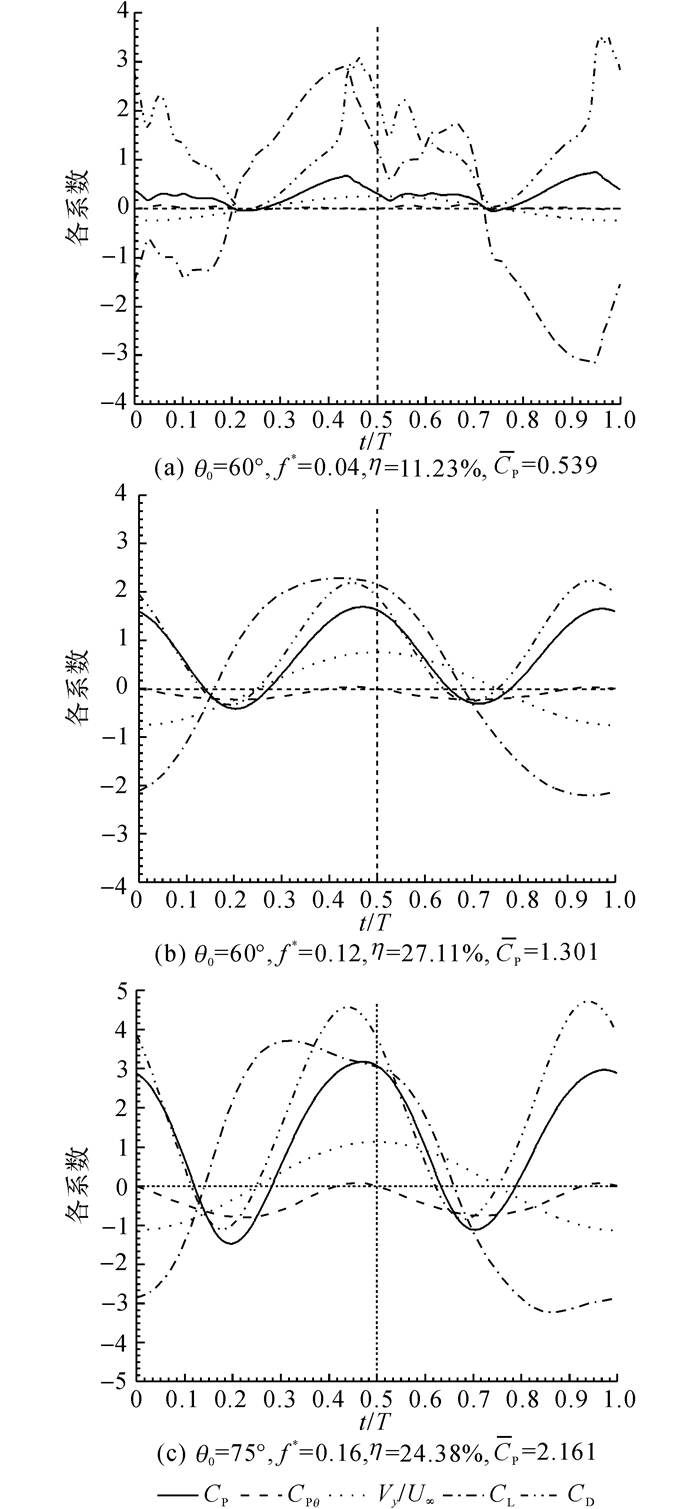
|
图 8 典型运动参数下水翼2各力系数及功率系数变化曲线 Fig. 8 Force coefficient and power coefficient of foil 2 under typical motion parameters |
如图 8(a)所示, 当俯仰振幅为60°, 折算频率为0.04时, 水翼在最大攻角时刻附近, 即周期起点及T/2处, 各力系数曲线有较大的波动, 此时水翼的水动力性能较差; 当水翼的振荡频率较大(见图 8(b), 折算频率为0.12) 时, 水翼的最大攻角降低, 攻角未超过失速角, 此时水翼具有良好的水动力性能, 各系数曲线比较平滑.
如图 9所示为与图 8相对应参数下不同时刻的漩涡结构图.图 9(a)中, 在T/4时刻水翼1前缘产生的漩涡随着水翼1的俯仰运动重新附着在水翼的尾部, 并随着绕流体的流动流向水翼的尾缘, 在T/2时刻出现漩涡的脱落, 并伴随着新的前缘涡附着在水翼1上.水翼2的后缘边界层已经发生了分离; 当水翼运动至T/2时, 水翼1在1/4周期产生的漩涡已经脱落, 并在水翼后缘发生新的漩涡脱落, 水翼2的前缘产生新的漩涡, 并且伴随着边界层的分离.在该运动参数下, 水翼运动过程中不断发生边界层的分离及漩涡脱落现象造成图 8(a)中水翼各力系数及功率系数曲线波动比较大.图 9(b)中, 水翼1与水翼2在T/4和T/2时均未出现漩涡的产生及脱落现象.由图 6可知, 在该运动参数下, 水翼的攻角始终低于失速角, 且水翼的边界层逐渐变薄, 因此在图 8(b)中, 水翼的各力系数及功率系数曲线比较平滑.图 9(c)中, 增大的折算频率及俯仰振幅使水翼的边界层相对图 9(b)增大, 因此水翼的升力系数曲线不如图 9(b)平滑, 但图 9(c)中的升力极值比图 9(b)中的升力极值大.增大的俯仰振幅和折算频率使垂直方向的速度及俯仰角速度增加, 根据式(5) 可知, 水翼的时均功率与捕能效率均较大.选择合适的俯仰振幅和折算频率, 可以在获得较好的捕能效率的同时, 具有较好的水动力特性.
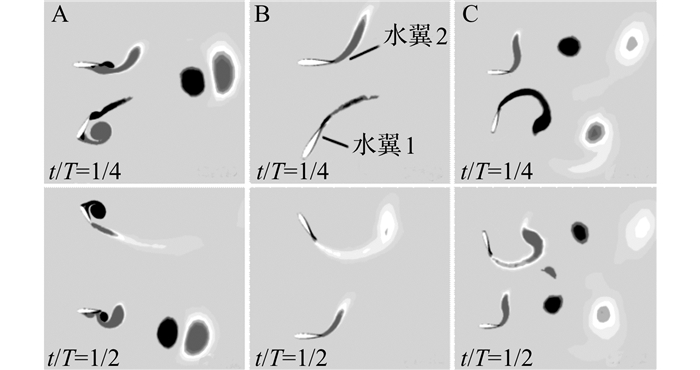
|
图 9 不同运动参数下的漩涡结构图 Fig. 9 Vortex structure under different motion parameters |
图 9(c)中, 当水翼的折算频率为0.16时, 在整个运动周期内水翼的攻角都较小, 未超过水翼的失速角, 因此水翼的各力系数曲线及功率系数曲线具有较好的连续性.如图 10所示为与图 9(c)在相同运动参数条件下, 水翼在不同时刻的总压力云图.在3T/8时刻, 水翼2的下表面压力场比上表面压力场高, 水翼的垂直方向分力与升沉运动一致, 具有能量提取的能力.水翼1的俯仰力矩方向与俯仰运动方向相反, 因此维持水翼1的俯仰运动需要消耗能量; 在5T/8时刻, 水翼1周围的压力情况与3T/8时刻的水翼2相似, 此时, 水翼1的下表面压力场比上表面的压力场高, 且水翼的垂直分力方向与升沉运动方向一致, 因此具有能量提取的能力.水翼2周围的压力情况与3T/8时刻的水翼1相似, 俯仰力矩的方向与水翼俯仰运动的方向相反, 维持水翼2的俯仰运动需要消耗能量.由图 8(c)可知, 水翼2在3T/8时功率系数为正, 且捕获的功率远大于水翼2;在5T/8时, 维持俯仰运动消耗的功率.可知, 3T/8时刻水翼上、下表面的压力差比5T/8时刻水翼上、下表面的压力差大.
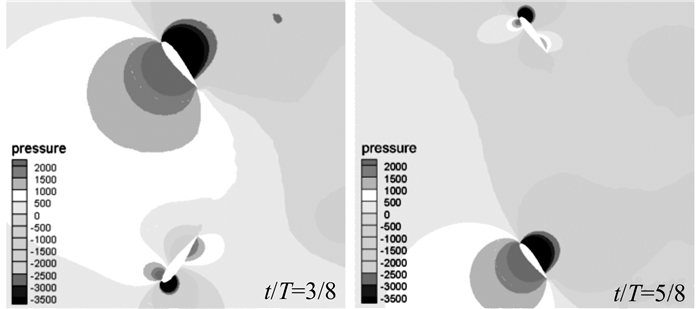
|
图 10 典型运动参数下水翼周围的总压力云图 Fig. 10 Total stress deflectable around foils under typical motion parameters |
当升沉振幅为c, 俯仰振幅为75°和80°时, 水翼在不同振荡频率下的捕能特性和稳定性效果的数值计算结果如表 3所示.双水翼的捕能效率随着折算频率的升高而增大, 当0.14<f*<0.20时, 水翼的捕能达到较高水平.当折算频率为0.18, 俯仰振幅为80°时, 水翼的能量捕获效率最高可达43.18%.此时水翼的效率时均阻力系数较小, 水翼的工作稳定性相对较差; 当0.14<f*<0.18时, 水翼在俯仰振幅为75°时的捕能效率与俯仰振幅为80°时的捕能效率相差较少, 但效率时均阻力系数较大, 表明该参数下水翼的稳定性较好.在兼顾捕能效率和系统稳定性的前提下, 选择系统的折算频率为0.14<f*<0.18, 俯仰振幅为75°~80°.
| 表 3 不同折算频率下数值计算结果(y0=c, θ0=75°) Table 3 Numerical calculation versus reduced frequency (y0=c, θ0=75°) |
(1) 翼型的相对厚度对双水翼捕能系统的时均功率影响随运动参数的变化而变化, 其中, NACA0009翼型的水动力特性较差, NACA0018翼型的水动力特性及捕能性能最好.
(2) 在小的折算频率下, 升沉振幅是影响时均功率系数的主要因素, 但对能量捕获效率的影响较小.随着振荡频率的增加, 在低的俯仰振幅下, 升沉振幅对能量捕获效率的影响逐渐减弱; 在较高的俯仰振幅下, 升沉振幅对时均功率系数的影响较明显.
(3) 当升沉振幅y0=c时, 不同的俯仰振幅下均存在“最优振荡频率”, 使得水翼的捕能效率达到最大值, 且较高的俯仰振幅对应较大的“最优振荡频率”.
(4) 当俯仰振幅为75°或80°时, 振荡翼的效率时均阻力系数随振荡频率的增大先增大后减小; 当0.14<f*<0.18时, 振荡翼的效率时均阻力系数较大, 表明在该运动参数范围内, 系统的稳定性较好.
(5) 综上所述, NACA0018翼型在0.14<f*<0.18, 俯仰振幅为75°~80°时, 双水翼振荡系统的捕能效率较高, 且系统稳定性较好; 系统的最高捕能效率可达43.18%.
| [1] | MCKINNEY W, DELAURIER J. Wingmill: an oscillating-wing windmill[J]. Journal of Energy, 1981, 5(2): 109–115. DOI:10.2514/3.62510 |
| [2] | PLATER M, ASHRAF M, YONG J, et al. Development of a new oscillating-wing wind and hydropower generator[M]. Oriando: AIAA, 2009. |
| [3] | SEMLER C. Experimental investigation of an oscillating flow generator [D]. Monterey: Naval Postgraduate School, 2010. https://www.researchgate.net/publication/235115042_Experimental_Investigation_of_an_Oscillating_Flow_Generator |
| [4] | ZHU Q, PENG Z. Mode coupling and flow energy harvesting by a flapping foil[J]. Physics of Fluids, 2009, 21(3): 33601. DOI:10.1063/1.3092484 |
| [5] | PENG Z, ZHU Q. Energy harvesting through flow-induced oscillating of a foil[J]. Physics of Fluids, 2009, 21(12): 123602. DOI:10.1063/1.3275852 |
| [6] | SIMPSON B J. Experimental studies of flapping foils for energy extraction [D]. Boston: MIT, 2009. https://www.researchgate.net/publication/44024320_Experimental_studies_of_flapping_foils_for_energy_extraction |
| [7] | XIAO Q, LIAO W, YANG S, et al. How motion trajectory affects energy extraction performance of a biomimic energy generator with an oscillating foil?[J]. Renewable Energy, 2012, 37(1): 61–75. DOI:10.1016/j.renene.2011.05.029 |
| [8] | LU K, XIE Y, ZHANG D. Nonsinusoidal motion effects on energy extraction performance of a flapping foil[J]. Renewable Energy, 2014, 64(2): 283–293. |
| [9] | KINSEY T, DUMAS G. Parametric study of an oscillating airfoil in a power-extraction regime[J]. AIAA Journal, 2008, 46(6): 1318–1330. DOI:10.2514/1.26253 |
| [10] | KINSEY T, DUMAS G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils[J]. Journal of Fluids Engineering, 2012, 134(2): 21104. DOI:10.1115/1.4005841 |
| [11] | KINSEY T, DUMAS G. Optimal tandem configuration for oscillating-foils hydrokinetic turbine[J]. Journal of Fluids Engineering, 2012, 134(3): 31103. DOI:10.1115/1.4005423 |
| [12] | KINSEY T, DUMAS G, LALANDE G, et al. Prototype testing of a hydrokinetic turbine based on oscillating hydrofoils[J]. Renewable Energy, 2011, 36(6): 1710–1718. DOI:10.1016/j.renene.2010.11.037 |
| [13] | 王勇, 逯建伟, 谢玉东, 等. 升降式振荡水翼捕获潮流能发电装置: 201310473753. X[P]. 2013-10-11. |
| [14] | AMIRALAEI M R, ALIHANBARI H, HASHEMI S M. An investigation into the effects of unsteady parameters on the aerodynamics of a low Reynolds number pitching airfoil[J]. Journal of Fluids and Structures, 2010, 26(6): 979–993. DOI:10.1016/j.jfluidstructs.2010.06.004 |
| [15] |
逯建伟, 王勇, 谢玉东. 振荡翼捕获能量系统的流体动力性能[J].
山东大学学报:工学版, 2013, 43(5): 93–97.
LU Jian-wei, WANG Yong, XIE Yu-dong. Fluiddynamic performance of an oscillating airfoil in an energy extraction system[J]. Journal of Shandong University: Engineering Science, 2013, 43(5): 93–97. |



