如今汽车保有量不断地增加, 高速公路网络不断地扩展, 车速不断地提高, 对汽车的行车安全提出了更高的要求.随着电子技术和制动控制理论的成熟和发展, 汽车制动技术朝着线控制动的方向发展.其中, 电子机械制动(electronic mechanical brake, EMB)系统具有体积小、结构简单、响应速度快的特点, 已经成为重点发展的方向[1-2].
车辆制动器随着使用磨耗, 制动间隙会逐渐增大, 引起制动响应变慢, 甚至因各轮制动时序差别较大导致车辆侧滑、跑偏等情况, 严重影响行车安全.传统液压制动器一般通过如制动间隙调整器、自调整摩擦圈的机械结构实现间隙调节补偿.电子机械制动器具有旋转-直线运动转换环节, 结构组成与传统液压制动器不同.针对其中的制动间隙调整问题, 主要有两种解决方案.1) 通过具有间隙补偿功能的机械结构装置来进行间隙调整[3-4], 但该方法使得制动器结构臃肿, 增加了制动器的安装空间.2) 通过采集制动器力学信号, 并通过控制策略进行间隙调整[5-9], 如利用电机角度、扭矩、制动器输出力、位移等传感器采集到的信息进行间隙调整中关键过程控制点的识别, 但该方法增加了额外的传感装置(各类传感器), 不但增大了制动器安装所需的空间, 而且增加了成本.
针对上述问题, 本文提出通过电流信号识别制动过程临界点的电子机械制动器间隙调整控制策略, 利用电流信号的变化特征识别出制动过程中的两个关键临界点, 解决了增加额外传感器或辅助机械机构带来的安装空间和成本增加的问题.
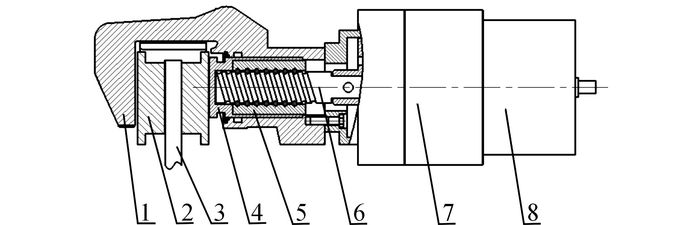
1 EMB执行器建模电子机械制动器如图 1所示.当有制动命令给入时, 电机旋转, 继而通过减速器驱动滚珠丝杠、螺母推动活塞推压制动片来实现制动;当缓解命令给入时, 电机反转, 活塞缩回, 制动片和制动盘分离.
|
1-制动钳体;2-制动片;3-制动盘;4-活塞;5-螺母;6-丝杠;7-减速器;8-电机 图 1 EMB执行器结构图 Fig. 1 EMB actuator structure |
根据该结构, 电子机械制动执行器系统总体模型包括驱动电机模型、电机摩擦模型、传动以及负载模型, 如图 2所示.其中根据电机是否堵转, 可以将传动模型分为2种状态.

|
图 2 EMB执行器总体模型 Fig. 2 General model of EMB actuator |
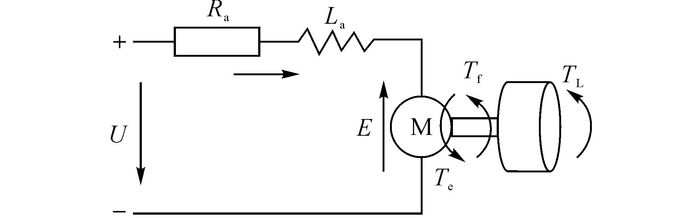
采用永磁直流力矩电机作为EMB执行机构的驱动电机, 如图 3所示.动态方程[10]如下.
|
图 3 直流电机工作原理图 Fig. 3 Direct current motor working principle |
| $ U = {I_{\rm{a}}}{R_{\rm{a}}} + {L_{\rm{a}}}\frac{{{\rm{d}}{I_{\rm{a}}}}}{{{\rm{d}}t}} + E. $ | (1) |
| $ E = {C_{\rm{e}}}{\mathit{\Phi }_n} = {K_{\rm{t}}}{\omega _{\rm{m}}}. $ | (2) |
| $ {J_{\rm{m}}}\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} = {T_{\rm{e}}} - {T_{\rm{f}}} - {T_{\rm{L}}}. $ | (3) |
| $ {T_{\rm{e}}} = {C_{\rm{t}}}\mathit{\Phi }{I_{\rm{a}}} = {K_{\rm{t}}}{I_{\rm{a}}}. $ | (4) |
式中:U为电枢电压, Ia为电枢电流, Ra为电枢电阻, La为电枢电感, E为反电动势, n为电机转速, Te为电机电磁转矩, Tf为电机摩擦转矩, TL为负载转矩, Jm为等效转动惯量, Ce为电动势常数, Ct为转矩常数, Φ为每极气隙磁通, ωm为电机转速, Kt为转矩系数.
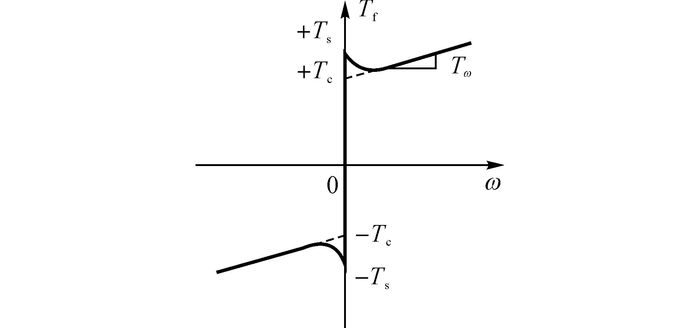
1.2 电机摩擦模型选择如图 4所示的静态摩擦模型中的Stribeck摩擦模型.通过试验已证明, 该模型对真实摩擦力的拟合准确性能达到90%[11].
|
图 4 Stribeck摩擦模型 Fig. 4 Stribeck friction model |
Stribeck摩擦模型的数学表达式[12]如下:
| $ \begin{array}{l} {T_{\rm{f}}} = \\ \left\{ \begin{array}{l} {T_{\rm{e}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\omega = 0\;且\;\left| {{T_{\rm{e}}}} \right| < {T_{\rm{s}}};\\ {T_{\rm{s}}} \cdot {\mathop{\rm sgn}} \left( {{T_{\rm{e}}}} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\omega = 0\;且\;\left| {{T_{\rm{e}}}} \right| \ge {T_{\rm{s}}};\\ {T_{\rm{c}}} + \left( {{T_{\rm{s}}} - {T_{\rm{c}}}} \right)\exp \left[ { - {{\left( {\omega /{\omega _{\rm{s}}}} \right)}^\delta }} \right] + {B_{\rm{v}}}\omega ,\;\;\;\;\;\omega \ne 0. \end{array} \right. \end{array} $ | (5) |
式中:ω为电机转速;ωs为Stribeck速度;Bv为黏性摩擦系数;ωs和δ都为经验常数, 本文设定δ=1.
1.3 传动模型 1.3.1 非堵转状态下的传动模型Saric等[13]提出非堵转状态下制动力与电机转子转角符合以下三次多项式的非线性关系:
| $ {F_{\rm{c}}} = {A_1}\theta _{\rm{m}}^3 + {A_2}\theta _{\rm{m}}^2 + {A_3}{\theta _{\rm{m}}}. $ | (6) |
式中:Fc为制动力, A1、A2、A3为系统刚度, θm为电机转角.
电机在非堵转状态下, 制动片和制动盘刚发生接触直至电机堵转, 制动片的物理形变从零开始逐渐增大, 形变量与电机转角呈线性关系.式(6) 中的未知量可以通过实验确定.
1.3.2 堵转状态下的传动模型电机在堵转状态下, 转速为零, 电机呈现阻性特性, 堵转电流为
| $ {I_{\rm{a}}} = \frac{U}{{{R_{\rm{a}}}}}. $ | (7) |
电机的堵转转矩与电枢电压满足以下关系:
| $ {T_{\rm{e}}} = {K_{\rm{t}}} \cdot \frac{U}{{{R_{\rm{a}}}}}. $ | (8) |
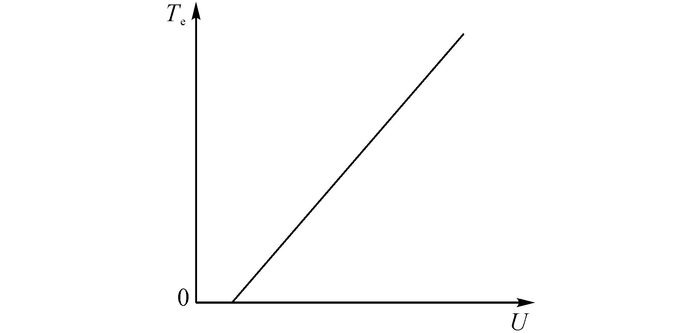
如图 5所示,在制动时, 电机输出的堵转转矩与给定的电枢电压成正比, 可以通过改变电机输入的电枢电压控制制动力.
|
图 5 电压—堵转转矩特性 Fig. 5 Voltage and stall torque characteristics |
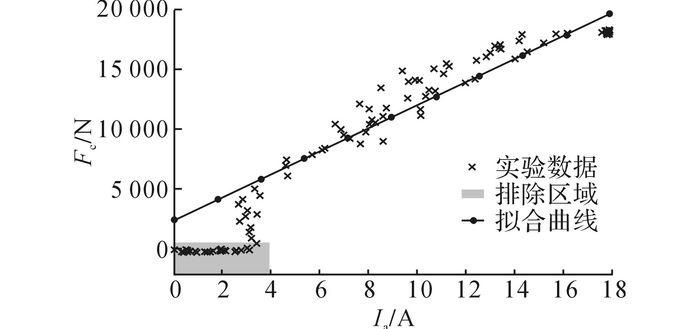
将0~10 V斜坡电压信号加载到驱动电机上, 利用万能试验机得到关于电机堵转时电流和夹紧力的实验数据, 如图 6所示.
|
图 6 夹紧力-电流关系[14] Fig. 6 Relationship between clamping force and current |
由于在间隙消除阶段, 负载较轻, 电机电流较小, 制动力几乎为零, 剔除这部分数据后, 制动力和电机电流基本满足线性关系, 拟合可得[14]
| $ {F_{\rm{c}}} = 953.7{I_{\rm{a}}} + 2477. $ | (9) |
制动片与制动盘间的正压力是由滚珠丝杠副驱动的, 滚珠丝杠的驱动力矩与制动夹紧力有如下关系:
| $ {T_{\rm{s}}} = \frac{{{F_{\rm{c}}} \cdot L}}{{2{\rm{ \mathsf{ π} }}}}. $ | (10) |
式中:Ts为作用在滚珠丝杠上的驱动转矩, L为滚珠丝杠导程.
电机的负载转矩通过行星轮减速器传动输出给滚珠丝杠, 因此电机的负载转矩为
| $ {T_{\rm{L}}} = {T_{\rm{s}}}/i. $ | (11) |
式中:i为行星轮减速器传动比.
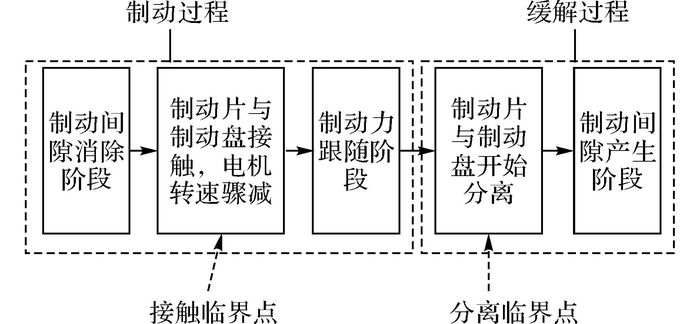
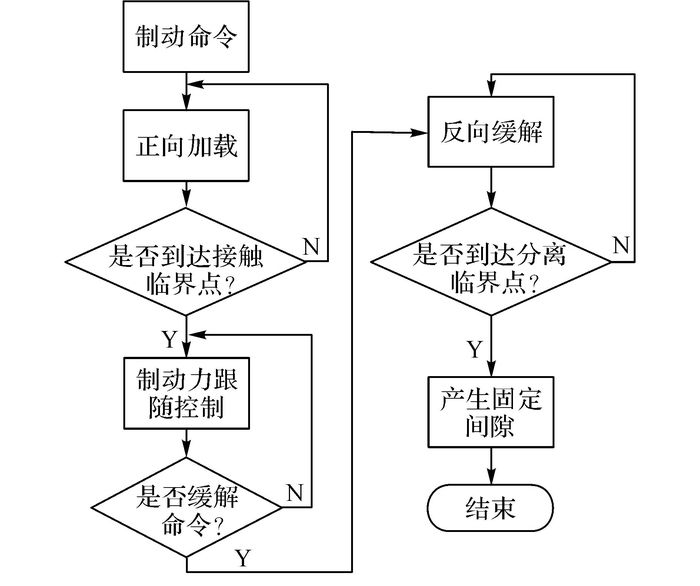
1.5 EMB制动过程建模电子机械制动器一个完整的制动过程, 分为3个阶段, 依次是制动间隙消除阶段、制动力跟随阶段和制动间隙产生阶段, 如图 7所示.制动间隙消除到制动力跟随需要经过制动片与制动盘开始接触这一临界点, 即接触临界点.制动力跟随到制动间隙产生, 需要经过制动片与制动盘开始分离这一临界点, 即分离临界点.上述两个临界点的识别是进行间隙调整的关键.
|
图 7 EMB制动器制动过程示意图 Fig. 7 Schematic diagram of EMB braking process |
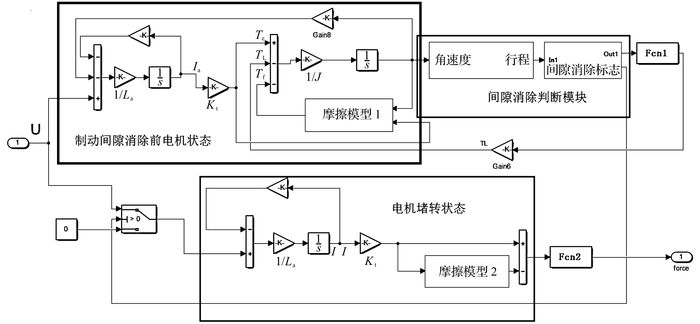
本文执行器使用的是直流力矩电机, 具有较强的堵转性能, 在制动间隙消除后, 电机的转速迅速降为零, 进入制动力跟随阶段.如图 8所示,本文的EMB执行器数学模型由制动间隙消除前和制动间隙消除后(即电机堵转状态时)两部分组成.模型的输入为电机电压, 输出为制动力.当制动间隙消除完毕时, 制动器切换到电机堵转模块.
|
图 8 EMB执行器仿真模型 Fig. 8 Simulation model of EMB actuator |
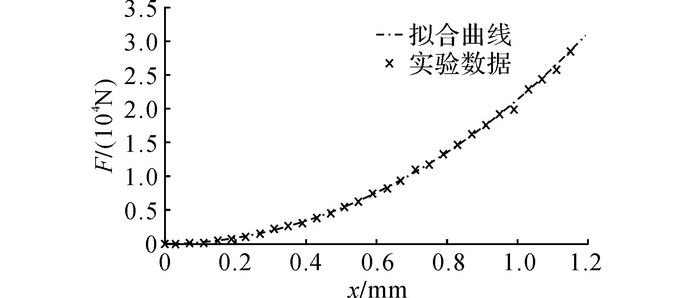
对于一套制动器部件, 刚度主要由所有零件中刚度最小的制动片决定.通过研究制动片的物理特性, 可得制动片的位移形变x和所受正压力F的关系, 如图 9所示.
|
图 9 制动片的刚度特性曲线 Fig. 9 Stiffness characteristic curve of brake pad |
利用最小二乘法对实验数据进行拟合, 可得如下关系式:
| $ F = 1048.5{x^3} + 20162.9{x^2} + 154.3x. $ | (12) |
一个制动过程中, 在到达目标制动力前, 当制动片产生0.2 mm形变后, 施加在制动片上的压力迅速增大, 同时TL迅速增大.由式(1)~(3) 可知:当驱动电机的输入电压不变时, 随着TL的突然增大, 电机转速会迅速减小.由于电机上的反电动势与电机转速呈正比, 导致反电动势突然减小, 此时Ia会发生突变增大.
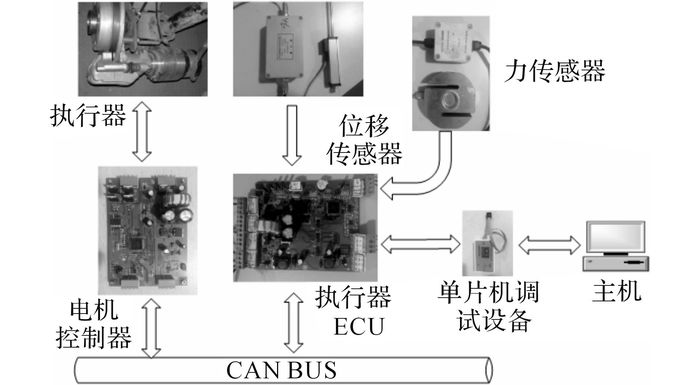
通过实验研究制动片和制动盘接触时电流和制动力之间的关系, 在剔除电机启动电流突变部分的数据之后, 如图 10所示.在经过前0.1 s的间隙消除后, 电机电流和夹紧力逐渐增大, 这与图 14中在0.1 s之后电流和力趋势相同, 说明可以用电流来判断间隙是否消除完毕, 即当电流突破设定值时, 可以认为制动间隙消除完毕.

|
图 10 间隙消除临界点处力-电流特性趋势图 Fig. 10 Force and current trend chart of the critical point in gap elimination |
|
图 14 EMB控制系统的硬件配置图 Fig. 14 Hardware configuration of EMB control system |
从2.1节可知, 电机在反转产生制动间隙前, 制动片的位移形变量是一个不断减小的过程;由式(1)~(3) 可以反推得出:当驱动电机的输入电压不变时, 随着TL的不断减小, Ia减小;当TL减小为零时, Ia不再变化, 即
| $ \frac{{{\rm{d}}{I_{\rm{a}}}}}{{{\rm{d}}t}} = 0. $ | (13) |
如图 11所示, 通过实验数据可以得出, 以电机开始反转为零点, 由于此时制动片和制动盘处于夹紧状态, 一旦电机上施加反向电压, 制动片与制动盘之间的夹紧力开始减小;当电流经历过0.2 s的电机启动上升过程之后, 电流斜率从负半轴逐渐靠近零轴.当夹紧力完全变为零时, 电机电流变化的斜率变为零, 可以认为这是刹车制动结束时间隙产生的起点, 图 13中在1 s之后电流和力的趋势反映了上述情况.可以将电流斜率变为零处作为刹车片和刹车盘的分离点, 即间隙调整(间隙开始产生)的临界点.

|
图 11 间隙调整临界点处力-电流趋势图 Fig. 11 Force and current trend chart of critical point in gap adjustment |
|
图 13 EMB控制策略仿真结果 Fig. 13 Simulation results of EMB control strategy |
对于直流力矩电机, 在已知电流的情况下, 电机的转速按下式确定:
| $ {n_{{\rm{rea}}}} = \left( {1 - \frac{{{I_{{\rm{rea}}}}}}{{{I_{\max }}}}} \right){n_{\max }}. $ | (14) |
式中:nrea为电机的实际转速, nmax为电机最大空载转速, Irea为电机的实际电流, Imax为电机堵转时的最大电流.
在分离临界点后, 再令电机旋转固定时间, 可将制动间隙控制在所需距离.
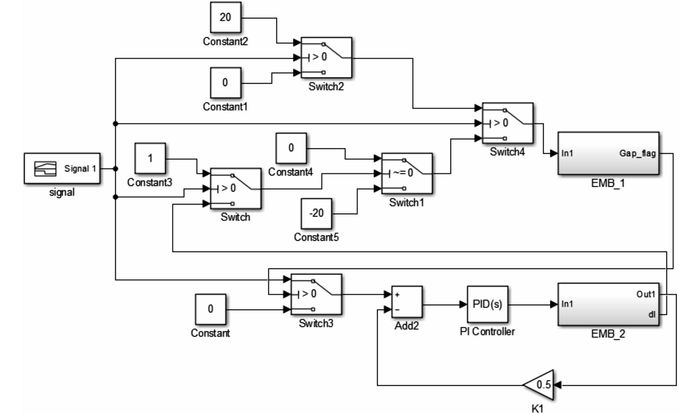
3 控制策略设计与仿真分析基于上述临界点的识别, 制定EMB制动器控制策略, 如图 12所示.当有制动力命令输入时, 先根据电流信号判断制动间隙是否消除, 如果没有, 则快速进行制动间隙消除.然后进入制动力跟随阶段, 当缓解信号输入, 即制动结束时, 进行最后的制动间隙调整.根据电流信号判断是否达到制动间隙开始产生的临界点, 一旦满足, 则设定延时器, 利用电机特性产生固定的制动间隙.
|
图 12 EMB间隙调整控制策略逻辑图 Fig. 12 Logic diagram of EMB control strategy for brake clearance adjustment |
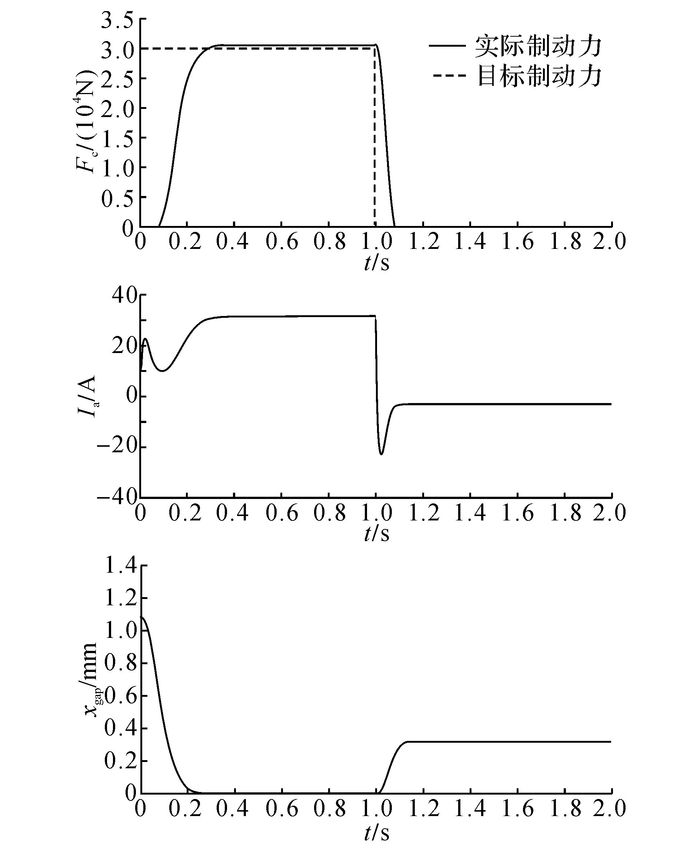
根据EMB执行器的仿真模型, 并结合控制策略, 对控制策略进行离线仿真分析.在仿真时, 输入一个30 kN持续1 s的制动力信号来验证算法的有效性, 仿真结果如图 13所示.图中,xgap为刹车片与制动盘的间隙.当输入制动命令后, 前0.1 s内制动力没有发生变化, 该阶段处于制动间隙消除过程.电机在启动电流的冲击后, 电流经间隙消除逐渐增大至堵转值.制动力在0.3 s左右, 基本达到目标制动力命令要求.当制动命令在1 s时解除后, 电机上施加反向电压, 迅速反转;此时, 电流经过启动突变后, 减小至稳定状态.制动片和制动盘之间的间隙最后稳定在0.3 mm左右.
4 实验验证为了验证提出的EMB控制策略的有效性, 搭建基于飞思卡尔电子嵌入式系统的硬件试验平台, 如图 14所示.利用位移传感器模拟制动力信号, 将位移传感器的数值转换为目标制动力.自制制动器的主要零部件规格参数如表 1所示.
| 表 1 制动器主要零部件的规格参数 Table 1 Parameters of main components of brake |
为了对比制动效果, 人为模拟放大制动片的磨损量, 如图 15所示.将制动钳体置于万能试验机的支撑底座和运动臂之间, 利用力传感器来测量制动力;在制动过程中, 制动钳活塞会随着试验机运动臂的上升而外伸, 通过控制试验机运动臂向上的位移量能够模拟制动片的磨损.
|
图 15 制动片磨损模拟实验图 Fig. 15 Brake pad wear simulation test diagram |
在有间隙调整控制策略和无间隙调整控制策略两种模式下进行实验, 每种模式下进行两次制动.在第一次制动开始前, 两种模式下的制动钳活塞的起始位置相同, 此时的初始制动间隙为0.3 mm.在每种模式下的第一次制动过程中, 将万能试验机运动臂上移0.2 mm, 人为模拟制动片0.2 mm的磨损.由于控制策略的差异, 在第一次制动缓解过程中, 两种模式下产生的制动间隙会有差异, 造成两种制动模式下的第二次制动响应时间不同, 如图 16所示.结果表明, 有间隙调整策略时的制动器输出最大目标制动力响应时间为0.63 s, 无间隙调整控制策略的制动器输出最大目标制动力响应时间约为0.70 s, 间隙调整控制策略令制动器具有更快的制动响应速度, 响应时间缩短10%.

|
图 16 不同控制策略下的第二次制动实验结果 Fig. 16 Experimental results of second braking under different control strategies |
(1) 基于电流信号特征识别制动过程临界点的电子机械制动器间隙调整控制策略, 能够在制动片磨损后, 准确控制制动间隙, 从而有效地缩短制动器的响应时间.
(2) 通过电流信号的特征可以有效地识别制动过程中制动片与制动盘接触、分离这两个临界点, 解决了安装额外的传感器或机械辅助机构所带来的成本增加和安装空间增大等问题.
| [1] |
王政军, 李星, 李源清, 等. 汽车线控技术的研究现状及展望[J].
科技创新导报, 2015(21): 8–9.
WANG Zheng-jun, LI Xing, LI Yuan-qing, et al. Research status and prospect of automotive X-by-wire technology[J]. Science and Technology Innovation Herald, 2015(21): 8–9. DOI:10.3969/j.issn.1674-098X.2015.21.004 |
| [2] |
李昂. 浅谈汽车线控制动技术与发展[J].
电子技术与软件工程, 2014(05): 118.
LI Ang. Discussion on automobile brake-by-wire technology and development[J]. Electronic Technology and Software Engineering, 2014(05): 118. |
| [3] |
王维锐, 葛正, 傅云峰, 等. 具有间隙调节功能的车用电子机械制动器: 中国, 201120510037. 0[P]. 2012-07-25.
WANG Wei-rui, GE Zheng, FU Yun-feng, et al. Vehicle electronic mechanical brake with gap regulating function: CN, 201120510037.0[P]. 2012-07-25. |
| [4] | SHIN D H, PARK T S, JINS H, et al. Study of mechanism for wear adjustment with electro wedge brake[J]. Key Engineering Materials, 2014, 625: 712–716. DOI:10.4028/www.scientific.net/KEM.625 |
| [5] | YAO Y. Brake system and method of control with air gap estimation: US, 20150260246A1 [P]. 2014-03-14. |
| [6] | KI Y H, LEE K J, CHEON J S, et al. Design and implementation of a new clamping force estimator in electro-mechanical brake systems[J]. International Journal of Automotive Technology, 2013, 14(5): 739–745. DOI:10.1007/s12239-013-0081-4 |
| [7] | JO C, HWANG S, KIM H. Clamping-force control for electromechanical brake[J]. IEEE Transactions onVehicular Technology, 2010, 59(7): 3205–3212. DOI:10.1109/TVT.2010.2043696 |
| [8] | SHIN D H, PARK T S, JEONG C P, et al. Motor control system and method for wear compensation of electromechanical brake: US, 20150308530A1 [P]. 2015-10-29. |
| [9] | NARULA P, ROBERTS P, KNOOP D. Method and system for setting a braking component running clearance: US, 20160076609A1 [P]. 2016-03-17. |
| [10] |
汪贵平, 马建, 闫茂德. 永磁直流电动机驱动汽车的数学模型[J].
中国公路学报, 2011, 24(1): 122–126.
WANG Gui-ping, MA Jian, YAN Mao-de. Study of mathematical model of electric vehicle driven by permanent magnet DC motor[J]. China Journal of Highway and Transport, 2011, 24(1): 122–126. |
| [11] |
黄进, 叶尚辉. 含摩擦环节伺服系统的分析及控制补偿研究[J].
机械科学与技术, 1999, 18(1): 1–4.
HUANG Jin, YE Shang-hui. Analysis and control of servo system with friction and servo system[J]. Mechanical Science and Technology for Aerospace Engineering, 1999, 18(1): 1–4. |
| [12] | MARTON L, LANTOS B. Control of mechanical systems with Stribeck friction and backlash[J]. Systems and Control Letters, 2009, 58(2): 141–147. DOI:10.1016/j.sysconle.2008.10.001 |
| [13] | SARIC S, BAB H A, HOSEINNEZHAD R. Clamp-force estimation for a brake-by-wire system: a sensor-fusion approach[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 778–786. DOI:10.1109/TVT.2007.905251 |
| [14] |
傅云峰. 汽车电子机械制动系统设计及其关键技术研究[D]. 杭州: 浙江大学, 2013.
FU Yun-feng. Automotive electromechanical brake system design and its key technology [D]. Hangzhou: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013303600.htm |



