2. 上海卫星工程研究所, 上海 200240
2. Shanghai Institute of Satellite Engineering, Shanghai 200240, China
随着制造业的发展, 高精度双驱龙门机床运动平台在航空航天、电力设备、机器人、汽车、船舶等领域已具有广泛的应用[1-2].在双驱龙门机床中, 横梁由两台平行布置的电机驱动, 两电机之间存在着机械耦合关系.当滑块沿横梁移动时, 横梁两端电机的负载参数将发生变化, 并引进时变干扰.为了提高双驱龙门机床的控制精度, 研究同步控制问题具有重要的现实意义.
近年来, 国内外学者针对双驱龙门机床同步控制问题进行了一定的研究.在系统建模方面, Chu等[3]将双驱运动系统等效为一阶惯性环节, 未考虑双驱系统的机械耦合关系.李玉霞等[4]基于动力学分析建立龙门机床双驱间的机械耦合模型, 但忽略了滑块运动对两端等效负载的影响.Teo等[5]利用拉格朗日方程建立反映滑块运动的双驱龙门机床动态模型, 将沿导轨方向的库仑摩擦力视为恒值, 但实际运用中因滑块运动产生的库仑摩擦力呈大幅度变化.Garciaherreros等[6]简化了上述动力学模型, 主要考虑因速度变化导致的摩擦力变化, 未考虑滑块运动导致的摩擦力变化.在双驱同步控制算法方面, 为了减小跟踪误差, Tomizuka等[7]设计零相位误差跟踪控制器, 但同步误差较大.为了减小同步误差, Koren等[8]提出一种交叉耦合控制结构, 根据同步误差生成校正信号并反馈至单轴控制环路中, 从而提高同步性能.Yeh等[9]设计一种干扰观测器, 以减小外部干扰对机床同步控制精度的影响.Hu等[10]针对高速龙门机床中的动态耦合现象, 提出一种自适应鲁棒控制算法.为了提高轮廓精度, Xi等[11]设计一种积分滑模控制算法.赵希梅等[12]针对龙门定位平台上双直线电动机伺服系统的位置精确同步控制问题, 提出了具有快速跟踪能力以及鲁棒性的交叉耦合互补滑模控制算法.Liu等[13]针对系统未建模部分和外部干扰, 采用H∞控制提高双驱单轴的鲁棒性.朱国昕等[14]采用H∞次优方法设计交叉耦合控制器, 从而减小轮廓误差, 但未考虑因滑块移动带来的参数不确定性和时变干扰.综上所述, 这些文献很少涉及具有较大质量滑块的大型双驱龙门机床.在该情况下, 大质量滑块运动会使横梁两边的等效负载质量剧烈变化, 带来参数不确定性和时变干扰, 增加了同步误差, 加大了高精度同步运动的难度, 甚至损坏物理结构.对于该类大型双驱动龙门机床, 不能直接采用上述方法实现高精度同步运动.
本文研究的主要问题是在参数不确定性和时变干扰情况下的双驱龙门机床高精度同步控制.首先基于拉格朗日方程建立动力学模型, 该模型中的摩擦力可以反映系统的机械耦合和滑块运动.针对该模型, 设计H∞-交叉耦合同步控制算法, 提高系统的鲁棒性以处理参数不确定性和时变干扰, 保证了高精度同步运动控制的要求.最后在某大型双驱龙门机床进行实验, 通过与Yao[15]设计的PID同步控制算法比较跟踪误差和同步误差, 说明该算法在处理不确定性和时变干扰方面有显著的效果, 能够保证高精度同步运动.
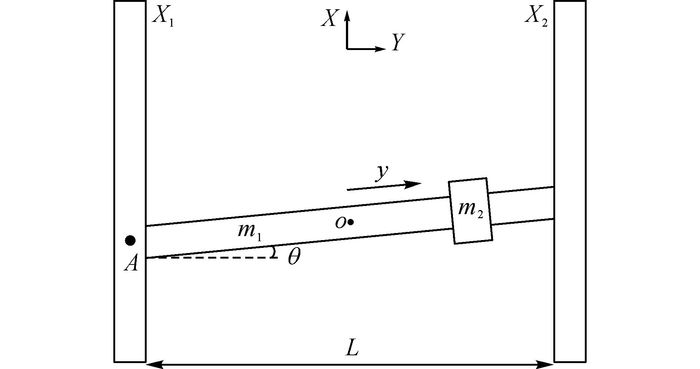
1 双驱龙门机床动力学建模如图 1所示, 双驱龙门机床一般由2个导轨(X1轴和X2轴)和横梁(Y轴)构成, 横梁由2台平行布置的直线电机驱动.在一般情况下, X1轴和X2轴配备相同的驱动电机, 但受外部干扰、工艺等因素的影响, 双驱动电机很难实现高精度的同步运动.特别是大质量滑块沿横梁移动, 带来的系统参数不确定性和时变干扰.为了提高含有大质量滑块的双驱龙门机床同步运动的控制精度, 必须建立动力学模型.
|
图 1 双驱龙门机床平面简化模型 Fig. 1 Diagram of dual-drive gantry stage |
图 1中, m1为横梁的质量;m2为滑块的质量;L为横梁的长度;点o为横梁的重心;y为滑块重心到点o的距离;x1和x2分别为X1轴和X2轴电机的位移量;x为横梁的位移量;θ为由于不同步导致横梁微小转动的角度;I1和I2分别为横梁和滑块的转动惯量, I1=m1L2/12, I2=m2y2.
由图 1可得,
| $ \left[ {\begin{array}{*{20}{c}} x\\ \theta \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1/2}&{1/2}\\ { - 1/L}&{1/L} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right]. $ | (1) |
进一步, 可得横梁和滑块的速度如下:
| $ {\mathit{\boldsymbol{v}}_{m1}} = \left[ {\begin{array}{*{20}{c}} {\dot x}\\ 0 \end{array}} \right],{\mathit{\boldsymbol{v}}_{m2}} = \left[ \begin{array}{l} \dot x + \dot y\sin \theta + y\dot \theta \cos \theta \\ \dot y\cos \theta - y\dot \theta \sin \theta \end{array} \right]. $ | (2) |
建立能够反映滑块运动的动力学方程如下:
| $ \left. \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot \varphi }_i}}}} \right) - \frac{{\partial L}}{{\partial {\varphi _i}}} = {R_i},\\ L = T - V;{\varphi _i} = x,\theta ,y;{R_i} = {F_x},{F_\theta },{F_y}. \end{array} \right\} $ | (3) |
式中:T为系统的动能,
| $ T = \frac{1}{2}{m_1}\mathit{\boldsymbol{v}}_{m1}^{\rm{T}}{\mathit{\boldsymbol{v}}_{m1}} + \frac{1}{2}{m_2}\mathit{\boldsymbol{v}}_{m2}^{\rm{T}}{\mathit{\boldsymbol{v}}_{m2}} + \frac{1}{2}\left( {{I_1} + {I_2}} \right){{\dot \theta }^2}; $ | (4) |
V为系统的弹性势能, 假设龙门机床是刚体结构, 则V=0;Fx和Fy分别为沿x、y方向的广义力, Fθ为使横梁转动θ角度的广义力矩,
| $ \begin{array}{l} {F_x} = {F_1} - {f_1} + {F_2} - {f_2},\\ {F_\theta } = \left( {{F_2} - {f_2} - {F_1} + {f_1}} \right)\cos \theta \cdot L/2,\\ {F_y} = {F_3} - {f_3}, \end{array} $ | (5) |
Fi、fi分别为电机驱动力和摩擦力(i=1、2、3分别表示沿x1、x2、y方向).
将式(2)、(4) 和(5) 代入式(3), 可得动力学方程:
| $ \mathit{\boldsymbol{M\dot \eta + C\dot \eta + Bf = BF}}\mathit{\boldsymbol{.}} $ | (6) |
| $ \left. \begin{array}{l} \mathit{\boldsymbol{M = }}\left[ {\begin{array}{*{20}{c}} \begin{array}{l} {m_1} + {m_2}\\ {m_2}y\cos \theta \\ {m_2}\sin \theta \end{array}&\begin{array}{l} {m_2}y\cos \theta \\ {I_1} + {I_2} + {m_2}{y^2}\\ 0 \end{array}&\begin{array}{l} {m_2}\sin \theta \\ 0\\ {m_2} \end{array} \end{array}} \right],\\ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ 0\\ 0 \end{array}&\begin{array}{l} 2{m_2}\dot y\cos \theta - {m_2}\dot y\sin \theta \\ 4{m_2}\dot yy\\ - 2{m_2}y\dot \theta \end{array}&\begin{array}{l} 0\\ 0\\ 0 \end{array} \end{array}} \right],\\ \mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} \begin{array}{l} 1\\ - \frac{{L\cos \theta }}{2}\\ 0 \end{array}&\begin{array}{l} 1\\ \frac{{L\cos \theta }}{2}\\ 0 \end{array}&\begin{array}{l} 0\\ 0\\ 1 \end{array} \end{array}} \right],\\ \mathit{\boldsymbol{\eta = }}{\left[ {x,\theta ,y} \right]^{\rm{T}}},\mathit{\boldsymbol{F = }}{\left[ {{F_1},{F_2},{F_3}} \right]^{\rm{T}}},\mathit{\boldsymbol{f = }}{\left[ {{f_1},{f_2},{f_3}} \right]^{\rm{T}}}. \end{array} \right\} $ | (7) |
式中:M为惯量矩阵, C为科里奥利向心矩阵.
当滑块和横梁质量相近时, 滑块运动位置对摩擦力有很大的影响, 建立一个能够反映滑块位置的摩擦力模型:
| $ \left. \begin{array}{l} {f_1}\left( y \right) = \mu \left[ {\frac{1}{2}{m_1}g + \left( {\frac{1}{2} - \frac{y}{L}} \right){m_2}g} \right] + \gamma {{\dot x}_1} = \\ \;\;\;\;\;\;\;\;\;\overline {{f_1}} \left( y \right) + \gamma {{\dot x}_1},\\ {f_2}\left( y \right) = \mu \left[ {\frac{1}{2}{m_1}g + \left( {\frac{1}{2} - \frac{y}{L}} \right){m_2}g} \right] + \gamma {{\dot x}_2} = \\ \;\;\;\;\;\;\;\;\;\overline {{f_2}} \left( y \right) + \gamma {{\dot x}_2}. \end{array} \right\} $ | (8) |
式中:γ为黏滞摩擦系数, μ为库仑摩擦系数.与Chu等[3-6]提出的建模方法相比可知, 上述摩擦力模型能够有效地反映大型龙门机床双驱之间的机械耦合关系和大质量滑块运动的影响.
由于系统机械结构的限制, θ远小于0.01 rad, 可以假设sin θ≈0和cos θ≈1.在文献[15]中已经证明了科里奥利向心力可以忽略不计, 即式(7) 中C可以忽略.进一步, 模型(6) 可以简化为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\dot x}_1}}\\ {{{\ddot x}_1}}\\ {{{\dot x}_2}}\\ {{{\ddot x}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ 0&{ - \gamma {Q_{11}}}&0&{ - \gamma {Q_{12}}}\\ 0&0&0&1\\ 0&{ - \gamma {Q_{21}}}&0&{ - \gamma {Q_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{{\dot x}_1}}\\ {{x_2}}\\ {{{\dot x}_2}} \end{array}} \right] + \\ \;\;\;\;\left[ {\begin{array}{*{20}{c}} 0&0\\ { - {Q_{11}}}&{ - {Q_{12}}}\\ 0&0\\ { - {Q_{21}}}&{ - {Q_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\overline {{f_1}} }\\ {\overline {{f_2}} } \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&0\\ {{Q_{11}}}&{{Q_{12}}}\\ 0&0\\ {{Q_{21}}}&{{Q_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}} \end{array}} \right]. \end{array} $ | (9) |
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}\\ {{Q_{21}}}&{{Q_{22}}} \end{array}} \right] = \frac{1}{{m_2^2{y^2} + 2{m_1}{m_2}{y^2} + {I_1}\left( {{m_1} + {m_2}} \right)}} \times \\ \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 2{m_2}{y^2} + {m_2}Ly + \\ {I_1} + \frac{{{L^2}}}{4}\left( {{m_1} + {m_2}} \right) \end{array}&\begin{array}{l} 2{m_2}{y^2} + {I_1} - \\ \frac{{{L^2}}}{4}\left( {{m_1} + {m_2}} \right) \end{array}\\ \begin{array}{l} 2{m_2}{y^2} + {I_1} - \\ \frac{{{L^2}}}{4}\left( {{m_1} + {m_2}} \right) \end{array}&\begin{array}{l} 2{m_2}{y^2} - {m_2}Ly + {I_1} + \\ \frac{{{L^2}}}{4}\left( {{m_1} + {m_2}} \right) \end{array} \end{array}} \right]. \end{array} $ | (10) |
对于大型双驱龙门机床, 滑块运动会使系统产生参数不确定性和时变干扰.为了保证双驱龙门机床具有较高同步控制精度, 采用H∞控制算法来解决参数不确定性和时变干扰问题.
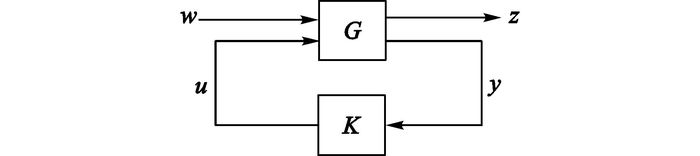
标准的H∞控制问题的基本框图如图 2所示.图中, w为外部输入信号(包括参考信号、干扰和噪声等), u为控制输入, z为被控输出信号, y为测量输出, G(s)为系统给定的广义控制对象, K(s)为待设计的控制器.系统的状态空间实现[16]为
|
图 2 标准H∞控制问题的基本框图 Fig. 2 Block diagram of standard H∞ control problem |
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\dot x = Ax + }}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u}},\\ \mathit{\boldsymbol{z = }}{\mathit{\boldsymbol{C}}_1}\mathit{\boldsymbol{x + }}{\mathit{\boldsymbol{D}}_{11}}\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{D}}_{12}}\mathit{\boldsymbol{u}},\\ \mathit{\boldsymbol{y = }}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{x + }}{\mathit{\boldsymbol{D}}_{21}}\mathit{\boldsymbol{w + }}{\mathit{\boldsymbol{D}}_{22}}\mathit{\boldsymbol{u}}. \end{array} \right\} $ | (11) |
式中:x为状态变量.可得广义控制对象:
| $ \mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_2}}\\ {{\mathit{\boldsymbol{C}}_1}}&{{\mathit{\boldsymbol{D}}_{11}}}&{{\mathit{\boldsymbol{D}}_{12}}}\\ {{\mathit{\boldsymbol{C}}_2}}&{{\mathit{\boldsymbol{D}}_{21}}}&{{\mathit{\boldsymbol{D}}_{22}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{11}}}&{{\mathit{\boldsymbol{G}}_{12}}}\\ {{\mathit{\boldsymbol{G}}_{21}}}&{{\mathit{\boldsymbol{G}}_{22}}} \end{array}} \right]. $ | (12) |
于是, 从w到z的闭环传递函数为
| $ {\mathit{\boldsymbol{T}}_{zw}} = {\mathit{\boldsymbol{G}}_{11}} + {\mathit{\boldsymbol{G}}_{12}}\mathit{\boldsymbol{K}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{G}}_{22}}\mathit{\boldsymbol{K}}} \right)^{ - 1}}{\mathit{\boldsymbol{G}}_{21}}. $ | (13) |
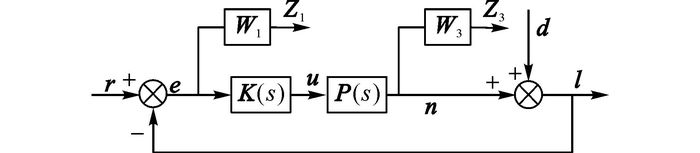
基于混合灵敏度控制问题的H∞设计方法是针对权函数W1和W3的H∞最优控制问题, W1和W3表示跟踪误差和输出的加权, 结构图如图 3所示.图中, P(s)为系统的标称控制对象, K(s)为待设计的控制器[17].
|
图 3 双驱控制系统混合灵敏度问题 Fig. 3 Mixed sensitivity problem of dual-drive controlsystem |
系统的灵敏度函数S和补灵敏度函数T的表达式如下:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{S}}\left( s \right) = {\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}\left( s \right)\mathit{\boldsymbol{K}}\left( s \right)} \right)^{ - 1}},\\ \mathit{\boldsymbol{T}}\left( s \right) = {\left( {\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{P}}\left( s \right)\mathit{\boldsymbol{K}}\left( s \right)} \right)^{ - 1}}\mathit{\boldsymbol{P}}\left( s \right)\mathit{\boldsymbol{K}}\left( s \right) = \mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}\left( s \right). \end{array} \right\} $ | (14) |
为了保证系统的性能和鲁棒稳定性, S(s)和T(s)必须满足如下关系式:
| $ \begin{array}{l} \bar \sigma \left| {\mathit{\boldsymbol{S}}\left( {{\rm{j}}w} \right)} \right| \le \bar \sigma \left| {\mathit{\boldsymbol{W}}_1^{ - 1}\left( {{\rm{j}}w} \right)} \right|,\\ \bar \sigma \left| {\mathit{\boldsymbol{T}}\left( {{\rm{j}}w} \right)} \right| \le \bar \sigma \left| {\mathit{\boldsymbol{W}}_3^{ - 1}\left( {{\rm{j}}w} \right)} \right|. \end{array} $ | (15) |
式中:
| $ {\left\| {{\mathit{\boldsymbol{T}}_{zr}}\left( {\mathit{\boldsymbol{G}},\mathit{\boldsymbol{K}}} \right)} \right\|_\infty } \le \lambda . $ | (16) |
根据DGKF算法[18]可知, H∞控制器具有如下形式:
| $ \mathit{\boldsymbol{K}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{\rm{f}}}}&{ - {\mathit{\boldsymbol{Z}}_{\rm{f}}}{\mathit{\boldsymbol{L}}_{\rm{f}}}}\\ {{\mathit{\boldsymbol{F}}_{\rm{f}}}}&0 \end{array}} \right]. $ | (17) |
式中:
| $ {\mathit{\boldsymbol{A}}_{\rm{f}}} = \mathit{\boldsymbol{A + }}{\lambda ^{ - 2}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{B}}_1^{\rm{T}}\mathit{\boldsymbol{X + }}{\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{F}}_{\rm{f}}} + \mathit{\boldsymbol{ZL}}{\mathit{\boldsymbol{C}}_2}, $ | (18) |
| $ {\mathit{\boldsymbol{F}}_{\rm{f}}} = - \mathit{\boldsymbol{B}}_2^{\rm{T}}{\mathit{\boldsymbol{X}}_\infty }, $ | (19) |
| $ {\mathit{\boldsymbol{L}}_{\rm{f}}} = - {\mathit{\boldsymbol{Y}}_\infty }\mathit{\boldsymbol{C}}_2^{\rm{T}}, $ | (20) |
| $ {\mathit{\boldsymbol{Z}}_{\rm{f}}} = {\left( {\mathit{\boldsymbol{I}} - {\lambda ^{ - 2}}{\mathit{\boldsymbol{Y}}_\infty }{\mathit{\boldsymbol{X}}_\infty }} \right)^{ - 1}}. $ | (21) |
式(19)、(20) 中, 矩阵X∞和Y∞分别满足如下Riccati方程:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_\infty } + {\mathit{\boldsymbol{X}}_\infty }\mathit{\boldsymbol{A + }}{\mathit{\boldsymbol{X}}_\infty }\left( {{\lambda ^{ - 2}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{B}}_1^{\rm{T}} - {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{B}}_2^{\rm{T}}} \right){\mathit{\boldsymbol{X}}_\infty } + \\ \;\;\;\;{\mathit{\boldsymbol{C}}_1}\mathit{\boldsymbol{C}}_1^{\rm{T}} = {\bf{0}}. \end{array} $ | (22) |
| $ \begin{array}{l} \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{Y}}_\infty } + {\mathit{\boldsymbol{Y}}_\infty }{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{Y}}_\infty }\left( {{\lambda ^{ - 2}}\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{C}}_1} - \mathit{\boldsymbol{C}}_2^{\rm{T}}{\mathit{\boldsymbol{C}}_2}} \right){\mathit{\boldsymbol{Y}}_\infty } + \\ \;\;\;\;\mathit{\boldsymbol{B}}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1} = {\bf{0}}. \end{array} $ | (23) |
为了设计所提H∞控制器, 给出如下引理.
引理[17] 存在H∞控制器(17), 使图 2的闭环系统内部稳定, 且满足||Tzw||∞≤λ的充分条件如下.
1) D11足够小, 且满足D11<λI.
2) Riccati方程(22) 的解X∞为正定矩阵.
3) Riccati方程(23) 的解Y∞为正定矩阵.
4) ρ(X∞Y∞)<λ.
其中, ρ(X)为矩阵X中绝对值最大的特征值.控制系统的性能与λ密切相关, λ越大, 系统的控制性能越差.在设计过程中, 应尽量选择较小的λ.通过二分法, 可以确定最小的λ.
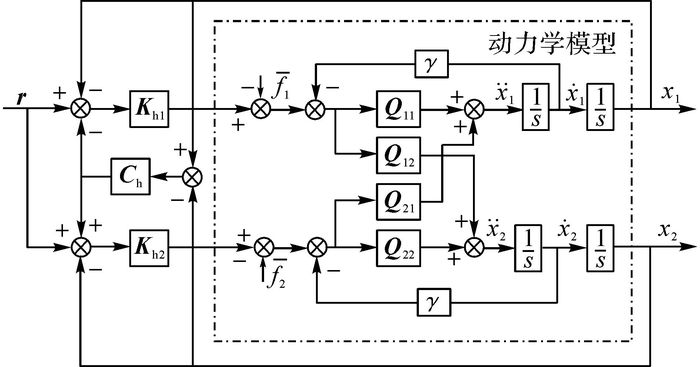
图 4给出基于H∞-交叉耦合算法的双驱龙门机床同步控制原理框图.图中, 动力学模型参数与式(9) 的各参数相对应;Kh1和Kh2分别为x1轴和x2轴的H∞控制器, 通过基于混合灵敏度问题的H∞设计方法进行设计, 求解Riccati方程求得;Ch为交叉耦合控制器, 以双驱间的同步误差作为控制输入, 经内部算法处理产生补偿信号, 分别对x1轴和x2轴进行补偿.为了提高系统响应速度, 增加系统稳定性, 交叉耦合控制器采用PD控制方式.
|
图 4 H∞-交叉耦合同步控制原理框图 Fig. 4 H∞ cross-coupled synchronous control structure |
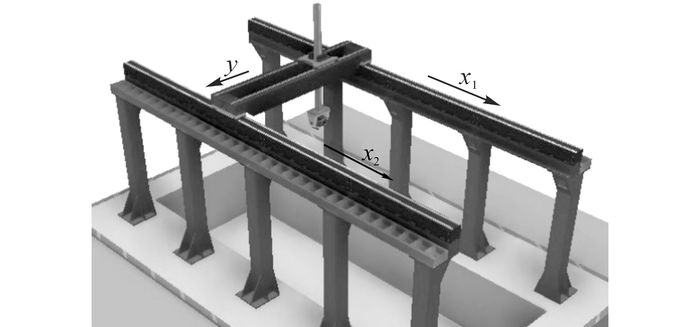
为了验证设计的H∞-交叉耦合同步控制算法的可用性和有效性, 针对某大型双驱龙门机床进行具体实验.应用的大型双驱龙门机床机构如图 5所示.横梁和滑块分别由KOLLMORGEN IC44-075直线电机驱动, 推力常数Kf=305 N/A, 峰值推力Fp=3 750 N;测量系统采用Renishaw RGS-40直线光栅尺, 分辨率为1 μm.龙门机床的主要参数如下:m1=4 000 kg, m2=4 000 kg, L=5 m, μ=0.005, γ=0.003.
|
图 5 某大型双驱龙门机床示意图 Fig. 5 Structure of dual-drive gantry stage |
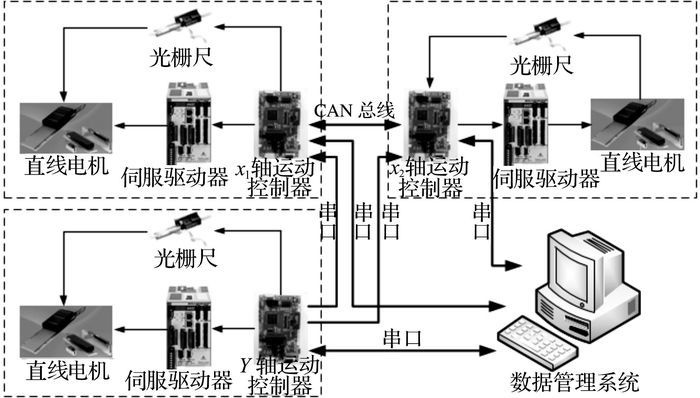
图 6给出该大型双驱龙门机床的实验平台构成示意图.实验平台工作过程如下:由实时控制平台发送指令给各轴的运动控制器, 经DSP内部处理产生控制信号传送到伺服驱动器, 伺服驱动器驱动直线电机, 由直线光栅尺反馈位置信号, 构成反馈回路.X1和X2轴通过CAN总线通讯, 传递位置信号给交叉耦合控制器, 同时Y轴的位置信号通过串口实时传送给X1和X2轴.该平台的采样时间为2 ms.
|
图 6 某大型双驱龙门机床实验平台构成 Fig. 6 Experimental platform constitutes of dual-drive gantry stage |
下面进行H∞控制器权函数的设计.W1反映了灵敏度函数的特性, 为了获得较小的灵敏度函数, 选取W1如下:
| $ {W_1} = 0.75 \times \frac{{\left( {{s^2} + 5.196s + 12} \right)}}{{s\left( {s + 0.014} \right)}}. $ | (24) |
W3反映了补灵敏度函数的特性, 为了保证W3G为真的实有理函数, 选取W3如下:
| $ {W_3} = \frac{{s\left( {s + 100} \right)}}{{1000}}. $ | (25) |
利用MATLAB鲁棒控制工具箱求解Riccati方程, 得到H∞控制器:
| $ \begin{array}{l} {K_{{\rm{h1}}}} = {K_{{\rm{h2}}}} = \\ \;\;\;\;\frac{{1.379 \times {{10}^8}\left( {s + 1.927} \right)\left( {s + 0.207} \right)\left( {s + 0.194} \right)}}{{\left( {{s^2} + 0.214s + 0.012} \right)\left( {{s^2} + 183.4s + 9380} \right)}}. \end{array} $ | (26) |
根据工程参数整定法可得交叉耦合控制器为
| $ {C_{\rm{h}}} = 15 + 0.5s. $ | (27) |
实验中, 分别令大型双驱龙门机床X向双驱作匀速运动(即以-6 000 mm处为起始点, 系统输入r=200t-6 000 (mm), 记为实验Ⅰ)和正弦运动(即以-1 000 mm处为起始点, 系统输入r=1 000 sin(t/5-π/2) (mm), 记为实验Ⅱ);同时, 滑块以200 mm/s和1 000 mm/s的速度沿横梁运动.通过与Yao[14]设计的PID同步控制算法比较跟踪误差和同步误差, 得到如下几组实验结果.
实验Ⅰ 匀速运动
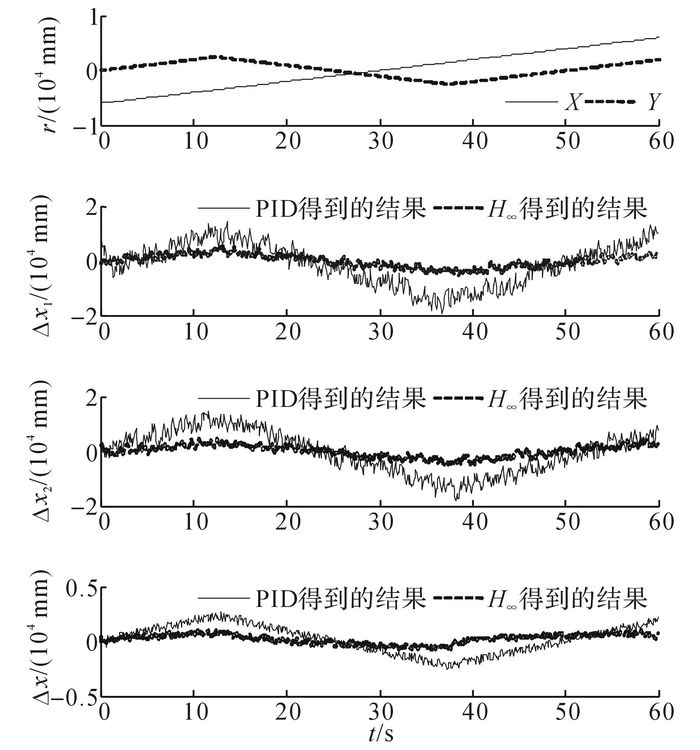
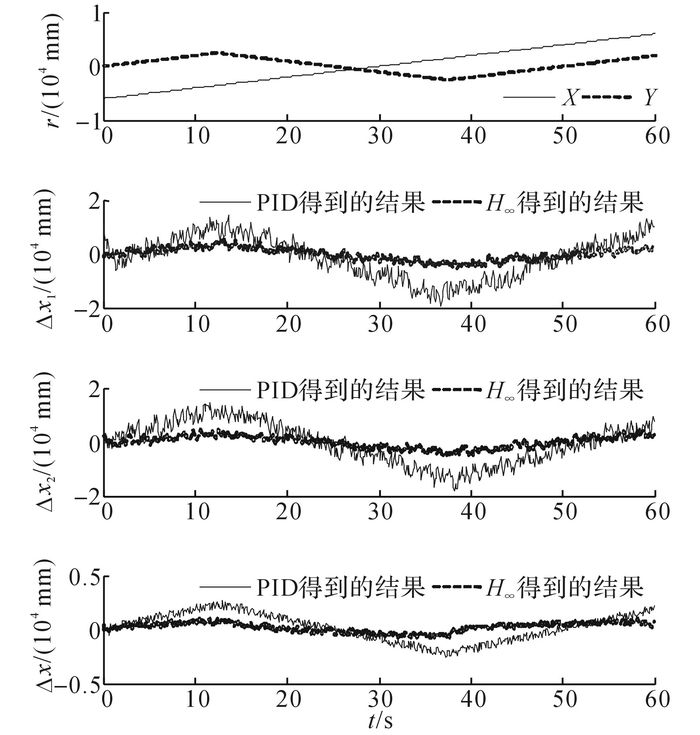
图 7、8给出X向双驱作匀速运动的情况下, 滑块分别以200和1 000 mm/s运动的跟踪误差和同步误差实验结果.图中, r为系统的给定量, Δx1为x1向的跟踪误差, Δx2为x2向的跟踪误差, Δx为x向的同步误差.由图 7、8可以看出, 当滑块在横梁的一端时, 跟踪误差和同步误差都将增大.当滑块速度增加时, 会加剧系统的不确定性和时变干扰的幅值.与传统PID控制算法相比, 采用提出的H∞交叉耦合控制算法能够得到较小的跟踪误差和同步误差.
|
图 7 X轴的跟踪误差和同步误差曲线(200 mm/s) Fig. 7 Tracking and synchronous error curves (200 mm/s) |
|
图 8 X轴的跟踪误差和同步曲线(1 000 mm/s) Fig. 8 Tracking and synchronous error curves (1 000 mm/s) |
实验Ⅱ 正弦运动
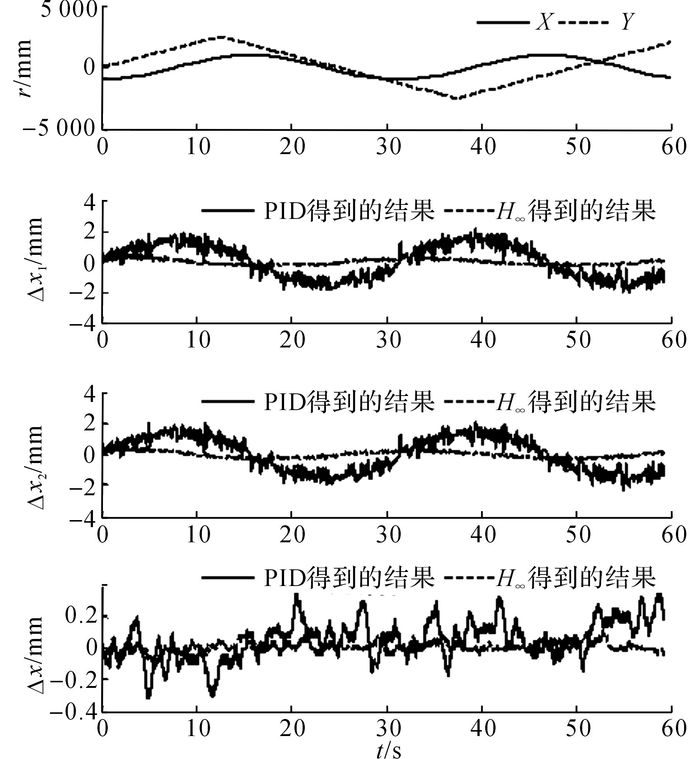
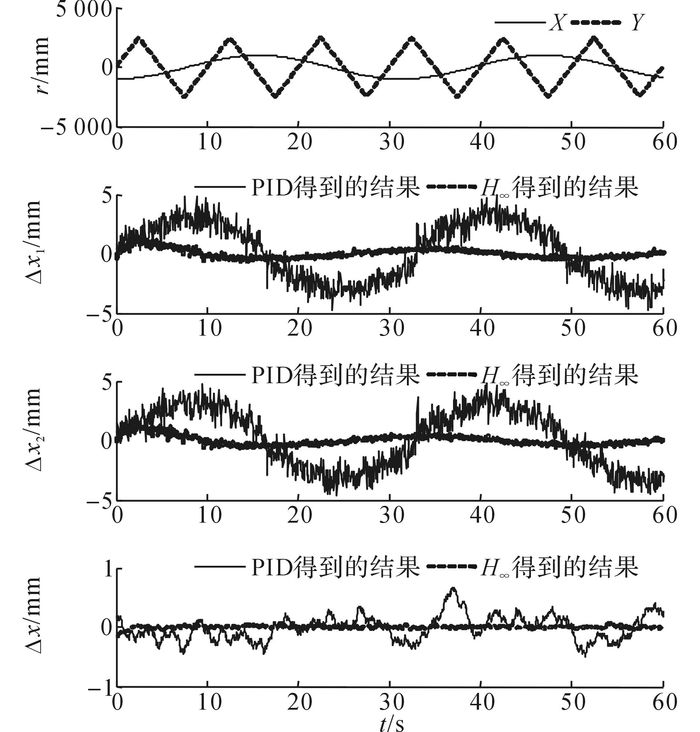
图 9、10给出X向双驱作正弦运动情况下, 滑块分别以200和1 000 mm/s的速度运动的跟踪误差和同步误差实验结果.当滑块速度由200 mm/s增加到1 000 mm/s时, 系统的不确定性和时变干扰的幅值都将增大, 采用提出的H∞交叉耦合控制算法能够保证系统高精度同步运动.由表 1可以看出, 无论是匀速运动还是正弦运动, 采用PID控制算法得到的最大跟踪误差和最大同步误差至少是采用H∞控制算法的3倍.
|
图 9 X轴的跟踪误差和同步误差曲线(200 mm/s) Fig. 9 Tracking and synchronous error curves (200 mm/s) |
|
图 10 X轴的跟踪误差和同步曲线(1 000 mm/s) Fig. 10 Tracking and synchronous error curves (1 000 mm/s) |
| 表 1 最大跟踪误差和同步误差 Table 1 Maximum tracking error and synchronous error |
针对具有参数不确定性和时变干扰特点的大型双驱龙门机床, 采用拉格朗日方程建立能够反映大质量滑块运动的动力学模型, 设计一种基于H∞交叉耦合算法的同步控制方法.所设计的H∞控制器对由滑块运动引起的时变干扰和不确定性具有鲁棒性, 同时, 设计的交叉耦合算法能够有效降低机床双驱间的同步控制误差.在某大型双驱龙门机床平台进行实验, 实验结果表明, 与PID控制算法相比, 该算法具有较好的鲁棒性.特别当滑块运动速度较大时, 该算法具有较好的同步控制精度.值得注意的是, 本文在实验中仅分析不同滑块速度对双驱同步控制的影响, 未考虑不同滑块质量的影响.在仿真实验中, 引入滑块质量因素, 研究该因素对负载参数的不确定性、动态响应、时变干扰强度的影响是后续工作的重点.另外, 针对负载不确定性和时变干扰的H∞控制器, 本文是采用基于混合灵敏度方法设计的, 在后续工作中将对H∞控制器的设计进行深入研究.
| [1] | ZHANG G, WU J, LIU P, et al. Dynamic analysis and model-based feedforward control of a 2-DoF translational parallel manipulator driven by linear motors[J]. Industrial Robot, 2013, 40(6): 597–609. DOI:10.1108/IR-01-2013-307 |
| [2] | WANG T, CASSANDRAS C G, POURAZARM S. Optimal motion control for energy-aware electric vehicles[J]. Control Engineering Practice, 2015, 38: 37–45. DOI:10.1016/j.conengprac.2014.12.013 |
| [3] | CHU B, KIM S, HONG D, et al. Optimal cross-coupled synchronizing control of dual-drive gantry system for a SMD assembly machine[J]. JSME International Journal, 2004, 47(3): 939–945. DOI:10.1299/jsmec.47.939 |
| [4] |
李玉霞, 赵万华, 程瑶, 等. 动梁式龙门机床的双驱同步控制系统建模[J].
西安交通大学学报, 2012, 46(4): 119–124.
LI Yu-xia, ZHAO Wan-hua, CHENG Yao, et al. Synchronous control system modeling of gantry-typemachine tools[J]. Journal of Xi'an Jiaotong University, 2012, 46(4): 119–124. DOI:10.7652/xjtuxb201204020 |
| [5] | TEO C S, TAN K K, LIM S Y, et al. Dynamic modeling and adaptive control of an H-type gantry stage[J]. Mechatronics, 2007, 17(7): 361–367. DOI:10.1016/j.mechatronics.2007.04.004 |
| [6] | GARCIAHERREROS I, KESTELYN X, GOMAND J, et al. Model-based decoupling control method for dual-drive gantry stages: a case study with experimental validations[J]. Control Engineering Practice, 2013, 21(3): 298–307. DOI:10.1016/j.conengprac.2012.10.010 |
| [7] | TOMIZUKA M. Zero phase error tracking algorithm for digital control[J]. Journal of Dynamic Systems, Measurement, and Control, 1987, 109(1): 65–68. DOI:10.1115/1.3143822 |
| [8] | KOREN Y. Cross-coupled biaxial computer control for manufacturing systems[J]. Journal of Dynamic Systems, Measurement, and Control, 1980, 102(4): 265–272. DOI:10.1115/1.3149612 |
| [9] | YEH S S, TSAI Z H, HSU P L. Applications of integrated motion controllers for precise CNC machines[J]. International Journal of Advanced Manufacturing Technology, 2009, 44(9/10): 906–920. |
| [10] | HU C X, YAO B, WANG Q F. Coordinated adaptive robust contouring controller design for an industrial biaxial precision gantry[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(5): 728–735. DOI:10.1109/TMECH.2009.2032292 |
| [11] | XI X C, ZHAO W S, POO A N. Improving CNC contouring accuracy by robust digital integral sliding mode control[J]. International Journal of Machine Tools and Manufacture, 2015, 88: 51–61. DOI:10.1016/j.ijmachtools.2014.08.005 |
| [12] |
赵希梅, 赵久威. 精密直驱龙门系统的交叉耦合互补滑模控制[J].
电工技术学报, 2015, 30(11): 7–12.
ZHAO Xi-mei, ZHAO Jiu-wei. Cross-coupled complementary sliding mode control for precision direct-drive gantry system[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 7–12. DOI:10.3969/j.issn.1000-6753.2015.11.002 |
| [13] | LIU Z Z, LUO F L, RAHMAN M A. Robust and precision motion control system of linear motor direct drive for high-speed x-y table positioning mechanism[J]. IEEE Transactions on Industrial Electronics, 2005, 52(5): 1357–1363. DOI:10.1109/TIE.2005.855661 |
| [14] |
朱国昕, 郭庆鼎. 双直线电机伺服系统动态同步进给的鲁棒H∞控制[J].
沈阳工业大学学报, 2005, 27(5): 510–513.
ZHU Guo-xin, GUO Qing-ding. Robust H∞ control for dynamically synchronized feed in dual linear motor servo system[J]. Journal of Shenyang University of Technology, 2005, 27(5): 510–513. |
| [15] | YAO W S. Modeling and synchronous control of dual mechanically coupled linear servo system[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 37(4): 041109. |
| [16] | GARCIAHERREROS I, KESTELYN X, GOMAND J, et al. Decoupling basis control of dual-drive gantry stages for path-tracking applications [C]// 2010 IEEE International Symposium on Industrial Electronics(SIE). Bari: IEEE, 2010: 131-136. |
| [17] |
张木楷, COOKPeter. H-无穷控制器的设计及仿真(英文)[J].
大连工业大学学报, 2012, 31(5): 225–230.
ZHANG Mu-kai, COOK Peter. Design and simulation of H∞ controller[J]. Journal of Dalian PolytechnicUniversity, 2012, 31(5): 225–230. |
| [18] | DOYLE J C, GLOVER K, PRAMOD P, et al. State-space solutions to standard H2 and H∞ control problems[J]. IEEE Transactions on Automatic Control, 1989, 34(8): 831–847. DOI:10.1109/9.29425 |



