2. 杭叉集团股份有限公司, 浙江 临安 311305
2. Hangzhou Fork Group Limited Company, Lin'an 311305, China
冲击问题广泛存在于汽车船舶、航空航天、建筑桥梁等工程领域, 模拟计算方法的研究越来越受到人们的重视[1-3].冲击问题分为单次冲击和多次冲击, 对于单次冲击问题, 国内外普遍采用显式动力学方法进行计算, 无需考虑冲击效应的累积.对于多次冲击问题, 由于顺次冲击效应的耦合, 计算过程更复杂.
国内外关于多次冲击问题已有大量深入的研究, Khedmati等[4]对甲板结构的多次冲击进行有限元仿真分析, 结果表明, 动态仿真比静态仿真更符合实际情况, 且冲击行为与冲击时间间隔有关.程志胜等[5]建立瓦楞纸板多次冲击的非线性参数模型, 通过动力学计算和试验结果的比较进行验证.刘中华等[6]研究梁-梁多次弹塑性撞击问题的多次接触撞击分离, 提出将局部弹性接触模型与有限差分法相结合的方法.高震等[7]研究非线性有限元法在钢结构冲击(碰撞)计算中的有效性, 提出单点多次冲击累积损伤的模拟计算方法.Abdelkrim等[8-9]提出列车循环动载荷作用下路基的累积变形的计算方法.以上文献主要针对定点多次冲击问题进行模拟计算, 各次冲击位置不变, 不考虑加载间隔, 累积模拟时间短.
动点间歇性冲击问题是多次冲击的一种重要形式, 各次冲击的位置不同, 且顺次冲击存在一定的加载间隔, 累积模拟时间长.本文对动点间歇性冲击变形累积的问题进行研究, 在多次冲击普遍采用的并型变形叠加法[10]和串型变形累积法[8]的基础上, 提出可控串型变形累积的计算方法.以某型号叉车护顶架为例, 分别采用并型变形叠加法、串型变形累积法和可控串型累积法, 对护顶架动载试验的最终变形进行显式动力学计算.结合实际动载试验, 分析3种变形累积方法的精确性和有效性, 并型变形叠加法的计算时间短, 但结果误差较大;串型变形累积法要求有较大的冲击时间间隔, 计算时间较长;可控串型变形累积法解决了前两种方法存在的局限性, 在满足结果精确性的基础上大大缩短了计算时间.
1 动点间歇性冲击变形累积计算冲击变形是评估机械结构安全性的重要指标, 对于多次冲击的显式动力学数值计算, 存在冲击变形累积的问题.下面介绍3种变形累积方法的基本原理.
1.1 并型变形叠加法并型变形叠加法不考虑各次冲击之间的关系, 在初始状态的前提下, 对各个冲击点进行单独动力学分析.提取各个测点单次冲击的塑性变形, 然后直接进行线性叠加, 得到各个测点的总体变形, 计算公式如下:
| $\begin{array}{l} {U_{\rm{s}}}\left( {n,m} \right) = \sum\limits_{i = 1}^n {[u\left( {i,m} \right) - {u_{\rm{t}}}\left( {i,m} \right)]} = \\ \quad \quad \quad \quad \quad \sum\limits_{i = 1}^n {{U_{\rm{s}}}\left( {i,m} \right)} . \end{array}$ | (1) |
式中:u(i, m)、ut(i, m)、us(i, m)分别为第m点在第i次冲击时的总变形、弹性变形和塑性变形, Us(n, m)为第m个冲击点在第n次冲击后的总体塑性变形.
并型变形叠加法各个冲击点的计算相互独立, 可以同时进行, 节约时间成本, 但仅适用于小变形累积的计算, 在大变形累计的求解中会产生较大的误差.
1.2 串型变形累积法串型变形累积法充分考虑前、后冲击步之间的关联, 在前一次冲击的塑性变形、残余应力等的基础上进行连续的动力学计算, 更符合实际情况.对不同点的冲击计算需要先后进行, 计算时间较长.经过对计算过程的监控发现, 单次计算时间随冲击次数的增加呈递增趋势, 可能是由单元畸变或是残余应力等冲击条件的变化导致的.
1.3 可控串型变形累积法由于显式动力学计算方法是条件稳定的, 时间步长必须满足Courant准则[11].显式动力学分析可以计算每个单元的最高阶频率对应的稳定时间极限.
| ${\Delta _{{\rm{sta}}}} = \frac{{{L^{\rm{e}}}}}{{{C_{\rm{d}}}}}.$ | (2) |
式中:Le为单元在各个尺寸方向上的最小值;Cd为模型材料的波速,
| ${C_{\rm{d}}} = \sqrt {\frac{E}{\rho }} ,$ | (3) |
其中,E为材料的弹性模量,ρ为材料的密度.
由式(2)、(3) 可知:稳定时间极限与单元最小尺寸成正比, 与材料波速成反比.在材料不变的情况下, 单元最小尺寸增大n倍, 则稳定时间极限Δsta可以增大n倍, 不考虑网格密度的影响, 相应的计算时间缩短n倍;但单元尺寸过大, 会影响计算精度.在显式动力学计算中, 希望在不影响计算结果精度的同时, 单元的最小尺寸尽可能大[12].
由于在动点间歇性冲击数值模拟中, 随着冲击次数的增加, 局部单元产生畸变, 稳定极限减小, 会造成计算时间的增长.本文根据显式动力学条件稳定的特点, 在串型变形累积法的基础上, 提出基于单元重构的可控串型变形累积法.如图 1所示为该方法的整个过程.图中, t0为单次冲击模拟时间;ti为第i次冲击载荷从冲击接触开始到结束所用的时间;Δt为冲击之间的加载间隔, 是指前一次冲击接触结束到下一次冲击接触开始的时间, 可以使受冲击后的结构通过振荡达到状态稳定, 消除弹性变形和残余应力.
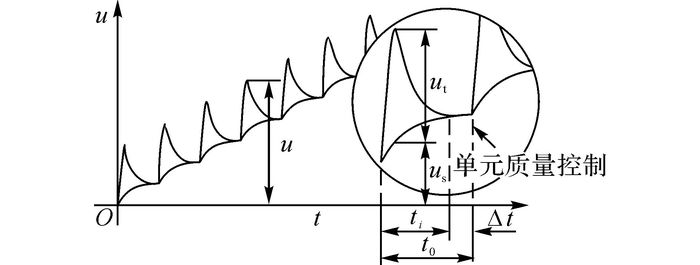
|
图 1 可控串型变形累积法示意图 Fig. 1 Sketch map of controllable cascade form deformation accumulation method |
在每一次计算结束后, 对影响下一次计算的单元质量进行控制, 原理如图 2所示.
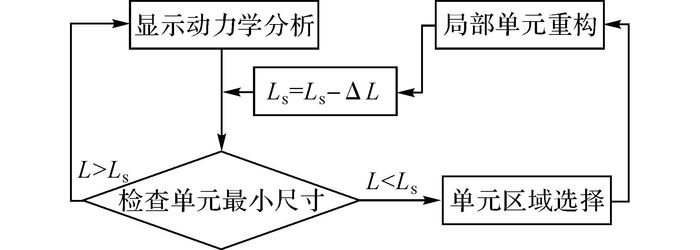
|
图 2 单元质量控制程序 Fig. 2 Mesh quality control procedures |
设置LS为标准单元最小尺寸, 此时对应的标准时间步长为ΔS.每隔时间S检查一次单元最小尺寸L, 若L>LS, 则继续计算;若单元长度L<LS, 则选取单元尺寸小于LS区域处的单元, 进行单元重构, 将LS减少单元基本长度ΔL, 再次检查L, 直至满足继续进行计算的条件为止.该方法可以对单元质量进行不断调整, 同时通过动态改变单元最小尺寸LS的方法, 消除了由于大变形区域单元无法达到既定要求造成的死循环现象.该方法在不降低计算精度的同时, 缩短了整体计算时间.
2 叉车护顶架动载试验及其模拟计算护顶架是叉车的主要防护结构, 承受意外跌落物冲击载荷, 具有抵抗永久变形的能力, 保障叉车驾驶员的生命安全[10, 13].ISO6055:2004明确规定了叉车护顶架动载试验的规范和要求, 主要采用动点间歇性冲击的方法, 对护顶架不同位置依次进行10次冲击, 每次冲击都是在前次冲击效应的基础上进行, 最终结果是10次冲击变形的累积.本文采用显式动力学方法, 对护顶架动载试验进行数值模拟, 按照上述提到的3种方法进行变形累积, 求解护顶架的最终变形, 将模拟结果与实际试验结果进行对比.
2.1 叉车护顶架的动载试验依据国际标准ISO6055《工业车辆护顶架技术要求和试验方法》[14]的要求, 开展护顶架动载试验.动载试验模型包括护顶架和跌落物体两部分, 跌落物是边长为300 mm的正方体, 质量为45 kg.试验要求跌落物从1500 mm的高处冲击护顶架不同位置10次.按照标准要求, 在动载试验中把护顶架安装在与所涉及配套叉车安装方式相同的测试底盘上进行试验, 护顶架动载试验现场如图 3所示.

|
图 3 护顶架动载试验 Fig. 3 Dynamic test of forklift overhead guard |
为了便于定位和测量, 落点标记在护顶架顶棚的上表面, 如图 4所示;测点标记在护顶架顶棚的下表面且易于测量的位置, 如图 5所示.用激光测距仪分别测量这些测点到某一固定参考面的垂直距离.跌落物通过悬挂装置定位, 使用激光测距仪测量重块到护顶架的距离, 并使重块位置与护顶架上的落点对应.定位完成后, 释放悬挂在护顶架上的绳子, 对护顶架进行冲击.分别测量这些点到参考面的垂直距离, 试验之前所测数值与试验后所测数值之差是护顶架测点的竖直变形量.按照上述方法, 对护顶架上方10个标定落点进行冲击, 得到各个测点的最终变形.
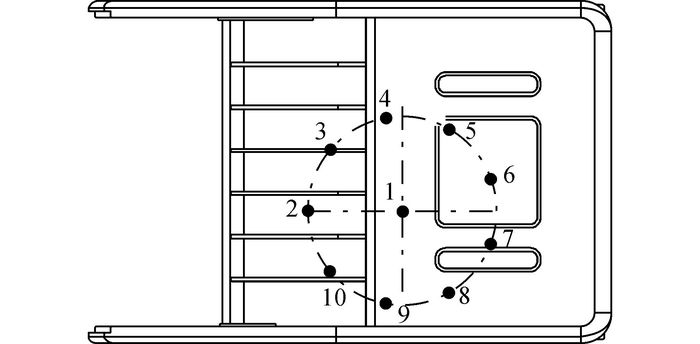
|
图 4 动载试验落点位置 Fig. 4 Markers of drop points |

|
图 5 动载试验测点位置 Fig. 5 Markers of measure locations |
冲击问题是接触和碰撞同时存在的复杂力学问题, 可以使用单自由度弹簧阻尼系统模拟[15], 运动方程如下:
| $m\ddot u + c\dot u + ku = F\left( t \right).$ | (4) |
式中:m为质量, k为弹簧刚度, c为阻尼系数, F(t)为外力, u为以静力平衡位置为基准的位移.
采用中心差分法, 得到速度和位移的关系如下:
| $\dot u\left( {{t_{n + \frac{1}{2}}}} \right) = \dot u\left( {{t_{n - \frac{1}{2}}}} \right) + \frac{1}{2}\left( {\Delta {t_{n + \frac{1}{2}}} + \Delta {t_{n - \frac{1}{2}}}} \right)\ddot u\left( {{t_n}} \right),$ | (5) |
| $u({t_{n + 1}}) = \dot u({t_n}) + \dot u({t_{n + \frac{1}{2}}})\Delta {t_{n + \frac{1}{2}}}.$ | (6) |
在整个时域范围内, 由式(4)~(6) 可以“显式”求得各个离散时间点处的位移、速度和加速度.所谓“显式”, 是指增量步结束的状态仅依赖于该增量步开始时的位移、速度和加速度.
2.2.2 显示动力学分析参数的设定在显示动力学分析过程中, 单元类型、初始单元最小尺寸L0、单次冲击模拟时间T0等、标准单元最小尺寸LS、单元质量控制程序运行间隔S、单元基本长度ΔL参数的设置对结果的准确度及计算时间的长短有直接影响.本文对采用3种变形累积方法进行显示动力学分析的参数设置, 如表 1所示.为了保证分析结果的可比性, 3种方法的模拟计算均在同一台计算机上完成.
| 表 1 动载试验显示动力学分析参数 Table 1 Explicit dynamics simulation parameters of dynamictest |
1) 单元参数.
由于护顶架结构以薄壁型钢和板材为主, 单元类型选用适用于薄壳结构的Belytschko-Tsay壳单元.对于所用的护顶架有限元模型, 采用不同的单元最小尺寸进行单次冲击, 并与单次冲击试验结果比较, 得出护顶架不同单元最小尺寸下的变形结果误差率和模拟计算时间, 如表 2所示.表中,Lmin为最小单元尺寸,ν为结果误差率,ts为模拟计算时间.分析计算结果可得:将单元最小尺寸设定为16 mm左右, 可以保证在不影响计算精度的情况下, 计算时间较短.
| 表 2 不同最小单元尺寸单次冲击模拟结果 Table 2 Single impact simulation results of different minimum mesh size |
为了使单元最小尺寸尽可能大, 在单元质量控制程序中, 设置可控串型变形累积法质量控制程序中LS设定为8 mm, ΔL设定为0.5 mm, S为30 min.
2) 单次冲击模拟时间.
由于护顶架动载试验属于动点间歇性冲击, 顺次冲击之间存在一定的加载间隔, 在实际试验中的加载间隔是由调整重块的高度以及对准试验点位置所用的时间来决定的, 每次冲击间隔约为5 min.在模拟计算时, 过大的加载间隔将会导致计算时间很长.通过对护顶架单次冲击进行模拟计算, 得到护顶架受单次冲击后的稳态曲线, 如图 6所示.图中, T为模拟时间, Y为护顶架受冲击部分某一点的变形.取护顶架达到稳态所用的最短时间1 100 ms作为单次冲击模拟时间T0.
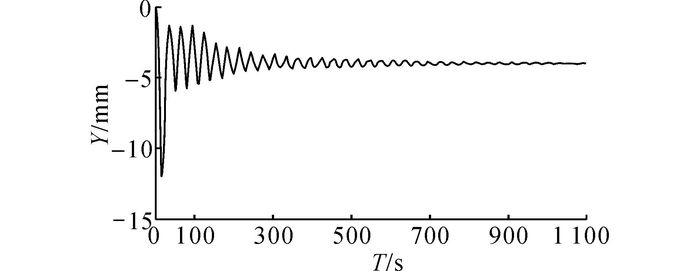
|
图 6 护顶架单次冲击稳态图 Fig. 6 Steady state diagram of single impact on overhead guard |
在护顶架动载试验仿真计算中, 能量分布是否合理是衡量模型准确性的重要因素.在碰撞过程中, 动能急剧下降, 内能迅速上升, 系统总能量由于重力的做功而增加.接触开始瞬间总能量E为跌落物的动能, 由式(7) 计算可得, 结果为662 J.
| $E = Mg\Delta h.$ | (7) |
式中:M为跌落物质量, g为重力加速度, Δh为跌落物到护顶架的距离.
在显式动力学分析过程中, 能量守恒方程为
| ${E_{\rm{T}}} = {E_{\rm{I}}} + {E_{\rm{K}}} + {E_{\rm{A}}} + {E_{\rm{W}}}.$ | (8) |
式中:ET为总能量(不包含势能);EI为内能;EK为动能;EA为伪应变能;EW为除重力外的其他外力做功, 在动载试验中, EW=0.
伪应变能主要由于沙漏因素、壳单元与梁单元的横向切应变存储的能量.按照显式动力学能量评估标准可知, 伪应变能所占的比例不高于5%, 所以需要对单点积分产生的沙漏进行控制, 本次分析采用Flanagan-Belytschko刚度公式来控制沙漏.
护顶架动载试验第一冲击的能量曲线如图 7所示.为了清楚地显示碰撞时的能量变化, 取0~80 ms区间的曲线.在3 ms左右跌落物体与护顶架发生接触, 此时的ET为667 J, 与理论计算一致.在8 ms左右, EK和EI达到了波谷和波峰, 此时跌落物和护顶架发生最大接触, 护顶架产生最大弹塑性变形;在13 ms左右, 护顶架弹性变形基本消失, 此时由于跌落物产生一定程度的反弹, 重力做负功, 动能和总能量的总体呈轻微下降的趋势.能量变化的总体趋势符合式(8) 所述的守恒条件.由此可知, 该仿真模型准确可靠.
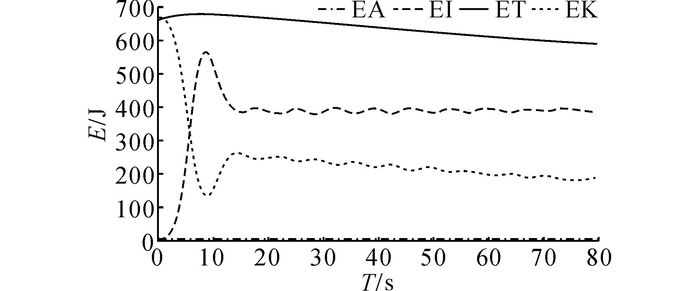
|
图 7 第一次冲击的能量曲线 Fig. 7 Energy curve of first dynamic load |
采用并型变形叠加、串型变形累积和可控串型变形累积法3种方法计算护顶架最终变形, 与实际试验结果相比较, 得出3种方法的误差率, 如表 3所示.各个测点试验测量和数值模拟变形的结果如图 8所示.
| 表 3 3种方法结果的误差率 Table 3 Result error rate of three methods |
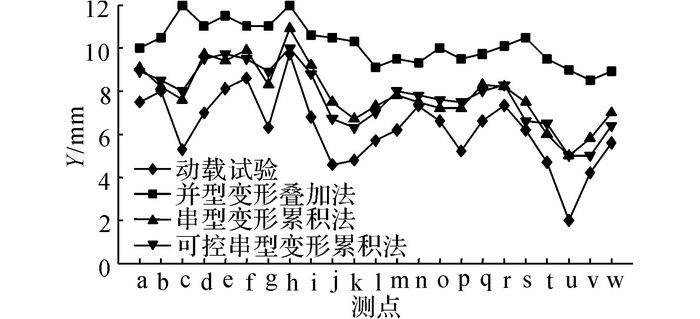
|
图 8 护顶架测点变形结果对比 Fig. 8 Deformation results comparison of measurelocations |
分析表 3和图 8可以得出, 采用模拟计算得出的结果均比实际试验结果略大, 采用并型叠加法得出的结果与实际试验结果相差较大, 误差率为48%.采用串型累积法和可控串型累积法得出的变形结果与实际试验结果较符合, 误差率分别减少到19%和20.5%, 并且不同测点的变形趋势与实际试验吻合.串型累积法和可控串型变形累积法能够更可靠地反映动点间歇性冲击的变形累积行为.
3.2 计算时间分析比较采用并型变形叠加、串型变形累积和可控串型变形累积法3种方法对护顶架动载试验所需的净计算时长, 如表 4所示.净计算时长是指显式动力学程序的运行时间, 不包括参数模型建立、修改等附加时间.可以得出:在相同的网格初始尺寸、单次冲击时间参数相同的情况下, 采用并型变形叠加法, 计算一次冲击所用时间平均为0.5 h, 10次冲击共需要净计算时长5 h;采用串型变形累积法, 求解完成净计算时长为88 h, 是并型变形叠加法的18倍左右;采用可控串型变形累积法对计算过程中的单元质量进行有效控制, 10次冲击完成所需的净计算时长为22.6 h, 比串型变形累积法减少了74%, 大大提高了计算效率.
| 表 4 3种方法的净计算时长 Table 4 Net computing time of three methods |
分析串型变形累积法和可控串型变形累积法得到的顺次冲击模拟计算时间的变化趋势如图 9所示.图中, i为冲击次数, Ti为每次冲击所用的时间.
使用串型变形累积法得到的顺次冲击计算时间呈指数增加, 最大单次计算时间为23.6 h.采用可控串型变形累积法得到的顺次冲击计算时间虽有增加, 但是增长速率十分缓慢, 最大单次计算时间仅为6 h.可控串型变形累积法通过单元质量的改善, 有效降低了动点间歇性冲击变形问题的计算时长, 在保证计算精度的基础上, 提高了计算效率.
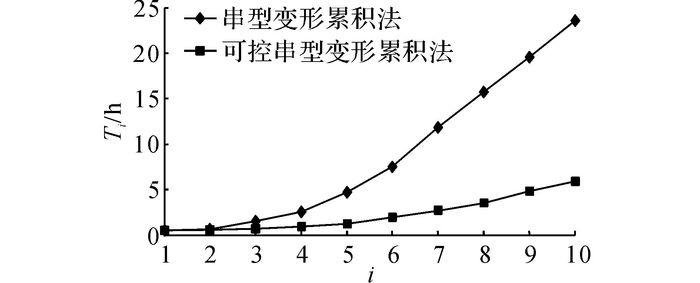
|
图 9 顺次冲击计算时间对比 Fig. 9 Computing time comparison of consequentlyimpact |
(1) 并型变形叠加法采用单次冲击变形线性叠加的方法计算最终变形, 计算简单方便、效率高, 但是结果误差率较大;串型变形累积法采用顺次冲击依次累积方法计算最终变形, 计算结果精度较并型变形叠加法提高40%, 但是计算时间较长, 是并型变形叠加法的18倍左右.
(2) 在动点间歇性冲击变形问题中, 单元的畸变会影响计算过程, 降低计算效率.本文提出的可控串型变形累积法对计算过程中的单元质量进行有效控制, 在保证良好计算精度的同时, 计算时间比串型变形累积法减少74%, 解决了并型变形叠加法存在的结果精度低和串型变形叠加法存在的计算时间长的问题.
(3) 采用提出的可控串型累积法计算所得的变形结果虽然与实际试验结果较吻合, 但是存在接近于20%的误差, 提高多次冲击模拟计算的精度是我们要关注和研究的现实问题.
| [1] |
王海峰. 冲击作用力学行为研究[J].
现代制造技术与装备, 2014(4): 43–44.
WANG Hai-feng. Studies on the contact mechanical behavior[J]. Modern Manufacturing Technology andEquipment, 2014(4): 43–44. |
| [2] |
王晨, 马卫华, 罗世辉, 等. 机车牵引销冲击动力学特性分析[J].
振动与冲击, 2016, 35(3): 34–40.
WANG Chen, MA Wei-hua, LUO Shi-hui, et al. Analysis on dynamic features of locomotive traction pin[J]. Journal of Vibration and Shock, 2016, 35(3): 34–40. |
| [3] |
丁问司, 丁元文, 范亚军. 交变气动冲击锤瞬态冲击特性分析[J].
机械工程学报, 2015, 51(3): 73–79.
DING Wen-si, DING Yuan-wen, FAN Ya-jun. Analysis of the transient impact performance of alternating pneumatic impact hammer[J]. Journal of Mechanical Engineering, 2015, 51(3): 73–79. |
| [4] | KHEDMATI M R, GHAVAMI K, EDALAT P. Static and dynamic structural analysis of aluminum craft deck structures, subjected to repeated impact load[J]. Latin American Journal of Solids and Structures, 2009, 6(3): 265–283. |
| [5] |
程志胜, 魏天路, 高德. 瓦楞纸板缓冲动态模型的建立及参数识别[J].
农业机械学报, 2000, 31(2): 100–103.
CHENG Zhi-sheng, WEI Tian-lu, GAO De. A model for dynamic compressive performance of corrugated board and its application[J]. Transactions of the Chinese Society of Agricultural Machinery, 2000, 31(2): 100–103. |
| [6] |
刘中华, 尹晓春. 自由梁对简支梁的多次弹塑性撞击[J].
机械工程学报, 2010, 46(10): 47–53.
LIU Zhong-hua, YIN Xiao-chun. Multiple elastic-plastic impacts between free-free beam and simply supported beam[J]. Journal of Mechanical Engineering, 2010, 46(10): 47–53. |
| [7] |
高震, 顾永宁, 胡志强. 结构冲击试验的校准计算[J].
船舶力学, 2005, 9(2): 77–82.
GAO Zhen, GU Yong-ning, HU Zhi-qiang. Benchmark study of structural impact test[J]. Journal of Ship Mechanics, 2005, 9(2): 77–82. |
| [8] | ABDELKRIM M, BONNET G, BUHAN P D. A computational procedure for predicting the long term residual settlement of a platform induced by repeated traffic loading[J]. Computers and Geotechnics, 2003, 30(6): 463–476. DOI:10.1016/S0266-352X(03)00010-7 |
| [9] |
边学成, 蒋红光, 申文明, 等. 基于模型试验的高铁路基动力累积变形研究[J].
土木工程学报, 2011, 44(6): 112–119.
BIAN Xue-cheng, JIANG Hong-guang, SHEN Wen-ming, et al. Study of accumulative deformation of high-speed railways based on physical model testing[J]. China Civil Engineering Journal, 2011, 44(6): 112–119. |
| [10] |
刘显贵, 刘诗彬, 李颖新, 等. 基于ISO6055的叉车护顶架动载安全性能的仿真及试验研究[J].
机械强度, 2014, 36(5): 757–761.
LIU Xian-gui, LIU Shi-bin, LI Ying-xin, et al. Simulation and experimental research of forklift overhead guard dynamic safety based on ISO 6055[J]. Journal of Mechanical Strength, 2014, 36(5): 757–761. |
| [11] |
余跃, 周鸿波, 童水光, 等. 大客车侧翻耐撞性的结构设计方法[J].
浙江大学学报:工学版, 2011, 45(4): 714–718.
YU Yue, ZHOU Hong-bo, TONG Shui-guang, et al. Structural design method for rollovers crashworthiness of large bus[J]. Journal of Zhejiang University: Engineering Science, 2011, 45(4): 714–718. |
| [12] | 庄茁, 由小川, 廖剑晖. 基于ABAQUS的有限元分析和应用[M]. 北京: 清华大学出版社, 2009: 204-206. |
| [13] | TODOROV G, KAMBEROV K, ROMANOV B, et al. Safety and reliability assesment of forklift truck cabine based on virtual prototype [C]//Proceedings of the International Conference on Manufacturing Systems. Bucharest: Romania Academy Press, 2009: 1842-3183. |
| [14] | ISO6055. Industrial trucks: overhead guards-specification and testing [S]. Switzerland: ISO, 2004. |
| [15] | 张策. 机械动力学[M]. 2版. 北京: 高等教育出版社, 2008: 117-123. |



