随着人类开发利用海洋资源的脚步不断加快, 各种水下机器人应运而生.传统的基于螺旋桨的水下推进器, 在推进过程中会产生侧向涡流, 增加能量消耗, 降低推进效率, 而且桨叶易被水草缠绕, 对环境扰动较大.在长期的自然选择中, 海洋生物进化出了优异的水下运动能力.由于仿生水下机器人游动机动性、游动效率以及对环境扰动小等方面的优势[1-2], 国内外研究人员根据鱼类的游动特性, 已经研究出了多种水下仿生机器人.
目前, 鱼类的运动推进模式主要分为两种:身体/尾鳍(body and/or caudal fin, BCF)推进模式和中央鳍/对鳍(median and/or paired fin, MPF)推进模式[3-4]. BCF推进模式仿生机器鱼最早问世[5], MPF推进模式仿生机器鱼起步较晚, 但由于在低速游动下, 推进效率、机动性、稳定性较BCF模式更出色[6], 更加适应水下搜救任务、环境监测、资源勘查、军事侦察等.其中, 鳐科(Rajiform)的胸鳍波动推进仿生机器鱼具有优异的游动性能, 国内外科研人员已经对胸鳍波动推进机理进行了相关研究, 并研制出胸鳍拍动推进仿生样机[7-10]、单长鳍推进仿生样机[11-12]、对称多长鳍推进仿生机器鱼样机[13-20].现有仿生样机实现了与仿生原型相似的游动运动, 但游动速度、机动性和稳定性与生物存在差距.
本文针对水下勘测和侦察任务需要机器人具有较高的机动性和稳定性的特点, 基于胸鳍波动推进鱼类魟鱼的生物学特征, 提出利用环形长鳍推进实现多自由度矢量推进的仿生机器魟鱼设计方案及游动控制策略.研制了仿生样机, 开展直线游动、机动转弯和动态浮沉实验, 分析波动参数对推进性能的影响.
1 仿生机器魟鱼设计 1.1 仿生原型的生物学特征分析魟鱼(见图 1)是一种以鳐科模式游动的底栖鱼类, 身体扁平, 呈圆盘状, 拥有围绕身体周围的宽大胸鳍及细长的尾.在游动时, 魟鱼通过胸鳍的波动运动实现灵活的水下运动, 游动稳定性高、机动性好, 并且能够在水下狭窄环境下实现原地的转弯和后退游动.

|
图 1 珍珠魟 Fig. 1 Freshwater stingray Potamotrygon motoro |
魟鱼胸鳍的波动运动具有较高的柔性, 骨骼结构中鳍条沿周向均布连接在体软骨上(见图 2)[21].在局部鳍条两侧肌肉纤维的差动拉动下, 能够实现鳍面的局部弯曲变形, 整个胸鳍内肌肉纤维的规律收缩和舒张使鳍面宏观上呈现出类似正弦波的运动.

|
MT-后鳍软骨;PR-前鳍软骨;R-鳍条;V-脊椎骨 图 2 珍珠魟骨骼的俯视图[21] Fig. 2 Dorsal view of cleared and stained skeleton of Potamotrygon motoro[21] |
仿生机器魟鱼旨在模仿魟鱼的外形和胸鳍结构, 实现与魟鱼相似的鳍波动运动和优异的游动性能.本文的仿生机器魟鱼“StingrayRobot Ⅲ”(见图 3)在原有仿生机器魟鱼设想[22]的基础上进行适当改进.该样机由端盖、上壳体、下壳体、环形长鳍、沉浮模块、姿态控制模块、控制电路板、电池和配重组成.

|
图 3 仿生机器魟鱼样机三维结构示意图 Fig. 3 Three-dimensional structure diagram of bionic robot prototype |
环形长鳍是仿生水下机器人的推进装置, 其中鳍条总数为20个, 且沿圆周均布, 每个舵机(Power HD1219MG)通过舵盘转接与一个鳍条固接, 便于控制鳍条带动鳍面呈现多种波形.姿态控制模块用于调整仿生样机的游动姿态, 针对原仿生样机设想中两轴滑台机构占用空间大、配重质量轻和调整能力弱的问题, 该仿生样机姿态控制模块采用4个圆周均布的离中心轴线较远的滑台机构, 降低了空间占用高度, 提高了姿态控制能力.
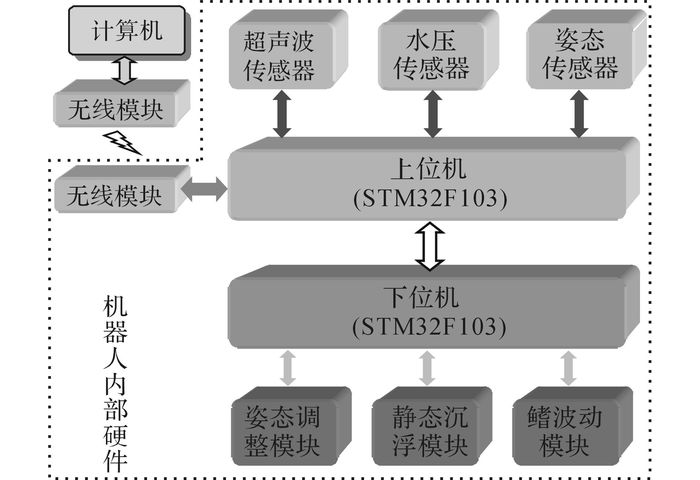
仿生机器魟鱼的控制系统(见图 4)包括:控制计算机、无线通信模块、主控上位机、运动控制下位机、超声传感器、水压传感器、姿态传感器、姿态调整模块、静态沉浮控制和鳍波动运动模块.计算机通过USB与无线通信模块连接, 将运动控制指令传送至仿生机器魟鱼.仿生机器魟鱼的主控上位机是一块STM32F103单片机, 与超声波传感器、水压传感器及姿态传感器组成主控模块, 主要功能是将机器人的运动指令进行解析, 将具体鳍的波动参数传输至运动控制下位机;同时, 通过超声、水压和姿态传感器来实时感知仿生水下机器人的运动状态参数.运动控制下位机选用一块STM32F103单片机, 功能是依据接收主控上位机的运动参数, 将具体控制信号输出给伺服舵机、静态沉浮模块和姿态控制模块中的步进电机.
|
图 4 仿生机器魟鱼控制系统结构图 Fig. 4 Control system diagram of robot |
仿生机器魟鱼样机(见图 5)采用3D打印技术制造了壳体结构, 环形鳍面为0.2 mm厚的硅胶薄膜.该样机的最大直径为460 mm, 其中壳体最大直径为380 mm, 高124 mm, 样机重10.8 kg.

|
图 5 仿生样机“Stingray Robot Ⅲ” Fig. 5 Bionic prototype "Stingray Robot Ⅲ" |
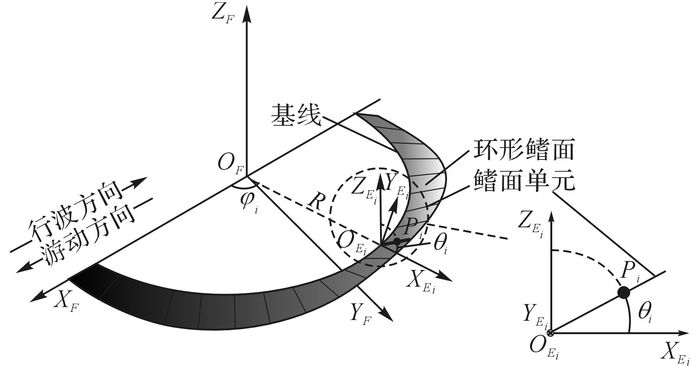
仿生机器魟鱼依靠环形长鳍的波动运动实现推进, 环形长鳍的波动波形近似为沿圆周方向的谐波.由于鳍面厚度与鳍面的宽度和长度相比为小量, 可以将环形长鳍的波动鳍面简化为无厚度空间曲面;环形鳍面可以看作由沿周向划分的鳍面单元构成, 波形为各鳍面单元规律运动的拟合运动.根据上述简化假设, 为了便于描述仿生样机环形长鳍的波动运动, 建立随体坐标系OFXFYFZF和鳍面单元坐标系OEXEYEZE, 如图 6所示.
|
图 6 环形胸鳍坐标系 Fig. 6 Coordinate system of annular pectoral fin |
第i个鳍面单元的运动为OEiXEiZEi平面内绕坐标原点的周期性摆动运动, 则鳍面单元上任意点Pi在鳍面单元坐标系中的坐标表示为
| $ ^{\rm{E}}{P_i} = {\left[ {l\cos {\theta _i},0,l\sin {\theta _i}} \right]^{\rm{T}}};l \in \left[ {0,L} \right]. $ | (1) |
式中:θi为第i个鳍面单元与OEiXEi轴的夹角, l为OEiPi长度, L为环形鳍面的宽度.
根据齐次坐标变换可知, 鳍面单元坐标系相对于随体坐标系的变换矩阵为
| $ _{\rm{E}}^{\rm{E}}T = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _i}}&{ - \sin {\varphi _i}}&0&{R\cos {\varphi _i}}\\ {\sin {\varphi _i}}&{\cos {\varphi _i}}&0&{R\sin {\varphi _i}}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]. $ | (2) |
式中:R为环形鳍面基线圆弧半径, φi为第i个鳍面单元坐标系OEiXEi轴与随体坐标系OFXF轴的夹角.
Pi在随体坐标系中的齐次坐标可以表示为
| $ ^{\rm{E}}{P_i} = _{\rm{E}}^{\rm{E}}T\left[ {\begin{array}{*{20}{c}} {^{\rm{E}}{P_i}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {l\cos {\theta _i}\cos {\varphi _i} + R\cos {\varphi _i}}\\ {l\cos {\theta _i}\sin {\varphi _i} + R\sin {\varphi _i}}\\ {l\sin {\theta _i}}\\ 1 \end{array}} \right]. $ | (3) |
在任意t时刻, 第i个鳍面单元的摆动角度可以表示为
| $ {\theta _i}\left( t \right) = {\theta _{\max }}\left( i \right)\sin \left( {2{\rm{\pi }}{f_i}t + {\psi _i}} \right). $ | (4) |
式中:θmax(i)为第i个鳍面单元的最大摆角, fi为第i个鳍面单元的摆动频率, ψi为第i个鳍面单元的初始相位角.
由于鳍面单元为绕随体坐标系Z轴呈圆周排列, 相邻两个鳍面单元的运动初始相位差Δψi与鳍面单元位置夹角Δφi之间的关系为
| $ \frac{{\Delta {\psi _i}}}{{2{\rm{\pi }}}} = n\frac{{\Delta {\varphi _i}}}{{2{\rm{\pi }}}}, $ | (5) |
| $ \frac{{\sum\nolimits_{j = 1}^i {\Delta {\psi _j}} }}{{2{\rm{\pi }}}} = n\frac{{\sum\nolimits_{j = 1}^i {\Delta {\varphi _j}} }}{{2{\rm{\pi }}}}. $ | (6) |
式中:Δψi=ψi-1-ψi, Δφi=φi-φi-1, n为环形鳍面上的波数.
整理式(5)、(6) 后, 第i个鳍面单元的初始相位角为
| $ {\psi _i} = {\psi _1} - n\left( {{\varphi _i} - {\varphi _1}} \right). $ | (7) |
将式(7) 代入式(4), 可得第i个鳍面单元的运动规律为
| $ {\theta _i}\left( t \right) = {\theta _{\max }}\left( i \right)\sin \left( {2{\rm{\pi }}{f_i}t + {\psi _1} - n\left( {{\varphi _i} - {\varphi _1}} \right)} \right). $ | (8) |
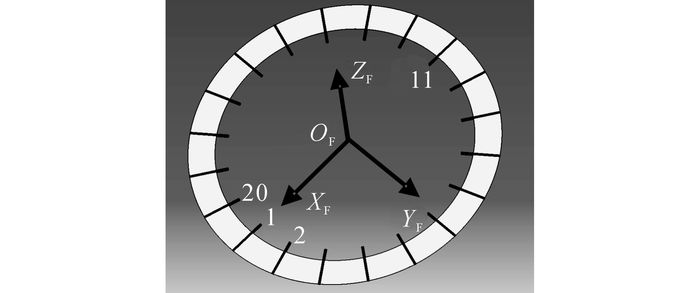
仿生机器魟鱼的环形长鳍由20个舵机驱动的碳纤维鳍条致动, 将致动鳍条按逆时针方向进行编号, 如图 7所示.
|
图 7 鳍条编号示意图 Fig. 7 Schematic diagram of fin ray number |
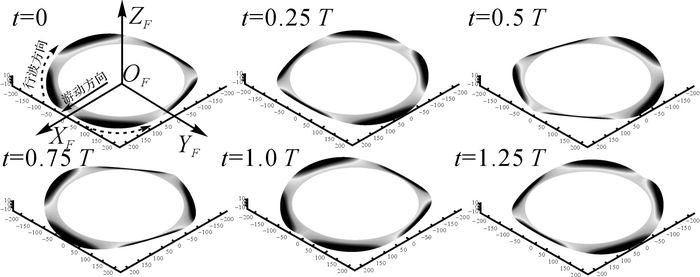
仿生机器魟鱼的环形长鳍结构能够通过不同的规律运动方式, 提供随体坐标系OFXFYF平面内任意径向方向的推力.以任意时刻XF正方向游动为例, 直线游动控制策略为游动过程中鳍面沿1号和11号鳍条所在的OFXFZF平面对称, 呈两侧对称的波动运动(见图 8).因为φ1=0, 鳍条的运动规律为
|
图 8 直线游动鳍面仿真波形 Fig. 8 Simulated waveforms of straight-line swimming |
| $ \begin{array}{*{20}{c}} {{\theta _i}\left( t \right) = {\theta _{\max }}\left( i \right)\sin \left( {2{\rm{ \mathsf{ π} }}{f_i}t + {\psi _1} - n{\varphi _i}} \right);}\\ {i = \left\{ {\begin{array}{*{20}{c}} {k,}&{k \in \left[ {1,11} \right];}\\ {22 - k,}&{k \in \left[ {12,20} \right].} \end{array}} \right.} \end{array} $ | (9) |
式中:k为致动鳍条编号, φi=(i-1)π/10.
3.2 机动转弯方式本文的仿生魟鱼样机有2种机动转弯方式.在直线巡游方式中, 仿生魟鱼两侧的波动幅值是相等的, 通过改变式(9) 的θmax(i), 即第i根鳍条的最大幅值, 使得OFXFZF两侧的波动幅值不一样, 两侧产生不相等的前向推力, 实现转弯.该转弯半径较大, 因此提出另一种机动转弯方式, 即通过环形长鳍鳍面呈现沿圆周方向的波动运动的策略, 实现原地的转弯运动.以从1号鳍条开始的原地右转波动运动为例, 鳍条运动规律为
| $ \left. \begin{array}{l} {\theta _i}\left( t \right) = {\theta _{\max }}\left( i \right)\sin \left( {2{\rm{\pi }}{f_i}t + {\psi _1} - n{\varphi _i}} \right);\\ i = k,\;\;\;\;\;\;\;\;\;k \in \left[ {1,20} \right]. \end{array} \right\} $ | (10) |
式中:
| $ {\varphi _i} = \left( {i - 1} \right){\rm{\pi /10}}{\rm{.}} $ |
仿生机器魟鱼样机主要是通过静态沉浮模块能够实现样机在水中的静态悬浮, 而在机动游动中主要依靠姿态控制模块与游动速度进行配合实现动态的上浮和下潜.样机动态浮沉策略为:在胸鳍巡游时, 通过样机内部的重心调节机构实现俯仰角的改变, 即改变鱼体的攻角实现动态浮沉.
4 仿生胸鳍波动推进器游动实验与分析为了研究样机的推进性能, 搭建实验平台, 如图 9所示.实验水箱为200 cm×80 cm×70 cm(长×宽×高)的钢化玻璃水箱, 实验水箱内装有测量标尺, 采用摄像机记录样机游动视频, 通过处理实验过程的图像序列可以获得样机游动的相关数据.

|
图 9 仿生水下机器人实验平台 Fig. 9 Testing platform of bionic underwater robot |
魟鱼直线巡游时, 胸鳍作类似正弦波运动, 单侧推进波的波数为1.2~1.5.当仿生机器魟鱼样机进行直线游动实验时, 鳍面为等波幅匀速波动, 每个鳍条的最大摆动角度和波动频率相等, 将样机鳍条的运动学参数设定为:n=2.5;θmax∈[0, 30°], 且每5°一个间隔;ψ1=0;每个鳍条的波动频率相同, fi∈[0.2, 1.2] Hz, 且每0.2 Hz一个间隔.
如图 10所示为当θmax为20°, 频率f为0.8 Hz时的仿生机器魟鱼样机直线巡游的图像序列.可以看出, 当仿生样机的环形胸鳍按直线游动控制策略游动时, 鳍面能够呈现出与游动方向相反的波动波形, 且波形较平滑, 样机游动稳定性好.

|
图 10 直线游动图像序列 Fig. 10 Video sequence of Stingray Robot Ⅲ during steady forward swimming |
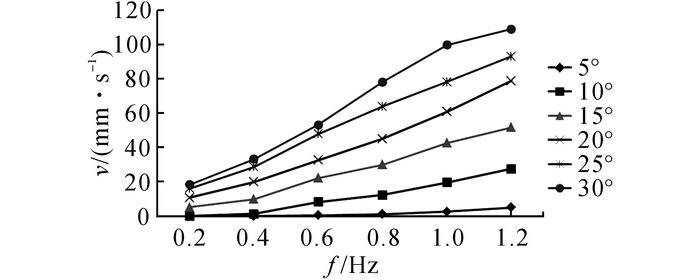
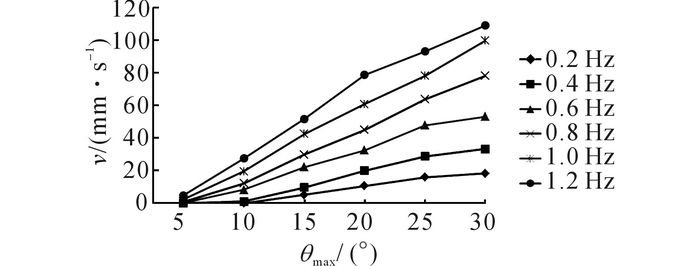
为了研究环形鳍面波动频率和波动幅值对仿生样机推进速度的影响, 通过分组实验对不同参数条件下的样机游动速度v进行测量, 实验结果如图 11、12所示.实验结果表明:当波动频率为0.4 Hz、波动幅值为15°以下时, 样机推进速度变化不明显;当频率和幅值继续增大时, 样机的游动速度随波动频率和波动幅值的增大而明显增大;当波动频率为1.2 Hz、波动幅值为30°时, 样机游动速度达到最大值109 mm/s(0.24体长/s).由于样机波动鳍面宽度与壳体宽度的比值小于生物原型, 波动产生的推进速度小于文献[21]中提及的生物游动速度0.9~3 BL/s.
|
图 11 频率对推进速度的影响 Fig. 11 Effect of frequency on average propulsion velocity |
|
图 12 幅值对推进速度的影响 Fig. 12 Effect of amplitude on average propulsion velocity |
在仿生样机原地转弯实验中, 整个环形鳍面上呈现2个完整的正弦波, 其他实验运动参数与直线游动实验相同.
如图 13所示为仿生样机原地顺时针转弯的图像序列.图中, 箭头表示机器鱼随体坐标系X轴的正方向.此时, 仿生样机鳍条最大摆角为20°, 频率为0.8 Hz, 转向速度约为42.8°/s.仿生样机在原地转弯游动过程中, 最大中心偏移量为18 mm, 并且游动非常平稳.较小偏移量的产生主要是由于水流扰动和鳍条摆动误差导致的.

|
图 13 顺时针原地旋转图像序列 Fig. 13 Video sequence of clockwise turning |
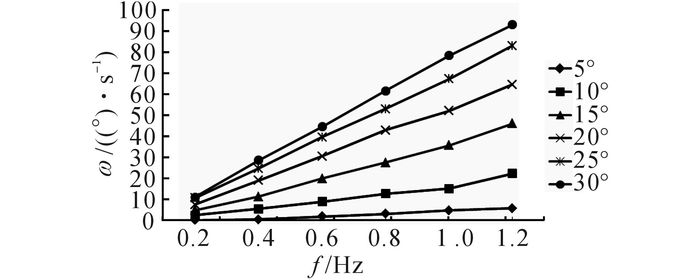
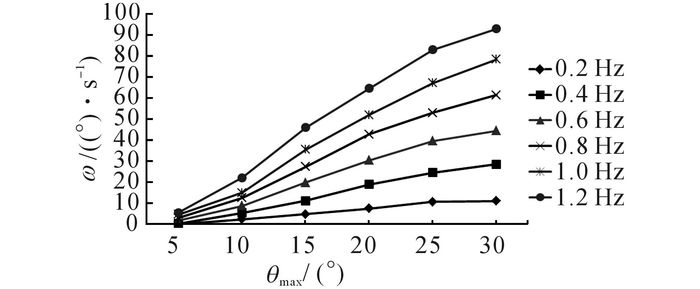
在不同的波动频率与波动幅值条件下, 对转弯速度ω的变化进行实验研究, 实验数据如图 14、15所示.通过实验发现, 在幅值相同的情况下, 随着波动频率的增加, 转弯速度随之增大, 且转弯速度与波动频率呈现近似的线性关系.在频率相同的情况下, 幅值越大, 对应的转弯速度随之增大.最大转弯速度为93°/s, 出现在波动频率为1.2 Hz、波动幅值为30°的情况下.
|
图 14 频率对机动转弯速度的影响 Fig. 14 Effect of frequency on average angular velocity of turning |
|
图 15 幅值对机动转弯速度的影响 Fig. 15 Effect of amplitude on average angular velocity of turning |
如图 16所示为仿生样机动态下沉图像序列.通过控制机器鱼内部重心调整机构, 实现重心前移, 使整个机器鱼与水平面成一定攻角, 如图 16中箭头所指的前进方向所示, 进而在游动时, 实现下潜, 此时θmax=30°, f=1 Hz, 下潜攻角约为25°.

|
图 16 下潜图像序列 Fig. 16 Video sequence of diving |
如图 17所示为仿生样机动态上浮图像序列.此时, 控制样机内部重心调整机构, 使得重心向后移, 实现与下潜相反的效果, 实现机器鱼的上浮, 此时θmax=30°, f=1 Hz, 上浮攻角约为25°.

|
图 17 上浮图像序列 Fig. 17 Video sequence of rising |
本文在分析仿生原型魟鱼形态和肌肉、骨骼结构的基础上, 设计一种仿生机器魟鱼.分析仿生环形长鳍的波动机理, 建立仿生样机在直线游动和原地转弯游动时, 鳍条致动单元的控制策略.仿生样机的实验结果表明, 环形胸鳍能够实现与生物近似的波动运动, 直线和转弯控制策略能够有效地控制仿生样机实现运动, 游动速度和原地转弯速度随波动频率和波动幅值的增大而增大, 最大直线游动速度可达109 mm/s, 最大原地转弯速度可达93°/s.样机游动平稳、机动性好, 为未来高性能水下机器人研究提供了一种新的仿生推进方式.在后续研究中, 将采用CFD仿真与DPIV技术对环形鳍波动推进的水动力学机理和高效推进机制进行深入研究, 并对现有的仿生样机进行继续改进和优化.针对高波动频率下的高速巡游性能开展深入研究, 以期获得更好的综合性能.
| [1] | TRIANTAFYLLOU M S, TRIANTAFYLLOU G S. An efficient swimming machine[J]. Scientific American, 1995, 272(3): 64–70. DOI:10.1038/scientificamerican0395-64 |
| [2] | BANDYOPADHYAY P R. Trends in biorobotic autonomous undersea vehicles[J]. IEEE Journal of Oceanic Engineering, 2005, 30(1): 109–139. DOI:10.1109/JOE.2005.843748 |
| [3] | WEBB P W. Form and function in fish swimming[J]. Scientific American, 1984, 251(1): 72–83. DOI:10.1038/scientificamerican0784-72 |
| [4] | SFAKIOTAKIS M, LANE D M, DAVIES J B C. Review of fish swimming modes for aquatic locomotion[J]. IEEE Journal of Oceanic Engineering, 1999, 24(2): 237–252. DOI:10.1109/48.757275 |
| [5] | BARRETT SCOTT D. The design of a flexible hull undersea vehicle propelled by an oscillating foil [D].Massachusetts: Massachusetts Institute of Technology, 1994. https://www.researchgate.net/publication/37603717_The_design_of_a_flexible_hull_undersea_vehicle_propelled_by_an_oscillating_foil |
| [6] | HIROYOSHI S, NAOMI K, KOICHI S. Load characteristics of mechanical pectoral fin[J]. Experiments in Fluids, 2008, 44(5): 759–771. DOI:10.1007/s00348-007-0432-x |
| [7] | CAO Y, BI S, CAI Y, et al. Applying central pattern generators to control the robofish with oscillating pectoral fins[J]. Industrial Robot, 2015, 42(5): 392–405. DOI:10.1108/IR-03-2015-0044 |
| [8] | MA H, CAI Y, WANG Y, et al. A biomimetic cownose ray robot fish with oscillating and chordwise twisting flexible pectoral fins[J]. Industrial Robot, 2015, 42(3): 214–221. DOI:10.1108/IR-11-2014-0426 |
| [9] | RUSSO R S, BLEMKER S S, FISH F E, et al. Biomechanical model of batoid (skates and rays) pectoral fins predicts the influence of skeletal structure on fin kinematics: implications for bio-inspired design[J]. Bioinspiration and Biomimetics, 2015, 10(4): 2–15. |
| [10] | YANG S B, QIU J, HAN X Y. Kinematics modeling and experiments of pectoral oscillation propulsion robotic fish[J]. Journal of Bionic Engineering, 2009, 6(2): 174–179. DOI:10.1016/S1672-6529(08)60114-6 |
| [11] | BIOLEAU R, FAN L, MOORE T. Mechanization of rajiform swimming motion: the making of Robo-ray [R]. Vancouver: Engineering Physics Project Laboratory, University of British Columbia, 2002. |
| [12] |
胡天江. 仿生长鳍波动适应性理论与控制方法研究[D]. 长沙: 国防科学技术大学, 2008.
HU Tian-jiang. Undulation adaptability theory and control for the biomimetic undulating fins [D]. Changsha: National University of Defense Technology, 2008. |
| [13] | ALVARADO P V, CHIN S, LARSON W, et al. A soft body under-actuated approach to multi degree of freedom biomimetic robots: a stingray example [C]// Proceedings of the 2010 3rd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics. Tokyo: IEEE, 2010: 473-478. |
| [14] | RAHMAN M M, SUGIMORI S, MIKI H, et al. Braking performance of a biomimetic squid-like underwater robot[J]. Journal of Bionic Engineering, 2013, 10(3): 265–273. DOI:10.1016/S1672-6529(13)60222-X |
| [15] |
高飞, 王玉魁, 王振龙, 等. 形状记忆合金丝驱动的仿生墨鱼水下机器人的原型设计[J].
机器人, 2013, 35(3): 346–351.
GAO Fei, WANG Yu-kui, WANG Zhen-long, et al. Prototype design of a kind of biomimetic cuttlefish underwater robot actuated by SMA wires[J]. Robot, 2013, 35(3): 346–351. |
| [16] | WEI Q P, WANG S, DONG X, et al. Design and kinetic analysis of a biomimetic underwater vehicle with two undulating long-fns[J]. Acta Automatica Sinica, 2013, 39(8): 1330–1338. DOI:10.1016/S1874-1029(13)60049-X |
| [17] |
章永华, 何建慧. 仿生蓝点魟的结构设计及建模[J].
机械科学与技术, 2012, 31(4): 627–632.
ZHANG Yong-hua, HE Jian-hui. Mechanism design and modeling of a biomimetic bluespotted ray[J]. Mechanical Science and Techology for Aerospace Engineering, 2012, 31(4): 627–632. |
| [18] |
王扬威. 仿生墨鱼机器人及其关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
WANG Yang-wei. Biomimetic cuttlefish robot and its key technology research [D]. Harbin: Harbin Institute of Technology, 2011. |
| [19] |
杭观荣, 王振龙, 王扬威, 等. 肌肉性静水骨骼原理的仿乌贼鳍推进器[J].
哈尔滨工业大学学报, 2009, 41(11): 59–64.
HANG Guan-rong, WANG Zhen-long, WANG Yang-wei, et al. Squid fin-like propeller based on the principle of muscular hydrostat[J]. Journal of Harbin Institute of Technology, 2009, 41(11): 59–64. DOI:10.3321/j.issn:0367-6234.2009.11.012 |
| [20] |
谢海斌. 基于多波动鳍推进的仿生水下机器人设计、建模与控制[D]. 长沙: 国防科学技术大学, 2006.
XIE Hai-bin. Design, modeling, and control of bionic underwater vehicle propelled by multiple underlatory fins [D]. Changsha: National University of Defense Technology, 2006. |
| [21] | ROSENBERGER L J, WESTNEAT M W. Functional morphology of undulatory pectoral fin locomotion in the stingray taeniura lymma (chondrichthyes: Dasyatidae)[J]. The Journal of Experimental Biology, 1999, 202: 3523–3539. |
| [22] | 王扬威, 赵东标, 刘凯, 等. 仿生机器魟鱼及其运动方式: 201110428002. 7[P]. 2012-06-27. |


