2. 火箭军工程大学 空间工程系, 陕西 西安 710025
2. School of Space Engineering, Rocket Force University of Engineering, Xi'an 710025, China
在超音速流场中, 激波是一种必然出现的物理现象.在模拟高超声速流动时, 激波位置及强度的预测将直接影响气动力计算的精度, 对于激波位置与强度的预测一直以来都是计算流体力学的一个重要领域.在计算过程中, 为了保证流场中物理量变化剧烈区域(如激波区域)的数值解的精度, 需要较高的网格分辨率.若在全流场区域统一采用较小的网格尺度, 会导致网格数量急剧增大, 致使计算效率降低;若统一采用较大的网格尺度, 虽然网格数量减小, 计算效率增高, 但不能保证流场(尤其是激波区域)的计算精度.为了平衡计算效率与计算精度之间的关系, 最有效的解决途径是采用自适应网格方法.
Berger[1]首次将自适应网格技术引入超音速流场领域.该方法利用简单的Richardson截断误差来确定激波等强梯度压力变换区域, 在这些区域内自适应地增加了网格密度.Lohner[2]针对结构网格, 采用自适应网格方法对转捩问题进行求解.蒋跃文等[3]针对非结构网格, 首次将图像处理思想应用到自适应网格方法中, 获得了较好的实验结果.Dadone等[4-7]对基于结构网格中的自适应方法进行系统的研究, 提出2种改进的自适应网格方法:对称面方法(symmetry technique, ST)和曲面修正对称面方法(curvature corrected symmetry technique, CCST).随后, Dadone等[8]针对结构网格, 在激波等流场敏感区域同时采用2种网格进行插值计算来自适应地增加网格密度, 这种重叠网格的方法称为Iblanking方法[9].Wang等[10]针对二维非结构网格进行自适应网格方法研究.以上所有都是基于二维网格结构进行的研究, 但是现实中的流场具有三维特征.邹建锋等[11-12]将自适应网格方法扩展到三维非网格结构中, 分别针对各向异性非结构网格和Delaunay三角形的非结构化网格, 自适应地增加网格密度.
已有的自适应网格方法大多基于结构网格和非结构网格, 但是这两种网格对于具有复杂边界的物面生成难度大, 需要消耗巨大的存储资源, 计算效率低.针对这些问题, 本文针对三维笛卡尔网格, 提出基于图像处理思想的自适应网格方法.该方法充分考虑了激波流场区域的特征.1) 将流场计算网格与图像像素类比, 以较粗的笛卡尔网格覆盖流场全域.2) 对全域进行流场计算, 根据计算的结果将流场区域分割成3部分:加密区、稀疏区和过渡区, 并为各区域赋予不同的权值, 其中加密区是压力梯度较大的区域, 即需要增加密度的区域;稀疏区是压力梯度较小的区域, 即不需要增加密度的区域;过渡区介于两者之间.3) 在需要较高分辨率的激波区域(即加密区), 将网格按照权值的大小进行细分, 权值越大, 细分的程度越高;稀疏区权值为零, 所以保持原网格不变;为了避免网格畸变, 即避免将笛卡尔网格中细分程度较高的加密区和细分程度较低的稀疏直接连接, 过渡区根据两者的权重差对中间区域的网格进行细分, 从而保证了整个流场的光滑性、连续性和稳定性.4) 重新对流场进行计算, 反复迭代步骤2)、3), 直至达到所需的网格分辨率, 算法终止.
1 控制方程设流动的绝对速度为q=ui+vj+wk, 其中i、j、k分别表示速度坐标系下3个坐标轴的单位矢量, u、v、w分别表示速度的3个分量.在速度坐标系下, 积分形式的流场控制方程, 即Navier-Stokes方程组, 可以表示如下:
| $ \frac{\partial }{{\partial t}}\iiint\limits_\mathit{\Omega } {\mathit{\boldsymbol{Q}}{\rm{d}}\mathit{\Omega }} + \iint\limits_S {\left( {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{q}}_{\rm{b}}}} \right) \cdot {\rm{d}}\mathit{\boldsymbol{S}}} = \frac{1}{{\operatorname{Re} }}\iint\limits_S {{\mathit{\boldsymbol{F}}^{\rm{V}}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}}. $ | (1) |
式中:
| $ \mathit{\boldsymbol{Q = }}{\left[ {\rho ,\rho u,\rho v,\rho w,\rho {e_{\rm{t}}}} \right]^{\rm{T}}}, $ |
| $ {\tau _{xx}} = \lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial u}}{{\partial x}}, $ |
| $ \mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} {\rho u}&{\rho v}&{\rho w} \\ {\rho {u^2} + p}&{\rho vu}&{\rho wu} \\ {\rho uv}&{\rho {v^2} + p}&{\rho wv} \\ {\rho uw}&{\rho vw}&{\rho {w^2} + p} \\ {\rho u{h_{\rm{t}}}}&{\rho v{h_{\rm{t}}}}&{\rho w{h_{\rm{t}}}} \end{array}} \right],{\mathit{\boldsymbol{F}}^{\rm{V}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ {{\tau _{xx}}}&{{\tau _{yx}}}&{{\tau _{zx}}} \\ {{\tau _{xy}}}&{{\tau _{yy}}}&{{\tau _{zy}}} \\ {{\tau _{xz}}}&{{\tau _{yz}}}&{{\tau _{zz}}} \\ {{\phi _x}}&{{\phi _y}}&{{\phi _z}} \end{array}} \right], $ |
| $ {\tau _{yy}} = \lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial v}}{{\partial y}}, $ |
| $ {\tau _{zy}} = {\tau _{yz}} = \mu \left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right), $ |
| $ {\tau _{zz}} = \lambda \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + 2\mu \frac{{\partial w}}{{\partial z}}, $ |
| $ {\tau _{xy}} = {\tau _{yx}} = \mu \left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right), $ |
| $ {\tau _{xz}} = {\tau _{zx}} = \mu \left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right), $ |
| $ {\phi _x} = u{\tau _{xx}} + v{\tau _{xy}} + w{\tau _{xz}} + k\frac{{\partial T}}{{\partial x}}, $ |
| $ {\phi _y} = u{\tau _{yx}} + v{\tau _{yy}} + w{\tau _{yz}} + k\frac{{\partial T}}{{\partial y}}, $ |
| $ {\phi _z} = u{\tau _{zx}} + v{\tau _{zy}} + w{\tau _{zz}} + k\frac{{\partial T}}{{\partial z}}. $ |
ρ、(u, v, w)、E、H、p、T、μ和k分别为密度、速度的分量、总能、总焓、压强、温度、黏性系数和热传导系数.式(1) 不封闭, 需要引入完全气体热力学关系式p=(γ-1)ρ[E-0.5(u2+v2+w2)]和Stokes假设H=E+p/ρ.由Stokes假设可得, λ和μ的关系为3λ+2μ=0, 其中γ为比热系数, 对于空气, 可以取γ=1.4.
2 自适应网格方法自适应网格方法要解决的首要问题是判断一个网格是否需要进行加密(即增加密度), 然后将需要加密的网格区域从整个流场的网格中准确地分离出来.这个判断和分离的过程可以借鉴图像处理问题中识别和标示目标物体的过程, 即将流场中的网格类比于图像处理中的像素, 由于流场中出现激波的区域流动变化比较剧烈, 该区域的压力梯度较大, 可以将流场中每个网格的压力作为该网格的特征值, 并将其类比于图像处理中每个像素的灰度.下面给出针对三维笛卡尔网格的一种基于图像处理思想的自适应网格方法的具体步骤.
1) 初始网格.以较粗的笛卡尔网格覆盖流场全域.
2) 标识网格.按照式(1) 对全域进行流场计算, 根据计算的结果将流场区域分割成3部分:加密区、稀疏区和过渡区, 并为各区域赋予不同的权值, 其中加密区是压力梯度较大的区域, 即需要增加密度的区域;稀疏区是压力梯度较小的区域, 即不需要增加密度的区域;过渡区介于两者之间.流场区域分割和权值计算的具体过程如下.
首先, 定义网格i的两个特征函数如下:
| $ \left. \begin{array}{l} {G_a}\left( i \right) = \left| {\Delta {p_i}} \right| \cdot V_i^a,\;\;a < 1;\\ {G_b}\left( i \right) = \left| {\Delta {p_i}} \right| \cdot V_i^b,\;\;b > 1. \end{array} \right\} $ | (2) |
式中:Ga(i)和Gb(i)分别为网格i的稀疏特征函数和加密特征函数, Δpi为网格i的压力梯度, Vi为网格i的体积, 指数a和b分别为给定的调节参数.
借鉴图像处理中图像二值化的概念, 将流场网格进行三值化扩展, 定义如下所示的初始权值函数:
| $ f\left( i \right) = \left\{ \begin{array}{l} 1,\;\;{G_a}\left( i \right) < {\mathit{\Phi }_a};\\ - 1,\;\;{G_b}\left( i \right) > {\mathit{\Phi }_b};\\ 0,\;\;\;\;\;其他. \end{array} \right\} $ | (3) |
根据式(3) 给出的权值将整个网格分割成加密区、稀疏区和过渡区3个部分.式(3) 中, Φa和Φb分别为稀疏区和加密区的阈值.若网格i的稀疏特征函数值Ga(i)小于给定的稀疏阈值Φa, 则网格i属于稀疏区;若加密特征函数值Gb(i)大于给定的加密阈值Φb, 则网格i属于加密区;否则, 网格i属于过渡区.
为了避免单纯梯度计算可能带来的噪声(即造成孤立加密点), 将相邻网格之间的相互影响考虑到权值函数的计算中.在三维笛卡尔网格中, 每个网格i有6个邻居, 分别记为L1、L2、L3、L4、L5和L6, 则网格i的中间权值函数定义如下:
| $ \begin{array}{l} {h_1}\left( i \right) = f\left( i \right) + f\left( {{L_1}} \right) + f\left( {{L_2}} \right) + f\left( {{L_3}} \right) + f\left( {{L_4}} \right) + \\ \;\;\;\;\;\;\;\;\;\;f\left( {{L_5}} \right) + f\left( {{L_6}} \right). \end{array} $ | (4) |
对网格i进行多轮迭代更新, 网格i的中间权值称为网格i的第一轮中间权值.定义网格i的第j轮中间权值函数如下:
| $ \begin{array}{l} {h_j}\left( i \right) = {h_{j - 1}}\left( i \right) + {h_{j - 1}}\left( {{L_1}} \right) + {h_{j - 1}}\left( {{L_2}} \right) + {h_{j - 1}}\left( {{L_3}} \right) + \\ \;\;\;\;\;\;\;\;\;\;{h_{j - 1}}\left( {{L_4}} \right) + {h_{j - 1}}\left( {{L_5}} \right) + {h_{j - 1}}\left( {{L_6}} \right). \end{array} $ | (5) |
实验表明, 只要对式(5) 进行两轮迭代(j=2), 就可以使激波区域网格的中间权值函数值比其他区域明显增加.给定两个阈值N1和N2, 网格i的最终权值函数k(i)如下所示:
| $ k\left( i \right) = \left\{ \begin{array}{l} - 1,\;\;\;\;\;{h_j}\left( i \right) < 0;\\ 1,\;\;\;\;\;\;\;{h_j}\left( i \right) > {N_1};\\ 2,\;\;\;\;\;\;{h_j}\left( i \right) > {N_2};\\ 0,\;\;\;\;\;\;其他. \end{array} \right. $ | (6) |
由式(6) 可知, 当k(i)=1和k(i)=2时, 网格i属于加密区, 且网格i的权值越大, 说明激波强度越大, 该区域被细分的程度越高;当k(i)=-1时, 网格i属于稀疏区, 说明该区域的流动变化较平缓, 可不作任何加密处理;当k(i)=0时, 网格i属于过渡区, 说明该区域位于加密区和稀疏区的中间过渡区域.
3) 自适应加密.在需要较高分辨率的激波区域(即加密区), 将网格按照权值的大小进行细分, 权值越大, 细分的程度越高;稀疏区权值为零, 所以保持原网格不变;为了避免网格畸变, 即避免将笛卡尔网格中细分程度较高的加密区和细分程度较低的稀疏直接连接, 过渡区根据两者的权重差对中间区域的网格进行细分, 从而保证了整个流场的光滑性、连续性和稳定性.
4) 终止判断.重新对流场进行计算, 反复迭代步骤2)、3), 直至达到所需的网格分辨率, 算法终止.
3 实验与结果分析以某型超声速飞机为例, 外形如图 1所示, 流场计算取速度M=2.4, 迎角α=0, 在该计算条件下, 飞机头部和机翼表面将出现激波.通过激波处的网格加密情况来验证提出的自适应网格方法的有效性.算法参数设置如下:a=0.42, b=1.03, Φa=3.2, Φb= 0.45, N1=8, N2=12.

|
图 1 超声速飞机计算数模 Fig. 1 Computational model of the supersonic aircraft |
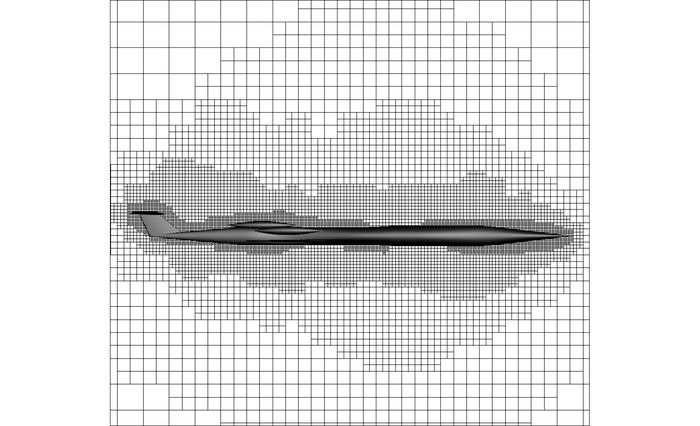
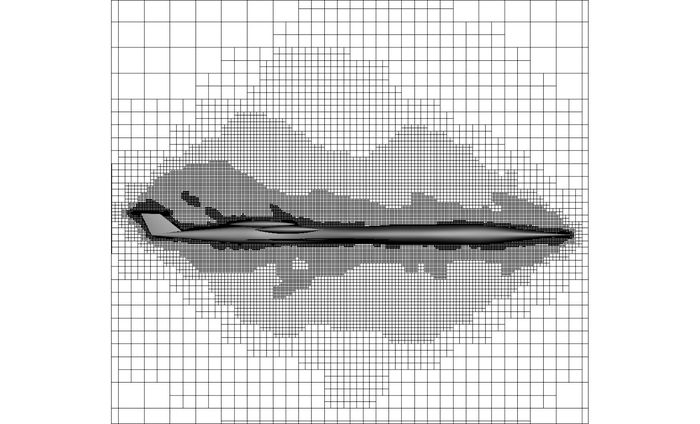
对于流场, 采用三维笛卡尔网格作为初始网格.图 2给出初始网格的生成情况.由图 2可以看出, 初始网格在飞机的头部和中部出现密集区, 这是由于飞机头部曲率变化较大, 中部有机翼及发动机, 因而在这两处区域会生成较密集的网格.初始网格加密依据的是飞机的外形复杂度, 但是飞机的外形复杂区域不一定是激波出现区域.图 3给出采用所提自适应网格方法求得的网格加密情况.可以看出, 在飞机头部、中部机翼及尾翼部分出现激波, 这3个区域的网格较图 2而言更密集, 即加密效果更好.从图 3还可以看出, 在加密区和稀疏区之间的过渡区域, 采用所提算法生成的网格更光滑, 过渡更平缓, 避免了畸形区域的产生.
|
图 2 初始网格 Fig. 2 Initial grid |
|
图 3 自适应后的网格 Fig. 3 Adaptive grid |
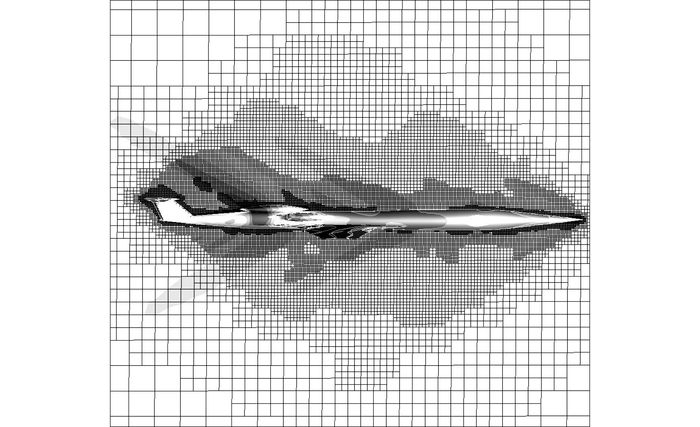
为了验证提出算法的加密区域是激波出现的区域, 图 4给出飞机表面及对称面的压力云图.从图 4可以看出, 对称面上在飞机中部和尾部的箭头阴影区域表征了流场中激波出现的位置, 应用算法对自适应网格加密后, 加密区域与激波区域一致.可见, 采用所提算法能够有效地捕捉激波并在激波区域进行加密, 提高了激波的辨识度.为了更直观地体现这一结论, 图 5给出飞机的三维网格示意图.可以看出, 在对称面和机翼延展方向网格均有明显的加密, 加密区域与激波区域一致, 再次验证了采用提出算法能够有效地捕捉激波, 并在激波区域进行加密.
|
图 4 对称面压力云图 Fig. 4 Symmetric surface pressure distribution |

|
图 5 三维网格示意图 Fig. 5 Three-dimension grid |
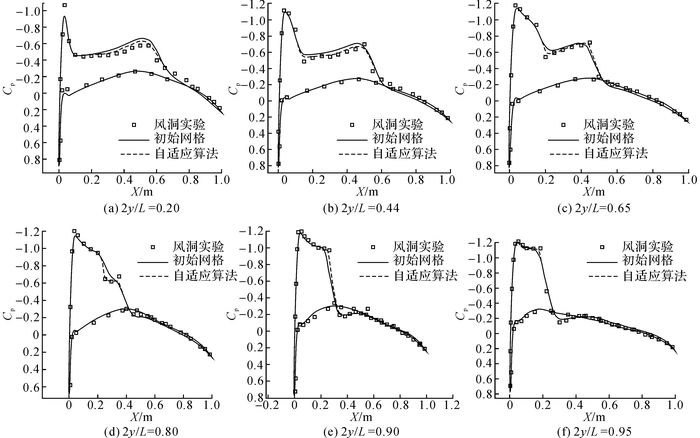
以上是通过直观的网格生成情况对算法进行分析, 下面从压力分布、升力系数与阻力系数3个方面, 将提出的自适应算法获得的计算值与真实风洞实验值[13]进行比较, 通过两者的吻合程度来验证算法的有效性;将提出的自适应算法获得的计算值与采用初始网格(即不采用自适应加密技术的网格)进行流场计算获得的计算结果进行对比, 验证了所提算法的有效性和高效性.图 6给出沿机翼展6个剖面的压力分布情况.图中, X/C为单位化的弦长, Cp为压力.从图 6(a)~(c)可以看出, 在20%、44%及65%位置处, 出现双激波(压力系数急剧下降区域), 采用提出算法得到的计算值与风洞实验值保持一致, 而初始网格对应的计算值与实验值存在较明显的误差.由图 6(d) ~(f)可以看出, 在80%、90%及95%截面处, 只出现了一道激波, 计算值与实验值能够很好地吻合, 且吻合度明显优于初始网格对应的计算结果.可见, 在6个剖面, 采用所提算法获得的计算值与风洞实验值均能保持一致, 即采用该算法能够有效地捕捉激波.
|
图 6 机翼不同剖面压力分布图 Fig. 6 Pressure distributions of different sections of wing |
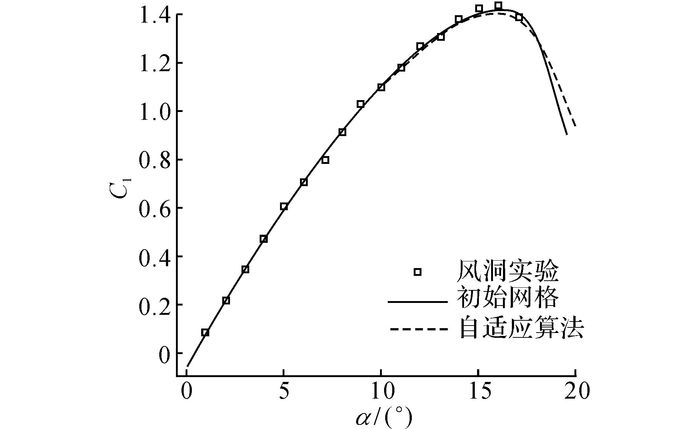
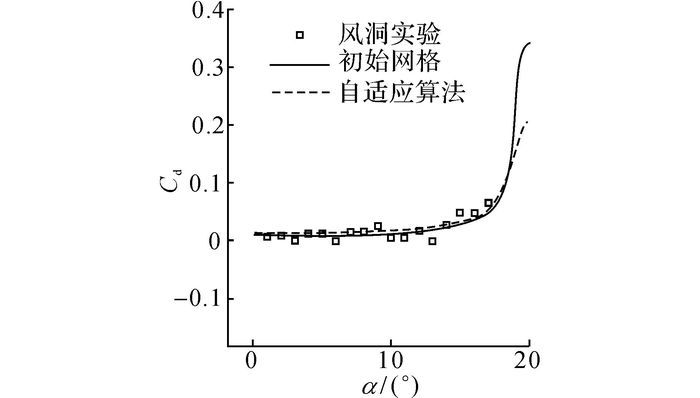
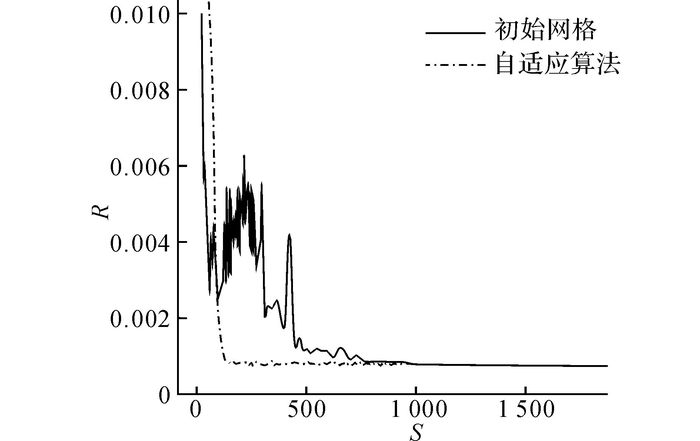
图 7、8分别给出升力系数Cl与阻力系数Cd的计算值与风洞实验值的对比结果.可以看出, 采用提出算法获得的升力系数和阻力系数均与风洞实验值相一致, 可见采用该算法能够有效地捕捉激波, 从而进一步验证了该算法的有效性.将所提自适应算法的收敛速度与采用初始网格进行流场计算的收敛速度进行比较, 如图 9所示.图中, S为算法的迭代步数;R为收敛残差, 即相邻两次迭代计算结果的差值.从图 9可以看出, 若采用初始网格进行计算, 则算法迭代1 000次后才能收敛, 但所提算法在迭代300次后即可收敛, 可见所提算法的高效性.
|
图 7 升力系数结果对比图 Fig. 7 Comparison results of lift coefficient |
|
图 8 阻力系数结果对比图 Fig. 8 Comparison results of drag coefficient |
|
图 9 算法收敛速度对比图 Fig. 9 Comparison on convergence speed of algorithms |
本文借鉴图像处理的思想, 提出基于笛卡尔网格的自适应网格方法.该方法充分考虑了激波流场区域的特征, 根据压力梯度将流场区域分割为加密区、稀疏区和过渡区3个部分, 并为各区域赋予不同的权值;将网格按照权值的大小进行细分, 权值越大, 细分的程度越高;为了避免网格中细分程度较高的加密区和细分程度较低的稀疏直接连接, 过渡区根据两者的权重差对中间区域的网格进行细分, 从而保证了整个流场的光滑性、连续性和稳定性.以某型飞机超音速流动为例, 从压力分布、升力系数与阻力系数3个方面对算法进行验证.结果表明, 采用该方法能够有效地捕捉到激波附近的流场信息, 提高了激波的辨识度.
| [1] | BERGER M J. Adaptive mesh refinement for hyperbolic partial differential equations[J]. Journal of Computational Physics, 1984, 53(84): 484–512. |
| [2] | LOHNER R. Adaptive remeshing for transient problems[J]. Computer Methods in Applied Mechanics and Engineering, 1989, 75: 195–214. DOI:10.1016/0045-7825(89)90024-8 |
| [3] |
蒋跃文, 叶正寅, 王刚. 基于图像处理思想的自适应网格技术[J].
空气动力学学报, 2009, 27(6): 713–717.
JIANG Yue-wen, YE Zheng-yin, WANG Gang. Methods of adaptive unstructured grid based on image process methodology[J]. Acta Aerodynamica Sinica, 2009, 27(6): 713–717. |
| [4] | DADONE A, GROSSMAN B. Surface boundary conditions for the numerical solution of the Euler equations[J]. AIAA Journal, 2012, 32(2): 285–293. |
| [5] | CARAMIA G, DADONE A. A general purpose adjoint formulation for inviscid 2D/3D fluid dynamic optimization [C]//10th AIAA Multidisciplinary Design Optimization Conference. National Harbor, Maryland: AIAA, 2014: 1174. |
| [6] | DADONE A, GROSSMAN B. Fast convergence of viscous airfoil design problems[J]. AIAA Journal, 2015, 40(10): 1997–2005. |
| [7] | DADONE A, GROSSMAN B. Ghost-cell method for inviscid two-dimensional flows on Cartesian grids[J]. AIAA Journal, 2012, 42(12): 2499–2507. |
| [8] | DADONE A, GROSSMAN B. Ghost-cell method with far-field coarsening and mesh adaptation for Cartesian grids[J]. Computers and Fluids, 2006, 35(7): 676–687. DOI:10.1016/j.compfluid.2006.01.013 |
| [9] | DURBIN P A, IACCARINO G. An approach to local refinement of structured grids[J]. Journal of Computational Physics, 2002, 181(2): 639–653. DOI:10.1006/jcph.2002.7147 |
| [10] | WANG Z J, SUN Y. Curvature-based wall boundary condition for the Euler equations on unstructured grids[J]. AIAA Journal, 2012, 41(1): 27–33. |
| [11] |
邹建锋, 盛东, 邢菲, 等. 基于各向异性非结构网格的超声速流动自适应计算[J].
空气动力学学报, 2013, 31(1): 47–51.
ZOU Jian-feng, SHENG Dong, XING Fei, et al. Anisotropic unstructured mesh adaption for supersonic flow simulation[J]. Acta Aerodynamica Sinica, 2013, 31(1): 47–51. |
| [12] |
杜华坤, 冯德山, 汤井田. 基于Delaunay三角形的非结构化有限元GPR正演[J].
中南大学学报:自然科学版, 2015, 46(4): 1326–1334.
DU Hua-kun, FENG De-shan, TANG Jing-tian. GPR simulation by finite element method of unstructured grid based on Delaunay triangulation[J]. Journal of Central South University: Science and Technology, 2015, 46(4): 1326–1334. |
| [13] | GOYNE C P, RODRIGUEZ C G, KRAUSS R H, et al. Experimental and numerical study of a dual-mode scramjet combustor[J]. Journal of Propulsion and Power, 2015, 22(3): 481–489. |



