变几何桁架(variable geometry truss, VGT)机械臂是一种拥有广阔前景的机械臂.相对于连杆机械臂, VGT机械臂拥有更大的刚度、灵活性和工作空间等优点[1-3].VGT机械臂在空间大载荷转运, 工业自动化生产流水线和新型柔性机器人在轨服务中有着重要的作用, 一直受到广泛的关注[4-5].多节双八面体VGT机械臂是变几何桁架机械臂中的一种, 它由多个双八面体VGT单元组成.通过改变每个单元驱动平面上驱动器的长度来改变单元构形, 使末端运动平面发生移动和偏转来完成给定任务.对于多节双八面体VGT机械臂, 快速准确的逆运动学算法是轨迹规划和运动控制的基础, 有着重要的研究意义.
对于多节并联机械臂逆运动学算法, 目前研究主要分为雅可比矩阵法[6-7]、神经网络法[8]、优化方法[9]、解析方法等[10].雅可比矩阵方法利用机械臂的雅可比矩阵, 通过设定初值后迭代修正, 获得逆运动学解.雅可比矩阵法在求解串联机械臂和节数较少的并联机械臂时, 可以取得比较好的效果.由于并联机械臂含有多个驱动器, 在节数较多时雅可比矩阵维数很大, 在迭代计算过程中需要多次调用雅可比矩阵伪逆和正运动学, 计算速度和精度受到影响[6].采用神经网络法, 离线学习驱动器和末端运动平面移动的映射关系, 得到逆运动学的解.学习结果受到多驱动器输入的影响, 收敛性较难保证.优化方法适用于处理多驱动器的机械臂的规划问题, 然而较长的计算时间让它不适合在线使用, 并且算法通常不具有全局收敛性.解析方法依赖于对机械结构的几何分析, 直接根据给定的末端位置求解作动器的参数, 难点在于如何高效求解复杂的多节非线性约束方程.若能够解决非线性约束方程求解问题, 则解析方法相对于其他方法可以取得更准确和快速的效果.
针对单节双八面体VGT机械臂的逆运动学问题, 姜柏森等[11]推导了逆运动学解析解.对于多节双八面体VGT机械臂的逆运动学问题, 吴江等[2]采用神经网络拟合法求解三节机械臂逆运动学, 然而该方法在处理多节的机械臂逆运动学求解时, 速度和收敛性不能保证.Yang等[12]利用凸优化求解多节双八面体VGT机械臂逆运动学解, 然而构造凸函数需要额外加入一些驱动器杆长约束条件, 机械臂工作空间受到限制, 同时计算速度较慢.杭鲁滨等[13]利用Groebner基对单节双八面体单元进行运动学分析.由于Groebner基求解耗时, 同时容易出现增根和丢根的情况, 不适合于多节机械臂的逆运动学求解.
为了实现多节双八面体变几何桁架机械臂实时准确的运动控制, 使末端运动平面的位置和法向量按照到达指令值, 本文根据双八面体VGT机械臂对称特性, 推导逆运动学解析算法.建立2个辅助坐标系:P坐标系和M坐标系.将整体逆运动学问题分解为求解辅助坐标系旋转矩阵子问题和求解辅助坐标系内位置矢量子问题, 得出两节双八面体VGT机械臂的逆运动学解, 将两节逆运动学推广得出多节双八面体VGT机械臂逆运动学解析算法.仿真和实验结果表明, 采用该逆运动学解析算法可以快速准确地得出计算结果.
1 机械臂运动学模型双八面体变几何桁架机械臂的结构如图 1所示.每个单元包含两个连接平面和一个驱动平面.对于第k个单元, 定义固定在连接平面上的两个坐标系为k-1和k坐标系.0坐标系代表基座坐标系.机械臂的简化模型如图 1所示, 每个三角形表示一个连接平面, 两个相邻三角形表示一个桁架单元.定义k-1和k坐标系的位姿变换关系为
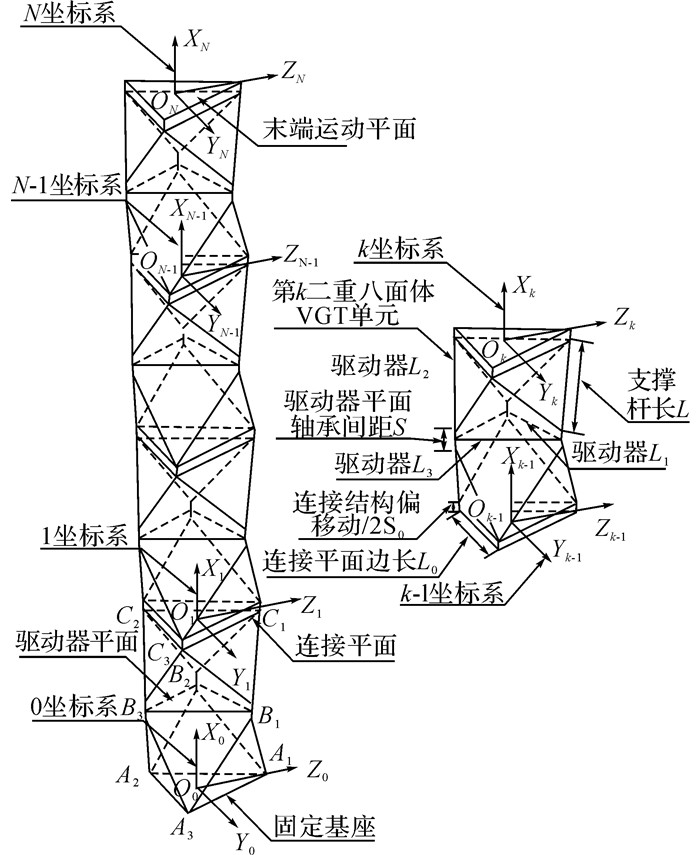
|
图 1 双八面体变几何桁架机械臂的简化模型 Fig. 1 Simplified model of double-octahedral variable geometry truss |
| $ \left. {\begin{array}{*{20}{c}} {^{k - 1}{\mathit{\boldsymbol{T}}_k} = \left[ {\begin{array}{*{20}{c}} {^{k - 1}{\mathit{\boldsymbol{R}}_k}}&{^{k - 1}{\mathit{\boldsymbol{P}}_k}}\\ 0&1 \end{array}} \right]{;^{k - 1}}{\mathit{\boldsymbol{R}}_k} \in {{\bf{R}}^{3 \times 3}},}\\ {^{k - 1}{\mathit{\boldsymbol{P}}_k} \in {{\bf{R}}^{3 \times 1}},{{\left( {^{k - 1}{\mathit{\boldsymbol{R}}_k}} \right)}^{{\rm{T}}k - 1}}{\mathit{\boldsymbol{R}}_k} = \mathit{\boldsymbol{I}}.} \end{array}} \right\} $ | (1) |
式中:k-1Rk为k-1和k坐标系之间的旋转矩阵;k-1Pk为k-1和k坐标系之间位移矢量Pk在k-1坐标系内的坐标;I∈R3×3为单位矩阵.对于一个向量X, 在k-1和k坐标系内的坐标分别为k-1X和kX.定义向量X的长度为x,
| $ ^{k - 1}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{ = }}^{k - 1}}\mathit{\boldsymbol{R}}_k^k\mathit{\boldsymbol{X = }}{\left[ {^{k - 1}{x_x},\;\;{\;^{k - 1}}{x_y},\;\;\;{\;^{k - 1}}{x_z}} \right]^{\rm{T}}}. $ | (2) |
对于一个多节双八面体变几何桁架机械臂, 定义末端运动平面的位置和方向在基座坐标系分别为
| $ \begin{array}{*{20}{c}} {^0{\mathit{\boldsymbol{P}}_{\rm{e}}} \in {{\bf{R}}^{3 \times 1}}和{^0}{\mathit{\boldsymbol{n}}_{\rm{e}}} \in {{\bf{R}}^{3 \times 1}}.}\\ {\left. \begin{array}{l} ^0{\mathit{\boldsymbol{P}}_{\rm{e}}}{ = ^0}{\mathit{\boldsymbol{P}}_{\rm{1}}} + \sum\limits_{i = 2}^N {{{\left( {\prod\limits_{k = 1}^{i - 1} {^{k - 1}{\mathit{\boldsymbol{R}}_k}} } \right)}^{i - 1}}{\mathit{\boldsymbol{P}}_i}} ,\\ ^0{\mathit{\boldsymbol{n}}_{\rm{e}}} = \left( {\prod\limits_{k = 1}^N {^{k - 1}{\mathit{\boldsymbol{R}}_k}} } \right){\left[ {1,\;\;\;\;0,\;\;\;\;0} \right]^{\rm{T}}}. \end{array} \right\}} \end{array} $ | (3) |
多节双八面体变几何桁架机械臂的逆向运动学问题为:给定0Pe和0ne, 根据式(3) 求解每个单元驱动器L1~L3的长度.将上述过程分解为:1) 求解每个模块的位置向量k-1Pk;2) 根据k-1Pk计算出每个单元驱动器L1~L3的长度.因为单节逆运动学解析已经在文献[11]中给出, 本文着重解决问题1).
2.2 桁架机械臂的旋转矩阵根据文献[11]中的推导, 双八面体变几何桁架机械臂有结构对称的特点, 即每个八面体单元关于其驱动器平面呈镜面对称, 并且镜面垂直于Pk, 如图 2所示.将坐标系的Xk-1轴反转得到-Xk-1轴, 则-Xk-1 Yk-1 Zk-1 Ok-1系与Xk Yk Zk Ok系关于驱动器平面对称.根据这个性质, 提出以下旋转矩阵:
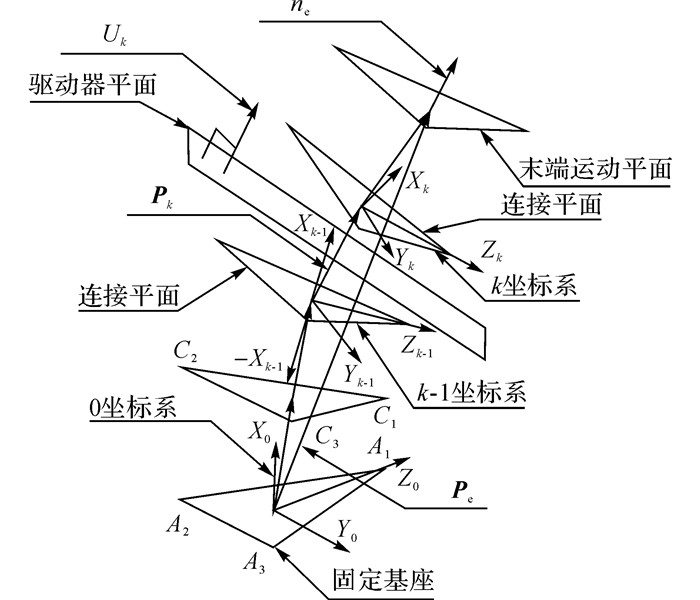
|
图 2 M坐标系与P坐标系的定义 Fig. 2 Definition of M coordinate frame and P coordinate frame |
| $ \left. \begin{array}{l} ^{k - 1}{\mathit{\boldsymbol{R}}_k} = \left( {\mathit{\boldsymbol{I}} - {2^{k - 1}}{\mathit{\boldsymbol{U}}_k}{{\left( {^{k - 1}{\mathit{\boldsymbol{U}}_k}} \right)}^{\rm{T}}}} \right)\mathit{\boldsymbol{D}};\\ \mathit{\boldsymbol{D = }}\left[ {\begin{array}{*{20}{c}} { - 1}&{}&{\bf{0}}\\ {}&1&{}\\ {\bf{0}}&{}&1 \end{array}} \right],\\ ^{k - 1}{\mathit{\boldsymbol{U}}_k}{ = ^{k - 1}}{\mathit{\boldsymbol{P}}_k}/{p_k},{p_k} = \left\| {^{k - 1}{\mathit{\boldsymbol{P}}_k}} \right\|. \end{array} \right\} $ | (4) |
式中:k-1Uk表示向量k-1Pk的方向;pk表示k-1Pk的大小.式(4) 使用k-1Uk计算第k个桁架单元的旋转矩阵.
2.3 最小工作单元要使末端运动平面能够按照指令平移和向指定方向偏转, 即到达给定的0Pe和0ne, 机械结构的任务空间至少需要5个自由度.在双八面体变几何桁架机械臂中, 每个单元有3个自由度.因为两个连接平面之间的位移和偏转是耦合的, 使用2个单元就可以实现末端平面位置和指向定位的功能.定义2个单元构成的机构称为最小工作单元.本文先求解最小工作单元的逆运动学解析解, 然后推广至N节机械臂.最小工作单元的逆运动学问题如下:给定0Pe和0ne, 根据
| $ \left. {\begin{array}{*{20}{c}} {^0{\mathit{\boldsymbol{P}}_{\rm{e}}}{ = ^0}{\mathit{\boldsymbol{P}}_{\rm{1}}}{ + ^0}{\mathit{\boldsymbol{R}}_{\rm{1}}}^1{\mathit{\boldsymbol{P}}_{\rm{2}}},}\\ {^0{\mathit{\boldsymbol{n}}_{\rm{e}}}{ = ^0}{\mathit{\boldsymbol{R}}_{\rm{1}}}^1{\mathit{\boldsymbol{R}}_{\rm{2}}}{{\left[ {1,\;\;\;\;0,\;\;\;\;0} \right]}^{\rm{T}}},} \end{array}} \right\} $ | (5) |
求解:0P1和1P2.
2.4 辅助坐标系旋转矩阵子问题由式(5) 可知, Pe、P1和P2在同一个平面内:
| $ {\mathit{\boldsymbol{P}}_{\rm{2}}} \cdot \left( {{\mathit{\boldsymbol{P}}_{\rm{e}}} \times {\mathit{\boldsymbol{P}}_{\rm{1}}}} \right) = 0. $ | (6) |
由式(6) 的共面关系定义该平面为M平面, 包括向量Pe、P1和P2, 如图 2所示.求出M平面的方向和M坐标系旋转矩阵子问题的解, 可以先求出式(5) 关于向量所在平面的信息.以Pe方向为Y轴, M平面法线方向为X轴定义M.定义辅助坐标系Pe, 其与基座坐标系的旋转矩阵为
| $ \left. \begin{array}{l} ^P{\mathit{\boldsymbol{R}}_{\rm{0}}} = \left[ {\begin{array}{*{20}{c}} {{c_3}} & {{s_3}} & 0\\ { - {s_3}} & {{c_3}} & 0\\ 0 & 0 & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{c_2}} & 0 & { - {s_2}}\\ 0 & 1 & 0\\ {{s_2}} & 0 & {{c_2}} \end{array}} \right];\\ {\sigma _2} = - a\tan \left( {\frac{{^0{u_{{\rm{e}}z}}}}{{^0{u_{{\rm{e}}x}}}}} \right),{\sigma _3} = - a\cos \left( {^0{u_{{\rm{e}}y}}} \right). \end{array} \right\} $ | (7) |
式中:cos σi=ci, sin σi=si. P坐标系由Pe向量唯一确定且为Y轴.M坐标系可以通过P坐标系绕Y轴旋转φ角得到, 如图 3所示.P坐标系将求解M平面方向的问题转化为求单变量旋转角的问题:
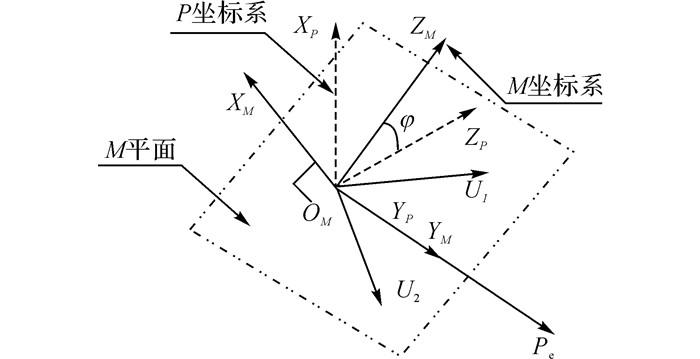
|
图 3 向量Pe、P1和P2在M平面上的关系 Fig. 3 Vector relationship between Pe, P1 and P2 on M plane |
| $ ^M{\mathit{\boldsymbol{R}}_P} = \left[ {\begin{array}{*{20}{c}} {\cos \varphi }&0&{ - \sin \varphi }\\ 0&1&0\\ {\sin \varphi }&0&{\cos \varphi } \end{array}} \right]. $ | (8) |
考察式(5) 中有关0ne的关系, 结合式(4), 有
| $ \left. {\begin{array}{*{20}{c}} {^0{\mathit{\boldsymbol{n}}_{\rm{e}}}{ = ^0}{\mathit{\boldsymbol{R}}_{\rm{1}}}\left( {\mathit{\boldsymbol{I}} - {2^1}{\mathit{\boldsymbol{U}}_2}{{\left( {^1{\mathit{\boldsymbol{U}}_2}} \right)}^{\rm{T}}}} \right){\mathit{\boldsymbol{D}}^0}\mathit{\boldsymbol{b}},}\\ {^0\mathit{\boldsymbol{b}} = {{\left[ {1,\;\;\;\;0,\;\;\;\;0} \right]}^{\rm{T}}}.} \end{array}} \right\} $ | (9) |
将式(9) 的关系变换到M坐标系内,
| $ {\left( {\mathit{\boldsymbol{I}} - {2^M}{\mathit{\boldsymbol{U}}_2}{{\left( {^M{\mathit{\boldsymbol{U}}_2}} \right)}^{\rm{T}}}} \right)^M}{\mathit{\boldsymbol{n}}_{\rm{e}}} = {\left( {\mathit{\boldsymbol{I}} - {2^M}{\mathit{\boldsymbol{U}}_1}{{\left( {^M{\mathit{\boldsymbol{U}}_1}} \right)}^{\rm{T}}}} \right)^M}\mathit{\boldsymbol{b}}. $ | (10) |
式(10) 表示向量ne和b在被U1和U2所构成的反射矩阵变换后的值相等.式中:MU1和MU2分别为向量U1和U2在M坐标系中的坐标.根据M平面的定义可知, U1和U2向量处于M坐标系的YZ平面上, 所以坐标MU1和MU2的X分量为零, 有下列关系:
| $ \mathit{\boldsymbol{I}} - {2^M}{\mathit{\boldsymbol{U}}_1}{\left( {^M{\mathit{\boldsymbol{U}}_1}} \right)^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0& * & * \\ 0& * & * \end{array}} \right]. $ | (11) |
| $ \mathit{\boldsymbol{I}} - {2^M}{\mathit{\boldsymbol{U}}_2}{\left( {^M{\mathit{\boldsymbol{U}}_2}} \right)^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0& * & * \\ 0& * & * \end{array}} \right]. $ | (12) |
由于将式(11)、(12) 代入式(10) 后不改变向量ne和b在M坐标系中的X坐标, 根据式(10), 可以直接令ne和b在M坐标系中的坐标X分量相等,
| $ {\left( {^M{\mathit{\boldsymbol{R}}_P}^P{\mathit{\boldsymbol{n}}_{\rm{e}}}} \right)_x} = {\left( {^M{\mathit{\boldsymbol{R}}_P}^P\mathit{\boldsymbol{b}}} \right)_x}. $ | (13) |
式(13) 导出一个关于φ的单变量方程, 可得M平面的方向:
| $ \left. \begin{array}{l} \sin \left( {\beta + \varphi } \right) = 0;a = {\left( {^P{\mathit{\boldsymbol{n}}_{\rm{e}}}} \right)_x} - {\left( {^P\mathit{\boldsymbol{b}}} \right)_x},\\ b = {\left( {^P\mathit{\boldsymbol{b}}} \right)_z} - {\left( {^P{\mathit{\boldsymbol{n}}_{\rm{e}}}} \right)_z},\beta = {\rm{atan2}}\left( {a,b} \right). \end{array} \right\} $ | (14) |
式中:atan2为四象限反正切函数.式(14) 有2个相差π的解, 因为不考虑M平面的正反面, 只需一个可以解出辅助坐标系M的旋转矩阵.
| $ \varphi = - \beta . $ | (15) |
由于U1和U2在M平面内, 求出它们相对于M坐标系Y轴的夹角, 结合M坐标系的旋转矩阵, 即可求出在0、1坐标系中的坐标. M坐标系将式(5) 转换为如图 3所示的三角关系.令向量ne和b在M坐标系中的YZ分量为nep和bp.根据式(10), 定义nep和bp经过U1和U2为法向量的镜像变换后的结果为nepm和bpm.由于向量U1和U2都落在M平面上, 镜像变换关系可以用角度的方式表示在图 4和式(16) 中.
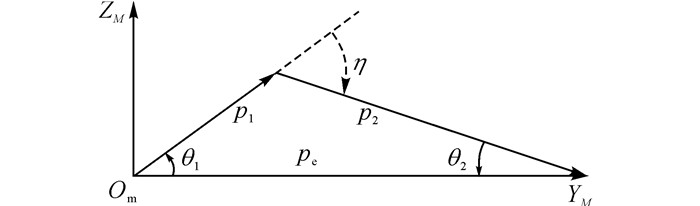
|
图 4 M平面上θb, θt, θ1和θ2角度关系 Fig. 4 Relatioship among θb, θt, θ1 and θ2 on M plane |
| $ \left. {\begin{array}{*{20}{c}} {{\theta _{{\rm{tm}}}} = {\theta _2} + {\rm{\pi }} - \left( {{\theta _{\rm{t}}} - {\theta _{\rm{2}}}} \right) = 2{\theta _2} + {\rm{\pi }} - {\theta _{\rm{t}}},}\\ {{\theta _{{\rm{bm}}}} = {\theta _1} + {\rm{\pi }} - \left( {{\theta _{\rm{b}}} - {\theta _{\rm{1}}}} \right) = 2{\theta _1} + {\rm{\pi }} - {\theta _{\rm{b}}},}\\ {{\theta _{\rm{t}}} = {\rm{atan2}}\left( {^M{n_{{\rm{e}}z}}{,^M}{n_{{\rm{e}}y}}} \right),}\\ {{\theta _{\rm{b}}} = {\rm{atan2}}\left( {^M{b_z}{,^M}{b_y}} \right).} \end{array}} \right\} $ | (16) |
式(10) 表明, θtm和θbm必须相等或者相差2π,
| $ \left. \begin{array}{l} {\theta _2} = {\theta _1} + \frac{{{\theta _{\rm{t}}} - {\theta _{\rm{b}}}}}{2},\\ {\theta _2} = {\theta _1} + \frac{{{\theta _{\rm{t}}} - {\theta _{\rm{b}}}}}{2} + {\rm{\pi }}{\rm{.}} \end{array} \right\} $ | (17) |
根据图 4, 定义η和两个值η1和η2如下:
| $ \left. {\begin{array}{*{20}{c}} {{\eta _1} = {\rm{atan2}}\left( {{\rm{s}}\left( {\frac{{{\theta _{\rm{t}}} - {\theta _{\rm{b}}}}}{2}} \right),\;\;\;{\rm{c}}\left( {\frac{{{\theta _{\rm{t}}} - {\theta _{\rm{b}}}}}{2}} \right)} \right),}\\ {{\eta _2} = {\rm{atan2}}\left( {{\rm{s}}\left( {\frac{{{\theta _{\rm{t}}} - {\theta _{\rm{b}}}}}{2} + {\rm{\pi }}} \right),\;\;\;{\rm{c}}\left( {\frac{{{\theta _{\rm{t}}} - {\theta _{\rm{b}}}}}{2} + {\rm{\pi }}} \right)} \right),}\\ {\eta = {\eta _1}或{\eta _2},\left| {{\theta _1}} \right| + \left| {{\theta _2}} \right| = \left| \eta \right|.} \end{array}} \right\} $ | (18) |
根据双八面体结构的尺寸, 首先设定p1的值, 结合pe、η1和η2, 计算出图 3中θ1、θ2和p2, 步骤如下.由正弦定理, 可得
| $ \left. {\begin{array}{*{20}{c}} {\sin {\theta _2} = \frac{{{p_1}\sin \eta }}{{{p_{\rm{t}}}}},}\\ {{\theta _2} = \arcsin \left( {\frac{{{p_1}\sin \eta }}{{{p_{\rm{t}}}}}} \right)或{\rm{\pi }} - \arcsin \left( {\frac{{{p_1}\sin \eta }}{{{p_{\rm{t}}}}}} \right).} \end{array}} \right\} $ | (19) |
根据余弦定理可得p2:
| $ \left. {\begin{array}{*{20}{c}} {{\theta _1} = \left| \eta \right| - {\theta _2},}\\ {{p_2} = \sqrt {p_{\rm{t}}^2 + p_{\rm{1}}^2 - 2{p_1}{p_{\rm{t}}}\cos {\theta _1}} .} \end{array}} \right\} $ | (20) |
| $ \left[ {\begin{array}{*{20}{c}} {{\theta _1}}\\ {{\theta _2}} \end{array}} \right] = {\mathop{\rm sgn}} \left( \eta \right)\left[ {\begin{array}{*{20}{c}} { - {\theta _1}}\\ {{\theta _2}} \end{array}} \right]. $ | (21) |
| $ \left. \begin{array}{l} ^M{\mathit{\boldsymbol{U}}_1} = {\left[ {0,\;\;\;\;\cos {\theta _1},\;\;\;\;\;\sin {\theta _1}} \right]^{\rm{T}}},\\ ^M{\mathit{\boldsymbol{U}}_2} = {\left[ {0,\;\;\;\;\cos {\theta _2},\;\;\;\;\;\sin {\theta _2}} \right]^{\rm{T}}}. \end{array} \right\}. $ | (22) |
θ1和θ2的符号根据式(21) 作相应改变.利用式(22) 计算出U1、U2、p1和p2.算法流程如图 5所示.根据式(18) 可知, η有两个值:η1和η2.根据式(19) 可知, 对于每一个η有两个θ1和θ2, 所以根据式(21) 和(22), θ1和θ2的解有4组.算法使用这4组解计算4组驱动器长度.在算法输出结果时, 只输出驱动器长度, 满足结构限制的解.
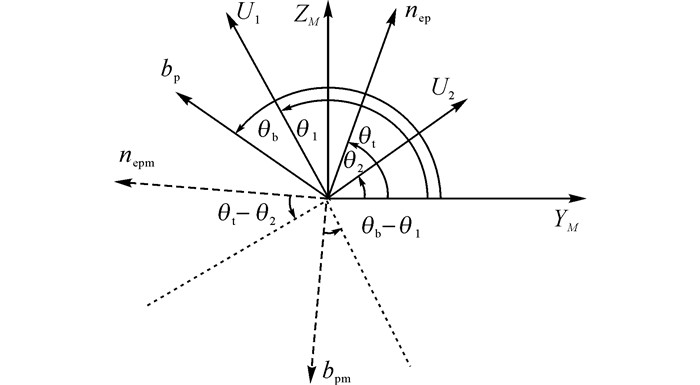
|
图 5 最小工作单元逆运动学解析算法 Fig. 5 Analytical inverse kinematics of minimum taskunit |
研究最小工作单元逆运动学解的特例.令0P1=1P2, 可得
| $ \mathit{\boldsymbol{c}} \cdot \left( {{\mathit{\boldsymbol{P}}_2} \times {\mathit{\boldsymbol{P}}_1}} \right) = {\bf{0}}. $ | (23) |
式中:c为基座法向量.式(23) 说明M平面与基座平面垂直.对于N1节机械臂, 令0P1=i-1Pi, i=2, 3, …,N1, 则所有i-1Pi将会落在同一个M平面上.以M平面为XY平面, 定义P2坐标系. Pe处于P2坐标系的XY平面上.如图 6所示, 因为所有i-1Pi相等, 它们构成一系列全等的等腰三角形的底, 并且连接点会构成一个圆弧.在给定Pe后, 圆弧的半径r和对应的圆心角θ由式(26) 算出.定义角σ如下:
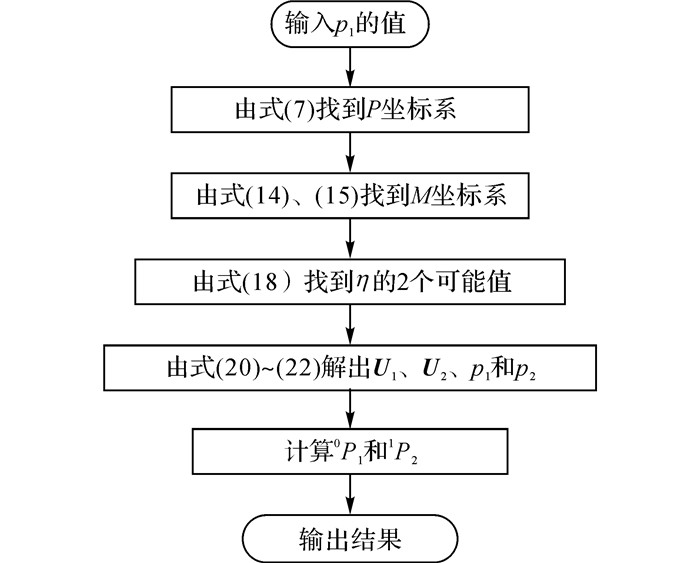
|
图 6 同向偏转简化 Fig. 6 Equal turn mode simplification |
| $ \sigma = {\rm{atan2}}\left( {^{{P_2}}{p_{{\rm{e}}z}}{,^{{P_2}}}{p_{{\rm{e}}y}}} \right). $ | (24) |
| $ \left. \begin{array}{l} ^{{P_2}}{\mathit{\boldsymbol{R}}_0} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \sigma }&{\sin \sigma }\\ 0&{ - \sin \sigma }&{\cos \sigma } \end{array}} \right];\\ \delta = \arccos \frac{{^{{P_2}}{p_{{\rm{e}}y}}}}{{{p_{\rm{e}}}}},r = \frac{{{p_{\rm{e}}}}}{{2\cos \delta }},\\ \theta = {{ { π} }} - 2\delta ,\gamma \equiv \theta /{N_1}. \end{array} \right\} $ | (25) |
对于N1节机械臂, 末端位置为Pe, 使用同向偏转简化, 得到每个单元的i-1Pi:
| $ \left. \begin{array}{l} ^{{P_2}}{\mathit{\boldsymbol{P}}_1} = r{\left[ {\sin \gamma ,\;\;\;1 - \cos \gamma ,\;\;\;0} \right]^{\rm{T}}};\\ ^0{\mathit{\boldsymbol{P}}_1}{ = ^0}{\mathit{\boldsymbol{R}}_{{P_2}}}^{{P_2}}{\mathit{\boldsymbol{P}}_1}{,^{i - 1}}{\mathit{\boldsymbol{P}}_i}{ = ^0}{\mathit{\boldsymbol{P}}_1},i = 2, \cdots ,{N_1}. \end{array} \right\} $ | (26) |
同向偏转简化将多节机械臂等效为一个大的单节机械臂, 同时3自由度和镜像对称的特点会被保留下来.推导同向偏转形式的意义在于将N1节机械臂逆向运动学简化为一节逆向运动学.
3.2 N节机械臂的逆运动学解析算法将一个N节的机械臂分成2组, 在每组中使用同向偏转简化, 将每组中所有VGT机构单元简化为一个最小工作单元, 如图 6所示.利用最小工作单元逆运动学算法得出结果.算法流程如图 7所示.
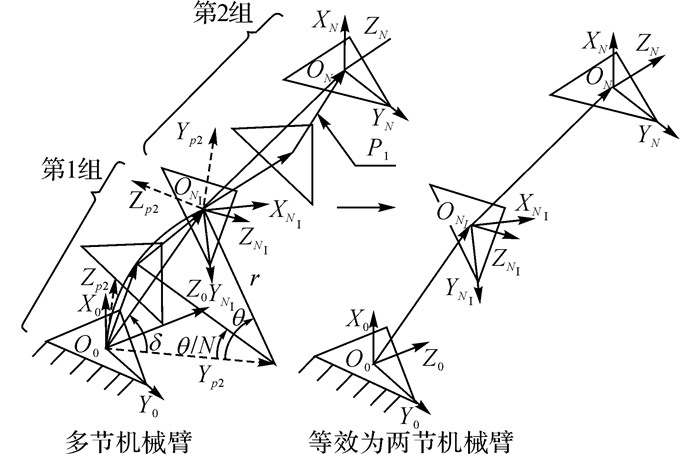
|
图 7 N节VGT机械臂的逆运动学算法 Fig. 7 Inverse kinematics of VGT manipulator with N sections |
双八面体VGT单元尺寸参数为:L=280 mm, L0=280 mm, S=58 mm, S0=16 mm.
为了验证逆运动学算法的有效性, 对2节双八面体VGT机械臂, 在MATLAB中建立机械臂运动学模型.仿真电脑配置为4核i7-4710M、2.5 GHz处理器, 16 GB内存.仿真场景为一典型操作场景, 包括机械臂头部的对准、伸出和矫正环节.将整个过程分成编号为i=1, 2, …, 30的位置点, 在逆运动学得出解后, 将结果代入正运动学中, 计算末端位置和偏转误差.本文提出的方法是在线实时方法, 而神经网络和优化方法都是离线方法, 所以在仿真比较中, 将该方法和目前应用最广泛的实时在线逆运动学方法雅可比矩阵法进行计算速度和误差比较.定义末端运动平面的位置误差perr和方向误差nerr如下:
| $ \left. \begin{array}{l} {p_{{\rm{err}}}} = \left\| {^0{\mathit{\boldsymbol{P}}_{{\rm{e,d}}}}{ - ^0}{\mathit{\boldsymbol{P}}_{{\rm{e,c}}}}} \right\|,\\ {n_{{\rm{err}}}} = \left\| {^0{\mathit{\boldsymbol{n}}_{{\rm{e,d}}}}{ - ^0}{\mathit{\boldsymbol{n}}_{{\rm{e,c}}}}} \right\|. \end{array} \right\} $ | (27) |
式中:0Pe, d和0ne, d分别表示期望的末端运动平面位置和法向量.0Pe, c和0ne, c分别表示根据逆运动学解计算出的末端运动平面位置和法向量.根据图 8和表 1可知, 本文方法的位置计算误差相对于雅可比方法下降约104倍, 法向量计算误差下降约10倍, 计算速度提升约60倍.当末端运动平面的位置比较接近初始值时, 雅可比矩阵法误差稍有下降, 如图 8中1~10号位置.当末端运动平面的位置离初值较远时, 如图 8中10~30号位置, 位置误差和法向量误差在1 mm和5×10-7左右波动.由于本文方法求解出的是理论上没有误差的解析解, 因此图 8展示的本文方法计算误差的来源为计算机在仿真时的舍入误差.由于舍入误差一般为随机分布, 所以本文方法的计算误差表现出随机分布特性.
|
图 8 雅可比矩阵法和本文方法的位置方向计算误差 Fig. 8 Position and normal vector error between Jacobian matrix method and proposed method |
| 表 1 本文方法和雅可比矩阵方法的平均计算时间和误差 Table 1 Average computation time and error of proposed method and Jabobian matrix method |
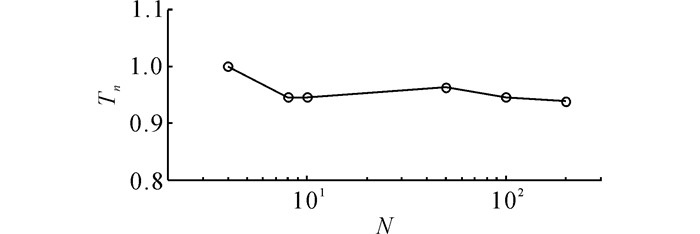
对于k=4、8、10、50、100和200节机械臂, 运行本文的逆向运动学并记录每次运行所消耗的时间, 定义归一化时间Tn:
| $ {T_n} = {T_k}/{T_2}. $ | (28) |
图 9中, 计算时间波动幅度在5%以内, 表明本文方法在处理多节机械臂逆运动学问题时, 有较高的计算速度.

|
图 9 本文提出方法的计算时间和节数的关系 Fig. 9 Computation time with respect to number of sections of manipulator |
实物测试平台如图 10所示.主控电脑为硕华610H工控机, 驱动器为MAXON32017步进电机+Epos2驱动板.驱动形式为步进电机+丝杠套筒.测试机械臂由两节双八面体VGT机械臂和Stewart平台构成. Stewart平台在机械臂的运动过程中保持不动, 相当于将末端运动平面按VGT机械臂末端法向量平移380 mm.机械臂尺寸与仿真验算模型相同.具体实验步骤如下.
|
图 10 VGT机械臂运动测试平台 Fig. 10 VGT manipulator motion test platform |
1) 给定一组期望的末端运动平面位置和方向后, 利用本文的逆运动学算法解出驱动器长度, 根据计算结果操作机构运动.
2) 如图 10所示, 将坐标纸铺在基座坐标系上, 利用铅锤、卷尺测量出末端运动平台在X0Y0Z0O0坐标系中坐标.利用铅锤和量角器测出末端运动平台的偏转角.对每个位置多次测量求平均值, 再将测量出的偏转角转换为末端运动平面在X0Y0Z0O0坐标系中的法向量.位置测量精度为±5 mm, 角度测量误差为±2°.
3) 从表 2可以看出, 位置误差大多数在5%以内, 方向误差在10%以内, 而且呈现一定的递增趋势.这些误差并不是由于逆运动学的算法引起的, 而是部分来源于测量误差, 部分来源于轴承间隙和重力作用下的杆件弯曲.在相对基座X轴较远的地方, 重力使杆部件弯曲和变形, 同时轴承间隙使得机构中等效杆长变长, 产生比在X轴附近区域更大的定位误差. 表 2的测量结果可以证明, 采用本文的逆向运动学方法可以准确地计算期望末端位置所对应的作动器杆长.
| 表 2 本文的逆运动学算法在测试平台中的实验结果 Table 2 Experiment results of proposed IK algorithm from test platform |
针对多节双八面体VGT机械臂的逆向运动学问题, 本文提出一种解析逆向运动学求解方法.定义最小工作单元, 利用辅助平面方法, 将复杂的立体几何问题简化为M平面上的平面几何问题;利用逆向运动学解的同向偏转简化, 使得多节结构可以看成一节结构;将N节机械臂分组, 每组利用同向偏转简化为一节问题, 代入最小工作单元求解逆向运动学问题.在数值仿真和物理实验中, 提出的解析方法具有计算速度快和精度高的特点, 适合于实时控制.
| [1] | BATRAM ATILLA. Trajectory Tracking of a redundant hybrid manipulator using a switching control method[J]. World Academy of Science, Engineering and Technology, International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 2016, 10(6): 920–929. |
| [2] |
吴江, 徐礼钜, 雷勇. 基于神经网络的冗余度二重八面体变几何桁架机器人运动学求解[J].
四川大学学报:工程科学版, 2000, 32(2): 90–103.
WU Jiang, XU Li-ju, LEI Yong. The kinematics ofredundant double-octahedron variable geometry truss manipulators based on neural network[J]. Journal of Sichuan University: Engineering Science Edition, 2000, 32(2): 90–103. |
| [3] | MACARENO L, AGIRREBEITIA J, ANGULO C, et al. FEM subsystem replacement techniques for strength problems in variable geometry trusses[J]. Finite Elements in Analysis and Design, 2008, 44(6/7): 346–357. |
| [4] | ATSUHIKO S, KOSUKE O, MORIO T, et al. Vibration reduction by natural frequency optimization formanipulation of a variable geometry truss[J]. Structural and Multidisciplinary Optimization, 2013, 48(5): 939–954. DOI:10.1007/s00158-013-0933-6 |
| [5] | DE Z I O, AGUIRREBEITIA J, AVILES R, et al. A finite element approach to the inverse dynamics andvibrations of variable geometry trusses[J]. Finite Elements in Analysis and Design, 2011, 47(3): 220–228. DOI:10.1016/j.finel.2010.10.009 |
| [6] | TONDU B. Closed-form redundancy solving of serial chain robots with a weak generalized inverse approach[J]. Robotics and Autonomous Systems, 2015, 74(PB): 360–370. |
| [7] | DULEBA I, OPAKA M. A Comparison of jacobian-based methods of inverse kinematics for serial robotmanipulators[J]. International Journal of Applied Mathematics and Computer Science, 2013, 23(2): 373–382. |
| [8] | GIORELLI M, RENDA F, CALISTI M, et al. Learning the inverse kinetics of an octopus-like manipulator in three-dimensional space[J]. Bioinspiration and Biomimetics, 2015, 10(3): 1–13. |
| [9] | SHUKLA, SINGLA E, WAHI P, et al. A direct variational method for planning monotonically optimal paths for redundant manipulators in constrained workspaces[J]. Robotics and Autonomous Systems, 2013, 61(2): 209–220. DOI:10.1016/j.robot.2012.08.012 |
| [10] | YAHYA S, MOGHAVVEMI M, MOHAMMED A. Geometrical approach of planar hyper-redundant manipulators: inverse kinematics, path planning and workspace[J]. Simulation Modelling Practice and Theory, 2011, 19(1): 406–422. DOI:10.1016/j.simpat.2010.08.001 |
| [11] |
姜柏森, 杨永胜, 胡士强. 八面体变几何桁架机器人的运动学分析及仿真研究[J].
制造业自动化, 2015, 37(3): 20–22.
JIANG Bai-sen, YANG Yong-sheng, HU Shi-qiang. The solution and simulation for the kinematic problem of octahedral VGT manipulator[J]. ManufacturingAutomation, 2015, 37(3): 20–22. |
| [12] | YANG Y, JIANG B, HU S. Fast trajectory planning for VGT manipulator via convex optimization[J]. International Journal of Advanced Robotic Systems, 2015, 12(9): 1–17. |
| [13] |
杭鲁滨, 王彦, 邓辉宇, 等. 基于Groebner基的八面体变几何桁架机构位置正解分析[J].
机械科学与技术, 2004, 23(6): 745–747.
HANG Lu-bin, WANG Yan, DENG Hui-yu, et al. Forward displacement analysis of the octahedron variable geometry truss based on Groebner basis[J]. Mechanical Science and Technology, 2004, 23(6): 745–747. |



