冗余机械臂可以利用系统的冗余特性完成更复杂的操作任务, 例如在不影响操作任务的情况下避免同环境发生碰撞, 保持可观的可操作度以避免位形奇异等.然而, 冗余机械臂的运动受到驱动元件的约束限制.例如, 关节坐标应位于物理结构所限定的范围内;关节转速应位于驱动器最大输出转速及减速器所允许的最大输出转速范围内;关节驱动力矩应在驱动器最大输出力或力矩范围内.以上约束限制了机械臂关节的运动能力, 通过正向运动学映射影响了机械臂在操作空间的运动性能.如果缺乏恰当的考虑, 那么机械臂的控制算法将产生无法实现的逆运动学解, 导致操作任务的执行出现偏差[1], 甚至为系统带来损害.
关节力矩约束对于关节力矩控制和速度控制都起着重要的制约作用, 通过动力学模型制约关节加速度范围, 从而限定关节速度以及关节坐标的变化.针对关节力矩约束下机械臂的控制问题, 众多学者采用不同的方法来求解.根据采用的求解思路, 这些方法大致可分为两类:力矩优化法和约束求解法.前者通过对与关节力矩相关的性能指标的优化, 以减小关节力矩指令, 使其在驱动器的输出范围之内.
例如, Hollerbach等[2]通过设计零空间关节加速度使关节力矩向量与代数中心距离的2范数最小.Liu等[3-4]求解了操作任务运动学约束下关节力矩2范数最优问题.Zhao等[5-7]分别通过对关节加速度加权范数优化来减小接近输出饱和的关节的指令力矩.郭宪等[8]通过对关节力矩的无穷范数优化实现最小力矩幅值.闫彩霞等[9]通过对关节力矩进行加权优化来平衡各关节力矩负荷.金波等[10]通过对系统能耗进行优化来完成力矩分配.这些优化指标将各个关节力矩综合为单一指标, 没有直接考虑各个关节力矩的输出范围, 不能严格保证关节力矩指令在物理允许范围内.
约束求解法将最大关节输出力矩作为关节力矩指令的边界, 对操作任务求解以确保遵循关节力矩约束.例如, Bianco等[11]通过对操作任务轨迹切向速率及高阶导数规划的办法来求解关节力矩有限的约束问题.该方法在逆运动学求解过程中没有考虑系统冗余特性, 不适合冗余机械臂.陈伟海等[12]对关节力矩再分配, 以保证各关节的实际输出力矩在其驱动能力范围内.该方法需要进行二次计算, 不仅增加了运算量, 并且再分配的结果可能导致新的关节发生力矩饱和.Zhang等[13]将关节力矩约束和操作任务作为二次型优化问题求解的可行域.该方法未考虑到操作任务与关节驱动力矩约束相矛盾的情况.
针对上述方法的缺点, 本文提出基于GWLN的冗余机械臂有限关节力矩约束求解方法:将有限关节力矩的非线性约束局部线性化为线性约束, 引入辅助变量将非齐次约束转化为扩展系统变量的齐次约束, 采用GWLN方法进行求解, 保证关节力矩约束.由于该方法直接对力矩约束进行求解, 避免了力矩再分配方法需要二次计算运算量大的缺点.该算法的有效性通过理论分析得到证明, 对比仿真结果表明, 采用该方法更有效地保证了关节力矩约束.
1 机械臂运动学动力学模型假定机械臂m维运动学操作任务可以通过二阶运动学模型表示为
| $ \mathit{\boldsymbol{J\ddot q + \dot J\dot q = \ddot x}}. $ | (1) |
式中:q∈Rn为关节坐标, x∈Rm为操作任务坐标, J(q)=∂x/∂q∈Rm×n为操作任务坐标对关节坐标的雅可比矩阵.为了实现期望的操作空间的加速度ẍd, 要求关节空间加速度指令
| $ {{\mathit{\boldsymbol{\ddot q}}}_{\rm{c}}} = {\mathit{\boldsymbol{J}}^ + }\left( {{{\mathit{\boldsymbol{\ddot x}}}_{\rm{d}}} - \mathit{\boldsymbol{\dot J\dot q}}} \right) + \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{J}}^ + }\mathit{\boldsymbol{J}}} \right)\mathit{\boldsymbol{z}}. $ | (2) |
式中:(I-J+J)z∈Rn为雅可比矩阵零空间内加速度项, 取z=0n×1可得最小2范数的关节加速度指令.当机械臂具有冗余自由度时, 操作空间的加速度∂d可以对应不同的关节加速度指令
由动力学模型可知, 机械臂在q和关节速度
| $ \mathit{\boldsymbol{\tau = M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{q}} \right). $ | (3) |
式中:M(q)∈Rn×n为系统惯性矩阵,
| $ {\tau _{i,\min }} \leqslant {\tau _i} \leqslant {\tau _{i,\max }}. $ | (4) |
式中:τi, max、τi, min分别为第i关节驱动力矩τi允许取值范围的上、下限.当关节加速度指令过大时, 所需关节力矩指令τc会超出驱动器的输出能力范围.由于驱动力不足, 实际关节加速度与规划关节加速度出现偏差, 从而导致操作任务出现执行误差.
为了避免这一问题, 需要在机械臂的控制过程中考虑驱动器输出能力有限的约束.综合式(1)、(4), 可得关节力矩约束下的机械臂控制问题:
| $ \left. {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\ddot q}}}_{\rm{c}}}\mathit{\boldsymbol{ + \dot J\dot q = }}{{\mathit{\boldsymbol{\ddot x}}}_{\rm{d}}};}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}{\tau _{\min }} \le \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right){{\mathit{\boldsymbol{\ddot q}}}_{\rm{c}}} + \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{q}} \right) \le {\tau _{\max }}.} \end{array}} \right\} $ | (5) |
式(5) 中的约束为关节加速度指令的非线性约束, 且约束边界随关节坐标及关节速度的变化而变化, 增加了求解难度.考虑到关节力矩约束仅在指令关节力矩超过驱动元件的输出范围时产生作用, 仿照Flacco等[14]采用的方法, 可将力矩饱和关节的输出力矩限定在饱和输出极限τi=τi, max或τi=τi, min, 以充分利用关节驱动能力, 从而将不等式约束转化为等式约束, 即
| $ \left. {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\ddot q}}}_{\rm{c}}}\mathit{\boldsymbol{ + \dot J\dot q = }}{{\mathit{\boldsymbol{\ddot x}}}_{\rm{d}}};}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}{\tau _{i,{\rm{c}}}} = {\mathit{\boldsymbol{M}}_i}\left( \mathit{\boldsymbol{q}} \right){{\mathit{\boldsymbol{\ddot q}}}_{\rm{c}}} + {\mathit{\boldsymbol{C}}_i}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)\mathit{\boldsymbol{\dot q}} + {\mathit{{g}}_i}\left( \mathit{\boldsymbol{q}} \right) = {\tau _{i,\lim }}.} \end{array}} \right\} $ | (6) |
式中:τi>0.5(τi, max+τi, min)时, 力矩约束边界τi, lim=τi, max, 否则τi, lim=τi, min;Mi和Ci分别为惯性矩阵M和科里奥利力矩阵C的第i行.式(6) 为线性约束作用下的线性系统的求解问题, 可以采用梯度投影法或基于任务优先级的方法求解[15-16].基于优先级的方法的分层算法结构较复杂, 并且在任务优先级变化时可能导致控制量的不连续, 不利于系统的平稳运行.此外, 由于约束条件具有高优先级, 相应关节的力矩将始终处于饱和输出的状态, 不会随操作任务的变化而退出饱和状态, 约束将持续作用.
2 基于GWLN的有限关节力矩控制采用基于广义加权最小范数的方法来求解冗余机械臂关节力矩约束控制问题.广义加权最小范数法[17-18]被应用于线性齐次约束下线性系统的最小二乘问题的求解, 成功地解决了冗余机械臂关节限位和操作空间避障问题.注意到, 式(6) 中的约束为非齐次约束, 不能直接应用广义加权最小范数法进行求解.对广义加权最小范数法进行扩展:引入辅助变量s并且令
| $ \mathit{\boldsymbol{\dot{\bar{J}}\dot{\bar{q}}}}=\left[ \begin{matrix} \mathit{\boldsymbol{J}} & {{\bf{0}}_{m\times 1}} \\ {{\bf{0}}_{1\times n}} & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{{\mathit{\boldsymbol{\ddot{q}}}}}_{\rm{c}}} \\ {\ddot{s}} \\ \end{matrix} \right]=\left[ \begin{matrix} {\mathit{\boldsymbol{\ddot{\tilde{x}}}}} \\ 1 \\ \end{matrix} \right]=\mathit{\boldsymbol{\ddot{\bar{x}}}}\mathit{.} $ | (7) |
式中
| $ \left[ {{\mathit{\boldsymbol{M}}}_{i}},{{\mathit{\boldsymbol{C}}}_{i}}\left( \mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot{q}}} \right)\mathit{\boldsymbol{\dot{q}}}+{{\mathit{{g}}}_{i}}\left( \mathit{\boldsymbol{q}} \right)-{{\tau }_{i,\lim }} \right]\mathit{\boldsymbol{\ddot{\bar{q}}=}}\bf{0}. $ | (8) |
记
| $ \left. \begin{align} & \mathit{\boldsymbol{\bar{J}\ddot{\bar{q}}=\ddot{\bar{x}}}}; \\ & \rm{s}\rm{.}\ \rm{t}\rm{.}\ \ {{\mathit{\boldsymbol{K}}}_\mathit{i}}\mathit{\boldsymbol{\ddot{\bar{q}}}}=\bf{0}. \\ \end{align} \right\} $ | (9) |
式(9) 为线性齐次约束下的线性系统求解问题, 可以应用广义加权最小范数法求解.构建所有力矩饱和关节的约束任务矩阵
| $ \left. \begin{matrix} {{{\mathit{\boldsymbol{\bar{J}}}}}_{{{\mathit{\boldsymbol{T}}}^{-1}}}}{{{\mathit{\boldsymbol{\ddot{\bar{q}}}}}}_{\mathit{\boldsymbol{T}}}}=\mathit{\boldsymbol{\ddot{\bar{x}}}}, \\ \rm{s}\rm{.}\ \rm{t}\rm{.}\ \ \ \left[ \begin{matrix} {{\mathit{\boldsymbol{I}}}_{p\times p}} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ \end{matrix} \right]{{{\mathit{\boldsymbol{\ddot{\bar{q}}}}}}_{\mathit{\boldsymbol{T}}}}={{\bf{0}}_{p\times 1}}. \\ \end{matrix} \right\} $ | (10) |
式中:虚拟关节变量
| $ \mathit{\boldsymbol{W=}}\left[ \begin{matrix} {{\mathit{\boldsymbol{W}}}_{1}} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & {{\mathit{\boldsymbol{W}}}_{2}} \\ \end{matrix} \right]. $ | (11) |
式中:子对角加权矩阵W1=diag(w1, …, wp)∈Rp×p为约束方向K的权值, 子对角加权矩阵W2=diag (wp+1, …, w(n+1))∈R(n-p+1)×(n-p+1)为正交补方向(K⊥)T的权值.采用加权最小范数法求解式(10), 可得具有最小加权范数
| $ {{{\mathit{\boldsymbol{\ddot{\bar{q}}}}}}_{\mathit{\boldsymbol{T}}}}={{\mathit{\boldsymbol{W}}}^{-1}}{{\left( {{{\mathit{\boldsymbol{\bar{J}}}}}_{{{\mathit{\boldsymbol{T}}}^{-1}}}}{{\mathit{\boldsymbol{W}}}^{-1}} \right)}^{+}}\mathit{\boldsymbol{\ddot{\bar{x}}}}. $ | (12) |
对式(12) 两边左乘T-1, 可得扩展系统变量:
| $ \begin{align} & \mathit{\boldsymbol{\ddot{\bar{q}}}}={{\mathit{\boldsymbol{T}}}^{-1}}{{\mathit{\boldsymbol{W}}}^{-1}}{{\left( {{{\mathit{\boldsymbol{\bar{J}}}}}_{{{\mathit{\boldsymbol{T}}}^{-1}}}}{{\mathit{\boldsymbol{W}}}^{-1}} \right)}^{+}}\mathit{\boldsymbol{\ddot{\bar{x}}}}= \\ & {{\left( \mathit{\boldsymbol{WT}} \right)}^{-1}}{{\left( \mathit{\boldsymbol{WT}} \right)}^{-\rm{T}}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}}{{\left( \mathit{\boldsymbol{\bar{J}}}{{\left( \mathit{\boldsymbol{WT}} \right)}^{-1}}{{\left( \mathit{\boldsymbol{WT}} \right)}^{-\rm{T}}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}} \right)}^{-1}}\mathit{\boldsymbol{\ddot{\bar{x}}}}. \\ \end{align} $ | (13) |
根据广义加权最小范数法可知, 当W1→∞时, 满足力矩约束式(8), 可以通过下面的定理证明.
定理:当约束对应的权值wi趋于无穷时, 式(13) 满足
证明:设约束任务矩阵K的奇异值分解为K=USVT, 其中U∈Rp×p、V∈R(n+1)×(n+1)为酉矩阵, S=[Σp, 0p×(n-p+1)]∈Rp×(n+1)的奇异值位于对角子矩阵Σp∈Rp×p中.将V分块为V=V1|V2, 其中V1∈R(n+1)×p, V2∈R(n+1)×(n+1-p), 则K⊥=V2.此时, 变换矩阵T为
| $ \begin{align} & \mathit{\boldsymbol{T=}}\left[ \begin{matrix} \mathit{\boldsymbol{U }}\!\!\mathit{\boldsymbol{\Sigma}}\!\!\rm{ V}_{1}^{\rm{T}} \\ \mathit{\boldsymbol{V}}_{2}^{\rm{T}} \\ \end{matrix} \right]=\left[ \begin{matrix} \mathit{\boldsymbol{U}} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & {{\mathit{\boldsymbol{I}}}_{n+1-p}} \\ \end{matrix} \right]\times \\ & \ \ \ \ \ \ \left[ \begin{matrix} {{\mathit{\boldsymbol{ }}\!\!\mathit{\boldsymbol{\Sigma}}\!\!\rm{ }}_{p}} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & {{\mathit{\boldsymbol{I}}}_{n+1-p}} \\ \end{matrix} \right]\left[ \begin{matrix} \mathit{\boldsymbol{V}}_{1}^{\rm{T}} \\ \mathit{\boldsymbol{V}}_{2}^{\rm{T}} \\ \end{matrix} \right]. \\ \end{align} $ | (14) |
将式(11)、(14) 代入式(13), 可得
| $ \begin{align} & \mathit{\boldsymbol{\ddot{\bar{q}}}}=\mathit{\boldsymbol{V}}\left[ \begin{matrix} \mathit{\boldsymbol{W}}_{1}^{-2}\mathit{\boldsymbol{ }}\!\!\mathit{\boldsymbol{\Sigma}}\!\!\rm{ }_{p}^{-2} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & \mathit{\boldsymbol{W}}_{2}^{-2} \\ \end{matrix} \right]{{\mathit{\boldsymbol{V}}}^{\rm{T}}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}}\times \\ & \ \ \ \ \ \ \ {{\left( \mathit{\boldsymbol{\ddot{J}V}}\left[ \begin{matrix} \mathit{\boldsymbol{W}}_{1}^{-2}\mathit{\boldsymbol{ }}\!\!\mathit{\boldsymbol{\Sigma}}\!\!\rm{ }_{p}^{-2} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & \mathit{\boldsymbol{W}}_{2}^{-2} \\ \end{matrix} \right]{{\mathit{\boldsymbol{V}}}^{\rm{T}}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}} \right)}^{-1}}\mathit{\boldsymbol{\ddot{\bar{x}}}}. \\ \end{align} $ | (15) |
当W1的对角元素趋于∞时, W1-1→0p×p, 有
| $ \begin{align} & \mathit{\boldsymbol{\ddot{\bar{q}}}}\approx \mathit{\boldsymbol{V}}\left[ \begin{matrix} {{\bf{0}}_{p\times p}} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & \mathit{\boldsymbol{W}}_{2}^{-2} \\ \end{matrix} \right]{{\mathit{\boldsymbol{V}}}^{\rm{T}}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}}\times \\ & \ \ \ \ \ {{\left( \mathit{\boldsymbol{\bar{J}V}}\left[ \begin{matrix} {{\bf{0}}_{p\times p}} & {{\bf{0}}_{p\times \left( n+1-p \right)}} \\ {{\bf{0}}_{\left( n+1-p \right)\times p}} & \mathit{\boldsymbol{W}}_{2}^{-2} \\ \end{matrix} \right]{{\mathit{\boldsymbol{V}}}^{\rm{T}}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}} \right)}^{-1}}\mathit{\boldsymbol{\ddot{\bar{x}}}}= \\ & \ \ \ \ \ {{\mathit{\boldsymbol{V}}}_{2}}\mathit{\boldsymbol{W}}_{2}^{-2}\mathit{\boldsymbol{V}}_{2}^{\rm{T}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}}{{\left( \mathit{\boldsymbol{\bar{J}}}{{\mathit{\boldsymbol{V}}}_{2}}\mathit{\boldsymbol{W}}_{2}^{-2}\mathit{\boldsymbol{V}}_{2}^{\rm{T}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}} \right)}^{-1}}\mathit{\boldsymbol{\ddot{\bar{x}}}}. \\ \end{align} $ | (16) |
此时
| $ K\mathit{\boldsymbol{\ddot{\bar{q}}}}={{\mathit{\boldsymbol{U}}}_{p}}{{\mathit{\boldsymbol{ }}\!\!\mathit{\boldsymbol{\Sigma}}\!\!\rm{ }}_{p}}\mathit{\boldsymbol{V}}_{1}^{\rm{T}}{{\mathit{\boldsymbol{V}}}_{2}}\mathit{\boldsymbol{W}}_{2}^{-2}\mathit{\boldsymbol{V}}_{2}^{\rm{T}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}}{{\left( \mathit{\boldsymbol{\bar{J}}}{{\mathit{\boldsymbol{V}}}_{2}}\mathit{\boldsymbol{W}}_{2}^{-2}\mathit{\boldsymbol{V}}_{2}^{\rm{T}}{{{\mathit{\boldsymbol{\bar{J}}}}}^{\rm{T}}} \right)}^{-1}}\mathit{\boldsymbol{\ddot{\bar{x}}}}. $ | (17) |
由V1T与V2的正交性可知, V1TV2=0p×(n+1-p).于是,
注:当加权后的扩展雅可比矩阵奇异时, 需要引入阻尼项来保证加权后的扩展雅可比矩阵的伪逆有界.然而, 引入阻尼后的扩展后系统方程存在残差, 即扩展的辅助变量值可能不严格等于1.这一问题可以通过采用变权重最小二乘法[19]来解决, 在此不作详述.
基于GWLN方法的约束求解与基于动力学灵活性指标优化算法[5]均采用加权范数法进行求解, 然而两者略有不同, 分析比较如下.
1) 基于动力学灵活性指标优化算法忽略了科里奥利力及重力项, 仅对关节加速运动所需力矩进行优化, 当关节重力矩和科里奥利力之和超过力矩输出极限时, 该方法将失效;基于GWLN的方法通过辅助变量的引入, 将科里奥利力及重力的影响考虑在内, 因而能够严格保证关节力矩约束.
2) 基于动力学灵活性指标优化算法的优化效果使得关节加速运动所需力矩在输出饱和关节的投影分量趋于零, 未充分利用临近饱和关节的驱动能力且易造成指令关节力矩跳变及振荡;基于GWLN的方法借助辅助变量, 使相应关节的指令力矩在饱和输出边界上, 控制的结果更平滑.
基于GWLN的方法与基于动力学灵活性指标的优化算法相比, 更加具有优点, 可以看作对后者的补充和完善.
3 仿真结果为了验证该算法的有效性, 在MATLAB Robotic Toolbox工具箱[20]中对PUMA 560机械臂在关节力矩约束下的操作任务进行仿真.仿真的设定如下.PUMA 560机械臂的连杆Denavit-Hartenberg参数如表 1所示.在机械臂腕关节末端添加了执行器.执行器的端点在关节6坐标系下的坐标为6pe=[0, 0, 0.2] m, 执行器的惯性模型被简化为质量为2.5 kg的质点, 质心位置在关节6坐标系中的坐标为6pc=[0, 0, 0.1] m.机械臂的初始关节坐标q(0)=[0, π/4, π, 0, π/4, 0] rad.操作任务轨迹为沿Ox方向的线段, 任务轨迹方程为
| 表 1 PUMA560机械臂Denavit-Hartenberg参数表 Table 1 Denavit-Hartenberg parameters of PUMA 560manipulator |
| $ {{\mathit{\boldsymbol{x}}}_{r}}\left( t \right)=\left[ \begin{matrix} 38.4{{t}^{5}}-48{{t}^{4}}+16{{t}^{3}}+0.7963 \\ -0.1501 \\ -0.0144 \\ \end{matrix} \right]. $ | (18) |
式中:t为时间坐标.任务持续的时间为0.5s, 仿真步长设定为5 ms.各个关节的关节力矩输出范围均为[-60, 60] N·m.由于末端执行机构的轨迹逐渐远离机械臂的基座, 整个操作过程机械臂作伸展动作, 水平方向2、3关节的重力矩增加.为了避免离散化误差, 在此引入闭环误差反馈:
| $ {{{\mathit{\boldsymbol{\ddot{x}}}}}_{\rm{d}}}\left( t \right)={{{\mathit{\boldsymbol{\ddot{x}}}}}_{\rm{r}}}\left( t \right)-{{k}_{\rm{p}}}\mathit{\boldsymbol{e}}\left( t \right)-{{k}_{\rm{v}}}\mathit{\boldsymbol{\dot{e}}}\left( t \right). $ | (19) |
式中:e(t)为操作任务误差,e(t)=x(t)-xr(t);kp=kv=20为误差反馈系数.
在不考虑关节力矩约束控制的情况下, 最小2范数关节加速度逆运动学解所需的关节力矩峰值可以达到120 N·m, 大大超出了关节驱动器的能力范围, 如图 1所示.由于关节驱动器无法满足关节力矩输出要求, 实际输出的关节力矩仅能保持在饱和极限值.因系统驱动力不足, 实际的关节加速度将偏离最小范数关节加速度指令, 如图 2所示.图中,

|
图 1 最小2范数关节加速度控制率下关节力矩指令 Fig. 1 Command torque by joint acceleration least 2-norm method |
|
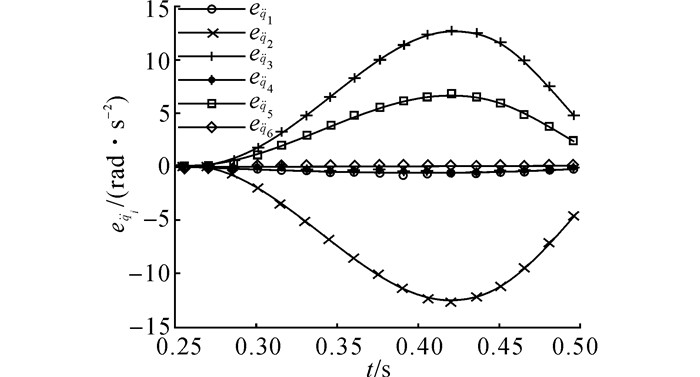
图 2 关节加速度最小2范数控制率下规划关节加速度指令与实际关节加速度的偏差 Fig. 2 Discrepancy between joint acceleration command and actual joint acceleration by joint acceleration least 2-norm method |
采用本文方法来求解关节力矩约束.注意到式(8) 将使得关节力矩保持在饱和极限值.为了避免在关节力矩约束未被激活时使关节力矩幅度增长的副作用, 仅当第i关节的力矩τi超过设定阈值τthres时, 关节力矩约束任务Ki被激活.将约束任务矩阵修改为
| $ \begin{align} & {{\mathit{\boldsymbol{K}}}_{i}}\left( k \right)= \\ & \ \ \ \ \left[ {{\mathit{\boldsymbol{M}}}_{i}}\left( \mathit{\boldsymbol{q}} \right),\ \ \ -{{\mathit{\boldsymbol{C}}}_{i}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\dot{q}}}-{{g}_{i}}\left( \mathit{\boldsymbol{q}} \right)+{{\tau }_{i}}\left( k-1 \right) \right]. \\ \end{align} $ | (20) |
式中:k表示当前控制周期, k-1表示上一控制周期.当
| $ {{w}_{i}}=\left\{ \begin{matrix} \frac{{{\tau }_{i,\lim }}-{{\tau }_{i,\rm{thres}}}}{{{\tau }_{i,\lim }}-{{\tau }_{i}}}, & \Delta \left| {{\tau }_{i}} \right|\ge 0,{{\tau }_{i}}>{{\tau }_{i,\rm{thres}}}; \\ 1, & 其他. \\ \end{matrix} \right. $ | (21) |
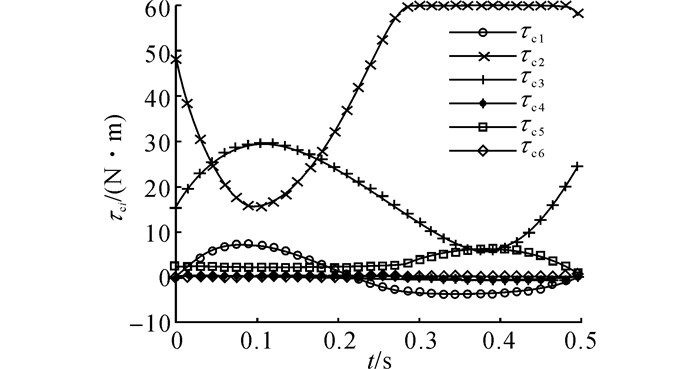
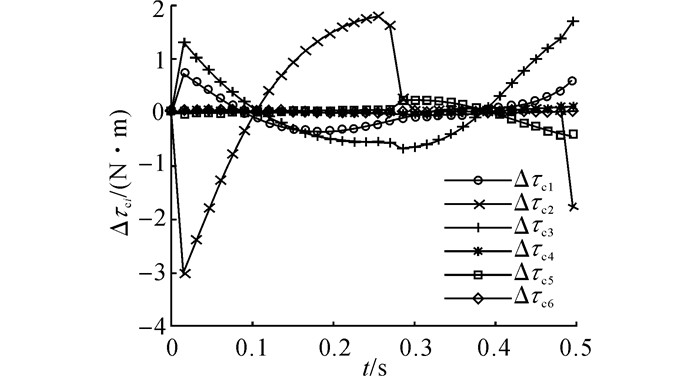
由式(21) 可知, 当τi≤τi, thres时, wi=1, 式(13) 退化为关节加速度最小2范数解.当τi=τi, lim时, wi=∞, 关节力矩指令τi, c将保持在输出极限τi, lim.在式(13) 的作用下, 整个过程的指令关节力矩曲线如图 3所示.从图 3可以看出, 各关节的指令力矩平滑变化, 且均保持在设定的输出范围内, 因而关节实际输出力矩与关节力矩指令一致.其中, 关节2力矩的最大值为59.994 N·m, 几乎在其饱和输出边界上, 满足关节力矩约束.算法的有效性可以从相邻控制周期关节力矩的增量变化中看出, 如图 4所示.在t=0.3 s前后, 随着关节2的力矩值趋向输出极限, 指令力矩的增量Δτc2逐渐减小到0, 即满足约束
|
图 3 基于GWLN方法的关节力矩指令 Fig. 3 Joint torque command by proposed method |
|
图 4 基于GWLN方法的相邻周期关节力矩指令增量 Fig. 4 Increment of command torque by proposed method |
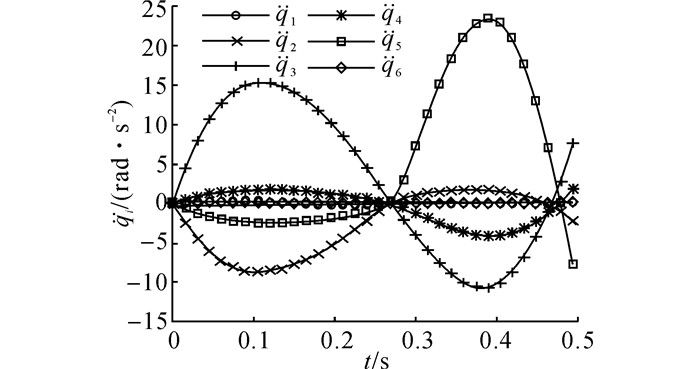
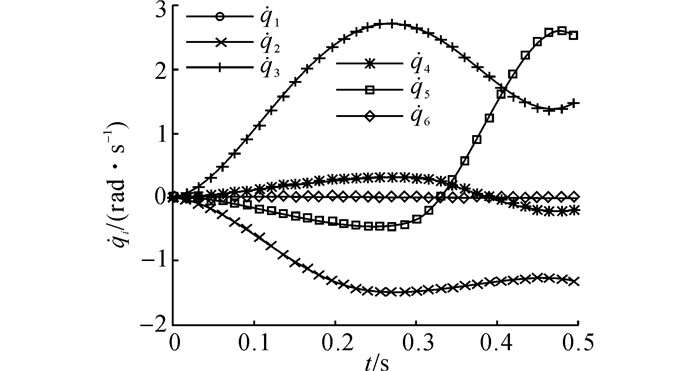
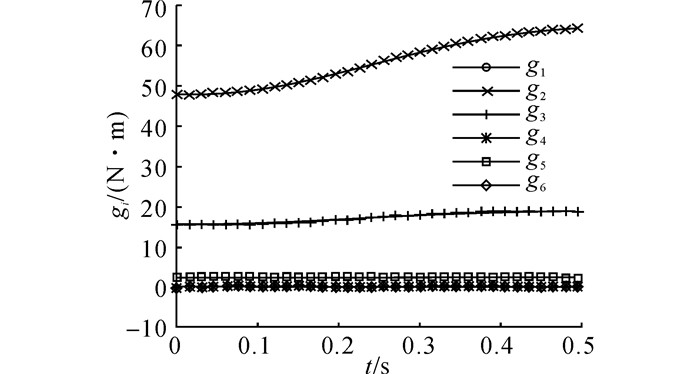
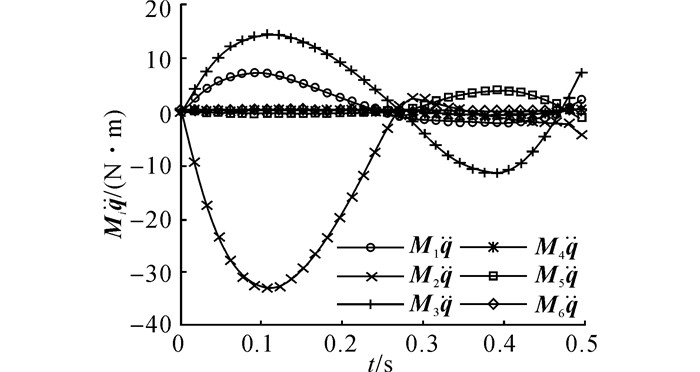
在式(13) 的控制下, 整个过程的关节加速度曲线及关节速度曲线分别如图 5、6所示.由于关节驱动力矩未超出极限, 实际关节加速度与规划关节加速度指令一致, 从而保证了操作任务的准确性.当操作任务结束时, 关节速度及关节加速度不为零, 该现象是由关节力矩约束导致的.随着操作任务的进行, 各个关节的重力负荷逐渐增加, 如图 7所示.在t=0.3 s之后, 关节2的重力负荷已经超过了关节力矩极限.此时, 机械臂系统不能在该位形下保持零关节速度和零关节加速度的静止状态.在式(13) 的作用下, 关节力矩约束使得关节2加速力矩子项
|
图 5 基于GWLN方法的关节加速度 Fig. 5 Joint acceleration by proposed method |
|
图 6 基于GWLN方法的关节速度 Fig. 6 Joint velocity by proposed method |
|
图 7 基于GWLN方法的重力矩g(q) Fig. 7 Gravity item g(q) by proposed method |
|
图 8
基于GWLN方法的关节加速所需力矩 |
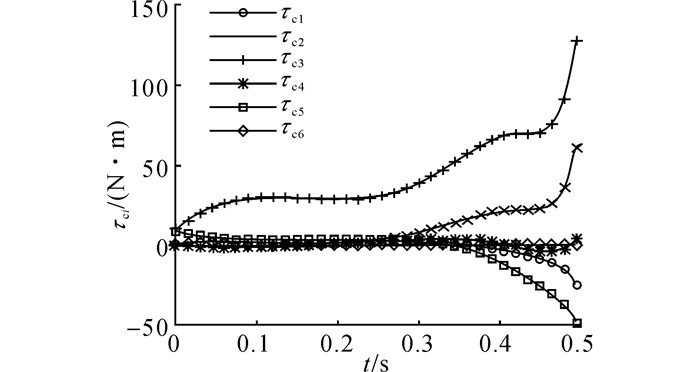
采用Hollerbach提出的零空间力矩优化算法以及赵占芳提出的动力学灵活性指标优化算法对同一力矩约束下的操作任务进行求解, 得到的指令关节力矩结果如图 9、10所示.零空间力矩优化算法在t=0.38 s后, 关节3的指令关节力矩超出了实际关节输出极限, 如图 9所示.此时, 实际关节加速度和指令关节加速度之间将出现偏差, 导致操作任务产生执行偏差.这一结果验证了关节力矩指标优化不保证关节力矩约束的结论.
|
图 9 零空间力矩优化算法控制下关节力矩指令 Fig. 9 Joint torque command and actual output joint torque by null space optimization method |
|
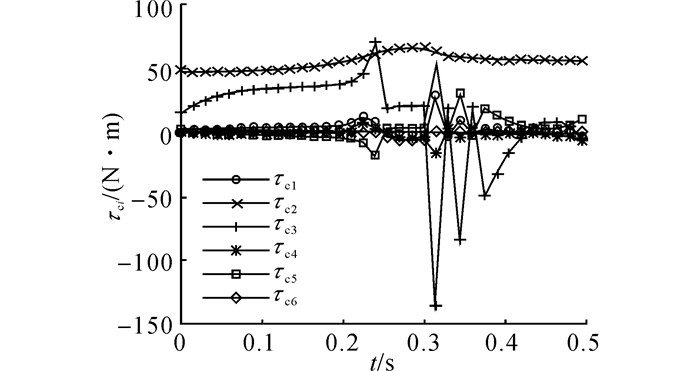
图 10 动力学灵活性优化算法控制下关节力矩指令 Fig. 10 Joint torque command by dynamic dexterityoptimization method |
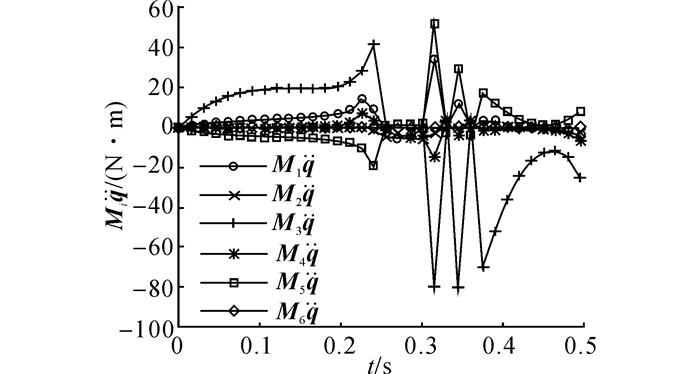
基于动力学灵活性指标优化算法的结果如图 10所示.当某一关节指令力矩趋近输出饱和极限时, 对动力学灵活性指标的优化作用使得相应关节所需要的加速力矩项
|
图 11
动力学灵活性优化算法控制下关节加速所需力矩 |
针对有限关节力矩约束下冗余机械臂的控制问题, 本文提出基于广义加权最小范数法的求解算法.该方法在保证关节力矩约束的同时, 准确地完成了操作任务, 充分利用了系统的冗余特性.算法的有效性既通过理论分析得到了证明, 也由在MATLAB Robotic Toolbox中的仿真结果得到了验证.与现有加权算法的结果对比可知, 基于GWLN方法的控制算法更加有效地保证关节力矩约束.
当操作任务的要求完全超出关节力矩范围时, 关节力矩约束不能通过基于GWLN的运动学规划求解方法得以实现, 任务轨迹的执行将产生偏差.此时, 须对操作任务规划调整来保证对任务轨迹的跟踪, 具体方法还有待研究.此外, 本文提出的算法未考虑机械臂模型偏差及外界扰动存在的情况.如何在模型偏差以及扰动存在的情况下, 实现冗余机械臂的力矩约束控制是今后的研究方向之一.
| [1] | KIRCANSKI M, KIRCANSKI N. Resolved rate and acceleration control in the presence of actuator constraints[J]. IEEE Control Systems, 1998, 18(1): 42–47. DOI:10.1109/37.648628 |
| [2] | HOLLERBACH J M, SUH K C. Redundancy resolution of manipulators through torque optimization[J]. IEEE Journal of Robotics and Automation, 1987, 3(4): 308–316. DOI:10.1109/JRA.1987.1087111 |
| [3] | LIU S, WANG J. Bi-criteria torque optimization ofredundant manipulators based on a simplified dual neural network[C]//2005 IEEE International Joint Conference on Neural Networks. Montreal: IEEE, 2005:2796-2801. https://www.researchgate.net/publication/4202856_Bi-criteria_torque_optimization_of_redundant_manipulators_based_on_a_simplified_dual_neural_network |
| [4] | 熊有伦. 机器人学[M]. 北京: 机械工业出版社, 1993: 263-266. |
| [5] | ZHAO Z, WU Z, LU J, et al. Dynamic dexterity of redundant manipulators[C]// IEEE International Conference on Systems, Man and Cybernetics. Vancouver: IEEE, 1995: 928-933. http://www.researchgate.net/publication/224098766_Dynamic_dexterity_of_redundant_manipulators |
| [6] |
陈伟海. 冗余自由度机器人优化控制研究[D]. 北京: 北京航空航天大学, 1996.
CHEN Wei-hai. Research on control of robot with redundant degree of freedom[D]. Beijing: Beihang University, 1996. http://d.wanfangdata.com.cn/Thesis/Y219667 |
| [7] |
郭大忠, 柳洪义, 张威, 等. 冗余度机器人运动学和动力学同时优化[J].
东北大学学报:自然科学版, 2008, 29(7): 1008–1011.
GUO Da-zhong, LI Hong-yi, ZHANG Wei, et al. Simultaneously kinematical and dynamical optimizations of redundant robots[J]. Journal of Northeastern University: Natural Science, 2008, 29(7): 1008–1011. |
| [8] |
郭宪, 王明辉, 李斌, 等. 基于最小无穷范数的蛇形机器人最优力矩控制[J].
机器人, 2014, 36(01): 8–13.
GUO Xian, WANG Ming-hui, LI Bin, et al. Optimal torque control of a snake-like robot based on the minimum infinity norm[J]. Robot, 2014, 36(01): 8–13. DOI:10.3969/j.issn.1004-6437.2014.01.001 |
| [9] |
闫彩霞, 闫楚良, 陆震. 基于加权矩阵的过驱动并联机构驱动力矩调节法[J].
吉林大学学报:工学版, 2008, 38(5): 1215–1219.
YAN Cai-xia, YAN Chu-liang, LU Zhen. Approach to coordinate driving torque of redundant actuated parallel manipulator based on weighted matrix[J]. Journal of Jilin University: Engineering and Technology Edition, 2008, 38(5): 1215–1219. |
| [10] |
金波, 陈诚, 李伟. 基于能耗优化的六足步行机器人力矩分配[J].
浙江大学学报:工学版, 2012, 46(07): 1168–1174.
JIN Bo, CHEN Cheng, LI Wei. Optimization of energy-efficient torque distribution for hexapod walking robot[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(07): 1168–1174. |
| [11] | BIANCO C G L, GERELLI O. Trajectory scaling for a manipulator inverse dynamics control subject to generalized force derivative constraints[C]//International Conference on Intelligent Robots and Systems. St. Louis: IEEE, 2009: 5749-5754. Trajectory scaling for a manipulator inverse dynamics control subject to generalized force derivative constraints |
| [12] |
陈伟海, 武桢, 丁希伦, 等. 冗余度机器人动力学容错控制技术研究[J].
北京航空航天大学学报, 2000, 26(6): 726–730.
CHEN Wei-hai, WU Zhen, DING Xi-lun, et al. Research on fault tolerant control of dynamically redundant manipulators[J]. Journal of Beijing University of Aeronautics And Astronautics, 2000, 26(6): 726–730. |
| [13] | ZHANG Yu-nong, WANG Jun. A dual neural network for constrained joint torque optimization of kinematically redundant manipulators[J]. IEEE Transactions on Systems Man and Cybernetics Part B, 2002, 32(5): 654–662. DOI:10.1109/TSMCB.2002.1033184 |
| [14] | FLACCO F, LUCA A D, KHATIB O. Motion control of redundant robots under joint constraints: saturation in the null space[C]//2012 IEEE International Conference on Robotics and Automation (ICRA). St. Paul: IEEE, 2012: 285-292. http://www.researchgate.net/publication/254041442_Motion_control_of_redundant_robots_under_joint_constraints_Saturation_in_the_Null_Space |
| [15] | LIEGEOIS A. Automatic supervisory control of the configuration and behavior of multibody mechanisms[J]. IEEE Transactions on Systems Man and Cybernetics, 1977, 7(12): 868–871. DOI:10.1109/TSMC.1977.4309644 |
| [16] | NAKAMURA Y, HANAFUSA H, YOSHIKAWA T. Task-priority based redundancy control of robot manipulators[J]. International Journal of Robotics Research, 1987, 6(2): 3–15. DOI:10.1177/027836498700600201 |
| [17] | XIANG J, ZHONG C W, WEI W. General-weighted least-norm control for redundant manipulators[J]. IEEE Transactions on Robotics, 2010, 26(4): 660–669. DOI:10.1109/TRO.2010.2050655 |
| [18] |
钟琮玮. 仿人型乒乓球机械手运动学及动力学控制方法研究[D]. 杭州: 浙江大学, 2011.
ZHONG Cong-wei. Kinematic and dynamic control of a humanoid pingpong manipulator[D]. Hangzhou: Zhejiang University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10335-1012313880.htm |
| [19] | XIANG J, ZHONG C W, WEI W. A varied weights method for the kinematic control of redundant manipulators with multiple constraints[J]. IEEE Transactions on Robotics, 2012, 28(2): 330–340. DOI:10.1109/TRO.2011.2173834 |
| [20] | CORKE P. Robotics, vision and control[M]. Berlin: Springer, 2011. |



