生产计划和调度不仅是企业生产和管理的重要环节之一, 而且是生产决策的有效依据, 计划和调度方案的优劣决定了企业的经济效益.为了保证生产决策的可行性和最优性, 越来越多的学者开始关注生产计划和调度的集成问题[1-2].在生产计划和调度执行的过程中, 存在很多不确定性因素, 例如环境不确定因素和系统不确定因素.环境不确定因素主要包括需求不确定性和供应不确定性.系统不确定性因素主要包括产量不确定性、处理时间不确定性、产品质量不确定性和设备故障[3].以上不确定性因素对生产计划和调度有重要的影响, 可能使优化结果不是最优解甚至是非可行解, 从而严重影响企业的生产效率和经济效益.
目前, 对于不确定条件下的生产计划和调度问题已经取得了一定的研究成果.处理生产过程中不确定性因素的方法主要分成以下3种[4]:随机规划方法、模糊规划方法和鲁棒优化方法.Andre等[5]建立两阶随机规划模型来处理采矿生产调度中供应量的不确定性问题, 使得优化结果与传统优化方法相比提高了净现值, 有效地改善了矿资源的管理和可持续使用.Xu等[6]评估了场景树的复杂程度对随机规划模型性能的影响, 利用蒙特卡洛法来决定所需要的场景数量, 有效地降低了模型的规模, 提高了模型性能.Iris等[7]利用模糊线性规划模型来解决集约生产计划(aggregate production planning)问题, 将用户需求、库存和托单的不确定性引入到计划模型中, 基于不同的模糊参数, 为企业提供了更全面、准确的决策依据.Yang等[8]为带有模糊交货期的并行机调度问题建立模糊拖期调度模型, 以工件的拖期惩罚成本最小化作为优化目标.Donya等[9]建立基于多产品两阶段的鲁棒优化模型, 考虑了需求和生产成本的不确定性问题, 有效地降低了不确定性参数波动对生产计划的影响.田野等[10]利用产量关联对多周期生产计划与调度问题进行集成, 使用场景方法描述需求不确定性, 实例结果验证了采用该方法可以最大限度地降低产品的短缺费用, 降低生产成本, 实现生产操作性和经济性的综合优化.
考虑不确定性因素的生产计划和调度问题虽然引起了越来越多学者的关注, 但是大都集中于需求和处理时间等不确定性参数.对于公用工程的不确定性问题的研究较少.在实际生产过程中, 公用工程被广泛地应用并分配给不同的生产线来支撑生产的正常运行, 例如蒸汽、冷凝水、电力等.在通常情况下, 这些公用工程的供给量存在波动, 影响生产的平稳性甚至可能导致设备的停机.目前, 大部分生产调度模型没有考虑公用工程的不确定性因素, 只是把公用工程看作确定性参数来处理, 这样会严重影响生产调度结果的最优性和有效性, 甚至可能导致调度结果的不可行.另外, 公用工程的供给量与实际生产过程紧密相关, 包括生产速率、处理时间等.在生产计划和调度模型中, 考虑公用工程的不确定性因素是十分重要的[11].
本文建立生产计划和调度的双层集成模型, 同时考虑了需求和公用工程的不确定性问题.首先建立计划和调度的确定性模型, 分别在计划层和调度层引入机会约束方法和模糊理论来描述不确定参数, 建立带有不确定性约束的优化模型.利用集成优化求解法和滚动优化策略对每一个计划周期内的计划和调度模型进行分层求解, 通过双层模型间的迭代使得计划和调度结果达成一致.通过经典算例论证了采用提出的模型, 不但有效地降低了两种不确定参数对优化结果的影响, 而且提高了设备和公用工程的利用率.
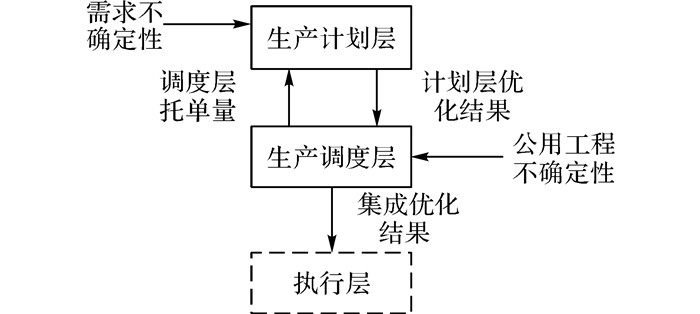
1 集成模型双层结构及求解策略很多文献将订单需求作为确定性参数来处理, 但实际上订单需求受到很多因素的影响, 是生产计划问题中主要的不确定性因素, 严重影响生产计划的可行性.公用工程是生产过程中的另一种不确定因素.一些公用工程, 例如蒸汽、冷凝水和电力等是生产正常运行的重要保障.在通常情况下, 这些公用工程同时供应给不同的生产线, 若供给量发生扰动, 则将对生产过程造成严重的影响, 使得生产无法按照预定计划完成.本文提出计划和调度双层集成模型来分层处理需求和公用工程的不确定性问题.生产计划和调度的双层结构如图 1所示.
|
图 1 生产计划和调度的双层结构 Fig. 1 Bi-level structure of production planning andscheduling |
生产计划和调度层次模型通常用于解决大规模的计算问题, 但是计划和调度的层次结构适用于逐一处理不同时间尺度的不确定性问题[11].需求和公用工程的不确定性具有各自的时间尺度, 需求不确定性应该在相对较长的时间尺度内处理, 然而公用工程的不确定性应该在较短的时间尺度内考虑.在计划层和调度层分别处理需求和公用工程的不确定性是更合理的.
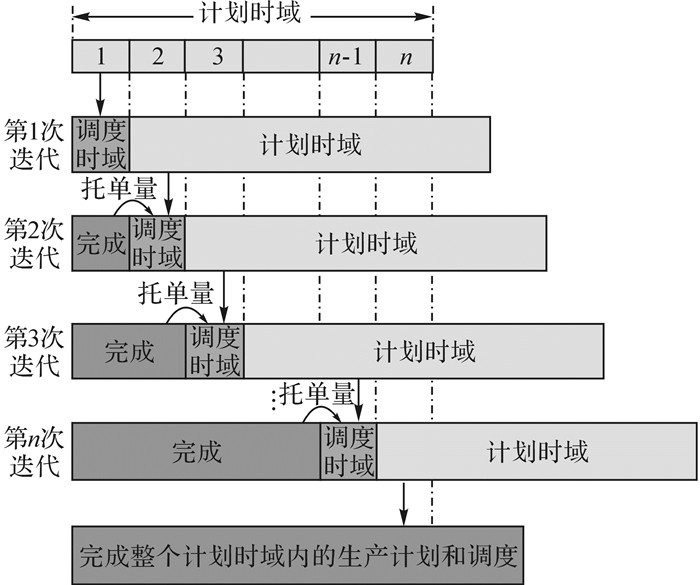
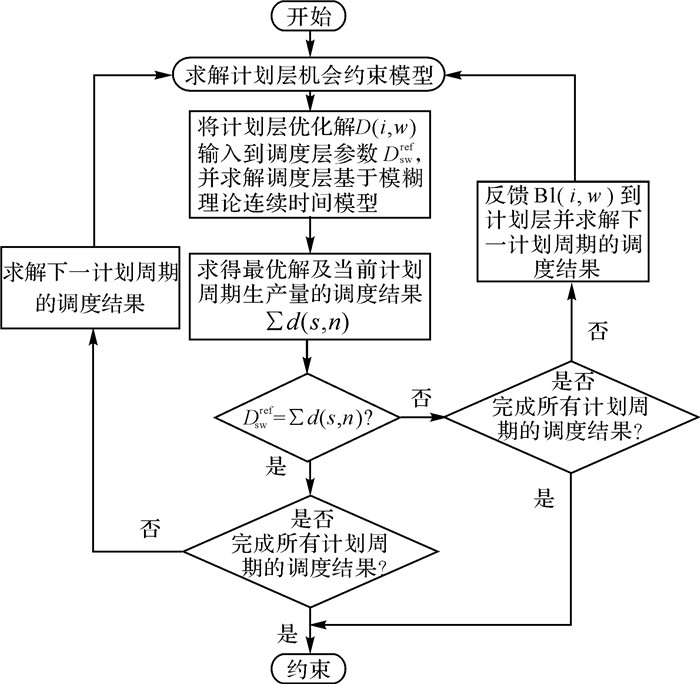
在计划层建立离散时间模型, 利用机会约束方法来表示需求不确定性, 但在计划层不考虑公用工程的不确定问题, 即计划层的优化模型建立在不受公用工程限制的条件下.在调度层建立连续时间模型, 利用模糊理论来描述公用工程的不确定性.计划层离散模型的计划时域(planning horizon)由n个时间相等的计划周期(planning period)组成.调度层连续模型的调度时域与计划层的计划周期时间长度相等.利用滚动时域优化策略, 对计划层和调度层模型进行迭代求解, 来实现双层模型的集成.第1次迭代时, 如图 2所示, 计划层模型在整个计划时域内求得最优解, 并只将第一个计划周期内的生产任务分配给调度层模型, 调度层的目标是尽可能多地完成计划层分配的生产任务, 并完成第一个计划周期内的优化调度.在计划层和调度层模型的迭代求解过程中, 允许托单情况的发生, 即存在调度层没有完全完成计划层分配的生产任务的情况.对于没有完成的托单量, 将重新作为订单需求反馈到下一次计划层的优化求解中.此时, 第一个计划周期内的生产计划和调度已经确定.在第2次迭代时, 计划层的优化时域从第二个计划周期开始, 并向后滚动一个计划周期, 重新求解计划层模型.然后, 计划层将当前计划时域内的第一个计划周期的生产任务分配给调度层模型, 完成该计划周期的优化调度.如此滚动优化, 直至整个计划时域内的生产优化全部完成.计划层和调度层的迭代求解流程图如图 3所示.
|
图 2 滚动时域优化求解策略示意图 Fig. 2 Sketches of rolling horizon optimization strategy |
|
图 3 计划和调度层迭代求解流程图 Fig. 3 Flowchart of iterative solving process between planning and scheduling layers |
由于计划层的时间尺度较大, 主要涉及能力约束和物料平衡.在计划层建立离散时间线性规划模型, 以利益最大化作为目标函数, 同时考虑了生产率波动和库存水平超限约束.在计划层引入机会约束方法来表示订单需求的不确定性, 并假设订单需求服从正态分布;最后通过数学变换将机会约束不确定性模型转化成带有指定置信水平的确定性模型, 并加以求解.
2.1.1 确定性模型1) 物料平衡方程如下:
| $ \begin{array}{l} I\left( {i,w} \right) = I_i^0 + P\left( {i,w} \right) - D\left( {i,w} \right) - \\ \;\;\;\;\;\;\;\sum\limits_{j \in {Q_i}} {{a_{ij}}P\left( {i,w} \right);i \in A,w = 1} . \end{array} $ | (1) |
| $ \begin{array}{l} I\left( {i,w} \right) = I\left( {i,w - 1} \right) + P\left( {i,w} \right) - D\left( {i,w} \right) - \\ \;\;\;\;\;\;\;\sum\limits_{j \in {Q_i}} {{a_{ij}}P\left( {i,w} \right);i \in A,w > 1.w \in W} . \end{array} $ | (2) |
式中:Ii0为物料状态i的初始库存量;A为所有物料状态的集合, 包括原料、中间品和产品;Qi为物料状态i的下游物料状态集合;aij为物料状态i与物料状态j之间的转化系数.约束(1)、(2) 分别表示物料在初始周期和后续周期内的物料平衡水平.物料状态i在计划周期w末的库存量I(i, w)等于前一周期末的库存量I(i, w-1) 加上物料状态i当前周期的产量P(i, w), 再减去当前周期物料状态i的交货量D(i, w)和消耗量∑j∈QiaijP(j, w).
2) 能力约束如下:
| $ p_i^{\min } \le p\left( {i,w} \right) \le p_i^{\max };i \in {A_2},w \in W. $ | (3) |
| $ I_i^{\min } \le I\left( {i,w} \right) \le I_i^{\max };i \in A,w \in W. $ | (4) |
式中:A2为中间品和产品的集合.约束(3)、(4) 分别表示物料的生产能力约束和库存能力约束.物料状态i在计划周期w内的生产量被限定在最小生产能力pimin和最大生产能力pimax之间;物料状态i在计划周期w末的库存量介于库存下限Iimin和库存上限Iimax之间.
3) 生产率波动约束为
| $ \left. \begin{array}{l} P\left( {i,w} \right) - x\left( {i,w} \right) \le P\left( {i,w - 1} \right) \le \left( {i,w} \right) + x\left( {i,w} \right);\\ i \in {A_2},w \in W. \end{array} \right\} $ | (5) |
为了降低生产率波动对生产过程的影响, 在约束(5) 中引入辅助变量x(i, w), 并在目标函数中设置相应的惩罚权值λ, 使得下一周期的生产量尽可能接近前一周期生产量, 避免了相邻周期的生产率出现过大波动.
4) 库存水平超限约束如下:
| $ \left. \begin{array}{l} I_i^{{\rm{lb}}} - z\left( {i,w} \right) \le I\left( {i,w} \right) \le I_i^{{\rm{ub}}} + z\left( {i,w} \right);\\ i \in {A_2},w \in W. \end{array} \right\} $ | (6) |
为了增加生产流程的鲁棒性, 考虑了库存水平的超限问题.在约束(6) 中引入辅助变量z(i, w), 并设置库存的参考上、下限Iiub和Iilb, 使得物料状态的库存水平I(i, w)尽量在参考范围内, 可以有效地避免库存水平过低或过高的情况发生.
5) 需求约束如下:
| $ \left. \begin{array}{l} D\left( {i,w} \right) \le {O_{iw}} + {\rm{Bl}}\left( {i,w - 1} \right) + {\rm{b}}{{\rm{l}}_{i,w - 1}};\\ i \in {A_3},w \in W. \end{array} \right\} $ | (7) |
| $ \left. \begin{array}{l} {\rm{Bl}}\left( {i,w} \right) = {\rm{Bl}}\left( {i,w - 1} \right) + {O_{iw}} - D\left( {i,w} \right);\\ i \in {A_3},w \in W. \end{array} \right\} $ | (8) |
式中:bli, w-1为来自调度层优化结果的反馈托单量, A3为产品集合.约束(7) 表达交货量D(i, w)应小于等于当前周期订单量、前一周期拖单量以及来自调度层的托单量的总和.约束(8) 表达产品i在周期w的托单量Bl(i, w)由前一周期的托单量Bl(i, w-1)、当前周期的订单量Oiw和交货量D(i, w)决定.在目标函数中设有相关惩罚权值γ来避免托单情况的发生.
6) 目标函数为
| $ \begin{array}{l} \max \sum\limits_{i \in {A_2}} {\sum\limits_{w \in W} {\left[ {{m_i} \cdot D\left( {i,w} \right) - \gamma \cdot {m_i} \cdot {\rm{Bl}}\left( {i,w} \right) - } \right.} } \\ \;\;\;\left. {\theta \cdot z\left( {i,w} \right) - \lambda \cdot x\left( {i,w} \right)} \right]. \end{array} $ | (9) |
式中:mi为产品的市场价格.计划层模型的目标函数是利益最大化, 其中第一项是销售利润, 第二项是托单惩罚项, 最后两项是关于库存超限和生产率波动的惩罚项.以上3个惩罚项的惩罚权值分别为γ、θ、λ, 关于惩罚权值的取值决定于企业对不同惩罚项的重视程度.在一般情况下, 托单的发生会导致企业赔偿高额的违约金, 严重影响企业信誉.设置γ为100, 远高于其他两项惩罚权值.库存超限和生产率波动项是辅助惩罚项, 不应过多影响优化结果, 权值应设置得相对小, 因此, 后两个惩罚项权值设置为θ=0.001, λ=0.001.
2.1.2 机会约束规划模型Sliver和Peterson首次提出报童模型, 并且使用随机变量来描述需求不确定性[12].目前, 采用随机规划来处理需求的不确定问题已经取得了很多研究成果.机会约束是随机规划的一个重要分支, 是在随机规划的理论基础上, 考虑到所做决策在不利情况下可能存在不满足约束条件的情况发生, 即允许所做决策在一定程度上不满足约束条件, 但该决策应该使约束条件成立的概率不小于某一置信水平.机会约束更真实地反映了不确定变量的属性.在计划层, 采用机会约束方法来表示生产计划中订单需求的不确定性.在约束(7)、(8) 中, 参数Oiw是随机变量, 表示产品i在周期w的订单需求量.假设该参数服从正态分布, 即Oiw~N(E{Oiw}, var{Oiw}).在置信水平α和β下, 约束(7)、(8) 可以改写成
| $ \left. \begin{array}{l} \Pr \left\{ {{O_{iw}} \ge D\left( {i,w} \right) - {\rm{Bl}}\left( {i,w - 1} \right) - {\rm{b}}{{\rm{l}}_{i,w - 1}}} \right\} \ge \alpha ;\\ i \in {A_3}. \end{array} \right\} $ | (10) |
| $ \left. \begin{array}{l} \Pr \left\{ {{O_{iw}} \ge D\left( {i,w} \right) + {\rm{Bl}}\left( {i,w} \right) - {\rm{Bl}}\left( {i,w - 1} \right)} \right\} \ge \beta ;\\ i \in {A_3}. \end{array} \right\} $ | (11) |
式中:Pr{·}为概率计算运算符.将Oiw转化成服从标准正太分布.利用概率密度函数, 式(10)、(11) 可以进一步转化成
| $ \begin{array}{*{20}{c}} {\frac{{\left( {D\left( {i,w} \right) - {\rm{Bl}}\left( {i,w - 1} \right) - {\rm{b}}{{\rm{l}}_{i,w - 1}}} \right) - E\left\{ {{O_{iw}}} \right\}}}{{\sqrt {{\mathop{\rm var}} \left\{ {{O_{iw}}} \right\}} }} \le }\\ {{\mathit{\Phi }^{ - 1}}\left( {1 - \alpha } \right);\;\;\;i \in {A_3}.} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {\frac{{\left( {D\left( {i,w} \right) + {\rm{Bl}}\left( {i,w} \right) - {\rm{Bl}}\left( {i,w - 1} \right)} \right) - E\left\{ {{O_{iw}}} \right\}}}{{\sqrt {{\mathop{\rm var}} \left\{ {{O_{iw}}} \right\}} }} \le }\\ {{\mathit{\Phi }^{ - 1}}\left( {1 - \beta } \right);\;\;\;i \in {A_3}.} \end{array} $ | (13) |
式(12)、(13) 中的不等式右侧可以通过简单的计算求得, 于是将机会约束规划模型转化成了带有置信水平的确定性模型.
2.2 调度层连续模型调度模型时间尺度相对较短, 不仅需要能力约束和物料平衡, 而且涉及任务的处理量、开始和结束时间.在调度层, 采用基于特定单元事件点的连续时间表达法来建立调度层模型.特定单元事件点的连续时间模型允许任务发生在调度时域内的任意时刻, 具有可变的时间间隔, 使得数学规划问题的规模更小, 需要的计算时间更少, 被认为是更准确并能够真实描述生产情况的建模方法.调度层模型的目标是在公用工程不确定的条件下, 完成计划层分配的任务.在调度层, 采用模糊理论来呈现公用工程的不确定性, 利用数学工具将不确定性模型转化成等价的确定性模型再求解.
2.2.1 确定性模型1) 分配约束为
| $ \sum\limits_{i \in {I_j}} {w\left( {i,n} \right) \le 1;j \in J,n \in {\bf{N}}} . $ | (14) |
式中:w(i, n)为0-1变量, 若任务i在事件点n执行, 则w(i, n)=1, 否则w(i, n)=0;J和N分别为设备和事件点的集合;Ij为可以在设备j上执行的任务集合.约束(14) 限制每个设备j在同一事件点n(event point)最多只能执行一个任务i.
2) 能力约束为
| $ \left. \begin{array}{l} B_i^{\min } \cdot w\left( {i,n} \right) \le b\left( {i,n} \right) \le B_i^{\max } \cdot w\left( {i,n} \right);\\ \forall i \in I,n \in {\bf{N}}. \end{array} \right\} $ | (15) |
式中:I为全部的任务集合.约束(15) 限定了生产批量的范围.若任务i在事件点n执行, 即w(i, n)=1, 则任务i的物料处理量b(i, n)受批量上下限Bimax和Bimin的限制;否则, 强制b(i, n)为0.
3) 物料平衡如下.
当n=1时,
| $ \left. {\begin{array}{*{20}{c}} {{\rm{ST}}\left( {s,n} \right) = {\rm{ST}}_s^0 + \sum\limits_{i \in I_s^c} {\rho _{is}^cb\left( {i,n} \right)} ;}\\ {\forall s \in {S^{\rm{R}}},{S^{\rm{I}}},n = 1.} \end{array}} \right\} $ | (16) |
| $ {\rm{ST}}\left( {s,n} \right) = {\rm{ST}}_s^0 - d\left( {s,n} \right),\forall s \in {S^{\rm{R}}},n = 1. $ | (17) |
当n>1时,
| $ \left. {\begin{array}{*{20}{c}} {{\rm{ST}}\left( {s,n} \right) = {\rm{ST}}\left( {s,n - 1} \right) + \sum\limits_{i \in I_s^c} {\rho _{is}^cb\left( {i,n} \right)} ;}\\ {\forall s \in {S^{\rm{R}}},n \in {\bf{N}},n > 1.} \end{array}} \right\} $ | (18) |
| $ \begin{array}{l} {\rm{ST}}\left( {s,n} \right) = {\rm{ST}}\left( {s,n - 1} \right) + \sum\limits_{i \in I_s^{\rm{p}}} {\rho _{is}^{\rm{p}}b\left( {i,n - 1} \right)} + \\ \;\;\;\sum\limits_{i \in I_s^c} {\rho _{is}^cb\left( {i,n} \right)} ,\forall s \in {S^{\rm{I}}},n \in {\bf{N}},n > 1. \end{array} $ | (19) |
| $ \begin{array}{l} {\rm{ST}}\left( {s,n} \right) = {\rm{ST}}\left( {s,n - 1} \right) + \sum\limits_{i \in I_s^{\rm{p}}} {\rho _{is}^{\rm{p}}b\left( {i,n - 1} \right)} - \\ \;\;\;d\left( {s,n} \right),\forall s \in {S^{\rm{P}}},n \in {\bf{N}},n > 1. \end{array} $ | (20) |
式中:SR、SI、SP和S分别为原料集合、中间品集合、产品集合以及3种物料的全集;STs0为状态s的初始库存量;Isp和Isc分别为物料状态s的生产任务和消耗任务集合;ρisp和ρisc分别为任务i生产和消耗物料状态s的比例系数, 且ρisp>0, ρisc < 0.约束(16)、(17) 分别是初始事件点原料、中间品和产品的物料平衡约束.约束(18)~(20) 分别是3种物料状态s在初始事件点之后的物料平衡方程.3种物料状态的库存量ST(s, n)由上个事件点物料状态的库存量ST(s, n-1) 和生产量∑(i∈Isp)ρispb(i, n-1) 以及当前事件点物料状态的消耗量∑(i∈Isc)ρiscb(i, n)和交货量d(s, n)来确定.
4) 需求约束为
| $ \sum\limits_{n \in {\bf{N}}} {d\left( {s,n} \right) \le D_{sw}^{{\rm{ref}}}} ,\;\;\;\forall s \in {S^{\rm{P}}},w \in W. $ | (21) |
| $ \left. {\begin{array}{*{20}{c}} {{\rm{bl}}\left( {s,w} \right) = D_{sw}^{{\rm{ref}}} - \sum\limits_{n \in {\bf{N}}} {d\left( {s,n} \right)} ;}\\ {\forall s \in {S^{\rm{P}}},w \in W.} \end{array}} \right\} $ | (22) |
约束(21) 表示指定计划周期w内物料状态s的总交货量∑n∈Nd(s, n)应该小于等于计划层下达的参考任务量Dswref.约束(22) 中的bl(s, w)是调度层的托单量, 由参考任务量Dswref和总交货量∑n∈Nd(s, n)决定, 并被反馈到计划层的下一个周期.
5) 持续约束为
| $ \left. {\begin{array}{*{20}{c}} {{T^{\rm{f}}}\left( {i,n} \right) = {T^{\rm{s}}}\left( {i,n} \right) + {\alpha _i} \cdot w\left( {i,n} \right) + {\beta _i} \cdot b\left( {i,n} \right);}\\ {i \in I,n \in {\bf{N}}.} \end{array}} \right\} $ | (23) |
式中:αi·w(i, n)、βi·b(i, n)分别为任务持续时间的常数项和变化项.任务i在事件点n的结束时间Tf(i, n)等于开始时间Ts(i, n)加上任务的持续时间.
6) 顺序约束如下.
a) 在相同设备上执行相同任务,
| $ {T^{\rm{s}}}\left( {i,n + 1} \right) \ge {T^{\rm{f}}}\left( {i,n} \right);i \in I,n \in {\bf{N}},n < N. $ | (24) |
约束(24) 表达n+1事件点任务i的开始时间应该大于等于上一事件点在相同设备上执行的任务i的结束时间.
b) 在相同设备上执行不同任务,
| $ \begin{array}{*{20}{c}} {{T^{\rm{s}}}\left( {i,n + 1} \right) \ge {T^{\rm{f}}}\left( {i',n} \right);i,i' \in {I_j};}\\ {i \ne i',j \in J,n \in {\bf{N}},n < N.} \end{array} $ | (25) |
约束(25) 表示在同一个设备上执行不同任务的时间约束关系.n+1事件点任务i的开始时间要大于等于n事件点任务i′的结束时间.
c) 在不同的设备上执行不同任务,
| $ \left. \begin{array}{l} {T^{\rm{s}}}\left( {i,n + 1} \right) \ge {T^{\rm{f}}}\left( {i',n} \right) - M\left( {1 - w\left( {i',n} \right)} \right);s,i,i',\\ j,j',n \in {\bf{N}},n < N,i \in {I_j},i' \in {I_{j'}},i \ne i',j \ne j',\\ i \in I_s^{\rm{c}},i' \in I_s^{\rm{p}}. \end{array} \right\} $ | (26) |
式中:M为松弛约束中的较大正数, 此处取值为500.根据生产工艺可知, 若不同任务在不同设备上生产或消耗相同的物料, 则约束(26) 限制消耗任务i的开始时间不能小于生产任务i′的结束时间.若w(i′, n)=1, 即任务i′在事件点n生产物料状态s, 则Ts(i, n+1)≥Tf(i′, n)成立;否则约束(26) 被松弛.
7) 紧约束为
| $ \sum\limits_{i \in {I_j}} {\sum\limits_{n \in {\bf{N}}} {\left( {{\alpha _i} \cdot w\left( {i,n} \right) + {\beta _i} \cdot b\left( {i,n} \right)} \right) \le H;j \in J} } . $ | (27) |
约束(27) 表示每个设备j的总加工时间应该不大于调度时域H.
8) 公用工程约束为
| $ \left. {\begin{array}{*{20}{c}} {\sum\limits_{i \in {I_u}} {\left( {{\gamma _{iu}} \cdot w\left( {i,n} \right)} \right)} + \sum\limits_{i \in {I_u}} {\left( {{\delta _{iu}} \cdot b\left( {i,n} \right)} \right)} \le U_u^{\max };}\\ {\forall u \in U,n \in {\bf{N}}.} \end{array}} \right\} $ | (28) |
式中:U为公用工程集合, Iu为消耗公用工程u的任务集合.约束(28) 表示在相同事件点同一公用工程u的消耗总量应该不大于最大供给量Uumax.公用工程的消耗量由常数项γiu·w(i, n)和变化项δiu×b(i, n)来确定, γiu和δiu为任务i对公用工程u的消耗系数.
| $ T_u^{\rm{s}}\left( {u,n + 1} \right) \ge T_u^{\rm{s}}\left( {u,n} \right);u \in U,n \in {\bf{N}},n < N. $ | (29) |
式中:Tus(u, n)为在事件点n、公用工程u的开始消耗时间.约束(29) 与约束(24) 相似, 表示下一事件点公用工程开始消耗的时间应大于等于当前事件点开始消耗的时间.
为了准确计算公用工程的消耗总量, 约束(30)、(31) 强制消耗同一公用工程的所有任务的开始时间与该公用工程被消耗的起始时间相等.
| $ \left. {\begin{array}{*{20}{c}} {T_u^{\rm{s}}\left( {u,n} \right) \ge {T^{\rm{s}}}\left( {i,n} \right) - M\left( {1 - w\left( {i,n} \right)} \right);}\\ {u \in U,i \in {I_u},n \in {\bf{N}}.} \end{array}} \right\} $ | (30) |
| $ \left. {\begin{array}{*{20}{c}} {T_u^{\rm{s}}\left( {u,n} \right) \le {T^{\rm{s}}}\left( {i,n} \right) + M\left( {1 - w\left( {i,n} \right)} \right);}\\ {u \in U,i \in {I_u},n \in {\bf{N}}.} \end{array}} \right\} $ | (31) |
若w(i, n)=1, 则约束(30)、(31) 变为Tus(u, n)≥Ts(i, n)且Tus(u, n)≤Ts(i, n), 即有Tus(u, n)=Ts(i, n), 因此强制消耗同一公用工程的所有任务的开始时间与该公用工程被消耗的开始时间相等.若w(i, n)=0, 则约束(30) 和(31) 同时被松弛.
| $ \left. {\begin{array}{*{20}{c}} {{T^{\rm{f}}}\left( {i,n - 1} \right) \le T_u^{\rm{s}}\left( {u,n} \right) + M\left( {1 - w\left( {i,n - 1} \right)} \right);}\\ {u \in U,i \in {I_u},n \in {\bf{N}},n > 1.} \end{array}} \right\} $ | (32) |
在约束(32) 中, 若w(i, n-1)=1, 即上一事件点任务i被执行, 则消耗公用工程u的任务结束时间Tf(i, n-1) 应小于等于当前事件点公用工程u的开始消耗时间Tus(u, n);否则, 约束(32) 被松弛.
9) 存储约束为
| $ {\rm{ST}}\left( {s,n} \right) \le {\rm{ST}}_s^{\max },\forall s \in {S^{{\rm{dfis}}}},n \in {\bf{N}}. $ | (33) |
| $ \begin{array}{l} {T^{\rm{f}}}\left( {i',n} \right) \ge {T^{\rm{s}}}\left( {i,n} \right) - M\left( {1 - w\left( {i',n} \right)} \right),\forall s \in {S^{{\rm{dfis}}}},\\ j,j' \in J,n < N,i \in {I_j},i' \in {I_j},i \ne i',j \ne j',i \in I_s^{\rm{c}},\\ i' \in I_s^{\rm{p}}. \end{array} $ | (34) |
式中:STsmax为物料状态s的最大存储能力, Sdfis为指定有限存储政策下的物料状态集合.约束(33) 采用无限存储和指定的有限存储政策, 表达物料有限的存储能力.为了处理指定的有限存储政策, 引入约束(34)、(26) 来共同避免虚假存储现象.若约束(26)、(34) 不被松弛, 则有
| $ {T^{\rm{s}}}\left( {i,n} \right) \le {T^{\rm{f}}}\left( {i',n} \right) \le {T^{\rm{s}}}\left( {i,n + 1} \right). $ | (35) |
约束(35) 要求当前事件点物料状态s的生产任务i′的结束时间大于等于消耗任务i的开始时间, 并小于等于下一事件点消耗任务的开始时间, 这样可以避免在事件点n发生指定有限库存的虚假超限现象.
10) 变量界限约束如下:
| $ \left. \begin{array}{l} T_u^{\rm{s}}\left( {u,n} \right) = 0,\;\;\;n = 1,u \in U;\\ T_u^{\rm{s}}\left( {u,n} \right) \le H,n \in {\bf{N}},u \in U;\\ {T^{\rm{s}}}\left( {i,n} \right) \le H,\;\;\;{T^{\rm{f}}}\left( {i,n} \right) \le H,i \in I,n \in {\bf{N}}. \end{array} \right\} $ | (36) |
为了简便计算, 约束(36) 设定公用工程的最初开始消耗时间为0, 并限制公用工程开始的消耗时间以及任务的开始和结束时间都在调度时域内.
11) 目标函数为
| $ \min \;\;\;D_{sw}^{{\rm{ref}}} - \sum\limits_{n \in {\bf{N}}} {d\left( {s,n} \right);s \in {S^{\rm{P}}},w \in W.} $ | (37) |
调度层的优化目标是在指定的计划周期内完成计划层下达的生产任务, 所以调度层的目标函数是计划层的参考任务量与调度层的任务完成量之差.
2.2.2 模糊调度模型某些不确定变量的历史数据较少、很难获得, 或者无法找到具体的分布函数来描述不确定变量的变化规律.采用模糊理论对不确定变量进行描述是一种有效的方法, 因为确定模糊数的隶属度函数比确定随机变量的分布函数容易.公用工程不同于订单需求, 受能源系统的影响很大, 而能源系统受到很多因素的干扰, 很难确定具体的分布函数来表示公用工程的不确定性.采用模糊理论来描述公用工程的不确定性.约束(28) 中的公用工程供给量Uumax是一个不确定性参数.假设Uumax的隶属度函数为三角形隶属度函数, 如下:
| $ {\mu _{\rm{A}}}\left( u \right) = \left\{ \begin{array}{l} \frac{{u - {u_{\rm{a}}}}}{{{u_{\rm{b}}} - {u_{\rm{a}}}}},\;\;\;{u_{\rm{a}}} \le u \le {u_{\rm{b}}};\\ \frac{{{u_{\rm{c}}} - u}}{{{u_{\rm{c}}} - {u_{\rm{b}}}}},\;\;\;{u_{\rm{b}}} < u \le {u_{\rm{c}}};\\ \;\;\;\;0,\;\;\;\;\;\;\;\;\;\;\;\;\;其他. \end{array} \right. $ | (38) |
利用模糊理论将不确定性约束(28) 转化成确定性约束:
| $ \begin{array}{l} \sum\limits_{i \in {I_u}} {\left( {{\gamma _{iu}} \cdot w\left( {i,n} \right)} \right)} + \sum\limits_{i \in {I_u}} {\left( {{\delta _{iu}} \cdot b\left( {i,n} \right)} \right)} \le \\ \;\;\;{w_{\rm{a}}} \cdot U_{{\rm{a,}}\alpha }^{\max } + {w_{\rm{b}}} \cdot U_{{\rm{b,}}\alpha }^{\max } + {w_{\rm{c}}} \cdot U_{{\rm{c,}}\alpha }^{\max };u \in U,n \in {\bf{N}}. \end{array} $ | (39) |
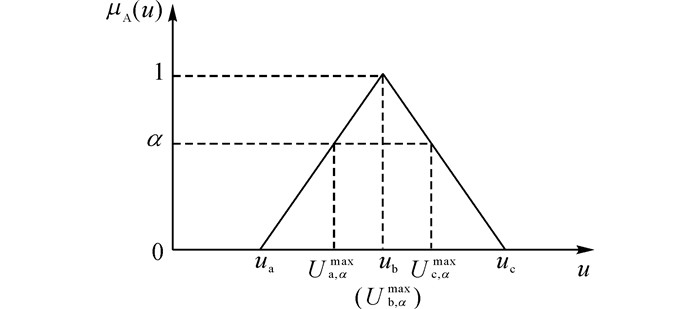
式中:wa、wb、wc为权值, 并满足wa+wb+wc=1;Ua, αmax、Ub, αmax、Uc, αmax分别为不确定性参数Uumax的三角隶属度函数在α截集下的边界点, 计算公式如下:
| $ U_{{\rm{a,}}\alpha }^{\max } = {u_{\rm{a}}} + \alpha \left( {{u_{\rm{b}}} - {u_{\rm{a}}}} \right). $ | (40) |
| $ U_{{\rm{b,}}\alpha }^{\max } = {u_{\rm{b}}}. $ | (41) |
| $ U_{{\rm{c,}}\alpha }^{\max } = {u_{\rm{c}}} + \alpha \left( {{u_{\rm{c}}} - {u_{\rm{b}}}} \right). $ | (42) |
Ua, αmax、Ub, αmax、Uc, αmax的关系如图 4所示.
|
图 4 参数Uumax的三角隶属度函数 Fig. 4 Triangle-shape grade of membership function for parameter Uumax |
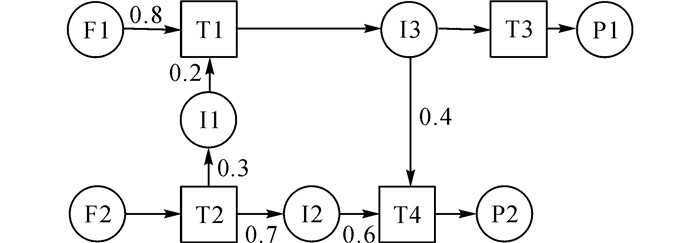
使用经典算例来验证计划、调度双层模型在处理需求和公用工程不确定问题时的可行性和有效性.该算例首次由Maravelias等[13]引入, 并被其他学者用以验证不同的模型[14].采用状态任务网络(state task network, STN)表示法对生产流程进行描述, 如图 5所示.两种原料(F1、F2) 经过吸热反应和放热反应生产两种产品(P1、P2), 并且经历3种中间物料状态(I1、I2、I3).反应1(T1) 和反应3(T3) 是吸热反应, 需要高压蒸汽(HS);反应2(T2) 和反应4(T4) 是放热反应, 需要冷凝水(CW).T1和T2可以在反应器1和反应器2上执行.T3和T4只能在反应器3上执行.在不同设备上执行的同种任务被视为两个不同的生产任务, 因此该算例共涉及6个不同的生产任务.由于能源系统的限制, 高压蒸汽(HS)和冷凝水(CW)的平均供给量分别是24和29 kg/min.另外, 原料和产品采用无限存储政策, 中间物料采用指定的有限存储政策.算例的相关数据见表 1~3.表 3中,Ps为物料状态s的单位状态.
|
图 5 状态任务网络示意图 Fig. 5 State task network representation for case study |
| 表 1 生产能力数据和处理时间系数 Table 1 Data of production capability and coefficients of processing time |
| 表 2 公用工程消耗系数 Table 2 Coefficients of utility consumption |
| 表 3 中间物料相关数据 Table 3 Related data of materials |
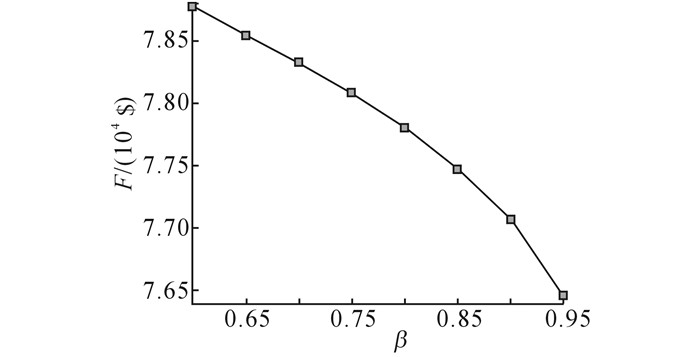
在计划层引入机会约束方法来表示订单需求的不确定性, 利用概率理论将不确定性模型转化为某置信水平下的确定性模型.置信水平取值的不同对优化结果存在一定的影响, 如图 6所示.图中,β为置信水平,F为目标函数最大利润.置信因子从0.6增加到0.95, 目标函数利润最大化呈现递减的趋势, 而且递减速度越来越快.这是因为在置信水平低的情况下, 企业承担的风险大, 可能获得的最大利润更大;相反, 在置信水平高的情况下, 企业承担的风险低, 可能获得的利润相对更小.该现象和风险投资的道理是相同的.置信因子的具体取值依赖于企业愿意承担的风险系数, 在仿真分析部分, 将置信因子取值为0.9.
|
图 6 不同置信水平下最大利润的变化趋势 Fig. 6 Trend of maximum profit under differentconfidence levels |
调度层采用三角形隶属度函数来表达公用工程的不确定性, 利用模糊理论将不确定性模型转化为确定性模型.转化后的确定性模型需要确定模糊权值的取值.在调度层的模糊不确定性模型中, 高压蒸汽(HS)的模糊参数取值为ua=22, ub=24, uc=28;冷凝水(CW)的模糊参数取值为ua=27, ub=29, uc=33.以第1个计划周期为例, 分析模糊权值wa、wb、wc的不同取值对优化结果的影响.
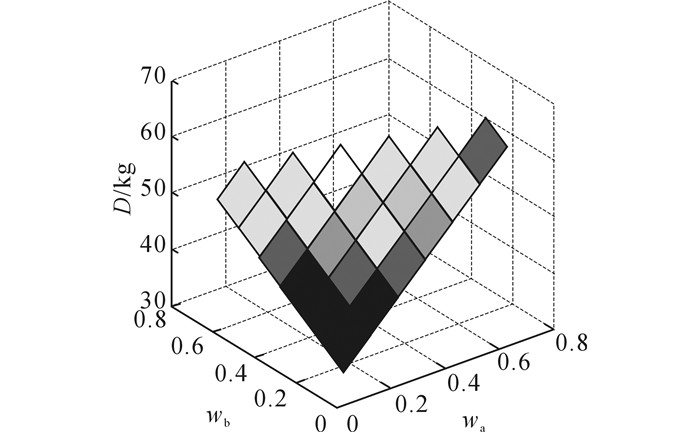
由于模糊权值满足wa+wb+wc=1, 使用wa、wb和调度层最优解为坐标系的三维立体图形来展示wa和wb的不同取值对调度层最优解(最小化计划层任务量和调度层生产量之差)的影响.如图 7所示, D为调度层优化结果.当wa固定不变时, 随着wb的增加, 优化结果增加, 这是因为当wa固定不变时, 随着wb的增加, 转化成确定的公用工程供给量Uumax降低.资源约束缩小了可行域的范围, 导致最小化的优化结果增加.当wb固定不变时, 随着wa的减少, 优化结果减少, 这是因为当wb固定不变时, 随着wa的减少, 转化成确定的公用工程供给量Uumax增加.资源约束扩大了可行域的范围, 使得最小化的优化结果降低.
|
图 7 不同模糊权值下的调度层优化结果 Fig. 7 Optimized solution of scheduling layer under different fuzzy weights |
该分析给出了模糊权值的取值对调度层最优解的影响趋势.实际上, 模糊权值选取的重要准则是能够更准确地描述模糊变量的模糊性, 并且需要对历史数据进行分析.根据相关文献对模糊权值的选取经验, 设置wa=0.1, wb=0.5, wc=0.4.
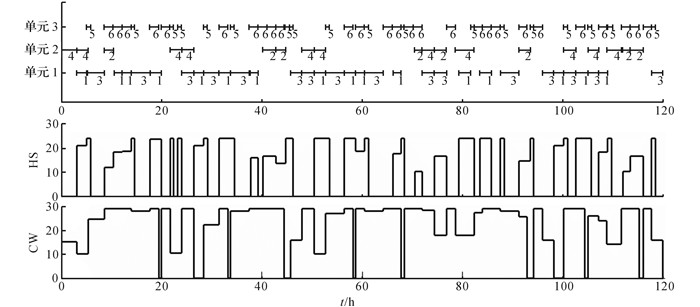
3.3 计划和调度层集成模型仿真分析已知两种产品在未来9个计划周期内的订单数据和两种公用工程的平均供给量, 利用提出的计划和调度双层模型及滚动优化策略, 完成前5个计划周期的计划和调度任务.该算例利用优化软件Lingo 11.0, 并在2.20 GHz的计算机上进行计算.在计划层采用离散模型, 计划时域为5 d, 计划周期为1 d.在调度层采用连续模型, 调度时域为1 d.如图 8、9所示分别为传统方法和不确定性方法的仿真分析, 包括甘特图和公用工程的使用水平.
|
图 8 传统方法的甘特图及公用工程使用水平 Fig. 8 Gantt chart and utility utilization level by traditional method |
|
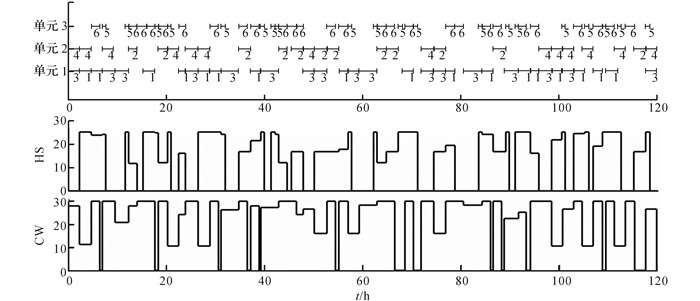
图 9 不确定性方法的甘特图及公用工程使用水平 Fig. 9 Gantt chart and utility utilization level by uncertain method |
从图 8、9中甘特图的对比来看, 不确定性方法中的任务数量及密度明显大于传统方法, 传统方法执行96个生产任务, 不确定性模型执行107个生产任务.采用提出的不确定性方法有效地提高了设备的利用率.如表 4所示为传统方法和不确定方法的对比分析.表中,P1plan、P2plan分别为P1、P2计划生产量,P1sch、P2sch分别为P1、P2调度生产量,RHS、RCW分别为高压蒸汽利用率和冷凝水利用率.传统方法的计划层最优解为79 187.97美元;产品P1、P2的计划生产量分别为870.00、1 330.00 kg.不确定性方法使用机会约束理论描述需求的不确定性, 在0.9的置信水平下, 计算上层计划层模型, 求得最优解为77 070.07美元;产品P1、P2的计划生产量分别为843.37、1 297.01 kg.传统方法的调度层最优解为150.00 kg;产品P1、P2的调度生产量分别为720.00、1 330.00 kg.不确定性方法的调度层最优解为50.91 kg;产品P1、P2的调度生产量分别为820.60、1 268.88 kg.从调度结果可以看出, 采用不确定性方法缩小了计划生产量和调度生产量之间的差距, 更多地完成了计划层下达的生产任务, 使得不确定性方法的实际最优解75 320美元优于传统方法的实际最优解74 800美元.
| 表 4 传统方法和不确定性方法的对比分析 Table 4 Comparative analysis between traditional and uncertain methods |
从公用工程的使用水平分析, 图 9中的高压蒸汽(HS)的使用水平与图 8中HS的使用水平相比, 采用不确定方法更有效地利用了公用工程HS, 并且使用情况较连续.经计算可知, 传统方法的HS和CW利用率分别为45.78%和80.81%;不确定性方法的HS和CW利用率分别为53.75%和82.34%.由此可见, 不确定性方法在调度层采用模糊理论有效地降低了不确定参数对优化结果的影响, 不仅更真实地反映了生产的实际情况, 而且有效地提高了设备对公用工程的利用率.
4 结语本文建立生产计划和调度双层集成模型, 分别在计划层和调度层采用机会约束和模糊理论来描述需求和公用工程的不确定性, 利用滚动优化策略对双层模型进行迭代求解.算例的仿真结果表明了所提方法的有效性和优越性.机会约束方法可以结合不确定信息优化产品的产量, 为决策者提供更准确的参考依据, 有利于决策的合理性和有效性.使用模糊理论表示公用工程的不确定性更真实地描述了公用工程的供给量, 增加了调度结果的可行性, 降低了不确定参数对优化结果的影响, 同时提高了设备和公用工程的利用率.
| [1] | WANG W, LI X, GAO L, et al. Application of interval theory and genetic algorithm for uncertain integrated process planning and scheduling [C]// 2013 IEEE International Conference of Systems, Man, and Cybernetics (SMC). Manchester: IEEE, 2013: 2796-2801. http://www.researchgate.net/publication/262313216_Application_of_Interval_Theory_and_Genetic_Algorithm_for_Uncertain_Integrated_Process_Planning_and_Scheduling |
| [2] | CHU Y F, YOU F Q, WASSICK J M, et al. Integrated planning and scheduling under production uncertainties: bi-level model formulation and hybrid solution method[J]. Computers and Chemical Engineering, 2015, 72: 255–272. DOI:10.1016/j.compchemeng.2014.02.023 |
| [3] | MULA J, POLER R, GARCIA-SABATER J P, et al. Models for production planning under uncertainty: areview[J]. International Journal of Production Economics, 2006, 103(1): 271–285. DOI:10.1016/j.ijpe.2005.09.001 |
| [4] | CHAKRABORTTY R K, HASIN M A A, SARKER R A, et al. A possibilistic environment based particle swarm optimization for aggregate production planning[J]. Computers and Industrial Engineering, 2015, 88: 366–377. DOI:10.1016/j.cie.2015.07.021 |
| [5] | ANDRE L, ROUSSOS D. Stochastic optimization of mine production scheduling with uncertain ore/metal/waste supply[J]. International Journal of Mining Science and Technology, 2014, 24(6): 755–762. DOI:10.1016/j.ijmst.2014.10.004 |
| [6] | XU B, ZHONG P A, ZAMBON R C, et al. Scenario tree reduction in stochastic programming with recourse for hydropower operations[J]. Water Resources Research, 2015, 51(8): 6359–6380. DOI:10.1002/2014WR016828 |
| [7] | IRIS C, CEVIKCAN E. A fuzzy linear programming approach for aggregate production planning[M]. Berlin: Springer, 2014: 355-374. |
| [8] | YANG H B, MAO F Y, XU J H, et al. Parallel machine scheduling with fuzzy due date using improved simulated annealing in lean production [C] // Applied Mechanics and Materials. Shenzhen: Trans Tech Publications, 2014, 457: 470-473. http://www.researchgate.net/publication/272599047_parallel_machine_scheduling_with_fuzzy_due_date_using_improved_simulated_annealing_in_lean_production |
| [9] | DONYA R, REZA R, PARVIZ F, et al. A robust optimization model for multi-product two-stage capacitated production planning under uncertainty[J]. Applied Mathematical Modeling, 2013, 37(20): 8957–8971. |
| [10] |
田野, 董宏光, 邹雄, 等. 考虑需求不确定性的化工生产计划与调度集成[J].
化工学报, 2014, 65(09): 3552–3558.
TIAN Ye, DONG Hong-guang, ZOU Xiong, et al. Chemical production planning and scheduling integration under demand uncertainty[J]. CIESC Journal, 2014, 65(09): 3552–3558. DOI:10.3969/j.issn.0438-1157.2014.09.033 |
| [11] | WANG Y, SU H Y, SHAO H S, et al. Hierarchical approach of planning and scheduling with demand uncertainty and utility disturbance [C]//The 5th International Symposium on Advanced Control of Industrial Process. Hiroshima, Japan: [s. n.], 2014: 28-30. |
| [12] |
于春云, 赵希男, 彭艳东, 等. 模糊随机需求模式下的扩展报童模型与求解算法[J].
系统工程, 2006, 24(9): 103–107.
YU Chun-yun, ZHAO Xi-nan, PENG Yan-dong, et al. Extended Newsboy problem based on fuzzy random demand[J]. Systems Engineering, 2006, 24(9): 103–107. |
| [13] | MARAVELIAS C T, GROSSMANN I E. New general continuous-time state-task network formulation for short-term scheduling of multipurpose batch plants[J]. Industrial and Engineering Chemistry Research, 2003, 42(13): 3056–3074. DOI:10.1021/ie020923y |
| [14] | WANG Y, SU H Y, SHAO H S, et al. Unit-specific event-based and slot-based hybrid model framework with hierarchical structure for short-term scheduling[J]. Mathematical Problems in Engineering, 2015, 501: 906280. |



