2. 上海海洋大学 海洋科学学院, 上海 201306;
3. 天津地质调查中心, 天津 300170
2. College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China;
3. Tianjin Institute of Geology and Mineral Resources, Tianjin 300170, China
黄骅港(38°18′N, 117°53′E)位于渤海湾西南岸, 坐落在河北、山东两省交界处, 距河北省沧州市90 km, 是滨海新区的三大港口之一[1].黄骅港的导堤工程始建于1997年, 至2012年已基本形成典型的半封闭式港区.黄骅港主要由综合港区与煤炭港区组成, 核心功能为煤炭运输.作为国家西煤东运第二条大通道的出海口, 黄骅港肩负着带动“滨海新型发展带”发展, 并推动京津冀“一轴三带”规划实施的重任[2].
黄骅港所在的粉沙淤泥质海岸对港口、航道的影响巨大, 滩面泥沙活动性大、易起动、易沉降、密实快, 在大风作用时易造成港口与航道的淤积[3-4].同时, 该海区的风暴潮常导致黄骅港水位暴涨、泥沙骤淤, 最典型的是2003年10月发生的45年一遇特大寒潮风暴潮, 该风暴潮过后黄骅港外航道淤积量高达970万m3, 航道水深骤减3.6 m.为了解决泥沙淤积问题, 黄骅港于2004年5月开始实施外航道整治工程, 2009年3月开始修建综合港区防沙堤.工程的不断建设使得黄骅港水动力特性发生显著改变, 学者对黄骅港泥沙淤积问题展开了系列研究.Feng等[5]利用实测资料分析黄骅港水动力和泥沙特性, 指出强风是引起黄骅港外航道骤淤的重要原因, 通过理论分析得到风能与骤淤厚度之间的计算公式.匡翠萍等[6]运用Delft3D建立黄骅港二维潮流泥沙数学模型, 模拟不同工程在单一风况作用下的水动力环境与泥沙输运过程.研究结果表明:在ENE向8级大风作用下, 黄骅港潮流动力失衡, 涨、落潮输沙不等, 近岸含沙量高.高进[7]通过分析黄骅港卫星图像与数值模拟结果发现, 外航道粉沙淤积量远大于预测值的原因是堤头旋涡的输沙作用.
潮流作为海洋水动力中最重要的因素之一, 影响悬浮颗粒物输运、温盐分布以及海床冲淤演变等, 垂向结构变化会对水工建筑物与海岸地貌造成显著的影响[8-11], 而平面二维潮流数学模型不能反映水流的垂向特征.大风对水体紊动有显著影响, 紊动是泥沙起动、悬浮、输运的关键因素, 分布特征与工程建设密切相关, 而鲜有学者研究三维水体紊动与海岸工程的相互影响.研究不同风况作用下风生流及紊动的三维特性, 对进一步探究水体中物质(例如:泥沙、污染物)输运有十分重要的科学意义.本文采用Delft3D建立黄骅港三维潮流数学模型和紊流模型, 基于典型风况ENE向6、8级风下的计算结果, 定量分析不同风力等级作用下风生流与紊动能的时空分布特征, 探究风与流对紊动能分布的影响机理.
1 数学模型建立Delft3D-FLOW模块是Delft3D中最核心和基础的水动力模块.该模块基于浅水假定与Boussinesq假定, 求解不可压缩流体的Navier-Stokes方程.数值离散采用ADI法, 通过联立偏微分基本方程, 结合初始条件与边界条件进行求解[12-14].
1.1 基本方程潮流数学模型和紊流模型的基本方程如下.
连续方程为
| $ \begin{array}{l} \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \left[{\left( {d + \zeta } \right)U\sqrt {{G_{\eta \eta }}} } \right]}}{{\partial \xi }} + \\ \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \left[{\left( {d + \zeta } \right)V\sqrt {{G_{\xi \xi }}} } \right]}}{{\partial \eta }} = \left( {d + \zeta } \right)Q{\rm{ }}. \end{array} $ | (1) |
式中:Q为单位面积的源汇项;ζ为水位;d为基准面下的水深;H为总水深, H=d+ζ;t为时间;Gξξ、Gηη分别为正交曲线坐标系与笛卡尔坐标系之间的转换系数;U、V分别为ξ、η向上的垂向平均流速.
动量方程为
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial u}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial u}}{{\partial \eta }} + \frac{\omega }{{d + \zeta }}\frac{{\partial u}}{{\partial \sigma }}-\\ \frac{{{v^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \xi }} + \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\xi \xi }}} }}{{\partial \eta }}-fv = \\ -\frac{1}{{{\rho _0}\sqrt {{G_{\xi \xi }}} }}{P_\xi } + {F_\xi } + \frac{1}{{{{\left( {d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left( {{v_V}\frac{{\partial u}}{{\partial \sigma }}} \right) + {M_\xi }, \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial v}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial v}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial v}}{{\partial \eta }} + \frac{\omega }{{d + \zeta }}\frac{{\partial v}}{{\partial \sigma }} + \\ \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \xi }}-\frac{{{u^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\xi \xi }}} }}{{\partial \eta }} + fu = \\ -\frac{1}{{{\rho _0}\sqrt {{G_{\eta \eta }}} }}{P_\eta } + {F_\eta } + \frac{1}{{{{\left( {d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left( {{v_V}\frac{{\partial v}}{{\partial \sigma }}} \right) + {M_\eta }. \end{array} $ | (3) |
式中:u、v分别为ξ、η向上的流速分量;σ为相对垂向坐标, 由实际垂向坐标z、ζ及H确定, σ=(z-ζ)/H;ω为σ坐标系中的垂向流速;f为柯氏力参数, 由地球自转角速度Ω与纬度ϕ确定, f=2Ωsin ϕ;Pξ和Pη为压力梯度;Fξ和Fη为水平雷诺应力的不平衡项;Mξ和Mη为外来源汇项引起的附加动量;vv为垂向涡黏系数.σ坐标系中的垂向速度ω由下列连续方程求解:
| $ \begin{array}{l} \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \left[{\left( {d + \zeta } \right)u\;\sqrt {{G_{\eta \eta }}} } \right]}}{{\partial \xi }} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }} \times \\ \frac{{\partial \left[{\left( {d + \zeta } \right)v\sqrt {{G_{\xi \xi }}} } \right]}}{{\partial \eta }} + \frac{{\partial \omega }}{{\partial \sigma }} = \left( {d + \zeta } \right)({q_{{\rm{in}}}} -{q_{{\rm{out}}}}). \end{array} $ | (4) |
式中:qin和qout分别为单位体积的源和汇.
z坐标系中的垂向速度w可用ω和水平流速、水深、水位等进行计算, 转换成
| $ \begin{array}{l} w = \omega + \left( {\sigma \frac{{\partial H}}{{\partial t}} + \frac{{\partial \zeta }}{{\partial t}}} \right) + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }} \times \\ \left[{u\;\sqrt {{G_{\eta \eta }}} \left( {\sigma \frac{{\partial H}}{{\partial \xi }} + \frac{{\partial \zeta }}{{\partial \xi }}} \right) + v\sqrt {{G_{\xi \xi }}} \left( {\sigma \frac{{\partial H}}{{\partial \eta }} + \frac{{\partial \zeta }}{{\partial \eta }}} \right)} \right]. \end{array} $ | (5) |
垂向涡黏系数vv由紊动能k与紊动能耗散ε计算:
| $ {v_v} = {c_\mu }\frac{{{k^2}}}{\varepsilon }. $ | (6) |
标准k-ε紊流模型的k、ε输运方程分别为
| $ \begin{array}{l} \frac{{\partial k}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial k}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial k}}{{\partial \eta }} + \frac{\omega }{{d + \zeta }}\frac{{\partial k}}{{\partial \sigma }} = \\ \frac{1}{{{{\left( {d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left( {\frac{{{v_V}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial \sigma }}} \right) + {P_k}-\varepsilon, \end{array} $ | (7) |
| $ \begin{array}{l} \frac{{\partial \varepsilon }}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial \varepsilon }}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial \varepsilon }}{{\partial \eta }} + \frac{\omega }{{d + \zeta }}\frac{{\partial \varepsilon }}{{\partial \sigma }} = \\ \frac{1}{{{{\left( {d + \zeta } \right)}^2}}}\frac{\partial }{{\partial \sigma }}\left( {\frac{{{v_V}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial \sigma }}} \right) + {P_\varepsilon }-{c_{2\varepsilon }}\frac{{{\varepsilon ^2}}}{k}. \end{array} $ | (8) |
式中:Pk、Pε分别为k、ε生成项;σk、σε分别为k、ε普朗特-施密特数, 分别为1.0、1.3;c2ε、cμ分别为常数1.92、0.09.
1.2 计算范围及网格平面坐标系统采用大地坐标, 高程以黄骅港理论最低潮面为零点.为了保证计算边界不受工程建设的影响, 模型东北边界(NE)距黄骅港煤炭港区外航道口门43 km, 西北边界(NW)、东南边界(SE)分别距黄骅港30 km和36 km.计算区域为东经117°36′~118°40′, 北纬38°07′~38°51′的海域, 如图 1所示.模型计算网格采用197×125的非均匀正交曲线网格, 对工程区域与航道的网格加密, 网格步长为70~1 482 m, 垂向均分为10层.
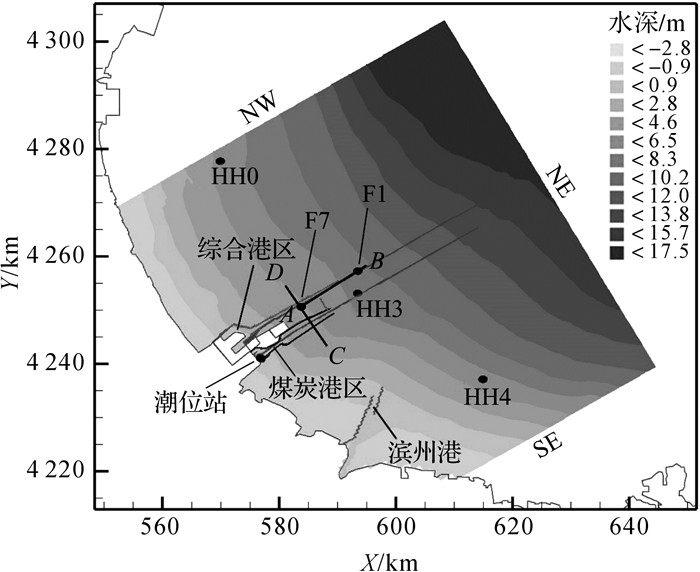
|
图 1 研究区域与观测点位置 Fig. 1 Study area and observation stations |
数学模型的3条海域开边界(NW、NE、SE)通过大小模型嵌套的方式由渤海模型[15]计算取得, 岸线闭边界采用流速为零的不可滑移条件, 自由表面边界的风切应力τs由下式确定:
| $ |{{\boldsymbol{\tau}} _{\rm{s}}}| = {\rho _{\rm{a}}}{C_{\rm{d}}}U_{10}^2. $ | (9) |
式中:ρa为空气密度;U10为海平面以上10 m处的风速;Cd为风拖曳力系数, Cd=0.000 63+0.000 066U10.
水平紊动黏滞系数取20 m2/s, 曼宁系数由底部泥沙粒径分布与水深确定, 取值为0.011~0.016.滩地干湿交换过程采用动边界处理, 临界水深为0.1 m.时间步长取1 min, 对应柯朗数小于10, 满足模型计算稳定性的要求.
2 模型验证采用NOAA提供的6 h 1次的风场数据作为风的输入条件, 使用潮位站2012年10月15日0:00至16日23:00实测潮位数据与测站HH0、HH3、HH4 2012年10月15日5:00至16日6:00实测潮流数据对数学模型进行验证(站点位置如图 1所示).图 2、3的验证结果表明, 潮位计算值与实测值基本一致, 潮流计算值在大小和相位上均与实测值吻合较好.图中,θ为流向,v0为流速.
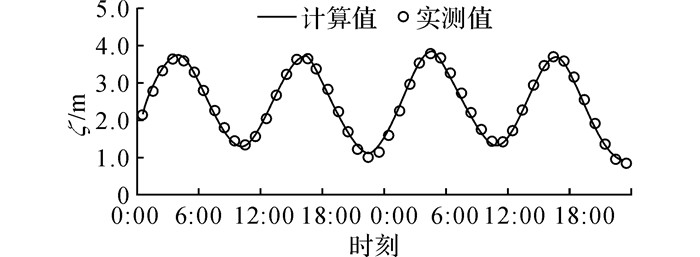
|
图 2 潮位验证(2012.10.15 0:00 ~ 10.16 23:00) Fig. 2 Verification of tidal level (Oct.15 0:00~1623:00, 2012) |
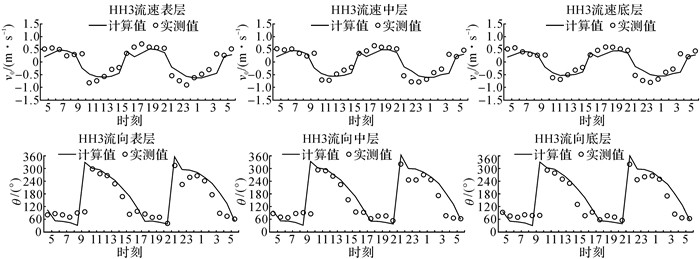
|
图 3 流速、流向三维验证(2012.10.15 5:00 ~ 10.16 6:00) Fig. 3 Three-dimensional verification of velocity and its direction (Oct.15 5:00~16 6:00, 2012) |
针对黄骅港在大风作用下泥沙淤积的问题已有不少研究[3-7, 15-17], 学者们普遍认为:黄骅港易在6级以上大风作用下发生骤淤, 且ENE向为主要引起泥沙淤积的风向.选取ENE向6级(风速为12.3 m/s)和8级(风速为19.0 m/s)风作为典型风况分别进行模拟, 通过位于综合港区深水航道上的纵断面A-B、横跨黄骅港工程的横断面C-D以及位于断面A-B之上的分析站点F1(港外)、F7(港内)上的计算结果讨论黄骅港风生流及紊动的三维特性(分析站点位置见图 1).
3.1 水平分布特征如图 4所示为ENE向3种风况下(无风、6级和8级)涨、落急时刻的垂向平均流场.总体来看, 随着风力等级的提高, 涨急流速增加, 流向几乎不变;落急流速减小, 流向由东北向北偏转, 且涨急平均流速大于落急平均流速.其中, 6级风对流速大小、方向的改变有限, 8级风使得流速显著变化, 落急流向明显偏转.黄骅港堤头、口门及近岸局域区域和滨州港堤头附近区域的流速较大, 港池内的流速一般小于0.2 m/s.
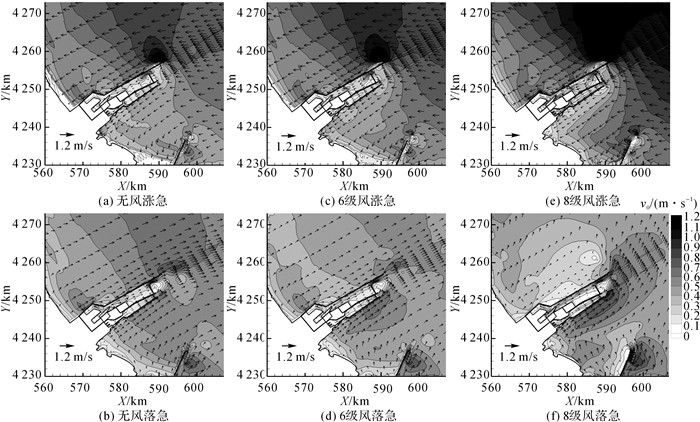
|
图 4 3种风况下涨、落急时刻垂向平均流场 Fig. 4 Depth-averaged current fields at maximum flood and ebb under three wind scenarios |
如图 5所示为ENE向风作用下的净垂向平均风生流场(潮汐周期为2012.10.15 5:00 ~ 10.16 5:00).由图 5可知, 黄骅港风生流由东南向西北方向运动, 在工程堤头外侧有显著绕流现象, 且外海风生流流速最大, 港池最小.港区南导堤与滨州港之间形成明显的顺时针环流, 而港区北导堤外侧形成向岸沿堤风生流, 即ENE向风使得外海和港区北导堤外侧涨潮流增强, 落潮流减弱;港区南导堤外侧涨潮流减弱、落潮流增强;滨州港北导堤外侧涨潮流增强、落潮流减弱.随风力等级的提高, 风生流对潮流场的影响加剧.
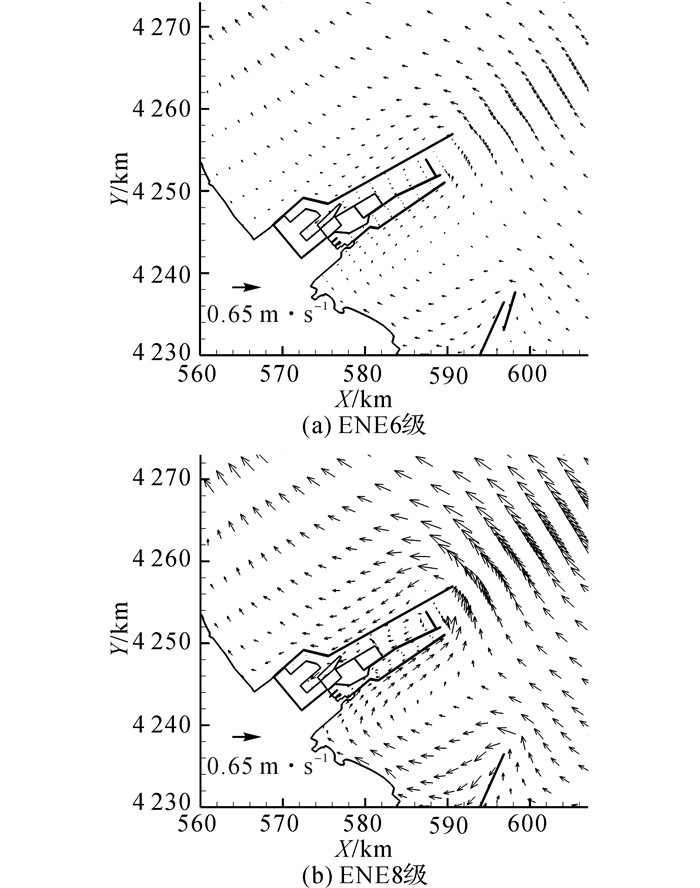
|
图 5 ENE向风作用下的净垂向平均风生流场(潮汐周期:2012.10.15 5:00~10.16 5:00) Fig. 5 Net depth-averaged wind-induced current fields under ENE wind(tide period: Oct.15 5: 00~Oct.16 5: 00, 2012) |
图 6中,h/H为相对高程.为了探究流速沿航道的垂向分布特征, 分析3种风况下断面A-B的涨、落急流速(见图 6)可知:在涨急时刻, 风向与流向相同, 风对水流垂向结构几乎无影响, 流速等值线以抛物线簇的形式存在, 断面流速随风力等级的提高而增大, 且点B、堤头以及口门处增幅明显;在落急时刻, 风向与流向相反, 水体近表层受到的风切应力作用沿水深方向减小, 水流垂向结构由抛物线簇变化为同心椭圆曲线簇, 断面流速随风力等级的提高而减小, 且流速在垂直方向上趋于均一化, 梯度减小.8级风对流速在量值、水平分布、垂向结构上的影响均大于6级风.在断面A-B上分别选取F1(港外)和F7(港内)两个站点, 流速的垂向分布如图 7所示.可知, 黄骅港港池内外站点流速受风的影响变化相反:随着风力等级的提高, 港内站点涨急流速减小、落急流速增大;港外站点涨急流速增大、落急流速减小.随着风力的加强, 流速的垂向梯度变大, 并且形成一定的垂向环流.

|
图 6 3种风况下涨、落急时刻流速沿断面A-B的垂向分布 Fig. 6 Vertical distributions of velocity magnitude along profile A-B at maximum flood and ebb under three wind scenarios |
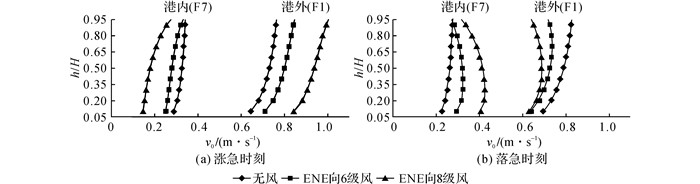
|
图 7 3种风况下涨、落急时刻站点F1、F7的流速垂向分布 Fig. 7 Vertical distributions of velocity magnitude at points F1 and F7 at maximum flood and ebb under three wind scenarios |
风作用下的紊动能三维特征受潮流和风切应力的共同影响.3种风况下, 涨、落急时刻的垂向平均紊动能(见图 8)与垂向平均流速(见图 4)的分布规律基本一致, 由于流速愈大, 紊动愈强, 相应的紊动能愈大, 因此强紊动区域为黄骅港堤头、口门及近岸局部区域和滨州港堤头附近区域.3种风况下的垂向平均紊动能在涨急时刻大于落急时刻, 6级风作用时变化小, 8级风作用时增加显著等特征.
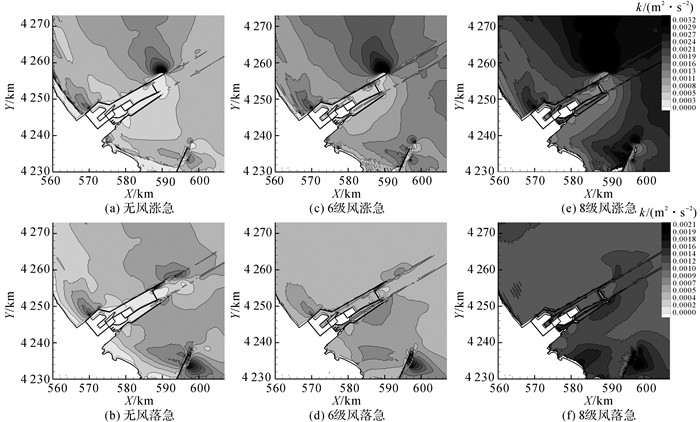
|
图 8 3种风况下涨、落急时刻垂向平均紊动能场 Fig. 8 Depth-averaged turbulence energy fields at maximum flood and ebb under three wind scenarios |
如图 9所示为3种风况下涨、落急时刻紊动能沿断面A-B的垂向分布, 无风作用时, 断面A-B涨、落急时刻紊动能沿水深方向的增加(与流速垂向分布特征相反(见图 6(a)、(b)), 为底部边界层的作用, 且点B、堤头、口门处紊动能较大.在ENE向风影响下, 紊动能沿断面A-B的垂向分布呈非线性, 其中ENE向6级风作用时, 点B、堤头、口门等流速较大的区域紊动强, 紊动能沿水深方向增加, 而其余导堤掩护段内平缓水流的紊动主要由风切应力产生, 故紊动能沿水深方向减小.ENE向8级风作用时, 风切应力在水体表层产生的紊动强于底部边界层的作用, 可达2.5倍, 紊动能基本都沿水深从表层向底部减小;由于风向与涨潮流方向一致, 涨潮期间的紊动明显强于落潮.
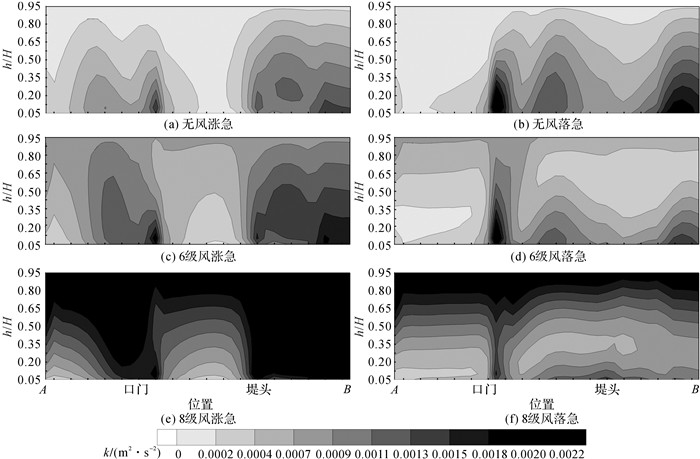
|
图 9 3种风况下涨、落急时刻紊动能沿断面A-B的垂向分布 Fig. 9 Vertical distributions of turbulence energy along profile A-B at maximum flood and ebb under three windscenarios |
为了进一步探究导堤对港池的掩护作用, 对3种风况下涨、落急时刻紊动能沿断面C-D的垂向分布(见图 10)进行分析.在无风作用时, 港池内的紊动能基本维持在10-5~10-4 m2/s2的极低水平.在ENE向6、8级风作用下, 港池内的紊动能主要由风切应力产生, 沿水深向底部减小, 水体近表层的紊动能最大值分别为7×10-4和2.25×10-3 m2/s2, 近底层的紊动能分别为10-4~5×10-4、3×10-4~9×10-4 m2/s2.长导堤环抱港池内的水体流速和紊动能与港池外相比大幅减弱.
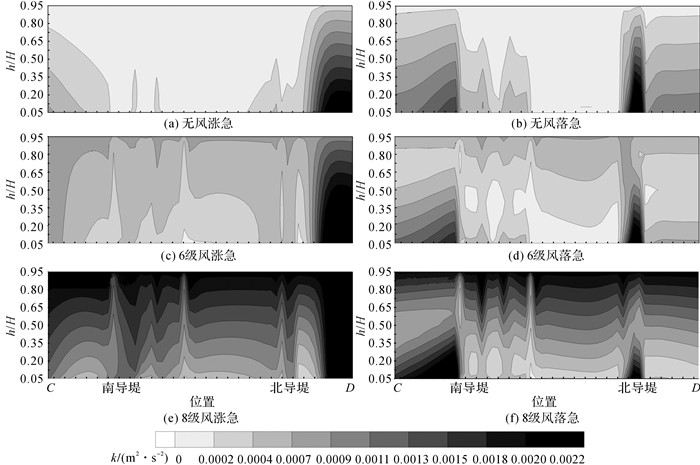
|
图 10 3种风况下涨、落急时刻紊动能沿断面C-D的垂向分布 Fig. 10 Vertical distributions of turbulence energy along profile C-D at maximum flood and ebb under three windscenarios |
(1) 在ENE向风作用下, 黄骅港风生流由东南向西北方向运动, 在工程堤头外侧有显著的绕流现象.随着风力等级的提高, 风生流对潮流场的影响加剧.
(2) 与无风相比, 6级风作用时流速与紊动能的量值、水平分布以及垂向结构变化较小, 但8级风作用时流速与紊动能的水平分布与垂向结构变化显著, 紊动能增加近2倍.
(3) 垂向平均紊动能与垂向平均流速的平面分布规律基本一致, 呈现黄骅港堤头、口门及近岸局部区域和滨州港堤头附近区域较大, 港池较小;紊动能在涨潮期间较落潮期间强.
(4) 紊动能在无风时, 由于底部边界层作用下从水面向海底递增, 但在强风切应力作用下, 从水面向海底递减.在8级风作用时, 风应力在水体表层产生的紊动能明显强于底部边界层作用产生的紊动能, 可达2.5倍.
(5) 长导堤环抱港池内的水体流速和紊动能与港池外相比大幅减弱.
| [1] |
淦学甄, 刘虎. 黄骅港港口竞争力分析[J].
物流工程与管理, 2010, 32(07): 110–111.
GAN Xue-zhen, LIU Hu. Harbor competitive poweranalysis to Huanghua port[J]. Logistics Engineering and Management, 2010, 32(07): 110–111. DOI:10.3969/j.issn.1674-4993.2010.07.044 |
| [2] |
张会强. 神华黄骅港外航道整治工程分析研究[J].
价值工程, 2012, 23: 81–83.
ZHANG Hui-qiang. Analysis of Shenhua Huanghua harbor waterway regulation project[J]. Value Engineering, 2012, 23: 81–83. DOI:10.3969/j.issn.1006-4311.2012.01.057 |
| [3] |
曹祖德, 孔令双. 粉沙质海岸泥沙运动特性研究[J].
海洋学报, 2011, 33(5): 152–162.
CAO Zu-de, KONG Ling-shuang. Sediment problems of harbor on silt-sandy beach[J]. Acta Oceanologica Sinica, 2011, 33(5): 152–162. |
| [4] |
杨华. 黄骅港外航道泥沙问题的治理及其效果[J].
水道港口, 2009, 30(04): 233–240.
YANG Hua. Regulation and effect on siltation in outer channel of Huanghua Harbor[J]. Journal of Waterway and Harbor, 2009, 30(04): 233–240. DOI:10.3969/j.issn.1005-8443.2009.04.002 |
| [5] | FENG X X, LI J B, HAO P Z, et al. Relation between sudden sedimentation and wind energy in outer channel of Huanghua Port and its application in Binzhou Port[J]. China Ocean Engineering, 2008, 22(1): 161–170. |
| [6] |
匡翠萍, 刘鹏晨, 顾杰, 等. 黄骅港外航道整治工程对风暴潮流下泥沙输运的影响[J].
泥沙研究, 2014(01): 39–46.
KUANG Cui-ping, LIU Peng-chen, GU Jie, et al. Influence of Huanghua port regulation project on sediment transport under currents induced by storm surge[J]. Journal of Sediment Research, 2014(01): 39–46. |
| [7] |
高进. 黄骅港外航道大风骤淤的机理及其整治[J].
科技导报, 2005(01): 29–31.
GAO Jin. Mechanism and control of abrupt aggradation after gales in the outerchannel of the Huanghua harbor[J]. Engineering and Technology, 2005(01): 29–31. DOI:10.3321/j.issn:1000-7857.2005.01.007 |
| [8] | KOCYIGIT M B, FALCONER R A. Modelling of wind-induced currents in water basins[J]. Proceedings of the ICE-Water Management, 2004, 157(4): 197–210. |
| [9] | YANG Y, STRAATMAN A G, HANGAN H, et al. An engineering model for countercurrent flow under wind-induced waves and current[J]. Environmental Fluid Mechanics, 2008, 8(1): 19–29. DOI:10.1007/s10652-008-9052-0 |
| [10] | GOOSSENS L H J, VAN PAGEE H J A, TESSEL P J. Vertical turbulent diffusion in air-driven water flows[J]. Journal of the Hydraulics Division, 1982, 108(9): 995–1009. |
| [11] | 张弛, 王义刚, 郑金海. 波生流垂向结构研究综述[J]. 水科学进展, 2009, 20(5): 739–746. |
| [12] | Deltares. Delft3D-FLOW user manual[M]. Delft: Deltares, 2013. |
| [13] | LESSER G R, ROELVINK J A, VAN KESTER J A T M, et al. Development and validation of a three-dimensional mor-phological model[J]. Coastal Engineering, 2004, 51(8-9): 883–915. DOI:10.1016/j.coastaleng.2004.07.014 |
| [14] | HU K L, CHEN Q, WANG H Q. A numerical study of vegetation impact on reducing storm surge by wetlands in a semi-enclosed estuary[J]. Coastal Engineering, 2015, 95: 66–76. DOI:10.1016/j.coastaleng.2014.09.008 |
| [15] | 匡翠萍, 刘鹏晨, 姚凯华, 等. 渤海新区近岸海洋水动力环境数值模拟研究报告[R]. 上海: 同济大学, 2012. |
| [16] | KUANG C P, MAO X D, LIU P C, et al. Influence of wind force on a silt-muddy coast: Huanghua Harbor Coast, China[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2015, 141(6): 05015001. DOI:10.1061/(ASCE)WW.1943-5460.0000299 |
| [17] | 侯志强. 黄骅港外航道整治工程后沿堤流分析[J]. 水运工程, 2008, 11: 121–127. DOI:10.3969/j.issn.1002-4972.2008.07.025 |



