2. 天津大学 滨海土木工程结构与安全教育部重点实验室, 天津 300072
2. Key Laboratory of Coast Structures Safety of Education Ministry, Tianjin University, Tianjin 300072, China
钢桥疲劳问题一直受到持续的关注, 而钢桥的疲劳敏感细节更是钢桥疲劳评估研究的重点对象.名义应力法考虑不同的疲劳细节分类, 给出不同的疲劳设计曲线, 但是对于复杂的构造细节, 名义应力难于确定[1], 疲劳寿命结果的离散性大;热点应力法考虑焊接接头结构几何不连续对疲劳应力的贡献, 降低了疲劳评估对细节分类的依赖, 但是仅仅局限于评估焊趾失效的情况[2];有效缺口应力法[3-5]以仅仅依靠单一S-N曲线就能实现不同焊接构造细节形态和不同载荷条件的疲劳评估, 且相比名义应力和热点应力能够有更好的评估结果, 获得了学者们的青睐和兴趣.
Park等[6]研究将有效缺口应力法用于大尺寸焊接接头疲劳评估的适用性, 结果表明, 基于最大主应力假设, 该方法可以有效地区分起始裂纹位于焊趾或者焊根处, 试样尺寸效应对疲劳强度的影响不明显, 已有的有效缺口应力疲劳强度试验数据位于FAT300设计曲线的上方.Pedersen等[7]采用有效缺口应力法, 对大量的高强钢焊接接头疲劳试验数据进行重分析发现, 薄板对接焊接接头采用FAT225疲劳设计曲线会得到偏于不保守的结果, 并建议设计曲线统一降为FAT200.Nguyen等[8]考虑随时间非线性变化的锈蚀损耗对构件细节厚度的影响, 采用有效缺口应力评估了油轮局部细节焊趾处的腐蚀疲劳寿命.Oh等[9]对板厚小于1.5 mm殷钢材质的天然气储藏容器构造细节进行疲劳评估, 提出相应的有效缺口应力疲劳设计曲线的建议.祝志文等[10]基于有效缺口应力进行正交异性钢桥面板的疲劳评价, 结果表明, 增加U肋的厚度会使U肋与横隔板端焊缝处更易产生疲劳裂纹.Aygül等[11]比较了热点应力法和有效缺口应力法, 开展带工艺孔正交异性板的疲劳寿命评估, 结果表明, 后者评估寿命与足尺试验结果吻合很好, 采用忽略焊缝几何壳单元会使热点应力过大.Shahri等[12]采用缺口应力法和临界距离法, 对摩擦搅拌焊T形和搭接焊接接头进行疲劳寿命评估.尽管如此, 将有效缺口应力法用于钢桥焊接接头疲劳评估的适用性评价研究比较缺乏.
本文介绍了有效缺口应力法的基本概念、计算方法及疲劳设计曲线, 开展3种典型钢桥焊接构造细节的疲劳试验, 包括不等厚对接焊接接头、十字形非传力和传力角焊缝接头.以疲劳试验结果为基础, 通过ABAQUS有限元软件分析构造细节焊趾或焊根处的有效缺口应力, 探讨3种构造细节的失效模式, 得到有效缺口应力S-N曲线, 并与推荐的FAT225疲劳设计曲线和名义应力S-N曲线进行对比分析.
1 有效缺口应力法原理有效缺口应力概念主要分为以下2种方法.1) 参考半径rref=1.0 mm, 主要用于壁厚t>5 mm的大型焊接结构[13], 如工业建筑和桥梁结构等;2)rref=0.05 mm主要用于t < 5 mm的薄壁结构[14], 如汽车工业.本文研究主要针对前者.
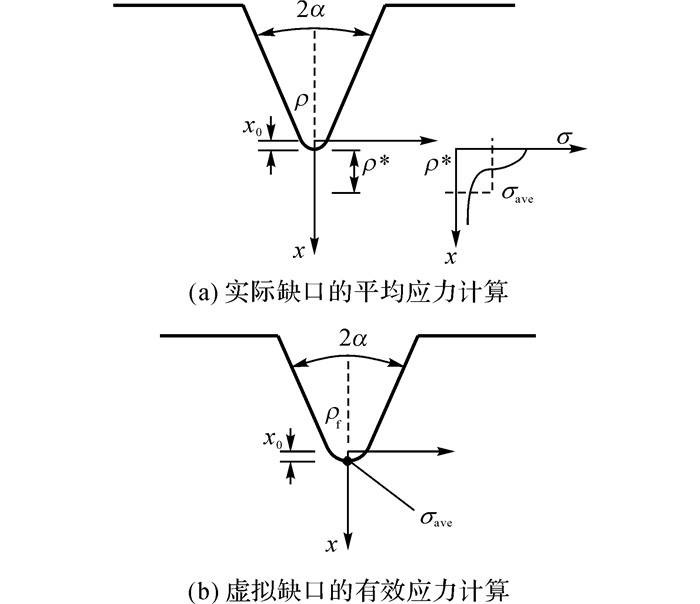
1.1 有效缺口应力概念Neuber的微观支撑理论[15]认为在较大的缺口尖端区域应力和应力梯度下, 应该考虑材料微观各向异性对疲劳行为的影响, 即材料微观支撑长度ρ*区域范围的约束作用.理论最大缺口应力不是产生疲劳裂纹的关键, 而在裂纹萌生一定区域内的平均缺口应力起着重要的作用.平均缺口应力σave可以通过对理论缺口应力沿ρ*的积分求得, 如图 1(a)和式(1) 所示.为了简化平均缺口应力的计算, Neuber提出用包含微观支撑效应在内的虚拟缺口半径ρf来代替实际缺口半径ρ, 如图 1(b)和式(2) 所示, 用虚拟圆弧上反映实际强度的最大缺口应力代替平均缺口应力.
|
图 1 Neuber微观支撑理论 Fig. 1 Neuber's micro-support hypothesis |
| ${{\sigma }_{\text{ave}}}=\frac{1}{{{\rho }^{*}}}\int\limits_{{{x}_{0}}}^{{{x}_{0}}+{{\rho }^{*}}}{\sigma \text{d}x}, $ | (1) |
| $ {\rho _{\rm{f}}} = \rho + s{\rho ^*}. $ | (2) |
式中:s为与应力多轴度和强度准则相关的系数.
Radaj等[16-17]基于钢材微观结构支撑理论, 提出虚拟参考半径1 mm的概念, 基于平面应变状态和von Mises多轴强度准则, 建议应力幅S取值为2.5, ρ*取值为0.4 mm.在实际缺口根部半径为ρ=0的最不利条件下, 由式(2) 得到虚拟参考半径rref=ρf=1 mm.有效缺口应力可以通过虚拟参考半径圆弧上的最大应力计算得到.
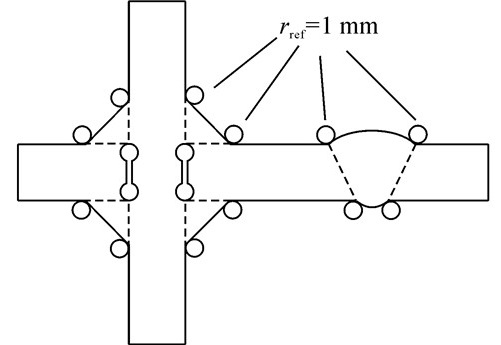
1.2 有效缺口应力的计算方法线弹性有效缺口应力法的基本思想是通过rref=1.0 mm的圆弧来代替焊趾或焊根处的缺口尖角, 从而避免实际缺口尖角的应力奇点.基于有限元方法或者边界元法, 采用二维平面应变单元或三维实体单元模型, 计算虚拟圆弧处的最大主应力或者von Mises应力[18], 作为S-N曲线疲劳评估的有效缺口应力, 如图 2所示.
|
图 2 有效缺口应力计算模型示意图 Fig. 2 Schematic diagram for calculation model of effective notch stress |
在有限元分析计算时, 单元形状、位移插值函数及网格质量对计算结果的收敛性有着明显的影响.国际焊接协会(International Institute of Welding, IIW)给出缺口处网格划分大小的基本规定, 如表 1所示.当结构模型比较复杂时, 为了保证网格质量, 可以采用子模型或者超单元技术.Baumgartner等[19]研究网格划分和单元类型选择对有效缺口应力计算的影响, 指出单元形状的选择一定要能反映应力梯度的变化, 对二次单元推荐采用四边形和六面体单元, 对线性单元不宜采用四面体单元.
| 表 1 平行和垂直缺口表面的推荐单元尺寸 Table 1 Recommended element sizes in direction parallel and perpendicular to notch surface |
表 2给出具有97.7%概率保证和循环次数N=2×106时, 钢材焊接接头对应的正应力和切应力疲劳强度FAT值[5].不同的强度假设, 对应不同的正应力和切应力疲劳强度.
| 表 2 不同参考半径和强度假设对应的FAT值 Table 2 FAT values corresponding to different reference radius and strength hypothesizes |
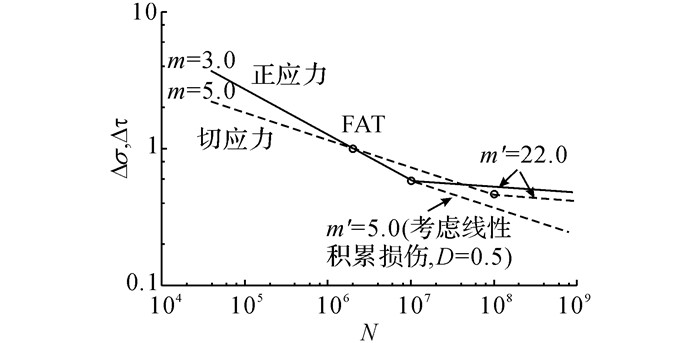
图 3给出IIW推荐的厚板和带加劲肋焊接结构的疲劳设计曲线[5].图中, Δσ和Δτ为归一化正应力幅和切应力幅,m、m′为斜率.对于正应力疲劳, 当N < 107时, m=3.0;当N>107时, m=22.0.考虑Palmgren-Miner线性疲劳累积损伤, 当N>107时, 取m′=5.0, 允许累积损伤量D=0.5;对于切应力疲劳, 当N < 108时, m=5.0, 当N>108时, m′=22.0.
|
图 3 IIW推荐的基于有效缺口应力疲劳设计曲线 Fig. 3 Fatigue design curves in notch stress systemrecommended by IIW |
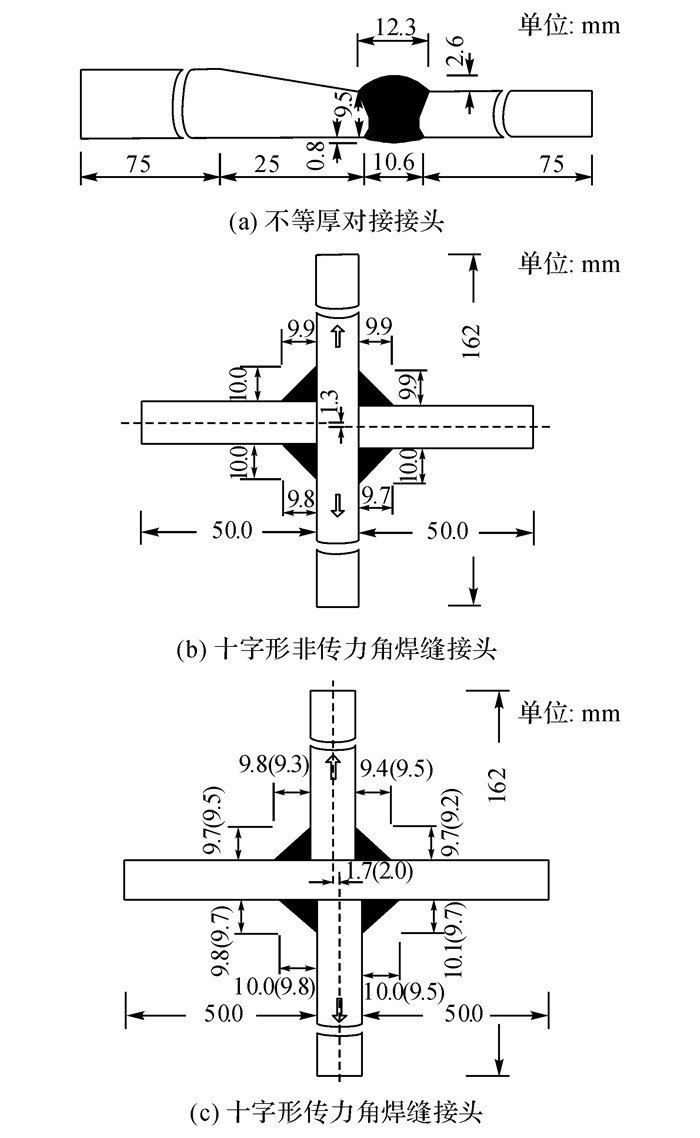
选取钢桥3种典型的焊接构造细节, 包括不等厚对接焊缝接头(26个)、十字形传力角焊缝接头(26个)和十字形非传力角焊缝接头(26个), 如图 4所示, 开展高周疲劳试验.钢板为Q345qD材质, 板厚为12 mm, 其中不等厚接头薄板厚度为8 mm.焊接工艺为CO2气体保护焊, 对接接头选用E501T-1L药芯焊丝, 十字形接头选用ER50-6实心焊丝.
|
图 4 钢桥典型焊接细节试样的几何尺寸 Fig. 4 Geometric dimensions for welded joint specimens of steel bridges |
为了为有限元模型建模分析提供准确的几何参数, 对试样的焊缝局部细节几何尺寸进行测量.详细的测量结果均值如图 4所示.针对十字形传力角焊缝接头, 对焊根破坏和焊趾破坏模式的几何尺寸分别进行统计.图 4(c)中, 括号表示为焊趾失效试样尺寸.
2.2 试验方案3种钢桥焊接细节的疲劳试验在清华大学力学系的PLG-200高频疲劳试验机上开展, 如图 5所示, 应力比R=0.1.针对每种焊接细节, 取7个不同等级的应力幅进行试验, 每个等级应力水平至少完成3个有效试样.试验以疲劳循环次数达到500万次或者试验加载频率降低10 Hz作为试验停机准则.

|
图 5 疲劳试验装置示意图 Fig. 5 Experimental setup of fatigue tests |
不等厚对接焊接接头的失效位置均为薄板与焊缝连接的焊趾处, 十字形非传力角焊缝接头的失效位置均为焊趾处, 十字形传力角焊缝接头接头的失效位置包括焊趾和焊根.
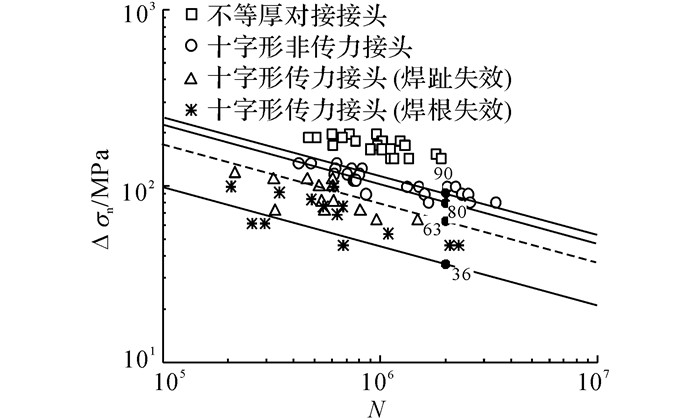
如图 6所示, 给出3种构造细节的名义应力S-N曲线.图中, Δσn为名义应力幅.给出IIW推荐的相应构造细节分组的疲劳设计曲线.可以看出, 不等厚对接焊接接头的所有试验数据均位于FAT90曲线的上部, 十字形非传力角焊缝接头有个别数据点位于FAT80曲线的下方.对于十字形传力角焊缝接头, 分焊趾和焊根失效, 给出相应的疲劳试验数据.可以看出, 除3个数据点外, 其余焊根失效数据点均位于IIW推荐的针对焊根失效的FAT36曲线上方, 这可能是由于疲劳试样本身的焊接质量引起的;焊趾失效大部分数据点位于IIW推荐的针对焊趾失效的FAT63曲线下方;整体来看, 焊趾失效疲劳强度高于焊根失效疲劳强度, Eurocode3规范仅给出十字形传力角焊缝接头的焊根失效FAT36疲劳设计曲线是合理的.
|
图 6 钢桥典型构造细节试样的名义应力S-N曲线 Fig. 6 Nominal stress S-N curves for constructionaldetail specimens of steel bridges |
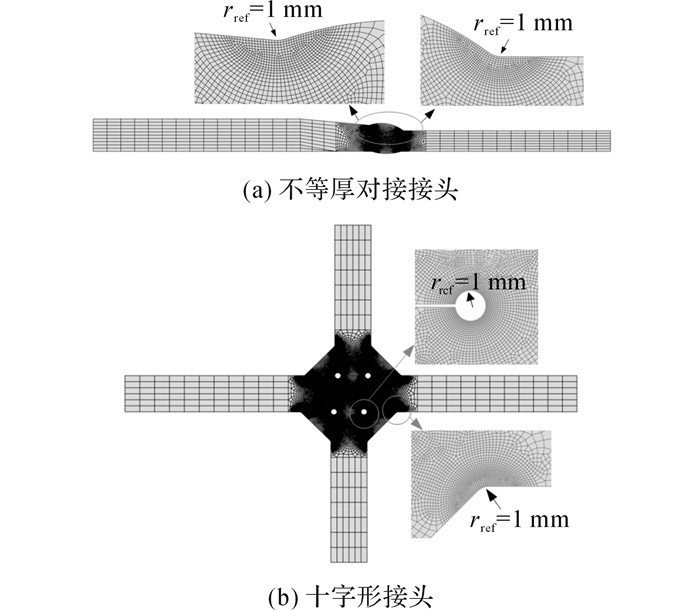
图 7给出不等厚对接焊接接头、十字形非传力角焊缝接头和十字形传力角焊缝接头的二维平面应变有限元模型, 采用二次8节点四边形单元CPE8.焊接接头局部细节的几何尺寸如图 4所示, 其中十字形接头考虑了焊接位错的影响, 焊趾和焊根处的尖角采用有效缺口半径rref=1 mm的虚拟圆弧代替.其中, 焊根采用keyhole模型, 十字形接头焊根处未熔合空隙统一取为0.2 mm.疲劳试样均施加单位拉伸荷载1 MPa, 弹性模量和泊松比分别为206 GPa和0.3.借鉴文献[6~12]的理论分析经验, 考虑到本文试样经过热变形矫正和线切割的应力释放, 有限元模型中不再考虑残余应力的影响.
|
图 7 典型构造细节试样的有限元模型 Fig. 7 Finite element models of constructional detailspecimens |
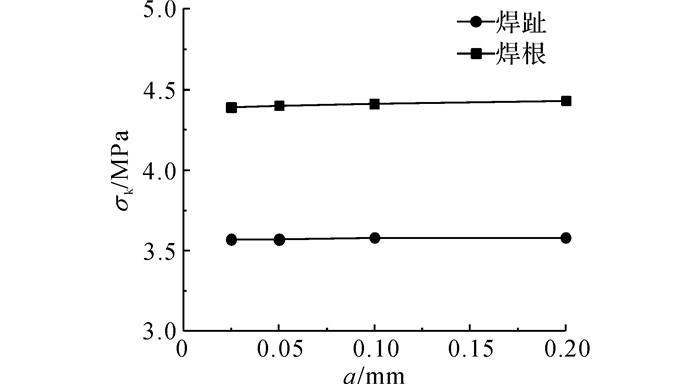
以十字形传力角焊缝接头为算例, 不考虑焊接位错的影响, 统一取焊脚尺寸hf=10 mm, 施加单位荷载, 计算焊趾和焊根处的网格尺寸对有效缺口应力的影响.如图 8所示, 给出最大主应力强度准则下, 有效缺口应力σk随网格尺寸a的变化规律.可以看出, 随着网格尺寸的加密, 焊趾和焊根处有效缺口应力的变化不明显, 这证明在IIW推荐的网格尺寸范围内, 有效缺口应力的计算足够精确.在后续的有效缺口应力计算分析中, 3种焊接细节焊趾或焊根处的网格最小尺寸统一取0.1 mm.
|
图 8 十字形传力角焊缝接头的网格敏感性分析 Fig. 8 Effect of element size on stress variation at weld toe or root of load-carrying fillet-welded cruciform joint |
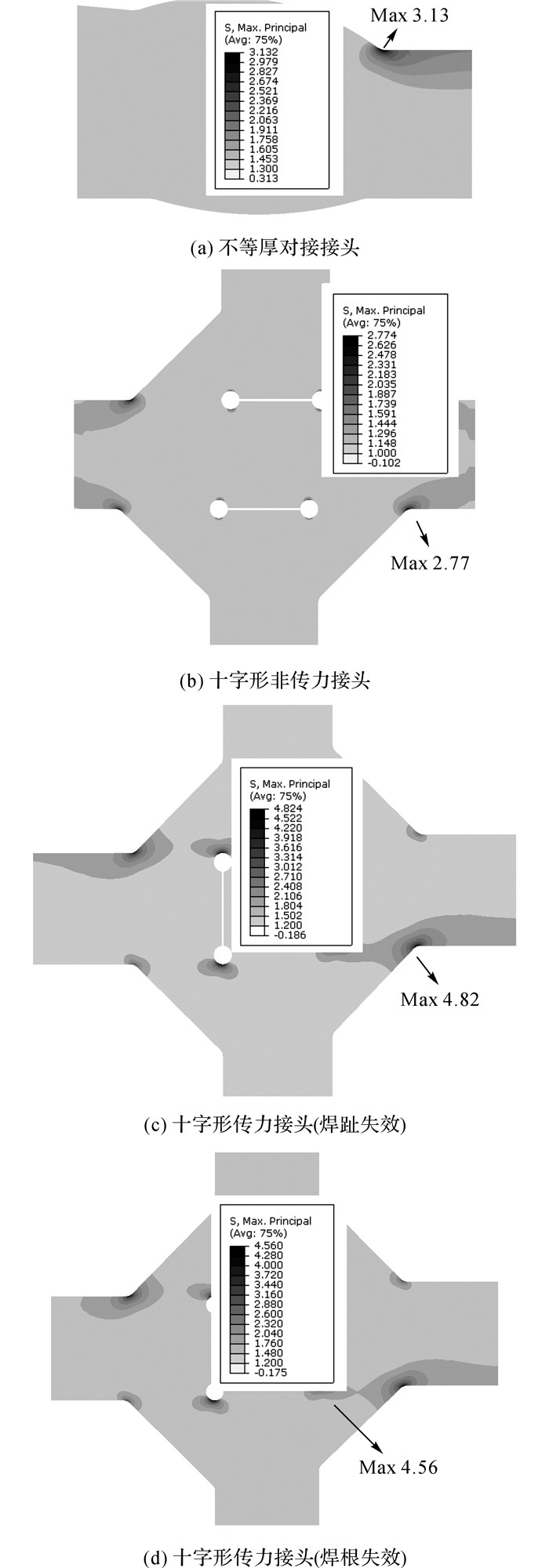
如图 9所示, 给出3种典型焊接构造细节的有效缺口应力计算结果, 计算了焊趾和焊根缺口处的最大主应力.可知, 在最大主应力强度的假设条件下, 不等厚对接焊接接头的最大应力出现在薄板和焊缝的连接处, 十字形非传力角焊缝接头的最大应力出现在焊趾处.对发生焊趾失效的十字形传力角焊缝而言, 最大应力出现在焊趾处;对发生焊根失效的十字形传力角焊缝而言, 最大应力出现在焊根处.
|
图 9 构造细节试样的有效缺口应力计算(最大主应力) Fig. 9 Effective notch stress calculation of constructional detail specimens (maximum principle stress) |
如表 3所示, 在单位拉伸荷载作用下, 分最大主应力强度假设和von Mises应力强度假设, 给出3种焊接构造细节焊趾或焊根失效位置处的有效缺口应力集中系数Kf.比较而言, 十字形传力角焊缝接头的焊趾或焊根处表现出更大的应力集中, 具有更低级别的疲劳细节分组.
| 表 3 有效缺口应力集中系数 Table 3 Effective notch stress intensity factors |
由疲劳试验结果可知, 不等厚对接焊接试样在薄板与焊缝连接焊趾处出现疲劳裂纹, 十字形非传力角焊缝在焊趾处出现疲劳裂纹, 十字形传力角焊缝在焊趾处或焊根处出现疲劳裂纹.由图 9所示, 对比试验结果和有效缺口应力的有限元分析结果发现, 疲劳失效出现的位置与最大有效缺口应力出现的位置是相对应的.这表明采用有效缺口应力法能够有效地判断裂纹起始位置, 区分焊趾和焊根失效, 弥补了热点应力只能针对焊趾失效进行疲劳评估的不足.
4.2 焊接位错和焊脚尺寸对失效模式的影响焊趾或焊根处的有效缺口应力相对大小直接影响了十字形传力角焊缝接头的失效模式.以本文的十字形传力角焊缝接头为算例背景, 假设4个焊脚尺寸相同, 通过有限元计算焊趾和焊根处的有效缺口应力, 分析焊接位错量e和hf对失效模式的影响程度.
从图 10可以看出, 对十字形传力角焊缝接头而言, 在满足构造要求的焊脚尺寸条件下, 焊接位错是决定十字形传力角焊缝接头失效模式的主要因素.在较小的焊接位错量条件下, 十字形传力角焊缝接头主要以焊根失效为主;当焊接位错量大于某值时, 十字形传力角焊缝接头主要以焊趾失效为主.Kainuma等[20]基于断裂力学方法, 指出不考虑焊接位错时, 疲劳失效模式从焊根到焊趾转变的临界焊脚尺寸比(焊脚尺寸/主板厚度)是1.2.根据本文方法可知, 当hf=16 mm时, 失效位置仍然在焊根, 值得进一步商榷.

|
图 10 十字形传力角焊缝接头失效模式的影响因素分析 Fig. 10 Effects of misalignment and weld size on failure mode of load-carrying fillet-welded cruciformjoints |
采用有限元方法, 表 3给出3种构造细节的有效缺口应力集中系数.根据下式可以将名义应力转化为有效缺口应力[7]:
| $ \Delta {\sigma _{\rm{k}}} = {K_{\rm{f}}}\Delta {\sigma _{\rm{n}}}. $ | (3) |
式中:Δσk为有效缺口应力幅.图 11给出有效缺口应力系统下的3种典型构造细节的S-N曲线.

|
图 11 钢桥典型构造细节试样的有效缺口应力S-N曲线(主应力假设) Fig. 11 Effective notch stress S-N curves for constructional detail specimens of steel bridges (maximum principal stress) |
如图 11(a)可以看出, 对接焊接接头的疲劳试验数据均位于有效缺口应力FAT225疲劳设计曲线的上方, 并具有较高的安全富裕度, 这可能是由于不等厚对接接头在受力时存在偏心二次弯矩, 增大了焊趾处的缺口应力集中系数.如图 11(b)、(c)所示, 十字形非传力和传力角焊缝接头疲劳试验数据绝大部分位于FAT225曲线的偏安全一侧, 与FAT225曲线吻合较好;与名义应力系统下具有相同情形的是有个别数据落在疲劳设计曲线的下方, 可能是由于较大焊接位错或个别疲劳试样焊缝局部缺陷造成的, 毕竟FAT225疲劳设计曲线是针对有较高焊趾轮廓质量焊缝提出来的[7].尽管如此, 针对十字形两种试验疲劳寿命偏低的接头, 采用实际的试样尺寸, 重新计算焊趾和焊根处的有效缺口应力, 结果如图 11(d)所示, 但情况不能让人满意.
比较图 6的名义应力系统和图 11(d)的有效缺口应力系统下3种焊接构造细节的疲劳试验数据.可以看出, 有效缺口应力系统的疲劳试验数据表现较小的离散性和较高的一致性, 证明了有效缺口应力法的有效性.图 11(d)给出Pedersen等[7]提出的FAT200疲劳设计曲线.除了十字形传力角焊缝接头3个焊根失效数据点落在FAT200曲线的下方, 可能是由于焊接质量不足造成的, 其余数据均位于FAT200曲线的上方.另外, 名义应力系统下的疲劳试验数据几乎均位于相应疲劳设计曲线的上方, 这说明与有效缺口应力系统的FAT225设计曲线相比, 前者的疲劳设计曲线具有更高的安全保证.
由于成本的限制, 本文相关类型的试验数据不十分丰富以及部分疲劳试样焊接质量的影响, 在缺口应力系统下, 图 11(d)表现出不等厚对接接头和十字形接头疲劳数据的些许差异;考虑到疲劳试验的离散性及疲劳试验结果在S-N曲线数据图中存在一定的离散分布带宽, 这些差异是允许存在的.此外, 会继续展开钢桥焊接细节的疲劳试验和数值分析工作, 完善有效缺口应力法的研究.
5 结论(1) 3种焊接构造细节的疲劳试验数据结果表明, 大部分疲劳试验数据与FAT225疲劳设计曲线吻合较好, 名义应力疲劳设计曲线相比有效缺口应力FAT225设计曲线具有更高的安全豁余度.
(2) 采用有效缺口应力法能够区分焊接构造细节的疲劳裂纹在焊趾或焊根的起始位置, 焊接位错量会严重影响十字形传力角焊缝接头的疲劳失效模式.
(3) 有效缺口应力法可以很好地用于钢桥焊接构造细节的疲劳寿命评估.基于本文疲劳试验数据、有限元分析结果以及文献[7]的建议可知, 在最大主应力强度准则条件下, 对于焊接质量满足抗疲劳设计要求的构造细节, 建议使用FAT200疲劳设计曲线.
| [1] | HOBBACHER A F. The new IIW recommendations for the fatigue assessment of welded joints and components-A comprehensive code recently updated[J]. International Journal of Fatigue, 2009, 31: 50–58. DOI:10.1016/j.ijfatigue.2008.04.002 |
| [2] | AYGÜL M, BOKESJÖ M, HESHMATI M, et al. A comparative study of different fatigue failure assessments of welded bridge details[J]. International Journal of Fatigue, 2013, 49: 62–72. DOI:10.1016/j.ijfatigue.2012.12.010 |
| [3] | HOBBACHER A F. Recommendations for fatiguedesign of welded joints and components [R]. Paris:International Institute of Welding, 2008. |
| [4] | FRICKE W. IIW recommendations for the fatigueassessment by notch stress analysis for welded structures [R]. Paris: International Institute of Welding, 2010. |
| [5] | SONSINO C M, FRICKE W, BRUYNE F D, et al. Notch stress concepts for the fatigue assessment of welded joints: background andapplications[J]. International Journal of Fatigue, 2012, 34(1): 2–16. DOI:10.1016/j.ijfatigue.2010.04.011 |
| [6] | PARK W, MIKI C. Fatigue assessment of large-size welded joints based on the effective notch stressapproach[J]. International Journal of Fatigue, 2008, 30(9): 1556–1568. DOI:10.1016/j.ijfatigue.2007.11.012 |
| [7] | PEDERSEN M M, MOURITSEN O Ø, HANSEN M R, et al. Re-analysis of fatigue data for welded jointsusing the notch stress approach[J]. International Journal of Fatigue, 2010, 32(10): 1620–1626. DOI:10.1016/j.ijfatigue.2010.03.001 |
| [8] | NGUYEN K T, GARBATOV Y, SOARES G. Fatigue damage assessment of corroded oil tanker details based on global and local stress approaches[J]. International Journal of Fatigue, 2012, 43: 197–206. DOI:10.1016/j.ijfatigue.2012.04.004 |
| [9] | OH D J, LEE J M, KIM M H. Fatigue strength assessment of Invar alloy weld joints using the notch stressapproach[J]. Engineering Failure Analysis, 2014, 42: 87–99. DOI:10.1016/j.engfailanal.2014.04.003 |
| [10] |
祝志文, 钱六五. 基于有效缺口应力法的正交异性钢桥面板疲劳评价[J].
湖南大学学报:自然科学版, 2015, 42(9): 59–67.
ZHU Zhi-wen, QIAN liu-wu. Fatigue assessment of orthotropic steel bridge deck based on the effective notch stress method[J]. Journal of Hunan University: Natural Sciences, 2015, 42(9): 59–67. |
| [11] | AYGVL M, AL-EMRANI M, URUSHADZE S. Modelling and fatigue life assessment of orthotropic bridge deck details using FEM[J]. International Journal of Fatigue, 2012, 40: 129–142. DOI:10.1016/j.ijfatigue.2011.12.015 |
| [12] | SHAHRI M M, SANDSTRÖM R. Effective notch stress and critical distance method to estimate the fatigue life of T and overlap friction stir welded joints[J]. Engineering Failure Analysis, 2015, 25: 250–260. |
| [13] | MORGENSTERN C, SONSINO C M, HOBBACHER A, et al. Fatigue design of aluminum welded joints by the local stress concept with the fictitious notch radius of rf =1mm[J]. International Journal of Fatigue, 2006, 28(8): 881–890. DOI:10.1016/j.ijfatigue.2005.10.006 |
| [14] | ZHANG G, RICHTER B. A new approach to thenumerical fatigue-life prediction of spot-welded structures[J]. Fatigue and Fracture of Engineering Materials and Structures, 2008, 23(6): 499–508. |
| [15] | NEUBER H. Vber die berücksichtigung der Spannungskonzentration bei Festigkeitsberechnungen[J]. Konstruktion, 1968, 20(7): 245–251. |
| [16] | RADAJ D. Design and analysis of fatigue resistant welded structures[M]. Cambridge: Abington, 1990. |
| [17] | RADAJ D, SONSINO C M, FRICKE W. Fatigueassessment of welded joints by local approaches[M]. Cambridge: Woodhead, 2006. |
| [18] | SONSINO C M. A consideration of allowable equivalent stresses for fatigue design of welded joints according to the notch stress concept with the reference radii rref = 1.00 and 0.05 mm[J]. Welding in the World, 2013, 53(3/4): 64–75. |
| [19] | BAUMGARTNER J, BRUDER T. An efficient meshing approach for the calculation of notch stresses[J]. Welding in the World, 2013, 57(1): 137–145. DOI:10.1007/s40194-012-0005-3 |
| [20] | KAINUMA S, MORI T. A study on fatigue crack initiation point of load-carrying fillet welded cruciform joints[J]. International Journal of Fatigue, 2008, 30(9): 1669–1677. DOI:10.1016/j.ijfatigue.2007.11.003 |



