2. 浙江大学 计算机科学与技术学院,浙江 杭州 310058
2. College of Computer Science and Technology, Zhejiang University, Hangzhou 310058, China
互联网在极大地提高人们获取信息效率的同时,产生了信息过载的问题. 为了让人们愈加高效地从互联网获取所需信息,需要科学、系统地对互联网信息进行组织和呈现. 推荐算法能够针对个体有效地将用户感兴趣的潜在信息推送给用户,提高了用户获取信息的效率和体验,能够为平台和企业带来可观的商业利益,因此具有十分重要的现实意义.
从方法上划分,推荐算法主要分为基于内容的推荐[1]、基于近邻的协同过滤推荐[2-3]及基于模型的协同过滤推荐[4-5]. 基于内容的推荐依据物品的元数据计算物品的相关性,然后基于用户的历史偏好推荐类似物品给用户. 协同过滤推荐依据用户对物品的偏好计算物品或用户的相关性,然后基于这些关联性进行推荐.
从数据类型上划分,可以分为显式反馈和隐式反馈. 显式反馈是用户主动进行的评分,展现的是用户的喜好和不喜好;隐式反馈是点击、购物等记录,展现的是用户的兴趣. 隐式反馈一般用0-1二值矩阵来描述用户-物品的行为,对于0-1矩阵来说,1代表用户对该物品感兴趣,0有2种含义:1)用户见过该物品但是不感兴趣,没有点击;2)用户没有见过该物品. 如果我们能够对矩阵中出现的0值进行较好地区分,那么可以给用户见过的物品赋予更高的置信度,降低0值数据中的噪音数据,进而提高模型的预测效果. 面对隐式推荐中的0值二义性问题,现有的推荐方法主要是利用物品本身的流行度对0值数据赋予不同的置信度,未考虑社交信息对0值数据置信度的影响.
针对隐式数据推荐中的稀疏性和二义性问题,本文在充分利用社交数据和分析0值数据的基础上,提出基于社交信息和物品曝光度的矩阵分解推荐算法.
1 相关工作研究人员针对推荐系统中的稀疏性以及隐式推荐中的0值二义性进行广泛而深入的研究. 下文介绍当前主流的潜在因子模型、结合曝光度的潜在因子模型以及结合社交信息的潜在因子模型.
1.1 潜在因子模型潜在因子模型将用户和物品分解为低维度的用户潜在向量和物品潜在向量,物品潜在向量体现物品的潜在特征属性,用户潜在向量体现用户对于这些潜在特征的偏好.
最初的潜在因子模型是奇异值分解(singular value decomposition, SVD)[6],通过最小化评分误差对用户和物品潜在因子进行学习. Koren[7]对SVD方法进行改进,通过随机梯度下降法和交替最小二乘法来优化求解低秩矩阵,提出加入用户、物品偏置以及额外上、下文信息的SVD++模型. Koren在SVD++的基础上,为用户、物品偏置及用户潜在因子增添时序特征,提出timeSVD++[8]模型,进一步提高了预测准确率. 此外,Mnih等[9]假设用户潜在因子、物品潜在因子以及观测噪声都服从高斯分布,提出概率矩阵分解算法(probabilistic matrix factorization, PMF),从概率分布的角度诠释了矩阵分解. Liang等[10]提出CoFactor模型,将词向量运用于物品之间的相互关系挖掘,运用挖掘出的物品关系来约束矩阵分解中的物品潜在因子向量,从而更好地模拟物品特征.
Rendle等[11]针对隐式反馈数据的topN推荐,提出基于贝叶斯后验优化的个性化推荐模型(Bayesian personalized ranking, BPR). BPR假设用户之间偏好以及同一用户对不同物品的偏好都彼此独立,将观测值处理成(用户、物品i、物品j)的三元组集合表示用户相对j更喜欢i,利用随机梯度下降法优化贝叶斯后验目标函数来学习用户和物品的潜在因子. Yu等[12]认为仅仅为固定用户构建物品对采样还不够充分,因为不同用户对同一物品的偏好差异无法显示区分出来,由此提出排名感知的互惠贝叶斯个性化推荐,在BPR的基础上引入物品相对于不同用户之间的偏序信息,在多个数据集上取得了更优的召回率和平均准确率. Zhang等[13]首先利用PageRank算法计算物品的重要性,然后将物品PR值作为权重结合到矩阵分解模型中,利用BPR进行模型学习.
1.2 结合曝光度的潜在因子模型隐式数据推荐往往比显式数据推荐更加困难,因为显式数据同时展示用户喜欢和不喜欢的物品,隐式数据只展示用户喜欢的物品. 隐式数据的值只有0和1,因此当预测用户的偏好时,必须用到未点击的0值用户-物品对,很多镜像的显式数据推荐方法直接将0值数据视为用户不喜欢,该假设不符合现实情况. 隐式数据推荐的一个关键问题是:我们知道用户会点击他们感兴趣的物品,但是不知道一个物品为什么没有被用户点击.
Hu等[14]提出WMF模型,在SVD模型的损失函数中加入观测值的置信度wui,为观测到的“1”值赋予大的置信度,未观测到的“0”值赋予小的置信度,从而降低“0”值观测值对模型的影响. WMF模型对于缺失的“0”值数据,都是赋予相同的置信度,在真实情况中,越流行的物品被用户见过的概率越大,因此流行物品的“0”值数据更有可能是用户见过但是真得不感兴趣,应该具有更大的置信度.
为了更好地模拟物品之间的差异,He等[15]提出eALS模型. 首先通过物品的被点击频率,计算每个物品的流行度;然后根据物品的流行度,对缺失的“0”值数据进行加权,得到物品被用户见过但是没被点击的置信度,加入到损失函数中未观测数据预测值的惩罚项中,取得了更好的预测效果和性能.
Liang等[16]首次引入物品曝光度的概念,表示用户是否接触过物品,结合PMF提出更加通用化的基于物品曝光度的矩阵分解模型Expo-MF. Expo-MF模型假设物品曝光度服从伯努利分布,在知道曝光度的条件下,用户的兴趣服从矩阵分解模型. Expo-MF模型分别用物品流行度及物品主题、位置等信息对物品曝光度进行建模发现,加入物品主题、位置信息后,Expo-MF相比WMF模型在召回率上有明显提升.
Lin等[17]认为仅仅考虑物品曝光度不足以准确刻画用户偏好,额外引入社交曝光度来表示用户之间是否了解彼此,提出TranSIV生成模型. 利用迁移学习,将社交和评分信息整合到统一的模型中,从而更好地学习用户偏好,在Ciao数据集中相对Expo-MF模型取得了更好的预测效果.
1.3 结合社交信息的潜在因子模型随着社交网络的飞速发展,许多互联网平台都加入了社交功能,比如Lastfm、网易云音乐、豆瓣. 社交功能将具备共同兴趣爱好的用户汇集在一起,增强了用户之间的联系,同时为推荐算法提供了新的数据源.
Purushotham等[18]在CTR的基础上加入社交关系,提出CTR-SMF模型. 通过LDA对物品文本信息主题建模来约束物品潜在因子,利用矩阵分解将社交矩阵分解成用户偏好潜在因子和社交潜在因子,通过社交关系来约束用户偏好潜在因子,最后通过评分矩阵约束用户偏好因子和物品特征因子,相比PMF和CTR模型取得更好的效果. Jamali等[19]提出SocialMF,该方法假设一个用户的偏好与好友的平均偏好相似,在MF的损失函数中加入社交正则化项. Ma等[20]在SocialMF的基础上提出Soreg,该模型考虑到每个用户的好友偏好有差异,同个用户的不同好友之间可能出现兴趣相异从而相互抵消的情况,因此该方法更强调用户之间个体化的社交关系,关系越强的好友对目标用户的影响越大. Hu等[21]提出MR3模型对评分、物品评论和社交关系同时建模,从而更有效地分析出潜在因子和隐藏主题. Guo等[22]提出3种基于隐式反馈的融合社交信任的物品相似度模型,根据用户-用户和物品-物品相似度,利用矩阵分解来计算用户对评分物品和未评分物品的偏好. 柳玲等[23]综合考虑用户的局部影响力和全局影响力,提出基于用户影响力游走模型的社会化推荐算法. 该算法根据用户信任关系和历史行为分析用户的局部影响力,通过评估用户的评分质量研究用户的全局影响力;然后将二者有机结合,计算随机游走模型中各节点之间的转移概率,在一定程度上提高了推荐的性能. Chaney等[24]假设用户喜爱物品受到自身偏好和社交关系的共同影响,基于PF[25]提出SPF模型,在多个数据集上取得更好的推荐效果.
在现有研究中,针对隐式反馈中的物品曝光度,大多只是考虑了物品本身的流行度和属性,以往社交信息的作用主要是约束用户的潜在偏好相似度,没有考虑到用户社交影响力对物品曝光度的影响. 众所周知,随着社交功能的日渐发展,用户之间的接触和分享越来越常见和频繁,对用户-物品曝光度的影响不可忽视. 不同于Expo-MF[16]模型利用物品信息对物品曝光度建模以及TranSIV[17]模型将社交信息应用于社交曝光度,本文将社交信息应用于物品曝光度及用户潜在因子模型,通过概率生成模型进行建模.
2 基于社交信息和物品曝光度的矩阵分解推荐算法用户社交信息不仅影响用户的潜在偏好,而且影响用户对物品的曝光度,因此利用用户社交信息和用户影响力对物品曝光度建模;然后在已有物品曝光度的条件下,同时对用户-用户社交矩阵和用户-物品观测值矩阵进行矩阵分解;最后利用求出的用户潜在偏好矩阵和物品潜在特征矩阵进行TopN推荐,算法流程如图1所示.

|
图 1 基于社交信息和物品曝光度的矩阵分解推荐流程图 Fig. 1 Framework of matrix factorization recommendation algorithm based on social information and item exposure |
在推荐系统的社交行为中,用户会和好友分享自己的兴趣爱好,比如购买了某个商品,听了某首音乐. 用户对于物品的曝光度一方面受到物品本身流行度的影响,另一方面受到用户的好友对该物品曝光度的共同影响,并且影响力越大的好友对用户的物品曝光度影响越大,例如拥有大量关注者的微博大V分享的物品被其他用户浏览或转发的概率更大. 基于以上假设,将社交关系和用户影响力运用到物品曝光度计算模型.
由于推荐系统中的社交关系为图结构,每个用户都可以由图中的一个节点代表,用户之间的关系通过有向边代表,因此先根据用户之间的社交关系建立有向图,然后运用PageRank[26]来计算每个用户的影响力,如算法1所示.
算法 1 幂迭代法计算用户的PR影响力
1:输入:用户社交矩阵sNXN,其中N为用户数量.
2:初始化常量d和δ. d=0.85,
3:计算对角矩阵
4:计算矩阵
5:初始化向量X和Z.
6:while max (abs (X−Z)) > 0.000 1 do:
Z=X;
4:计算矩阵A.
5:初始化向量X和Z.
6:while max (abs (X-Z)) > 0.000 1 do:
X=AX;
end while
7:输出用户影响力向量X
其中,d为PageRank算法中的阻尼系数,表示用户继续访问当前页面所提供的链接的概率,一般取值为0.85,1−d表示用户随机访问任一页面的概率;A为谷歌矩阵,用于在每次迭代中更新PageRank向量X;Z为前一次迭代的PageRank向量.
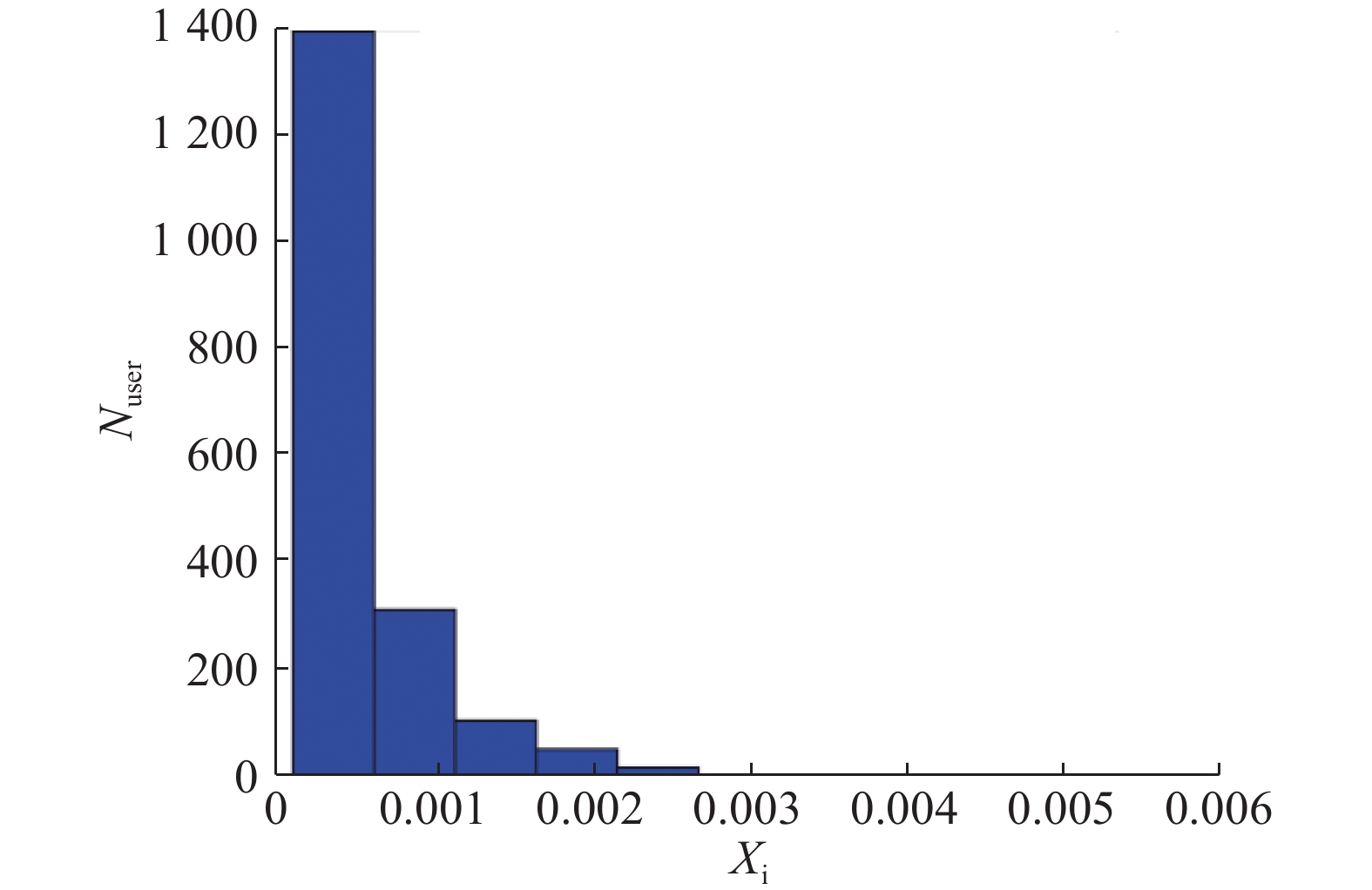
计算出用户的PR值后,得到Lastfm[27]上的用户影响力分布,如图2所示. 图中,Xi为用户影响力,Nuser为对应的用户数量. 从图2可以发现,用户影响力符合幂律分布,影响力越大,用户数量越少.
|
图 2 Lastfm数据集用户影响力分布图 Fig. 2 Distribution of user influence on Lastfm dataset |
该模型将用户影响力作为权重,应用于用户间的物品曝光度影响中,考虑将不同区间的PR映射到对应的权重中,如表1所示.
| 表 1 用户影响力的权重映射 Table 1 Weight mapping of user influence |
随着网络社交行为的越来越普遍和多样性,人们每天都能够主动或被动地从社交互动中接触到朋友或是被关注者分享的大量信息,而这部分信息往往没有有效的记录方式. 对于物品曝光度来说,这些浏览信息起到极关键的作用,尤其在社交活动频繁的场景下. 将社交影响力和社交关系加入物品曝光度模型中,从而更好地刻画物品曝光度.
如图3所示为曝光度与观测值的关系. 图中,Y的取值中括号左侧为观测数据,括号里为预测的偏好. 矩阵A=[aui]为物品曝光度,表示用户u是否接触过物品i,在计算曝光度的条件上进行观测值的预测,以此来解决0值数据的二义性问题. 其中,u1见过i2(a12=1),u3见过i1(a31=1),但是没有点击(y12=0,y31=0),所以认为u1不喜欢i2,u3不喜欢i1. 对于曝光度为0(aui=0)来说,无法确定用户的兴趣(yui=?).

|
图 3 曝光度矩阵作为观测值矩阵的条件 Fig. 3 Exposure matrix as condition of observation matrix |
假设曝光度aui服从先验概率为μui的伯努利分布. μui为u见过i的概率,受到物品本身的流行度及用户社交关系的共同影响. 一般来说,流行的物品更容易受到曝光,因此用户接触过它的可能性更大;在社交网络中,好友之间经常会分享彼此的兴趣,产生交流,可能互相推荐各自感兴趣的物品,因此用户对物品的曝光度会受到好友对该物品曝光度的影响. 基于以上2个假设,设置μui为
| ${\mu _{ui}} \sim {e_i} + f\left( {{{{S}}_{{u}}}} \right).$ | (1) |
式中:ei为物品i本身的流行度,物品被用户见过的次数越多则越流行,因此用伯努利分布的共轭先验Beta分布表示ei~Beta(α1,α2);f(Su)表示用户u的好友对曝光度μui的影响,用户的影响力越大,则对好友的曝光度影响程度越大. 通过影响力加权用户u的好友对物品i的曝光度先验来计算f(Su),具体如下:
| $f\left( {{{{S}}_u}} \right) = \mathop \sum \nolimits_{f \in {\rm{Friends}}\left( u \right)} {X_f} {\mu _{fi}}.$ | (2) |
式中:Friends(u)为用户u的好友集合,Xf为用户f的影响力.
2.3 基于社交信息和物品曝光度的矩阵分解方法(SI-Expo-MF)假定用户偏好θu、物品因子βi以及用户社交偏好zk都服从均值为0、方差为λθ−1的高斯分布;社交矩阵元素suk服从均值为θuTzk、方差为λs−1的高斯分布;曝光度aui服从先验概率为μui的伯努利分布;在已知曝光度的条件下,用户的观测值yui服从均值为θuTβi、方差为λy−1的高斯分布,完整的概率图模型如图4所示.

|
图 4 SI-Expo-MF的图模型 Fig. 4 Graph model of SI-Expo-MF |
假定潜在因子维度为K,则具体概率模型如下:
| $\left.\begin{array}{l} {{{\theta}} _u} \sim N\left( {0,\lambda _\theta ^{ - 1}{{{I}}_K}} \right),\\ {{{\beta}} _i} \sim N\left( {0,\lambda _\beta ^{ - 1}{{{I}}_K}} \right),\\ {{{z}}_k} \sim N\left( {0,\lambda _z^{ - 1}{{{I}}_K}} \right),\\ {a_{ui}} \sim {\rm{Bernoulli}}\left( {{\mu _{ui}}} \right),\\ {s_{uk}} \sim N\left( {{{{\theta}} _u}^{\rm{T}}{{{z}}_k},{\lambda _s}^{ - 1}} \right),\\ {y_{ui}}|{a_{ui}} = 1 \sim N\left( {{{{\theta}} _u}^{\rm{T}}{{{\beta}} _i},{\lambda _y}^{ - 1}} \right),\\ {y_{ui}}|{a_{ui}} = 0 \sim {\delta _0}. \end{array}\right\}$ | (3) |
式中:λθ、λβ、λy、λz、λs为超参数,IK为K维单位矩阵,δ0表示
对于观测值矩阵Y来说,当yui>0时,aui=1;当yui=0时,aui是潜在的,此时有以下2种情况:1)用户u见过物品i但是没有点击(aui=1,yui=0);2)用户u没有见过物品i(aui=0,yui=0). 由于Y通常是非常稀疏的,大多数aui属于潜在变量.
由式(3)可以推导出aui、yui和suk的对数联合概率:
| $\begin{array}{l} \log p\left( {{a_{ui}},{y_{ui}},{s_{uk}}{\rm{|}}{\mu _{ui}},{{{\theta}} _u},{{{\beta}} _i},{{{z}}_k},{\lambda _{{y}}}^{ - 1},{\lambda _s}^{ - 1}} \right) = \\ \log {\rm{Bernoulli}}\left( {{a_{ui}}{\rm{|}}{\mu _{ui}}} \right) + \\ {a_{ui}}\log N\left( {{y_{ui}}{\rm{|}}{{{\theta}} _u}^{\rm{T}}{{{\beta }}_i},{\lambda _{{y}}}^{ - 1}} \right) +\\ \left( {1 - {a_{ui}}} \right)\log l\left( {{y_{ui}} = 0} \right)+\\ \log N\left( {{s_{uk}}{\rm{|}}{{{\theta}} _u}^{\rm{T}}{{{z}}_k},{\lambda _s}^{ - 1}} \right). \end{array}$ | (4) |
式中:l(b)为指示函数,b为真时为1,否则为0.
2.4 模型训练由于该模型中含有未观测到的隐含数据曝光度,可以利用期望最大化算法进行参数估计,如算法2所示.
算法2 EM算法推导模型参数
输入:
Y;s;X;模型超参数λθ,λβ,λz,λy,λs,α1,α2,曝光度先验µ的初始值μini;潜在因子数量K.
输出:
用户潜在因子矩阵θ1:U;物品潜在因子矩阵β1:I
1:初始化:
θ1:U,β1:I,用户社交潜在因子z1:U,μ
2:while 验证集的NDCG比上一次迭代更好时 do:
E步骤:
计算曝光度的期望E [aui](见式(5))
M步骤:
更新θ1:U(见式(6))
更新z1:U (见式(7))
更新β1:I(见式(8))
更新μui(见式(9))
end while
在E步骤,已知当yui>0时,aui=1. 对每个未观测到(yui=0)的用户物品观测值对,计算曝光度的期望E [aui],如下所示:
| $\begin{array}{l} E\left[ {{a_{ui}}{\rm{|}}{\theta _u},{\beta _i},{\mu _{ui}},{y_{ui}} = 0} \right] = \\ \displaystyle\frac{{{\mu _{ui}} N\left( {0{\rm{|}}{{{\theta}} _u}^{\rm{T}}{{{\beta}} _i},{\lambda _y}^{ - 1}} \right)}}{{{\mu _{ui}} N\left( {0{\rm{|}}{{{\theta}} _u}^{\rm{T}}{{{\beta}} _i},{\lambda _y}^{ - 1}} \right) + \left( {1 - {\mu _{ui}}} \right)}}. \end{array}$ | (5) |
为了方便表述,定义
在M步骤,目标是找到使对数似然函数最大化的参数,可以利用梯度下降对参数求解偏导等于0进行更新. θu、zk和βi的更新如下所示:
| $\begin{split} &\!\!\!\!\!\!\!\!{{{{\theta}} _u} \leftarrow {{\left( {{\lambda _y}\displaystyle\sum\nolimits_i {{p_{ui}}} {{{\beta}} _i}{{{\beta}} _i}^{\rm{T}} + {\lambda _\theta }{{{I}}_K} + {\lambda _s}\sum\nolimits_k {{{{z}}_k}} {{{z}}_k}^{\rm{T}}} \right)}^{ - 1}}} \times \\ &{\left( {\displaystyle\sum\nolimits_i {{\lambda _y}} {p_{ui}}{y_{ui}}{{{\beta}} _i} + \sum\nolimits_k {{\lambda _s}} {{{s}}_{uk}}{{{z}}_k}} \right)}, \end{split}$ | (6) |
| ${{{z}}_k} \leftarrow {\left( {{\lambda _s}\mathop \sum \nolimits_u {{{\theta}} _u}{{{\theta}} _u}^{\rm{T}} + {\lambda _z}{{{I}}_K}} \right)^{ - 1}}\left( {\mathop \sum \nolimits_u {\lambda _s}{{{s}}_{uk}}{{{\theta}} _u}} \right),\qquad\;$ | (7) |
| ${{{\beta}} _i} \leftarrow {\left( {{\lambda _y}\mathop \sum \nolimits_u {p_{ui}}{{{\theta}} _u}{{{\theta}} _u}^{\rm{T}} + {\lambda _\beta }{{{I}}_K}} \right)^{ - 1}}\left( {\mathop \sum \nolimits_u {\lambda _y}{p_{ui}}{y_{ui}}{{{\theta}} _u}} \right).$ | (8) |
对数似然相对于
| ${\mu _{ui}} \leftarrow \frac{{{\alpha _1} + \displaystyle\sum\nolimits_u {{p_{ui}}} + \sum\nolimits_f^{{\rm{Friends}}\left( u \right)} {{X_f}} {p_{fi}} - 1}}{{{\alpha _1} + {\alpha _2} + U + \displaystyle\sum\nolimits_f^{{\rm{Friends}}\left( u \right)} {{X_f}} {p_{fi}} - 2}}.$ | (9) |
式中:
矩阵分解协同过滤的预测是通过计算用户潜在因子和物品潜在因子的点积,对预测值排序后进行TopN推荐,计算方式如下:
| ${E_y}\left[ {{y_{ui}}{\rm{|}}{{{\theta}} _u},{{{\beta}} _i}} \right] = {{\theta}} _u^{\rm{T}}{{{\beta}} _i}.$ | (10) |
该实验在Lastfm数据集[24]上开展. Lastfm是一个提供音乐分享服务的个性化网站. 用户在注册后可以收听不同歌手的音乐,对歌手标记标签,同时用户之间可以互相关注形成社交关系. 数据集中包含了用户对歌手的收听信息以及用户之间的社交关系,是开展实验的理想平台.
用到的数据集包含1 892个用户和17 632个歌手,具体的统计结果如表2所示. 表中,观测值密度为0.28%,相对比较稀疏;用户的社交密度为0.71%,相对于观测数据来说更加丰富.
| 表 2 Lastfm数据集统计结果 Table 2 Data statistics in Lastfm |
实验采用召回率(recall)、平均准确率(MAP)和归一化折损累计增益(NDCG)作为评价指标. MAP认为推荐结果是二元相关性(感兴趣或不感兴趣),NDCG可以以实数的形式进行相关性打分.定义rank(u,i)为用户u的推荐列表中物品i的排名,yutest为测试集中用户u点击过的物品i的集合.
召回率(recall):表示测试集中推荐列表命中的物品数与用户点击的物品集合大小的比例,召回率越大,效果越好. 对于每个用户u,召回率的计算方式如下:
| ${\rm{Recall}}@k = \mathop \sum \nolimits_{i \in y_u^{{\rm{test}}}} \frac{{l\left\{ {{\rm{rank}}\left( {u,i} \right) \leqslant k} \right\}}}{{{\rm{min}}\left( {k,\left| {y_u^{{\rm{test}}}} \right|} \right)}}.$ | (11) |
式中:k为设置的推荐物品数量.
平均准确率(AP):在准确率的基础上考虑位置因素,推荐物品排名越靠前,则AP越高. 对于每个用户u,平均准确率的计算方式如下:
| ${\rm{AP}}@k = \mathop \sum \nolimits_{n = 1}^k \frac{{{\rm{Precision}}@n}}{{\min \left( {n,\left| {y_u^{{\rm{test}}}} \right|} \right)}},$ | (12) |
| ${\rm{MAP}}@k = \frac{1}{m}\mathop \sum \nolimits_u {\rm{AP}}@{k_u}.$ | (13) |
归一化折损累计增益(NDCG):NDCG是针对连续值的指标,随着排名的靠后,折损值越大,因此对排序靠前的结果给予更大的重要性. 计算方式如下:
| ${\rm{DCG}}@k = \displaystyle\mathop \sum \nolimits_{i = 1}^k \frac{{{2^{{\rm{rel}}{_i}}} - 1}}{{{\rm{log}}_2^{ {i + 1} }}},$ | (14) |
| ${\rm{NDCG}}@k = \frac{{{\rm{DCG}}@k}}{{{\rm{IDCG}}@k}}.$ | (15) |
式中:IDCG@k为正则化因子,确保NDCG为0~1.0. 在隐式反馈的场景中,如果i∈yutest,那么reli=1;否则,reli=0.
3.2 实验方案开展3组不同类型的实验,包括模型在不同参数下的召回率比较、模型自身模块比较以及模型与其他优秀算法的预测效果比较.
首先随机将观测数据分成70%训练集、20%测试集和10%验证集,然后通过网格搜索方法训练参数,获取最好效果下的参数值. 在EM算法迭代过程中,θ1:U、z1:U、β1:I和μui的更新都是可并行的矩阵操作,因此利用Python的Multiprocessing和Joblib库并行计算,从而提高效率.
在实验中,计算验证集的归一化折损累计增益(NDCG)作为迭代的评价指标,发现一般迭代次数在10次以内能够达到收敛,因此设置EM算法的最大迭代次数为10.
3.3 模型参数选择设置曝光度aui的Beta先验μui的参数α1、α2都为1;在实验中发现,用户潜在因子的逆方差λθ、物品潜在因子的逆方差λβ和用户社交潜在因子的逆方差λz在同一量级时具有较好的效果,用户-物品观测值的逆方差λy和用户-用户社交值的逆方差λs在同一量级时具有较好的效果. 设置潜在因子的逆方差λθ=λβ=λz=λ l,设置观察值的逆方差λy=λs=λ o.
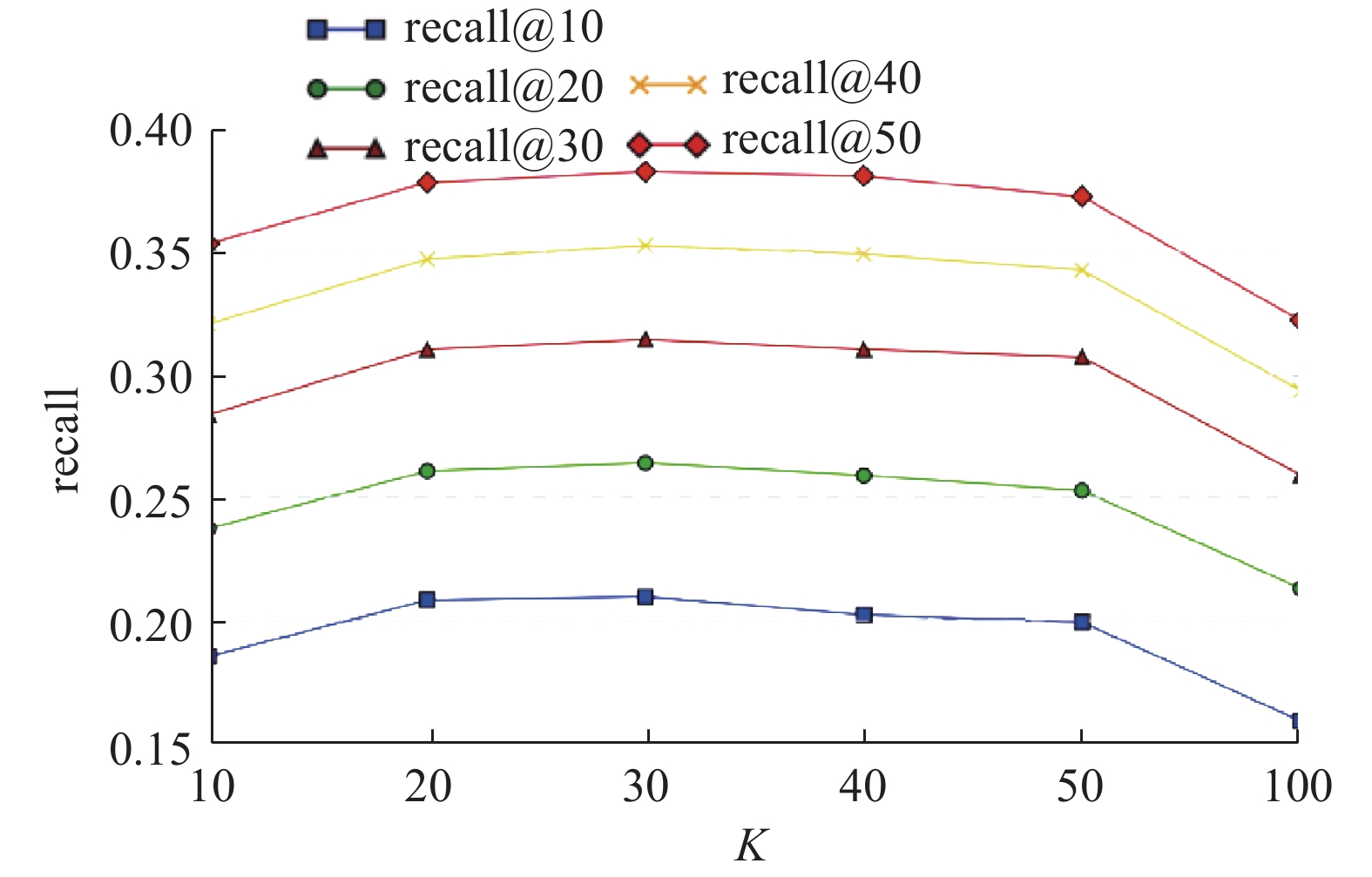
3.3.1 潜在因子数对模型的影响潜在因子数K为用户潜在向量、物品潜在向量、用户社交潜在向量的维度,不同的推荐场景和数据集中的潜在因子数不同. 首先设置μini=0.01,潜在因子逆方差λl=0.01,观测值逆方差λo=1;然后调整不同的K,对θ、β进行训练. 为了更加直观地体现模型效果,使用TopN推荐中不同N的召回率来体现模型的效果. 如图5所示为K对模型的影响. 可知,当K=20、30、40时,模型的召回率较高;当K=30时,模型达到最好的预测效果;当K=10时,召回率很低;当K>50时,召回率急剧下降. 对于Lastfm数据集来说,最合适的K为30.
|
图 5 不同潜在因子K下模型的召回率 Fig. 5 Recall with different number of latent factor |
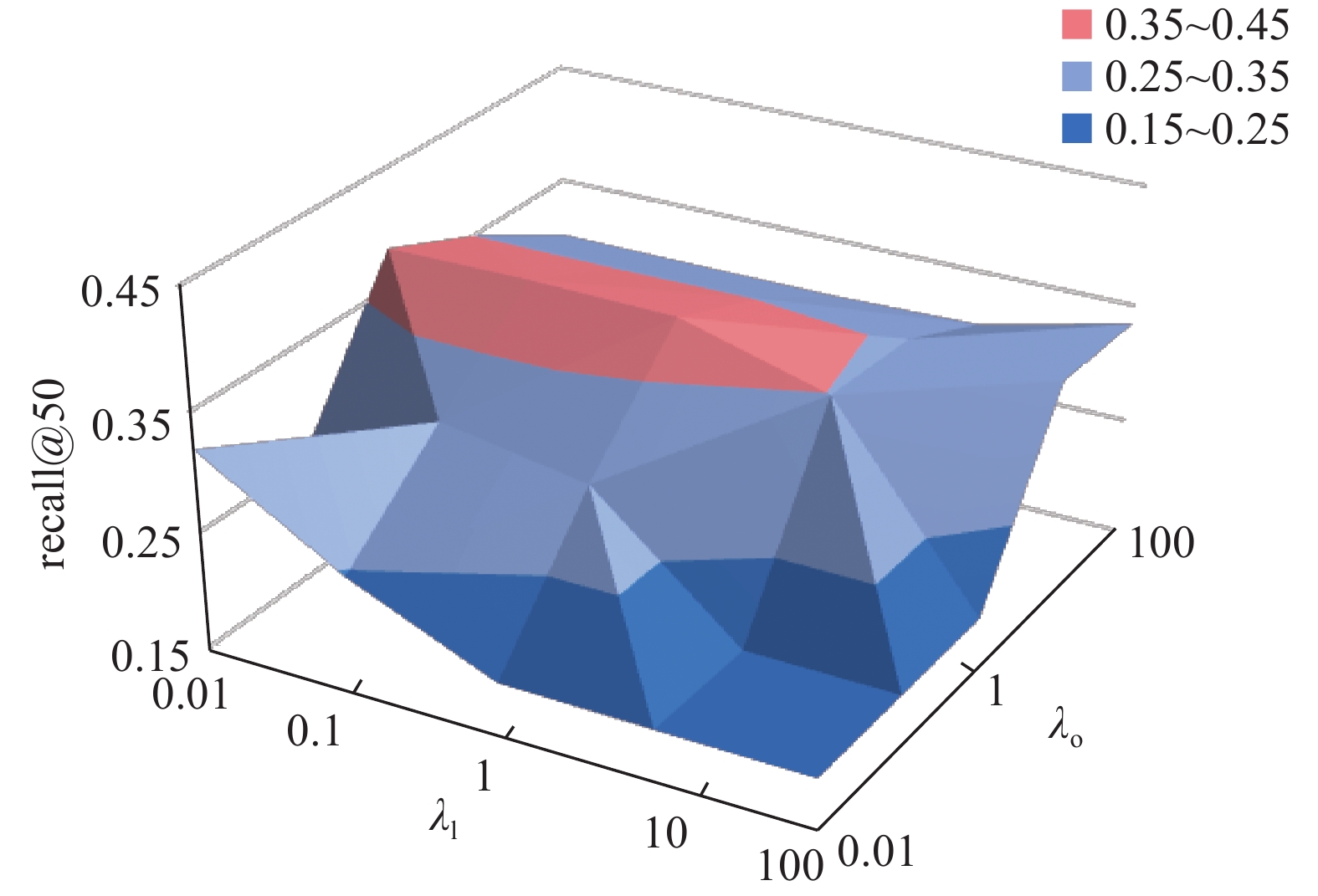
设置K=30,μini=0.01,利用网格搜索来调整λl和λo. 为了直观地体现模型效果,使用推荐物品数量为50的召回率作为评价指标. 从图6可知,当λo较小时,召回率较低;当λo=1时,模型的预测效果最好;随着λo的继续增加,召回率开始逐渐下降. λl的取值变化对模型的影响非常小;当λl=0.1,λo=1时,具有最高的召回率.
|
图 6 不同λl和λo下模型的召回率 Fig. 6 Recall@50 with different λl and λo |
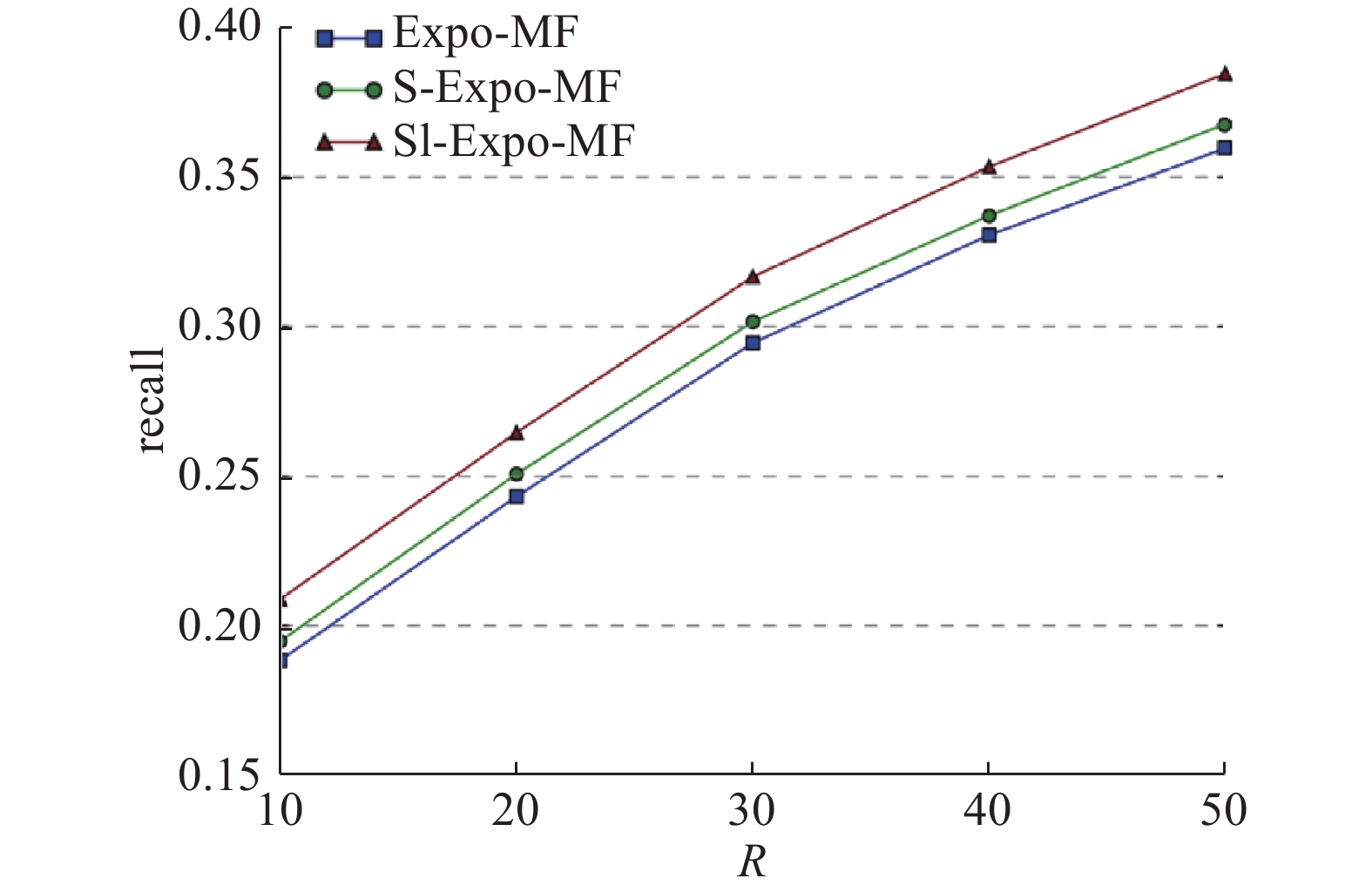
为了验证用户社交关系和影响力能够增强模型预测的效果,将完整模型(SI-Expo-MF)、去掉曝光度中用户影响力的模型(S-Expo-MF)、完全去掉用户社交关系(Expo-MF)的模型进行召回率比较,结果如图7所示. 图中,R表示预测结果召回排前多少位. 可以发现,Expo-MF效果最差,S-Expo-MF效果略有提升,SI-Expo-MF模型的效果最好,并且相对于S-Expo-MF来说提升的效果更加明显. 说明在曝光度和矩阵分解中加入社交信息,能够显著提升模型的推荐效果.
|
图 7 用户社交关系和用户影响力对模型的影响 Fig. 7 Impact of social information and user influence |
依据用户的关注好友数量,将用户划分为0~5个好友,6~15个好友和16个好友以上3部分,计算每部分用户的召回率. 在S-Expo-MF和SI-Expo-MF模型中开展实验,设定推荐个数为50,结果如图8所示. 一方面,2个模型中随着用户好友数目的增加,用户预测召回率明显提升,并且随着好友数的增加,召回率提升的比例越高,说明好友越多,该用户预测效果越好. 另一方面,对比S-Expo-MF和SI-Expo-MF结果发现,在相同的好友规模情况下,SI-Expo-MF的效果都更好;随着好友数量的增加,SI-Expo-MF相对于S-Expo-MF的提升更加明显,说明曝光度的用户影响力因素对模型的影响较大.

|
图 8 不同好友数量用户的召回率 Fig. 8 Recall@50 of users with different number of friends |
将提出的模型与其他优秀的隐式反馈推荐模型进行召回率、平均准确率和归一化折损累计增益3个评价指标的对比.
WMF[14]:加权矩阵分解模型,作为隐式反馈数据推荐的标准模型,WMF假设所有未观测到的用户-物品值比观测到的值具有更低的置信度,在概率矩阵分解的基础上,将置信度作为真实值和预测值残差的权重.
eALS[15]:不同于WMF对所有未观测到的“0”值数据赋予相同的权重,eALS利用物品的流行度对缺失值赋予不同的置信度. 通过在WMF损失函数的基础上加上一个未观测到的用户-物品对预测值的惩罚项,更好地利用未观测数据.
BPR-MF[11]:贝叶斯个性化排名矩阵分解模型,强调不同物品对用户的影响力. BPR-MF假设用户之间偏好以及同一用户对不同物品的偏序都彼此独立,将观测值处理成(用户,物品i,物品j)的三元组集合表示用户相对j更喜欢i,通过随机梯度下降法优化贝叶斯后验目标函数来学习用户和物品的潜在因子向量.
Expo-MF[16]:物品曝光度矩阵分解模型,在WMF的基础上引入物品曝光度的概念,将符合伯努利分布的物品曝光度作为观测值的条件,通过最大化观测值和物品曝光度的联合概率来学习出用户和物品的潜在因子向量.
首先利用网格搜索,对WMF模型、eALS模型、BPR-MF模型、Expo-MF模型和本文的SI-Expo-MF模型的参数进行调优;然后对各个模型的性能进行对比,结果如表3所示. 在WMF模型中,K=10,λ=0.01,α=1;在eALS模型中,K=10,λ=0.01,c0=64,α=0.5;在BPR-MF模型中,K=30,用户特征正则项λu=0.002 5,物品特征正向更新正则项λv+=0.002 5,物品特征负向更新正则项λv−=0.000 25;在Expo-MF模型中,K=30,λθ=λβ=0.1,λy=1,μini=0.01;在SI-Expo-MF模型中,K=30,λθ=λβ=0.1,λy=1,μini=0.01.
| 表 3 不同模型在Lastfm数据集上的表现对比 Table 3 Performance comparison of different models in Lastfm |
在recall、NDCG和MAP 3个评价指标上,WMF的效果最差,引入物品曝光度的Expo-MF比WMF和BPR-MF稍好. 由于eALS和Expo-MF都是仅从不同的角度和方式利用了物品的流行度,两者效果差不多;引入社交信息的SI-Expo-MF模型具有最好的预测结果. 具体来说,SI-Expo-MF在recall@20上相比WMF、BPR-MF、Expo-MF和eALS的提升分别为10.16%、7.74%、4.50%和3.44%;在recall@50上相比WMF、BPR-MF、Expo-MF和eALS的提升分别为6.12%、5.20%、4.06%和3.36%;在NDCG@100上相比WMF、BPR-MF、Expo-MF和eALS的提升分别为10.81%、7.25%、4.22%和3.57%;在MAP@100上相比WMF、BPR-MF、Expo-MF和eALS的提升分别为11.50%、10.56%、6.32%和4.77%.
综合以上实验结果发现,SI-Expo-MF模型具有最好的推荐性能. 利用用户的社交矩阵来约束用户潜在因子向量,加入了额外的辅助信息;利用社交关系、用户影响力及物品流行度来提高物品曝光度预测,从而更好地区分稀疏用户-物品观测值矩阵中的噪音数据,提高整体的预测效果.
4 结 语针对隐式反馈数据推荐中存在的数据稀疏性问题和未观测值的二义性问题,提出基于用户社交网络和物品曝光度的概率矩阵分解模型,利用社交信息同时对潜在因子和曝光度进行建模. 在Lastfm数据集上开展一系列实验,分析社交信息和用户影响力对模型的影响;将本文模型与WMF、eALS、BPR-MF、Expo-MF模型在recall、MAP和NDCG多个指标下的预测效果进行对比,验证了本文模型具有更加优秀的预测效果.
未来的工作展望可以从如下几个方面入手:对于具有明显区分特征的用户-物品数据集,可以利用谱聚类,将用户-物品矩阵分解成多个具有相似上、下文场景的用户-物品子矩阵,分别进行协同过滤;对物品的文本内容进行主题建模,提取物品特征,改进物品潜在特征因子;利用文本特征或地理特征,结合用户社交信息对物品的曝光度进行建模,更好地解决隐式反馈数据未观测值的二义性问题;通过更复杂、有效的影响力模型或信息传播模型来刻画用户之间的物品曝光度影响.
| [1] |
PAZZANI M J, BILLSUS D. Content-based recommendation systems [M]//The adaptive web. Berlin: Springer, 2007: 325–341.
|
| [2] |
李伟霖, 王成良, 文俊浩. 基于评论与评分的协同过滤算法[J]. 计算机应用研究, 2017, 34(2): 361-364. LI Wei-lin, WANG Cheng-liang, WEN Jun-hao. Reliability analysis of manipulator based on fourth-moment estimation[J]. Application Research of Computers, 2017, 34(2): 361-364. DOI:10.3969/j.issn.1001-3695.2017.02.009 |
| [3] |
DESROSIERS C, KARYPIS G. A comprehensive survey of neighborhood-based recommendation methods [M]//Recommender systems handbook. Boston: Springer, 2011: 107–144.
|
| [4] |
李博, 陈志刚, 黄瑞, 等. 基于LDA模型的音乐推荐算法[J]. 计算机工程, 2016, 42(6): 175-179. LI Bo, CHEN Zhi-gang, HUANG Rui, et al. Music recommendation algorithm based on LDA model[J]. Computer Engineering, 2016, 42(6): 175-179. DOI:10.3969/j.issn.1000-3428.2016.06.031 |
| [5] |
CHEN C, ZHENG X, WANG Y, et al. Context-aware collaborative topic regression with social matrix factorization for recommender systems [C] // 28th AAAI Conference on Artificial Intelligence. Québec: AAAI, 2014, 14: 9–15. https://www.researchgate.net/publication/302907972_Context-ware_Collaborative_Topic_Regression_with_Social_Matrix_Factorization_for_Recommender_Systems
|
| [6] |
PATEREK A. Improving regularized singular value decomposition for collaborative filtering [C] // Proceedings of KDD Cup and Workshop. San Jose: ACM, 2007: 5–8.
|
| [7] |
KOREN Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model [C] // Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Las Vegas: ACM, 2008: 426–434. https://www.researchgate.net/publication/221654609_Factorization_meets_the_neighborhood_A_multifaceted_collaborative_filtering_model
|
| [8] |
KOREN Y. Collaborative filtering with temporal dynamics[J]. Communications of the ACM, 2010, 53(4): 89-97. DOI:10.1145/1721654 |
| [9] |
MNIH A, SALAKHUTDINOV R R. Probabilistic matrix factorization [C] // Advances in Neural Information Processing Systems. Vancouver: ACM, 2007: 1257–1264.
|
| [10] |
LIANG D, ALTOSAAR J, CHARLIN L, et al. Factorization meets the item embedding: regularizing matrix factorization with item co-occurrence [C] // Proceedings of the 10th ACM Conference on Recommender Systems. Boston: ACM, 2016: 59–66. https://www.researchgate.net/publication/307573310_Factorization_Meets_the_Item_Embedding_Regularizing_Matrix_Factorization_with_Item_Co-occurrence?ev=auth_pub
|
| [11] |
RENDLE S, FREUDENTHALER C, GANTNER Z, et al. BPR: Bayesian personalized ranking from implicit feedback [C] // Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence. Montreal: UAI Press, 2009: 452–461. https://www.researchgate.net/publication/224943864_BPR_Bayesian_Personalized_Ranking_from_Implicit_Feedback?ev=auth_pub
|
| [12] |
YU L, ZHOU G, ZHANG C, et al. Rankmbpr: rank-aware mutual Bayesian personalized ranking for item recommendation [C] // International Conference on Web-Age Information Management. Nanchang: WAIM, 2016: 244–256. https://www.researchgate.net/publication/303601210_RankMBPR_Rank-Aware_Mutual_Bayesian_Personalized_Ranking_for_Item_Recommendation
|
| [13] |
ZHANG H, GANCHEV I, NIKOLOV N S, et al. Weighted matrix factorization with Bayesian personalized ranking [C] // SAI Computing Conference. London: SAI, 2017.
|
| [14] |
HU Y, KOREN Y, VOLINSKY C. Collaborative filtering for implicit feedback datasets [C] // 8th IEEE International Conference on Data Mining. Taipei: IEEE, 2008: 263–272. https://www.researchgate.net/publication/220765111_Collaborative_Filtering_for_Implicit_Feedback_Datasets
|
| [15] |
HE X, ZHANG H, KAN M Y, et al. Fast matrix factorization for online recommendation with implicit feedback [C] // Proceedings of the 39th International ACM SIGIR Conference on Research and Development in Information Retrieval. Pisa: ACM, 2016: 549–558. http://xueshu.baidu.com/usercenter/paper/show?paperid=f9e67dc8ad8adab8166c3362203cc956&site=xueshu_se&hitarticle=1
|
| [16] |
LIANG D, CHARLIN L, MCINERNEY J, et al. Modeling user exposure in recommendation [C] // Proceedings of the 25th International Conference on World Wide Web. Montréal: International World Wide Web Conferences Steering Committee, 2016: 951–961. https://www.researchgate.net/publication/312635232_Modeling_User_Exposure_in_Recommendation
|
| [17] |
LIN X, ZHANG M, ZHENG Y F, et al. Learning and transferring social and item visibilities for personalized recommendation [C] // Proceedings of the 2017 ACM on Conference on Information and Knowledge Management. Singapore: ACM, 2017: 337–346. https://www.researchgate.net/publication/320882164_Learning_and_Transferring_Social_and_Item_Visibilities_for_Personalized_Recommendation
|
| [18] |
PURUSHOTHAM S, LIU Y, KUO C C J. Collaborative topic regression with social matrix factorization for recommendation systems [C] // International Conference on International Conference on Machine Learning. Edinburgh: Omni Press, 2012. https://www.researchgate.net/publication/227716505_Collaborative_Topic_Regression_with_Social_Matrix_Factorization_forRecommendation_Systems
|
| [19] |
JAMALI M, ESTER M. A matrix factorization technique with trust propagation for recommendation in social networks [C] // Proceedings of the 4th ACM Conference on Recommender Systems. Barcelona: ACM, 2010: 135–142. https://www.researchgate.net/publication/221141035_A_matrix_factorization_technique_with_trust_propagation_for_recommendation_in_social_networks
|
| [20] |
MA H, ZHOU T C, LYU M R, et al. Improving recommender systems by incorporating social contextual information[J]. ACM Transactions on Information Systems (TOIS), 2011, 29(2): 1-23. |
| [21] |
HU G N, DAI X Y, QIU F Y, et al. Collaborative filtering with topic and social latent factors incorporating implicit feedback[J]. ACM Transactions on Knowledge Discovery from Data (TKDD), 2018, 12(2): 23. |
| [22] |
GUO G, ZHANG J, ZHU F, et al. Factored similarity models with social trust for top-N item recommendation[J]. Knowledge-Based Systems, 2017, 122: 17-25. DOI:10.1016/j.knosys.2017.01.027 |
| [23] |
柳玲, 马艺, 文俊浩, 等. 基于用户影响力游走模型的社会化推荐算法[J]. 计算机工程与应用, 2017(10): 61-67. LIU Ling, MA Yi, WEN Jun-hao, et al. Social recommendation algorithm based on user influence walk model[J]. Computer Engineering and Applications, 2017(10): 61-67. DOI:10.3778/j.issn.1002-8331.1512-0289 |
| [24] |
CHANEY A J B, BLEI D M, ELIASSI-RAD T. A probabilistic model for using social networks in personalized item recommendation [C] // Proceedings of the 9th ACM Conference on Recommender Systems. Vienna: ACM, 2015: 43–50. https://www.researchgate.net/publication/301432440_A_Probabilistic_Model_for_Using_Social_Networks_in_Personalized_Item_Recommendation
|
| [25] |
GOPALAN P, HOFMAN J M, BLEI D M. Scalable recommendation with hierarchical poisson factorization [C] // Proceedings of the 31st Conference on Uncertainty in Artificial Intelligence. Amsterdam: UAI, 2015: 326–335.
|
| [26] |
DUHAN N, SHARMA A K, BHATIA K K. Page ranking algorithms: a survey [C] // IEEE International Conference on Advance Computing. Patiala: IEEE, 2009: 1530–1537. https://www.researchgate.net/publication/224398728_Page_Ranking_Algorithms_A_Survey
|
| [27] |
Lastfm data set [EB/OL]. [2018-03-22]. https://grouplens.org/datasets/hetrec-2011/.
|



