肝脏是人体的重要器官之一，肝脏疾病一直是医学难题. 在多数情况下，手术是治疗肝脏疾病的唯一途径. 计算机辅助手术（computer assisted surgery, CAS）^[1]提供了术前模拟、术中支持和术后评估等功能，使得计算机辅助肝手术（例如肝肿瘤切除^[2]、活体肝移植^[3]和微创手术^[4-5]等）在临床治疗中发挥越来越重要的作用. 准确地从腹部CT 图像中分割出肝脏区域是保证手术可靠性的重要前提. 然而，腹部CT图像对比度低，肝脏的灰度值与毗邻的组织器官相近，导致肝脏的边缘模糊，并且肝脏的形状复杂多变，使得从CT图像中完成准确的肝脏分割变成一项具有挑战性的任务. 目前，手动描出肝脏边缘仍是医疗机构广泛采用的方法，但是这项工作十分枯燥、耗时. 据统计，手动完成一个肝脏序列分割平均需要30 min以上^[6]，并且，分割结果具有主观性. 因此，为了快速准确地分割肝脏，研究学者们尝试结合图像处理理论与其他技术，提出了不同的肝脏分割方法. 根据是否需要用户交互辅助完成肝脏分割，可以将这些方法统分为自动和半自动分割.

对于肝脏的自动分割，基于统计形状模型（statistic shape model, SSM）的方法被证明可以得到较准确的结果^[7]. 在医学图像计算和计算机辅助干预“medical image computing and computer assisted intervention （MICCAI） 2007 grand challenge”的肝脏分割竞赛中，自动分割方法的前三名都是基于SSM^[8-11]. 其中，Kainmüller等^[9]通过训练112个肝脏模型构建了一个含有7 000个标记点的SSM用于分割肝脏，最后通过形变网格优化结果. Heimann等^[10]通过训练35个肝脏模型构建了一个含有2 500个标记点的SSM模型，通过基于此SSM模型提供的内力和图像数据提供的外力来驱使形变网格进行肝脏分割. Saddi等^[11]使用符号距离函数表示训练样本，构建SSM，将算法嵌入到变分框架中完成肝脏分割. 然而，由于肝脏形状复杂多变，SSM往往不能准确地适应新图像中形状更精细的局部细节^[12]，导致分割精度降低. 近年来，基于对SSM的优化，Zhang等^[13]提出了稀疏形状组合模型（sparse shape composition, SSC）用于腹部器官的分割. Wang等^[14]描述了一种稀疏先验统计形状模型用于肝脏自动分割. Shi等^[15]结合矩阵低秩与稀疏分解的形状先验模型和概率图谱将分割适用对象扩展至腹部病变器官，该方法在病变肝脏和病变肺组织上的分割验证表明了该方法的有效性和准确性. 此外，Wang等^[16]尝试先基于概率图谱对肝脏进行粗分割，后提出由一种由形状−灰度先验模型约束的水平集方法进行优化分割. Ding等^[17]提出了一种基于局部决策融合的多图谱肝脏快速自动分割方法. 越来越多的研究学者尝试结合图割方法^[18-21]、深度学习与神经网络^[22-24]等技术完成自动分割任务.

自动分割方法有时需要大量的训练样本，并且稳定性不高，分割误差较大. 半自动分割方法由于交互操作融入先验知识，稳定性更高，所得分割结果往往比自动分割更准确. 因此，只需简易、耗时少的交互操作就能带来准确分割结果的半自动分割方法具有竞争力，更符合现今临床实践需求^[8]. 半自动分割的交互操作根据交互时间的长短分为3级：少于1 min为低耗交互；少于5 min为中耗交互；高于5 min为高耗交互^[8].

对于半自动分割方法的研究，Beichel 等^[25]使用基于图割的方法进行肝脏分割，首先利用标记区分肝脏区域与背景，然后利用图割方法分割肝脏. Dawant 等^[26]构建了一个新颖的动态速度函数，通过交互操作在肝脏内部画出大致的初始化轮廓曲线，基于水平集进行演化得到最终的结果. Beck等 ^[27]提出了一种基于3D种子增长的分割方法，通过用户指定种子点进行增长分割，达到自定义的非线性耦合标准时停止算法，然后通过交互操作改善分割结果. Yang等^[28]采用了基于混合水平集的半自动分割算法. 首先，根据肝脏区域的大小，在肝脏区域内适当地选取种子点，结合选取的种子点的灰度信息，使用快速行进水平集方法^[29]来获取初始的肝脏区域，然后通过基于阈值的水平集方法^[30]演化初始的肝脏区域得到最终的分割结果. Yamaguchi等^[31]尝试对非增强CT序列进行肝脏半自动分割，先通过手动排除肝脏血管部分，划分肝脏候选区域，然后结合局部直方图之间的相互关系与概率图谱进行肝脏分割. Chartrand等^[32]先通过手动定义一簇轮廓线，接着对这些轮廓线进行变分插值得到肝脏的初始轮廓，然后采用拉普拉斯网格法对模型进行迭代变形得到肝脏分割结果，最后对结果进行手动矫正改善. Eapen等^[33]提出了一种半监督式的半自动肝脏分割技术，主要在贝叶斯水平集框架下，通过对病人数据集的连续性学习来调整分割参数进行肝脏分割. Zareei等^[34]采用一种监督式的半自动分割方法，首先通过交互调整阈值进行预处理，获得初始肝脏轮廓，然后采用遗传算法和改进的活动轮廓演化获得最终的结果. 上述的多数方法需要较多的交互操作，例如需要人工设定过多的标记点、种子点和需要人工后处理提高分割准确度等，并且分割准确度有待提高.

本文旨在融入更少交互操作的同时获得更加准确的分割结果，提出一种基于区域增长和统一化水平集的半自动肝脏图像分割方法. 该方法包括混合图像预处理、基于区域增长的肝脏的初步分割、基于统一化水平集的肝脏优化分割和形态学后处理.

1）传统区域增长中增长阈值的设定不当以及种子点位置的选择不适，都会影响分割结果. 为此，本文通过图像预处理得到CT二值图像，为种子提供良好的增长环境，解决增长阈值的设定以及种子点位置选择的困难. 在避免过分割的同时，只需少量种子点，即能够较完整地初步提取肝脏区域.

2）提出一种由图像边缘信息与区域信息共同驱动的统一化水平集，相比由单图像信息驱动的水平集，能够适应更大的气球力与更多的迭代次数，从而既能保证活动轮廓在足够大的气球力下或者足够多的迭代次数下演化至肝脏边缘，又不轻易发生边缘泄漏，得到更准确的结果.

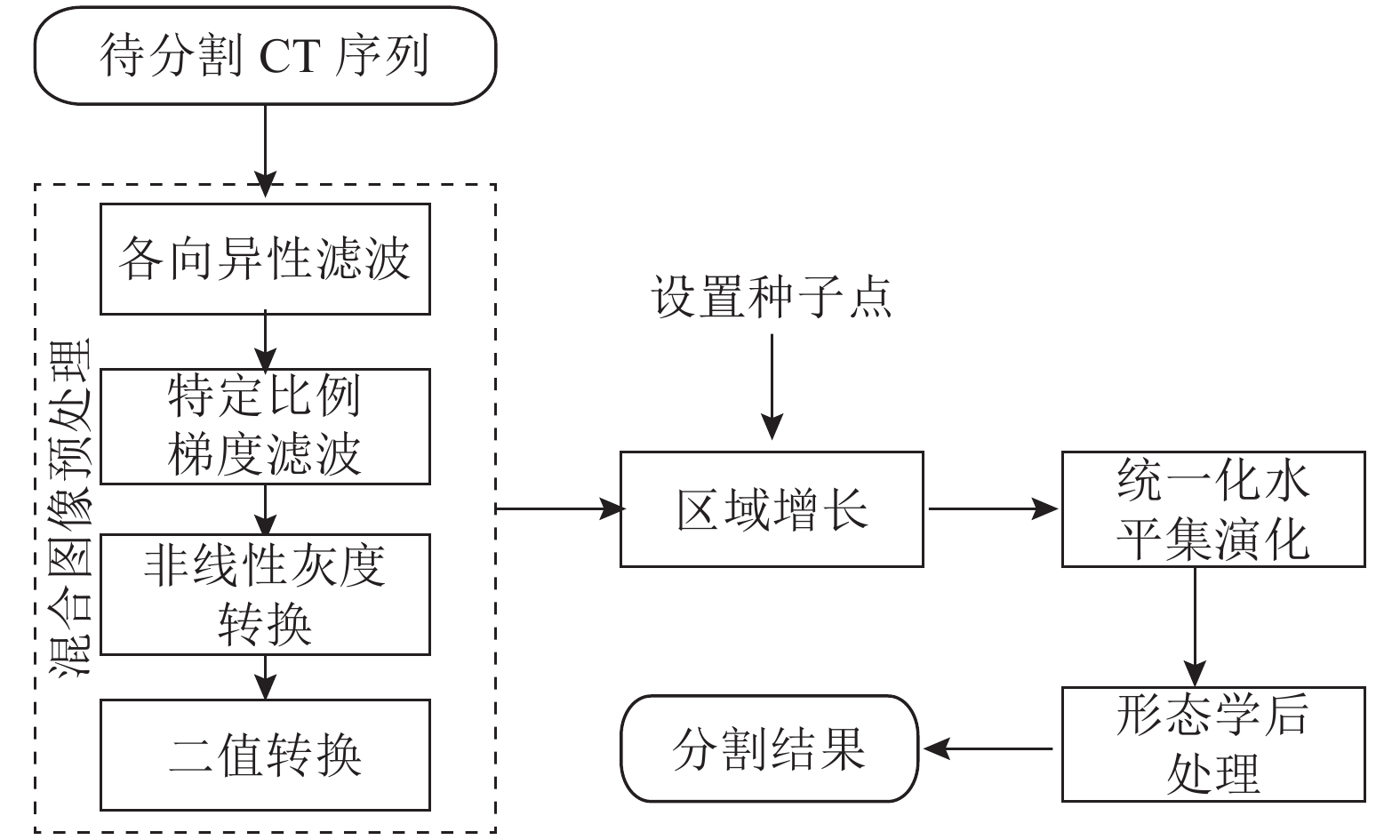
1 肝脏图像分割算法综述 1.1 算法流程

首先，对图像进行混合预处理得到CT序列的二值图像. 然后，设置种子点进行区域增长，得到肝脏的初步分割. 接着，利用肝脏的初步分割初始化统一水平集，通过统一化水平集演化得到优化分割结果. 最后，通过形态学后处理得到结果. 本文方法流程图如图1所示.

1.2 混合图像预处理

混合图像预处理的目的是将CT原图转化为二值图像，为种子提供良好的区域增长环境. 主要分为4个步骤，预处理结果如图2所示，其中图2（a）为原始CT图像.

1）为了减少噪声对肝脏分割的影响，采用各向异性滤波^[35]对图像进行滤波，如图2（b）所示. 该滤波器的优点在于去除噪声的同时能够保持良好的图像边缘，方程如下：

$\frac{{\partial I}}{{\partial {{t}}}} = {\rm{div}}\,\left( {c(\left| {\nabla I} \right|) \cdot \nabla I} \right).$

(1)

式中： ${\rm{div}}$ 为散度算子， $I$ 为输入图像， $c\left( \cdot \right)$ 为扩散系数.

2）特定比例梯度滤波^[36]. 通过各向异性滤波得到降噪之后的图像 ${f_{\rm{I}}}\left( {x,y} \right)$ . 将 ${f_{\rm{I}}}$ 进行高斯滤波，得到滤波后的图像 ${f_{\rm{E}}}\left( {x,y} \right)$ ：

${f_{\rm{G}}}\left( \gamma \right) = \frac{1}{\sqrt{{{{{2\text{π}}}}}}\gamma}\exp\; \left({ - \left( {{x^2} + {y^2}} \right)/2{\gamma ^2}}\right),$

(2)

${f_{\rm{E}}} = {f_{\rm{I}}} * {f_{\rm{G}}}.$

(3)

式中： $\gamma $ 为高斯滤波的标准偏差，控制边缘增强的程度，本文设置 $\gamma {\rm{ = }}0.5$ ^[37]. “ $ * $ ”为卷积运算. 计算 ${f_{\rm{E}}}\left( {x,y} \right)$ 每个像素点的梯度幅值，得到肝脏边缘增强图像 ${f_{\rm{M}}}\left( {x,y} \right)$ （见图2（c））：

${f_{\rm{M}}} = \left| {\nabla {f_{\rm{E}}}} \right| = \sqrt {{{\left( {\frac{{\partial {f_{\rm{E}}}}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial {f_{\rm{E}}}}}{{\partial y}}} \right)}^2}} .$

(4)

3）非线性灰度转换. 基于Sigmoid函数，对 ${f_{\rm{M}}}$ 进行灰度转化，得到转化后的图像 ${f_{\rm{s}}}$ （见图2（d））：

${f_{\rm{s}}} = \frac{1}{{1 + {{\exp }\;{\left( { - \left( {{f_{\rm{M}}} - \beta } \right)/\kappa } \right)}}}}.$

(5)

式中：参数 $\kappa $ 控制灰度加强的范围，参数β为灰度加强范围内的中心值. 本文设置 $\kappa {\rm{ = - }}1.5$ ，β=0.4^[37].

4）二值转换. 提出一种自定义二值转换规则，方程如下：

${f_{\rm{s}}} = \left\{ {{f_{\rm{s}}} \geqslant \left( {\max \left( {{f_{\rm{s}}}} \right) + \min \left( {{f_{\rm{s}}}} \right)} \right)/\theta } \right\}.$

(6)

式中： $\max \left( {{f_{\rm{s}}}} \right)$ 表示图中最大的灰度值， $\min \left( {{f_{\rm{s}}}} \right)$ 表示图中最小的灰度值， $\theta > 1$ 为控制转化的阈值. 该规则将图像灰度从阈值处划开，大于等于该阈值的灰度值转化为1，小于该阈值的灰度值转化为0，图像转换成二值图像.

二值转换规则的作用有以下3个方面：

1）在上文步骤2）“特定比例梯度滤波”中增强边缘的同时增强了噪声，二值转换使得高于阈值的噪声灰度变为1，在一定程度上减轻噪声加强. 如图2（e）~（h）所示，分别为取 $\theta = 1.1$ 、1.2、1.7和2.5得到的二值图像，可以看出，随着θ值的增加，噪声的过滤效果逐渐加强. 但是 $\theta $ 值不能无限增大，如图2（h）圆圈处所示，部分肝脏边缘已经被消除，会导致区域增长过分割. 由于不同的腹部序列存在着不同的灰度值与噪声情况，在实验中需要取不同的 $\theta $ 值来获取合适的二值转化阈值. 本文设置 $\theta$ =1.1~1.5.

2）为后续的区域增长提供良好的增长环境. 相对于传统的区域增长，本文的区域增长阈值设置简单（0或1），并且种子点的初始位置可以在灰度值为1的区间内任意选择，同时避免了过分割.

3）二值转换后，肝脏区域基本连通，灰度值基本为1，只需设置少量种子点，即可完成区域增长，得到大致完整的肝脏区域.

1.3 基于区域增长的肝脏初步分割

如图2（g）所示，经过预处理得到的二值图像肝脏区域基本连通，只需要1个种子点即可完成初步分割. 然而，有些情况需要设置多个种子点：1）CT中的肝脏非连续，呈离散状态；2）肝脏内有明显的血管；3）肝脏内有明显的病变区域，如肿瘤.

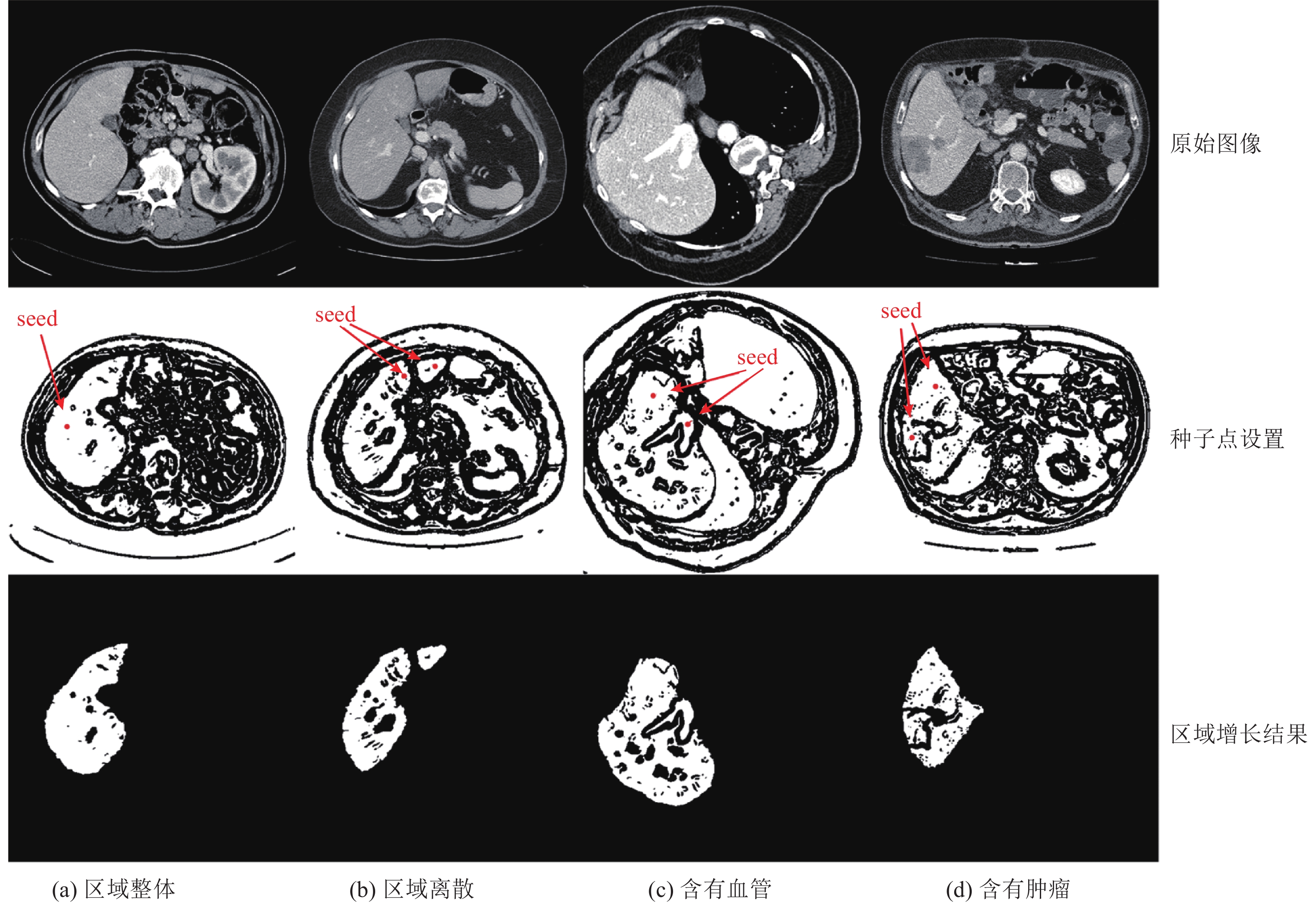
如图3所示为种子点设置的4种基本情况，从上到下依次为原始图像，二值图像中的种子点设置（图中箭头所指圆点为种子点）和区域增长结果. 图3（a）：非离散的均匀肝脏区域，二值图像的肝脏区域整体联通，设置1个种子点；图3（b）：离散为两部分的均匀肝脏，二值图像的肝脏区域两部分分别连通，设置2个种子点；图3（c）：肝脏内部有明显血管，二值图像的肝脏区域与血管不连通，设置2个种子点；图3（d）肝脏内部有明显肿瘤，二值图像的肿瘤区域与健康区域不连通，需要设置种子点. 另外，复杂情况为以上基本情况混合出现，此时需要相应增设种子点. 由区域增长得到的肝脏初始轮廓将用于初始化本文的统一化水平集，通过水平集演化，优化分割结果.

1.4 基于统一化水平集的肝脏优化分割 1.4.1 统一化水平集

水平集方法于1988年由Osher和Sethian首次提出^[38]，其主要思想是将可变形的曲线作为零水平集嵌入到更高一维的函数中，该函数称为水平集函数. 水平集方法被广泛地应用于医学图像处理，包括肝脏分割^{[16, 26, 28, 36-37, 39]}. 目前多数用于肝脏分割的水平集都是基于边缘的方法，通过结合边缘信息的气球力驱动水平集演化.

由于肝脏内部普遍存在血管和肿瘤等非肝脏均匀组织，如果气球力过小或者迭代次数过少，水平集演化会在灰度变化明显处（如血管边缘和肿瘤边缘）停止，或者无法演化至期望的肝脏边界上，导致分割不准确. 因此，用于肝脏分割的水平集往往设置较大的气球力或较多的迭代次数. 一方面，如果气球力过大或者迭代次数过多，很容易发生边缘泄漏. 因此，选择合适的气球力和迭代次数是相对困难的. 另一方面，基于区域信息的水平集通过结合曲线内外灰度信息的气球力进行驱动，在弱边缘或者无边缘处相对于基于边缘信息的水平集有更好的表现，并且对噪声更加稳定^[40]. 因此，本文结合两者的气球力，构造一个兼具两者优点的统一化水平集，并证明能够适应更大的气球力与迭代次数（证明见2.3节），从而既能保证活动轮廓在足够大的气球力下或者足够多的迭代次数下演化至肝脏边缘，又能保证不轻易发生边缘泄漏，得到更准确的结果.

本文采用的水平集框架是由Li等^[41]提出的距离正则化水平集（distance regularized level set evolution, DRLSE）.

给定一个水平集方程 $\varphi $ ：图像域 $\varOmega \to R$ ，定义一个能量函数：

$\varepsilon \left( \varphi \right){\rm{ = }}\mu D\left( \varphi \right) + {\varepsilon _{{\rm{ext}}}}\left( \varphi \right).$

(7)

式中： $\mu > 0$ ； $D\left( \varphi \right)$ 是正则惩罚项，避免了水平集的重新初始化，提高算法效率，定义如下，

$D\left( \varphi \right) = \int_\Omega {p\left( {\left| {\nabla \varphi } \right|} \right)} {\rm{d}}x.$

(8)

$p\left( {\left| {\nabla \varphi } \right|} \right) = \left\{ \begin{aligned}& \frac{1}{{{{\left( {2\pi } \right)}^2}}}\left( {1 - \cos \left( {2\pi \left| {\nabla \varphi } \right|} \right)} \right), &\nabla \varphi \leqslant 1; \\& \frac{1}{2}{\left( {\left| {\nabla \varphi } \right| - 1} \right)^2}, &\nabla \varphi > 1. \\ \end{aligned} \right.$

(9)

其中， $p\left( {\left| {\nabla \varphi } \right|} \right)$ 为一个双势阱函数，主要作用是允许二值阶跃函数可以直接作为水平集的初始化；函数 ${\varepsilon _{{\rm{ext}}}}\left( \varphi \right)$ 是外部力，可以根据图像的边缘信息或者区域信息来定义，驱动水平集的演化.

文献[41]通过将图像的边缘信息加入 ${\varepsilon _{{\rm{ext}}}}\left( \varphi \right)$ ，构建了基于边缘的DRLSE水平集. 令 $I$ 为图像，定义边缘指示函数：

$g = \frac{1}{{1 + {{\left| {\nabla {G_\sigma } * I} \right|}^2}}}.$

(10)

式中： ${G_\sigma }$ 为方差为 $\sigma $ 的高斯核函数. 在灰度变化较大的区域， $g$ 取值较小；在灰度变化较小的区域， $g$ 较大，且最大值为1.

定义 ${\varepsilon _{{\rm{ext}}}}\left( \varphi \right)$ 为

$\begin{split} {\varepsilon _{{\rm{ext}}}}\left( \varphi \right) = & \lambda L\left( \varphi \right) + \alpha A\left( \varphi \right) = \\ & \lambda \int_\varOmega {g\delta \left( \varphi \right)} \left| {\nabla \varphi } \right|{\rm{d}}x + \alpha \int_\varOmega {gH\left( { - \varphi } \right)} {\rm{d}}x .\\ \end{split} $

(11)

式中： $\lambda $ 和 $\alpha $ 为常数系数； $\delta $ 为Dirac函数； $H$ 为Heaviside函数； $L\left( \varphi \right)$ 为曲线的加权长度； $A\left( \varphi \right)$ 为气球力，控制曲线的演化.

Zhang等^[40]重构了一个新的基于区域信息的气球力（signed pressure force, SPF）.本文将该气球力结合到基于边缘的DRLSE中， ${\alpha _{\rm{SPF}}}\left( {I\left( x \right)} \right)$ 定义如下：

${\alpha_{\rm{SPF}}}\left( {I\left( x \right)} \right) = \frac{{I\left( x \right) - \left({{{c_1} + {c_2}}}\right)/{2}}}{{\max\, \left( {\left| {I\left( x \right) - \left({{{c_1} + {c_2}}}\right)/{2}} \right|} \right)}}.$

(12)

式中： ${c_1}$ 和 ${c_2}$ 分别为曲线内、外的平均灰度常值，可以通过求解C-V模型^[42]得到. C-V模型定义如下：

$\begin{split} E = & {\lambda _1}{\int_{{\rm{inside}}\left( c \right)} {\left| {I\left( x \right) - {c_1}} \right|} ^2}{\rm{d}}x\;+ \\ & {\lambda _2}{\int_{{\rm{outside}}\left( c \right)} {\left| {I\left( x \right) - {c_2}} \right|} ^2}{\rm{d}}x,\;x \in \varOmega \end{split} .$

(13)

其中，inside(c)表示曲线内部的区域，outside(c)表示曲线外部的区域.

假设

$\left. \begin{array}{l}c = \left\{ {x \in \varOmega :\varphi \left( x \right) = 0} \right\},\\{\rm{inside}}\left( c \right) = \left\{ {x \in \varOmega :\varphi \left( x \right) > 0} \right\},\\{\rm{outside}}\left( c \right) = \left\{ {x \in \varOmega :\varphi \left( x \right) < 0} \right\}.\end{array} \right\}$

(14)

通过对式（13）最小化求解，可解得

${c_1}\left( \varphi \right) = \frac{{\int_\varOmega {I\left( x \right) \cdot H\left( \varphi \right){\rm{d}}x} }}{{\int_\varOmega {H\left( \varphi \right){\rm{d}}x} }},\quad\quad$

(15)

${c_2}\left( \varphi \right) = \frac{{\int_\varOmega {I\left( x \right) \cdot \left( {1 - H\left( \varphi \right)} \right){\rm{d}}x} }}{{\int_\varOmega {\left( {1 - H\left( \varphi \right)} \right){\rm{d}}x} }}.$

(16)

将式（15）和（16）代入式（12）求得 ${\alpha_{\rm{SPF}}}\left( {I\left( x \right)} \right)$ ，将其结合到式（11）的气球力中，得到新的外部能量泛函方程：

$\begin{split} {\varepsilon _{{\rm{uni}}}}\left( \varphi \right) = & \lambda \int_\varOmega {g\delta \left( \varphi \right)} \left| {\nabla \varphi } \right|{\rm{d}}x + \\ & {\rm{ }}\alpha \int_\varOmega {g \cdot {\alpha_{\rm{SPF}}}\left( {I\left( x \right)} \right)H\left( { - \varphi } \right)} {\rm{d}}x \end{split} .$

(17)

因此，本研究的统一化水平集能量泛函可以写为

$\varepsilon \left( \varphi \right){\rm{ = }}\mu D\left( \varphi \right) + {\varepsilon _{{\rm{uni}}}}\left( \varphi \right).$

(18)

1.4.2 统一化水平集演化

令 ${I_0}$ 为区域增长得到的肝脏初始轮廓二值图像. 由于DRLSE框架中存在双势阱函数 $p\left( {\left| {\nabla \varphi } \right|} \right)$ ，允许直接使用二值阶跃函数初始化水平集函数 ${G_0}$ ，简化了使用符号距离函数（signed distance function, SDF）初始化的步骤. 本研究采用的初始化方程如下：

${G_0} = \omega \cdot \left( {{I_0} - \frac{1}{2}} \right).$

(19)

式中： $\omega $ 为变量参数，控制SDF的宽度. 由于图像域为离散网格化，符号距离函数在零水平集轮廓两侧至少有1个网格点，宽度至少为2^[41]，建议取 $\omega \geqslant 2$ . 本文设置 $\omega = 4$ .

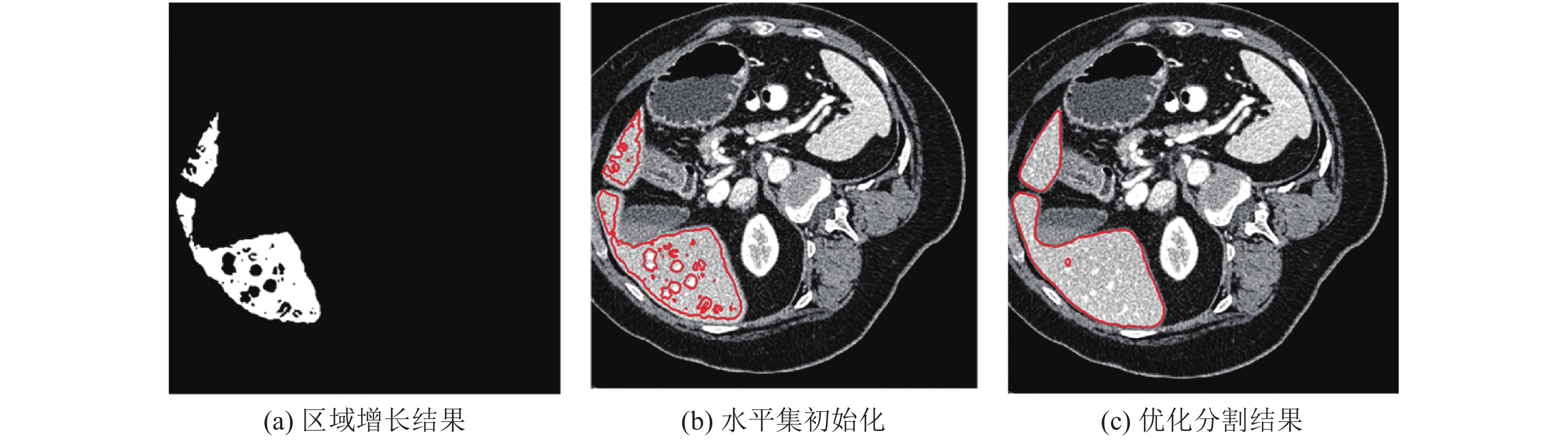
将初始化之后的水平集进行演化，得到优化分割结果，如图4所示. 本文中统一化水平集的相关参数如下设置：根据文献[42]中提出的 ${\lambda _1} = {\lambda _2} = 1$ 适用于绝大多数的图像分割，本文式（13）中同样设置 ${\lambda _1} = {\lambda _2} = 1$ ；由于DRLSE模型对 $\lambda $ 和 $\mu $ 的取值不敏感，根据文献[41]中的设置，本文式（17）中设置 $\lambda = 5$ ，式（18）中设置 $\mu = 0.04$ ，设置步长 $\Delta t = 1$ . 至于式（17）中的 $\alpha $ 与最大迭代次数 $t$ 的设置，进行大量尝试性地取值应用分割后，确定 $\alpha $ 的候选值为5、10、15，最大迭代次数 $t$ 的候选值为50、100、150，两两组合后得到9种组合. 为了寻找最优的组合，在40个数据集中随机选择10个数据集进行分割测试. 控制水平集初始化相同，水平集到达最大迭代次数后停止，将分割结果与金标准对比，误差评价标准采用相对体积误差σ_rv（数据集与误差评价标准具体见2.1与2.2节）. σ_rv绝对值越小则表明组合越优，具体结果如表1所示. 可以看出，当组合为（ $\alpha = 5$ ， $t = 150$ ）时误差最小；当组合为（ $\alpha = 10$ ， $t = 100$ ）时次之，两者结果仅相差0.2%，但是前者的迭代次数是后者的1.5倍. 综合考虑准确性与效率性，本文设置 $\alpha {\rm{ = }}10$ ， $t$ =100，用于肝脏图像的分割.

为了进一步提高分割的准确性，对于存在明显的弱边缘或者无边缘的肝脏区域分割，本文采用交互操作强制终止水平集演化.

1.5 形态学后处理

由于肝脏内部噪声的影响，水平集演化后得到的肝脏分割结果内部可能会存在孔洞，导致体素偏小，影响分割结果，本文采用形态学孔洞填充解决该问题.

2 实验结果与分析 2.1 实验数据集与实验平台

实验数据集：包含2个数据库，总共40个腹部序列，分别来自SLIVER07提供的20个腹部CT和3Dircadb提供的20个腹部CT. SLIVER07数据集的像素大小为0.57~0.81 mm，数目为512 $ \times $ 512，层间距为0.7~5.0 mm. 3Dircadb数据集的像素大小为0.56~0.81 mm，数目为512 $ \times $ 512，层间距为1.0~4.0 mm. 实验所用系统为Window 10，inter（R）core 3.10 GHz. 软件平台为Matlab^® 2016（美国Mathwork公司）.

2.2 误差评价指标

本文采用来自文献[8]中的5个评价指标进行结果误差分析，分别为体积重叠误差σ_vo、相对体积误差σ_rv、平均对称表面距离误差σ_ad、均方根对称表面距离误差σ_rd和最大对称表面距离误差σ_md.

${\sigma _{{\rm{vo}}}} = 100\left( {1 - \left( {\left| {M \cap N} \right|/\left| {M \cup N} \right|} \right)} \right),$

(20)

${\sigma _{{\rm{rv}}}} = 100\left( {\left( {\left| M \right| - \left| N \right|} \right)/\left| N \right|} \right),$

(21)

$\begin{gathered} {\sigma _{{\rm{ad}}}}\left( {M,N} \right) = \frac{1}{{\left| {S\left( M \right)} \right| + \left| {S\left( N \right)} \right|}} \;\times \; \quad\quad\quad\quad\quad\quad\quad\;\, \\ \left({\displaystyle\sum\nolimits_{{S_{\!M}} \in S( M )}} {d( {{S_{\!M}},S( N ))}} +{\displaystyle\sum\nolimits_{{S_{\!N}} \in S(N)}} {d( {{S_{\!N}},S(M))}}\right) , \end{gathered} $

(22)

$\begin{gathered} {\sigma _{{\rm{rd}}}}\left( {M,N} \right) = \sqrt {{{\left( {\left| {S\left( M \right) + S\left( N \right)} \right|} \right)}^{{\rm{ - 1}}}}} \;\times \;\quad\quad\quad\quad\quad\quad\;\,\\ {\left\{{\displaystyle\sum\nolimits_{{S_{\!M}} \in S( M )}} {d^2( {{S_{\!M}},S( N ))}}\,+\,{\displaystyle\sum\nolimits_{{S_{\!N}} \in S(N)}} {d^2( {{S_{\!N}},S(M))}}\right\} }^{1/2},\end{gathered}$

(23)

$\begin{split} {\sigma _{{\rm{md}}}}\left( {M,N} \right) = \max &\left\{ {\mathop {\max }\limits_{{S_M} \in S\left( M \right)} d\left( {{S_M},S\left( N \right)} \right),} \right. \\ & {\rm{ }}{\kern 1pt} {\kern 1pt} \left. {\mathop {\max }\limits_{{S_N} \in S\left( N \right)} d\left( {{S_N},S\left( M \right)} \right)} \right\}.\end{split} $

(24)

式中：M为令本文方法分割得到的肝脏分割结果；N为金标准（手动分割结果）；S（M）为M的表面体素集，S_M表示S（M）上的任意一点；表面S（N）为N的表面体素集，S_N表示S（N）上的任意一点； $d\left( \cdot \right)$ 表示最小欧氏距离.

2.3 不同水平集方法的比较

将基于边缘信息与基于区域信息的气球力相结合，加入至DRLSE的外部能量泛函中，构造出一个统一化水平集. 同时，分别与单独基于边缘信息驱动的DRLSE与基于区域信息驱动的DRLSE相比较，证明本文的水平集能够适应更大的气球力与更多的迭代次数，3个水平集定义如下.

1）本文构建的统一化水平集能量泛函：

$\begin{split}{\varepsilon _{{\rm{uni}}}}\left( \varphi \right) = & \lambda \int_\varOmega {g\delta \left( \varphi \right)} \left| {\nabla \varphi } \right|{\rm{d}}x + \\ &\alpha \int_\varOmega {g \cdot {\alpha _{\rm{SPF}}}\left( {I\left( x \right)} \right)H\left( { - \varphi } \right)} {\rm{d}}x\end{split}.$

(25)

2）基于边缘的DRLSE能量泛函：

$\begin{split}{\varepsilon _{{\rm{edg}}}}\left( \varphi \right) = & \lambda \int_\varOmega {g\delta \left( \varphi \right)} \left| {\nabla \varphi } \right|{\rm{d}}x + \\ &\alpha \int_\varOmega {g \cdot H\left( { - \varphi } \right)} {\rm{d}}x.\end{split}$

(26)

3）基于区域的DRLSE的能量泛函：

$\begin{split}{\varepsilon _{{\rm{reg}}}}\left( \varphi \right) =& \lambda \int_\varOmega {g\delta \left( \varphi \right)} \left| {\nabla \varphi } \right|{\rm{d}}x + \\ &\alpha \int_\varOmega {\alpha_{{\rm{SPF}}}\left( {I\left( x \right)} \right)H\left( { - \varphi } \right)} {\rm{d}}x.\end{split}$

(27)

在数据集中随机挑选3张腹部CT（图A、图B和图C）作为实验材料，进行如下比较.

1）采用上文的步骤对图C进行水平集初始化，分别使用上述3个水平集进行演化分割. 为了突出比较结果，设置较大的气球力与较多的迭代次数，其中对edge-DRLSE和region-DRLSE，设置 $\alpha {\rm{ = }}20$ ，对于本文的unified-DRLSE，设置 $\alpha {\rm{ = }}30$ . 最大迭代次数 $t$ 都设置为150，步长 $\Delta t = 1$ .

如图5所示为演化结果. 可以看出，edge-DRLSE能够完成肝脏分割，但是在较大的气球力驱动下，随着迭代次数的增加，在100次迭代之后就已经明显地发生边缘泄漏. region-DRLSE在较大气球力驱动下，能够适应较多的迭代次数，但是易于发生全局分割，将毗邻组织也进行分割. 本文的unified-DRLSE能够完成肝脏分割，并更加适应大气球力与多迭代次数，即使在150次迭代后，边缘泄漏的程度仍相对较低.

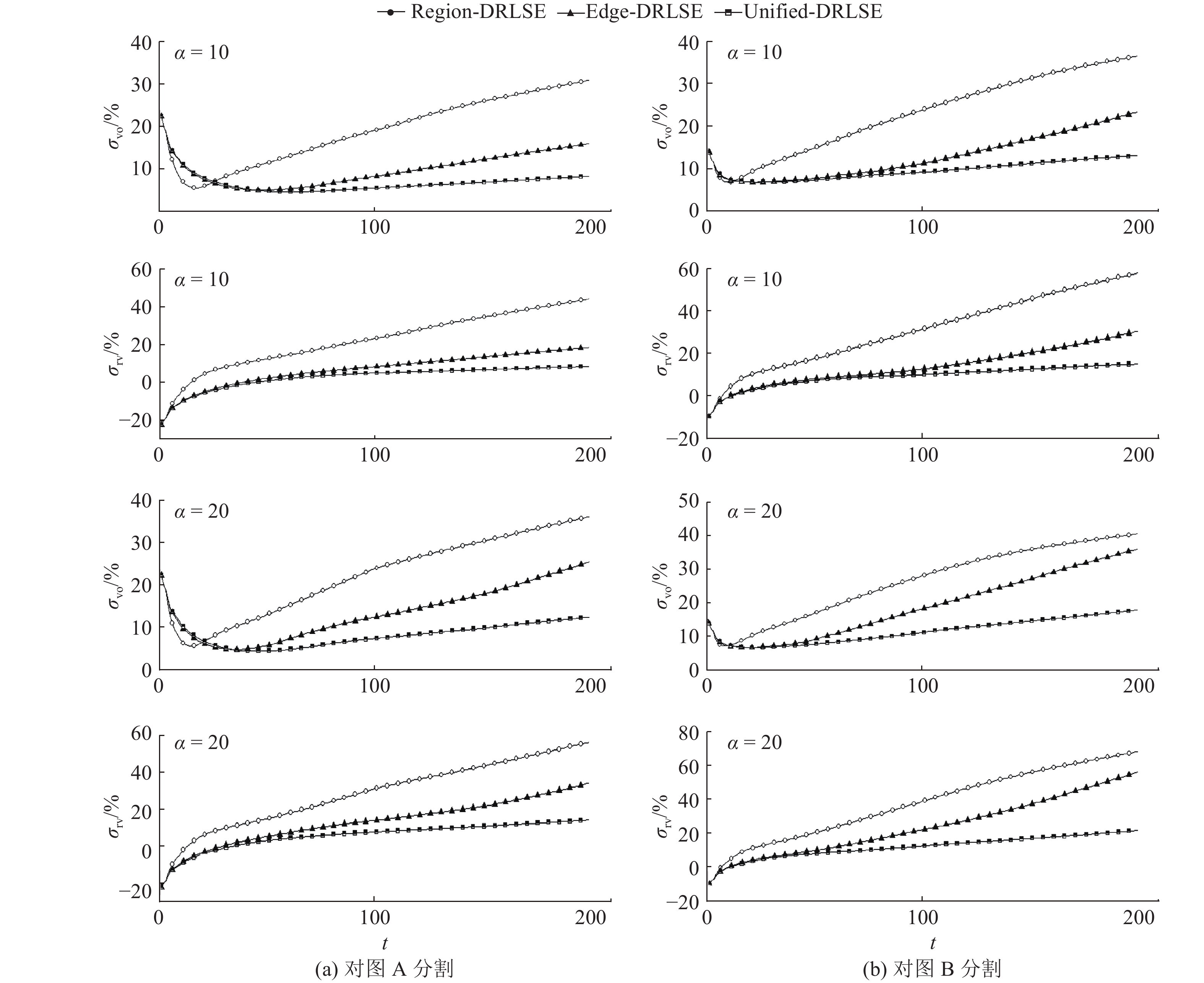
2）采用上文步骤对图A和图B进行水平集初始化，并令3个水平集进行演化分割. 为了突出比较结果，对3个水平集分别依次设置 $\alpha {\rm{ = }}10$ 和 $\alpha {\rm{ = }}20$ ，迭代最大次数 $t$ 设置为200，步长 $\Delta t = 1$ . 每次迭代演化结束后，将3个水平集的分割结果与金标准结果进行比较，误差评价标准采用σ_vo和σ_rv. 3个水平集的在图A和图B上的演化结果误差如图6所示. 其中σ_rv为负值表示分割结果的体素小于金标准体素. 可以看出，3条折线图中，随着迭代次数T的增多，unified-DRLSE的位置最低（取值最小，准确度最高），变化最为平缓，表明本文的统一化水平集适应大气球力、多迭代次数，同时能够带来更加准确的分割结果.

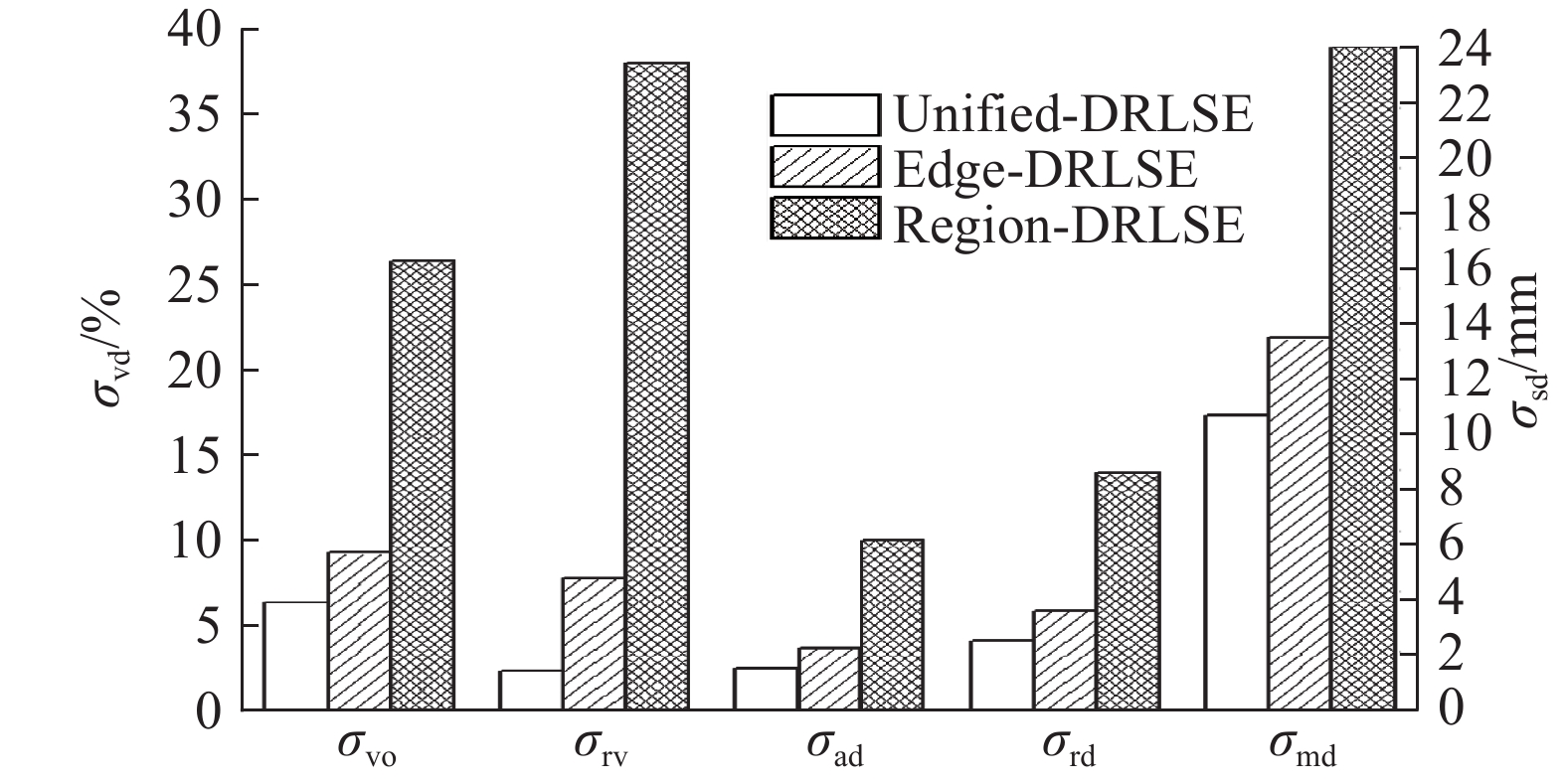
采用3种水平集方法对40个腹部序列进行分割. 为了突出比较结果，对每个水平集都设置 $\alpha {\rm{ = 15}}$ ，t=100， $\Delta t = 1$ . 采用上述步骤进行水平集初始化，水平集到达最大迭代次数后停止，将最终的分割结果与金标准进行比较，采用5个误差标准，分别得到体素误差σ_vd和距离误差σ_sd，平均结果如图7所示.其中，统一化水平集分割的结果误差指标为6.43%，2.40%，1.41，2.36和9.85 mm. edge-DRLSE的分割结果误差指标为9.35%，7.90%，2.13，3.36和12.38 mm. region-DRLSE分割的结果误差指标为26.46%，38.04%，5.70，7.92和22.01 mm. 可以看出，本文的统一化水平集的分割结果明显优于其他2个水平集得到的结果.

2.4 交互时间与算法运行时间分析 2.4.1 交互时间

本文方法的交互操作分为两部分：区域增长需要的种子点选择以及部分CT图中水平集演化的强制终止. 下面依次分析交互时间.

1）种子个数的主要影响因素为CT图中肿瘤、血管和肝脏离散区域的数量. 统计2个数据集每个序列平均单张CT所需的种子点个数N_av，如图8所示，N_al为整个数据集平均单张CT所需种子数. 其中，对于SLIVER07，每张CT的平均种子点个数为1.8±1.1；对于3Dircadb，每张CT的平均种子点个数为1.6±1.1. 在文献[26]中，水平集的初始化通过人工在肝脏内部画一条初始的活动轮廓完成，并且分割结果依赖于活动轮廓的初始化. 本文通过设置少量种子点进行区域增长，从而进行水平集初始化，交互时间与准确度都优于文献[26]. 在文献[27]中，区域增长容易发生过分割，需要进行人工改善分割结果，这种交互操作非常耗时. 本文区域增长不会发生过分割，也没有耗时的后处理操作. 在文献[28]的方法中，对于大肝脏区域，需要设置10~15个种子点；对于小肝脏区域，也需要设置至少2~6个种子点. 与文献[28]相比，本文的种子点个数明显减少，交互时间明显缩短. 在文献[32]中，需要对每张CT图人工定义3~10条初始肝脏轮廓线并进行手动后处理操作，其中平均一个数据集的后处理操作需要3 min. 这种方法所需的交互时间明显多于本文方法所需的交互时间.

2）水平集演化的强制终止仅针对于肝脏存在着明显的弱边缘或者无边缘的CT图. 首先，这类CT图所占比例较少，其次，单次交互时间短（本文采用鼠标右键交互终止水平集演化）. 整体而言，水平集的终止交互时间是极少量的.

通过统计得到，本实验中平均每个腹部序列的交互时间为85.7 s，属于中耗交互. 相比于上述提及的其他半自动分割方法，本文方法需要的交互时间更少.

2.4.2 算法运行时间

除去交互时间，算法运行时间包含图像预处理、区域增长和水平集演化的时间. 通过统计可得，加上交互时间，平均一个腹部序列交互时间为24.6±9.9 min. 相对于手动分割一个腹部序列所需时间为39.4±5.5 min^[36]，总时间减少了约37.6%，并极大地减少了人力劳动，人工的参与时间减少了约38 min.

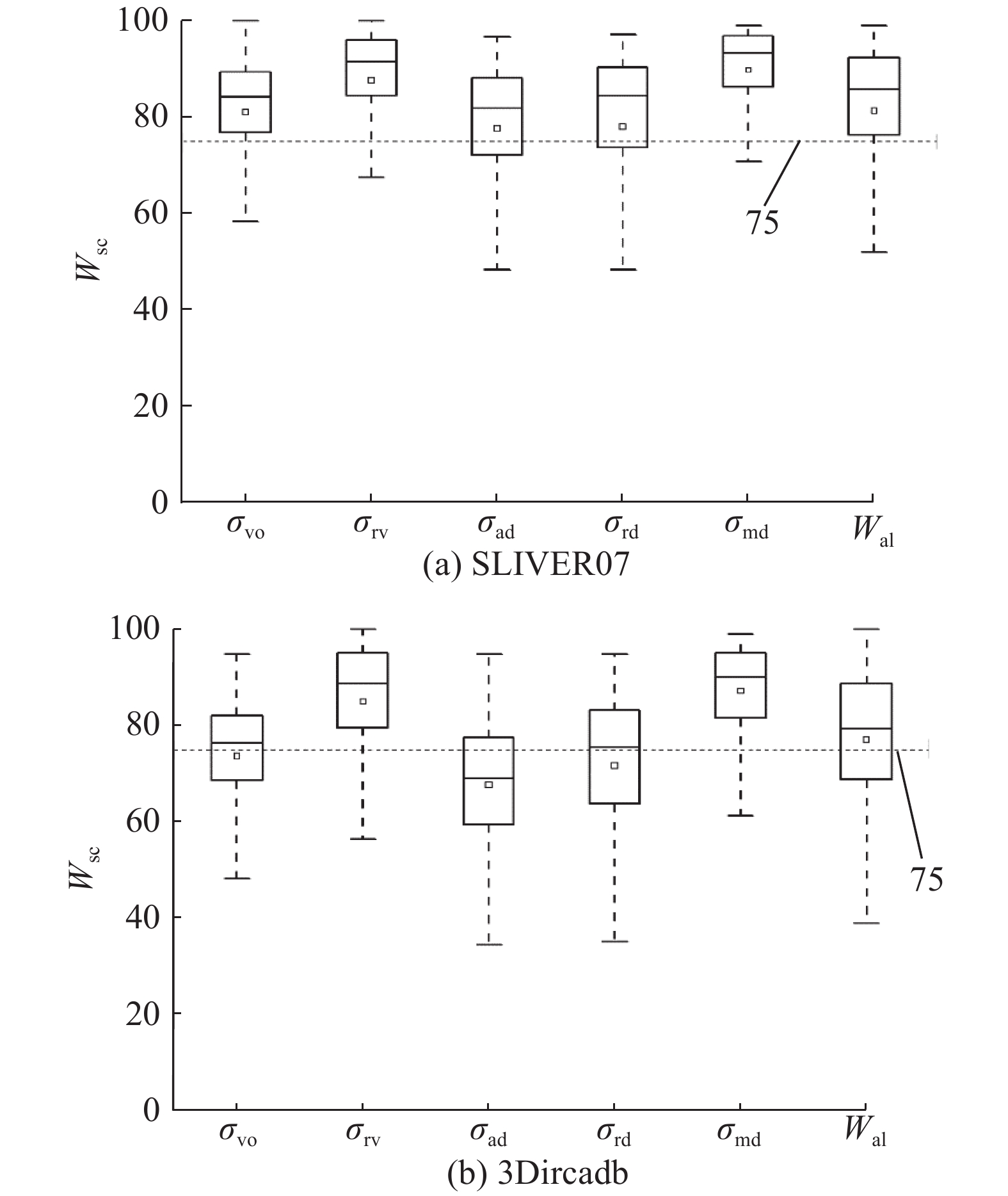
2.5 肝脏分割误差结果

本文对2个公共数据集进行验证，得到的误差结果如表2所示. 表2列出了5项误差指标的各个统计特征：平均值（C_me），标准误差（C_sd），最差值（C_wo）和最优值（C_be）. 其中，SLIVER07数据集的误差分别为4.9%±3.1%，−0.7%±3.3%，0.9±0.7 mm，1.6±1.4 mm和7.8±7.9 mm；3Dircadb数据集的误差分别为 6.73%±3.10%，−1.02%±3.76%，1.29±0.56 mm，2.04±1.18 mm和9.68±7.42 mm. 另外，根据文献[43]，将σ_vo=6.4%，σ_rv=4.7%，σ_ad=1.0 mm，σ_rd=1.8 mm和σ_md=19 mm作为分割得分75分的参考值，按照线性插值计算SLIVER07和3Dircadb数据集5个误差指标的得分W_sc，绘制标准箱体图，分别如图9所示（其中虚线表示75分，小正方形表示平均值，W_al表示加权总得分）. 可以看出，本文方法对于2个数据集都得到了良好的表现，总得分均在75分之上，分别为83±15分和77±15分. 相比而言，本文方法在SLIVER07上的表现要优于在3Dircadb上的表现，每项得分（包括最后的得分）都较高，主要原因在于后者含有肿瘤的CT序列比例要多于前者，并且肿瘤数量也多于前者，相对更难分割.

表3是本文方法与其他半自动分割方法在SLIVER07数据集上的分割误差比较. 本文方法的得分比文献[25]高1分，比文献[26]高7分，比文献[27]高6分，比文献[33]高5分. 相比其他多种方法，本文在融入更少交互操作的同时，得到了更加准确的分割结果.

表4是本文方法与其余2个自动分割方法在3Dircadb数据集上的分割误差比较. 可以看出，文献[19]、[44]的自动分割方法能够在更短的时间内完成分割任务，但是分割结果准确度低于本文的半自动分割方法.

从表3和表4中可以看出，本文方法的分割结果要相对优于其他方法，其中最明显的是σ_md误差指标，本文方法得到的σ_md平均值小于10 mm，要明显小于其他方法. 在分割过程中，导致σ_md偏大的主要因素如下：1）某些CT图中肝脏区域离散，没有完整地分割到全部肝脏区域；2）金标准中将血管包含在肝脏部分，没有将肝脏血管分割；3）对于弱边缘或者无边缘的肝脏区域，易于将毗邻组织分割，导致过分割. 本文采用交互操作，设置种子进行区域增长，能够确保完整地分割肝脏离散区域以及肝脏血管；另外，对于存在明显的弱边缘或者无边缘的肝脏区域，通过交互强制停止水平集演化，防止严重过分割. 以上措施能够限制σ_md过大，同时减小σ_ad与σ_rd，提高肝脏分割的准确度.

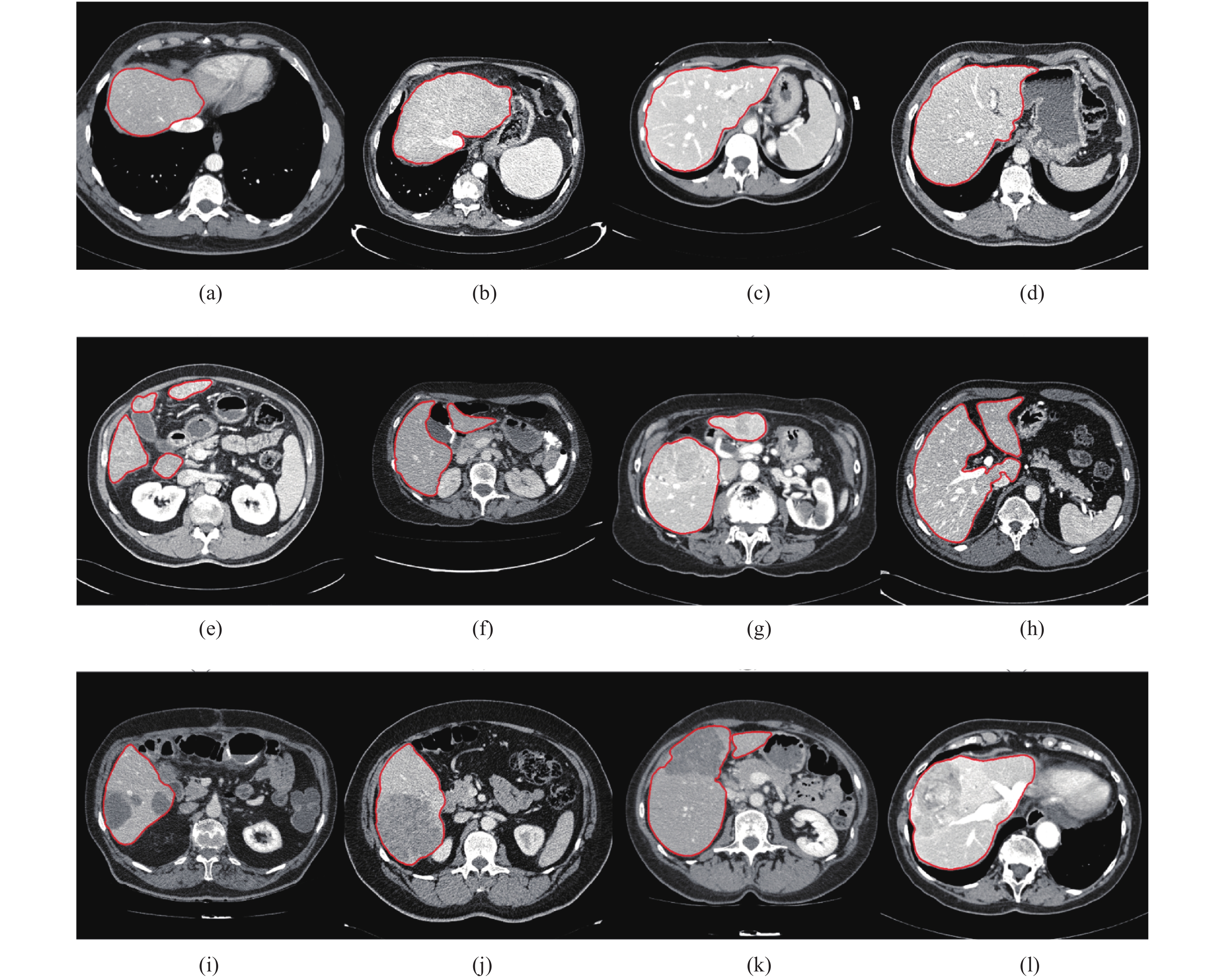
如图10所示，随机挑选3组共12张基于本文方法得到的肝脏分割结果（黑线表示），一行表示一组. 其中图10（a）~（d）是无病变无离散区域的整体肝脏分割结果，图10（e）~（h）是离散肝脏区域分割结果，图10（i）~（l）是病变肝脏的分割结果. 可以看出，本文的方法能够得到准确的分割结果. 例如：第一组的图10（a）中肝脏与心脏之间几乎不存在边缘，对于这种情况，该结果是采用交互强制中断水平集得到的；第二组的图10（e）中，肝脏离散成4个区域，对于这种情况，通过在离散的4个肝脏区域内设置种子点，能够确保分割出完整的肝脏区域；第三组的肝脏内部都包含了大肿瘤，从分割结果可以看出，本文的方法对于此类病变肝脏也具有良好的适用性与鲁棒性.

2.6 三维重建效果分析

肝脏分割精度影响三维模型重建的效果.为了检验重建效果，在40个肝脏序列分割结果中随机选择2个分割序列（表示为序列Ⅰ、序列Ⅱ），采用医学软件MIMICS^® 17.0（比利时Materialise公司）进行基于面绘制的三维重建^[45]. 将序列Ⅰ、序列Ⅱ导入软件，分别以 $x \times y \times z$ 为0.57 mm $ \times $ 0.57 mm $ \times $ 0.7 mm和0.57 mm $ \times $ 0.57 mm $ \times $ 1.0 mm进行重建，结果如图11所示. 其中，从上往下依次为序列Ⅰ、序列Ⅱ的模型重建，从左往右依次为：第1列为金标准重建模型，第2列为本文方法分割后的重建模型，第3列为前两者的颜色距离误差图，模型下方为颜色距离误差参考图，最大绝对值为10 mm. 序列Ⅰ和Ⅱ的具体3D距离误差数值如表5所示，包含σ_ad、σ_rd和σ_md三个指标. 从图11和表5中可以看出，三维重建模型与金标准模型之间的体积误差低，准确度高.

3 结　论

（1）针对传统区域增长中增长阈值和种子点位置选择的共同困难，本文通过混合图像预处理将CT图转化成二值图像，为种子提供良好的增长环境：增长阈值和种子点位置设定简单，避免了过分割，能够较完整地提取肝脏区域. 另外，本文方法种子点个数所需很少，平均每张CT图像仅需要1.73个种子点.

（2）针对基于边缘信息的水平集设定合适的气球力与迭代次数困难，对于噪声敏感等问题，结合图像区域信息，提出了统一化水平集，由边缘信息与区域信息共同驱动，该方法能够适应大气球力与多迭代次数，同时能够带来更准确的分割结果.

（3）本实验中交互操作包含种子点设定与弱边缘处强制终止水平集演化，总体交互时间短，平均每个腹部序列的交互时间为85.7 s，属于中耗交互，相比于其他半自动分割方法，交互时间更少. 算法运行平均时间为24.6±9.9 min，相比手动分割减少了37.6%.

（4）将本文方法在2个公共数据集共40个腹部序列中进行验证，发现误差指标σ_md明显低于其他方法，本文方法得到的σ_md均值小于10 mm，其他方法得到的σ_md均值基本都大于15 mm. 另外，基于本文方法的肝脏模型三维重建精度较高，重建模型与金标准模型之间的3D距离误差较小.

（5）本文的算法运行时间虽然相比手动分割大大减少，但是仍需进一步优化以提高效率. 今后的研究将尝试引入窄带^[46]、GPU加速^[47]或者相干传播^[48]等技术来加速水平集演化，进一步提高肝脏分割的效率. 另外，受文献[49-50]启发，考虑在水平集中加入形状约束信息和毗邻组织约束信息，进一步提高肝脏分割的准确度. 同时，将使用更多的数据集进行算法验证，进一步体现本文算法的普适性.

本文方法具有良好的适应性与鲁棒性，能够带来更加准确的结果. 相比于其他半自动分割方法，交互时间更少；相比人工手动分割，大大减少了人工投入，节省了分割时间，提高了分割效率. 本文方法能够为临床实践提供参考.