2. 河南工业大学 信息科学与工程学院,河南 郑州 450001;
3. 武汉大学 地球空间信息技术协同创新中心,湖北 武汉 430079
2. College of Information Science and Engineering, Henan University of Technology, Zhengzhou 450001, China;
3. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China
位姿测量是摄影测量与计算机视觉普遍关注的问题,在空间交会对接、机器人导航、工业机械手抓取物体、交通工具运动轨迹跟踪等方面有广泛的应用[1-4]. 位姿测量手段多种多样,整体可以分为两大类:直接在目标上装载GPS和IMU等设备进行位姿测量与利用各种摄影设备获取目标的影像资料进行位姿测量[5]. GPS和IMU设备的位姿测量精度高,但在运动目标快速变化时GPS信号容易丢失,IMU设备存在漂移现象且对使用环境有所限制,利用影像资料即基于视觉的位姿测量可以避免直接接触运动物体,受到了广泛的关注研究. 按照视觉传感器数量的不同可以将基于视觉原理测量物体的位姿方法分为单目视觉位姿测量、双目视觉位姿测量. 双目视觉位姿测量精度高,但其受到应用环境的限制,存在测量范围较小、立体匹配困难等缺陷. 单目视觉位姿测量结构简单,对应用环境限制少,且可以避免立体视觉中的场景小、立体匹配等不足,受到许多学者的广泛关注[6].
单目视觉位姿测量可以分为两类:基于合作目标的位姿测量[7-9]和非合作目标的位姿测量[10-12]. 基于合作目标的运动物体位姿测量是指在被测物体上设计若干标志点,利用目标上设计的空间相对位置已知的标志点,提取标志点并依据标志点的位置关系解求出目标的位姿. Guo等[9]将4个非共面的发光二极管作为特征点,采用Posit算法求解单相机获取图像中目标的相对位姿;吴立新等[13]等提出以序列编码图形路标作为合作特征,实现单目机器视觉系统在盲环境移动目标的定位;Pan等[14]采用改进的重力模型和多目标跟踪方法提高特征提取的精度,利用Levenberg-Marquardt方法(莱文贝格−马夸特方法)改善姿态估计的效率. 基于合作目标的单目视觉位姿测量方法设计了合理的人工标志,提取合作目标方法简单高效,位姿测量的精度与可靠性高,但该方法对使用场景有所限制,在某些情况下不具备在被测目标上布设特征的条件,使用范围有一定局限性.
非合作目标的物体位姿测量方式多样化,Éric等[10]在已知物体的三维非精细模型的条件下,通过人工交互选区图像与模型中4对以上同名点获取第一帧图像中目标的位姿,后续帧采取迭代求解代价函数获取单目序列图像中物体的位姿. 童张海[15]通过提取模板图像的特征点,将模板图像中的特征点与输入图像的特征点进行匹配,然后利用特征点间的关系实现非合作目标的位姿估计. Iwashita等[16]定义了复杂的力和扭矩模拟空间力场,求解扭矩极小值的代价函数以实现目标位姿参数的估计. Leng等[17]利用提取得到的轮廓生成距离图,快速构建2D-2D轮廓点的对应关系,然后确定2D-3D投影关系,迭代解算目标的姿态. Rosenhahn等[18]等利用目标的已知表面模型,构建代价函数,采用水平集的方法在分割图像获取物体边缘的同时测量物体的三维位姿. 非合作目标的位姿测量方法多种多样,由于缺少易于提取的目标特征,通常需要某些已知的附加信息. 此外,由于应用要求和环境的差别,没有适用于各种场合的普适方法,应针对应用环境以及测量要求的不同,选择合适的位姿测量方式.
本文根据相机参数以及运动目标的三维模型,采用OpenGL渲染生成位于不同位姿的运动目标模拟图像. 依据模拟图像与实际图像中目标轮廓两者之间的关系获取目标的位姿. 位姿的求解分为两部分:初始位姿的确定以及精确位姿的求解. 利用相机视野中物体的位姿集合事先建立轮廓剪影库,分析对比实拍图像轮廓与剪影库中轮廓,确定运动目标的初始位姿;根据实拍图像的目标轮廓与初始位姿的运动目标模拟图像中轮廓的距离关系,构建距离代价函数,采用非线性优化方式迭代求解运动目标的精确位姿. 本文提出的方法可以避免跟踪时手动给定第一帧运动目标的初值,在运动目标位姿初值的基础上进行跟踪,获取其精确位姿. 在仿真图像和实拍图像中验证本文提出方法的可靠性.
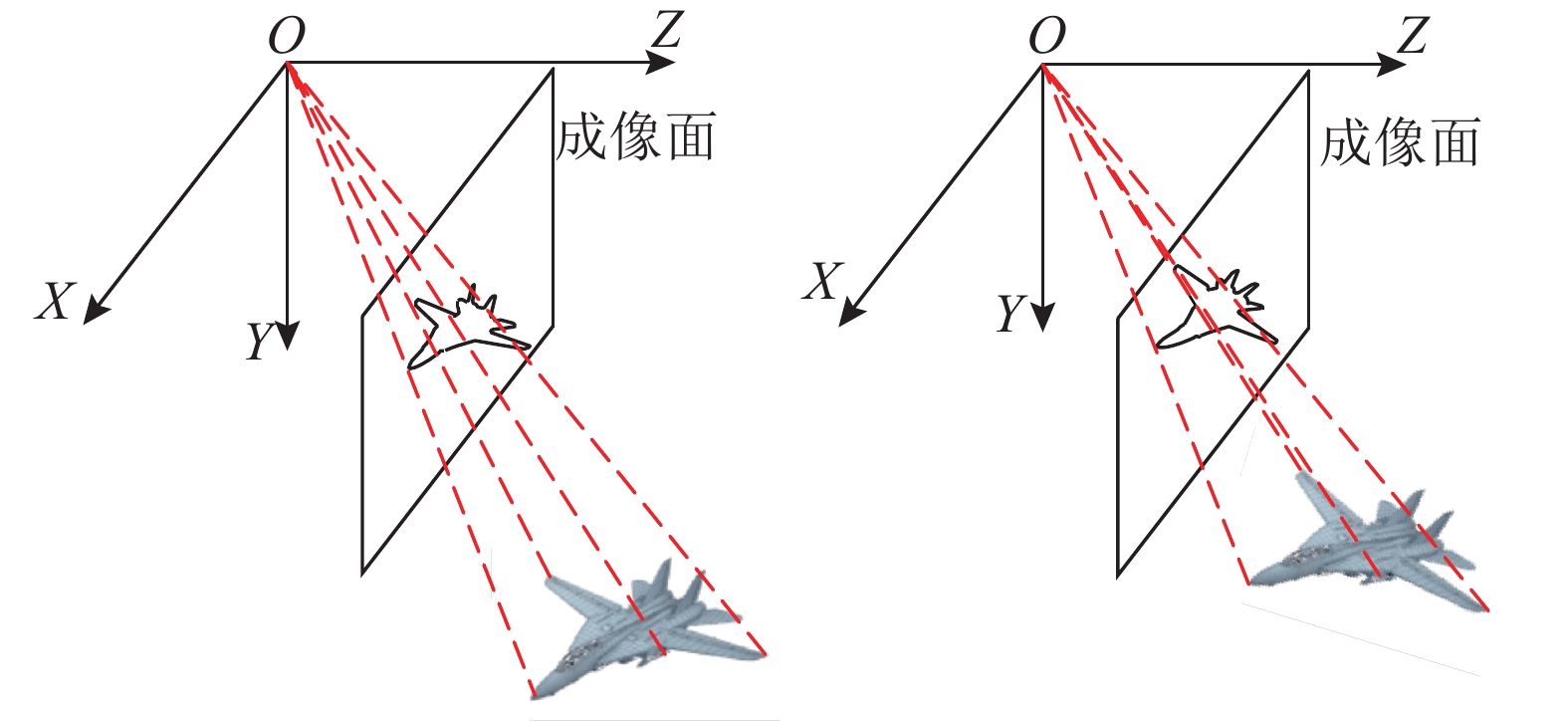
1 基于目标轮廓的单目位姿测量算法以目标的三维几何模型以及场景中布设相机的各项参数作为先验知识,可以通过目标的单幅图像来解算其位姿. 在先验知识下单目视觉位姿测量的基本原理如下:对于固定的相机而言,运动目标的位姿由其成像唯一确定. 当目标的位姿发生变化时,其相应的成像发生改变,运动目标的位姿与其成像之间存在对应关系,如图1所示.
|
图 1 不同位姿目标的成像示意图 Fig. 1 Imaging diagram of objects with different positions and orientations |
利用不同位姿目标成像唯一的特性确定运动目标的位姿. 已知目标的三维几何模型且相机参数已经标定的前提,采用OpenGL渲染生成不同位姿运动目标的模拟图像,通过构建模拟图像与实拍图像目标轮廓之间的关系,确定目标的位姿. 模拟图像与实拍图像包含的信息丰富程度不同,考虑到算法实用性以及目标边缘包含丰富的信息,选择采用运动目标的轮廓信息作为位姿测量的媒介,构建实拍图像与模拟图像目标轮廓间的关系,求解运动目标的位姿.
模拟图像与实拍图像通过边缘特征建立两者之间的关系,目前边缘提取方法种类多样[19],已经发展为具有高度复杂性、考虑多因素的边缘定义、采用较少噪声和纹理影响的轮廓提取机制,利用多尺度的高级别视觉信息的方法,不存在适用于各种应用的普适方法,需根据具体的应用场合选用合适的边缘提取方法. 本文依据实际环境事先对背景图像进行拍摄,通过背景差分算法获取运动目标,然后进行后处理,快速获取运动目标的轮廓. 利用目标轮廓进行位姿测量时,运动目标的位姿需要一个初值,某些方法中利用人工手动给定初值[20],或者通过人工选取若干个点进行初始位姿的确定[10]等,这些方法需要采用人工交互的方式,降低了方法的便捷性. 本文利用事先构建离散位姿运动目标轮廓集合,跟踪运动目标第一帧图像的初始位姿,由运动目标的轮廓与目标轮廓集合中的轮廓关系求得. 后续帧运动目标的初始位姿为上一帧的精确位姿,确定运动目标的初始位姿后,构建实拍图像和模拟图像目标轮廓之间的距离代价函数,采用非线性优化的方法迭代求解运动目标的精确位姿. 本文方法的整体流程如图2所示.

|
图 2 单目序列的刚体目标位姿测量流程图 Fig. 2 Flow chart of rigid object's position and orientation measurement based on monocular sequence |
根据已知的相机参数,预先获取该相机视野范围内目标的运动范围,并按照步长采样获取运动目标不同位姿的目标轮廓,可以通过离线的方式构建运动目标在各位姿的轮廓集合. 搜索实拍图像目标轮廓与各位姿模拟图像轮廓集合中套合最佳的轮廓,将套合最佳目标轮廓的位姿作为该运动目标的位姿初值.
当运动目标与相机的距离以及运动目标自身的角度发生变化时,对应目标轮廓位置间发生的偏差不同. 在搜索运动目标位姿初值时,需要综合考虑这些因素确保获取运动目标的可靠初值. 本研究在确定运动目标的初始位姿时,以实拍图像的目标轮廓为中心,按照距离确定图像中各像素为目标轮廓的可能性w,距离实拍图像轮廓点的远近反映出该点为初值位姿轮廓点的可能性:
| $w = \left\{ \begin{gathered} 0, \quad\quad\;\; d > T; \hfill \\ {{\rm e}^{ - 1 \times d}}, \quad d \leqslant T. \hfill \\ \end{gathered} \right.$ | (1) |
| $d = {\left\| {p - q} \right\|_2}.$ | (2) |
式中:d为离散采样目标轮廓集合中各位姿下目标轮廓点q距离实拍图像中最近的边缘轮廓点p之间的距离,T为设置的距离阈值. 如图3所示为按照距离提取边缘轮廓为中心构造的边缘点可能性结果.

|
图 3 像素与目标轮廓距离构成的概率图 Fig. 3 Probability image from distance between pixel and object contour |
运动目标位姿初值获取的具体步骤如下:
1)依据相机参数确定视场的范围,即确定运动目标出现的位姿范围,按照步长构建离散的位姿集合,同时生成离散位姿下运动目标的轮廓集合;
2)对拍摄得到的图像进行目标轮廓提取,并依据提取的目标轮廓生成距离概率图像;
3)根据得到的距离概率图像,将离散位姿集合中各位姿的目标轮廓进行相似性比较.
运动目标的位姿范围以集合形式表示为
| $\left\{ {\left( {X, Y, \theta } \right)|\;{X_1} \leqslant X \leqslant {X_2}, {Y_1} \leqslant Y \leqslant {Y_2}, {\theta _1} \leqslant \theta \leqslant {\theta _2}} \right\}.$ | (3) |
式中:X1、Y1分别为目标最小的X轴坐标与Y轴坐标,X2、Y2分别为目标最大的X轴坐标与Y轴坐标. θ1通常为0°,θ2通常为360°. 运动目标位姿范围是连续的,可能出现在该集合的任意位姿,通过离散采样构建离线特征集合表示为
| $\{ (X, Y, \theta )|\;X = {X_1} + m\Delta X, Y = {Y_1} + n\Delta Y, \theta = {\theta _1} + k\Delta \theta \}. $ | (4) |
式中:∆X、∆Y、∆θ为采样间隔,m、n与k由连续集合中出现的位姿范围确定,
| $ \left. \begin{aligned}& m = {\mathop{\rm floor}\nolimits} \;\left( {\frac{{{X_2} - {X_1}}}{{\Delta X}}} \right), \\& n = {\mathop{\rm floor}\nolimits} \;\left( {\frac{{{Y_2} - {Y_1}}}{{\Delta Y}}} \right), \\& k = {\mathop{\rm floor}\nolimits} \;\left( {\frac{{{\theta _2} - {\theta _1}}}{{\Delta \theta }}} \right). \end{aligned} \right\} $ | (5) |
式中:floor()表示向下取整操作. 通过上述公式确定离散的位姿集合,便于后续获取位姿的初始值.
实拍图像目标轮廓与离散位姿集合中各位姿目标轮廓的相似性ρ的具体求解如下:
| $\rho = \frac{1}{M}\sum\limits_{i = 1}^M \;{{w_i}} .$ | (6) |
式中:M为离散集合中某位姿目标轮廓点的数目,wi为该位姿目标轮廓各点的概率. 比较实拍图像轮廓与离散集合中各位姿轮廓的相似性,取相似性最大的位姿作为初始值.
实拍图像轮廓与离散位姿中轮廓相似性之间的关系如图4所示. 图中,每个坐标(X,Y)对应的角度θ的范围为[0°,360°],以圆心为起点,水平向右表示0°,竖直向上表示90°,水平向左表示180°,竖直向下表示270°,即逆时针方向构成360°. 圆内各条线的长度表示运动目标的位姿为(X,Y,θ)的相似性. 通过上述步骤,可以获取图像中运动目标的初始位姿. 如图5所示为搜索的位姿结果,左侧为目标的位姿在离散的位姿集合中时搜索的结果,右侧为目标的位姿不在离散位姿集合时搜索到的结果. 若对位姿精度要求不高,可以将初始位姿作为运动目标的位姿结果,无需进一步求解精确位姿;若对位置姿态精度要求高,则需要位姿的精确求解.

|
图 4 运动目标与离散集合中各位姿的相似性 Fig. 4 Similarity of moving object between different positions and orientations in discrete collection |

|
图 5 距离概率图与初始位姿轮廓叠加示意图 Fig. 5 Object contour of initial position and orientation superimposed on distance probability image |
采用OpenGL软件渲染位于初始位姿的运动目标模拟图像,提取模拟图像与实拍图像中运动目标的轮廓. 由实拍图像与模拟图像轮廓之间的距离关系,构建代价函数:
| $f = \frac{1}{N}\sum\limits_{i = 1}^N \;{{{\left\| {{p_i} - {q_i}} \right\|}_2}} .$ | (7) |
式中:N为实拍图像中提取运动目标轮廓离散点的数目,pi为提取实拍图像目标轮廓的离散点,qi为模拟图像目标轮廓中距离pi最近的离散点,||pi−qi||2为实拍图像轮廓点pi与模拟图像轮廓点qi的距离. 代价函数的意义如下:实拍图像的运动目标轮廓与模拟图像运动目标轮廓的整体距离,求解代价函数最小时模拟图像目标的位姿,即为运动目标的精确位姿,将其作为优化的指标.
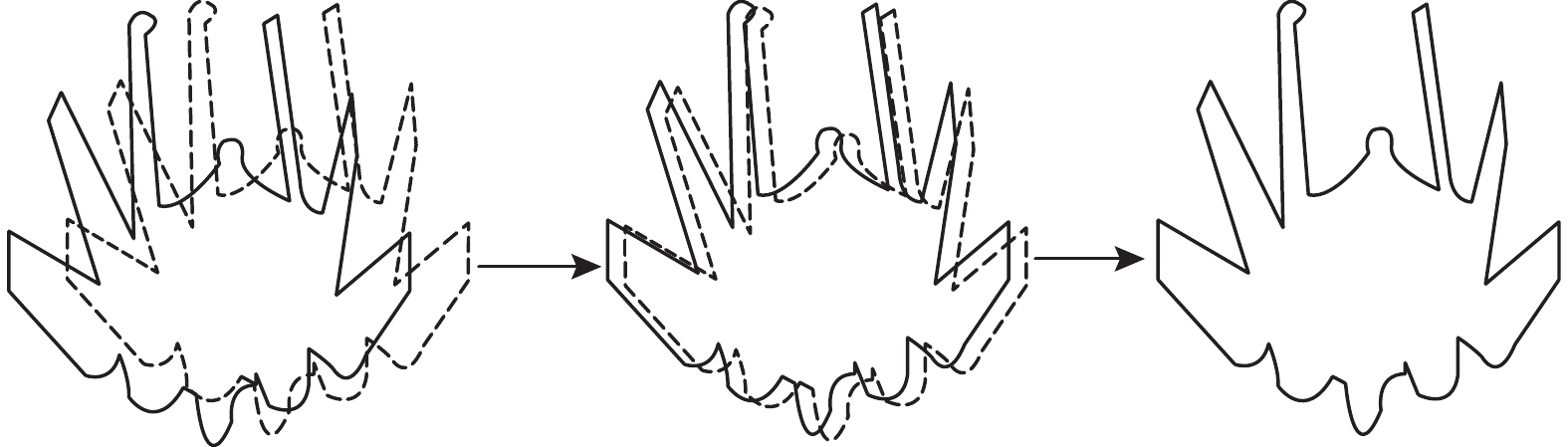
在求解代价函数最小值时,直接对位姿参数求偏导存在一定的困难,不能采用常规的线性化误差方程进行优化求解,本研究采用Powell[21-22]提出的“无偏导依赖项”的非线性最优化方法进行迭代求解,该方法适用于从初始值开始搜索精确值的问题. 初始位姿模拟图像目标轮廓与实拍图像目标轮廓之间不存在严格的对应关系,在迭代过程中逐步建立两者之间的关系,逐步缩小模拟图像目标轮廓与实拍图像目标轮廓之间的差异. 如图6所示,图中实线表示实拍图像目标轮廓,虚线为模拟图像目标轮廓.
|
图 6 迭代求解过程中图像目标轮廓逐渐重合示意图 Fig. 6 Schematic diagram of gradually overlapping of object contours in iterative solution process |
目标三维几何模型以及相机参数的获取可以采用三维激光扫描和相机标定技术. 采用OpenGL虚拟一个位于该位姿的相机,生成运动目标在不同位姿的渲染图像. 为了验证本文提出方法的可靠性,分别采用仿真图像以及实际图像测量运动目标的位姿,实验源码采用Visual C++编写,实验环境如下:CPU i7八核2.5 GHz、12 GB内存,Windows7 64位操作系统.
2.1 仿真图像模拟实验根据相机的各项参数,确定运动目标出现的视野范围,实验中运动目标出现的位姿范围如表1所示. 为了快速获取运动目标的初始位姿,构建离散的位姿集合,根据运动目标出现的范围进行离散采样,分别采用以下2种方案进行采样:
| 表 1 运动目标出现的位姿范围 Table 1 Position and orientation range of moving objects |
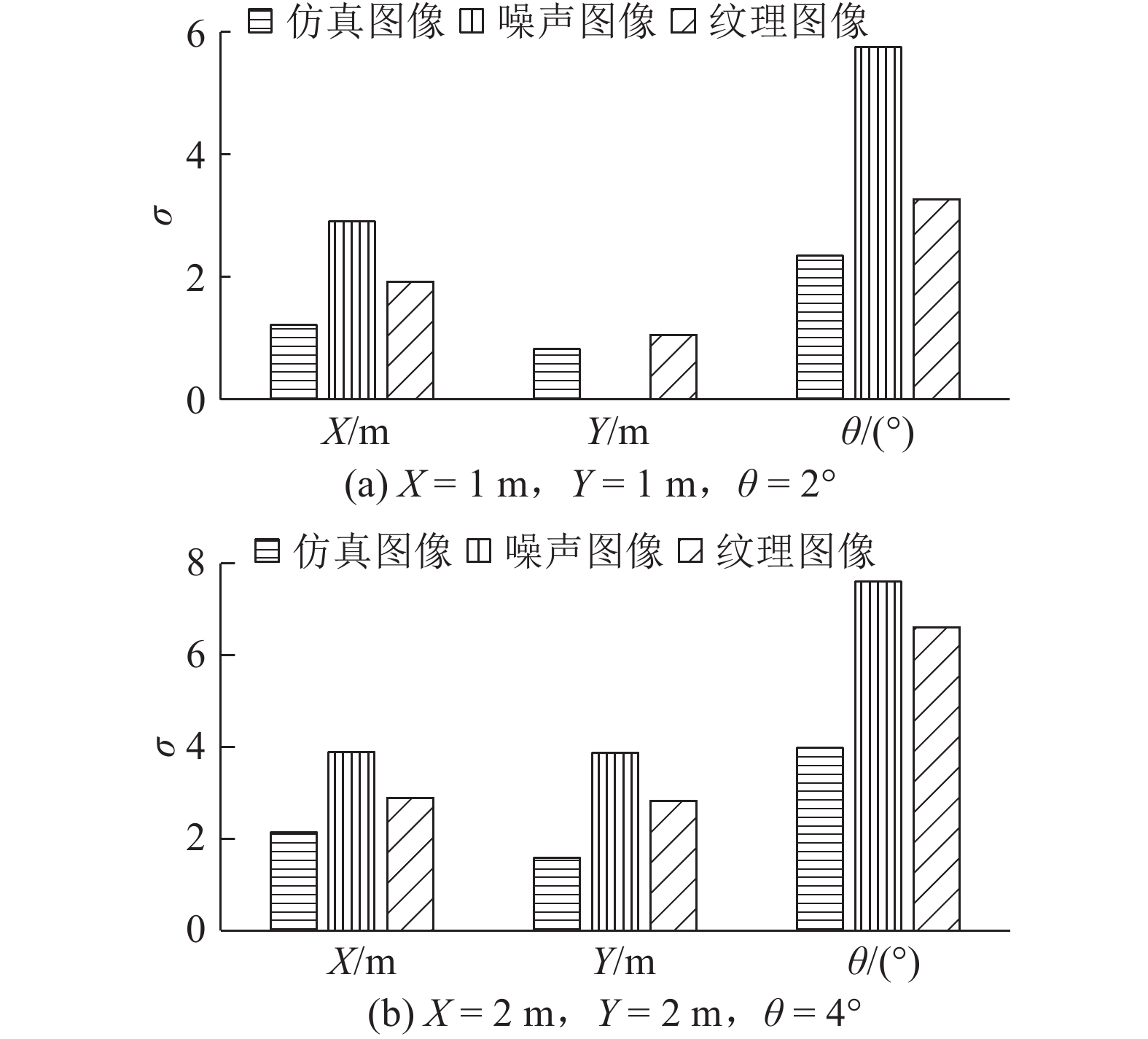
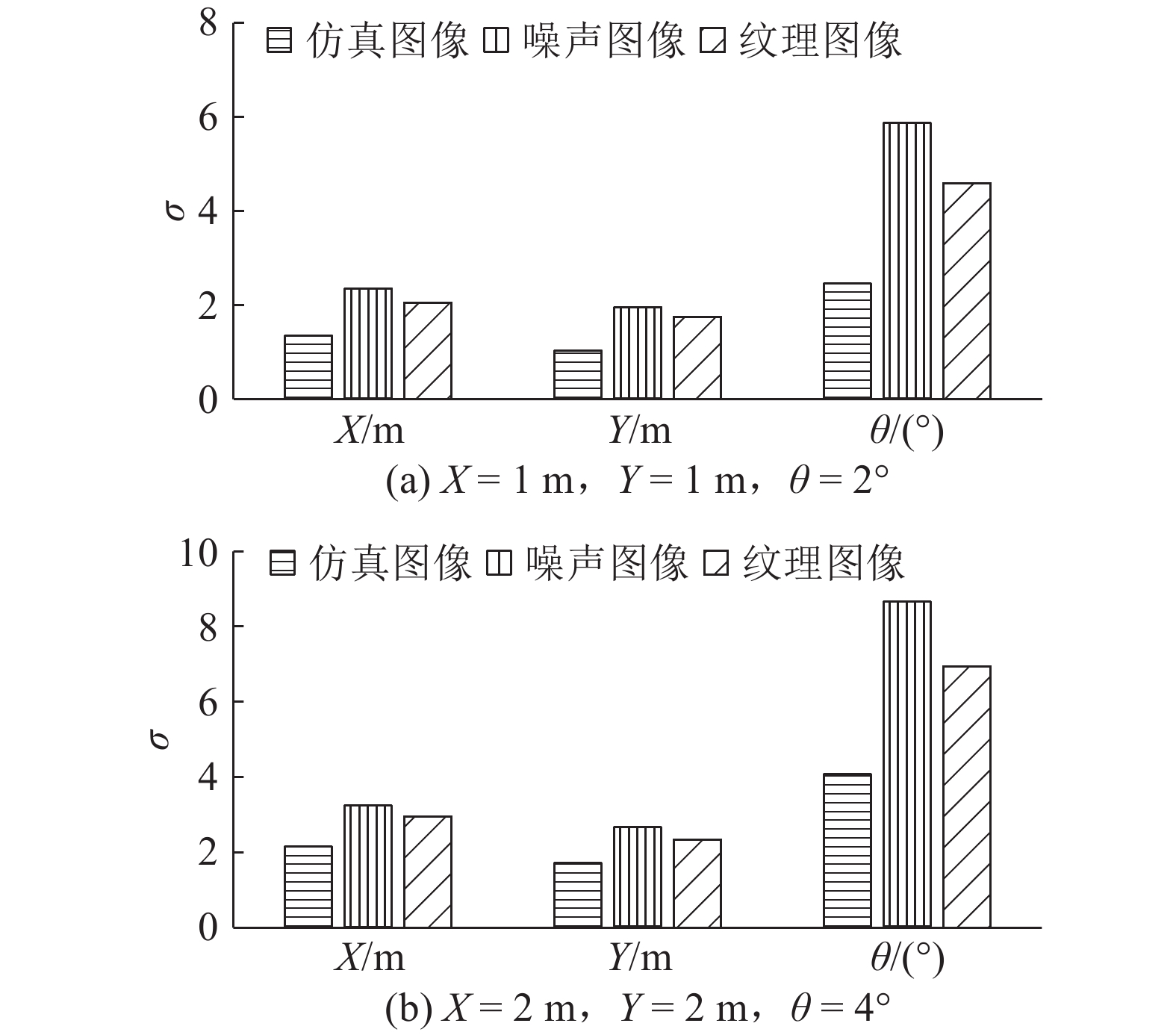
在2组位姿范围内,设计目标的运动轨迹并生成仿真图像序列,各以其中一条运动轨迹为例进行说明. 为了检验方法的可靠性,在仿真图像中分别加入噪声、纹理进行实验,用标准差σ衡量结果的可靠性. 如图7和8所示分别为第一组图像和第二组图像的初始位姿测量结果. 从图中可以看出,初始位姿的结果受采样间隔的影响,当采样间隔较小时,得到初始位姿的精度越高,当采样间隔较大时,初始位姿的可靠性降低. 加入纹理以及噪声图像的初始位姿误差相较于理想仿真图像的初始位姿有所增大,但其误差波动仍在一定范围内,可以满足提供初始值的精度需求. 统计分析图7与图8的耗时信息可知,图7(a)和8(a)比图7(b)和8(b)耗时更长,即采样间隔越大,耗时越短。此外,图8中的第二组耗时比图7中的第一组耗时更长,即离散位姿的规模越大,耗时越长. 采样间隔影响轮廓集合规模与初始位姿精度,集合规模的大小决定搜索时间. 当采样步长增大时,离散位姿目标轮廓集合规模减小,获取运动目标初始位姿的速度快,精度相对较低. 当采样步长减小时,离散位姿目标轮廓集合的规模增大,获取运动目标初始位姿的精度高,速度减慢. 采样间隔的选择受初始位姿精度与速度限制,由于初始位姿的获取仅需要序列图像第一帧中运动目标的初始位姿,通常对第一帧的速度限制较小,初始位姿的精度提供满足后续位姿精确求解初始值的要求即可. 由此可以看出,相机的视野范围对采样间隔影响较大,当视野范围较小时,运动目标出现在场景中的位姿范围小,采样步长可以相对较小,保证初始位姿精度且满足实时性;当相机视野范围较大时,采样步长可以适当增大,能够为精确位姿解算提供初始值即可.
|
图 7 第一组仿真图像中目标的初始位姿精度 Fig. 7 Accuracy of initial position and orientation of object in simulated images of first group |
|
图 8 第二组仿真图像中目标的初始位姿精度 Fig. 8 Accuracy of initial position and orientation of object in simulated images of second group |
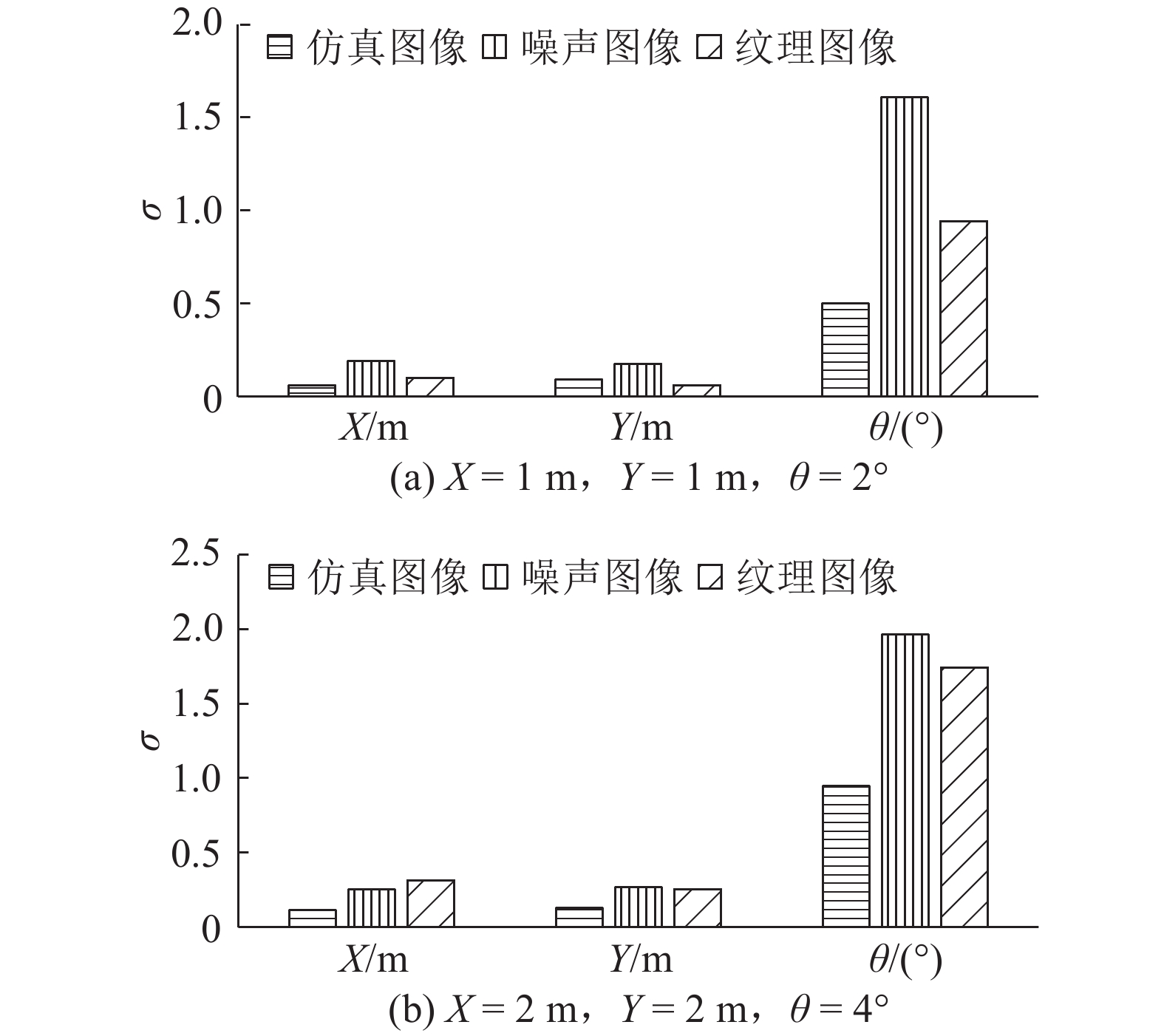
如图9、10所示分别为第一组和第二组仿真图像的精确位姿目标轮廓的套合结果. 如图11和12所示分别为2组图像采用不同采样间隔得到初始位姿作为跟踪初始值的精确位姿的结果. 从图11与12可以看出,理想仿真图像精度相对较高,当图像背景中包含噪声或纹理时,运动目标仍能够进行有效的跟踪,但测量的精度有所下降. 此外,由于采样步长不同得到的运动目标初始位姿的精度有所区别,精确位姿的求解结果受到初始位姿的影响. 初始位姿精度越高,求解得到精确位姿的可靠性越高. 求解的精确位姿相较于初始位姿结果精度明显有了较大的提升. 总体而言,本文提出的方法对理想仿真图像以及含有纹理、噪声的图像中运动目标的位姿测量能够得到较高的精度.

|
图 9 精确位置姿态下模拟图像的目标轮廓叠加在第一组仿真图像的结果 Fig. 9 Object contour under precise position and orientation superimposed on simulated images of first group |

|
图 10 精确位置姿态下模拟图像的目标轮廓叠加在第二组仿真图像的结果 Fig. 10 Object contour under precise position and orientation superimposed on simulated images of second group |
|
图 11 第一组仿真图像中目标的精确位姿结果 Fig. 11 Accuracy of precise position and orientation of object in simulated images of first group |

|
图 12 第二组仿真图像中目标的精确位姿结果 Fig. 12 Accuracy of precise position and orientation of object in simulated images of second group |
|
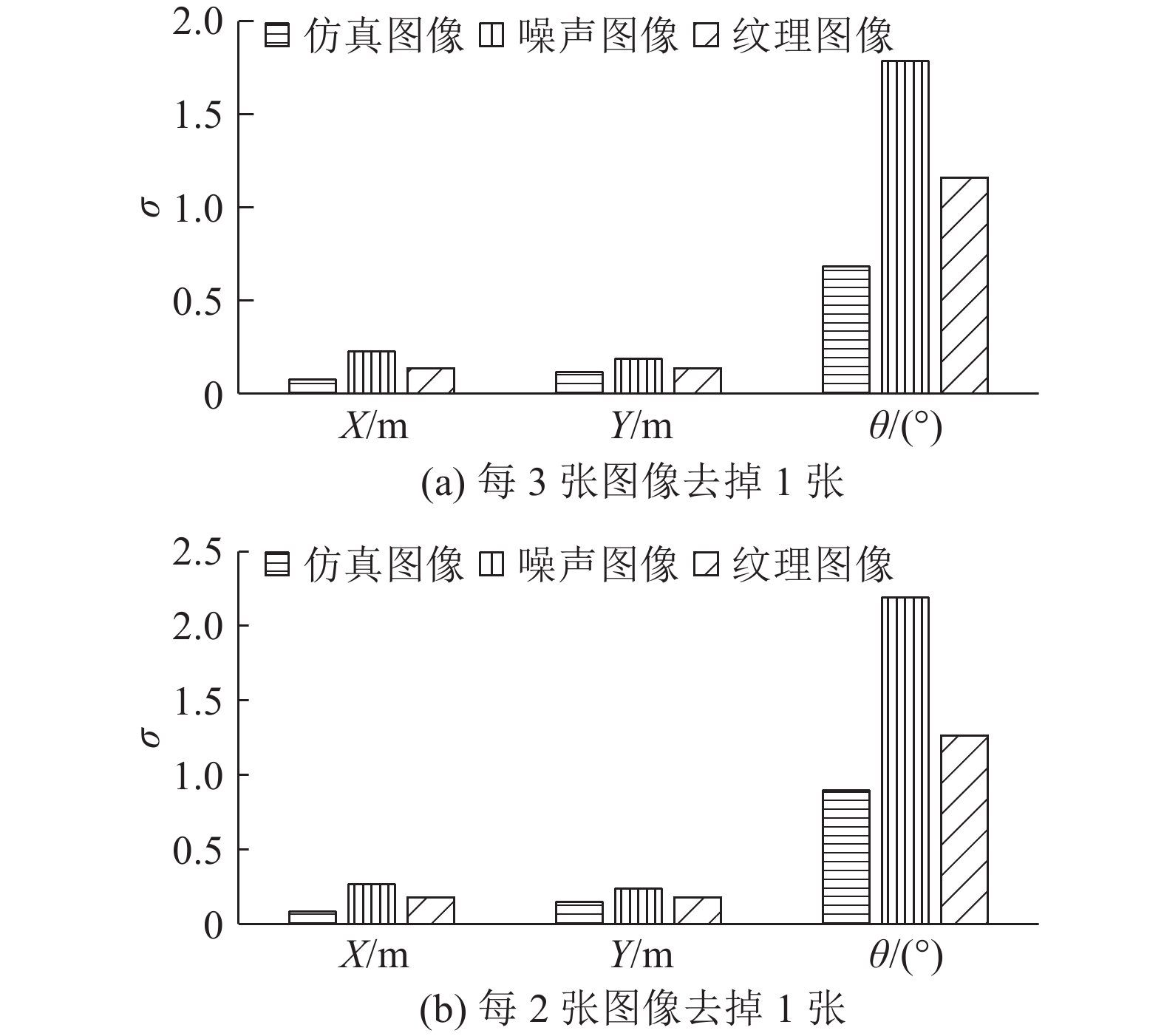
图 13 抽稀图像后运动目标的精确位姿结果 Fig. 13 Accuracy of precise position and orientation of object after thing images |
进一步分析运动目标的移动速度对位姿测量的影响,将仿真图像进行抽稀实验,对第一组仿真图像分别按照连续3张、2张图像剔除1张图像进行抽稀,按采样间隔1 m (X)、1 m (Y)、2°获取初始位姿,得到运动目标精确位姿测量结果如图13所示. 从图中可以直观地看出,位姿的精度受到运动目标移动间隔的影响,移动间隔越小,运动目标的位姿精度越高,当运动目标移动间隔有所增大时,运动目标的位姿精度有所下降.
2.2 实际图像模拟实验为了进一步验证本文提出方法的可靠性,测试在实际图像中运动目标的位姿测量结果. 采用Basler工业相机采集图像,采集图像前标定相机的内外方位元素,图像的大小为1 600×1 200,确定运动目标出现的位姿范围,其中X的范围为[0 m,0.7 m],Y的范围为[0.7 m,2 m],θ的范围为[0 °,360 °]. 采集2组图像进行实验验证,其中第一组图像受阴影的影响,第二组图像则存在遮挡、部分缺失的情况,2组各采集500幅图像进行运动目标的位姿测量.
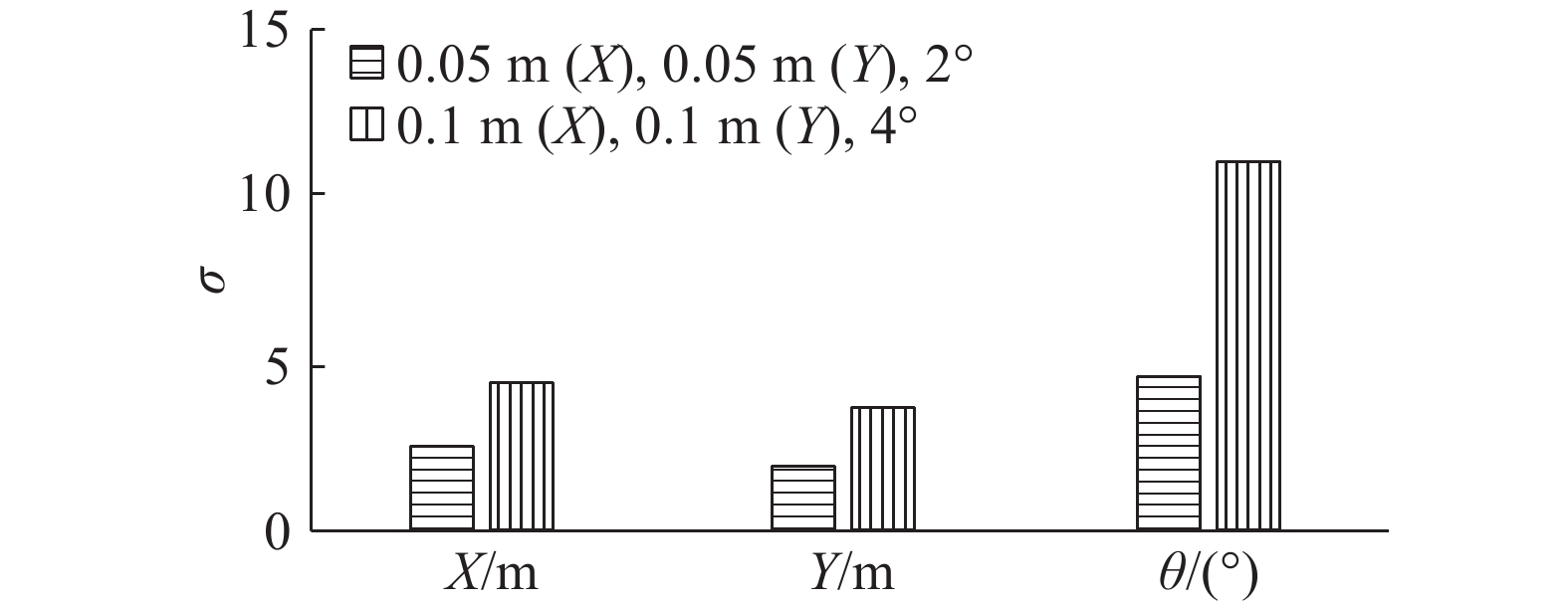
由于实际图像中运动目标位姿的真值并不是已知信息,无法采用上述仿真图像的方式直接比较运动目标的初始位姿与真值,将实际图像中运动目标的精确位姿作为真值分析初始位姿的精度. 每次跟踪只需获取初始帧中目标的初始位姿,为了评价初始位姿获取方法的可靠性,对第一组图像中的每一帧均进行初始位姿的获取,并将该结果与位姿求解得到的精确位姿进行比较. 采用2种不同的采样方式得到运动目标初始位姿的结果如图14所示. 可以看出,采样间隔越大,初始位姿与精确位姿间差距越大,初始位姿的精度则越低;采样间隔越小,初始位姿与精确位姿间差距越小,精度越高.
|
图 14 不同采样间隔下实拍图像中目标的初始位姿精度比较 Fig. 14 Comparison of initial position and orientation accuracy of objects in real images under different sampling intervals |
如图15所示为精确位姿的目标轮廓与实拍图像叠加显示. 2组图像通过目标轮廓距离概率获取第一帧图像中目标的初始位姿,然后进行位姿的精确求解. 图15中轮廓线为最终迭代的位姿OpenGL渲染生成的目标轮廓. 从图15可以看出,运动目标即使会受到阴影、部分遮挡缺失等影响,仍能有效地完成运动目标的位姿参数估计. 在物体跟踪的初始位姿相对准确的情况下,将当前帧的精确位姿作为下一帧的初始位姿,根据被测目标运动的连续性,即使存在遮挡、不完整等缺陷,仍能有效地进行位姿测量. 但需要指出的是,运动目标在初始位姿尽量不遮挡或仅有较小部分的遮挡缺失才能保证其初值的可靠性,此外,当运动目标被遮挡的部分较多时,运动目标的跟踪会出现问题.

|
图 15 精确位姿下模拟图像的目标轮廓叠加在实拍图像的结果 Fig. 15 Object contour under precise position and orientation superimposed on real images |
通过上述实验以及理论分析,影响运动目标位姿的因素主要包括:运动目标尺寸、相机的视野范围、运动目标初始位姿结果、运动目标移动间隔的影响等.
运动目标的尺寸影响其成像大小,对于同一相机而言,在相同位姿下,运动目标尺寸越大,得到运动目标轮廓点的数量越多,有利于采用代价函数求解精确的位姿,相应位姿的可靠性越高.
相机的视野范围影响着位姿的可靠性,采样间隔受视野范围的制约,同时运动目标的成像大小也受到影响. 视野范围越小,目标成像相对越大,选用的采样步长越小,获取精度越高;视野范围越大,目标成像相对越小,选用的采样步长越大,获取精度越低.
运动目标初始位姿受到距离概率图与采样步长的影响,阈值T影响距离概率图,阈值的选取要适当,阈值过大时易造成初始位姿搜索失误,阈值过小且采样间隔过大时易造成错过最为相似的初始位姿. 应当依据图像尺寸以及目标在图像中的成像大小设置阈值大小. 初始位姿的可靠性影响后续精确位姿的求解,初始位姿可靠性越高,后续精确位姿的精度越高.
运动目标移动间隔影响目标位姿的求解精度,抽稀仿真图像运动目标的位姿精度有所下降,抽稀程度越高,即运动目标移动间隔越大,位姿的精度越低.
3 结 语针对某些特殊情况下,采用单目视觉测量位姿时不具备采用合作目标的条件,本文提出了一种基于刚体目标轮廓的非合作目标单目视觉测量方法,利用相机参数以及运动目标的三维模型,构建了不同位姿目标轮廓集合,由离散集合中轮廓与拍摄图像中目标轮廓之间的关系确定运动目标的初始位姿. 在初始位姿已知的条件下,构建模拟图像中运动目标轮廓与实拍图像中目标轮廓之间的距离代价函数,迭代求解运动目标的精确位姿. 本文方法避免了手动给定运动目标第一帧的位姿初值,在纹理、阴影、部分遮挡等影响下,仍能有效地测量运动目标的位姿. 但若运动目标初始状态下受到遮挡或阴影的影响严重,则会造成初始位姿的获取错误,导致后续的跟踪存在问题,这是下一步研究的重点问题.
| [1] |
LI J, BESADA J A, BERNARDOS A M. A novel system for object pose estimation using fused vision and inertial data[J]. Information Fusion, 2017, 33(C): 15-28. |
| [2] |
SHARMA S, D'AMICO S. Comparative assessment of techniques for initial pose estimation using monocular vision[J]. Acta Astronautica, 2016, 123(1–2): 435-445. |
| [3] |
WANG X, YU H, FENG D. Pose estimation in runway end safety area using geometry structure features[J]. Aeronautical Journal, 2016, 120(1226): 675-691. DOI:10.1017/aer.2016.16 |
| [4] |
D'AMICO S, BENN M, JØRGENSEN J L. Pose estimation of an uncooperative spacecraft from actual space imagery[J]. International Journal of Space Science and Engineering, 2013(2): 171-189. |
| [5] |
陈娟, 陈乾辉. 空间目标三维姿态估计方法综述[J]. 长春工业大学学报:自然科学版, 2008, 29(3): 323-327. CHEN Juan, Chen Qian-hui. Summary of the 3D pose estimations for the space targets[J]. Journal of Changchun University of Technology: Natural Science Edition, 2008, 29(3): 323-327. DOI:10.3969/j.issn.1674-1374-B.2008.03.020 |
| [6] |
肖旭. 单目视觉位姿测量方法的研究[D]. 天津: 天津大学, 2009. XIAO Xu. Study on the monocular vision measurement method [D]. Tianjin: Tianjin University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10056-2010091282.htm |
| [7] |
PAN H, HUANG J Y, QIN S Y. Relative pose estimation under monocular vision in rendezvous and docking[J]. Applied Mechanics and Materials, 2013, 433–435: 799-805. |
| [8] |
DEMENTHON D F, DAVIS L S. Model-based object pose in 25 lines of code[J]. International Journal of Computer Vision, 1995, 15(1/2): 123-141. |
| [9] |
GUO Z, LI Z, ZHANG D, et al. Research on pose estimation method for cooperative target based on monocular images [C] // 20116th IEEE Conference on Industrial Electronics and Applications (ICIEA). Beijing: IEEE, 2011: 547–552.
|
| [10] |
ÉRIC M, PATRICK B, FRANÇOIS C. A 2D-3D model-based approach to real-time visual tracking [J]. Image and Vision Computing, 2001, 19(13): 941–955. http://www.sciencedirect.com/science/article/pii/S0262885601000543
|
| [11] |
ROMEIL S, SAMUEL D, ANTHONY Y, et al. A nonrigid kernel-based framework for 2D-3D pose estimation and 2D image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(6): 1098-1115. DOI:10.1109/TPAMI.2010.162 |
| [12] |
宋薇, 周扬. 基于CAD模型的单目六自由度位姿测量[J]. 光学精密工程, 2016, 24(4): 882-891. SONG Wei, ZHOU Yang. Estimation of monocular vision 6-DOF pose based on CAD model[J]. Optics and Precision Engineering, 2016, 24(4): 882-891. |
| [13] |
吴立新, 王植, 孔祥勤. 盲环境移动定位(Ⅱ):基于单目视觉系统的定位技术[J]. 东北大学学报:自然科学版, 2011, 32(5): 736-739. WU Li-xin, WANG Zhi, KONG Xiang-qin. Mobile positioning in blind environments (II): positioning moving targets based on a monocular vision system[J]. Journal of Northeastern University: Natural Science, 2011, 32(5): 736-739. DOI:10.3969/j.issn.1005-3026.2011.05.032 |
| [14] |
PAN H, HUANG J, QIN S. High accurate estimation of relative pose of cooperative space targets based on measurement of monocular vision imaging[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(13): 3127-3133. DOI:10.1016/j.ijleo.2013.12.020 |
| [15] |
童张海. 单目视觉空间目标位姿测量算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. TONG Zhang-hai. Alogrithm of relative pose estimation for space target based on monocular-vision[D]. Harbin: Harbin Institute of Technology, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D241018 |
| [16] |
IWASHITA Y, KURAZUME R, HASEGAWA T, et al. Fast alignment of 3D geometrical models and 2D color images using 2D distance maps [C] // International Conference on 3D Digital Imaging and Modeling. Ottawa: IEEE Computer Society, 2005: 164–171.
|
| [17] |
LENG D W, SUN W D. Iterative three-dimensional rigid object pose estimation with contour correspondence[J]. IET Image Processing, 2012, 6(5): 569-579. DOI:10.1049/iet-ipr.2010.0435 |
| [18] |
ROSENHAHN B, BROX T, WEICKERT J. Three-Dimensional shape knowledge for joint image segmentation and pose tracking[J]. International Journal of Computer Vision, 2007, 73(3): 243-262. DOI:10.1007/s11263-006-9965-3 |
| [19] |
PAPARI G, PETKOV N. Edge and line oriented contour detection: state of the art[J]. Image and Vision Computing, 2011, 29(2–3): 79-103. |
| [20] |
DELAMARRE Q, FAUGERAS O. 3D articulated models and multi-view tracking with silhouettes[C] // IEEE International Conference on Computer Vision. Kerkyra: IEEE, 1999: 716–721.
|
| [21] |
POWELL M J. Developments of NEWUOA for minimization without derivatives[J]. IMA Journal of Numerical Analysis, 2008, 28(4): 649-664. DOI:10.1093/imanum/drm047 |
| [22] |
POWELL M J. Beyond symmetric Broyden for updating quadratic models in minimization without derivatives[J]. Mathematical Programming, 2013, 138(1/2): 475-500. |



