关于制药车间的研究广泛关注药品加工的工艺设计、车间洁净环境的设计管理及成本控制等，针对制药车间生产调度问题的研究甚少. 为使制药车间有限的生产资源得到有效利用，并最大限度地提高顾客满意度，对药品加工作业进行合理调度，最小化药品生产的最长工期，是非常必要的.

制药车间可以视为一种特殊的作业车间，多种药品同时加工，每种药品包含多道工序，且有特定的加工顺序. 每道工序可以在多台平行设备中的任意一台上加工，该类生产车间为柔性作业车间（flexible job shop scheduling problem, FJSP）. 另外，药物作为一种化学制剂，来自外界的轻微细菌或病毒感染，都会造成其发生非预期的反应和变质，这些损失对整个生产过程来说是不可估量的. 因此无菌生产在目前的制药企业是普遍且必须的. 但是绝对的无菌生产是很难实现的，假设生产系统中两工序之间是无等待的，这样可以尽量减少药品在细菌环境中的暴露时间，减少重复消毒.

作业车间调度问题（job shop scheduling problem, JSP）作为一种经典车间调度问题被广泛研究，JSP问题早已经被证明是NP难的，即使对小规模的问题，也不可能通过遍历所有可行解的方式获得最优解. 赵诗奎^[1]针对作业车间调度问题，以优化最大完工时间为目标，提出一种融合新型邻域结构的混合求解方法. 该混合算法由具有全局搜索能力的遗传算法和基于邻域结构的邻域搜索算法构成. 张梅等^[2]针对作业车间调度问题，提出一种基于个体差异化自学习的改进教学算法，在收敛精度和鲁棒性能上均有较好的提高. Shahrabi等^[3]采用Q因子加强学习算法解决考虑随机的作业到达和机器故障的作业车间动态调度问题. Asadzadeh^[4]提出了一种并行的人工蜜蜂算法来解决作业车间的问题，采用并行化方法提高启发式算法的性能.

考虑到工序间的无等待约束，Allahverdi^[5]对含有无等待约束的车间调度问题作了总结，重点关注无等待的作业车间调度问题（no-wait job shop scheduling problem, NWJSP）. Liaw^[6]提出了一种结合禁忌搜索算法的两阶段启发式算法求解两阶段的无等待作业车间调度问题. Samarghandi等^[7]对两阶段的无等待作业车间问题建立数学模型并提出了一种遗传算法. Aitzai等^[8]对于多阶段的无等待作业车间问题提出了一种改进分支策略的分支定界算法. Li等^[9]用一种新的局部搜索算法，基于记忆和变邻域结构求解多阶段的无等待作业车间问题.

Koulamas等^[10]分析了无等待作业车间调度问题的复杂性，对于两阶段的无等待作业车间调度问题，表明当各个作业每道工序的作业时间相等（称为均衡车间）时，该问题是多项式可解的，并给出了求解策略. 该类问题为无等待均衡作业车间调度问题（no-wait proportionate job shop scheduling problem, NWPJSP）. 当存在某些作业只经过其中一台设备，即存在工序缺失的情况时，该问题依然是NP难的.

柔性作业车间调度问题（flexible job shop scheduling problem, FJSP）是JSP问题的扩展，不仅需要确定工序的加工顺序，还要给每个工序分配机器，是复杂的NP难问题. 宁涛等^[11]针对多目标环境下柔性作业车间调度问题，以最小化最大完工时间和惩罚值为目标，建立调度问题的数学模型，提出了基于混沌理论的量子粒子群算法. 徐华等^[12]提出了一种混合离散蝙蝠算法求解多目标柔性作业车间调度问题. 仲于江等^[13]针对柔性作业车间调度中的多目标优化问题，构建了满足约束条件的多目标优化模型，提出一种将小生境技术和粒子群算法相结合求最优解的优化策略. 蒋增强等^[14]结合基于设备状态−能耗曲线的低碳策略，提出包括能源消耗、最大完工时间、加工成本和成本加权加工质量的多目标柔性作业调度模型，设计了基于血缘变异的改进非支配排序遗传算法. 高丽等^[15]针对柔性作业车间调度问题中多种资源分配的复杂特性，建立了多目标集成优化模型，并设计了一种具有多重资源约束的多目标集成优化方法. 张国辉^[16]针对柔性作业车间调度完工时间最小问题，提出一种结合鼓—缓冲器—绳子（drum-buffer-rope, DBR）理论和改进遗传算法的方法. 朱伟^[17]设计了一种具有柔性资源约束的多目标集成优化方法，建立了多目标组合优化模型，采用规则导向的资源调度思想，并结合动态规划法求解最优人员分配方案. 肖华军等^[18] 提出了一种将化学反应算法和禁忌搜索相结合的混合算法. 田旻等^[19]提出了一种分层混合遗传算法求解以总拖期最短为目标的柔性作业车间调度问题. 李聪波等^[20]建立了一种面向能耗的多工艺路线柔性作业车间分批优化调度模型，并采用多目标模拟退火算法对模型进行优化求解. Pezzella等^[21]提出了一种整合不同策略的遗传算法求解柔性作业车间调度问题，并验证了算法的有效性. Roshanaei等^[22]建立了柔性作业车间调度问题的数学模型并提出了一种元启发式算法进行求解.

考虑到工序间的无等待约束，对于有无等待约束的柔性作业车间调度问题（no-wait flexible job shop scheduling problem, NWFJSP），Raaymakers等^[23]提出了一种模拟退火算法求解多阶段调度问题的方法.

本文考虑一种有无等待约束的柔性均衡作业车间调度问题（no-wait proportionate flexible job shop scheduling problem, NWPFJSP），提出一种基于列生成思路的JPCG_DB算法，试图得到问题的较优解.

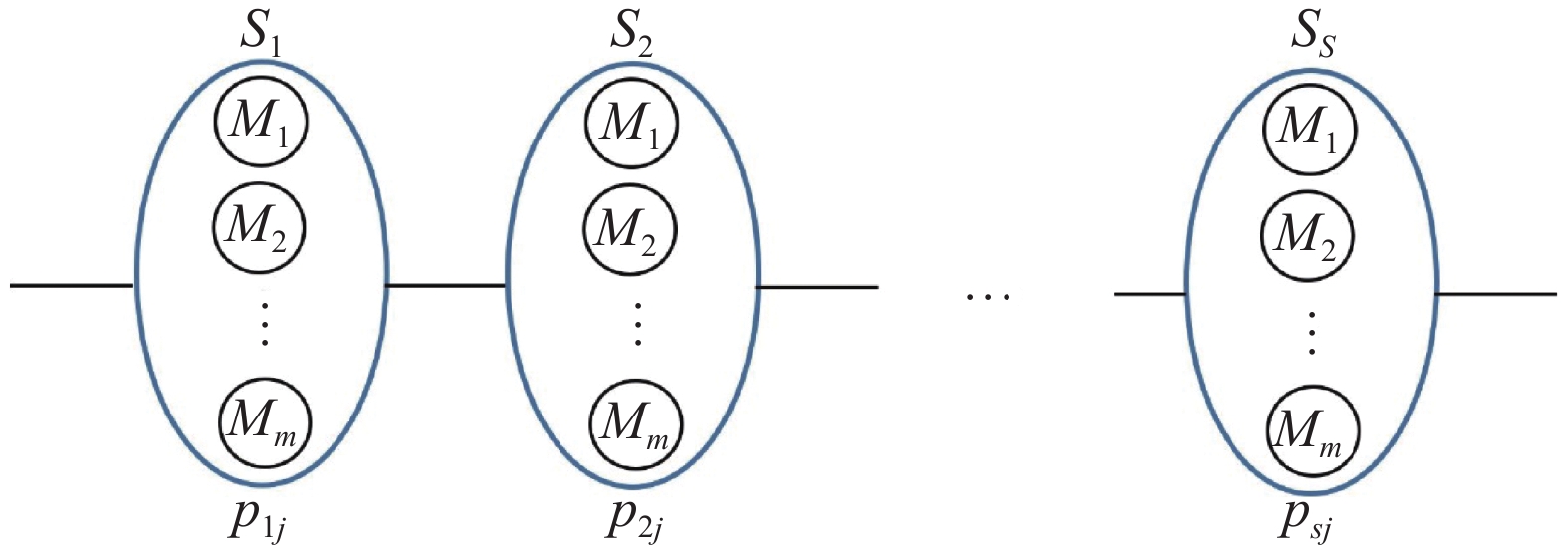
1 问题描述与建模 1.1 NWPFJSP问题描述

多阶段连续型制药车间调度模型如图1所示. 药品加工经过 $s$ 个阶段， $S = \left\{ {{{\rm{1}}},{{\rm{2}}},\cdots,{{{s}}}} \right\}$ ，每个阶段有 $m$ 台平行机， $M = \left\{ {{{\rm{1}}},{{\rm{2}}},\cdots,{m}} \right\}$ ，药品 $j$ 在阶段 s机器i上的加工时间为 ${p_{{}_{{ijs}}}}$ .

一批作业通过多道工序，在不同设备上完成加工，作业完成加工所需的工序数视为阶段 $s$ . 每个阶段包含 $m$ 台功能相同的平行设备，称该类车间为柔性作业车间. 作业 $j$ 在阶段 $s$ 的第 $i$ 台设备上的加工时间为 ${p_{{{ijs}}}}$ ，由于同一阶段中 $m$ 台机器功能相同，同一个作业在同一个阶段的不同机器上加工时间相同， ${p_{{\rm{1}}js}} = {p_{{\rm{2}}js}} = \cdots= {p_{{{ijs}}}} = \cdots = $ $ {p_{{{mjs}}}} = {p_{{{js}}}}$ . 假设同一个作业不同工序的加工时间相同，即 ${p_{{{j{\rm 1}}}}} = {p_{{{j{\rm 2}}}}} = \cdots = {p_{{j}}}$ . 同一作业不同工序之间满足无等待约束. 称该类车间为有无等待约束的柔性均衡作业车间（NWPFJSP）. 本研究考虑药品加工经过2个阶段的特殊情况 $S = \left\{ {{\rm{1}},2} \right\}$ .

制药车间一般存在批量问题，研究批量调度问题具有十分重要的现实意义. 在药品生产过程中，同一种产品通常组成一定数量的批次进行加工. 其中每批次作业可以分解为若干子批量进行加工，并将各子批量作为整体处理，甚至子批量大小均为可变的. 在考虑批量生产模式的柔性作业车间调度问题时，不仅要考虑作业分配和加工，还要考虑到作业可被分割为多个子批量，不同子批可选择不同调度方案. 适当的批量分割方法能有效减少设备的空闲等待时间，缩短生产周期.

在柔性作业车间的基础上，考虑作业批量问题. 假设有 $n$ 种待加工作业，每种作业有 ${D_{{n}}}$ 个，考虑以每个作业作为1个批量，将作业批量 ${D_{{n}}}$ 拆分为 $k$ 个子批，每个批次包含 $D_{{n}}^{{k}}$ 个作业，则对应于批量加工设备而言，加工作业量由 ${D_{{n}}}$ 减少为 $k$ ，本文的问题场景同样适用于该批量分割策略的批量生产柔性作业车间调度问题. 然而，当混合作业类型构成批次或同种作业加工时间波动较大时，则需要研究更为有效的批量分割策略.

柔性作业车间调度问题不仅需要安排各个作业的先后加工顺序，还要确定每个作业分别在各阶段中的哪一台设备上加工. 每个作业 $j$ 都含有2道工序 ${O_{{{{\rm 1}j}}}}{\text{和}}{\rm{ }}{O_{{{{\rm 2}j}}}}$ ，其中一部分作业按照 ${O_1} \to {O_2}$ （先加工工序1，再加工工序2）的工序顺序加工，其余部分作业按照 ${O_2} \to {O_1}$ （先加工工序2，再加工工序1)的工序顺序加工. 每个作业2道工序的加工时间相等，目标函数是最小化最大完工时间，具体描述如下.

1）有n个作业 ${{N}} = \left\{ {1,2,\cdots,n}\; \right\}$ 在2个阶段 ${{S}}= $ $ \left\{ {1,2} \right\}$ 完成加工；

2）每个阶段 $s \in {{S}}$ 有 $m$ 台同型机M = $ \left\{ {1,2,\cdots,m} \right\}$ ；

3）每个作业 $j \in {{N}}$ 包含2道工序 ${O_{{{sj}}}}(s \in S,j \in N)$ ，同一个作业的2道工序在2个阶段且每个阶段的任意一台设备上加工时间相等 ${p_{{\rm{1}}j}} = {p_{{\rm{2}}j}} = \cdots = {p_{{j}}}$ ；

4）加工过程中要满足无等待约束，也就是说同一个作业2个工序之间有先后约束，上一道工序 $O_{sj}$ 加工完成后立刻开始下一道工序 $O_{s + 1, j}$ . 同时，加工过程还要满足以下假设：在 $t = 0$ 时刻，所有作业都可以被加工；在 $t = 0$ 时刻，所有设备空闲，都可以被安排加工；同一时刻，同一台设备只能加工1道工序；工序一旦开始加工，不允许被打断，即每个阶段中每道工序只在1台设备上加工；各个作业之间是彼此独立的，不同作业的不同工序之间没有优先级约束.

1.2 NWPFJSP问题混合整数规划模型

对NWPFJSP问题，建立基于时间序列的混合整数规划模型.

${{N}}$ 为待加工药品集合， $N{\rm{ = }}\left\{ {{\rm{1,2,}}\cdots{\rm{,}}\;n} \right\}$ ； ${{M}}$ 为设备集合，每个阶段各有 $m$ 台同型机， ${{M = }}\left\{ {{\rm{1,2,}}\cdots{\rm{,}}m} \right\}$ ； ${{S}}$ 为阶段（工序）集合， ${{S = }}\left\{ {{\rm{1,2}}} \right\}$ ； ${p_{{j}}}$ 为作业 $j$ 在各阶段任意一台设备上的加工时间； ${{\rm{\psi }}_1}$ 表示工序顺序为 ${O_1} \to {O_2}$ 的作业集合； ${{\rm{\psi }}_{\rm{2}}}$ 表示工序顺序为 ${\rm{ }}{O_{\rm{2}}} \to {O_{\rm{1}}}$ 的作业集合.

自变量 ${x_{{{ijts}}}}{\rm{ = 1}}$ 表示 $t$ 时刻药品 $j$ 在阶段 $s$ 的第 $i$ 台设备上加工，否则 ${x_{{{ijts}}}}{\rm{ = 0}}$ ； ${S_{{j}}}$ 为作业 $j$ 开始加工时间； ${C_{{{js}}}}$ 为作业 $j$ 在阶段 $s$ 的完工时间； ${C_{{\rm{max}}}}$ 表示最长完工时间.

NWPFJSP问题的混合整数规划模型为

${\rm{Min}}\;{C_{{\rm{max}}}},$

(1)

${C_{{\rm{max}}}} \geqslant {C_{{{js}}}},\;\;j = 1,2,\cdots,n;\;s = 1,2.$

(2)

$\sum\limits_{{{i = 1}}}^{{m}} {\sum\limits_{{{t = 1}}}^{{T}}\; {{x_{{{ijts}}}} = {p_{{j}}}} } ;$

(3)

$\sum\limits_{{{j = 1}}}^{{n}}\; {{x_{{{ijts}}}}} \leqslant 1.$

(4)

$\sum\limits_{i = 1}^{m}\; {{x_{ijts}} \leqslant 1}. $

(5)

${C_{{{j1}}}} = {S_{{j}}} + {p_{{j}}},\;\;{{ }}{C_{{{j2}}}} = {S_{{j}}} + 2 \times {p_{{j}}}, \;\; j \in {\psi _1}.$

(6)

${C_{{{j2}}}} = {S_{{j}}} + {p_{{j}}},\;\;{{ }}{C_{{{j1}}}} = {S_{{j}}} + 2 \times {p_{{j}}}, \;\; j \in {\psi _2}.$

(7)

${C_{{{js}}}} - {p_{{j}}} + 1 \leqslant t + (1 - {x_{{{ijt}}}}) \times T.$

(8)

$\displaystyle\sum\limits_{{{t = 1}}}^{{T}}\; {{x_{{{ijts}}}}} \geqslant {p_{{j}}} \times {x_{{{ijts}}}}.$

(9)

${x_{ijts}} \in \left\{ {0,1} \right\}.$

(10)

目标函数（1）表示最小化所有待加工作业的最大完工时间. 式（2）表示最大完工时间的计算方法. 式（3）确保每个阶段中所有作业全部完成加工. 式（4）说明同一时刻，同一阶段的同一台设备上最多加工一个工序. 式（5）保证同一时刻，同一阶段中一个工序最多被分配到一台设备上加工. 式（6）和式（7）限制各个作业必须按照特定的工序顺序加工，同时满足无等待约束. 式（8）和式（9）保证不允许提前占用，式（8）确保同一阶段同一工序只能在一台设备上加工，式（9）确保工序连续加工不被打断. 式（10）指出变量 ${x_{{{ijts}}}}$ 的取值为0或1.

2 NWPFJSP问题的JPCG_DB算法

基于NWPFJSP问题的复杂性，设计一种基于列生成思路的JPCG_DB算法，试图求解该调度问题的较优解. JPCG_DB算法是在列生成算法^[24-25]的基础上，结合特定的排序策略J2_NWT规则，并在求解过程中结合使用动态规划和改进的分支定界策略，对NWPFJSP问题重新建模为由主问题和价格问题组成的整数规划模型并求解. JPCG_D算求解思路如下.

1）将所有作业按照J2_NWT规则组合为标准作业对并排序，将作业对重新编号.

2）生成一组初始解，并得到初始的限制性主问题.

3）循环：

a）求解限制性主问题，得到相应的对偶变量值；

b）将得到的对偶变量值带入价格问题中，求解价格问题；

c）将最小的reduced cost对应的新列加入到解集中，得到新的限制性主问题.

4）直到所有的reduced cost非负.

5）利用改进的分支定界策略得到整数解.

2.1 NWPFJSP问题的J2_NWT规则

Koulamas等^[10]分析了两阶段带有无等待约束的作业车间单机器调度问题（ ${\rm J2|prpt,nwt|}{C_{{\rm{max}}}}$ ）的复杂性，并对均衡车间，即各个作业2道工序加工时间相等的情况提出了最优排序策略. 该策略将显著减小求解NWPFJSP问题时的搜索空间. 考虑作业车间为柔性车间，即2个阶段分别有 $m$ 台同型机，用列生成方法将 $n$ 个作业安排到不同的机器上，而在同一设备上的各个作业的排序规则按照J2_NWT 规则进行排序.

定义一：作业对. $n$ 个被分为 ${\varPsi _1}$ 和 ${\varPsi _2}$ 两个集合，对任意作业 ${j_1} \in {\varPsi _1},{\rm{ }}{j_2} \in {\varPsi _2}$ ，在任意一对设备组合 ${M_1} \in {S_1},{M_2} \in {S_2}$ 上加工，作业 ${j_1}$ 第一道工序在设备 ${M_1}$ 上的完工时间为 ${C_{{{j{\rm 1}}}}}$ ，作业 ${j_2}$ 第一道工序在设备 ${M_2}$ 上的完工时间为 ${C_{{{j{\rm 2}}}}}$ ，若 ${C_{{{j{\rm 1}}}}} = {C_{{{j{\rm 2}}}}}$ ，作业 ${j_1}$ 第一道工序加工完成后立刻在 ${M_2}$ 上加工第二道工序，作业 ${j_2}$ 第一道工序完成后立刻在 ${M_1}$ 上加工第二道工序，实现作业工序间的无等待约束. 以这种形式存在的两个作业称为作业对 $p({j_1},{j_2})$ .

定义二：标准作业对. 满足以下条件的作业对为标准作业对.

标准作业对规则： ${\varPsi _1}$ 和 ${\varPsi _2}$ 集合中的作业分别按照SPT的规则进行排序， ${p_{{j}}}({q_{{j}}})$ 表示集合 ${\varPsi _1}({\varPsi _2})$ 中第 $j$ 个位置作业的加工时间. 如果 $\left| {{\varPsi _1}} \right| = \left| {{\varPsi _2}} \right|$ ，令 $k = \max \left\{ {\left| {{\varPsi _1}} \right|,\left| {{\varPsi _2}} \right|} \right\}$ ，加入必要的虚拟作业 ${p_{{j}}} = 0$ 或 ${q_{\rm{j}}} = 0$ 使得 $\left| {{\varPsi _1}} \right| = \left| {{\varPsi _2}} \right| = k$ . 此时集合 ${\varPsi _1}$ 和 ${\varPsi _2}$ 中分别有 $k$ 个作业，且按照加工时间从小到大的顺序排列. ${\varPsi _1}$ 和 ${\varPsi _2}$ 中相应位置的作业 $j$ 和 $j'$ 的作业对 $p(j,j')$ 称为标准作业对 $X(j,j')$ ，可以得到 $k$ 个标准作业对，每个作业对包含一个来自集合 ${\varPsi _1}$ 和一个来自集合 ${\varPsi _2}$ 的作业.

定义三：J2_NWT排序规则.

将 $k$ 个标准作业对根据 ${p_{{j}}}$ 和 ${q_{{j}}}$ 的大小关系分为两个不同的组，满足 ${p_{{j}}} \leqslant {q_{{j}}}$ 的作业对属于G1，满足 ${p_{{j}}} \geqslant {q_{{j}}}$ 的作业对属于G2. G1中 ${\alpha _{{j}}} = {q_{{j}}} - {p_{{j}}} \geqslant 0$ 和G2中 ${\beta _{{j}}} = {p_{{j}}} - {q_j} \geqslant 0$ 分别表示该作业对被安排加工时的机器空闲时间. 最终排序按照先G2后G1的顺序对所有作业对进行排序，其中G2内部按照 $\beta $ 的升序排列，G1内部按照 $\alpha $ 的降序排列. 可以得到最大完工时间：

${C_{\max }} = \sum\limits_{{{j}} = 1}^{{k}}\; {({p_{{j}}} + {q_{{j}}}) + {\alpha _{\max }} + {\beta _{\max }}}.$

(11)

定理2.1：按照J2_NWT排序规则可得到 ${\rm J}2|{\rm{prpt,nwt}}|{C_{\max }}$ 问题的最优排序.

证明：随机考虑集合 ${\rm{J}}12$ 按照加工时间从小到大顺序排列过的相邻2个作业 $j$ 和 $j + 1$ ，以及集合 ${\rm{J}}21$ 按照加工时间从小到大顺序排列过的相邻两个作业 $j'$ 和 $j' + 1$ . 按照上述定义，组成的标准作业对为 $(j,j')$ 和 $(j + 1,j' + 1)$ ，考虑不同的作业对组合方式 $(j,j' + 1)$ 和 $(j + 1,j')$ （此处称为新作业对）并验证其优良性. 集合 ${\rm{J}}12$ 中作业 $j$ 的加工时间为 ${p_{{j}}}$ ，集合 ${\rm{J}}21$ 中作业 $j'$ 的加工时间为 ${q_{{j}}}$ . 当作业对属于不同的组G1或 G2时，会影响作业对之间的排序顺序及最终的最大完工时间. 所以分以下几种情况进行讨论.

1）2对标准作业对和2对新作业对都属于G2组. 由

${p_{{{j + 1}}}} \geqslant {p_{{j}}},\;{q_{{{j + 1}}}} \geqslant {q_{{j}}}.$

可得

${p_{{{j + 1}}}} - {q_{{{j + 1}}}} \leqslant {p_{{{j + 1}}}} - {q_{{j}}},\;{p_{{j}}} - {q_{{j}}} \leqslant {p_{{{j + 1}}}} - {q_{{j}}}.$

因此，

$\max\, \left\{ {{p_{{j}}} - {q_{{j}}},{p_{{{j + 1}}}} - {q_{{{j + 1}}}}} \right\} \leqslant \max\, \left\{ {{p_{{j}}} - {q_{{{j + 1}}}},{p_{{{j + 1}}}} - {q_{{j}}}} \right\}.$

即 ${\beta _{\max }} \leqslant \beta _{\max }'.$ 又因为 ${\alpha _{{\rm{max}}}} = \alpha _{\max }'.$ 则

${\alpha _{\max }} + {\beta _{\max }} $ $\leqslant \alpha _{\max }' + \beta _{\max }',\;{C_{\max }} \leqslant C_{\max }'.$

得证. 当2对标准作业对和两对新作业对都G1组时，证明过程相同.

2）标准作业对中一对属于G2组，一对属于G1组，新作业对中一对属于G2组，一对属于G1组. 新作业对中

$\beta _{\max }' = {p_{{{j{\rm + 1}}}}} - {q_{{j}}},\alpha _{\max }' = {q_{{{j{\rm + 1}}}}} - {p_{{j}}}.$

若标准作业对中

${\beta _{\max }} = {p_{{{j{\rm + 1}}}}} - {q_{{{j{\rm + 1}}}}},{\alpha _{\max }} = {q_{{j}}} - {p_{{j}}}.$

则有

${\alpha _{\max }} + {\beta _{\max }} \leqslant \alpha _{\max }' + \beta _{\max }'.$

若标准作业对中

${\beta _{\max }} = {p_{{j}}} - {q_{{j}}},{\alpha _{\max }} = {q_{{{j{\rm + 1}}}}} - {p_{{{j{\rm + 1}}}}}.$

同样有

${\alpha _{\max }} + {\beta _{\max }} \leqslant \alpha _{\max }' + \beta _{\max }'.$

得证.

2对标准作业对都属于G2组，新作业对中一对属于G2组一对属于G1组. 标准作业对中

${\beta _{\max }} = \max \;\left\{ {{p_{{j}}} - {q_{{j}}},{p_{{{j + 1}}}} - {q_{{{j + 1}}}}} \right\}.$

新作业对中

$\beta _{\max }' = {p_{{{j + 1}}}} - {q_{{j}}},\;\alpha _{\max }' = {q_{{{j + 1}}}} - {p_{{j}}}{\rm{.}}$

则 ${\alpha _{\max }} \leqslant \alpha _{\max }',\;{\beta _{\max }} \leqslant \beta _{\max }'.$ 因此，

${\alpha _{\max }} + {\beta _{\max }} \leqslant \alpha _{\max }' +$ $ \beta _{\max }',\;{C_{\max }} \leqslant C_{\max }'.$

得证.

当2对标准作业对都属于G1组，新作业对一对属于G2组一对属于G1组时，证明过程相同.

2.2 NWPFJSP问题的主问题

假设各工序的加工时间 ${p_{\rm{j}}}(j = 1,2,\cdots,n)$ 都是整数，全部作业已按J2_NWT规则排序并重新编号，有标准作业对 ${{K}} = \left\{ {1,2,\cdots,k} \right\}$ .

定义四：列. $k$ 个标准作业对被分配到 $m$ 组设备组合上加工，设备组 ${M_{{m}}}$ 上的所有标准作业对 $X(j,j')$ 按照J2_NWT规则组成的序列成为“列”. 最终调度方案包含 $m$ 列.

用 $\theta $ 表示一列， $\vartheta $ 表示 $\theta $ 作为元素构成的集合 $(\theta \in \vartheta )$ . ${C_{{\rm{\theta max}}}}$ 为列 $\theta $ 的最大完工时间； ${{{a}}_{{{j\theta }}}} = 1$ 表示列 $\theta $ 中包含作业 $j$ ，否则 ${{{a}}_{{{j\theta }}}} = 0$ ； ${y_{\rm{\theta }}} = 1$ 表示最终调度方案中包含列 $\theta $ ，否则 ${y_{\rm{\theta }}} = 0$ .

根据式（11）， ${C_{{\rm{\theta max}}}}$ 可以表示为

${C_{{\rm{\theta max}}}} = \sum\limits_{{{j {\rm= 1}}}}^{{k}} \;{{a_{{{j{\rm \theta}}}}}({p_{{j}} } + {q_{{j}}}) + {\alpha _{{\rm{\theta max}}}} + {\beta _{{\rm{\theta max}}}}.} $

目标函数为

$\min \;{C_{\max }} = \min \max \;\left({C_{{\rm{\theta max}}}}{y_{\rm{\theta }}}\right).$

主问题可以表述为

$\min \;{C_{\max }};$

(12)

$\sum\nolimits_{{\rm{\theta }} \in \vartheta } \;\left({{a_{{{j{\rm\theta}}}}}{y_{\rm{\theta }}}}\right) = 1 , \;\; j \in K;$

(13)

$\sum\nolimits_{{\rm{\theta }} \in \vartheta } \;{{y_{\rm{\theta }}} = m;} $

(14)

${C_{\max }} \geqslant {C_{{\rm{\theta max}}}}{y_{\rm{\theta }}}, \;\; \theta \in \vartheta ;$

(15)

${y_{\rm{\theta }}} \in \left\{ {0,1} \right\}, \;\; \theta \in \vartheta .$

(16)

目标函数（12）是最小化所选择的列中最大的完工时间. 式（13）限制每个作业恰好在某设备组合上被加工1次. 式（14）说明最终调度方中刚好选择 $m$ 列，因为两个阶段分别有 $m$ 台设备并组成 $m$ 个设备组加工 $k$ 个作业组. 式（15）定义了调度方案的最大完工时间. 式（16）表明自变量 ${y_{\rm{\theta }}}$ 是0-1变量.

主问题MP是一个整数规划模型，将式（16） ${y_{\rm{\theta }}} \in \left\{ {0,1} \right\}$ 松弛为线性约束 ${y_{\rm{\theta }}} \in \left[ {0,1} \right]$ ，得到限制性主问题（RMP）. RMP是一个线性规划问题，对其求解得到相应的对偶变量值.

2.3 NWPFJSP问题的价格问题

利用限制性主问题得到的对偶变量值表示相应的价格问题，记 ${\pi _{{j}}}(j \in K)$ 为对应与式（13）的对偶变量值， $\pi $ 为对应于式（14）的对偶变量值，相应的价格问题可以表述为

${\min _{{\rm{\theta }} \in \vartheta }}\;{r_{\rm{\theta }}}.$

${r_{\rm{\theta }}} = {C_{{\rm{\theta max}}}} - \sum\nolimits_{{{j = 1}}}^{{k}}\;({{a_{{{j{\rm\theta}}}}}{\pi _{{j}}}) - \pi .} $

由于对任意的 $\theta \in \vartheta $ ， $\pi $ 是与 $\theta $ 无关的常数， $ - \pi $ 可以忽略. 于是，价格问题的目标函数可以表述为

$\begin{array}{l}\min \;\left[ {{C_{{\rm{\theta max}}}} - \displaystyle\sum\limits_{{\mathop{j}\nolimits} = 1}^{{k}} \;\Big({{a_{{{j{\rm \theta} }}}}{\pi _{{j}}}} }\Big) \right] = \\ \min \;\left[ {\displaystyle\sum\limits_{{{j {\rm = 1}}}}^{{k}} \;\Big({{a_{{{j{\rm \theta} }}}}({p_{{j}}} + {q_{{j}}})\Big) + {\alpha _{{\rm{\theta max}}}} + {\beta _{{\rm{\theta max}}}} - \displaystyle\sum\limits_{{{j {\rm= 1}}}}^{{k}} \;\Big({{a_{{{j{\rm \theta} }}}}{\pi _{{j}}}} } }\Big) \right].\end{array}$

价格问题的求解结果为满足该目标函数时所得到的一个列，对应一部分作业对在一组设备上加工，加工序列满足J2_NWT排序规则. 很明显，此处价格问题不是经典的背包问题或旅行商问题等可以直接用成熟算法求解的问题，所以考虑用动态规划求解价格问题.

动态规划算法步骤如下：

1）初始化

${F_0}(t) = \left\{ \begin{array}{l}0,\;\;\;\;\;\;\;\;\;\;t = 0;\\\infty ,\;\;\;\;\;\;\;\;t \ne 0.\end{array} \right.$

2）递推关系

$\begin{array}{l}{F_j}(t) = \left\{ \begin{array}{l}\min\; \left\{ {{{{F}}_{{{j {\rm - 1}}}}}(t),F_j^*(t)} \right\},\;\;\;\;\;t \geqslant {p_{{j}}} + {g_{{j}}};\\{{{F}}_{{{j - 1}}}}(t),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\quad\;\;\,{\text{其他}}.\end{array} \right.\end{array}$

3）求解

${\min _{{{j}} \in {{K}},0 \leqslant {{t}} \leqslant {{T}}}}{F_{{j}}}(t).$

步骤2）中T为所有作业均在一组设备上加工的时间总和：

${{T}} = {C_{\max }} = \sum\limits_{{{j{\rm = 1}}}}^{{k}} \;{({p_{{j}}} + {q_{{j}}}) + {\alpha _{{\rm max}}} + {\beta _{{\rm max}}}.} $

$F_{{j}}^{\rm{*}}(t)$ 的计算方法: 由于各个作业对存在一定的gap值（即 ${\alpha _{{j}}}$ 和 ${\beta _{{j}}}$ ），不同作业对组合时不是单纯的2个作业时间之和，需要考虑gap之间的连接关系. 对于当前药品 $j$ ，在当前时间 $t$ ，需要分别考察药品 $1:j - 1$ 与当前药品 $j$ 的组合可能性，如果当前时间区间 $t$ 足够容纳某个作业组合，计算该组合形式的目标函数值，所有组合可能中的最小值即为 $F_{{j}}^{\rm{*}}(t)$ .

上述动态规划算法的求解结果得到价格问题的最优解 $\theta *$ 和相应的目标值 $r_\delta ^*$ .

若 $r_\delta ^* \geqslant 0$ ，当前解即为限制性主问题的最优解；若 $r_\delta ^* < 0$ ，则在限制性主问题中添加新列 $\theta *$ ，再次求得相应的对偶变量值并求解新的子问题. 直到 $r_\delta ^* \geqslant 0$ .

2.4 改进的分支定界算法

通过主问题和价格问题的求解，得到一组由 ${y_{\rm{\theta }}}$ 组成的线性松弛解，其中包含多个列 $\theta $ ，当所有的自变量 ${y_{\rm{\theta }}}$ 都取1时，得到最优调度方案，恰好包含 $m$ 列， $k$ 个作业对恰好被分配在 $m$ 组设备上完成加工. 当自变量 ${y_{\rm{\theta }}}$ 存在分数解时，采用改进的分支定界算法，找到最优的整数解.

此处不能沿用传统的分支定界策略，即直接对自变量 ${y_{\rm{\theta }}}$ 进行分支. 因为若某个 ${y_{\rm{\theta }}} = 0$ 意味着该列中所有的作业对被从作业集合中去除，对应的这组设备组合上没有安排作业加工. 显然，此种策略无法得到对所有作业的有效排序. 所以考虑改进分支定界策略，对变量 ${x_{{{ij}}}}$ 进行分支，采用深度优先的策略.

用变量 ${x_{{{ij}}}}$ 表示在某台设备上作业 $j$ 在作业 $i$ 紧后加工；

${x_{{{i}}j}} = \sum\limits_{\rm{\theta }}\; \left({{x_{{{ij{\rm \theta}}}}}{y_{\rm{\theta }}}}\right) .$

如果作业 $j$ 和作业 $i$ 在同一台机器上加工，并且作业 $j$ 在作业 $i$ 紧后加工，则 ${x_{{{ij}}}} = 1$ ；否则 ${x_{{{ij}}}} = 0$ . 很明显，在得到的线性松弛解中，如果所有的变量 ${y_{\rm{\theta }}}$ 都是整数，则相应的变量 ${x_{{{ij}}}}$ 也全为整数；如果存在变量 ${y_{\rm{\theta }}}$ 不是整数，则一定存在相应的变量 ${x_{{{ij}}}}$ 非整. 选择满足 ${x_{{{hl}}}} = \arg {\min _{{{{x}}_{{{ij}}}}}}\left\{ {\left| {{x_{{{i}}j}} - 0.5} \right|} \right\}$ 的变量 ${x_{{{ij}}}}$ 分为2支： ${x_{{{hl}}}} = 0$ 和 ${x_{{{hl}}}} = 1$ . 如果另 ${x_{{{hl}}}} = 0$ ，则限制作业 $l$ 不能在作业 $h$ 的紧后加工；如果另 ${x_{{{hl}}}} = 1$ ，则限制作业 $l$ 一定要在作业 $h$ 的紧后加工.

3 算例分析

如表1所示，给出一些实际算例，用JPCG_DB算法求解并与CPLEX结果比较，验证算法的有效性. 其中JPCG_DB算法用Matlab 2016a 编写. 给出的算例中，待加工的作业的数量 $n$ 取值范围为[3，20]区间内的整数；机器台数 $m$ 取值为2、3、4、5；加工时间 $p$ 分别是区间[1，7]和[8，15]的均匀分布.表1分别列出了CPLEX和JPCG_DB算法的目标函数值和CPU时间. 表1中，V为目标函数值， $\eta $ 表示算法求解问题最优解所需要的CPU时间，g表示JPCG_DB算法所求得的最优解和CPLEX最优解的差值. 若在一小时之内得不到目标方案和目标函数值，用符号“—”表示.

由表1可以看出，CPLEX只能求得小规模算例 $(3 \leqslant n \leqslant 5)$ 的最优解，对于中大规模 $(6 \leqslant n \leqslant 20)$ 算例CPLEX无法在有效时间内求得目标函数值. 为了验证JPCG_DB算法的有效性，对于小规模算例，将JPCG_DB算法得到的目标函数值与CPLEX求得的最优解进行对比，结果表明JPCG_DB算法可以在很短的时间内得到最优解，从而验证了算法的有效性. 说明该算法对于求解复杂的大规模整数规划模型有很好的表现. 对于中大规模算例，没有有效的最优解可以用来验证JPCG_DB算法的有效性，但是计算结果表明该算法依然可以在较短时间内得到可行方案，该目标函数值可以作为问题的上界，并对实际生产制造有一定的指导作用.

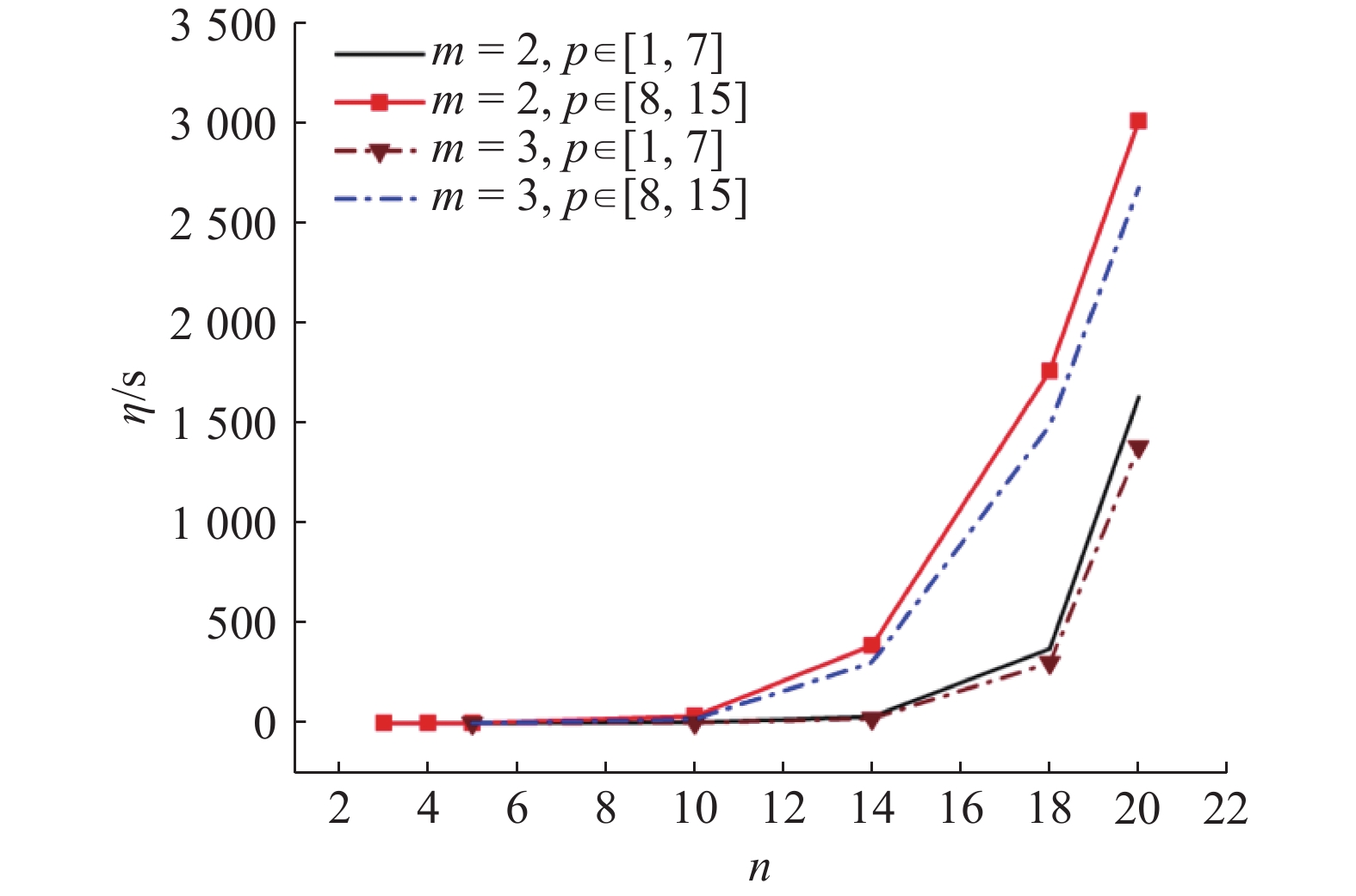
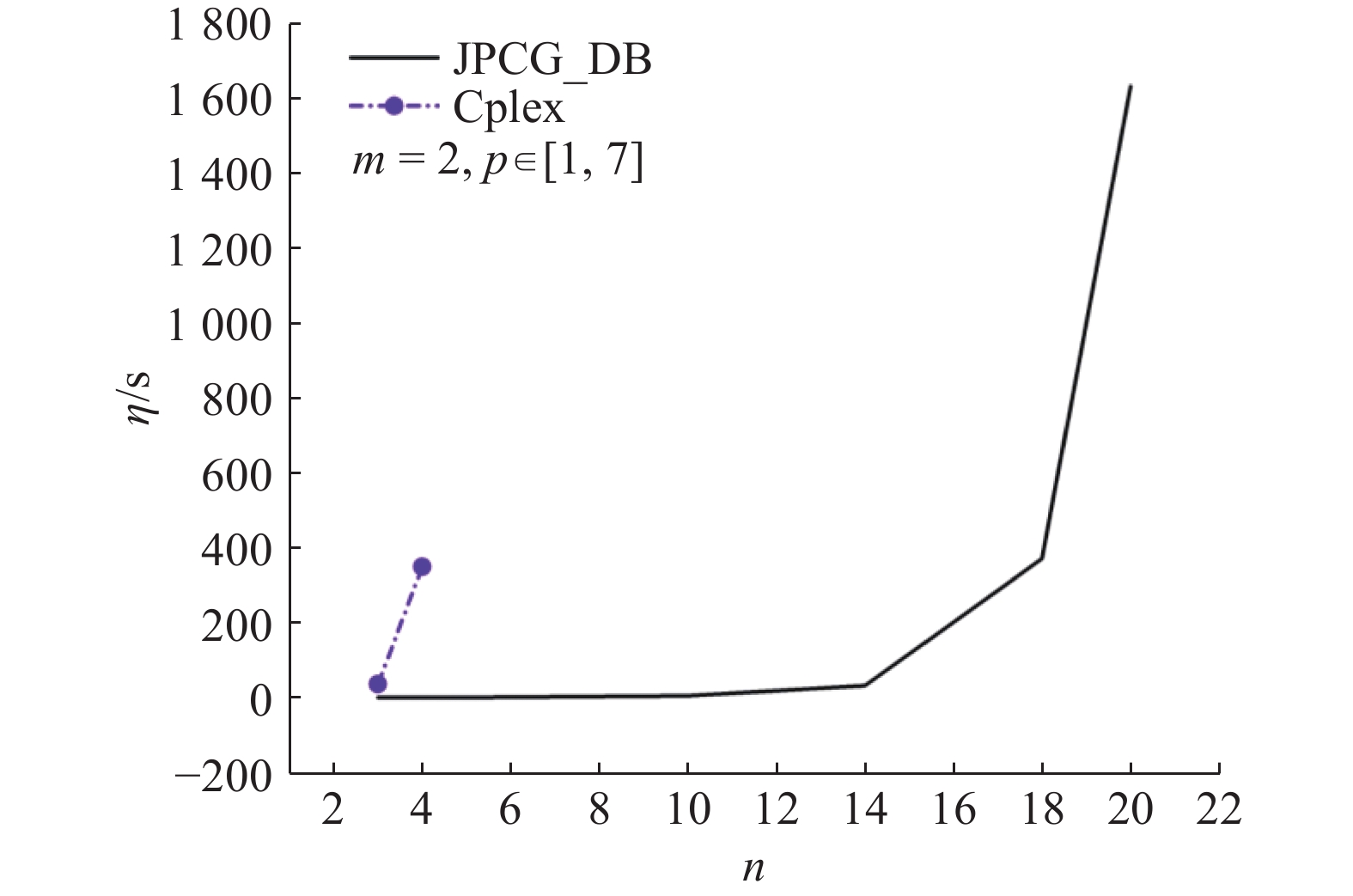
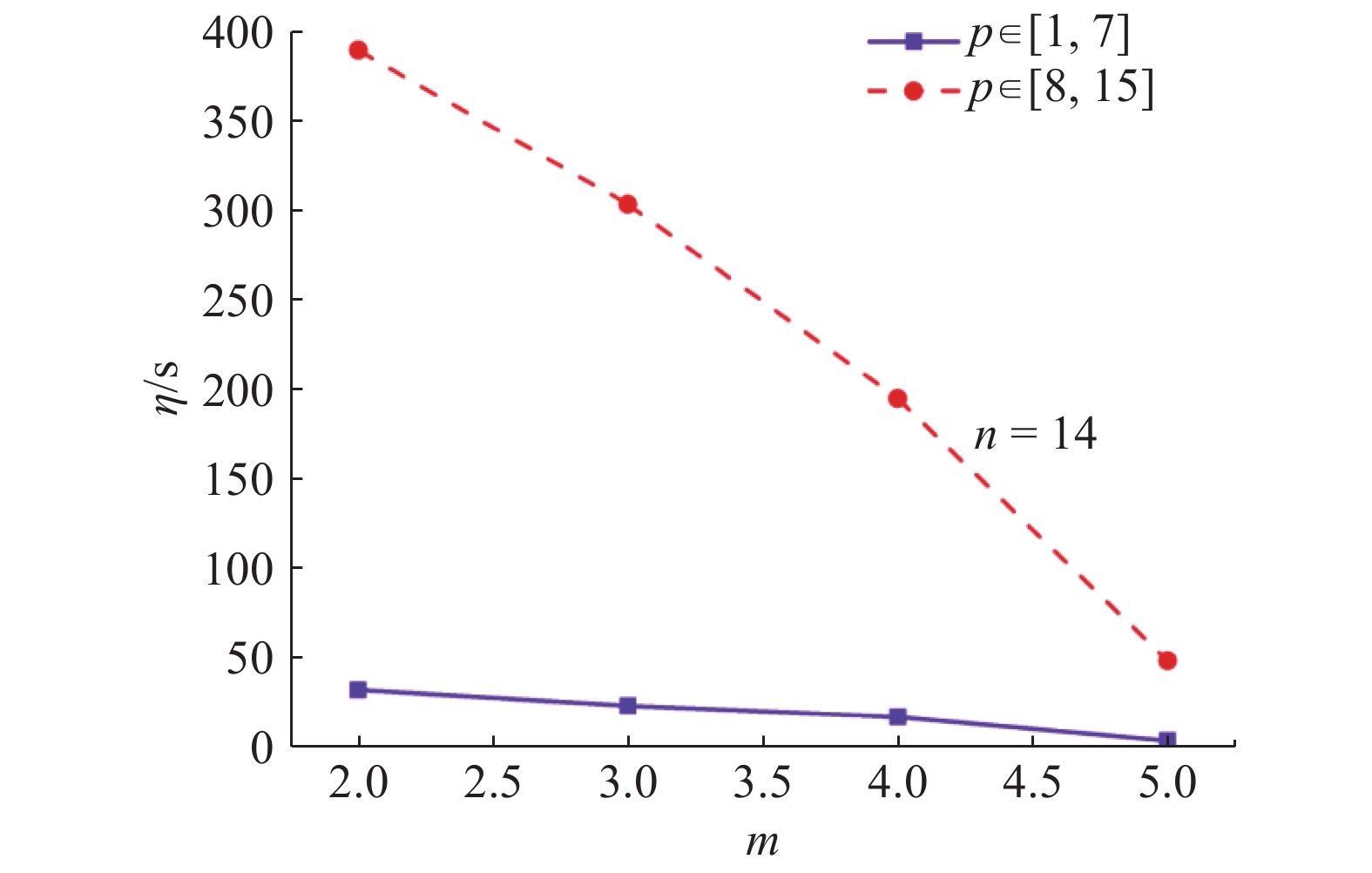
如图2所示为JPCG_DB算法计算时间与作业数的关系，如图3所示为当机器台数 $m = 2$ ，加工时间 $p \in \left[ {1,7} \right]$ 时，JPCG_DB算法计算时间与CPLEX的比较. 如图4所示为当作业数 $n = 14$ 时JPCG_DB算法计算时间与机器台数关系. 图2表明当机器台数一定时，JPCG_DB算法计算时间随作业数的增大而增大. 这与直观的结论是相符合的，当机器台数一定时，作业数越多，作业之间的组合和排序的可能性越多，问题求解则越复杂，计算时间越长. 由图3可知，CPLEX仅仅可以计算很小规模的算例，当作业数大于5时CPLEX无法求解，而本文提出的JPCG_DB算法依然可以在可接受的时间内得到有效的解，验证了算法的有效性. 值得注意的是，图4表明，当作业数一定时，机器台数越多JPCG_DB算法计算时间越小. 直观上，当机器台数越多时排序问题越复杂，但是恰恰相反. 试想一下，当机器台数大于作业个数时，只需简单地将各个作业分配到某几台机器上加工而已，并不涉及组合和排序的问题，所以机器台数越多，问题的复杂性越低，计算时间越短.

4 结　语

本文针对多阶段连续型制药柔性车间的调度问题，设计了基于列生成思路的JPCG_DB算法，结合特定的作业排序规则，用动态规划算法求解价格问题，并通过改进分支定界算法，尝试获得包含无等待约束的柔性均衡制药车间调度问题的近优解. 通过算例分析，对于小规模问题，JPCG_DB算法能在较短时间内得到最优解，对于较大规模问题，CPLEX无法在给定时间范围内得到可行解，而JPCG_DB算法却仍然能够在可接受时间范围内得到较优的结果. 本文提出的JPCG_DB算法可为多阶段连续型制药车间调度问题提供一类新的求解思路.