微小卫星[1]是以微机电技术为核心的新概念卫星,主要通过分散的星座结构[2]和编队[3-4]进行组网工作,协同完成空间大范围成像、立体成像和星间测距[5]等任务,将在未来的空间探索和商业应用中发挥重要作用. 随着集成电路的日益发展以及数字处理芯片能力的增强,应用于微小卫星的测控应答机正朝着小型化和低功耗的方向发展. 零中频架构[6]是目前集成度最高的发射架构之一,相比于传统的超外差架构,零中频架构有体积小、成本低、便于单片集成和实现多标准、多频段的发射等优点. 零中频发射架构具有巨大的商业价值,在无线通信领域也受到了广泛的关注,成为移动通信的主流方向.
在新一代微小卫星射频单片集成应答机的设计中,为了进一步压缩体积和降低功耗,模拟基带和射频处理一般由高度集成的软件无线电平台芯片来完成. 由于模拟器件的局限性,原本正交的I/Q两路并不一定呈90°,I/Q两路的幅度增益也不完全相同. 虽然高性能的模拟器件可以抑制I/Q不平衡的影响,但是设备的体积越大,功耗和成本越高. 此外,高性能的模拟器件在不同的环境(温度、频率等)下抑制I/Q不平衡的能力不同,在模拟域中不是抑制I/Q不平衡的有效途径. 但是,在数字域中,模拟器件对I/Q不平衡的估计是实时的,可以针对不同的环境作出相应的补偿. 在数字域使用I/Q不平衡校正算法进行补偿的成本比在模拟域低很多,并且具有较强的适应性.
针对I/Q不平衡的校正问题,Hsu等[7-8]提出利用训练序列联合估计和补偿信道、发射机和接收机的I/Q不平衡的方法,但是当系统引入相位噪声等干扰时,方法的性能急剧下降,而且实现联合估计的复杂度较高. Wang等[9-10]提出在正交频分复用(orthogonal frequency division multiplexing,OFDM)系统中基于频域最小二乘法的信道估计法,该方法结合了信道的时域特性,性能较好,但是计算较复杂. Shu等[11]建立了应用于稀疏无线信道的时域最小二乘法估计模型,提出迭代收缩信道估计方法,该方法简洁,但是难以实现对I/Q不平衡的补偿. 李建宇[12]提出基于查找表的开环发射机I/Q不平衡的补偿方法,但是只能补偿温度变化引起的I/Q不平衡,并且实现方法的工作量较大,不具有可移植性. 邹世源等[13]提出基于查找表的闭环发射机I/Q不平衡的补偿方法,稳定性比开环校正系统高,但是当系统引入频偏和噪声等影响时,系统性能大幅下降,并且实现方法的工作量较大.
提出基于模拟退火算法(simulated annealing algorithm, SAA)[14]的I/Q不平衡校正方法. 发射机射频端的反馈回路提供的反馈信息经过一定的数字信号处理后,表征当前补偿因子组合下的I/Q不平衡程度,结合SAA启发式随机搜索能力,快速、有效地搜索出用于补偿I/Q不平衡的幅度和相位因子. 利用补偿因子,在数字基带处提前补偿待发射的信号,实现对I/Q不平衡的校正.
1 I/Q不平衡的分析 1.1 非理想平衡下的信号分析假设I/Q两路的基带信号为正交的正弦信号,角频率为w0,各自的初始相位都为0:
| $I = \cos \;{\rm{ }}({w_0}t){\text{,}}$ | (1) |
| $Q = \sin \;{\rm{ }}({w_0}t). $ | (2) |
式中:I为同相支路信号,Q为正交支路信号,t为时间.
假设由非平衡传输链路所引入的相位差为p(w),其中,w为信号的频率. 实际相位差主要取决于信号的频率. 假设A为I路的幅度增益,B为Q路的幅度增益. 基带信号经过非平衡传输链路后变为
| $I = A\cos {\rm{ }}\;({w_0}t){\text{,}}$ | (3) |
| $Q = B\sin {\rm{ }}\;({w_0}t + p(w)). $ | (4) |
假设正交混频器是完全正交的,正交的本振信号角频率为
| ${I_{{\rm{LO}}}} = \cos {\rm{ }}\;({w_{{\rm{LO}}}}t){\text{,}}$ | (5) |
| ${Q_{{\rm{LO}}}} = \sin {\rm{ }}\;({w_{{\rm{LO}}}}t). $ | (6) |
经过正交调制后得到的射频输出信号为
| $\begin{array}{*{20}{c}}{{\rm{R}}{{\rm{F}}_{{\rm{out}}}} = I{I_{{\rm{LO}}}} - Q{Q_{{\rm{LO}}}} = }\\{A\cos \;({w_0}t)\;\cos \;({w_{{\rm{LO}}}}t) - B\sin \;\Big({w_0}t + p(w)\Big)\;\sin \;({w_{{\rm{LO}}}}t) = }\\{A\cos \;\Big[({w_{{\rm{LO}}}} + {w_0})t\Big] - \Big[C(w)/2\Big]\;\sin \;\Big[({w_{{\rm{LO}}}} + {w_0})t + \alpha\Big] + }\\{\Big[C(w)/2\Big]\;\sin \;\Big[({w_{{\rm{LO}}}} - {w_0})t - \alpha\Big] .}\\\end{array}$ | (7) |
式中:
| $C(w) = \bigg\{{{\Big[A - B\cos\; {\rm{ }}\big(p(w)\big)\Big]}^2} + {{\Big[B\sin\; {\rm{ }}\big(p(w)\big)\Big]}^2}\bigg\}^{1/2},$ | (8) |
| $\sin \;\alpha = \frac{{A - B\cos \;\big(p(w)\big)}}{{{\rm{\bigg\{ }}{{\Big[A - B\cos \;\big(p(w)\big)\Big]}^2} + {{\Big[B\sin \;\big(p(w)\big)\Big]}^2}{\rm{\bigg\}^{1/2} }}}},$ | (9) |
| $\cos \;\alpha = \frac{{B\sin \;\big(p(w)\big)}}{{{\rm{\bigg\{ }}{{\Big[A - B\cos \;\big(p(w)\big)\Big]}^2} + {{\Big[B\sin \;\big(p(w)\big)\Big]}^2}{\rm{\bigg\}^{1/2} }}}}.$ | (10) |
射频输出信号中包含3部分信号.
1)信号1 Acos [(w0+wLO)t]为有用信号,出现在射频本振的上边带;
2)信号2 [C(w)/2]sin [(wLO+w0)t+α]为与有用信号相差相位为α的一个同频干扰信号;
3)信号3 [C(w)/2]sin [(wLO−w0)t−α]为有用信号的镜像干扰信号,出现在射频本振的下边带.
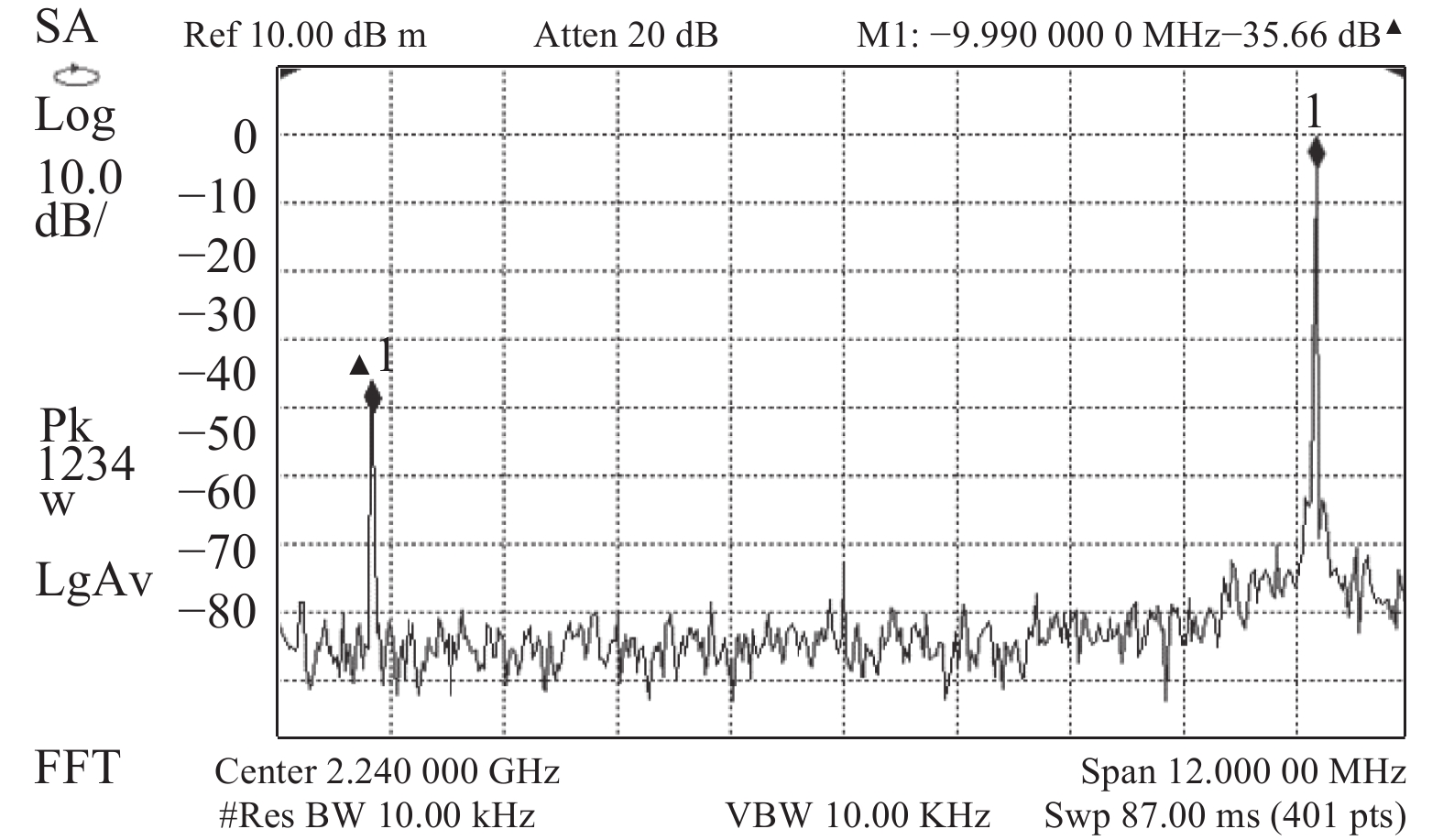
如图1所示,当存在I/Q不平衡时,发射机射频输出信号中,除了有用的上边带信号以外,在下边带还存在镜像干扰信号. 干扰信号不仅降低系统的发射效率,而且同频干扰信号大大增加了接收机的误码率,即使在发射机射频输出处采用窄带滤波器,也无法有效滤除. 对I/Q不平衡进行校正后,干扰信号的强度C(w)/2随之下降,同频干扰信号与镜像干扰信号的功率同时减小. 所以,对I/Q不平衡进行有效校正具有重要意义.
|
图 1 未进行I/Q不平衡校正的发射机射频输出处频谱 Fig. 1 Transmitter RF output spectrum before I/Q imbalance calibration |
在频谱上,有用信号Acos [(w0+wLO)t]和同频干扰信号[C(w)/2]sin [(wLO+w0)t+α]构成了有用信号的频谱,[C(w)/2]sin [(wLO−w0)t−α]构成了边带信号的频谱. 由于[C(w)/2]sin [(wLO+w0)t+α]对主信号的能量贡献较小,考虑边带抑制度时忽略这部分对有用信号频谱的影响. 边带抑制度(side band suppression, SBS)为有用信号和边带信号的能量差:
| ${\rm{SBS}} = 10 \times \lg \;[({A^2} - 2AB\cos \;(p(w)) + {B^2})/(4{A^2})]. $ | (11) |
为了简化讨论,假设由非平衡传输链路引入的相位差p(w)为与频率无关的量,即各个频率分量下引入的相位差是一致的,假设相位差为p',且I/Q两路的幅度不平衡度为D=20×lg (A/B). SBS可以表示为
| ${\rm SBS} = 10 \times \lg \;\Big[\left({({10^{D/20}})^2} - 2 \times {10^{D/20}} \times \cos \;p' + 1\right)/4\Big].$ | (12) |
当D∈[−30, 30] dB,p′∈[−

|
图 2 边带抑制度与不平衡关系 Fig. 2 Relationship between sideband suppression and I/Q imbalance |
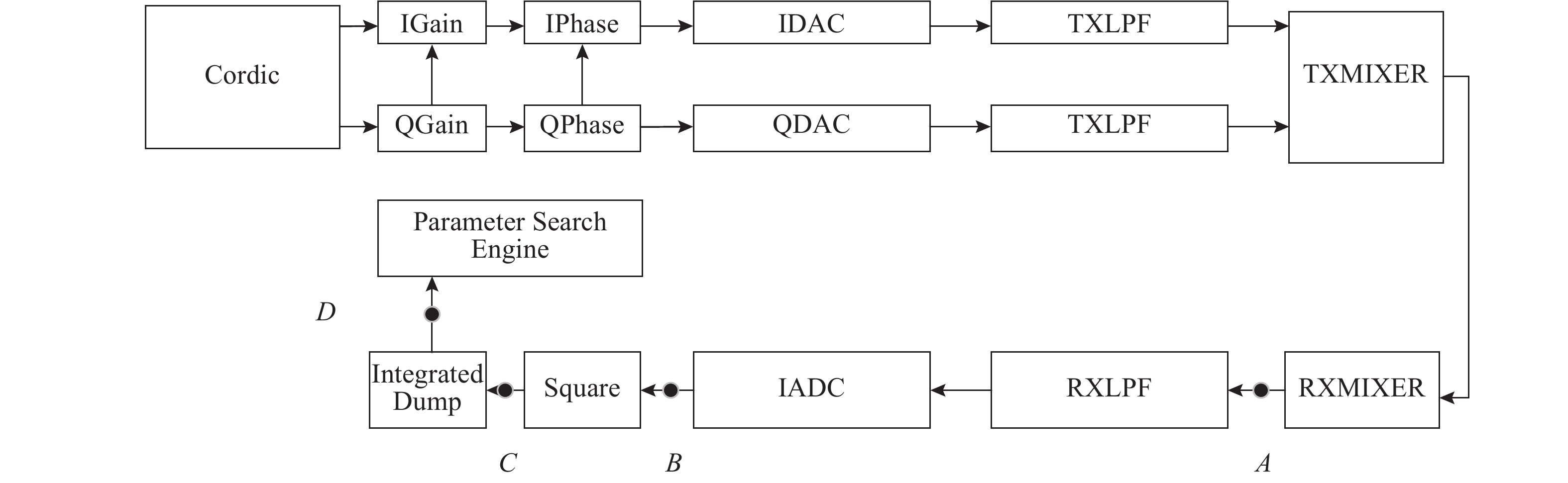
在发射机数字基带处,通过Cordic[16]模块产生频率为f0的两路正交的正弦信号. 经过发射机模拟基带和模拟射频端的不平衡传输链路后,假设不存在直流偏置不平衡的问题,发射机射频输出信号中将会出现有用信号、同频干扰信号和镜像干扰信号. 将发射机射频输出信号通过反馈回路输入到接收机射频输入端进行处理,假设发射机混频器的本振频率为fTXLO,接收机混频器的本振频率为fRXLO,且fTXLO-fRXLO>f0,其中f0为单音测试信号的频率. 经过接收机混频器的下混频后,镜像信号(图3点A处)的频率为f=fTXLO−fRXLO−f0,上边带有用信号与下边带镜像信号在频率上相距2f0,合理地设置接收机低通滤波器的带宽可以轻易滤除有用信号,只保留镜像信号. 此时,镜像信号(图3点B处)为
| ${s_{\rm{B}}} = \Big[C(w)/2\Big]{\rm{ }}\sin \;(2{\text{π}} ft - \alpha ).$ | (13) |
为了提取出信号中的C(w)表征此时干扰信号的强度,对信号进行平方操作(图3点C处):
| ${s_{\rm{C}}} = \Big[{C^2}(w){\rm{/}}4\Big]\Big[\sin \;\;(4{\text{π}} ft - 2\alpha ) + 1\Big].$ | (14) |
对信号进行积分抖落操作(图3点D处):
| ${s_{\rm D}}={{{C^2}(w)}/4}. $ | (15) |
利用信号表征现有的发射机数字基带补偿参数时,校正后的镜像会干扰信号的强度. 所提方案在利用接收端反馈回路的过程中,通过接收端的下混频、自平方和积分抖落来获取镜像干扰信号的强度,强度越大,I/Q不平衡程度越大. 由式(14)、(15)可知,积分抖落过程去除了接收本振和接收信号的相位差,接收本振不影响镜像信号强度的提取. 由图3可知,实际上只需要用到其中的一路(I路或者Q路)的接收端,接收端自身的I/Q不平衡程度对此没有影响. 所提方案在校正发射端I/Q不平衡的过程中,不受接收端本振和接收端I/Q不平衡的影响.
|
图 3 I/Q不平衡校正架构 Fig. 3 Architecture of I/Q imbalance calibration |
通过发射机I/Q不平衡整体校正架构可以将I/Q不平衡的校正问题转化为优化问题:
| $\begin{array}{l}\min\;\;\;f({G_{\rm{I}}},{G_{\rm{Q}}},{P_{\rm{I}}},{P_{\rm{Q}}});\\\left. \begin{array}{l}\quad\;\;\;{G_{\rm{I}}}> 0,\\\!\!{\rm{s}}.{\rm{t}}.\;\;\;{G_{\rm{Q}}} > 0,\\\quad\;\;\;{\text{π}}/2 > {P_{\rm{I}}} > - {\text{π}} /2,\\\quad\;\;\;{\text{π}} /2 > {P_{\rm{Q}}} > - {\text{π}} /2.\end{array} \right\}\end{array}$ | (16) |
式中:GI为I路的增益因子,GQ为Q路的增益因子,PI、PQ分别为I/Q两路的相移,函数f为C点处的信号强度,可以作为整个优化问题的目标函数. 在上述的约束条件下,找到该优化问题的最优解. 此时,该优化问题取得极小值,即使得干扰信号能量最低的点,同时系统在该点的I/Q不平衡程度最低.
如图2(a)所示,在理想情况下,优化问题具有唯一极小值点,利用GDA等[17]算法,可以快速找出优化问题的最优解. 但是如图2(b)所示,由于受到噪声和干扰的影响,实际曲面中会出现多处起伏,存在多个极小值点,GDA不再适用,难以找出全局极小值点. 此时可以使用SAA等启发式搜索算法[18]来寻找优化问题的最优解.
2.2 模拟退火算法及其应用SAA是20世纪80年代发展起来的求解组合优化问题的启发式随机搜索算法. 以组合优化问题的求解过程与物理系统中退火过程的相似性为基础,通过适当地控制温度的下降过程以及每个过程中的Markov[19-20]链来实现模拟退火. 在迭代过程中不仅接受使目标函数变好的点,而且以统计热力学中的Boltzmann概率[21]接受使目标函数变差的点,分布概率随着温度的下降逐渐减小. 整个解空间内取值的随机性使得算法跳出了局部最优解,获得了全局最优解. SAA的理论决定了SAA是全局最优搜索算法,以概率1接近最优值. SAA的具体实现步骤如下.
1) 初始化退火温度tk(令k=0),产生随机初始解x0.
2)在tk下重复执行如下操作,直至达到温度tk的平衡状态,完成1次Markov链的计算:在解x的邻域产生新的可行解x′;计算x′的目标函数f(x′)与旧解目标函数的差值∆E;依照概率
3)令
退火温度T控制了求解过程向目标函数最小值的优化方向进行,以概率 exp (−∆E/tk)接受劣解. 因此,SAA可以有效地跳出局部极值点. 只要初始温度足够高、退火过程足够慢,SAA就能收敛到全局最优点.
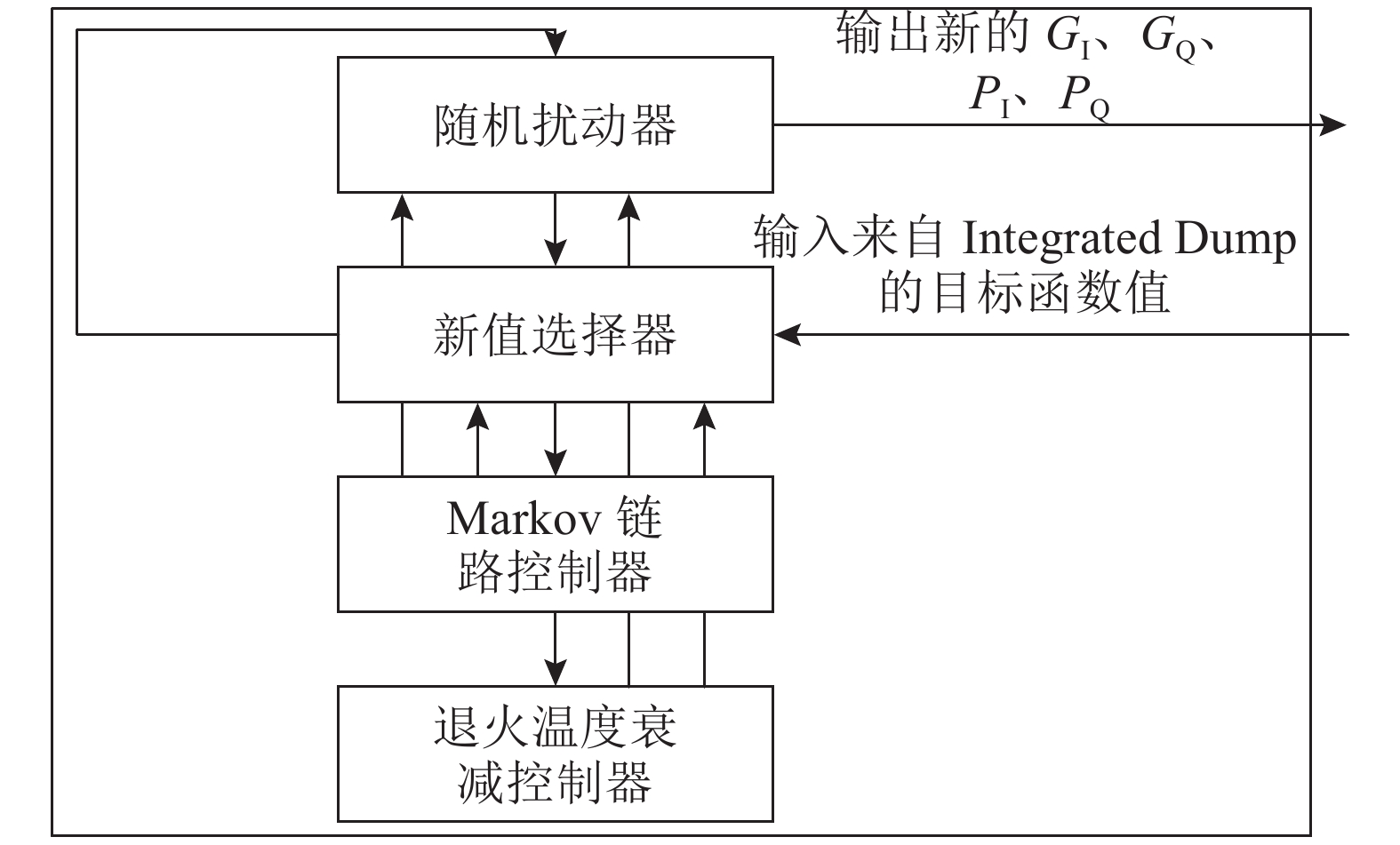
模拟退火参数搜索引擎是整个系统的核心部件,原理如图4所示. 基于模拟退火策略在解空间自动搜索满足要求的解向量,搜索过程如下.
|
图 4 模拟退火参数搜索引擎原理框图 Fig. 4 Block diagram of simulated annealing algorithm parameter searth engine |
1)设向量x={GI, GQ, PI,PQ},初始温度为t0,迭代次数i=0. 在随机扰动器中,从解空间内随机选择一个解向量x0,并且将向量x0的值分别传递到数字基带补偿模块IGain、QGain、IPhase和QPhase中,经过Integrated Dump模块的积分抖落处理后,所得结果作为目标函数值f(x0)送入新值选择器中. 令
| ${{x}_{{\rm{next}}}} = {{x}_{{\rm{opt}}}} = {{x}_0} {\text{,}}$ | (17) |
| ${f_{{\rm{opt}}}} = f({{x}_0}). $ | (18) |
式中:
2)令j=0,在温度Ti下重复执行如下操作:调用随机扰动器产生新的解向量xi,j;将新的解向量xi,j的值分别传递到数字基带补偿模块IGain、QGain、IPhase和QPhase中,新值选择器从Integrated Dump模块中,得到当前的目标函数值f(xi,j);如果f(xi,j)<fopt,表明当前解xi,j是目前所获得的最优解,令xopt=xi,j,fopt=f(xi,j);计算2次迭代的目标函数差值∆E=f(xi,j)-f(xnext). 如果∆E<0,接受更优解,即令xnext=xi,j;否则,依照概率
| $\exp \;( - \Delta E/{t_k}){\rm{ random}}\;[0,1.0]$ | (19) |
接受新解;j=j+1,如果j=k,完成1次Markov链,在Markov控制器控制下转到过程3);否则转到过程1).
3)令
| ${t_{i + 1}} = a {t_i};\;\;a \in (0,{\kern 1pt} {\kern 1pt} 1.0). $ | (20) |
式中:
退火温度控制器通过将当前温度与固定的衰减率相乘,实现指数式的温度衰减. 如果满足ti=tmin,程序结束;否则,在退火温度控制器控制下转到过程2).
具体实现所提方案时,由于数字基带预校正部分由LMS7002M单芯片无线电系统实现,只需要将相应的预校正参数(即向量x)配置到相应的寄存器中. 幅度预校正模块的寄存器位数是11位的无符号数,相位预校正寄模块的寄存器位数是12位有符号数. SAA搜索过程在场可编程门阵列(field-programmable gate array, FPGA)中以定点数计算的形式实现. 在搜索过程中,每次扰动的大小由随机扰动器中的移位伪随机过程决定,为了平衡随机干扰和总体稳定,设定扰动位数最小为1位,最大为3位. 由此可见,模拟退火参数搜索引擎不仅能为下一个状态接受更好的解,而且还能以一定的概率接受劣质解,有可能跳出局部最优解,获得全局最优解.
3 仿真验证利用MathWorks公司的Simulink软件[22]进行仿真. 系统的采样频率为40 MHz,数字基带正交的正弦信号频率f0=5 MHz,发射机混频器的本振频率fTXLO=2 240 MHz,接收机混频器的本振频率为fRXLO=2 234 MHz. 为了更好地验证SAA在不同信噪比条件下的优化效果,对比SAA和利用GDA编写的程序的优化性能差异. 设置使用SAA和GDA进行的最大搜索次数都为20 000,两者的搜索范围一致. 同时,设置温度衰减率为0.98,初始温度t0=120 °C. 为了使仿真结果更加可靠,每次仿真的初始I/Q不平衡程度设为随机. 信噪比的范围设为[−30, 30] dB,间隔为5 dB,在每个信噪比环境下进行5次仿真实验,取平均值作为该条件下的实验结果.
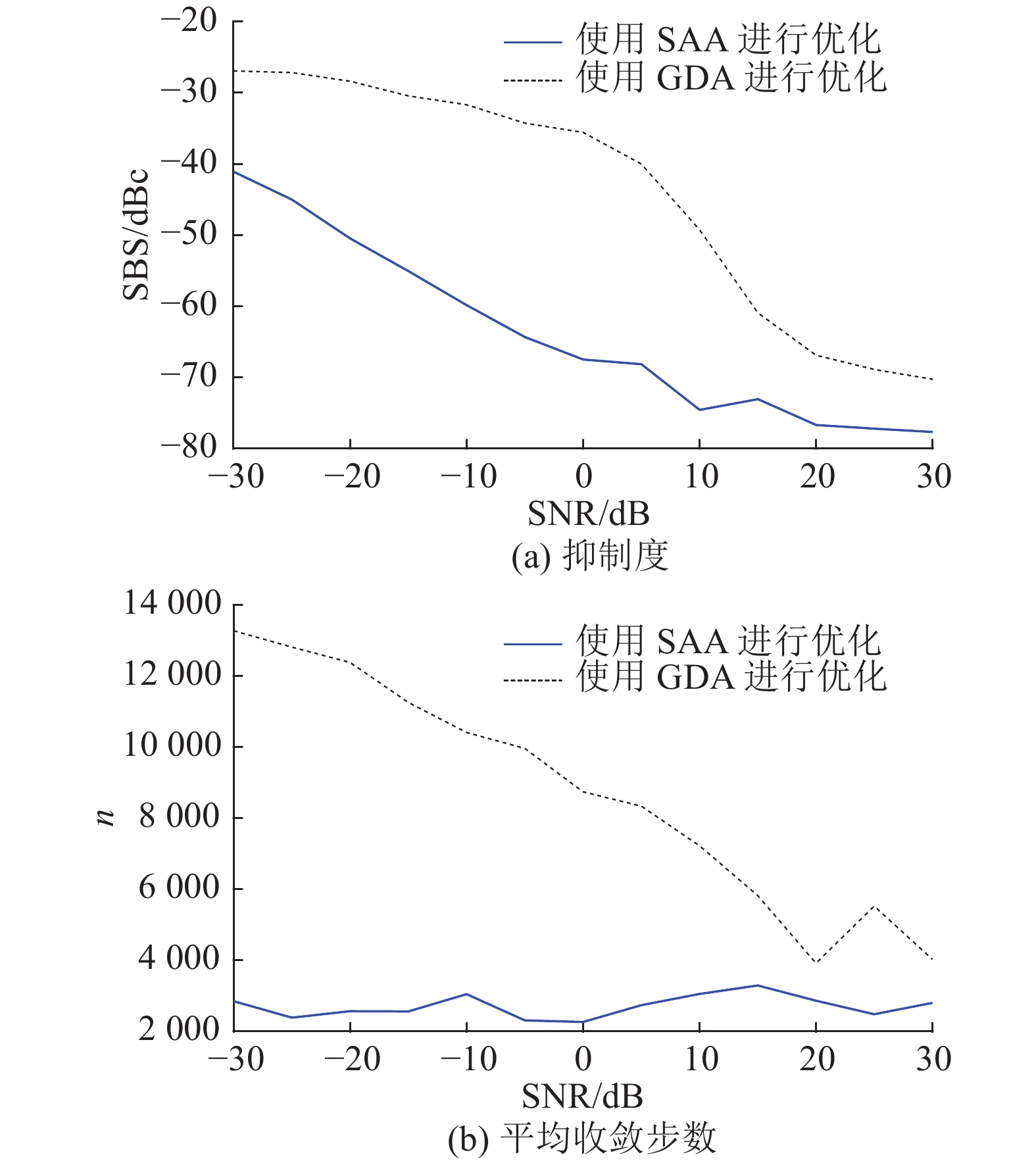
实际的仿真结果如图5所示,图中SNR为信噪比,n为该信噪比条件下收敛所需要的平均搜索步数,实线为使用SAA进行优化的曲线,虚线为使用GDA进行优化的曲线. 在加性高斯白噪声测试条件下,高信噪比时,使用SAA与使用GDA的优化结果相差不大. 中低信噪比时,使用SAA的优化结果明显优于使用GDA的优化结果. 这是因为基于梯度的优化算法只在当前迭代点的邻域内利用梯度信息进行局部搜索,没有在大范围内搜索的策略. SAA适当地控制温度的变化过程能够实现大范围粗略搜索与局部精细搜索相结合的搜索策略. 产生的随机概率密度函数以及接受试探点为新的当前迭代点的概率都与温度有关,当温度较高时,随机产生的试探点的散布范围较大,并且能够以较大的接受概率使目标函数值增加试探点,实现大范围粗略搜索. 当温度逐渐下降时,随机试探点的散布范围逐渐减小,接受使目标函数值增加的试探点的概率也逐渐减小,搜索过程逐渐变为局部精细搜索.
|
图 5 SAA与GDA在仿真中的抑制度与收敛步数对比图 Fig. 5 Comparison of image suppression and convergence steps between SAA and GDA in simulation |
如图5(b)所示,在同样的搜索终止条件下,SAA比GDA收敛得更快,运行效率更高. SAA采用大范围的粗略搜索与局部的精细搜索相结合的搜索策略,快速地搜索出全局最小值的大概位置后再进行局部精细搜索,减少了盲目搜索的次数,达到了快速收敛的效果. 同样得益于搜索策略,SAA的搜索步数受环境的影响较小. 在GDA的搜索过程中,噪声直接影响沿着梯度下降最快的搜索路线,噪声越大,搜索路线的偏移越大,搜索步数越多.
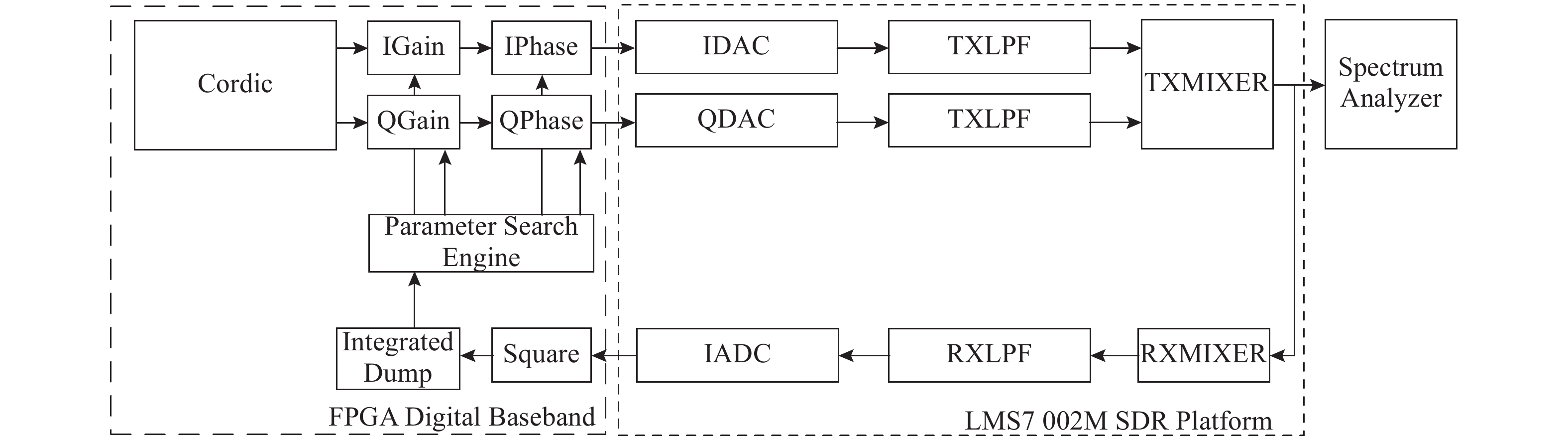
4 实验验证采用Xilinx公司的ISE Design Suite 14.7集成开发环境进行软件开发,在1块印刷电路板(printed circuit board,PCB)上同时集成了Xilinx Spartan-6 FPGA芯片、Lime Microsystem LMS7002M单芯片软件无线电系统和外围电路. 如图6所示,通过FPGA芯片实现对LMS7002M软件无线电系统的初始化配置和相关的数据处理. 系统的采样频率和系统的时钟频率都设为40 MHz,在FPGA中利用Cordic模块产生的正交正弦信号频率f0=5 MHz. 在温度变化实验中,发射机混频器的本振频率fTXLO=2 240 MHz,接收机混频器的本振频率为fRXLO=2 234 MHz. 将系统置于温度控制箱之中,系统温度的变化范围为−20~50°C. 在频率变化实验中,SAA的温度衰减率设为0.98,初始温度t0=120 °C. 发射机混频器的本振频率fTXLO的变化范围为[1 600, 2 400] MHz,接收机混频器的本振频率fRXLO的变化范围为[1 594, 2 494] MHz,中频频率保持为6 MHz,每个相邻频点的间隔为200 MHz,利用频谱仪观察发射机射频口的镜像抑制度,取每个条件下进行的5次实验的平均值作为该条件下的实验结果.
|
图 6 I/Q不平衡校正实验系统结构图 Fig. 6 Experiment system structure of I/Q imbalance calibration |
如图7(a)所示,t为温度,在不同温度点上使用SAA对I/Q不平衡进行校正,平均镜像抑制度为−57.5 dBc,比使用GDA得到的平均镜像抑制度低4.7 dBc. 如图7(b)所示,f为频率,在不同频点上使用SAA对I/Q不平衡进行校正,平均抑制度为−60.5 dBc,比使用GDA得到的平均镜像抑制度低6.56 dBc. 如果只在50 °C时对系统利用SAA进行校正,在整个温度变化范围内,镜像抑制度最大能够提高24.8 dBc. 如果只在1 600 MHz频点上利用SAA进行校正,在整个频率变化范围内,镜像抑度最大能够提高25 dBc. 这说明在温度和频率的变化影响下,在数字域进行实时有效的I/Q不平衡校正非常重要. 经由SAA优化后的镜像抑制度已经超出了一般实际应用所要求的−50 dBc的指标要求,并且SAA具有频率适应性和温度适应性. LMS7002M单芯片软件无线电系统所采用的集成模数转换器(analog-to-digital converter,ADC)器件是12位,考虑到ADC在量化过程中可能会出现饱和问题,在高位多预留1位符号位防止饱和,再加上原来的1位符号位,ADC的实际有效位数是10位,理论上所能表示的模拟信号的功率动态范围为20×lg 210≈60.2 dB. 在本次实验中,发射机射频输出的最大功率为−5 dBm,使用模拟退火算法优化得到−60.5 dBc镜像抑制度时,镜像干扰信号的功率为−62 dBm,优化过程中镜像信号功率的动态范围为59 dB. 如图8所示,考虑到实际系统中还存在滤波器通带内的噪声以及ADC所引入的量化噪声,优化结果已经接近系统所能达到的最大优化水平.

|
图 7 在不同温度和频率下的SAA优化效果图 Fig. 7 Results of SAA optimization under different temperatures and frequencies |

|
图 8 进行I/Q不平衡校正后的发射机射频输出处频谱 Fig. 8 Transmitter RF output spectrum after I/Q imbalance calibration |
提出了利用发射机射频前端的反馈回路提供的反馈信息结合SAA进行I/Q不平衡校正的方法. 在Simulink仿真中,当时间、搜索范围和搜索次数相同时,SAA比GDA的优化效果好. 在实际测试中,所提方案在不同的频率和温度点上分别能达到−57.5 dBc和−60.5 dBc的平均镜像抑制度,比GDA分别降低了4.7 dBc和6.56 dBc. 所提方案具有频率和温度适应性,所得到的优化效果满足实际应用需求. 在后续应用中,只需要在完成I/Q不平衡的校正后,修改中频滤波器的带宽,补偿参数的搜索范围,就可以将所提方案推广到发射机直流偏置不平衡的校正问题中. 在接下来的工作中,将尝试利用不同种类的启发式搜索算法来解决该问题,以达到更好的效果.
| [1] |
李明. 微小卫星发展的若干思考[J]. 航天器工程, 2016, 25(6): 1–5. LI Ming. Perspective on development of micro-small satellites[J]. Spacecraft Engineering, 2016, 25(26): 1–5. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=htqgc201606001 |
| [2] |
宗可, 曹桂兴, 闫忠文. 数据通信微小卫星星座系统的发展及应用[J]. 航天器工程, 2011(2): 66-71. ZONG Ke, CAO Gui-xing, YAN Zhong-wen. Development and application of data communication microsatellite constellation system[J]. Spacecraft Engineering, 2011(2): 66-71. DOI:10.3969/j.issn.1673-8748.2011.02.012 |
| [3] |
李亮, 王洪, 刘良玉,等. 微小卫星星座与编队技术发展[J]. 空间电子技术, 2017, 14(1): 1-3. LI Liang, WANG Hong, LIU Liang-yu, et al. Development of micro-satellite constellation and formation technologies[J]. Space Electronic Technology, 2017, 14(1): 1-3. DOI:10.3969/j.issn.1674-7135.2017.01.001 |
| [4] |
ROSE R, RUF C, ROSE D, et al. The CYGNSS flight segment; A major NASA science mission enabled by micro-satellite technology [C] // Aerospace Conference. Big Sky: IEEE, 2013: 1–13. https://www.researchgate.net/publication/261302621_The_CYGNSS_flight_segment_A_major_NASA_science_mission_enabled_by_micro-satellite_technology
|
| [5] |
FERNÁNDEZ F A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data[J]. Advances in Space Research, 2011, 47(5): 786-801. DOI:10.1016/j.asr.2010.10.002 |
| [6] |
戚秀真. 零中频发射机设计与实现[J]. 电子科技, 2014, 27(3): 73-76. QI Xiu-zhen. Design and implement of zero intermediate frequency transmitters[J]. Electronic Science and Technology, 2014, 27(3): 73-76. DOI:10.3969/j.issn.1007-7820.2014.03.022 |
| [7] |
HSU C J, SHEEN W H. Joint calibration of transmitter and receiver impairments in direct-conversion radio architecture[J]. IEEE Transactions on Wireless Communications, 2012, 11(2): 832-841. DOI:10.1109/TWC.2011.110811.110939 |
| [8] |
GU C F, LAW C L, WU W. Time domain IQ imbalance compensation for wideband wireless systems[J]. IEEE Communications Letters, 2010, 14(6): 539-541. DOI:10.1109/LCOMM.2010.06.091883 |
| [9] |
WANG J, YU H, WU Y, et al. Pilot optimization and power allocation for OFDM-based full-duplex relay networks with IQ-imbalances[J]. IEEE Access, 2017, 5: 24344-24352. DOI:10.1109/ACCESS.2017.2766703 |
| [10] |
SHU F, WANG J, LI J, et al. Pilot optimization, channel estimation and optimal detection for full-duplex OFDM systems with IQ-imbalances[J]. IEEE Transactions on Vehicular Technology, 2017, 66(8): 6993-7009. DOI:10.1109/TVT.2017.2667686 |
| [11] |
SHU F, ZHAO J H, YOU X H, et al. An efficient sparse channel estimator combining time-domain LS and iterative shrinkage for OFDM systems with IQ-imbalances[J]. Science China Information Sciences, 2012, 55(11): 2604-2610. DOI:10.1007/s11432-012-4691-7 |
| [12] |
李建宇. 射频单片集成应答机设计与实现[D]. 杭州: 浙江大学, 2014: 22–41. LI Jian-yu. Design and implementation of a RF monolithic integrated transponder [D]. Hangzhou: Zhejiang University, 2014: 22–41. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014162912.htm |
| [13] |
邹世源, 刘久文, 阳辉. 数字域校正零中频发射机IQ不平衡的研究[J]. 电视技术, 2013, 37(23): 163-166. ZOU Shi-yuan, LIU Jiu-wen, YANG Hui. Research of compensating zero-IF modulator IQ imbalance in digital domain[J]. Video Engineering, 2013, 37(23): 163-166. DOI:10.3969/j.issn.1002-8692.2013.23.042 |
| [14] |
RUTENBAR R A. Simulated annealing algorithms: an overview[J]. Circuits and Devices Magazine IEEE, 2015, 5(1): 19-26. |
| [15] |
DEBNATH S, TAMULI M, RAY A, et al. A review on accelerating scientific computations using the Conjugate Gradient method [C] // International Conference on Electronic Design, Computer Networks and Automated Verification. Shillong: IEEE, 2015: 150–153.
|
| [16] |
张朝杰, 金小军, 郑阳明,等. 基于CORDIC算法的微小卫星接收机设计及实现[J]. 浙江大学学报: 工学版, 2008, 42(6): 960-964. ZHANG Chao-jie, JIN Xiao-jun, ZHENG Yang-ming, et al. Design and implementation of micro-satellite receiver using CORDIC algorithm[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(6): 960-964. |
| [17] |
CHAU M, FU M C, QU H, et al. Simulation optimization: a tutorial overview and recent developments in gradient-based methods [C] // Winter Simulation Conference. Savanah: IEEE, 2015: 21–35. http://xueshu.baidu.com/s?wd=paperuri%3A%284c82314ae1e9aeda214d61c365745806%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdx.doi.org%2F10.1109%2FEDCAV.2015.7060557&ie=utf-8&sc_us=12541358251555775013&sc_as_para=sc_lib%3A
|
| [18] |
SUMAN B, HODA N, JHA S. Orthogonal simulated annealing for multiobjective optimization[J]. Computers and Chemical Engineering, 2010, 34(10): 1618-1631. DOI:10.1016/j.compchemeng.2009.11.015 |
| [19] |
LALAOUI M, AFIA A E, CHIHEB R. Hidden Markov model for a self-learning of simulated annealing cooling law [C] // International Conference on Multimedia Computing and Systems. Marrakech: IEEE, 2017: 558–563. https://www.researchgate.net/publication/316445645_Hidden_Markov_Model_for_a_self-learning_of_Simulated_Annealing_cooling_law
|
| [20] |
DIEKER A B, SALIOLA F V. Spectral analysis of random-to-random Markov chains [J]. Advances in Mathematics. 2018, 323: 427–485. http://www.sciencedirect.com/science/article/pii/S0001870816316425
|
| [21] |
ZHOU E, CHEN X. Sequential Monte Carlo simulated annealing[J]. Journal of Global Optimization, 2013, 55(1): 101-124. DOI:10.1007/s10898-011-9838-3 |
| [22] |
LEKD, NGUYEN H P, NGUYEN D N, et al. Simulink model and FPGA-based OFDM communication system: a simulation and hardware integrated platform[J]. International Journal of Modeling Simulation and Scientific Computing, 2010, 1(3): 369-404. DOI:10.1142/S1793962310000250 |



