聚类是挖掘潜在本质信息,对不同数据进行划分的过程. 聚类算法大致分为基于分割[1]、基于密度[2]、基于模型[3]、基于层次[4]、基于网格[5]的算法. 快速密度峰值聚类(clustering by fast search and find of density peaks,CFDP)算法是2014年Rodriguez等[6]在Science上提出的密度聚类算法. 核心思想是通过截断距离计算相对密度和最邻距离,使用绝对密度和最邻距离绘制决策图,主观地在决策图上选择出簇中心点. CFDP的主要贡献是给出分析和选择簇中心的启发式方法. 不少学者对该算法进行改进. Chen等[7]摒弃对单个初始中心点的寻找,通过用一半高密度的点生成初始聚类轮廓,把剩余点聚类,绕过了找中心的困境,把离群点剔除. Xie等[8]用k最近邻(k-nearest neighbor,kNN)的思想,根据最近的几个点的距离,估计出权值,聚类时按最大可能概率聚类. Xu等[9]以层次聚类的思想改进算法,使用ρδ做成阶梯,按照下降的大小区分平台,从最高的平台分层聚类,用比值决定外点,按属性和样本横竖分割数据空间,经过2次计算确定聚类结果.
从无监督角度对CFDP的改进,仍然存在问题. 中心点的自动选择有时存在误选、漏选;簇的数量需要人为给定;算法使用有场景局限,比如聚类效果依赖数据集结构与参数设置. 针对CFDP存在的问题,从半监督角度出发,结合集成学习,提出半监督约束集成的快速密度峰值聚类(semi-supervised constraint ensemble clustering by fast search and find of density peak,SiCE-CFDP)改进算法.
半监督学习的目的是通过先验知识降低算法对参数的依赖,扩展适用场合. 可分成基于约束的、基于距离的、基于非线性映射的和基于大间隔的这几类典型方法. 基于半监督约束的聚类目前研究较多. 按照所用约束信息粒度[10]大小,SiCE-CFDP属于对象级约束,在大部分数据没有标签的情况下,利用少部分数据的标签或者少部分数据之间的关系做到更好的聚类. 对于对象级约束,通过必须相连(Must-Link)约束和不可相连(Cannot-Link)约束来刻画数据间的相互关系,比如处于边界上的2个城市,通过Cannot-Link约束不属于一个国家. 基于对象级约束的半监督聚类算法包括属于密度聚类的CDBSCAN[11]、与EM相结合的Seeded-K-means[3]、强制满足约束的Constrained-K-means (COP-K-means)[12]、MPCK-means[13]方法、属于谱聚类的Constrained 1-Spectral Clustering[14]等. 这些算法通过半监督约束指导聚类,对传统算法进行改进,取得了不错的效果.
集成学习通过融合多个基结果得到更好的决策. 聚类集成主要通过多个聚类算法、或者同一算法的不同初始参数,得到不同的基聚类结果,以分歧为前提,利用一致性函数整合出更好的聚类结果[15]. 唐伟等[16]提出基于投票方法的集成函数,方法有4种投票策略,分别是选择投票、多数投票、选择加权投票和互信息加权投票. 集成方法充分利用聚类成员类标签信息,但是聚类准确率与当前聚类成员的质量有关,当聚类成员效果普遍较差时,准确率不高.
介绍SiCE-CFDP相关的理论前提,说明SiCE-CFDP的相关假设和步骤,对比提出的改进算法和现有典型算法,展示和讨论仿真结果,总结和展望SiCE-CFDP算法进一步优化的方向.
1 SiCE-CFDP方法原理与算法流程 1.1 相关工作与方法原理SiCE-CFDP是以CFDP和集成学习为基础的半监督聚类算法. CFDP算法假设簇中心是局部密度最大值,并且簇中心远离其他更高密度的点. 为了寻找符合假设的簇中心点,CFDP给出了点i的局部密度度量为
| ${\rho _i} = \sum\limits_{j \ne i} {\chi \left( {{d_{ij}} - {d_{\rm c}}} \right)} .$ | (1) |
点i的距离度量为
| ${\delta _i} = \min_{{j:\rho _j} > {\rho _i}} {{d_{ij}}} .$ | (2) |
式中:dij为两点间欧式距离;dc为截断距离,一般从所有dij距离从大到小排序后前1%到2%数据中取合适的dij值. χ函数计算节点i周围在截断距离dc范围内的点的个数. 如果dij-dc≥0,则χ(dij-dc)=1;如果dij-dc<0,则χ(dij-dc)=0. 截断距离dc的选择决定局部密度大小,决定聚类结果的稳定性和准确度. 式(2)中δi为节点i与比i拥有更高局部密度的点中最近的距离. 如果节点是全局密度最大点,赋予该点全局最大的距离值.
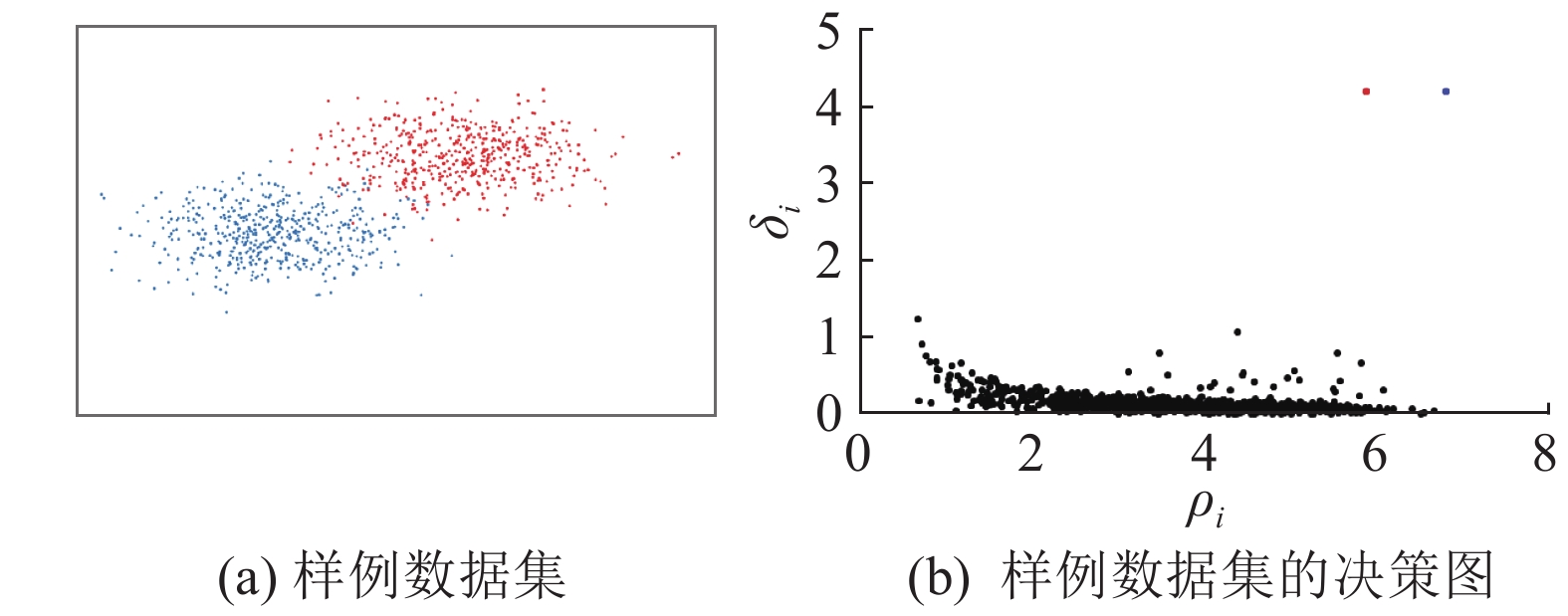
如图1所示,以δi为纵坐标,ρi为横坐标画出CFDP的决策图. 在决策图中,局部中心点一般具有高局部密度、高距离;噪声或边界点具有低局部密度、高距离. CFDP通过人工选择中心点的方式,确定簇数和簇中心点,把没有标签的点i归并到最近邻的拥有更高局部密度的点j所属的簇中,生成包含初始中心点的簇,完成整个聚类过程.
集成学习的宗旨是结合多个算法的结果,提高算法的准确率和稳定性. Hansen等[17]对集成学习的误差做过证明,假设m个单独的基算法,各基算法误差为p,如果基算法误差互相独立,使用投票法进行集成时,误差为
| $E = \sum\limits_{k > m/{\rm{2}}}^m { {{\rm C}^m_k} } {p^k}{(1 - p)^{m - k}}.$ | (3) |
当p<0.5时,E随m的增大单调递减. 只要每个基算法的准确率大于0.5,随着基算法的增多,集成性能提高,理论上无穷个基算法的集成错误率趋近0. 投票集成的方法主要有绝对投票法、相对投票法和加权多数投票法. 绝对投票法选择票数超过一半的类. 相对投票法选择票数最多的类别,如果最多票数的类别大于1,随机选择一个. 加权多数投票法与加权平均类似,用权重乘以选择,选出加权权重最大类别. 相关重要定义如下.
定义1 局部密度ρi:
| ${\rho _i} = 1\left/\sum\limits_{j{\rm{ = 1}}}^k \right.{{d_{ij}}} .$ | (4) |
采用相对密度[9],式(4)中点i的局部密度为与点i最邻近的k个数据点距离相加的倒数. 根据CFDP对密度的定义,2个在邻域内有相同数据点数的节点拥有相同密度,密度无法更加细致地区分2个节点谁更加稠密. 采用相对密度后,节点间密度值不会重复. 相对密度参考周围所有k个节点的情况,避免了对dc的选择,拥有更高的稳定性. 处在数据稠密区域的点与周围点的距离一般比较近,具有更大的ρi. 簇边界点与周围点的距离一般比较远,具有比较小的ρi. 一般情况下取k为总节点个数的2%,既能反映全局信息,又能体现局部特征.
定义2 Must-Link(ML)约束和Cannot-Link(CL)约束[11]为
Must-Link
Cannot-Link
Must-Link转移性:if Must-Link
Cannot-Link继承性:if Must-Link
定义3 主体违背。对于有n个节点的数据块和m个节点的初始中心点簇,理论存在的最大CL约束数为nm个. 假设数据块与初始中心点的簇属于同一类,约束信息随机分布,如果数据块n个节点中有n1个节点与初始中心点簇无CL约束,有n2个节点与初始中心点簇有CL约束,并且n1+n2=n. 实际可能产生的最大CL约束数为n2m个. n2个节点的CL约束可能由少部分误分类数据导致,假设块和簇属于同一类,误分类数据只占数据中的很小一部分,n2:n是一个很小的值,CL约束是由于随机分类时的错误造成.
为了衡量数据块或初始中心点簇中约束信息随机的程度,计算理论存在的ML约束数与实际ML约束数的比值. 数据块理论存在的ML约束数为n2,实际ML约束数为s1,数据块的随机度是s1:n2. 初始中心点簇理论存在的ML约束数为m2,实际ML约束数为s2,对于初始中心点簇的随机度是s2:m2.
主体违背时(n2m):(nm)=n2:n远大于s1:n2的数量级. 同理适用于初始中心点簇的主体违背判断. 主体违背主要应用于聚类过程.
1.2 SiCE-CFDP算法流程高效算法CFDP存在缺陷. 算法在决策图中需要主观确定中心点与类别数,当类别数未知时,算法应用受限;ρi和δi值的分布依赖截断距离参数dc,因此算法聚类的质量过度依赖参数dc的选择.
SiCE-CFDP有2点假设:簇的中心是局部密度的最大值,并且簇的中心远离其他更高密度的点;拥有相同密度分布,并且没有CL约束制约的簇,属于同一个类. 基于以上2点假设,给出SiCE-CFDP的算法流程.
1)参考k个周围节点的信息,按照式(4)和式(2)计算局部密度ρi和距离δi;
2)对决策图进行分析,通过对决策图的变换,结合3种状态综合选取初始中心点(置信度设为一般的0.05),把低密度点从初始中心点中排除;
3)采用KD-tree根据不同尺度对数据空间进行分割,按照约束信息对分割的数据空间进行合并与拆分,最终通过集成学习增加约束信息数量;
4)根据约束信息,对数据块和零散节点分块. 按照CFDP把点聚类到有更高密度的最邻近的对象所拥有的初始中心点标号上,同时进行约束信息检查,生成初始中心簇;
5)以算法假设为前提,采用Logistic回归分类器和分布检验(置信度设为一般的0.05),在不违背约束条件的前提下,对初始中心簇进行融合,生成最终的聚类结果.
1.2.1 局部密度与邻近距离计算采用k个周围点信息代替截断距离dc计算局部密度,按照式(4)和式(2)计算局部密度ρi与邻近距离δi. 对于重合的数据点,算法需要对原始数据进行小的摄动,在不破坏数据分布的情况下,使数据中节点不重合,保证密度最大点只有一个.
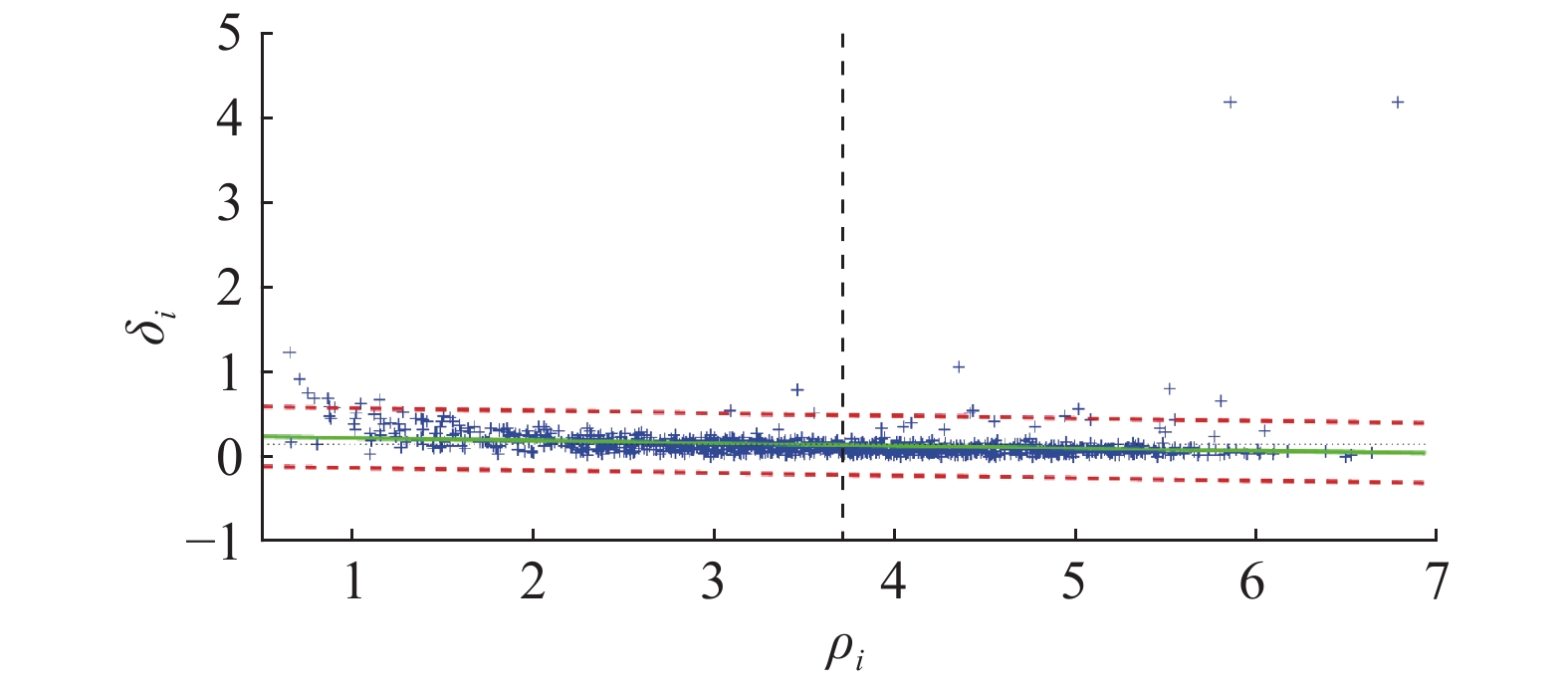
1.2.2 初始中心点选择在算法中,经过局部密度和邻近距离的计算,数据点可以分为4类情况. 针对如图1所示的样例数据集和原始决策图,图2利用Logistic回归对原始决策图进行分析,分离出系统簇中心点、边界点和局部中心点的示意图. 位于图2右上方的是拥有高密度高距离的簇全局中心点;靠近δi轴的是低密度高距离的簇边界点或离散点;处于图中央位置的是较高密度较高距离的局部中心点;贴近ρi轴的一般是低距离普通密度的簇内点.
|
图 1 样例数据集的决策图分析 Fig. 1 Analysis of decision graph for sample data |
在图2中通过对原始ρi-δi决策图采用Logistic回归,进行置信检验. 把置信区间外散布的点分离出来,分离的点集合记为pot1,包括簇的全局中心点、大部分簇边界点、部分簇的局部中心点.
|
图 2 决策图的Logistic回归分析图 Fig. 2 Logistic regression for analyzing decision graph |
同理把密度距离相乘得到ρδ=tmult,按从大到小绘制tmult分布图,得到具有阶梯结构的分布图,如图3所示. 从层次聚类角度看,tmult值变化能够反映数据从全局中心点到局部中心点的过程,局部中心点可以反映原始数据集的结构信息. 根据对原始决策图的认识,把拥有较大值的阶梯分离,分离的点集合记为pot2,包括簇的全局中心点、大部分簇的局部中心点、部分簇边界点.

|
图 3 tmult排序后的分布图 Fig. 3 Distribution of tmult after ranking |
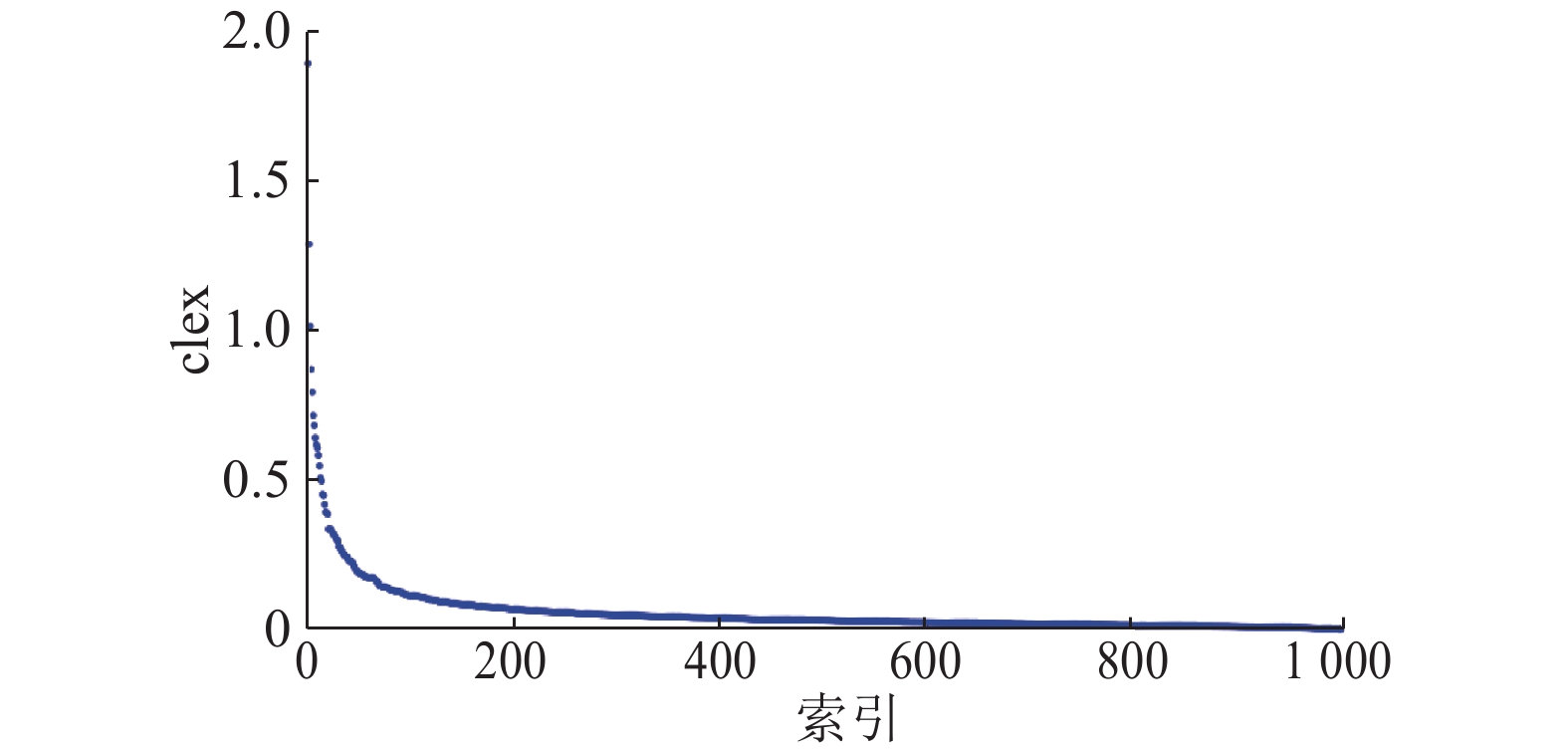
为了排除簇边界点,距离除以密度可以得到δi/ρi=clex. 按从大到小绘制clex分布图,如图4所示. clex分布图遵从箱体分布原则[9],按照拒绝假设,对于拥有较小密度的异常点数据进行筛查,标记为潜在容易引起中心点混淆的非中心点. 在clex的计算中,边界点一般都具有大距离小密度,因此边界点相比中心点一般拥有更大的clex值. 从clex分布图中分离异常点,分离的点集合记为pot3,包括簇边界点、小部分簇的局部中心点.
|
图 4 clex排序后的分布图 Fig. 4 Distribution of clex after ranking |
综合3种判断,对集合pot1和pot2进行交集运算后再与pot3进行差集运算,最终得到初始中心点集合fclust=(pot1∩pot2)-pot3=(簇的全局中心点,部分簇的局部中心点). 算法不仅选择了全局中心点,而且选择了部分簇的局部中心点,一方面保证算法在主观不知道类别数时不遗漏地聚类,使得所有簇都能有代表点,另一方面簇的局部中心点是数据层次结构的体现,指导性信息在后续聚类过程中帮助算法更好地聚类.
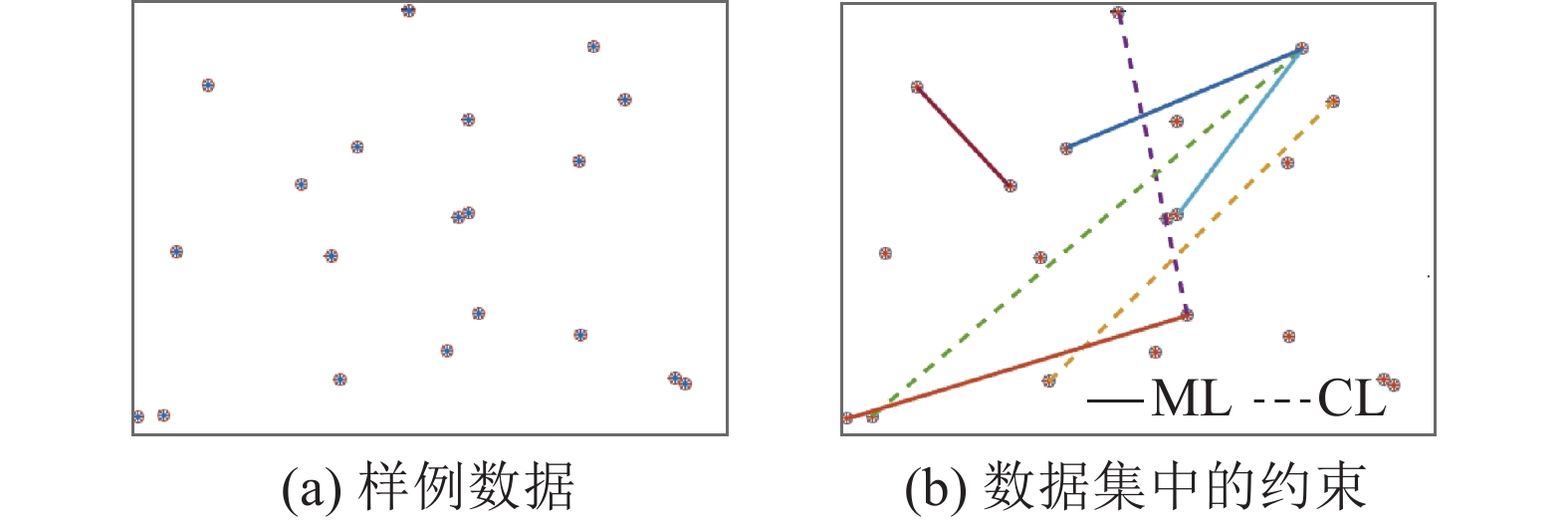
1.2.3 集成学习增加约束数量采用KD-tree对数据空间进行分割. 对被KD-tree分割的子空间中的点,根据约束情况进行合并. 如果整个子空间中不存在CL约束,认为子空间中的点都属于一类,分配到一个数据块中;如果存在CL约束,认为子空间内的点相互间不属于一类,不合并子空间内的点,使子空间中的点保持离散点的状态. 根据ML和CL约束信息,对存在ML约束,但是不存在CL约束的数据块和离散的数据点进行合并,生成多个大型的数据块. 数据块内不存在CL约束,保证对先验知识的不违背. 如图5所示,数据块生成过程将有ML连接的数据生成在一起,有CL约束的数据不会被分配在一个数据块.
|
图 5 样例数据与约束信息 Fig. 5 Sample data and constraint information |
当KD-tree对子空间划分时,影响最终数据块的最重要参数是每个子空间最多包含的节点数。考虑到CL约束需要有2个点才能成立,算法参考集成学习思想,从最多包含3个节点数开始,通过每轮改变每个子空间最多包含的节点数,使最多包含的节点数翻倍,生成不同的结果集,直到最多包含的节点数超过总节点数时停止迭代. 综合结果集进行多数投票,以80%作为阈值,如果2个节点在超过80%的结果集中属于同一个数据块,扩充ML约束.
比起单个的节点,经过ML、CL约束生成的数据块,节点在约束的帮助下看到了远处的数据与自己的归属情况,使得聚类过程能够有一种超前的视野,数据块更能代表数据集的结构分布情况.
1.2.4 根据约束信息进行聚类在通过集成学习增加约束信息数量后,重新使用KD-tree以最小的粒度(每个子空间最多3个点)进行数据空间的分割,按照约束信息生成最终的数据块.
把数据块和离散点聚类到中心点所属的簇中. 对数据块进行聚类的过程中,参考CFDP的邻近点聚类的思想,检查半监督约束信息,检测数据块与中心点簇是否存在CL约束. 对于数据块对象,将整个数据块并入最邻近的初始中心点所属的簇,使得初始中心点的簇也能够学习数据块对数据集的分布结构,增强系统的聚类精度. 某个数据块和所有初始中心点的簇都存在CL约束,可能是由少数误分类的节点引起,或者由数据块是一个新簇引起. 为了判断是否由少数误分类的节点引起,算法对数据块与中心点簇按照定义3进行主体违背检验,如果不存在主体违背,说明是少数误分类的节点引起. 把数据块中满足CL约束的点设置为离散点,合并数据块与中心点簇. 如果数据块与每个初始中心簇都存在主体违背,说明该数据块是一个新簇,算法需要生产一个新簇标签,防止类别遗漏.
1.2.5 簇融合由于初始中心节点数量一般大于真实类别数量,完成根据约束信息聚类之后,算法需要按照SiCE-CFDP提出的2点假设条件对初始中心簇进行融合.
约束信息使得数据能够跨越空间与远处的点相连,相同种类的簇之间可能会产生相互交错的情况,2个簇相互包含,节点区域重合严重. 产生这种情况的2个簇的密度中心并没有被明显的低密度区域隔离,并且没有来自先验知识的CL约束限制,因此两者应该同时归属于一个更大的簇. 从层次聚类的角度,把归属于同一层次下的2个并列的子层进行合并. 使用Logistic回归分类器寻找平面进行簇间相互交错度的判别,当2个簇充分混合时,平面无法区分两簇,此时理论准确率是50%. 以90%准确率作为阈值,大约有20%的数据相互混合. 当准确率低于阈值时,算法无法找到平面以较高的准确度区分交错的两簇,相互合并两簇.
算法假设拥有相同密度分布的数据可能属于同一个类别,当约束信息不足以让数据交错时,如果两类数据来自相同密度分布,需要被合并. 算法使用假设检验判断数据是否归属于相同密度发布,经过假设检验后,最终如果两簇符合相同分布,合并两簇. SiCE-CFDP的总体算法流程如下.
输入:邻近点数k,约束信息ML与CL
流程:
1 根据k、式(4)和式(2)计算局部密度和距离2 画出密度-距离图,用Logistic回归分离离群点得到点集合 pot13 画出密度×距离图,用Logistic回归分离离群点得到点集合 pot24 画出距离/密度图,用Logistic回归分离离群点得到点集合 pot35 pot1与pot2做交集后与pot3做差集运算,得到初始中心点6 从子空间包含最多数据点数为2开始迭代生产KD-tree的 结果集7 if KD-tree子空间里数据不存在CL约束,则把子空间 数据合并为数据块8 if 数据块与别的数据块或与离散点之间只存在ML 约束,则两者进行合并
9 回到第6步,并增倍子空间包含最多数据点数,直到最多 数据点数大于总数据点数
10 综合结果集进行多数投票,对在多数结果集中处于一类 的节点间扩充ML约束
11 对数据块和离散点聚类到离它最近的密度更大的节点所 属的包含初始中心点的簇上
12 if 数据块与所有中心点所属的簇存在CL约束
13 迭代检查数据块与中心点所属的簇是否存在主体 违背
14 if 数据块与簇不存在主体违背,则置数据块中 满足CL约束的点为离散点后再合并
15 else如果都存在主体违背,则以该数据块创建新 簇
16 回到第11步
17 迭代遍历中心点的簇
18 用Logistic分类器,判断两簇是否为一类
19 对密度分布进行置信检验判断两簇是否为一类
20 if 两簇是一类,则合并两簇
21 回到第17步
22 获得最终聚类结果
SiCE-CFDP经过局部密度与邻近距离计算(步骤1)、初始中心点选择(步骤2~5)、集成学习增强约束信息(步骤6~10)、根据约束信息聚类、簇融合(步骤11~21)后,按照CFDP的光晕点方法进行噪声点的剔除,得到最终聚类结果. SiCE-CFDP算法的步骤6~10时间复杂度比较高,其余步骤的时间复杂度比较小. 对于有n个实例的m维数据,建立单个KD-tree并且生产一次结果集的时间复杂度为O(mnlog n),算法需要遍历数据空间,因此算法总的时间复杂度为O(mn(logn)2).
改进算法的优点如下.
1)算法不需要预先知道类别数,只须知道计算密度时所需的最近邻点数量. 数量可以取经验值,一般是数据总数的2%,此外最近邻点数量的选择比dc的选择更具有鲁棒性.
2)算法不会漏选、误选初始中心点. 初始中心点数可能比想要聚类的类数多,因为算法所选取的候选中心点包括了反应系统层次信息的局部中心点.
3)算法在半监督信息帮助下能够适应于各种结构数据集.
4)算法在集成学习的帮助下,在专家给出的约束信息基础上,自我发现潜在的约束信息,随着数据量的增大,能够快速增强算法性能.
2 方法验证 2.1 聚类效果评价使用兰德指数(rand index)指标评价聚类结果. 兰德指数[18]通过刻画2个簇之间的一致度和不一致度描述了聚类结果与真实结果的相似度,并且在两个结果完全相同时有最大值1. 仿真中使用的数据集都有标签,因此数据的划分情况已知.
对于大小为N的数据集,集合中有N(N-1)/2个集合对. 兰德指数度量的正确的百分比为
| ${\rm RI}{\rm{ }} = \left( {\rm {TP + TN}} \right)/\left( {\rm TP + FP + FN + TN} \right).$ | (5) |
式中:TP为同一类的数据被分到同一个簇,TN为不同类的数据被分到不同簇,FP为不同类的数据被分到同一个簇,FN为同一类的数据被分到不同簇.
2.2 半监督信息产生规则参考Wagstaff等[12]和Halkidi等[19]的研究,使用测试数据集的类标签产生约束. 在给定一个约束量百分比(per)的情况下,如果测试数据集有3个类,每个类中节点的数量num1、num2、num3. Must-link是对相同标签对象的约束,Cannot-link是对不同标签数据的约束,理论上数据的全部Must-link总数为
| ${\rm numMLAll} = {\rm nu{m}_1}^2 + {\rm nu{m}_2}^2 + {\rm nu{m}_3}^2.$ | (6) |
理论上数据所拥有的全部Cannot-link总数numCLAll为
| ${\rm numCLAll} = {\sum\limits_{i = 1}^2} {\sum\limits_{j = i + 1}^3} {\rm{num}}{_i}\cdot {\rm{num}}{_j} .$ | (7) |
为了研究约束数量对算法效果的影响,变化约束量百分比,得到numMLAll·per和numCLAll·per作为真实约束数. 对于每种真实约束量,通过10次交叉验证计算平均兰德指数RI指标.
2.3 用于评测的数据集使用3组总共8个数据集来测试算法效果. 如图6所示给出了人工数据集的示意图. DS1代表桥结构的数据,2个数据集有相连但是没有重叠的边界. DS2代表不同密度结构的数据,不同簇的簇密度不同,可能一个稀疏、一个稠密. DS3代表重叠结构的数据,数据集之间有一部分数据在空间上相互包含. DS1、DS2和DS3是数据的基础结构,不同的数据集,是基础结构的组合和演化. 以基础结构为基础,衍生到对4个UCI数据集[20]的测试,评估算法在不同应用领域、维度数、数据量情况下的性能,证明算法应用场景的广泛性.

|
图 6 3个人工生成数据集 Fig. 6 Three synthetic datasets |
空调数据是针对某楼宇空调系统(如图7所示)的仿真数据,特征维度是在各种负荷下系统稳定后的各项设备参数,模型的建立来自真实的现场测试. 仿真模型与实际精度误差为5%~10%. 楼宇空调需要在不同负荷下,在满足设定值的情况下,调节压缩机、旁通阀、变频泵的频率等参数,控制室内机与室外机各自的压差,以及流量等指标. 对于控制而言,空调系统稳定后,尽管控制器可能选择不同控制算法实现,但是对应于给定负荷下的温度设定值,每种控制器会有稳定的压缩机开启台数、回水温度、新风占比等系统参数. 实验希望结合半监督信息与所得的特征数据,对数据进行半监督聚类,区分出所拥有的负荷区间,以及各种工况的占比,为控制系统的后续设计做基础,测试算法在真实环境下应用能力。如表1所示为所用所有数据集的特点描述.
| 表 1 用于评测的数据集基本信息 Table 1 Information of datasets used for evaluation |

|
图 7 仿真的楼宇空调系统示意图 Fig. 7 Schematic diagram of HVAC air conditioning system |
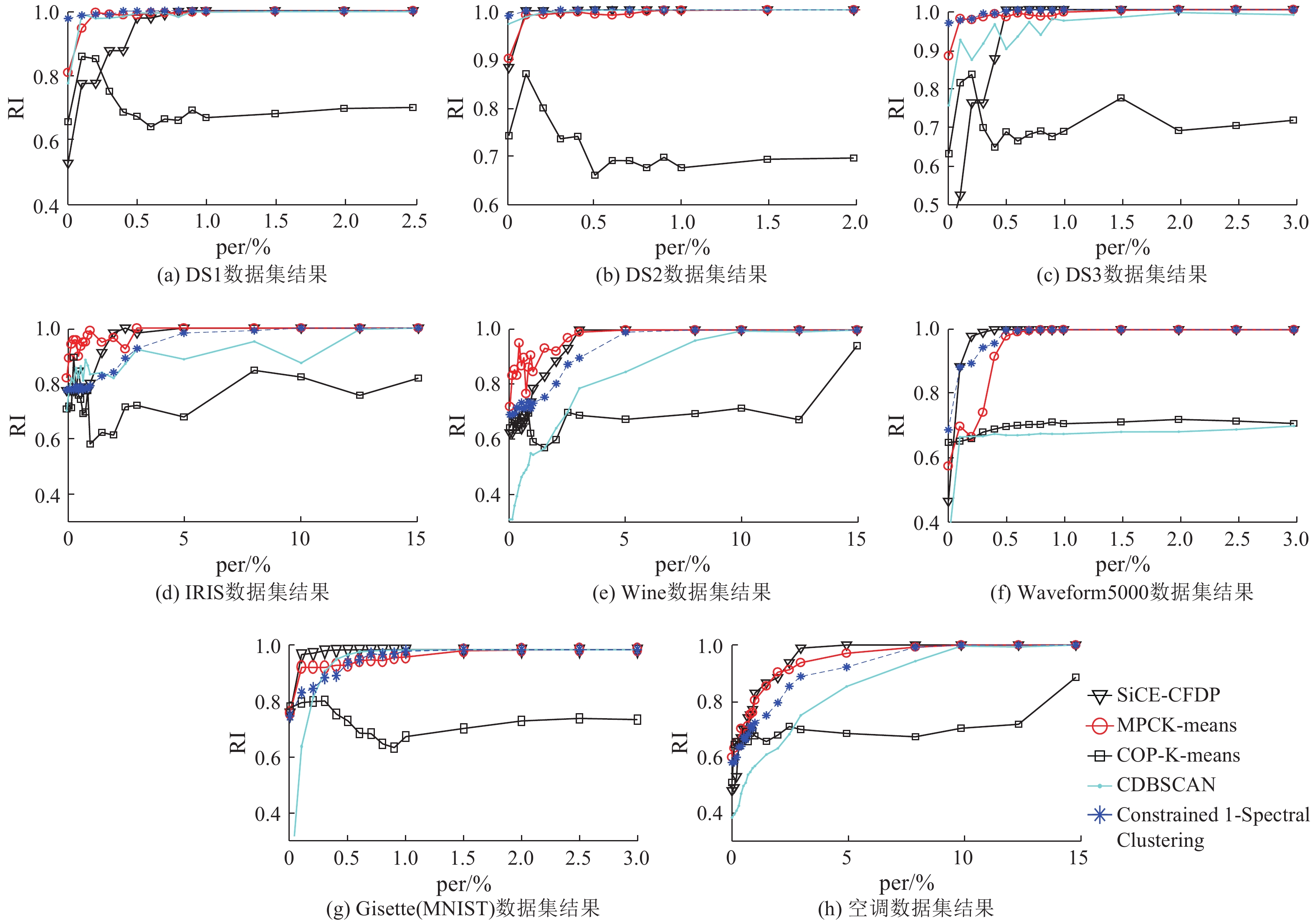
SiCE-CFDP在8个数据集基础上与CDB-SCAN、COP-K-means、MPCK-means、Constrained 1-Spectral Clustering等成熟的算法进行对比. 根据原文复现CDBSCAN算法,算法的参数选择参考笔者的选择方式,COP-K-means、MPCK-means、Constrained 1-Spectral Clustering来自于笔者提供的源码. 为了合理测试算法的性能,对约束强度选择25个数据点进行测试:0%,0.1%,0.2%,0.3%,0.4%,0.5%,0.6%,0.7%,0.8%,0.9%,1.0%,1.5%,2.0%,2.5%,3.5%,8.0%,10%,12.5%,15%,22%,30%,50%,75%,100%. 实验发现除了COP-K-means,其余算法后期都能收敛,因此为了更好地显示算法间的对比,如图8所示只画出前半段收敛阶段. 如表2所示通过对图8中per-RI曲线下方面积的积分对算法性能进行排名.
综合表2和图8发现,COP-K-means算法表现一直是最差的. COP-K-means算法通过约束信息修改初始中心点,在参考约束信息的情况下进行聚类. 在聚类过程中,COP-K-means算法继承了K-means只能对规则形状聚类的缺陷,导致算法无法有效利用约束信息区分数据分布的边界,因此算法在聚类过程中一直存在较大的波动,直到约束信息量很大时,算法性能才显现出稳定的上升趋势,但是偶尔会出现难以收敛的现象.
除去COP-K-means算法,表2和图8分析SiCE-CFDP、CDBSCAN、MPCK-means、Constrained 1-Spectral Clustering的效果分析如下,
| 表 2 对于不同的数据集5种算法性能排序 Table 2 Performance rank of five algorithms for different datasets |
1) 在对DS1数据集的测试中,所有算法展现了对约束信息的较高利用率和较快收敛性. 虽然SiCE-CFDP在约束少时RI较低,但是随着约束增多,RI迅速上升,并且快速收敛至稳定.
2)在DS2数据集的测试中,4种算法性能接近. 相对而言,Constrained 1-Spectral Clustering算法收敛速度最快,其次是SiCE-CFDP算法. 因为Constrained 1-Spectral Clustering算法对数据量中等的数据集效果比较好,当数据对象密度区分大、拥有明显边界时,更容易通过快速的谱图分割来找到最优的解.
3)在对DS3数据集的测试中,同为密度聚类算法的SiCE-CFDP和CDBSCAN的效果差距明显. 图8表明CDBSCAN无法像其他3种算法一样快速收敛. 因为密度聚类的前提假设是密度相连,密度接近却又相互重叠的2个簇是一个类. CDBSCAN只是利用约束信息生成了KD-tree,没有像SiCE-CFDP通过集成学习对约束信息进行进一步分析,也没有像SiCE-CFDP对中心点生成的簇结构进行更多分析和融合,对原始数据和约束信息的使用不如SiCE-CFDP. CBSCAN和SiCE-CFDP都属于密度聚类算法,但是CDBSCAN的性能远远不如SiCE-CFDP.
|
图 8 对于不同的数据集5种算法的性能对比 Fig. 8 Comparison of five algorithms’ performance for different datasets |
4)在对IRIS数据集的测试中,MPCK-means性能最好,SiCE-CFDP性能次之. Constrained 1-Spectral Clustering是基于谱图分割寻找最后函数解的算法,在DS3中表现不错,但是当重叠更加复杂时,Constrained 1-Spectral Clustering无法简单地寻找到合适的分割,所需要的约束增多. 与SiCE-CFDP相比,Constrained 1-Spectral Clustering出现了明显的效果差距. 由于EM算法的稳定性,采用EM估计的MPCK-means在小数据量、复杂数据空间特征情况下,脱颖而出.
5)Wine数据集与IRIS相似,但是数据重叠情况比IRIS严重. Constrained 1-Spectral Clustering仍然需要比较多的约束才能找到正确的分割.
6)在对Waveform5000数据集的测试中,SiCE-CFDP效果最好,Constrained 1-Spectral Clustering次之.
7)在对Gisette(Mnist)数据集的测试中,SiCE-CFDP效果最好. CDBSCAN效果比MPCK-means、Constrained 1-Spectral Clustering好. 不同手写数字数据的产生具有共性,根据每个人的风格,字在同一可辨识的标准范围内变化,数据集具有密度分布均匀的特征,适合使用CDBSCAN算法进行聚类.
8)在对空调数据集的测试中,SiCE-CFDP效果最好,MPCK-means次之. 对于数据量多、结构复杂的空调数据,SiCE-CFDP对约束利用较为充分,效果最好.
表3中选取最具代表性的DS1、DS2、DS3和空调数据集,分析了算法对需要人为确定的最重要参数最近邻点数量k的鲁棒性. 对于包含n个数据点的数据集,虽然不同的k导致初始中心点数目不同,但是经过有效的簇融合后,算法对参数k具有鲁棒性,并且能够聚类出准确的类别数. 算法中以多数投票增加ML约束时所使用的阈值,取值过小会导致错误约束增加,算法性能下降;取值过大会导致算法几乎难以发现可以增加的ML约束,建议阈值取值范围为75%~90%.
| 表 3 初始中心点数目和最终类别数随约束量的变化情况 Table 3 Changes of number of initial center points and final clusters under constraint numbers |
5种算法的性能关系为
SiCE-CFDP>Constrained 1-Spectral Clustering=MPCK-means>CDBSCAN>COP-K-means.
SiCE-CFDP通过集成学习对数据空间反复挖掘,在原有约束基础上,获得了更多合理的约束,对约束信息和约束信息代表的数据分布有了更深的认识. 结合反应层次信息的中心点,在后续的聚类过程中把同层的簇合并,拥有较高的稳定性. 除了SiCE-CFDP的其余4种算法需要预先知道类数,SiCE-CFDP算法能够在不需要知道类数的前提下,仅仅依靠少部分约束信息,快速提升聚类性能,获得精确的聚类结果. 当数据量小时,SiCE-CFDP与其他算法效果大致相近. 当数据集的数据量增多时,算法从已知约束结合数据分布增强约束信息,集成学习的优势越来越明显.
Constrained 1-Spectral Clustering通过函数对谱图进行划分,能够寻找到最优的解,但是类别多、数据重叠变得复杂时,需要更多的约束信息辅助进行划分,对约束信息量的需求和聚类效果不如SiCE-CFDP稳定.
MPCK-means通过EM和约束信息估计出合适的数据结构,但是没有深入考虑数据原始的层次分布结构,提取数据原始信息的能力比SiCE-CFDP稍差,聚类效果也逊色于SiCE-CFDP.
CDBSCAN算法与SiCE-CFDP算法虽然同属于基于半监督约束的密度聚类算法,但是CDBSCAN算法对约束信息的利用比较粗糙,只考虑了现有的约束信息,没有根据现有的数据和约束挖掘出新的可靠约束信息,相比SiCE-CFDP聚类效果有较大差距.
COP-K-means算法是最早提出的算法,对约束信息和原始数据信息的应用处于最浅层的阶段,相比其余4种算法,效果最差.
仿真结果证明通过挖掘原始数据层次信息和扩充约束信息以集成学习,算法能够得到更多可靠的聚类指引. 在CFDP基础上提出的SiCE-CFDP算法是稳定、自发掘的算法. SiCE-CFDP算法弥补了常见的典型算法缺陷,获得不逊于目前大部分主流半监督聚类算法的性能.
3 结 语提出半监督约束集成的快速密度峰值聚类算法(SiCE-CFDP). 算法通过集成学习增强约束信息、挖掘数据潜在结构,能够在更少的先验信息条件下,获得更好的聚类结果. 算法使用邻近的k个点计算密度和距离,以层次聚类思想选出多个中心点. 冗余选择初始中心点使得算法不会遗漏类别,在后期融合局部中心点簇. 算法对KD-tree设置不同参数,获得分歧信息,通过集成学习增加约束信息数量. 算法以初始中心点为核心,参考约束信息对数据集进行聚类,生成聚类簇. 结合线性判别器和分布检验的思想来合并簇,得到最终聚类结果. 对比SiCE-CFDP和典型算法的性能,结果表明对于各种结构的数据集,SiCE-CFDP可以在不预先知道类别数情况下,以少量约束获得更加精确的结果,原因是聚类过程中对数据结构分布的挖掘.
SiCE-CFDP算法可以进一步优化. SiCE-CFDP算法的优势体现在数据量变大之后. 当数据量较小时,算法效果与主流算法大致相当,因此提升小数据量时的性能值得继续研究. SiCE-CFDP对静态的数据有很好的处理效果,但是现在动态的流数据不断增多,考虑使用SiCE-CFDP算法处理在线动态数据量. 线性分类器的选择影响簇的融合,考虑尝试其他分类器.
| [1] |
SHAO J, HE X, BOHM C, et al. Synchronization-inspired partitioning and hierarchical clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(4): 893-905. DOI:10.1109/TKDE.2012.32 |
| [2] |
HUANG J, SUN H, SONG Q, et al. Revealing density-based clustering structure from the core-connected tree of a network[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(8): 1876-1889. DOI:10.1109/TKDE.2012.100 |
| [3] |
SHENTAL N, BAR-HILLEL A, HERTZ T, et al. Gaussian mixture models with equivalence constraints [M] //BASU S, DAVIDSON I, WAGSTAFF K. Constrained clustering: advances in algorithms, theory, and applications. Boca Raton: CRC Press, 2008: 33-58.
|
| [4] |
MORSIER D F, TUIA D, BORGEAUD M, et al. Cluster validity measure and merging system for hierarchical clustering considering outliers[J]. Pattern Recognition, 2015, 48(4): 1478-1489. DOI:10.1016/j.patcog.2014.10.003 |
| [5] |
PARIKH M, VARMA T. Survey on different grid based clustering algorithms[J]. International Journal, 2014, 2(2): 427-430. |
| [6] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [7] |
CHEN M, LI L, WANG B, CHENG J, et al. Effectively clustering by finding density backbone based-on kNN[J]. Pattern Recognition, 2016, 60: 486-498. DOI:10.1016/j.patcog.2016.04.018 |
| [8] |
XIE J, GAO H, XIE W, et al. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors[J]. Information Sciences, 2016, 354: 19-40. DOI:10.1016/j.ins.2016.03.011 |
| [9] |
XU J, WANG G, DENG W. DenPEHC: density peak based efficient hierarchical clustering[J]. Information Sciences, 2016, 373: 200-218. DOI:10.1016/j.ins.2016.08.086 |
| [10] |
RUIZ C, SPILIOPOULOU M, MENASALVAS E. User constraints over data streams [C] // 17th European Conference on Machine Learning and the 10th European Conference on Principles and Practice of Knowledge Discovery in Databases. Berlin: ECML /PKDD, 2006: 117-226.
|
| [11] |
RUIZ C, SPILIOPOULOU M, MENASALVAS E. Density-based semi-supervised clustering[J]. Data Mining and Knowledge Discovery, 2010, 21(3): 345-370. |
| [12] |
WAGSTAFF K, CARDIE C, ROGERS S, et al. Constrained K-means clustering with background knowledge [C] // Eighteenth International Conference on Machine Learning. San Francisco: Morgan Kaufmann Publishers Inc, 2001: 577-584. http://www.researchgate.net/publication/221345976_Constra
|
| [13] |
BILENKO M, BASU S, MOONEY R J. Integrating constraints and metric learning in semi-supervised clustering [C] // The Twenty-first International Conference on Machine Learning. Banff: ICML, 2004: 11. http://www.researchgate.net/publication/2942990_Integrating_Constraints_and_Metric_Learning_in_Semi-Supervised_Clustering
|
| [14] |
Rangapuram S S, Hein M. Constrained 1-Spectral Clustering [J]. Computer Science, 2015:1143-1151. http://www.oalib.com/paper/4075084
|
| [15] |
AZIMI J, FERN X. Adaptive cluster ensemble selection [C] // International Joint Conference on Artifical Intelligence. Pasadena: Morgan Kaufmann Publishers Inc, 2009: 992-997. http://www.researchgate.net/publication/220814546_Adaptive_Cluster_Ensemble_Selection
|
| [16] |
唐伟, 周志华. 基于Bagging的选择性聚类集成[J]. 软件学报, 2005, 16(4): 496-502. TANG Wei, ZHOU Zhi-Hua. Bagging-based selective clusterer ensemble[J]. Journal of Software, 2005, 16(4): 496-502. |
| [17] |
HANSEN L K, SALAMON P. Neural network ensemble[J]. IEEE Computer Society, 1990, 12(10): 993-1001. |
| [18] |
RAND W M. Objective criteria for the evaluation of clustering methods[J]. Journal of the American Statistical Association, 1971, 66(336): 846-850. DOI:10.1080/01621459.1971.10482356 |
| [19] |
HALKIDI M, GUNOPULOS D, KUMAR N. A framework for semi-supervised learning based on subjective and objective clustering criteria [C] // Fifth IEEE International Conference on Data Mining. Houston: IEEE, 2005: 637-640. http://doi.ieeecomputersociety.org/10.1109/ICDM.2005.4
|
| [20] |
BACHE K, LICHMAN M. UCI machine learning repository [EB/OL]. [2017-06-18]. https://archive.ics.uci.edu/ml/index.php
|



