随着移动通信网络的快速发展和移动终端定位技术的广泛应用,基于位置的服务(location based services, LBS)[1]影响着人类生产生活的方方面面. 通过LBS应用,移动终端用户构成了庞大的社会网络,产生了大量的位置数据. 群体是指2个及以上的个体由于特定的内在因素(兴趣、目标、利益等)自发或者有组织地聚集在一起形成的集合[2]. 群体发现是社会网络研究的重要内容[3],有助于进一步分析群体用户的行为模式与交互规律,实施舆情引导控制和异常群体监控[4]. 移动终端用户群体发现是指通过分析用户在使用LBS应用时产生的位置数据,挖掘具有相同内在因素的用户集合.
复杂网络的社团挖掘方法[5]主要依据用户关系拓扑图进行聚类,忽略了用户的其他属性,难以发现属性特征相似的群体[2]. 移动终端用户具有较强的位置属性,复杂网络的社团挖掘方法不适用于移动终端用户的群体发现. 在现有的针对位置社交网络(location-based social network, LBSN)的社团挖掘方法中,Hung等[6]和Boston等[7]根据位置数据提取用户的移动行为模式,将行为模式相似的用户聚类为一个社团/群体. 但是现实生活中行为模式相似的用户不一定具有社会关系,例如在相同路线经过的上班族、在同一个商圈居住的居民等,所以Boston等[7]所述方法发现的群体存在不准确性. Jayadevan等[8]根据位置共现信息估计用户社会关系强度,得到社会关系拓扑图,使用社团挖掘方法发现移动用户群体,但是该方法将共现信息转化为社会关系,弱化了用户的位置属性. 假定场景:给定3个用户(1、2、3)和3个位置(Ⅰ、Ⅱ、Ⅲ). 用户1频繁出现在Ⅰ和Ⅱ,用户2频繁出现在Ⅰ和Ⅲ,用户3频繁出现在Ⅱ和Ⅲ. 每2个用户通过共现位置建立了社会关系. 从社会关系的角度分析,3个用户可以属于同一个群体;但是从位置属性的角度看,三者没有共同的共现位置,属于不同的群体. Lim等[9]指出时空叠加关系发现的群体以位置为中心,具有高度的位置相似性. Brown等[10]根据网络结构图和用户签到的位置信息研究同一网络中线上和线下用户群体的差异性,指出线下用户群体具有位置聚集性. Brown等[11]和Liu等[12]利用用户社会关系和签到地点双重信息发现位置社团,根据签到信息计算用户的社会关系强度,将社会关系强度作为社会关系拓扑图中边的权值,删除权值小于阈值的边,用传统社团挖掘算法发现位置社团. 但是Brown等[11]和Liu等[12]将位置信息与社会关系相融合,根据社会关系拓扑图发现的群体同样可能存在位置属性不强的问题;同时移动终端上既有社交类应用,也有非社交类应用,在非社交类应用中用户间交流互动较少,无法直接提取用户的社会关系,因此Brown等[11]和Liu等[12]的方法在移动终端用户的群体发现中的普适性不强.
综上所述,位置数据不能直接表达用户的社会关系,复杂网络群体发现方法不能直接用于移动用户的群体发现;同时移动用户群体具有社会关系和位置聚集双重属性,现有以复杂网络和位置社交网络为对象的社团挖掘方法难以同时兼顾社会关系和位置属性,所发现群体具有不准确性。为此,以位置信息为对象,提取用户社会关系和位置属性,将前者作为用户关系拓扑图,后者作为用户标签,并通过标签传播算法将两者结合起来,提出一种有效的移动终端用户群体发现方法。
1 基本思路
移动终端用户群体发现的目的是从数量众多的用户中筛选出具有稠密社会关系和相似位置属性的用户群体。一方面,移动用户通常在多个地点签到,具有多个位置标签;另一方面,现实生活中每个用户拥有多种类型的社会关系,可能属于多个群体。同一群体成员的位置标签既有共性,也有差异。用户在某个群体中的标签差异性可能与用户所属的其他群体有关。现有方法不能很好处理上述位置属性多标签与社会关系多群体的问题。本研究提出基于反向标签传播算法(reverse label propagation algorithm, Reverse-LPA)的移动终端用户重叠群体发现方法。根据签到位置信息推断移动终端用户社会关系拓扑图,提取用户的时空共现区作为标签,通过标签初始化得到标签拓扑图。在标签拓扑图上进行反向标签传播,对于节点的每个标签,依据其在邻居节点中的状态,标记其状态为“保留”或“消除”;反复迭代,根据标签的状态将符合条件标签删除,得到稳定状态的用户标签拓扑图;最终在标签拓扑图上根据节点连接关系和标签分布情况提取用户群体。Reverse-LPA的结构如图1所示。
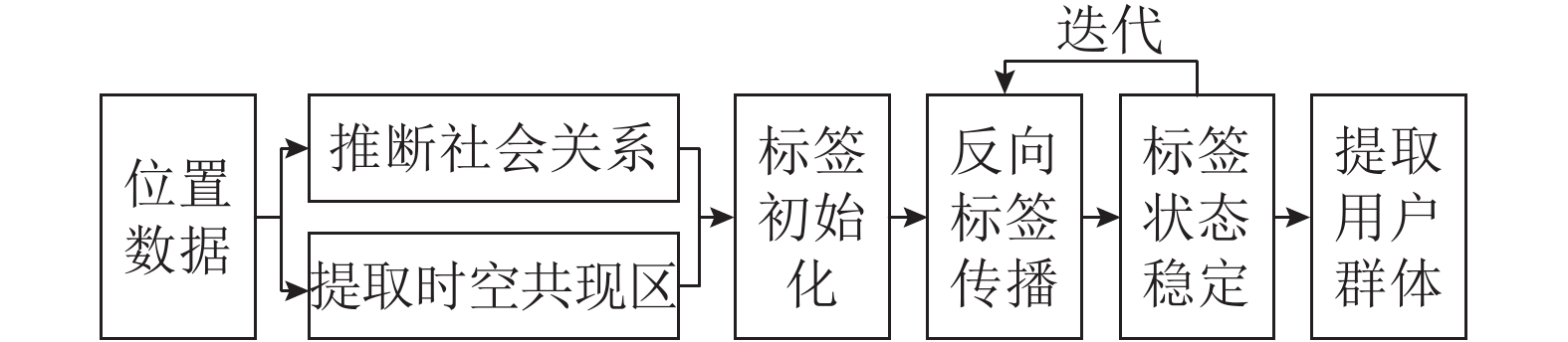
|
图 1 基于反向标签传播算法的结构图 Fig. 1 Structure of reverse label-propagation algorithm |
移动终端用户社会关系推断是指根据用户签到位置数据的时间和空间关系判断用户社会关系强度. 目前常用的方法有共现频次法[13]、轨迹相似法[14]和特征提取法[15-17]等. 选取马春来等[17]提出的方法,根据用户签到位置的总体属性、用户活跃性、位置多样性和位置特殊性等4类特征,使用改进的随机森林算法判断用户是否存在社会关系,在用户社会关系判断的基础上构建用户关系拓扑图.
2.2 时空共现区提取定义位置数据为
标签传播算法(label propagation algorithm, LPA)是一种复杂度较低的社团发现方法[19],包括标签初始化、标签传播和传播停止条件3个部分. 将用户时空共现区作为位置属性标签,结合标签初始化与用户社会关系拓扑图,有助于提高移动终端用户群体发现结果的准确性. 因为移动终端用户通常会在多个位置签到,对应多个时空共现区,所以标签初始化后的社会关系拓扑图中的每个用户节点拥有多个标签. 现有LPA大多为1个用户节点初始化1个标签,无法处理多标签的情况,因此本研究对现有的LPA进行改进,提出一种反向标签传播算法.
3.1 标签初始化设移动终端用户社会关系拓扑图为
现有LPA的标签传播是依据邻居节点标签的分布情况,采用一定的策略将节点标签置换为某一邻居节点标签. 节点的标签是算法随机分配的,不表示实际含义,置换标签不改变节点属性. 但是
数据集(见4.1节)上的统计结果显示每个用户的平均签到数量分布范围为
主标签反映了节点与群体的关系,伴随标签仅仅反映了节点与群体中部分节点的关系,因此改进标签传播方法是根据节点
1) 统计标签的节点集合. 统计与任意节点
2) 标记标签状态. Reverse-LPA中位置标签有2种可标记状态:保留和消除. “保留”状态指在当前节点中标签不需要消除;“消除”状态指在当前节点中标签可以消除. 标签的“保留”和“消除”状态是不断变化的,同一标签在不同的节点或者迭代次数中的状态可能不同. 初始状态为“保留”的标签最终不一定会被保留下来,状态为“消除”的标签需要满足一定的条件才可能被消除. 标记标签状态时,初始化所有标签状态为“保留”. 将标签集合
3) 传播标签状态. 每个节点向所有邻居节点传播自己的标签状态,并且接收邻居节点的标签状态. 对集合
4) 检查停止条件. 如果所有节点标签满足传播停止条件,停止标签传播,否则返回步骤2.
3.3 传播停止条件当任意标签
Reverse-LPA的伪代码如下.
Reverse-LPA Algorithm
Input:Label graph
Output:Group information matrix Group
1 For each
2 Do
3
4
5
6 For each
7 {If
8
9 Else If (
10
11 Propagate label state to neighbor nodes in
12 For each
13 {If
14 {
15 While (
16 Update
17 For each
18 {
19 For each
20 {If
21 {
Reverse-LPA的标签传播过程与现有的LPA差别比较大,需要证明可行性. Reverse-LPA的主要原理是在节点连接关系上经过多次传播获取标签的稳定状态,保留每个群体熵值最小的主标签. 根据Reverse-LPA的标签传播过程,可以通过证明节点标签稳定状态的存在性论证Reverse-LPA的可行性. 节点标签稳定状态的存在性可以从2个方面进行证明:伴随标签的稳定状态为“消除”;熵值最小主标签的稳定状态为“保留”,其他主标签的稳定状态为“消除”.
问题1可描述为:给定节点
证明:设
情况1:与
情况2:与
问题2可描述为:给定节点
证明:设
如果
同理可知,稳定状态时
问题1和问题2的证明结果表明,节点的稳定状态是存在的,Reverse-LPA是可行的.
5 实验及结果分析 5.1 数据集简介基于Reverse-LPA的移动终端用户群体发现方法,Boston等[7]和Jayadevan等[8]提出的对比方法只需要位置信息即可完成群体发现工作,但Liu等[12]提出的对比方法还需要用户社会关系信息,数据集需要同时具有用户签到位置和社会关系信息. 本研究选取来自社交网站Gowalla、Brightkite和Foursquare上的签到位置数据,通过实验验证Reverse-LPA的有效性. Gowalla、Brightkite数据集来源于Cho等[22]的研究,数据内容主要包括用户ID、位置、时间和关注关系. Foursquare数据集来源于Bao等[23]的研究,内容包括用户身份、签到事件、地点和关注关系. 由于Foursquare用户的签到频率比较稀疏,为了保证数据的可用性,选取签到事件不少于8次的用户进行实验. 为了分析Reverse-LPA群体发现的准确性,利用Foursquare数据集相对丰富的用户信息,使用问卷调查获取部分用户的真实群体信息. 根据身份信息和Foursquare网站定位用户的Facebook主页,获取用户的Email并且发送调查问卷. 问卷内容主要包括与用户有关注关系的Foursquare用户的Facebook昵称和社会关系类型选项. 根据问卷结果,将用户身份数据中家庭地址(Home City)一致并且有家人(Family)关系的用户划分为一个群体;将Facebook主页中工作地点(或单位)一致并且有同事(Colleague)关系的用户划分为一个群体. 在49 062个Foursquare用户中获取到Email账号31 049个,回收有效调查问卷648份,成功划分群体154个,涉及1 832个用户,命名为Fsqtrue数据集. 各数据集的统计信息如表1所示.
| 表 1 位置数据集属性信息 Table 1 Attribute information of location datasets |
已知群体背景信息时,使用标准互信息(normalized mutual information,NMI)评价群体发现算法的性能. NMI取值范围为[0, 1.0],数值越大表明群体发现算法输出结果与群体真实结构越接近,算法性能越好. 给定算法输出结果为
| $\begin{split}{\rm{NMI}}\left( {{G_{\rm{A}}},{G_{\rm{T}}}} \right) =& 2\displaystyle\frac{{H\left( {{G_{\rm{A}}}} \right) + H\left( {{G_{\rm{T}}}} \right) - H\left( {{G_{\rm{A}}},{G_{\rm{T}}}} \right)}}{{H\left( {{G_{\rm{A}}}} \right) + H\left( {{G_{\rm{T}}}} \right)}}=\\& \displaystyle\frac{{2{\mathop{\rm MI}\nolimits} \left( {{G_{\rm{A}}},{G_{\rm{T}}}} \right)}}{{H\left( {{G_{\rm{A}}}} \right) + H\left( {{G_{\rm{T}}}} \right)}}.\end{split}$ | (1) |
式中:
| $\begin{array}{l}H\left( {{G_{\rm{A}}}} \right) = \displaystyle\sum\limits_{i = 1}^{\left| {{G_{\rm{A}}}} \right|} {{N_{i\cdot}} \log\; \left( {\frac{{{N_{i \cdot }}}}{N}} \right)} ,\\H\left( {{G_{\rm{T}}}} \right) = \displaystyle\sum\limits_{j = 1}^{\left| {{G_{\rm{T}}}} \right|} {{N_{\cdot_j}} \log\; \left( {\frac{{{N_{\cdot j}}}}{N}} \right)} ,\\{\rm{NMI}}\left( {{G_{\rm{A}}},{G_{\rm{T}}}} \right) = \displaystyle\sum\limits_{i = 1}^{\left| {{G_{\rm{A}}}} \right|} {\displaystyle\sum\limits_{j = 1}^{\left| {{G_{\rm{T}}}} \right|} {{N_{ij}} \log\; \left( {\frac{{{N_{ij}}N}}{{{N_{i \cdot }}{N_{\cdot_j}}}}} \right)} } .\end{array}$ | (2) |
在群体背景信息未知的情况下,可以使用模块度
| ${Q_{{\rm{ov}}}}\left( {{G_{\rm{A}}}} \right) = \frac{1}{{2w}}\sum\limits_{G_{\rm{A}}^k \in G_{\rm{A}}^{}} {\sum\limits_{{v_i},{v_j} \in G_{\rm{A}}^{}} {\left( {{r_{ijk}}{w_{ij}} - {s_{ijk}}\frac{{d_i^{}d_j^{}}}{{2w}}} \right)} } . $ | (3) |
式中:
移动终端用户群体中不仅存在重叠现象,还具有位置属性. 如图2(a)所示,以模块度为衡量标准,节点
| ${S_{\rm{g}}}\left( {{G_{\rm{A}}}} \right) = \frac{1}{{\left| {{G_{\rm{A}}}} \right|}}\sum\limits_{k=1}^{\left| {{G_{\rm{A}}}} \right|} {{S_{\rm{g}}}\left( {G_{\rm{A}}^k} \right)} ,$ | (4) |
| ${S_{\text{g}}}\left( {G_{\text{A}}^k} \right) = \frac{1}{{\left| {G_{\text{A}}^k} \right|\left( {\left| {G_{\text{A}}^k} \right| - 1} \right)}}\sum\limits_{k{\text{ = 1}}}^{\big| {{G_{\text{A}}}^{}} \big|} {\sum\limits_{i = 1}^{\big| {G_{\text{A}}^k} \big|} {\sum\limits_{j = 1,j \ne i}^{\big| {G_{\text{A}}^k} \big|} {\frac{{\left| {z_{\text{c}}^{G_{\text{A}}^k - {v_i}} \cap z_{\text{c}}^{G_{\text{A}}^k - {v_j}}} \right|}}{{\left| {z_{\text{c}}^{G_{\text{A}}^k - {v_i}} \cup z_{\text{c}}^{G_{\text{A}}^k - {v_j}}} \right|}}} } } .$ | (5) |
式中:
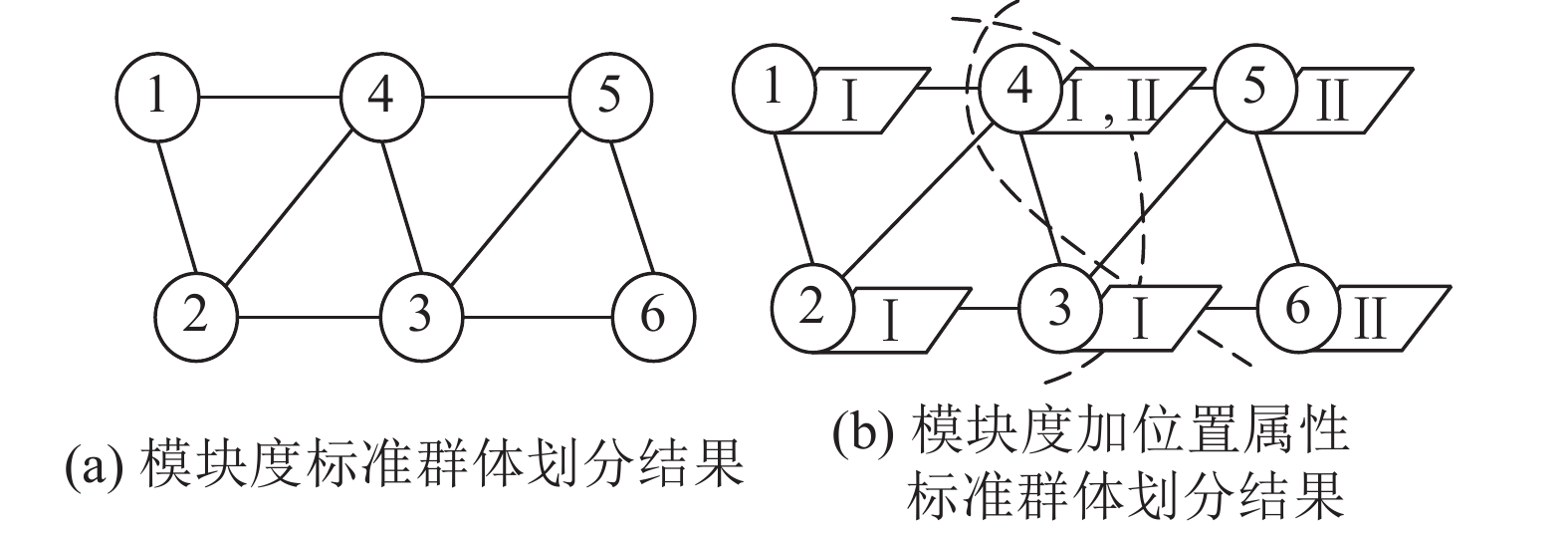
|
图 2 移动终端用户群体模块度与位置属性示例图 Fig. 2 Example diagram of group module degree and location attribute for mobile terminal users |
| $F\left( {{G_{\rm{A}}}} \right) = \frac{{2 {Q_{{\rm{ov}}}}\left( {{G_{\rm{A}}}} \right) {S_{\rm{g}}}\left( {{G_{\rm{A}}}} \right)}}{{{Q_{{\rm{ov}}}}\left( {{G_{\rm{A}}}} \right) + {S_{\rm{g}}}\left( {{G_{\rm{A}}}} \right)}}.$ | (6) |
实验结果分析包含两部分. 首先在4个数据集上观察评价指标NMI、
使用Reverse-LPA对4个数据集进行群体划分,在每次迭代中计算评价指标NMI、
Reverse-LPA算法流程、数据集特征和实验结果表明Reverse-LPA的迭代次数与用户平均签到次数存在关联关系.由 图3可知,数据集中用户平均签到次数越多,Reverse-LPA需要的迭代次数越多,但是后者的增速较前者慢. 原因是用户平均签到次数越多,初始标签越多,Reverse-LPA需要越多次迭代使所有节点标签达到稳定状态. 同时,初始标签越多,伴随标签越多,较多的伴随标签通过“消除传播效应”加速标签状态的确定,因此迭代次数的增幅低于平均签到次数.
函数
Reverse-LPA能够发现移动终端用户群体. 由图3(a)可知,Reverse-LPA在迭代过程中逐步提高了划分群体的NMI值,算法停止时NMI为0.85,说明Reverse-LPA对数据集Fsqtrue的群体划分结果是有效的. 函数F与

|
图 3 Reverse-LPA对Gowalla、Brightkite、Foursquare和Fsqtrue数据集进行群体划分时评价指标随迭代次数的变化 Fig. 3 Evaluation index changes with the number of iterations ingroup classification of Gowalla, Brightkite, Foursquare and Fsqtrueusing Reverse-LPA |
为了检验Reverse-LPA的有效性,对比Reverse-LPA和文献[7]、[8]、[12]中所述的基于共现位置轨迹的群体发现方法(group discovery using co-location traces,GDC)、面向位置区域的社会群体发现方法(local social groups discovery, LSGD)、基于位置的标签传播算法(location based label propagation algorithm,LBLPA)在4个数据集上的评价指标NMI、
| 表 2 Reverse-LPA、GDC、LSGD、LBLPA方法的群体发现效果对比 Table 2 Comparison of group discovery effects of Reverse-LPA, GDC, LSGD and LBLPA |
提出了基于Reverse-LPA的移动终端用户群体发现方法,根据位置数据推断用户社会关系拓扑图,提取用户时空共现区. 以时空共现区为标签标记社会关系拓扑图,在标签拓扑图上进行反向标签传播. 通过反复迭代,逐步消除伴随标签,最终保留每个用户所属群体的主标签. 将拓扑图上拥有相同主标签的用户划分为一个群体,得到移动终端用户群体结构. Reverse-LPA算法较好地考虑了用户社会关系和位置属性,其可行性和有效性在真实数据集上得到了验证,Reverse-LPA的评价指标
| [1] |
DEY A, HIGHTOWER J, LARA E D, et al. Location-based services[J]. IEEE Pervasive Computing, 2017, 9(1): 11-12. |
| [2] |
潘理, 吴鹏, 黄丹华. 在线社交网络群体发现研究进展[J]. 电子与信息学报, 2017, 39(9): 2097-2107. PAN Li, WU Peng, HUANG Dan-hua. Reviews on group detection in online social networks[J]. Journal of Electronics and Information Technology, 2017, 39(9): 2097-2107. |
| [3] |
方滨兴, 贾焰, 韩毅. 社交网络分析核心科学问题、研究现状及未来展望[J]. 中国科学院院刊, 2015(2): 187-199. FANG Bin-xing, JIA Yan, HAN Yi. The core scientific problems, research status and future prospects of social network analysis[J]. Bulletin of Chinese Academy of Sciences, 2015(2): 187-199. |
| [4] |
王桦, 韩同阳, 周可. 公安情报中基于关键图谱的群体发现算法[J]. 浙江大学学报: 工学版, 2017, 51(6): 1173-1180. WANG Hua, HAN Tong-yang, ZHOU Ke. Key graph-based community detection algorithm for public security intelligence[J]. Journal of Zhejiang University: Engineering Science, 2017, 51(6): 1173-1180. |
| [5] |
KIM J, LEE J G. Community detection in multi-layer graphs: a survey[J]. ACM SIGMOD Record, 2015, 44(3): 37-48. DOI:10.1145/2854006 |
| [6] |
HUNG C C, CHANG C W, PENG W C. Mining trajectory profiles for discovering user communities [C] // Proceedings of the 2009 International Workshop on Location Based Social Networks. Seattle: ACM, 2009: 1-8. http://www.cnki.com.cn/Article/CJFDTotal-ZGGX201608044.htm
|
| [7] |
BOSTON D, MARDENFELD S, PAN J, et al. Leveraging Bluetooth co-location traces in group discovery algorithms[J]. Pervasive and Mobile Computing, 2014, 11(6): 88-105. |
| [8] |
JAYADEVAN V, BHARADWAJ K, KUMAR A, et al. Discovering local social groups using mobility data[J]. International Journal of Computer Applications, 2015, 120: 15-19. |
| [9] |
LIM K H, CHAN J, LECKIE C, et al. Detecting location-centric communities using social-spatial links with temporal constraints [C] // Advances in Information Retrieval: 37th European Conference on IR Research. Vienna: ECIR, 2015: 489-494. http://link.springer.com/10.1007/978-3-319-16354-3_53
|
| [10] |
BROWN C, NICOSIA V, SCELLATO S, et al. Social and place-focused communities in location-based online social networks[J]. European Physical Journal B, 2013, 86(6): 1-10. |
| [11] |
BROWN C, NICOSIA V, SCELLATO S, et al. The importance of being placefriends: discovering location-focused online communities[C] // ACM Workshop on Online Social Networks. Helsinki: ACM, 2012: 31-36. http://www.researchgate.net/publication/234108127_The_importance_of_being_placefriends_discovering_location-focused_online_communities
|
| [12] |
LIU J, LI Y, LING G, et al. Community detection in location-based social networks: an entropy-based approach [C] // IEEE International Conference on Computer and Information Technology. Nadi: IEEE, 2017: 452-459. https://www.researchgate.net/publication/314955335_Community_Detection_in_Location-Based_Social_Networks_An_Entropy-Based_Approach
|
| [13] |
CRANDALL D J, BACKSTROM L, COSLEY D, et al. Inferring social ties from geographic coincidences[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(52): 22436-22441. DOI:10.1073/pnas.1006155107 |
| [14] |
XIAO X, ZHENG Y, LUO Q, et al. Inferring social ties between users with human location history[J]. Journal of Ambient Intelligence and Humanized Computing, 2014, 5(1): 3-19. DOI:10.1007/s12652-012-0117-z |
| [15] |
TAN R, GU J, CHEN P, et al. Link prediction using protected location history [C] // 2013 International Conference on Computational and Information Sciences. Shiyang: IEEE, 2013: 795-798. http://www.researchgate.net/publication/261159978_link_prediction_using_protected_location_history
|
| [16] |
WANG D, PEDRESCHI D, SONG C, et al. Human mobility, social ties, and link prediction [C] // ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM, 2011: 1100-1108. http://www.researchgate.net/publication/221654073_Human_mobility_social_ties_and_link_prediction
|
| [17] |
马春来, 单洪, 马涛, 等. 随机森林改进算法在LBS用户社会关系推断中的应用[J]. 小型微型计算机系统, 2016, 37(12): 2708-2712. MA Chun-lai, SHAN Hong, MA Tao, et al. An improved random forests algorithm with application to social ties inferring of LBS users [J]. Journal of Chinese Computer Systems, 2016, 37(12): 2708-2712. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xxwxjsjxt201612022 |
| [18] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [19] |
陈晶, 万云. 社交网络中基于模块度最大化的标签传播算法的研究[J]. 通信学报, 2017, 38(2): 25-33. CHEN Jing, WAN Yun. Research on label propagation algorithm based on modularity maximization in the social network[J]. Journal on Communications, 2017, 38(2): 25-33. |
| [20] |
WANG Z, ZHANG D, ZHOU X, et al. Discovering and profiling overlapping communities in location-based social networks[J]. IEEE Transactions on Systems Man and Cybernetics Systems, 2014, 44(4): 499-509. DOI:10.1109/TSMC.2013.2256890 |
| [21] |
LIU D, WEI W, SONG G, et al. Community discovery with location-interaction disparity in mobile social networks[J]. ZTE Communications, 2015(2): 53-61. |
| [22] |
CHO E, MYERS S A, LESKOVEC J. Friendship and mobility: user movement in location-based social networks [C] // ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Diego: ACM, 2011: 1082-1090. http://cn.bing.com/academic/profile?id=dadebb3a25c377e6fb082e4465eba412&encoded=0&v=paper_preview&mkt=zh-cn
|
| [23] |
BAO J, ZHENG Y, MOKBEL M F. Location-based and preference-aware recommendation using sparse geo-social networking data [C] // International Conference on Advances in Geographic Information Systems. Redondo Beach: ACM, 2012: 199-208. http://www.researchgate.net/publication/262237220_Location-based_and_preference-aware_recommendation_using_sparse_geo-social_networking_data
|
| [24] |
LANCICHINETTI A, FORTUNATO S, KERTÉSZ J. Detecting the overlapping and hierarchical community structure of complex networks[J]. New Journal of Physics, 2008, 11(3): 19-44. |
| [25] |
黄健斌, 钟翔, 孙鹤立, 等. 基于相似性模块度最大约束标记传播的网络社团发现算法[J]. 北京大学学报: 自然科学版, 2013, 49(3): 389-396. HUANG Jian-bin, ZHONG Xiang, SUN He-li, et al. A network community detection algorithm via constrained label propagation with maximization of similarity-based modularity[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2013, 49(3): 389-396. |
| [26] |
NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E Statistical Nonlinear and Soft Matter Physics, 2004, 69(2): 026113. DOI:10.1103/PhysRevE.69.026113 |
| [27] |
NICOSIA V, MANGIONI G, CARCHIOLO V, et al. Extending the definition of modularity to directed graphs with overlapping communities[J]. Journal of Statistical Mechanics Theory and Experiment, 2009(3): 3166-3168. |



