2. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058;
3. 浙江大学 宁波理工学院 土木建筑工程学院,浙江 宁波 315100;
4. 国网江苏省电力公司经济技术研究院,江苏 南京 210008
2. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China;
3. School of Civil Engineering and Architecture, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China;
4. State Grid Jiangsu Economic Research Institute, Nanjing 210008, China
剪切带萌生、发展和贯通是岩土体灾变过程中应变局部化的宏观表现,是多数岩土体破坏的征兆和前提[1-3]. 剪切带倾角决定了岩土体破裂发展方向,对精确再现岩土体渐进破坏过程有重要作用.剪切带倾角的理论和试验研究一直是岩土工程界的焦点. 试验方面,以室内双轴、三轴和空心圆柱扭剪试验为主. 大量试验结果表明,剪切带倾角与材料颗粒级配和形状、土样的密实度、有效平均正应力等有关[2,4-5]. 颗粒形状的不规则性增强、土体初始密实度增加,剪切带倾角增大;土颗粒平均粒径、土样初始围压增加,剪切带倾角减小. 理论方面,主要是围绕倾角的计算方法,具体分为2大类. 一类基于传统Mohr-Coulomb强度理论或滑移线场理论,由岩土体的极限破坏状态确定倾角. 该类方法的计算精度很低,计算值与试验值的偏差较大,故常用于计算各类砂土剪切带倾角的上、下限. 另一类是基于应变局部化判别的分叉理论[6],由剪切带产生时的临界塑性硬化模量推得. 相比于前者,后者计算精度没有本质上的提高,且依赖于本构模型形式[7]. 另外,传统Mohr-Coulomb、Drucker-Prager模型无法反映土体密实度和围压的影响,理论值变化规律与试验结果相矛盾[8]. 文献[9]引入附加塑性应变项,改进Mohr-Coulomb模型,计算精度稍有提高;文献[10~12]采用非共轴的塑性流动理论以及基于材料状态的临界状态本构模型,描述砂土应变局部化现象,得到的倾角变化规律与试验结果一致,但计算精度仍较低.
鉴于剪切带倾角在岩土体渐进破坏分析中的重要作用,系统收集国内外文献中各类砂土剪切带倾角的平面应变试验结果,在分析试验规律的基础上,提出考虑砂土颗粒形状、密实度和有效平均正应力等影响因素的剪切带倾角经验公式,以精确模拟岩土体灾变过程中的剪切带扩展.
1 试验结果与现有倾角计算方法 1.1 试验数据的收集与分析系统收集近40年来国内外文献中各类砂土剪切带倾角的平面应变试验结果[4,5,8,13-18],部分砂土的物理力学指标如表1所示,试验加载方式、边界条件、排水条件以及制样方法等基本相同. 表中d50为砂土平均粒径,Cu为不均匀系数,emax、emin分别为砂土最大孔隙比和最小孔隙比,
如图1所示为收集到的17种砂土剪切带倾角试验值与出现频次,图中,θt为剪切带倾角试验值,N为出现频次. 可以看出:1) 砂土剪切带倾角整体上服从正态分布规律,除极个别数据点外,大多数倾角集中分布于52°~67°;2) 砂土颗粒级配和形状的差异导致不同砂土的倾角分布区间相差很大,如棱角状的Hostun砂倾角分布于58°~70°,次圆球状的Masonry砂倾角则集中分布于59°~64°;3) 受土样初始密实度和围压的影响,同种砂土的倾角跨度很大. 以Hostun砂为例,相同密实度的试样随围压(100~800 kPa)的变化,倾角相差10°左右;同种围压下,不同相对密实度(25%、95%)的土样倾角差值约为5°. 由此可见,砂土剪切带倾角的影响因素多、跨度大、变化范围广,给精确的理论计算带来困难.

|
图 1 17种砂土剪切带倾角试验值在不同范围内的出现频次 Fig. 1 Appearance frequency for inclination angle of 17 kinds of sand shear band under different ranges |
现有剪切带倾角的计算方法很多,本文仅给出几种经典、常用的方法.
方法1 假定材料满足相关联的Mohr-Coulomb强度理论,剪切带平行于Mohr-Coulomb强度包络线对应的应力状态面,剪破面与最大主应力作用面夹角为
| ${\theta _1} = \displaystyle\frac{\text{\;π\;}}{\;4\;} + \displaystyle\frac{\;\varphi\; }{\;2\;}.$ | (1) |
式中:φ为土体峰值内摩擦角.
方法2 通过滑移线场理论,假定剪破面重合于无拉伸面,利用主应变增量莫尔圆,得到剪破面与大主应变增量作用面夹角:
| ${\theta _2} = \frac{\text{\;π\;}}{\;4\;} + \frac{\;\psi\; }{\;2\;}.$ | (2) |
式中:
方法3 Dunstan等[13]基于试验结果,提出同时考虑内摩擦角和剪胀角的剪切带倾角经验公式:
| ${\theta _3} = \frac{\text{ π }}{\;4\;} + \frac{{\varphi + \psi }}{4}.$ | (3) |
方法4 Bardet[19]由分叉理论得到剪切带产生时的临界塑性硬化模量,结合非关联的Mohr-Coulomb本构模型,推导得出剪切带倾角的解析解:
| ${\theta _4} = \frac{1}{2}\arccos \;\left( { - \frac{{\sin \; \psi + \sin \; \varphi }}{2}} \right).$ | (4) |
式(4)亦可通过非关联的Drucker-Prager本构模型得到.
方法5 Bardet[9]借鉴多重塑性机制方法,改进非关联的Mohr-Coulomb模型,在初始塑性应变率的基础上,叠加一个附加塑性应变率,调整屈服点方向,得到方法4的修正解:
| ${\theta _5} = \frac{\;1\;}{\;2\;}\arccos \; \left[ { - \frac{{\left( {1 - 2\kappa } \right)\sin \; \psi + \sin \; \varphi }}{{2\left( {1 - \kappa } \right)}}} \right].$ | (5) |
式中:
将如图1所示各类砂土剪切带倾角的平面应变试验结果与上述5种常用的剪切带倾角计算方法得到的理论值进行比较. 如图2所示为各计算方法理论值与试验值的关系图. 其中,图2(a)~2(c)分别为方法1~3计算值与试验值的分布图,对比发现:1) 由方法1、2得到的理论值分别过高和过低的估计了剪切带倾角,方法3得到的理论值介于两者之间,从试验值内部穿过,三种计算方法的精度均较低;2) 计算结果严重偏离于部分试验结果,方法1、2只能作为试验值的上、下限,界定各类砂土的剪切带倾角变化范围. 图2(d)~2(e)分别为方法4、5计算值与试验值的分布图,图中θ为剪切带倾角理论值,斜率1∶1对角线上理论值与试验值相等. 可见:1) ±5°偏差线以外分布大量数据点,由方法4、5得到的理论值与试验值仍存在较大偏差;2) 相比于图2(d),图2(e)在–5°偏差线外数据点减少,+5°偏差线外数据点变化不明显,说明方法5在高估试验值的问题上有所改善,计算精度略高于方法4.

|
图 2 剪切带倾角试验值与理论值的对比 Fig. 2 Comparison of test and calculated values for inclination angle of shear band |
理论值与试验值对比分析表明,方法3~5的计算精度高于方法1、2,说明同时考虑内摩擦角和剪胀角更为合理. 不少学者[15,19]通过理论推导证实方法4实为方法3的近似,方法5则是在方法4本构模型基础上的改进. 因此,方法3~5以及方法1都是由Mohr-Coulomb本构模型推导而来,满足Mohr-Coulomb强度理论的假定. 所以,同一种土,即初始密实度、颗粒级配及形状等参数相同的土,其内摩擦角是常数,剪切带倾角是唯一的,这是现有方法得到的理论值与试验值存在较大偏差,且无法对如图1所示试验结果变化规律作出合理解释的重要原因.
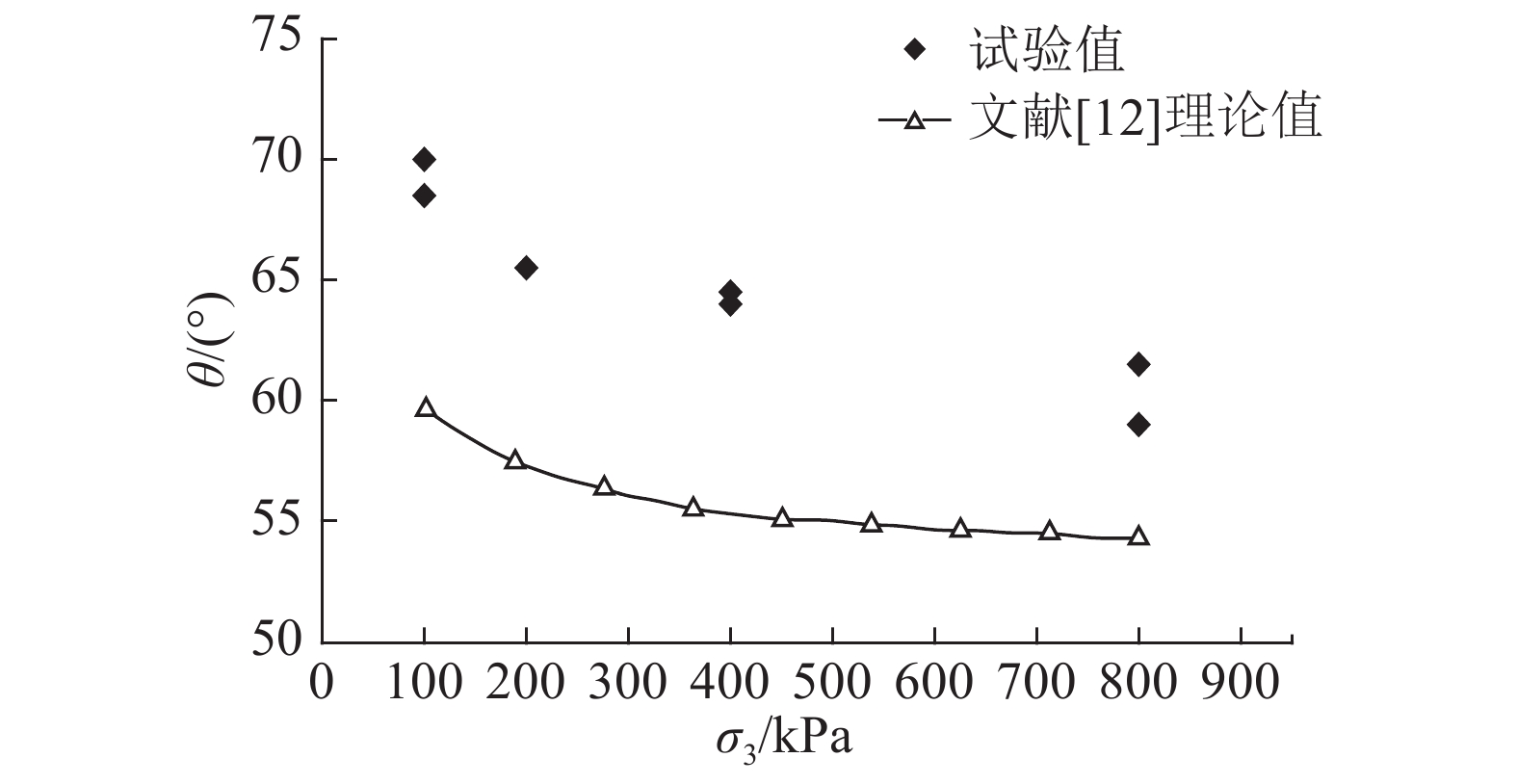
文献[12]采用与材料状态相关的砂土临界状态本构模型,分析了Hostun砂的应变局部化现象,如图3所示,从剪切带倾角与初始围压σ3的关系看,理论值随围压的增加而减小,这与试验结果的变化规律相同,但理论值却比试验值小10°左右,计算误差难以忽略.
|
图 3 不同初始围压下剪切带倾角理论值与试验值的对比 Fig. 3 Comparison of test and calculated values for inclination angle of shear band with different initial confining pressures |
考虑到现有方法计算值与试验值偏差较大,且无法解释试验结果的变化规律,基于上述分析,提出一种新的剪切带倾角计算方法.
2.1 公式提出细观特征(颗粒级配和形状)和初始状态(初始密实度和围压等)决定了材料宏观上的力学行为. 基于Mohr-Coulomb本构模型的计算方法不适用于剪切带倾角计算. 即使不考虑Mohr-Coulomb模型的局限性,方法1、2也分别过高、过低地估计了剪切带倾角,方法3取φ和
大量双轴和三轴试验表明,φ与
| $\varphi = {\varphi _{{\rm{crit}}}} + r\psi .$ | (6) |
式中:φcrit为临界内摩擦角,r为拟合参数. φcrit取决于材料级配、颗粒形状,对同种砂土而言近似为常数;本文所涉及砂土的φcrit值,除文献[8]中的Ottawa砂是由上式反演得到外,其余均由试验测定.
| $\theta = f\left( {{\varphi _{\rm{crit}}},\psi } \right) = \frac{\text{\;π\;}}{\;4\;} + \alpha {\varphi _{\rm{crit}}} + \beta \psi .$ | (7) |
式中:α、β为拟合参数. 由如图2所示的理论值与试验值分布关系及大量试验数据的拟合结果看,参数α可近似取为1/2,故式(7)可简化为
| $\theta = \frac{\text{\;π\;}}{\;4\;} + \frac{{{\varphi _{\rm{crit}}}}}{2} + \beta \psi .$ | (8) |
式(8)形式上与方法3~5类似,不同的是新增了拟合参数β,其具体取值如表1所示. 为了定量描述初始密实度和围压对剪胀角的影响,更直观地分析不同初始状态下的倾角变化规律,借鉴Cinicioglu等[21]提出的解耦土体密实度和围压的剪胀角经验公式:
| $\tan \; \psi = {\alpha _\psi }\frac{{{{p'}_{\!\!\!\!i}}}}{{{{{p}}_{\rm{a}}}}} + {m_\psi }{I_{\rm{D}}}.$ | (9) |
式中:
| $\theta = \frac{\text{\;π\;}}{\;4\;} + \frac{{{\varphi _{\rm{crit}}}}}{2} + \beta \; {\rm{arctan}} \; \left( {{\alpha _\psi }\frac{{{{p'}_{\!\!\!\!i}}}}{{{{{p}}_{\rm{a}}}}} + {m_\psi }{I_{\rm{D}}}} \right).$ | (10) |
式(8)、(10)中大部分控制变量的物理意义明确,但参数β由试验数据拟合而来,取值的依据及物理含义不清楚,不便于向其它种类的砂土推广应用. 为此,开展β与各类砂土物理、力学指标的相关性研究,发现β与Cu无明显相关性,但可能与d50以及emax、emin有关.
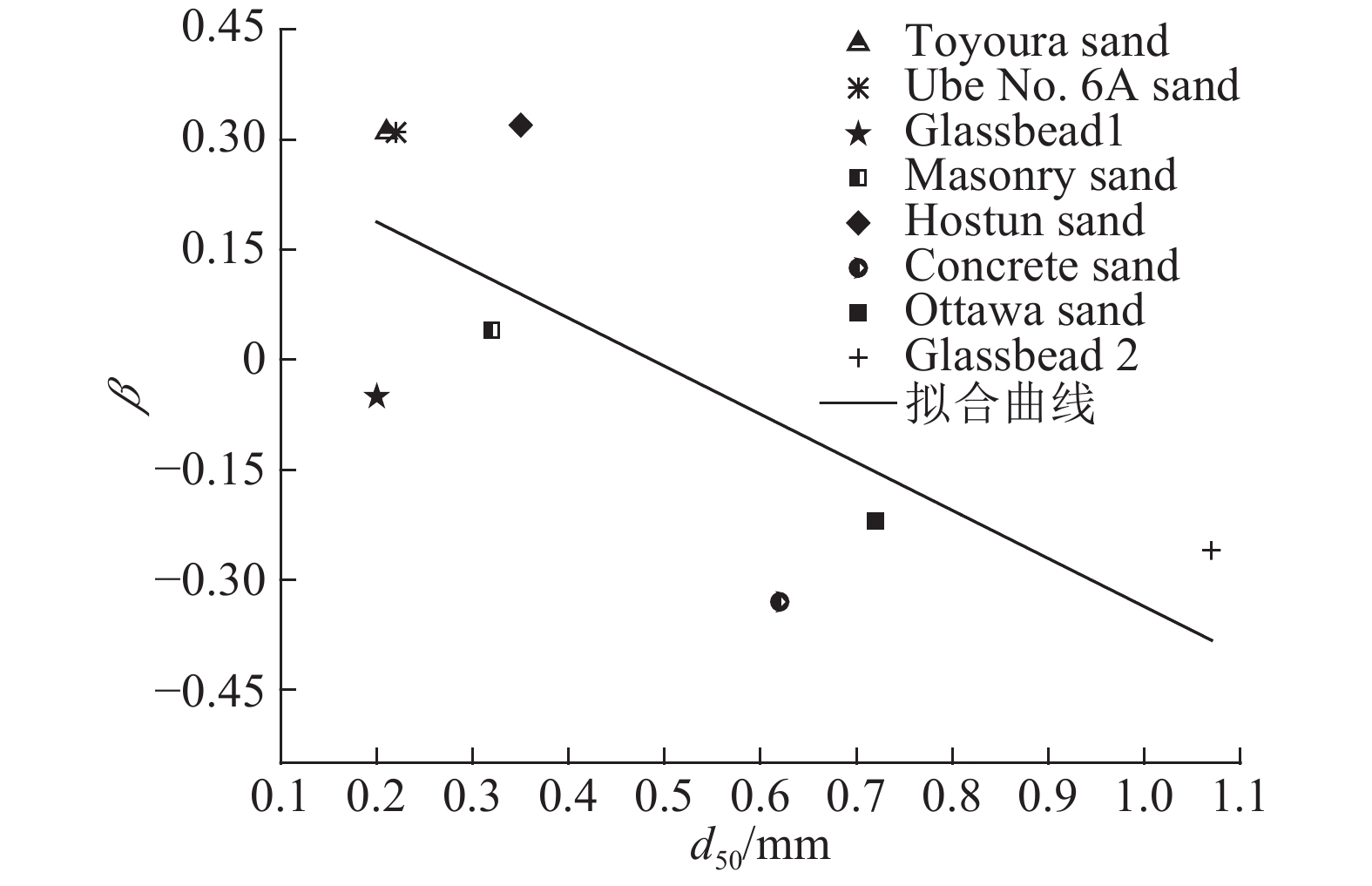
如图4所示为β与d50的关系图,并由此得到拟合公式:β=0.319–0.656d50. 由图可见,β随d50的增加整体上不断减小,二者呈负相关关系,但拟合度R2仅为0.49,拟合效果较差,不能据此说明β与d50间存在明确的相关关系.
|
图 4 拟合参数β与土体平均粒径关系 Fig. 4 Relationship between fitting parameter β and soil mean particle size |
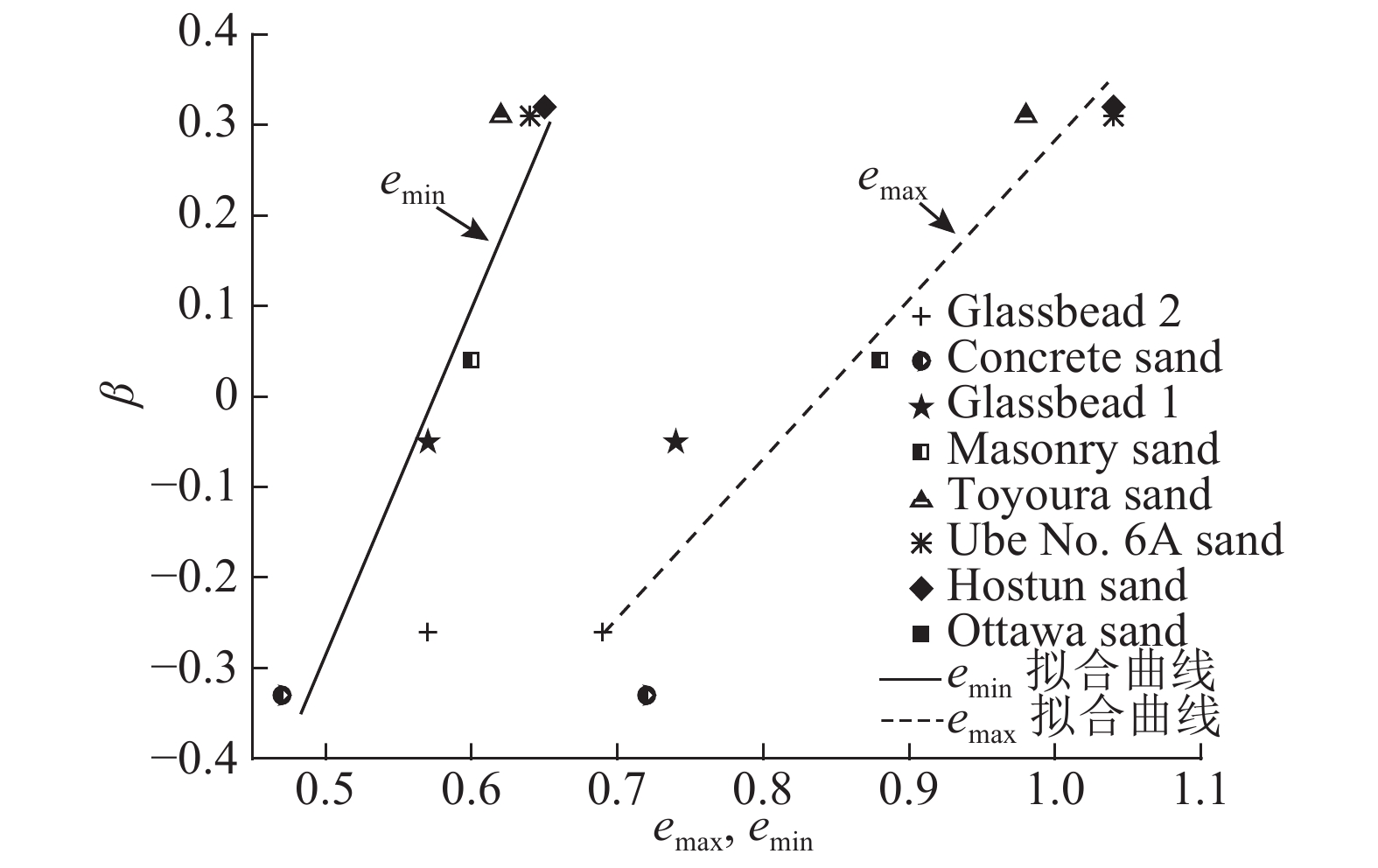
如图5所示为β与emax、emin的关系图,由数据点拟合得到公式:
|
图 5 拟合参数β与砂土最大孔隙比、最小孔隙比关系 Fig. 5 Relationship between fitting parameter β and the maximum, minimum void ratios in sands |
| $ \left.\begin{gathered} \beta {\rm{ = }} - 1.451 + 1.724{e_{\max }},\\ \beta {\rm{ = }} - 2.346 + 4.069{e_{\min }}.\\ \end{gathered}\right\} $ | (11) |
β与emax、emin的拟合度R2分别为0.902、0.897,β与emax、emin间存在良好的正相关性,随着emax或emin的增加,β线性增加. 因此,可通过砂土的emax或emin直接计算得到β,无需对试验数据进行拟合.
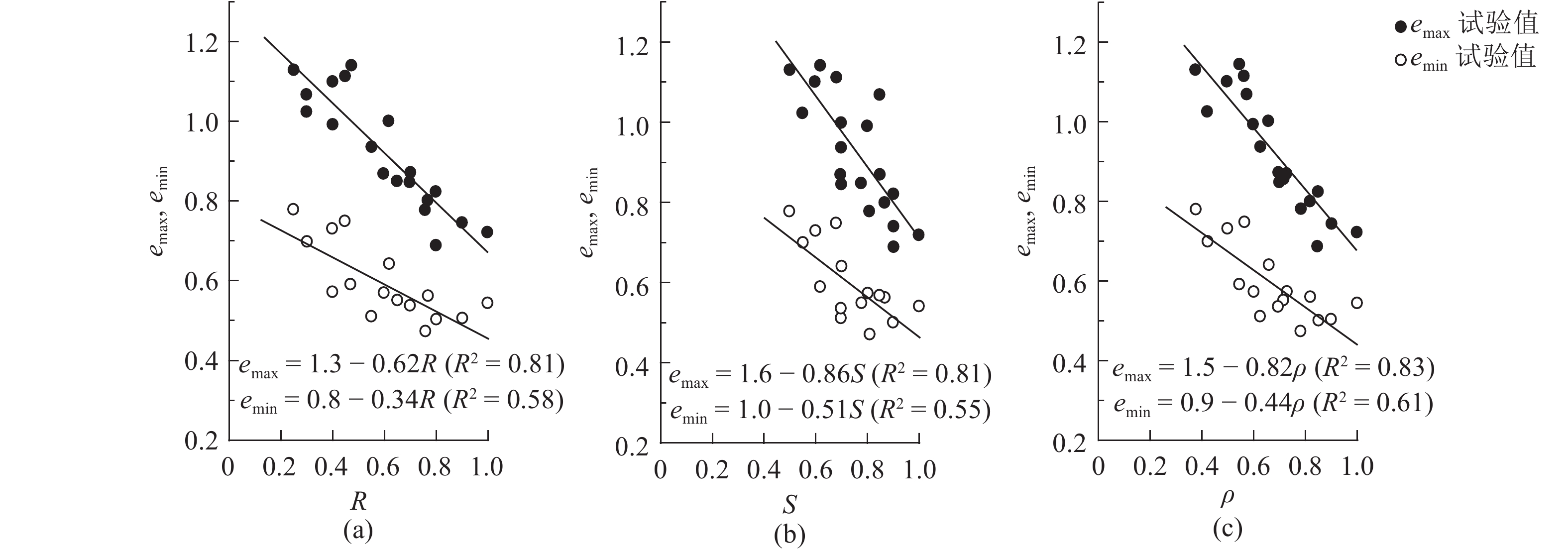
文献[22]以棱角度R、球形度S和不规则度ρ3个重要的细观特征参数表征土颗粒形状,研究颗粒形状对砂土物理、力学指标的影响. 如图6所示为各类砂土的emax、emin与颗粒形状的关系图,可见,随R、S和ρ增加,emax和emin减小,砂土各细观特征参数与最大或最小孔隙比之间呈显著的负相关性. 另外,土体孔隙比还与颗粒粒径有关,但本文收集到的大多数砂土的Cu值均小于2.5,粒径的影响可忽略[22].
|
图 6 颗粒形状与砂土最大孔隙比、最小孔隙比关系 Fig. 6 Relationship between particle shape and the maximum ,minimum void ratio in sands |
由图4~6可知,β与颗粒粒径无直接关联性,但砂土的颗粒形状,包括R、S和ρ,对剪切带倾角有一定影响.
将式(11)代入式(8)、(10)中,以β与emax的关系式为例,得到完全由砂土物理、力学指标表征的剪切带倾角计算公式:
| $\begin{array}{l}\!\!\!\!\!\!{\theta _6} =\displaystyle \frac{\text{\;π\;}}{\;4\;} + \frac{{{\varphi _{\rm{crit}}}}}{2} + \left( { - 1.451{\rm{ + }}1.724{e_{\max }}} \right)\psi ,\quad\quad\quad\quad\end{array}$ | (12) |
| $\begin{split}{\theta _7} =& \frac{\text{\;π\;}}{\;4\;} + \frac{{{\varphi _{\rm{crit}}}}}{2} +\\ &\left( { - 1.451{\rm{ + }}1.724{e_{\max }}} \right){\rm{arctan}} \; \left( {{\alpha _\psi }\frac{{{{p'}_{\!i}}}}{{{{{p}}_{\rm{a}}}}} + {m_\psi }{I_{\rm{D}}}} \right).\end{split}$ | (13) |
亦可根据β与emax、emin的拟合度大小,加权得到同时考虑emax、emin作用的倾角公式,以进一步提高计算精度,为了便于后文分析,此处不再详细列出. 式(12)、(13)即为所提经验公式的完整形式,式中各控制变量φcrit、
如表1所示,Hostun砂和Masonry砂除最大、最小孔隙比不同外,其它各项指标非常接近,适用于分析土体细观特征差异的影响. 如图1所示,Hostun砂和Masonry砂的倾角试验值范围分别为58°~70°和59°~64°. 由式(12),结合表1及文献[2]、[17]所列砂土物理、力学指标,求得2种砂土的倾角理论值范围分别为60.9°~66.0°和61.9°~63.1°. 理论值与试验值的分布区间较一致,所提方法能够较为精确地界定各类砂土的剪切带倾角变化范围,这是现有其他方法无法实现的.
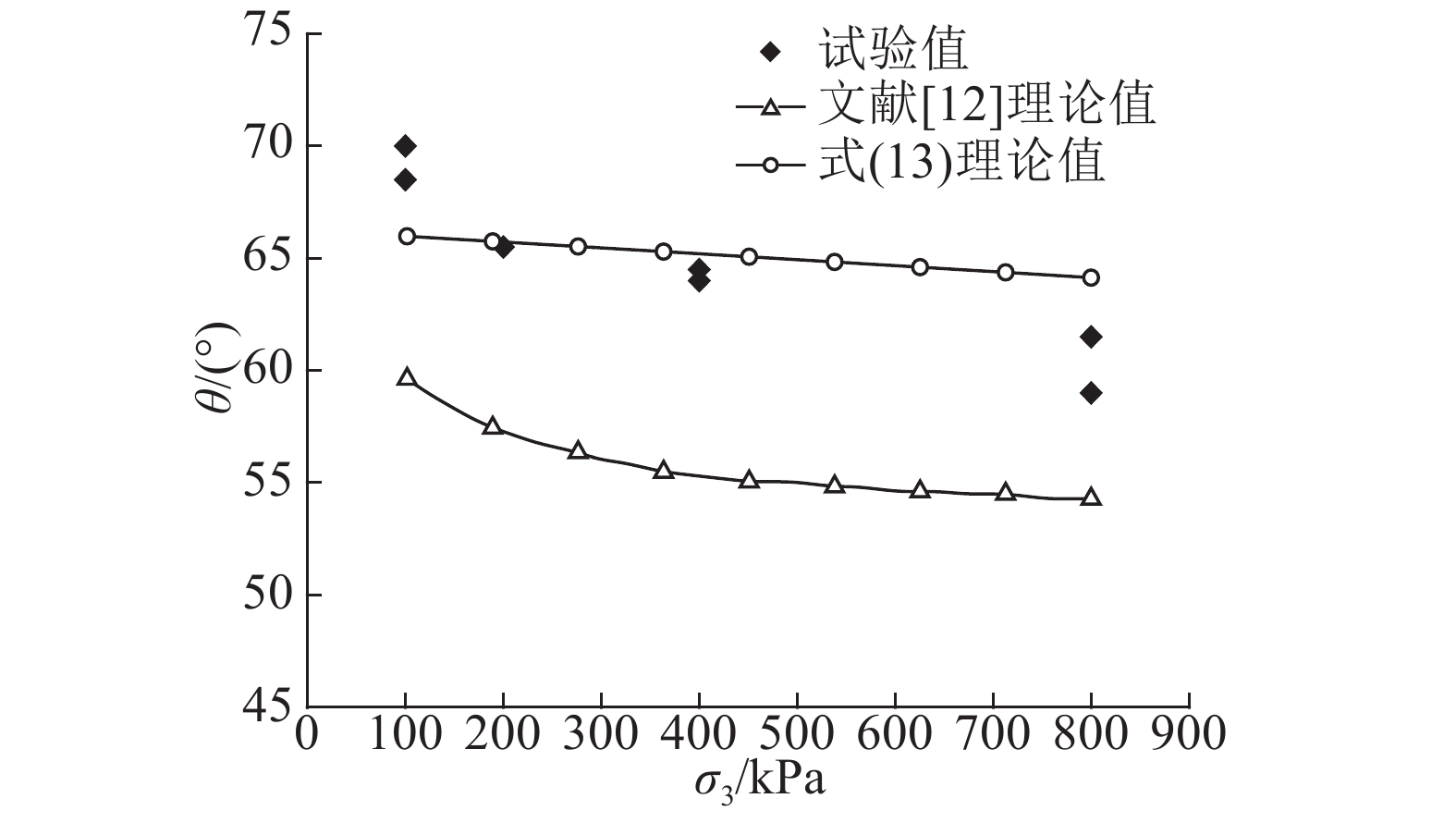
3.2 不同初始状态的砂土的剪切带倾角以Hostun砂为例,基于式(13)计算不同初始围压条件下的剪切带倾角. 在各土样初始相对密实度约为95%,围压为100~800 kPa的情况下,Hostun砂的剪切带倾角理论值与试验值如图7所示. 可见,所提方法较好地反映了随围压增加剪切带倾角减小这一试验规律,并且计算精度明显高于文献[12]的结果.
|
图 7 不同初始围压下剪切带倾角理论值与试验值的对比 Fig. 7 Comparison of test and calculated values for inclination angle of shear band with different initial confining pre-ssures |
以Toyoura砂为例,文献[4]中的Toyoura砂试验结果被用于所提公式拟合,文献[23~25]同样采用该类砂土开展剪切带倾角研究,因此可用于对拟合公式的验证. 如表2所示为Toyoura砂的剪切带倾角理论值与试验值. 可知,由式(12)、(13)得到的理论值与试验值非常接近,采用所提公式能够较好地预测同类砂土的剪切带倾角. 另外,所提公式不局限于如图1所示17种砂土,对其他基本物理、力学指标已知或可测,试验条件与本文相符的砂土,均适用.
| 表 2 Toyoura砂剪切带倾角试验值与理论值 Table 2 Test and calculated values for inclination angle of shear band for Toyoura sand |
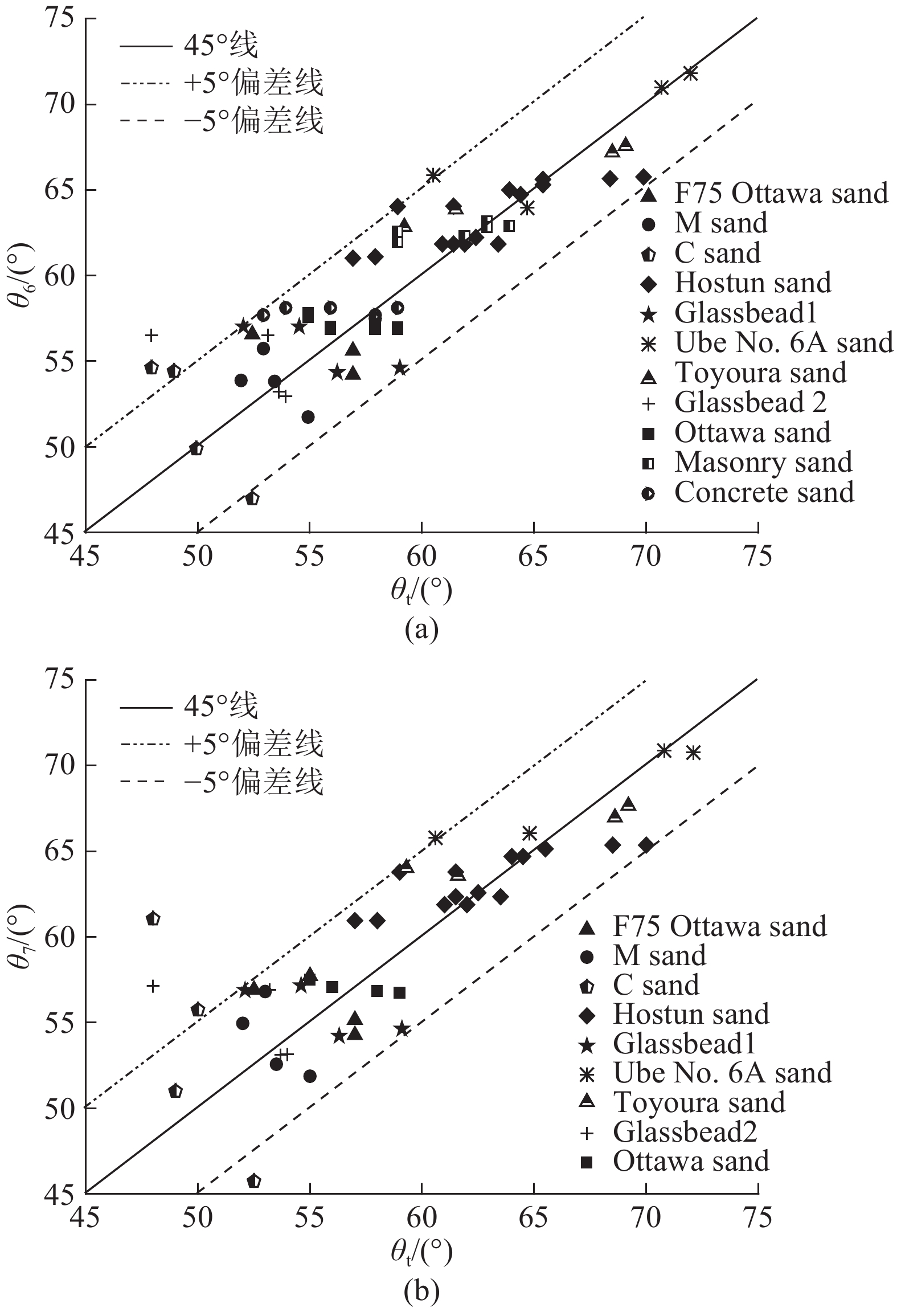
如图8所示为式(12)、(13)的理论值与试验值的关系图,可见,本文方法的计算偏差基本在−5°~5°,剪胀角由式(9)替换后,倾角计算精度无明显下降;相较于方法1~5的计算结果,本文方法的计算值与试验值的偏离程度较小,计算精度较高.
|
图 8 剪切带倾角试验值与提出的方法所得理论值的对比 Fig. 8 Comparison of test value and calculated value of the proposed method for inclination angle of shear band |
绝对误差反映理论值相对试验值的偏离程度:
| $\Delta \theta_i = {\theta _i} - {\theta _{\rm t}}.$ | (14) |
式中:i=1~7,分别代表方法1~5及本文所提方法.
平均误差反映计算结果误差的平均值:
| $E\left( {\Delta {\theta _i}} \right) = \frac{\;1\;}{\;n\;}\sum\limits_{j = 1}^n {\left| {\Delta {\theta _{ij}}} \right|} .$ | (15) |
式中:j代表第j个实验数据点,n为试验数据点总个数.
标准差反映计算结果绝对误差相对平均误差的偏离程度:
| ${\text{S}}{{\text{E}}_i} = \sqrt {\sum\limits_{j = 1}^n {{{\left( {\left| {\Delta {\theta _{ij}}} \right| - E(\Delta \theta{_i})} \right)}^2}} /n} .$ | (16) |
均方误差反映计算结果相对试验结果的离散程度:
| ${\text{SE}}{{\text{E}}_i} = \sqrt {\sum\limits_{j = 1}^n {{{\left( {\Delta {\theta _{ij}}} \right)}^2}} /\left( {n - 2} \right)} .$ | (17) |
由分析可知,方法3、4近似相等,方法5的计算精度高于方法4,故此处仅给出方法1、2、5以及本文所提方法的误差值,除特殊情况外,每种方法对应的试验数据来源相同,如表1所示. 如表3所示,f2、f3、f4、f5分别为计算值偏差范围在−2°~2°,−3°~3°,−4°~4°,−5°~5°的数据点个数占总数据点个数的百分比.
| 表 3 剪切带倾角计算结果统计表 Table 3 The error for inclination angle of shear band |
| 表 1 砂土物理力学指标与拟合参数 Table 1 Properties and fitting parameters in sands |
如表3所示,采用本文所提方法计算得出的平均误差、标准差以及均方误差约为现有其他方法结果的1/3,剪切带倾角偏差在−5°~5°的数据点占比90%以上,式(12)、(13)的各项统计指标和偏差水平均较低.
5 结 论(1) 砂土剪切带倾角一般分布于52°~67°,基于Mohr-Coulomb强度理论假定的现有其他方法无法反映土体细观特征参数和初始状态的影响,计算结果严重偏离试验结果,计算误差不可忽略.
(2) 基于砂土的力学指标φcrit和
(3) 提出的经验公式能够给出各类砂土在不同初始密实度和围压条件下的剪切带倾角,且计算偏差在−5°~5°的数据点占比90%以上,平均误差、标准误差和均方误差等各项统计指标约为现有其他方法结果的1/3.
| [1] |
凌道盛, 涂福彬, 卜令方. 基于黏聚区域模型的边坡渐进破坏过程强化有限元分析[J]. 岩土工程学报, 2012, 34(8): 1387-1393. LING Dao-sheng, TU Fu-bin, BU Ling-fang. Enhanced finite element analysis of progressive failure of slopes based on cohesive zone model[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(8): 1387-1393. |
| [2] |
DESRUES J, VIGGIANI G. Strain localization in sand: an overview of the experimental results obtained in Grenoble using stereophotogrammetry[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(4): 279-321. DOI:10.1002/(ISSN)1096-9853 |
| [3] |
WANG Q, LADE P. Shear banding in true triaxial tests and Its effect on failure in sand[J]. Journal of Engineering Mechanics, 2001, 127(8): 754-761. DOI:10.1061/(ASCE)0733-9399(2001)127:8(754) |
| [4] |
ZHUANG L, NAKATA Y, KIM U, et al. Influence of relative density, particle shape, and stress path on the plane strain compression behavior of granular materials[J]. Acta Geotechnica, 2014, 9(2): 241-255. DOI:10.1007/s11440-013-0253-4 |
| [5] |
ALSHIBLI K, STURE S. Shear band formation in plane strain experiments of sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(6): 495-503. DOI:10.1061/(ASCE)1090-0241(2000)126:6(495) |
| [6] |
RUDNICKI J, RICE J. Conditions for the localization of deformation in pressure-sensitive dilatant materials[J]. Journal of the Mechanics and Physics of Solids, 1975, 23(6): 371-394. DOI:10.1016/0022-5096(75)90001-0 |
| [7] |
MOLENKAMP F. Comparison of frictional material models with respect to shear band initiation[J]. Géotechnique, 1985, 35(2): 127-143. DOI:10.1680/geot.1985.35.2.127 |
| [8] |
HAN C, DRESCHER A. Shear bands in biaxial tests on dry coarse sand[J]. Soils and Foundations, 1993, 33(1): 118-132. DOI:10.3208/sandf1972.33.118 |
| [9] |
BARDET J. Orientation of shear bands in frictional soils[J]. Journal of Engineering Mechanics, 1991, 117(7): 1466-1485. DOI:10.1061/(ASCE)0733-9399(1991)117:7(1466) |
| [10] |
PAPARNICHOS E, VARDOULAKIS I. Shear band formation in sand according to model[J]. Géotechnique, 1995, 45(4): 649-661. DOI:10.1680/geot.1995.45.4.649 |
| [11] |
钱建固, 黄茂松. 土体变形分叉的非共轴理论[J]. 岩土工程学报, 2004, 26(4): 777-781. QIAN Jian-gu, HUANG Mao-song. Non-coaxiality for deformation bifurcation non-coaxial plasticity in soils[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 777-781. |
| [12] |
黄茂松, 扈萍, 钱建固. 基于材料状态相关砂土临界状态理论的应变局部化分析[J]. 岩土工程学报, 2008, 30(8): 1133-1139. HUANG Mao-song, HU Ping, QIAN Jian-gu. Strain localization of sand based on a state-dependent critical state model[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(8): 1133-1139. DOI:10.3321/j.issn:1000-4548.2008.08.005 |
| [13] |
DUNSTAN T, ARTHUR J, ALANIA, et al. Plastic deformation and failure in granular media[J]. Géotechnique, 1977, 27(1): 53-74. DOI:10.1680/geot.1977.27.1.53 |
| [14] |
DESRUES J, HAMMAD W. Shear band dependency on mean stress level in sand [C] // Proceeding of 2nd International Workshop on Numerical Methods for Localization and Bifurcation of Granular Bodies. Gdansk: Technical University of Gdansk, 1989: 57–67.
|
| [15] |
VARDOULAKIS I. Shear band inclination and shear modulus of sand in biaxial tests[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1980, 4(2): 103-119. DOI:10.1002/(ISSN)1096-9853 |
| [16] |
JANG E, JUNG Y, KIM J, et al. Assessment of shear band characteristics in granular soils using digital image analysis for plane strain tests[J]. Journal of the Korean Geotechnical Society, 2011, 27(4): 51–65.
|
| [17] |
RECHENMACHER A. Digital image correlation to evaluate shear banding in dilative sands[J]. Geotechnical Testing Journal, 2004, 27(1): 1-10. |
| [18] |
YOSHIDA T, TATSUOKA F, SSIDDIQUEE M, et al. Shear banding in sands observed in plane strain compression [C] // Proceedings of the 3rd Workshop Localization and Bifurcation Third for Soils and Rocks. Grenoble: [s. n.], 1993: 165–179.
|
| [19] |
BARDET J. A comprehensive review of strain localization in elastoplastic soils[J]. Computers and Geotechnics, 1990, 10(3): 163-188. DOI:10.1016/0266-352X(90)90034-S |
| [20] |
VAID Y, SASITHARAN S. The strength and dilatancy of sand[J]. Canadian Geotechnical Journal, 1992, 29(3): 522-526. DOI:10.1139/t92-058 |
| [21] |
CINICIOGLU O, ABADKON A. Dilatancy and friction angles based on in situ soil conditions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(4): 1-7. |
| [22] |
CHO G, DODDS J, SANTAMARINA J. Particle shape effects on packing density, stiffness, and strength: natural and crushed sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(5): 591-602. DOI:10.1061/(ASCE)1090-0241(2006)132:5(591) |
| [23] |
Tatsuoka F, Nakamura S, Huang C, et al. Strength anisotropy and shear band direction in plane strain tests of sand[J]. Soils and Foundations, 1990, 30(1): 35–54. http://www.sciencedirect.com/science/article/pii/014890629091068I
|
| [24] |
庄丽, 宫全美. 减围压平面应变压缩试验条件下丰浦砂中剪切带特性研究[J]. 岩土力学, 2016(增1): 201–208. ZHUANG Li, GONG Quan-mei. Shear band characteristics of Toyoura sand in plane strain compression with decreasing confining pressure[J]. Rock and Soil Mechanics, 2016(supp.1): 201–208. http://www.cnki.com.cn/Article/CJFDTotal-YTLX2016S1026.htm |
| [25] |
NAKARNURA S. Strain distribution of sand specimen in plane strain compression test [D]. Tokyo: University of Tokyo, 1987. http://cn.bing.com/academic/profile?id=58f470f2bdd656641210acfacc3bcbf7&encoded=0&v=paper_preview&mkt=zh-cn
|



