隧道建设是解决人们日益增长的出行需求的有效措施之一. 在现有隧道设计与施工过程中，尤其对于高压富水隧道，如何合理确定隧道涌水量与衬砌水压力是普遍存在的难点^[1]. 考虑到隧道渗流场受地层参数、隧道结构等众多因素影响，过去学者们往往将地层、水位、隧道断面形式等进行简化，采用复变函数保角变换方法^[2-4]、基于达西定律和无限含水层竖井理论的近似解法^[5-7]以及镜像法和达西定律相结合^{[1, 8]}等方法对隧道渗流场进行求解. 上述方法是基于常规排水方式的等效，即围岩渗水渗透进入隧道内并汇聚于侧沟，最终由侧沟、中心水沟共同排出的排水方式，计算思路清晰、结果能满足工程需求，普遍被研究人员接受与使用.

近年来，随着高压富水隧道建设项目的不断增多，沿用原有常规排水方式在隧道运营过程中易产生较高的衬砌水压力，改变衬砌结构受力特征^[9]，导致隧道衬砌开裂、仰拱隆起、翻浆冒泥等问题^[10]. 因此，工程师们提出了一种涌水量更大、排导能力更强，且能有效降低隧底水压力的深埋式中心水沟排水方式，且通过工程实践论证了该方法的可行性与有效性^[11]. 在该排水方式中，除通过边墙处排水孔有效排水外，隧底深埋水沟参与并主导排水，增加隧道排水路径，增大涌水量，即使在隧道防排水系统弱化（堵塞、部分失效）的情况下仰拱底部仍能保持较小水压力^[12].

深埋水沟排水方式工程应用不断增多，如何计算该排水方式下的渗透场解析解以进一步优化和指导工程施工成为工程师们普遍关心的问题. 依托武九客专石马寨隧道工程，结合镜像法和渗流力学，推导深埋水沟排水方式下半无限平面隧道渗流场解析解，并与数值解进行对比分析，进一步探讨不同参数下解析解的相关规律. 该方法的提出对进一步完善隧道渗流场理论、优化隧道设计以及指导工程实践等具有显著的现实意义.

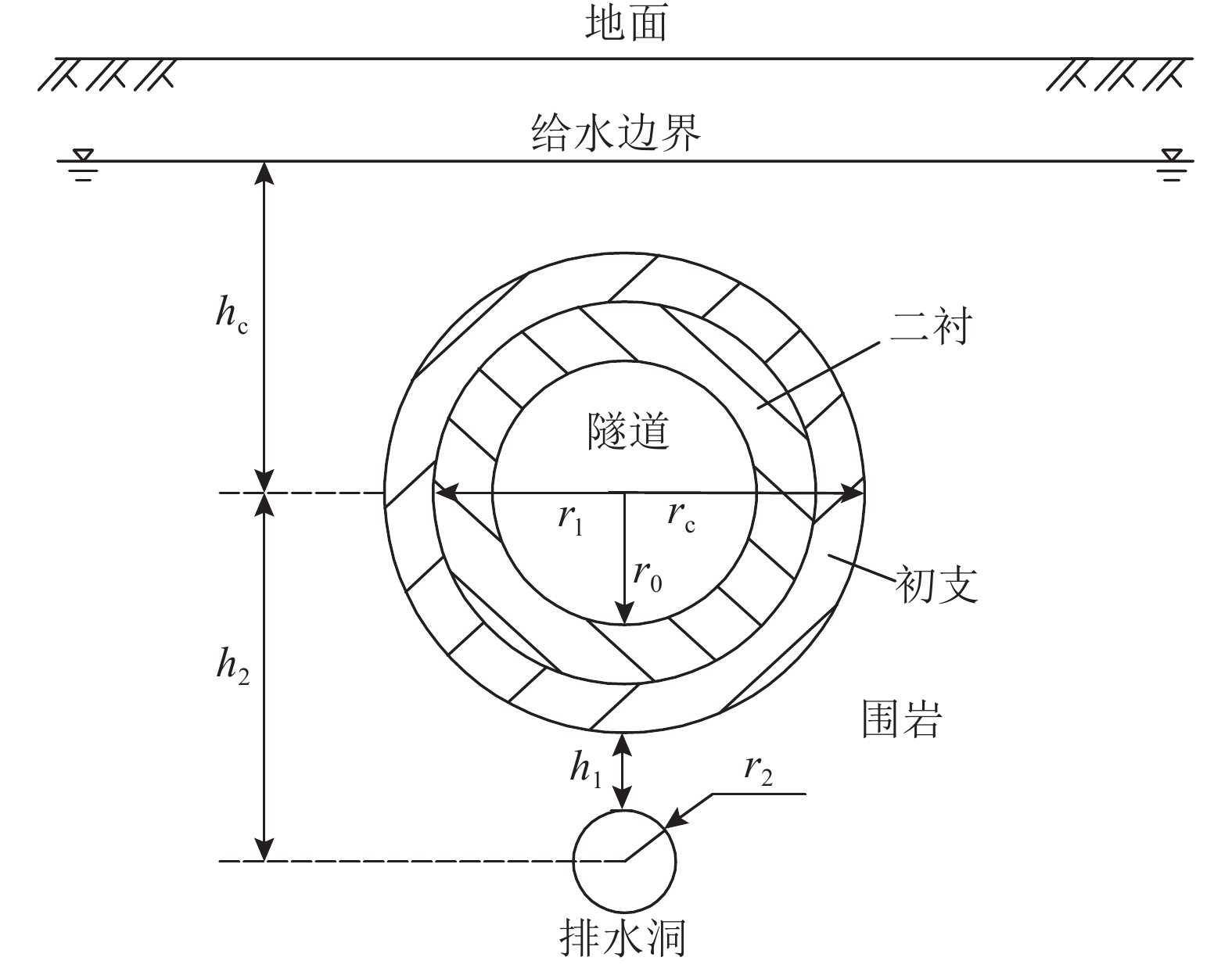
1 深埋水沟排水隧道渗流场解析解 1.1 基本假定及计算模型

根据深埋水沟排水方式及其渗流路径（见图1）建立渗流场计算模型. 地下水面为给水边界，将此边界定为计算模型上边界，并作以下假定：1）围岩、初支、二衬均为各向同性均匀连续介质，各含水介质及流体均不可压缩；2）隧道为水下大埋深；3）远场地下水补给充分，地下水给水水头不因隧道排水而降低，渗流方向以隧道径向为主；4）隧道渗流处于稳定层流状态，且服从Darcy定律；5）隧道通过全环衬砌均匀渗透排水，深埋水沟以隧底下方圆形毛洞的形式均匀排水，衬砌内壁、排水洞内壁水头为0，且不计隧道内侧位势水头的影响.

如图2所示为深埋水沟排水隧道渗流模型. 图中， ${k_{\rm s}}$ 为地层渗透系数； ${h_{\rm c}}$ 为圆形隧道中心与给水边界的距离，隧道结构包括初支、二衬， ${r_{\rm c}}$ 、 ${r_{\rm l}}$ 分别为初支外、内半径， ${r_0}$ 为二衬内半径， ${k_{\rm c}}$ 、 ${k_{\rm l}}$ 分别为初支、二衬渗透系数， ${h_1}$ 为圆形排水毛洞隧底埋深， ${r_2}$ 为毛洞半径， ${h_2}$ 为毛洞中心与隧道中心的距离.

1.2 渗流场解析思路

半无限平面深埋水沟排水隧道渗流场无法在笛卡尔坐标系或极坐标系内简单表示，故采取镜像法与渗流力学中势的叠加法联合进行求解，求解步骤如下.

1）根据渗流力学原理^[13]，求解无限平面内施加初支和衬砌的隧道渗流场，并退化求解毛洞形式的排水洞渗流场.

2）依据镜像法原则^[1]，将半无限平面深埋水沟排水隧道渗流场（如图3（a）所示）转化为无限平面内相互对称且涌水量异号的实际、虚拟深埋水沟排水隧道渗流场的叠加（如图3（b）所示），规定涌水量以流入隧道为正.

3）依据势的叠加法原则^[13]，同理于虚拟深埋水沟排水隧道渗流场，将无限平面实际深埋水沟排水隧道渗流场转化为无限平面实际隧道渗流场与实际排水洞渗流场的叠加. 最终可将半无限平面深埋水沟排水隧道渗流场转化为无限平面实际、虚拟隧道和实际、虚拟排水洞四洞渗流场的叠加.

4）根据单洞渗流场、叠加渗流场边界条件确定待定参数，求得深埋水沟排水隧道渗流场解析解.

1.3 无限平面单洞渗流场解析 1.3.1 施加初支和衬砌的单洞渗流场解析

施加初支和衬砌的隧道渗流场可划分为衬砌区域Ⅰ、初支区域Ⅱ、围岩区域Ⅲ. 当渗流处于层流时，渗流满足Darcy定理，在区域Ⅰ～Ⅲ有

$v = ki = k \frac{{{\rm d}\varPhi }}{{{\rm d}\rho }}.$

(1)

式中： $v$ 为渗流速度， $k$ 为渗透系数， $i$ 为水力梯度， $\varPhi $ 为总水头势函数， $\rho $ 为点到隧道圆心的距离.

根据涌水量和渗流速度关系，在区域Ⅰ～Ⅲ有

$Q = 2{\text{π}} \rho k \frac{{{\rm d}\varPhi }}{{{\rm d}\rho }}.$

(2)

式中： $Q$ 为隧道涌水量.

对式（2）在区域Ⅰ～Ⅲ分段积分有

$\varPhi = \left\{ \begin{array}{l}\displaystyle\frac{Q}{{2{\text{π}} {k_{\rm l}}}}\ln\; \rho + {c_1},\;{r_{\rm l}}{\rm{ > }}\rho \geqslant {r_0};\\\displaystyle\frac{Q}{{2{\text{π}} {k_{\rm c}}}}\ln\; \rho + {c_2},\;{r_{\rm c}}{\rm{ > }}\rho \geqslant {r_{\rm l}};\\\displaystyle\frac{Q}{{2{\text{π}} {k_{\rm s}}}}\ln\; \rho + {c_3},\;\rho \geqslant {r_{\rm c}}.\end{array} \right.$

(3)

式中： ${c_1}$ 、 ${c_2}$ 、 ${c_{\rm{3}}}$ 为对应积分常数.

对于区域Ⅰ、Ⅱ、Ⅲ，由相邻区域界面处总水头势函数相等可得

$\varPhi = \left\{ \begin{array}{l}\displaystyle\frac{Q}{{2{\text{π}} {k_{\rm l}}}}\ln\; \rho + {c_1},\;{r_{\rm l}}{\rm{ > }}\rho \geqslant {r_0};\\\displaystyle\frac{Q}{{2{\text{π}} {k_{\rm c}}}}\ln\; \frac{\rho }{{{r_{\rm l}}}} + \frac{Q}{{2{\text{π}} {k_{\rm l}}}}\ln\; {r_{\rm l}} + {c_1},\;{r_{\rm c}}{\rm{ > }}\rho \geqslant {r_{\rm l}};\\\displaystyle\frac{Q}{{2{\text{π}} {k_{\rm s}}}}\ln\; \frac{\rho }{{{r_{\rm c}}}} + \frac{Q}{{2{\text{π}} {k_{\rm c}}}}\ln\; \frac{{{r_{\rm c}}}}{{{r_{\rm l}}}} + \frac{Q}{{2{\text{π}} {k_{\rm l}}}}\ln\; {r_{\rm l}} + {c_1},\;\rho \geqslant {r_{\rm c}}.\end{array} \right.$

(4)

1.3.2 毛洞形式的排水洞渗流场解析

对于毛洞形式的排水洞，由于仅有围岩区域，不存在初支与二衬区域，对式（2）积分可得

$\varPhi = \frac{Q}{{2{\text{π}} {k_{\rm s}}}}\ln\; {\rho_0} + {c_4};\;{\rho_0} \geqslant {r_2}.$

(5)

式中： ${c_4}$ 为对应积分常数， $\rho_0 $ 为任意点到排水洞圆心的距离.

1.4 半无限平面深埋水沟排水隧道渗流场解析

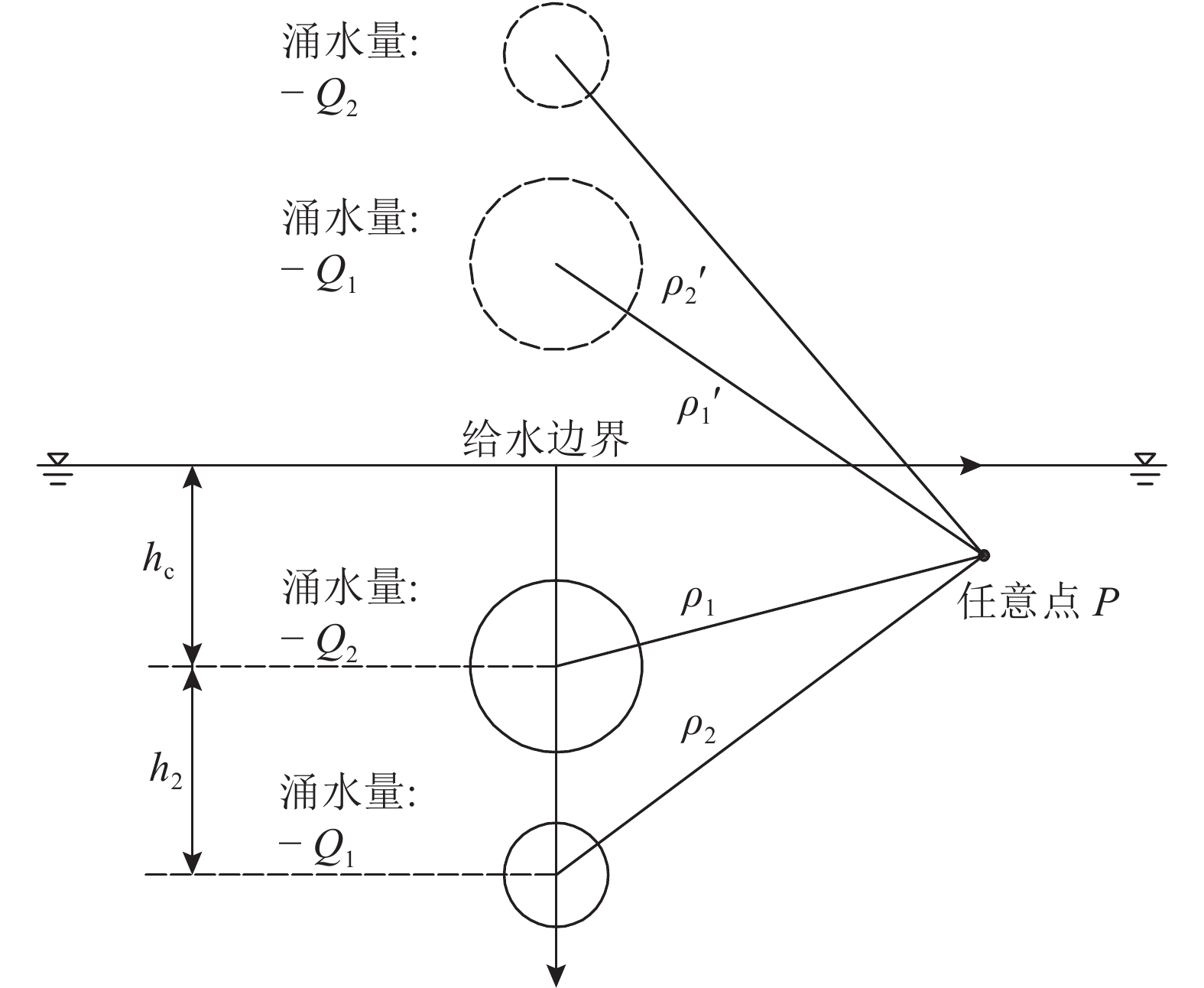
设实际半无限平面内任意点P到实际、虚拟隧道圆心的距离为 ${\rho _{_1}}$ 、 ${\rho _{_1}}'$ ，到实际、虚拟排水洞圆心的距离为 $ \rho _{\rm{_2}}$ 、 ${\rho _{_2}}'$ ，Q₁为隧道涌水量，Q₂为排水洞涌水量，如图4所示. 依据势的叠加原理^[13]，实际半无限平面内任意点总水头势函数有

$\varPhi = {\varPhi _{\rm{1}}} + \varPhi _{\rm{1}}' + {\varPhi _2}{\rm{ + }}\varPhi _2'.$

(6)

式中： ${\varPhi _1}$ 、 ${\varPhi _1}'$ 、 ${\varPhi _2}$ 、 ${\varPhi _2}'$ 分别为仅考虑实际隧道、虚拟隧道、实际排水洞、虚拟排水洞的无限平面水头势函数.

在实际半无限平面内， ${\varPhi _1}'$ 、 $ {\varPhi _2}$ 、 ${\varPhi _2}'$ 均可视作非分段函数（ ${\varPhi _1}' $ 虽为分段，但属于围岩区域），故仅 ${\varPhi _1}$ 需要分区域考虑. 因此，实际半无限平面总水头势函数 $\varPhi $ 是以实际隧道衬砌、初支、围岩分区的分段函数. 由式（4）~（6）可得总水头势函数为

$\varPhi = \left\{ \begin{array}{l}\displaystyle\frac{{{Q_1}}}{{2{\text{π}} {k_{\rm s}}}}\left( {\frac{{{k_{\rm s}}}}{{{k_{\rm l}}}}\ln\; \frac{{{\rho _1}}}{{{r_{\rm l}}}} + \frac{{{k_{\rm s}}}}{{{k_{\rm c}}}}\ln\; \frac{{{r_{\rm l}}}}{{{r_{\rm c}}}} + \ln\; \frac{{{r_{\rm c}}}}{{{\rho _{1}}'}}} \right) + \frac{{{Q_2}}}{{2{\text{π}} {k_{\rm s}}}}\ln\; \frac{{{\rho _2}}}{{{\rho _{2}}'}} + \\2{c_1}{\rm{ + 2}}{c_4},\;{r_{\rm l}} > \rho \geqslant {{{r}}_{\rm{0}}};\\\displaystyle\frac{{{{{Q}}_{\rm{1}}}}}{{{\rm{2}}{\text{π}} {{{k}}_{\rm{s}}}}}\left( {\frac{{{{{k}}_{\rm{s}}}}}{{{{{k}}_{\rm{c}}}}}\ln\; \frac{{{\rho _{\rm{1}}}}}{{{{{r}}_{\rm{c}}}}}{\rm{ + }}\ln\; \frac{{{{{r}}_{\rm{c}}}}}{{{\rho _{1}}'}}} \right){\rm{ + }}\frac{{{{{Q}}_{\rm{2}}}}}{{{\rm{2}}{\text{π}} {{{k}}_{\rm{s}}}}}\ln\; \displaystyle\frac{{{\rho _{\rm{2}}}}}{{{\rho _{2}}'}}{\rm{ + 2}}{{{c}}_{\rm{1}}}{\rm{ + 2}}{{{c}}_{\rm{4}}},\\{{{r}}_{\rm{c}}} > \rho \geqslant {{{r}}_{\rm{l}}};\\\displaystyle\frac{{{{{Q}}_{\rm{1}}}}}{{{\rm{2}}{\text{π}} {{{k}}_{\rm{s}}}}}\ln\; \displaystyle\frac{{{\rho _{\rm{1}}}}}{{{\rho _{1}}'}}{\rm{ + }}\frac{{{{{Q}}_{\rm{2}}}}}{{{\rm{2}}{\text{π}} {{{k}}_{\rm{s}}}}}\ln\; \displaystyle\frac{{{\rho _{\rm{2}}}}}{{{\rho _{2}}'}}{\rm{ + 2}}{{{c}}_{\rm{1}}}{\rm{ + 2}}{{{c}}_{\rm{4}}},\;\rho \geqslant {{{r}}_{\rm{c}}}.\end{array} \right.$

(7)

在给水边界处有 ${\rho _1} = {\rho _1}'$ 且 ${\rho _1} > {r_{\rm c}}$ 、 ${\rho _2} = {\rho _2}'$ ，设总水头 $\varPhi $ 为 $H$ ，代入式（7）可得

$2{c_1} + 2{c_4} = H.$

(8)

对于双洞渗流的相互影响，张丙强^[8]认为考虑的双洞有一定距离，以双洞圆心距作为等效影响距离. 本研究模型与文献[8]模型存在一定差异，为了综合考虑结构各点的影响，采取平均距离的方式进行等效. 如图5所示，以衬砌内壁与排水洞圆心平均距离 $\overline {{\rho _2}} $ 为例，将衬砌内壁等分为n段圆弧，每段弧长为 $l$ ，第i段圆弧到排水洞距离为 ${D_i}$ ，前i−1段圆弧对应圆心角为 ${\theta _i}$ ，依据余弦定理有

${D_i}{\rm{ = }}\big({{h_2}^2 + {r_0}^2 + 2{h_2}{r_0}\cos \;{\theta _i}} \big)^{1/2}.$

(9)

对衬砌内壁取积分，衬砌内壁到排水洞圆心的平均距离为

$\overline {{\rho _2}} = \mathop {\lim }\limits_{n \to + \infty } \sum\limits_{i=1}^n { {\frac{{{D_i}l}}{{2{\text{π}} {r_0}}}} } =\int_{\rm{0}}^{{\rm{2}}{\text{π}}} \frac{{{{\left( {{h_2}^2 + {r_0}^2 + 2{h_2}{r_0}\cos \;\theta } \right)}^{1/2}}}}{{2{\text{π}}}}{\rm{d}}\theta .$

(10)

同理可得排水洞内壁到隧道圆心的平均距离为

$\overline {{\rho _1}} =\int_{\rm{0}}^{{\rm{2}}{\text{π}}} \frac{{{{\left( {{h_2}^2 + {r_2}^2 + 2{h_2}{r_2}\cos \;\theta } \right)}^{1/2}}}}{{2{\text{π}} }}{\rm{d}}\theta .$

(11)

考虑到式（10）、（11）定积分的复杂性，解决具体问题时，可以采用Guass积分法等高精度数值积分法或借助计算机进行求解.

基于水下大埋深假定，对于隧道衬砌内壁，有 ${\rho _1} = {r_0}$ ， ${\rho _1}' \approx 2{h_{\rm c}}$ ， ${\rho _2}{\rm{ = }}\overline {{\rho _2}} $ ， ${\rho _2}' \approx 2{h_{\rm c}} + {h_2}$ ， $H = {h_{\rm c}}.$ 联立式（7）、（8），根据衬砌内壁水头恒为0的假定，可得隧道衬砌内壁水头为

$\begin{split}{\varPhi _1} =& \displaystyle\frac{{{Q_1}}}{{2{\text π} {k_{\rm s}}}}\left( {\frac{{{k_{\rm s}}}}{{{k_{\rm l}}}}\ln \frac{{{r_0}}}{{{r_{\rm l}}}} + \frac{{{k_{\rm s}}}}{{{k_{\rm c}}}}\ln \frac{{{r_{\rm l}}}}{{{r_{\rm c}}}} + \ln \frac{{{r_{\rm c}}}}{{2{h_{\rm c}}}}} \right){\rm{ + }}\\&\displaystyle\frac{{{Q_2}}}{{2{\text π} {k_{\rm s}}}}\ln \frac{{\overline {{\rho _2}} }}{{2{h_{\rm c}} + {h_2}}} + {h_{\rm c}} = 0.\end{split}$

(12)

同理，对于排水洞内壁，有 ${\rho _1} = \overline {{\rho _1}} $ ， ${\rho _1}' \approx 2{h_{\rm c}} + {h_2}$ ， ${\rho _2} = {r_2}$ ， ${\rho _2}' \approx 2{h_{\rm c}} + 2{h_2}$ ， $H = {h_{\rm c}} + {h_2}$ ，代入式（7），依据排水洞内壁水头恒为0的假定，可得

${\varPhi _2} = \frac{{{Q_1}}}{{2{\text{π}} {k_{\rm s}}}}\ln \frac{{\overline {{\rho _1}} }}{{2{h_{\rm c}} + {h_2}}} + \frac{{{Q_2}}}{{2{\text{π}} {k_{\rm s}}}}\ln \frac{{{r_2}}}{{2{h_{\rm c}} + 2{h_2}}} + {h_{\rm c}} + {h_2} = 0.$

(13)

联立式（12）、（13），解得深埋水沟排水方式下 ${Q_{1}}$ 及 ${Q_{2}}$ 分别为

$\left. \begin{array}{l}{Q_1} = {\rm{2}}{\text{π}} {k_{\rm s}}\displaystyle\frac{{D{h_{\rm c}} - B({h_{\rm c}} + {h_2})}}{{BC - AD}},\\{Q_2} = {\rm{2}}{\text{π}} {k_{\rm s}}\displaystyle\frac{{A({h_{\rm c}} + {h_2}) - C{h_{\rm c}}}}{{BC - AD}}.\end{array} \right\}$

(14)

式中：

$A = \displaystyle\frac{{{k_{\rm s}}}}{{{k_{\rm l}}}}\ln\; \frac{{{r_0}}}{{{r_{\rm l}}}} + \frac{{{k_{\rm s}}}}{{{k_{\rm c}}}}\ln\; \frac{{{r_{\rm l}}}}{{{r_{\rm c}}}} + \ln\; \frac{{{r_{\rm c}}}}{{2{h_{\rm c}}}},$ $B = \ln\; \displaystyle\frac{{{{\rho _2}} }}{{2{h_{\rm c}} + {h_2}}},$ $C = \ln\; \displaystyle\frac{{\overline {{\rho _1}} }}{{2{h_{\rm c}} + {h_2}}},$ $D = \ln\; \displaystyle\frac{{{r_2}}}{{2{h_{\rm c}} + 2{h_2}}}.$

将式（8）、（14）代入式（7）可得，当 ${\rho _1} = {r_{\rm l}}$ ， ${\rho _1}' \approx 2{h_{\rm c}}$ ， ${\rho _2}' \approx 2{h_{\rm c}} + {h_2}$ 时，对应隧道衬砌外表面，解得衬砌背后的水压力为

$\begin{aligned}{p_{\rm l}} = \varPhi {\gamma _{\rm w}} =& {\gamma _{\rm w}}\displaystyle\frac{{D{h_{\rm c}} - B({h_{\rm c}} + {h_2})}}{{BC - AD}}\left( {\frac{{{k_{\rm s}}}}{{{k_{\rm c}}}}\ln\; \frac{{{r_{\rm l}}}}{{{r_{\rm c}}}} + \ln\; \frac{{{r_{\rm c}}}}{{2{h_{\rm c}}}}} \right){\rm{ + }}\\&{\gamma _{\rm w}}\displaystyle\frac{{A({h_{\rm c}} + {h_2}) - C{h_{\rm c}}}}{{BC - AD}}\ln\; \frac{{{\rho _2}}}{{2{h_{\rm c}} + {h_2}}}{\rm{ + }}{\gamma _{\rm w}}{h_{\rm c}}.\end{aligned}$

(15)

式中： ${\gamma _{\rm w}}$ 为水重度，取10 kN/m³.

1.5 解的验证

若不考虑排水洞，即 ${r_2} \to {0^ + }$ ，有

$\left. \begin{array}{l}\mathop {\lim }\limits_{{r_2} \to {0^ + }}\displaystyle \frac{{D{h_{\rm c}} - B({h_{\rm c}} + {h_2})}}{{BC - AD}} = - \frac{{{h_{\rm c}}}}{A},\\\mathop {\lim }\limits_{{r_2} \to {0^ + }} \displaystyle\frac{{A({h_{\rm c}} + {h_2}) - C{h_{\rm c}}}}{{BC - AD}} = 0 .\end{array} \right\}$

(16)

将式（16）代入式（14），可得

$\left. \begin{array}{l}{Q_1} = \displaystyle\frac{{2{\text{π}} {k_{\rm s}}{h_{\rm c}}}}{{\displaystyle\frac{{{k_{\rm s}}}}{{{k_{\rm l}}}}\ln\; \displaystyle\frac{{{r_{\rm l}}}}{{{r_0}}} + \displaystyle\frac{{{k_{\rm s}}}}{{{k_{\rm c}}}}\ln\; \displaystyle\frac{{{r_{\rm c}}}}{{{r_{\rm l}}}} + \ln\; \displaystyle\frac{{2{h_{\rm c}}}}{{{r_{\rm c}}}}}},\\{Q_2} = 0 .\end{array} \right\}$

(17)

式（17）中隧道涌水量 ${Q_{1}}$ 与文献[1]中半无限平面单洞隧道最大涌水量计算公式相同. 文献[1]中不考虑隧底排水洞排水的隧道涌水量解析解仅为式（14）的特例，以此验证了本研究所推计算公式的正确性.

2 算例分析 2.1 计算参数

武九客专石马寨隧道位于湖北省阳新县，隧道起屹里程为DK140+077~DK143+763，全长3 686 m，最大埋深约350 m. DK140+840断面洞身围岩主要为中风化灰岩，岩体较破碎，岩溶发育，物探显示该断面拱顶上方存在异常区. 该断面埋深约300 m，地下水为以岩溶水为主，岩溶管道及裂隙发育，地下水量丰富，施工时易发生突水突泥事故. 针对此地质情况，为了有效控制隧身水压，减少后期病害的发生，建设单位于该断面所在区段采用深埋式中心水沟排水方式.

根据设计文件^①可知，DK140+840断面结构如图6所示，开挖面积为131.03 m²，采用等效面积法可以将隧道近似为外轮廓（初支外半径 ${r_{\rm c}}$ ）为6.5 m的圆形洞室；初支、二衬厚度分别为0.2、0.4 m，故初支内半径 ${r_{\rm l}}$ 为6.3 m，衬砌内半径 ${r_0}$ 为5.9 m；深埋水沟为隧底圆形排水洞，埋深 ${h_1}$ 取设计埋深0.5 m，半径 ${r_2}$ 取设计排水管半径0.4 m. 此外，文献[14]研究表明，复合式衬砌中防水板及排水盲管的防排水特性可以采用增大衬砌渗透性的方式进行等效模拟，因此本研究采用该方法将防水板及排水盲管的防排水作用进行等效. 地勘报告显示地下水位线到隧道的距离 ${h_{\rm c}}$ 为80 m，根据文献调研^{[6, 14-15]}及工程经验^[16]，围岩及初支渗透系数、二衬等效渗透系数取值如表1所示.

2.2 数值模型

根据2.1节中隧道特征参数，采用FLAC3D软件建立计算模型（130 m×100 m），如图7所示. 隧道顶面取为地下水位面，位于隧道上方80 m处，模型左、右边界及下边界距离隧道3倍洞径以上. 渗流边界条件为衬砌内壁、排水洞内壁孔隙水压力恒为0；地下水位线恒定于模型顶面，即水下埋深 ${h_{\rm c}}$ 恒为80 m；模型左、右及下边界均为透水边界. 同时，模型材料渗透系数均按表1取值.

2.3 算例解析与数值验证 2.3.1 隧道涌水量

涌水量解析解中包含有 $\overline {{\rho _1}} $ 、 $\overline {{\rho _2}} $ 的计算，因此，对算例中上述值的计算过程予以简要介绍. 排水洞特征参数埋置深度 ${h_1}$ =0.5 m，半径 ${r_2}$ =0.4 m，双洞圆心距 ${h_2}{\rm{ = }}{h_1} + {r_c} + {r_2}$ =7.4 m，将参数代入式（10）、（11），借助计算机求解可得

$\left. \begin{array}{l}{\rm{ }}\overline {{\rho _1}} = \displaystyle\int_{\rm{0}}^{{\rm{2}}{\text π} } \frac{{{{\left( {54.92 + 5.92\cos \;\theta } \right)}^{1/2}}}}{{2{\text{π}} }} {\rm{d}}\theta \approx 7.41{\rm{\;m}},\\{\rm{ }}\overline {{\rho _2}} = \displaystyle\int_{\rm{0}}^{{\rm{2}}{\text π}} \frac{{{{\left( {97.01 + 96.2\cos \;\theta } \right)}^{1/2}}}}{{2{\text{π}}}} {\rm{d}}\theta \approx 8.92{\rm{\;m}}.\end{array} \right\}$

(18)

将已知参数代入式（14），解得隧道及排水洞涌水量分别为2.35、6.60 m³/(m·d).

采取数值法计算渗流场，其渗流速度矢量图如图8所示. 由图8（a）可以看出，地下水渗流集中汇聚于隧底排水洞，且渗流速度为10⁻⁵ m/s量级；由图8（b）可知，衬砌结构（洞内排水）渗流速度仅为10⁻⁷～10⁻⁶ m/s量级，衬砌结构渗流速度明显小于排水洞，在对地下水的排泄中排水洞起主导作用. 为了进一步量化涌水量，编制FLAC^3D内置FISH语言提取渗流矢量并计算隧道、排水洞涌水量，如表2所示.

由表2可知，1）解析法与数值法求得的隧道及排水洞涌水量相差较小，其相差率分别为9.22%、1.64%（隧道、排水洞），表明解析解与数值解吻合程度较高；2）数值法和解析法解得的排水洞排量占比分别72.15%、73.73%，一方面数值结果与解析结果互为验证，另一方面表明在深埋水沟排水方式2种排水路径中，隧底排水洞是主要排水路径，主导地下水的排导.

2.3.2 衬砌水压力

将深埋水沟排水方式下衬砌水压力数值解p_a与依据式（15）得到的解析解p_b对比绘出，如图9所示. 可知，1）两法计算得到的衬砌水压力相差不大，最大差异位于边墙脚，该处解析解为276.3 kPa，数值解为249.6 kPa，相差率为9.66%，结果表明所推衬砌水压力解析解与数值模拟结果吻合较好；2）在深埋水沟有效排导下，隧底水压力得到有效控制，明显小于隧顶水压力，解析解、数值模拟得到的隧底、隧顶水压力比值分别为9.12%、9.20%，互为验证，亦证明深埋水沟排水方式在控制隧底水压力方面具有优越性. 表2、图9对比结果表明，所推解析解与采用FLAC3D软件所得数值解吻合较好，从数值分析的角度验证了所推公式的正确性.

2.4 衬砌水压力参数影响分析与探讨

衬砌水压力过高是富水隧道结构破坏的主要原因之一，而水压力过高与地层参数影响密不可分，因此从地层参数（水下埋深 ${h_{\rm c}}$ 、地层渗透性 ${k_{\rm s}}$ ）出发，探讨地层参数变化对衬砌水压力的影响规律.

2.4.1 衬砌水压力与隧道水下埋深的关系

改变式（15）中水下埋深 ${h_{\rm c}}$ ，探究水下埋深与衬砌水压力的关系，关系曲线如图10所示. 基于水下大埋深的假设，埋深下限取60 m. 由图10可知，1）衬砌水压力与隧道水下埋深呈线性正相关关系，且不同位置处增长斜率不同，其中隧底斜率最小，拱顶斜率最大，总体呈现“距离排水洞越远斜率越大”的分布规律，上述规律应是由于排水洞对衬砌结构的降压效应随距离的增长而逐渐衰减；2）当 ${h_{\rm c}}$ =250 m时，拱顶、拱脚、边墙角、隧底处的衬砌水压力分别为876.7、776.6、481.1、140.6 kPa，相较初始水头 ${h_{\rm c}}$ ，各处衬砌水压力均有一定程度的降低，尤其是隧底水压力仅为拱顶水压力的16.04%、 ${h_{\rm c}}$ 对应静水压力的5.62%. 结果表明，即使水下埋深较大，深埋水沟排水方式仍具有较好的降压效果，可将隧底水压力控制在合理范围内，对因隧底水压力过大导致的隧底隆起、轨道变形甚至结构破坏等病害起到防控作用.

2.4.2 衬砌水压力与围岩渗透性的关系

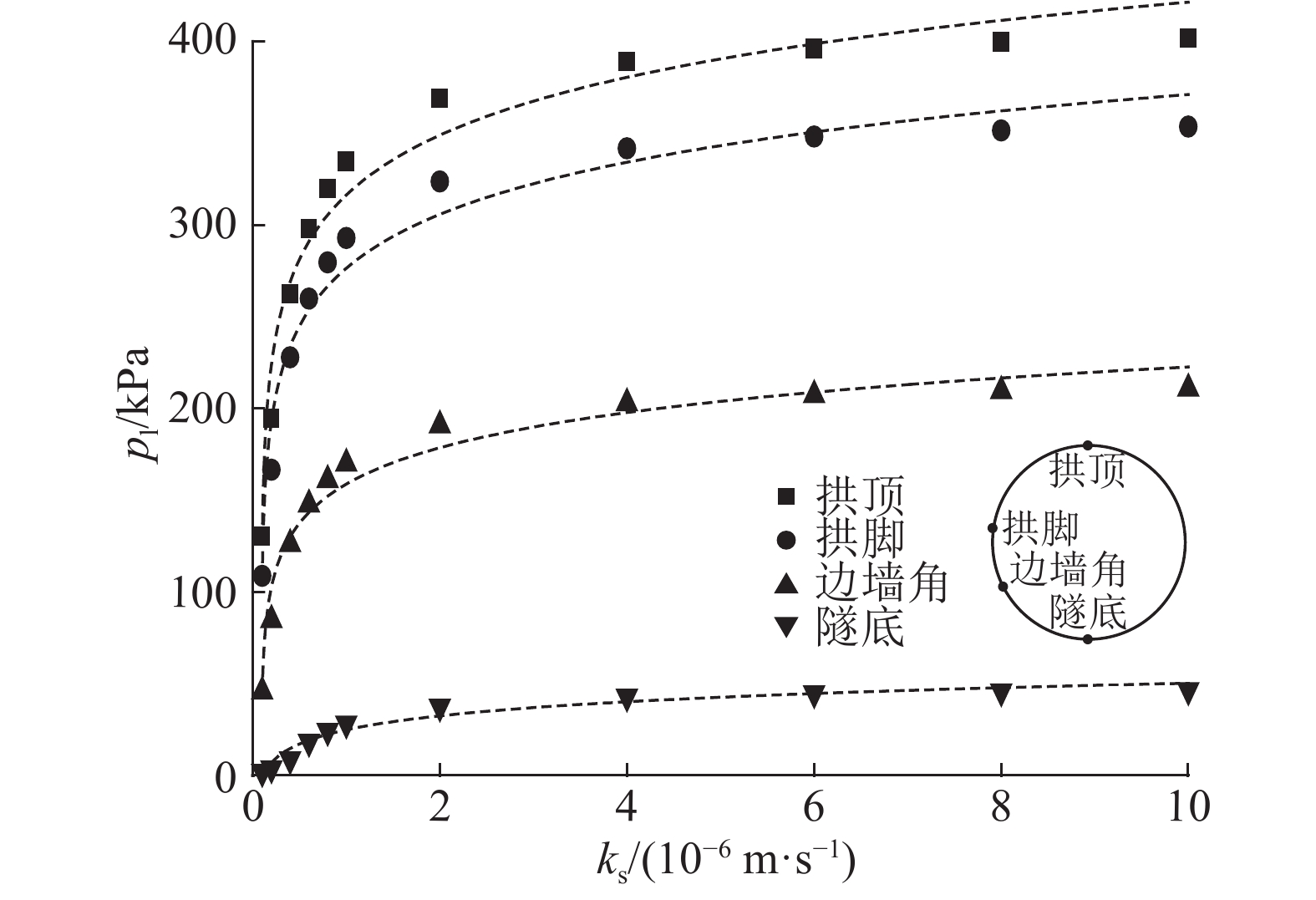
改变式（16）中围岩渗透系数 ${k_{\rm s}}$ ，探究围岩渗透性与衬砌水压力的关系，关系曲线如图11所示. 可知，1）衬砌水压力随围岩渗透性的增大而增大，且基本呈对数函数关系，同时不同位置处的增长速率不一，隧底增长速率最小、拱顶最大；2）随着围岩渗透系数从10⁻⁷ m/s增至10⁻⁵ m/s，隧底水压力从4.23 kPa增至46.52 kPa，水压力仍较小，若进一步提高围岩渗透性（至10⁻⁴ m/s），以拟合公式计算得到的隧底水压力仅为75.71 kPa，表明即使围岩裂隙发育，透水性好，深埋水沟排水方式仍可较好控制隧底水压力；随着围岩渗透性的增长，拱顶水压力增幅明显且量值较大（从130.14 kPa增至401.97 kPa），上述结果应是由排水系统在隧顶处的降压能力较弱且围岩渗水补给能力逐渐提升所导致的，因此当围岩渗透性较好时，对隧顶水压力应予以一定重视.

3 结　论

（1）深埋式中心水沟排水方式与传统排水方式在排水路径、排导能力等方面存在较大差异. 基于镜像法和渗流力学理论，推导了半无限平面内深埋式中心水沟排水隧道渗流场及涌水量解析解，并通过典型案例验证了所提公式的正确性. 公式的提出对于完善隧道渗流场理论、优化隧道设计以及指导工程实践等具有显著的现实意义.

（2）以武九客专石马寨隧道为算例，分别采用数值模拟和理论计算获得了深埋式中心水沟排水方式下隧道的涌水量和衬砌水压力分布规律. 2种方法计算结果相互验证和阐明了深埋式中心水沟排水方式在富水地层中的优越性. 其中，隧底排水洞排量大、有效排导能力强，是主要排水路径和控制隧底水压力的关键. 另外，数值模拟计算方法的提出为探讨深埋式中心水沟排水方式下隧道渗流场的相关规律提供了新思路.

（3）探讨了隧道水下埋深、围岩渗透性对深埋式中心水沟排水方式下隧道衬砌水压力的影响. 即使在水下埋深较大或围岩渗透性较好的情况下，深埋式中心水沟排水方式仍可有效降低衬砌水压力，控制隧底水压力，有效避免隧底隆起、轨道变形甚至隧底结构坏等病害的发生. 深埋式中心水沟排水在富水隧道建设中具有广泛应用前景.