自1995年被发明以来[1],超高性能混凝土UHPC或活性粉末混凝土RPC受到了越来越多的关注. 该材料致密性很高,具有超高的抗压性能[2-4]和耐久性[5-6]. 相对其超高的抗压强度,抗拉强度较低,较易脆性断裂[7]. 添加各种不同的纤维,利用纤维对微细裂缝的桥联作用,可以提高抗拉强度至12~18 MPa[8];尤其是超高性能钢纤维混凝土UHPFRC,断裂能可达40 kJ/m2,韧性可以与金属媲美,在抗爆抗冲击方面显示出极强的应用前景[9-11].
纤维对裂缝的桥联作用取决于纤维-水泥基体之间的界面黏结滑移性能,后者一般采用单根纤维的拉拔实验进行表征. Naaman等[12]较早开展3种钢纤维与水泥基体之间的单根拉拔实验,推导出剪切力-滑移关系. 李建辉等[13]开展异形钢纤维-砂浆的拉拔试验,建立柔性异型纤维的拉拔理论模型,理论模拟曲线与试验曲线吻合较好. 程俊等[14]开展UHPC基体中单根光滑钢纤维的拉拔试验,发现纤维拉拔力随着埋长的增加而提高,利用扫描电镜比较拉拔前、后纤维表面形态的变化. Naaman[15]首次发明一种由非圆截面纤维扭转而成的螺旋钢纤维(twisted steel fiber);Kim等[16]开展端钩和螺旋钢纤维-砂浆在不同加载速率下拉拔过程的对比实验,发现螺旋钢纤维拉拔曲线具有明显的平台段,拉拔能可达相同试验条件下端钩钢纤维的5倍. 螺旋钢纤维在UHPC基体中的拉拔实验与机理研究较少见,Lee等[17]开展不同埋设角度下的螺旋钢纤维-UHPC基体拉拔实验,发现当埋设角度为30°~45°时拉拔力最大. 在微观破坏机理方面,赵燕茹等[18]采用数字图像相关DIC技术,获得光滑钢纤维-混凝土基体拉拔过程中界面上应变的分布及变化,并实时观测了界面脱粘和滑移的全过程. 朋改非等[19]研究端钩和波纹钢纤维与混凝土基体之间的破坏过程,采用显微镜获得较直观的界面破坏形态. Qsymah等[20]对UHPFRC试样开展精度为24.8 μm的微观X光计算断层扫描(XCT),分析纤维走向以及孔洞的大小和统计分布,建立基于微观图像的有限元均匀化模型,但采用微观XCT扫描技术研究UHPFRC破坏机理尚未见报道.
本文开展UHPC基体下不同埋长的矩形截面螺旋钢纤维单根拉拔实验研究,得到拉拔全过程的拉拔力-位移曲线;采用微观XCT扫描,揭示螺旋钢纤维单根拉拔过程的“解螺旋”力学机理;基于拉拔力三折线的假设和塑性力学理论,推导解螺旋拉拔力的解析公式,采用实验结果进行验证.
1 拉拔实验 1.1 实验设计和实验结果UHPC的设计配合比如表1所示. 采用P.O52.5普通硅酸盐水泥和硅灰2种胶凝材料,将粒径为0.1~0.5 mm的石英砂和平均粒径为26 μm的石英粉作为填充剂,并添加固态聚羧酸系高效减水剂(减水率大于30%). 常温养护 28 d后,70.7 mm立方块的实测抗压强度为155 MPa. 实验采用如图1所示的矩形截面螺旋钢纤维,参数如表2所示. 表中,l为长度,De为等效直径,l0为扭转螺距,
| 表 1 UHPC设计配合比 Table 1 Mix design for UHPC |

|
图 1 螺旋钢纤维 Fig. 1 Twisted steel fibers |
| 表 2 螺旋钢纤维参数 Table 2 Parameters of twisted steel fibers |
单根纤维拉拔实验按照《钢纤维混凝土试验方法》[21]开展,考虑15、20、25 mm 3个纤维埋设长度,对每个埋长制作6个试件,常温养护28 d后进行实验. 实验装置和试件形状尺寸如图2所示. 试件制作过程分为纤维位置固定、前半试件浇筑、拆模、修剪纤维长度、后半试件浇筑、拆模养护等步骤. 拟静态加载采用位移控制,速率为0.01 mm/s.

|
图 2 单根钢纤维拉拔实验试件和装置 Fig. 2 Specimen and setup of single fiber pullout experiment |
采用浙江大学建工实验中心的Nikon XTH320 微观XCT仪(最高焦点精度为2 μm),如图3所示. 对纤维拉拔前、后的UHPC基体进行扫描,观察纤维与基体结合面的破坏情况,进行机理分析. 采用如下扫描参数:曝光时间为500 ms,电压为200 kV,电流为100 μA,扫描精度约为30 μm. 使用VGStudio MAX 3.0软件进行图像处理,根据XCT原始数据进行数据重构,获得二维切片和三维整体图像.

|
图 3 浙江大学微观计算断层扫描实验装置 Fig. 3 XTH320 micro X-ray computed tomography facility at Zhejiang University |
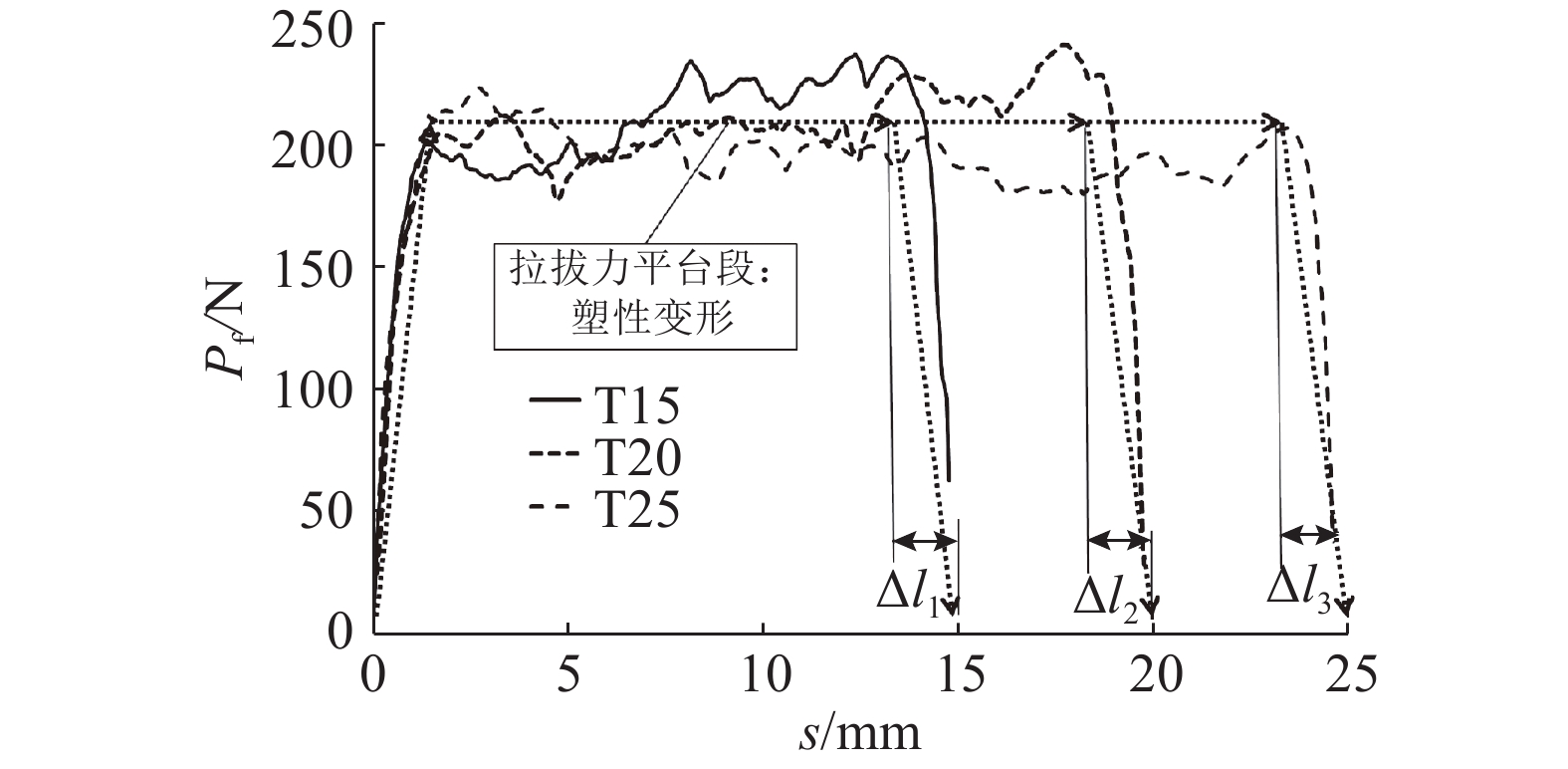
如图4、5所示为不同埋长6个试件的拉拔力P-位移s曲线和相应的平均线. 由图5可见,拉拔曲线存在较明显的拉拔力硬化平台段. Wille等[22]的实验中报道了该现象. 如图6所示为拉拔前、后纤维形态的变化. 可见,纤维在拔出后螺旋形状基本消失. 如图7所示为钢纤维拔出前、后UHPC基体典型的XCT图像. 可以看出,拉拔后纤维埋设通道的螺旋形状较完整,未见有明显的破坏.

|
图 4 不同埋长螺旋钢纤维-UHPC单根拉拔实验结果 Fig. 4 Twisted steel fibers-UHPC single pullout test results with different embedment length |
|
图 5 拉拔实验均线 Fig. 5 Averaged experimental pullout curves |

|
图 6 螺旋钢纤维拉拔前、后的形态对比 Fig. 6 Fibers before and after pullout |

|
图 7 典型UHPC基体在螺旋钢纤维拔出前后的XCT图像 Fig. 7 Typical XCT images of fiber channels in UHPC before and after fiber pullout |
以上实验现象出现的原因是螺旋钢纤维在拉拔过程中发生了塑性“解螺旋”变形,这可以由图8进行解释. 整个拉拔过程可以分为以下3个阶段. 1)拉拔力-加载位移开始为线性关系,在一定位移下,纤维与UHPC基体界面开始脱粘,拉拔力-加载位移关系变为微弱非线性. 2) 嵌入端纤维部分在脱粘后仅发生类似螺丝拧出的自由滑移和转动,两端UHPC基体受夹具约束没有相对的转动,因此会产生一个力矩,使得出口附近的纤维部分发生塑性“解螺旋”变形. 在该阶段,拉拔力来自于解螺旋段纤维的塑性变形,基本保持稳定,因此将该阶段的拉拔力称为解螺旋拉拔力. 3)当纤维剩余埋设长度小于某固定值(定义为有效解螺旋作用长度Δl)时,拉拔力迅速下降消失.

|
图 8 螺旋钢纤维的“解螺旋”机理 Fig. 8 “Untwisting” mechanism of twisted steel fibers |
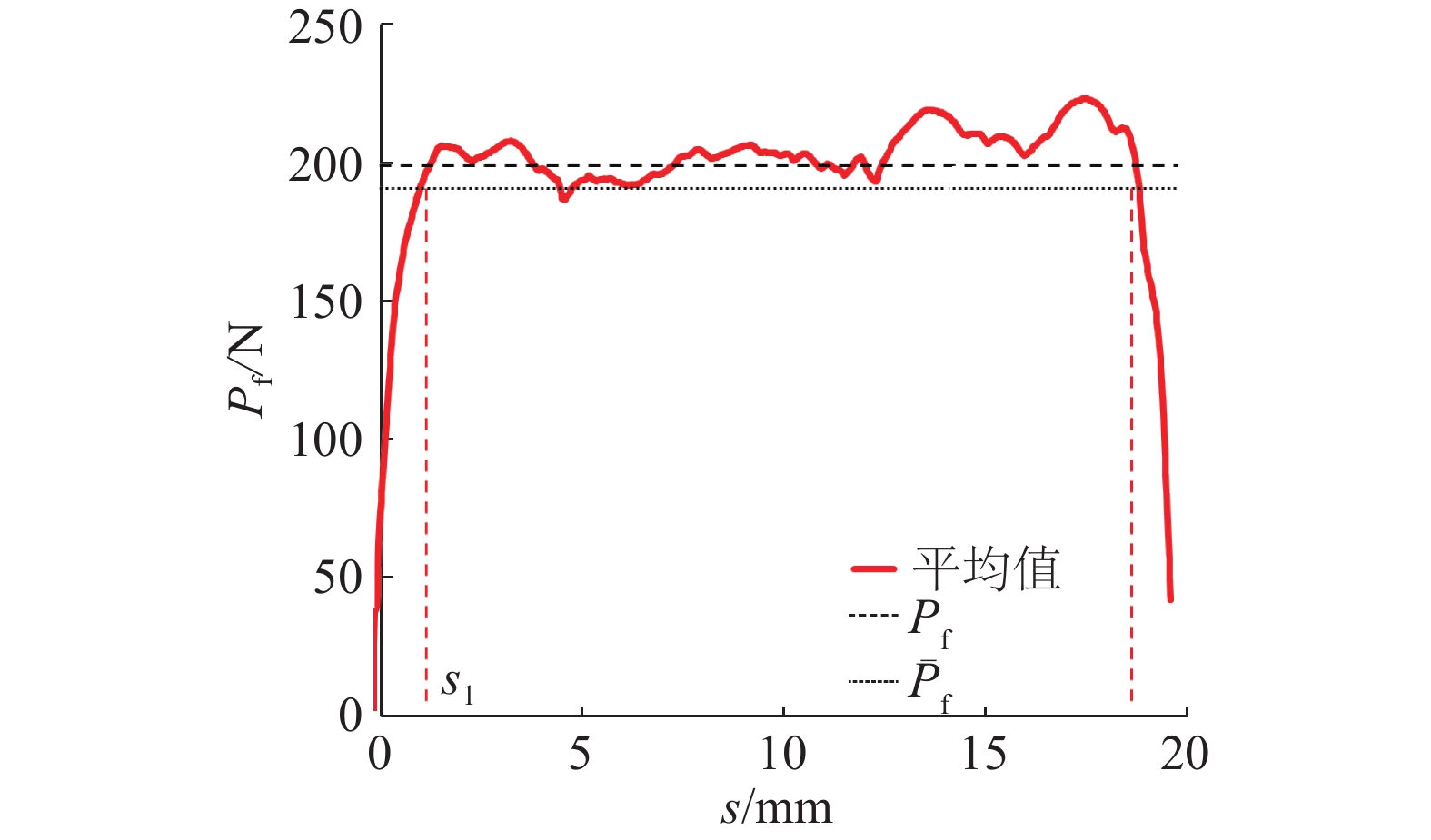
由图4可见,解螺旋拉拔力存在微弱波动,这可能是由纤维与基体之间的界面不均匀性引起的;解螺旋拉拔力的起点与终点通过平均拉拔力与拉拔曲线的交点确定. 为了方便定量分析,先定义拉拔全过程的平均拉拔力(见图9)为
| ${\bar P_{\rm f}} = \frac{{{E_{\rm p}}}}{{{l_{\rm e}}}} = \frac{{\displaystyle\int {{{P}} \left( s \right){\rm{d}}s} }}{{{l_{\rm e}}}}.$ | (1) |
式中:Ep为全过程拉拔能,即拉拔曲线所包裹的面积;le为纤维埋设长度;s为纤维拉拔位移;P(s)为拉拔位移为s时的拉拔力. 由
|
图 9 参数定义方法示意图 Fig. 9 Sketch of parameters definition method |
定义拉拔曲线第2阶段的解螺旋拉拔力为
| ${{{P}} _{\rm f}} = \frac{{\int_{{s_1}}^{{s_2}} {{{P}} (s){\rm{d}}s} }}{{{s_2} - {s_1}}}.$ | (2) |
实验结果如表3所示. 表中,有效解螺旋作用长度由Δl=le–s2计算,忽略了拉拔过程中纤维的轴向伸长. 如图10所示为Ep、

|
图 10 螺旋钢纤维单根拉拔实验结果 Fig. 10 Results of single fiber pullout tests |
| 表 3 螺旋钢纤维单根拉拔实验结果 Table 3 Results of single twisted steel fiber pullout tests |
基于以上螺旋钢纤维-UHPC单根拉拔实验结果及拉拔机理分析,拉拔力-位移曲线可以简化为如图11所示的三折线,对应于拉拔过程的3个阶段:线性脱粘段、塑性解螺旋段和骤降段. 为了推导解螺旋拉拔力解析解,引入3个假设:1)纤维解螺旋时,只要剩余埋长不小于Δl,则拉拔力恒定不变,此时的拉拔力为解螺旋拉拔力;2)纤维解螺旋时,有效解螺旋作用段之外的摩擦阻力忽略不计;3)钢纤维为理想塑性材料,在拉拔过程中,高强度UHPC基体不发生破坏.

|
图 11 螺旋钢纤维-UHPC基体拉拔曲线简化三折线模型 Fig. 11 Simplified trilinear model of pullout curve for twisted steel fiber-UHPC matrix |
针对2a×2b矩形截面螺旋钢纤维,如图12所示,在某截面上,假设基体对纤维表面的接触应力为线性分布,角点处接触应力为N1(y),且在平行的两面上反对称分布. 取长边上微段dx,该微段受到来自基体的压应力为
| $p = \frac{x}{b}{N_1}(y).$ | (3) |
沿长边进行积分,可得长边上受到的线荷载为
| ${p_{{X}}} = \int_0^b {\frac{x}{b}} {N_1}(y){\rm{d}}x.$ | (4) |
考虑长边螺旋面的倾角θ,压力在纤维轴线y方向的分量为
| ${p_y} = \int_0^b {\frac{x}{b}} {N_1}(y)\sin \theta {\rm{d}}x.$ | (5) |
螺旋面法向力px为
| ${p_x} = \int_0^b {\frac{x}{b}} {N_1}(y)\cos \theta {\rm{d}}x.$ | (6) |
假设基体与钢纤维之间的滑动摩擦系数为常数μ,则摩擦力在纤维轴线方向分量为
| ${f_y} = \mu \int_0^b {\frac{x}{b}} {N_1}(y)\cos \theta {\rm{d}}x.$ | (7) |
注意到短边螺旋面倾角为θ',4条边的轴向合力(线荷载)
| $\begin{split}{{{{P}}} _{\rm f}}^\prime = 2\displaystyle\int_0^b {\displaystyle\frac{x}{b}} {N_1}(y)(\sin \theta + \mu \cos \theta ){\rm{d}}x + \\2\displaystyle\int_0^a {\displaystyle\frac{x}{b}} {N_1}(y)(\sin {\theta ^\prime } + \mu \cos \theta '){\rm{d}}x.\end{split}$ | (8) |

|
图 12 矩形截面螺旋钢纤维受力分析简图 Fig. 12 Force analysis sketch of twisted steel fiber of rectangular section |
对
| $\begin{aligned} {{P}_{\text{f}}}= &\int_{0}^{\Delta l}{\left[ 2\int_{0}^{b}{\frac{x}{b}}{{N}_{1}}(y)(\sin \theta +\mu \cos \theta )\text{d}x+ \right.} \\ & \left. 2\int_{0}^{a}{\frac{x}{b}}{{N}_{1}}(y)(\sin {{\theta }^{\prime }}+\mu \cos {\theta }')\text{d}x \right]\text{d}y. \\ \end{aligned}$ | (9) |
螺旋扭矩为
| $\begin{split} T= & \int_{0}^{\Delta l}\left[ 2\int_{0}^{b}{\frac{x}{b}}{{N}_{1}}(y)(\cos \theta -\mu \sin \theta ) x\text{d}x+ \right. \\ & \left. 2\int_{0}^{a}{\frac{x}{b}}{{N}_{1}}(y)(\cos {{\theta }^{\prime }}-\mu \sin {\theta }') x\text{d}x \right]\text{d}y .\end{split}$ | (10) |
假设沿纤维轴向(Δl方向)压应力均匀分布,即N1(y)=N1,式(5)、(6)可以简化为
| $\begin{split}{{{P}} _{\rm f}} = 2\left[\displaystyle\int_0^b {\displaystyle\frac{x}{b}} {N_1}(\sin \theta + \mu \cos \theta ){\rm{d}}x +\right. \\\left.\displaystyle\int_0^a {\displaystyle\frac{x}{b}} {N_1}(\sin {\theta ^\prime } + \mu \cos \theta '){\rm{d}}x\right] \Delta l,\end{split}$ | (11) |
| $\begin{split}{{T}} = 2\left[\displaystyle\int_0^b {\displaystyle\frac{x}{b}} {N_1}(\cos \theta - \mu \sin \theta ) x{\rm{d}}x + \right.\\\left.\displaystyle\int_0^a {\displaystyle\frac{x}{b}} {N_1}(\cos {\theta ^\prime } - \mu \sin \theta ') x{\rm{d}}x\right] \Delta l.\end{split}$ | (12) |
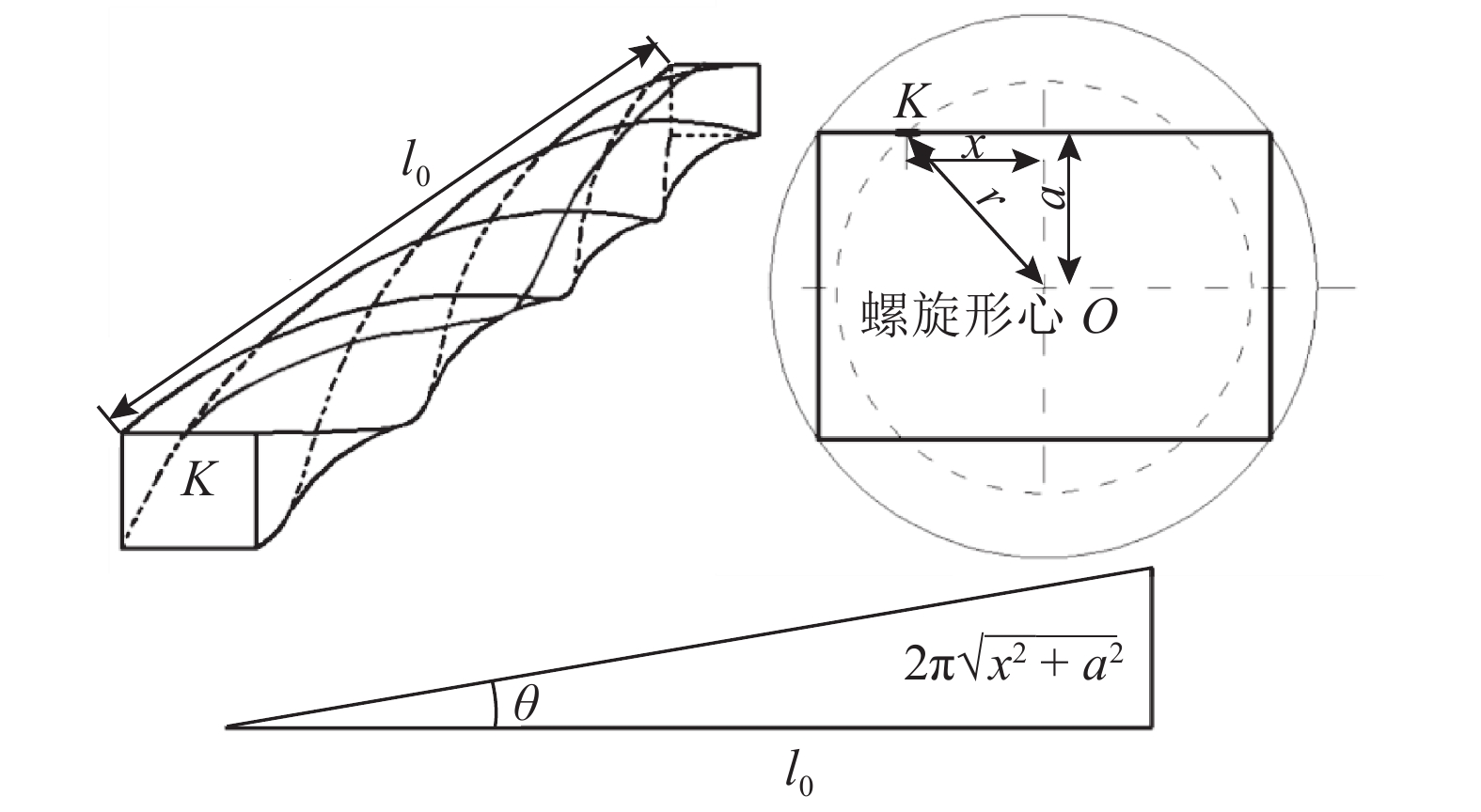
在几何关系上,如图13所示,对于钢纤维面上的任一点K,埋长方向(y方向)历经一个螺距l0,K点绕螺旋中心360°历经的距离为
|
图 13 螺旋面倾角示意图 Fig. 13 Sketch of twisted surface angle |
| $\left.\begin{array}{l}\sin \theta\! \! =\!\! \displaystyle\frac{{2{{\pi }}\sqrt {{x^2} + {a^2}} }}{{\sqrt {4{{\rm{\pi }}^2}({x^2} + {a^2}) + l_0^2} }},\cos \theta\!\! =\!\! \displaystyle\frac{{{l_0}}}{{\sqrt {4{{{\pi }}^2}({x^2} + {a^2}) + l_0^2} }}\!,\\\sin \theta '\! \!= \!\!\displaystyle\frac{{2{{\pi }}\sqrt {{x^2} + {b^2}} }}{{\sqrt {4{{\rm{\pi }}^2}({x^2} + {b^2}) + l_0^2} }}\!,\cos \theta '\!\! =\!\! \displaystyle\frac{{{l_0}}}{{\sqrt {4{{\rm{\pi }}^2}({x^2} + {b^2}) + l_0^2} }}.\end{array}\right\}$ | (13) |
将式(13)代入式(11)、(12),可得
| $\begin{split}{l}{{{P}} _{\rm f}} = \displaystyle\frac{{2{N_1}\Delta l}}{b}\left[\int_0^b x \displaystyle\frac{{2{{\pi }}\sqrt {{x^2} + {a^2}} + \mu {l_0}}}{{\sqrt {4{{\rm{\pi }}^2}({x^2} + {a^2}) + l_0^2} }}{\rm{d}}x +\right.\\ \left.\displaystyle\int_0^a x \displaystyle\frac{{2{{\pi }}\sqrt {{x^2} + {b^2}} + \mu {l_0}}}{{\sqrt {4{{{\pi }}^2}({x^2} + {b^2}) + l_0^2} }}{\rm{d}}x\right],\end{split}$ | (14) |
| $\begin{split}{l}{{T}} = \displaystyle\frac{{2{N_1}\Delta l}}{b}\left[\int_0^b {\displaystyle\frac{{{l_0} - \mu \times 2{{\pi }}\sqrt {{x^2} + {a^2}} }}{{\sqrt {4{{{\pi }}^2}({x^2} + {a^2}) + l_0^2} }} {x^2}{\rm{d}}x} + \right.\\\left.\displaystyle\int_0^a {\displaystyle\frac{{{l_0} - \mu \times 2{{\pi }}\sqrt {{x^2} + {b^2}} }}{{\sqrt {4{{{\pi }}^2}({x^2} + {b^2}) + l_0^2} }} {x^2}} {\rm{d}}x\right].\end{split}$ | (15) |
采用Mises屈服准则,可得
| ${\left( {\displaystyle\frac{\sigma }{{{\sigma _{\rm p}}}}} \right)^2} + 3{\left( {\displaystyle\frac{\tau }{{{\sigma _{\rm p}}}}} \right)^2} = 1.$ | (16) |
式中:σp为钢纤维单向拉伸屈服强度,本文取2 500 MPa;σ为钢纤维轴向正应力,σ=Pf/A, A=4ab;τ为钢纤维切向应力,由解螺旋矩引起.
矩形截面梁塑性极限扭矩[23]为
| ${{M}} = \displaystyle\frac{{4{b^2}\tau }}{3}(3a - b).$ | (17) |
在屈服极限状态(T=M)下,式(16)可以改写为
| ${\left( {\displaystyle\frac{{{P_{\rm f}}}}{{4ab}}} \right)^2} + {\displaystyle\left( {\frac{{9T}}{{4{b^2}\left( {3a - b} \right)}}} \right)^2} = {\sigma _{\rm p}}^2.$ | (18) |
已知钢纤维尺寸(a、b和l0)和强度σp以及由拉拔实验曲线确定的Δl,从式(14)、(15)和(18)可得N1、Pf和T.
2.3 实验验证由于实验数据有一定的离散性,取每个埋长的均值,与解析结果进行对比. 根据文献[24]可知,钢材与混凝土之间的摩擦系数μ取为0.5,Δl如表3所示. 表4给出拉拔力实验值与解析解的对比,结果吻合良好. 表中,
| 表 4 解螺旋拉拔力实验值与解析解对比 Table 4 Untwisting pullout force comparison of test results with analytical solution |
本文开展不同埋长的矩形截面螺旋钢纤维-UHPC基体的单根拉拔实验. 结果显示,由于UHPC基体的高强度,单根螺旋钢纤维的拉拔过程较明显地分为近似线性脱粘段、塑性解螺旋段和骤降段,拉拔力-位移曲线可以简化成三折线近似表示. 拔出后的钢纤维螺旋基本消失,表现出明显的塑性变形. 采用微观X光断层扫描,对拉拔前、后的UHPC基体内部细观结构进行比较. 结果发现,拉拔前、后基体的纤维拔出通道未见明显的破坏,纤维“旋转而出”,揭示了螺旋钢纤维单根拉拔过程的“解螺旋”塑性变形机理. 基于以上实验现象和塑性力学理论,推导了在纤维埋长大于有效解螺旋长度的情况下,矩形截面纤维的解螺旋拉拔力的简化解析解,结果与实验吻合良好.
| [1] |
RICHARD P, CHEYREZY M. Composition of reactive powder concretes[J]. Cement and Concrete Research, 1995, 25(7): 1501-1511. DOI:10.1016/0008-8846(95)00144-2 |
| [2] |
WANG C, YANG C, LIU F, et al. Preparation of ultra-high performance concrete with common technology and materials[J]. Cement and Concrete Composites, 2012, 34(4): 538-544. DOI:10.1016/j.cemconcomp.2011.11.005 |
| [3] |
ZHANG Y, SUN W, LIU S, et al. Preparation of C200 green reactive powder concrete and its static–dynamic behaviors[J]. Cement and Concrete Composites, 2008, 30(9): 831-838. DOI:10.1016/j.cemconcomp.2008.06.008 |
| [4] |
HABEL K, VIVIANI M, DENARIÉ E, et al. Development of the mechanical properties of an ultra-high performance fiber reinforced concrete (UHPFRC)[J]. Cement and Concrete Research, 2006, 36(7): 1362-1370. DOI:10.1016/j.cemconres.2006.03.009 |
| [5] |
王卫仑, 唐信, 柯玉伟, 等. 120MPa纤维超高强混凝土抗硫酸盐及氯离子侵蚀性能研究[J]. 混凝土, 2016(10): 5-7. WANG Wei-lun, TANG Xin, KE Yu-wei, et al. 120 MPa fiber ultra high strength concrete exposure to sulfate and chloride invading environment[J]. Concrete, 2016(10): 5-7. |
| [6] |
GU C, SUN W, GUO L, et al. Effect of curing conditions on the durability of ultra-high performance concrete under flexural load[J]. Journal of Wuhan University of Technology: Materials Science Edition, 2016, 31(2): 278. DOI:10.1007/s11595-016-1365-0 |
| [7] |
赵筠, 廉慧珍, 金建昌. 钢-混凝土复合的新模式——超高性能混凝土(UHPC/UHPFRC)之一: 钢-混凝土复合模式的现状, 问题及对策与UHPC发展历程[J]. 混凝土世界, 2013(10): 56-69. ZHAO Yun, LIAN Hui-zhen, JIN Jian-chang. Steel-concrete composite new model—ultra-high performance concrete (UHPC/UHPFRC): the present situation, problems and countermeasures of steel-concrete composite model and the development of UHPC[J]. Concrete, 2013(10): 56-69. DOI:10.3969/j.issn.1674-7011.2013.10.010 |
| [8] |
吴香国, 徐世烺, 吴明喜. 超高性能纤维改性混凝土断裂参数研究与应用[J]. 工程力学, 2009(3): 93-98. WU Xiang-guo, XU Shi-lang, WU Ming-xi. Fracture parameters study and application of ultra high performance fiber reinforcement concrete[J]. Engineering Mechanics, 2009(3): 93-98. |
| [9] |
HABEL K, GAUVREAU P. Response of ultra-high performance fiber reinforced concrete (UHPFRC) to impact and static loading[J]. Cement and Concrete Composites, 2008, 30(10): 938-946. DOI:10.1016/j.cemconcomp.2008.09.001 |
| [10] |
LIU J, WU C, CHEN X. Numerical study of ultra-high performance concrete under non-deformable projectile penetration[J]. Construction and Building Materials, 2017, 135: 447-458. DOI:10.1016/j.conbuildmat.2016.12.216 |
| [11] |
FANG Q, ZHANG J. Three-dimensional modelling of steel fiber reinforced concrete material under intense dynamic loading[J]. Construction and Building Materials, 2013, 44(7): 118-132. |
| [12] |
NAAMAN A E, NAJM H. Bond-slip mechanisms of steel fibers in concrete[J]. Materials Journal, 1991, 88(2): 135-145. |
| [13] |
李建辉, 邓宗才. 异型塑钢纤维-砂浆界面粘结性能[J]. 混凝土与水泥制品, 2005(2): 38-40. LI Jian-hui, DENG Zong-cai. The interface bonding property of the deformed steel fiber-mortar[J]. China Concrete and Cement Products, 2005(2): 38-40. DOI:10.3969/j.issn.1000-4637.2005.02.012 |
| [14] |
程俊, 刘加平, 张丽辉. 超高性能混凝土纤维-基体黏结性能测试与机理分析[J]. 混凝土与水泥制品, 2016(5): 62-66. CHENG Jun, LIU Jia-ping, ZHANG Li-hui. Performance test and mechanism analysis of fiber-matrix bonding in an UHPC[J]. China Concrete and Cement Products, 2016(5): 62-66. DOI:10.3969/j.issn.1000-4637.2016.05.014 |
| [15] |
NAAMAN A E. Engineered steel fibers with optimal properties for reinforcement of cement composites[J]. Journal of Advanced Concrete Technology, 2003, 1(3): 241-252. |
| [16] |
KIM D J, EL-TAWIL S, NAAMAN A E. Loading rate effect on pullout behavior of deformed steel fibers[J]. ACI Materials Journal, 2008, 105(6): 576-584. |
| [17] |
LEE Y, KANG S T, KIM J K. Pullout behavior of inclined steel fiber in an ultra-high strength cementitious matrix[J]. Construction and Building Materials, 2010, 24(10): 2030-2041. DOI:10.1016/j.conbuildmat.2010.03.009 |
| [18] |
赵燕茹, 邢永明, 黄建永, 等. 数字图像相关方法在纤维混凝土拉拔试验中的应用[J]. 工程力学, 2010, 27(6): 169-175. ZHAO Yan-ru, XING Yong-ming, HUANG Jian-yong, et al. Study on the fiber-reinforced concrete pull-out test using digital image correlation method[J]. Engineering Mechanics, 2010, 27(6): 169-175. |
| [19] |
朋改非, 牛旭婧, 赵怡琳. 异刑钢纤维对超高性能混凝土增强增韧的影响[J]. 建筑材料学报, 2016, 19(6): 1013-1018. PENG Gai-fei, NIU Xu-jing, ZHAO Yi-lin. Effect of deformed steel fiber on strengthening and toughening of ultra-high performance concrete[J]. Journal of Buiding Materials, 2016, 19(6): 1013-1018. DOI:10.3969/j.issn.1007-9629.2016.06.010 |
| [20] |
QSYMAH A, SHARMA R, YANG Z, et al. Micro X-ray computed tomography image-based two-scale homogenisation of ultra high performance fibre reinforced concrete[J]. Construction and Building Materials, 2017, 130: 230-240. DOI:10.1016/j.conbuildmat.2016.09.020 |
| [21] |
中国工程建设标准化协会.钢纤维混凝土试验方法: CECS13:89[S]. 北京: 中国计划出版社, 1989: 30–35.
|
| [22] |
WILLE K, NAAMAN A E. Pullout behavior of high-strength steel fibers embedded in ultra-high-performance concrete[J]. ACI Materials Journal, 2012, 109(4): 479-487. |
| [23] |
夏志皋. 塑性力学[M]. 上海: 同济大学出版社, 1991: 131–132.
|
| [24] |
BALTAY P, GJELSVIK A. Coefficient of friction for steel on concrete at high normal stress[J]. Journal of Materials in Civil Engineering, 1990, 2(1): 46-49. DOI:10.1061/(ASCE)0899-1561(1990)2:1(46) |



